Reinitializing Sea Surface Temperature in the Ensemble Intermediate Coupled Model for Improved Forecasts
Abstract
1. Introduction
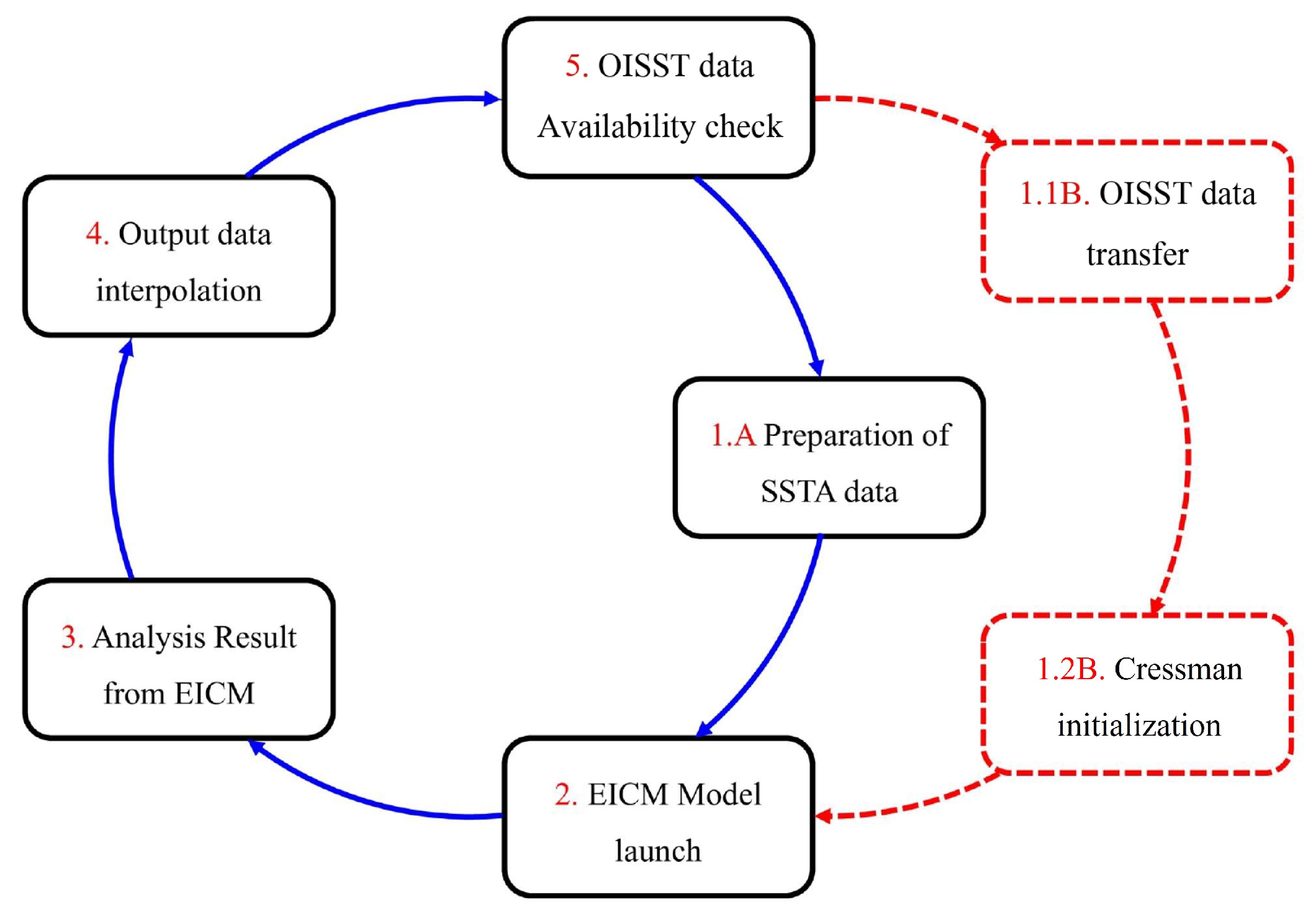
2. Materials and Methods
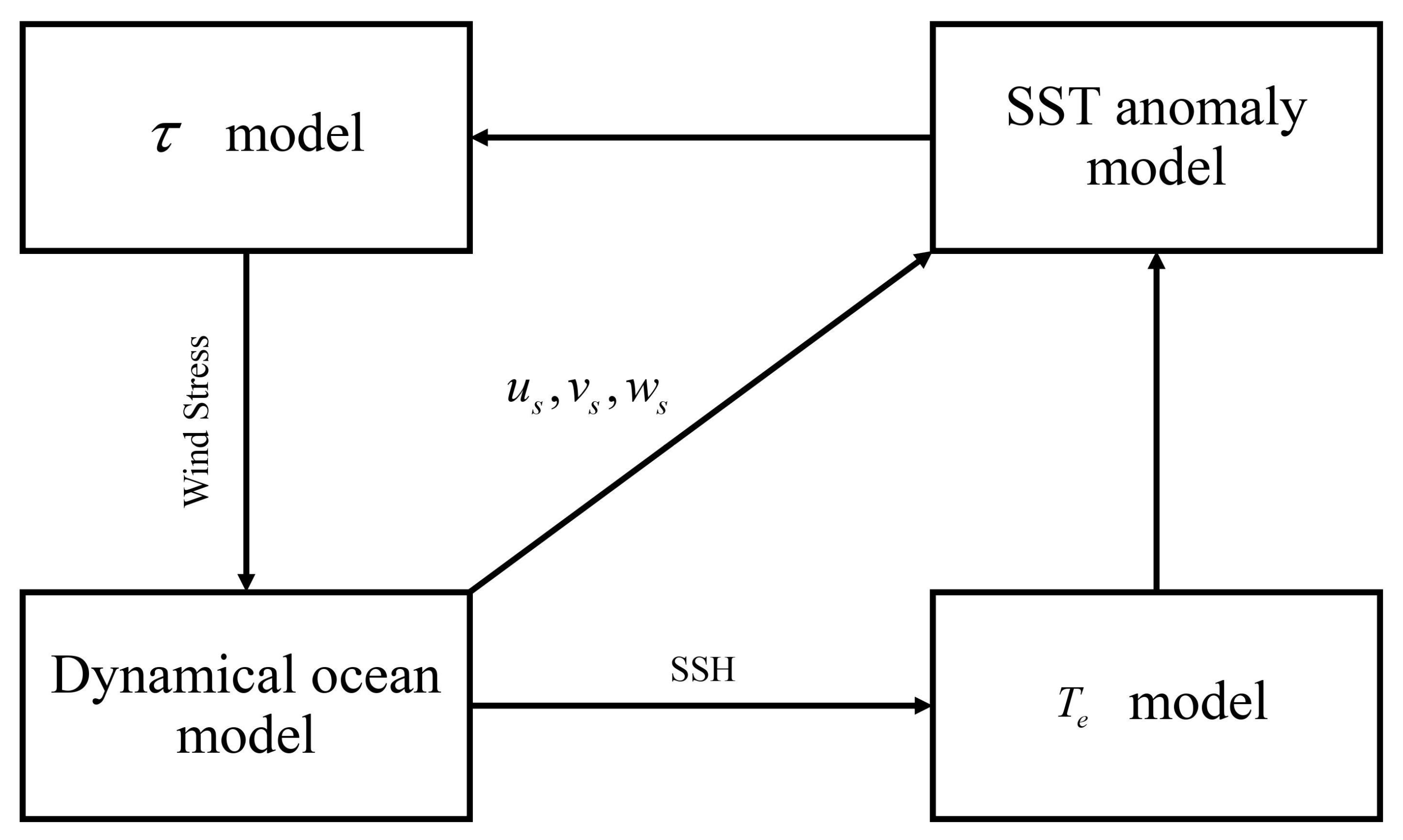
2.1. Ensemble Intermediate Coupled Model
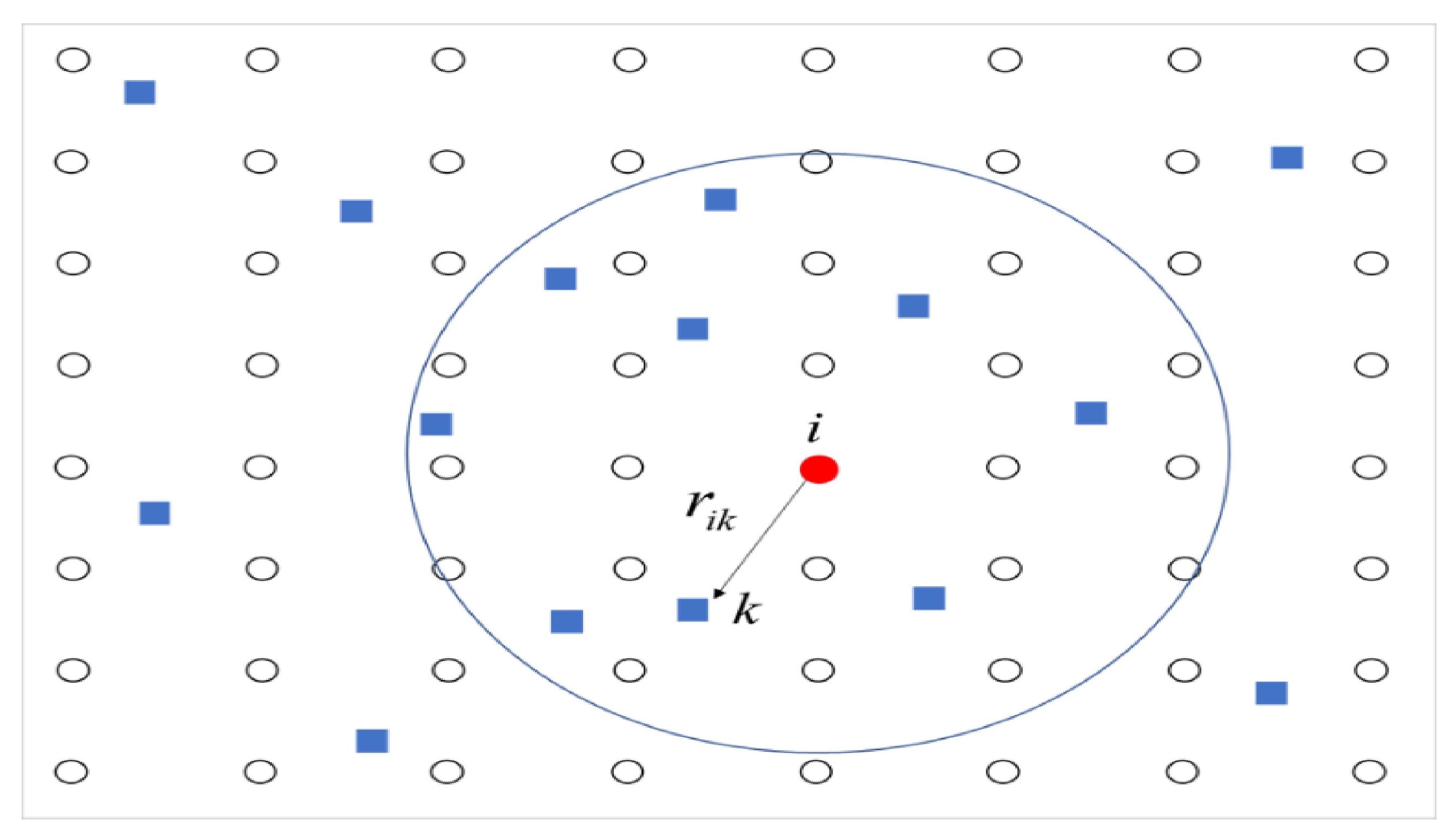
2.2. Cressman Scheme
2.3. Optimum Interpolation Sea Surface Temperature
2.4. Extended Reconstructed Sea Surface Temperature
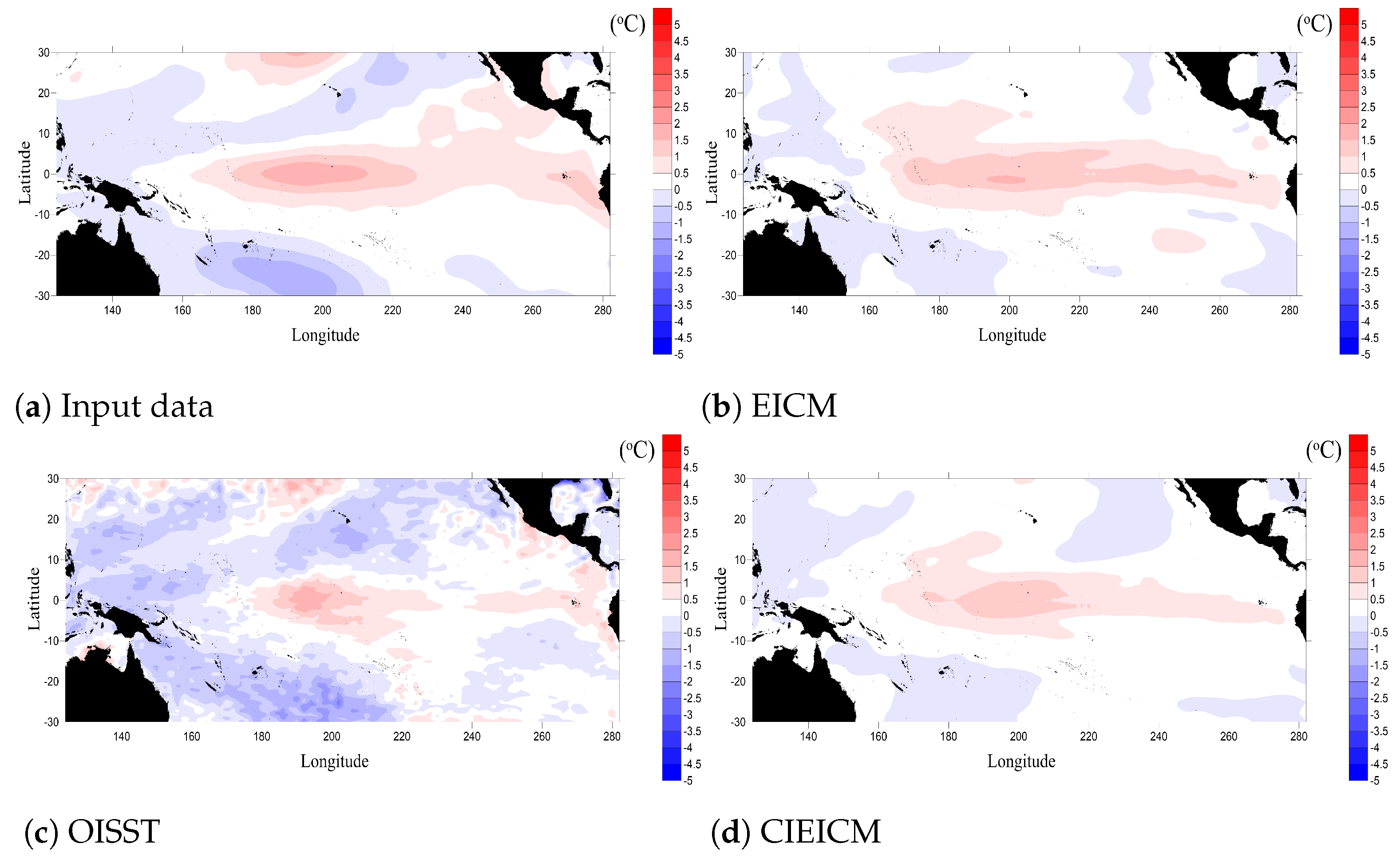
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AVHRR | Advanced Very High-Resolution Radiometer |
| EICM | Ensemble Intermediate Coupled Model |
| CIEICM | Cressman Initialized Ensemble Intermediate Coupled Model |
| ENSO | El Niño–Southern Oscillation |
| ERSST | Extended Reconstructed Sea Surface Temperature |
| HadISST | Hadley Center’s Sea Ice and Sea Surface Temperature |
| HCM | Hybrid Coupled Model |
| HRPT | High-Resolution Picture Transmission |
| ICM | Intermediate Coupled Model |
| IOM | Intermediate Ocean Model |
| MetOp | Meteorological Operational |
| NMAT | Night-time Marine Air Temperature |
| NOAA | National Oceanic and Atmospheric Administration |
| OISST | Optimum Interpolation Sea Surface Temperature |
| R | Correlation Coefficient |
| Root Mean Square Deviation | |
| Standard Deviation | |
| SST | Sea Surface Temperature |
| SSTA | Sea Surface Temperature Anomaly |
References
- Merchant, C.J.; Embury, O.; Roberts-Jones, J.; Fiedler, E.; Bulgin, C.; Corlett, G.K.; Good, S.; Mclaren, A.J.; Rayner, N.; Morak-Bozzo, S.; et al. Sea surface temperature datasets for climate applications from Phase 1 of the European Space Agency Climate Change Initiative (SST CCI). Geosci. Data J. 2014, 1, 179–191. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- McCreary, J.P., Jr. A model of tropical ocean-atmosphere interaction. Mon. Weather Rev. 1969, 111, 370–387. [Google Scholar] [CrossRef]
- Wyrtki, K. El Niño-the dynamic response of the equatorial Pacific Ocean to atmospheric forcing. J. Phys. Oceanogr. 1975, 5, 572–584. [Google Scholar] [CrossRef]
- Cane, M.A.; Zebiak, S.E.; Dolan, S.C. Experimental forecasts of El Niño. Nature 1986, 321, 827–832. [Google Scholar] [CrossRef]
- Zhang, R.-H.; Zheng, F.; Zhu, J.; Wang, Z. A successful real-time forecast of the 2010–11 La Niña event. Sci. Rep. 2013, 3, 1–7. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of Real-Time Seasonal ENSO Model Predictions during 2002–11: Is Our Capability Increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Barnett, T.P.; Latif, M.; Graham, N.; Flugel, M.; Pazan, S.; White, W. ENSO and ENSO-related predictability. Part I: Prediction of equatorial Pacific sea surface temperature with a hybrid coupled ocean-atmosphere model. J. Clim. 1993, 6, 1545–1566. [Google Scholar] [CrossRef]
- Kang, I.S.; Kug, J.S. An El Nino prediction system using an intermediate ocean and a statistical atmosphere. Geophys. Res. Lett. 2000, 27, 1167–1170. [Google Scholar] [CrossRef]
- Zhang, R.H.; Gao, C. The IOCAS intermediate coupled model (IOCAS ICM) and its real-time predictions of the 2015-16 El Niño event. Sci. Bull. 2016, 66, 1061–1070. [Google Scholar] [CrossRef]
- Zhang, S.; Harrison, M.J.; Wittenberg, A.T.; Rosati, A.; Anderson, J.L.; Balaji, V. Initialization of an ENSO forecast system using a parallelized ensemble filter. Mon. Weather Rev. 2005, 133, 3176–3201. [Google Scholar] [CrossRef]
- Webb, D.J.; Cowaed, A.C.; Snaith, H.M. A comparison of ocean model data and satellite observations of features affecting the growth of the North Equatorial Counter Current during the strong 1997–1998 El Niño. Ocean. Sci. 2020, 16, 565–574. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, R.-H. Ensemble hindcasts of SST anomalies in the tropical Pacific using an intermediate coupled model. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Zheng, F.; Zhu, J.; Wang, H.; Zhang, R.-H. Ensemble Hindcasts of ENSO Events over the Past 120 Years Using a Large Number of Ensembles. Adv. Atmos. Sci. 2009, 26, 359–372. [Google Scholar] [CrossRef]
- Chen, D.; Zebiak, S.E.; Busalacchi, A.J.; Cane, M.A. An improved procedure for El Niño forecasting: Implications for predictability. Science 1995, 269, 1699–1702. [Google Scholar] [CrossRef] [PubMed]
- Artur, N.; Lidia, D.G.; Macigj, J.; Macigi, K. Assimilation of the satellite SST data in the 3D CEMBS model. Oceanologia 2015, 57, 17–24. [Google Scholar]
- Abbasi, M.R.; Chegini, V.; Sadrinasab, M.; Siadatmousavi, S.M. Capabilities of data assimilation in correcting sea surface temperature in the Persian Gulf. Pollution 2017, 3, 273–283. [Google Scholar]
- Zheng, F.; Zhu, J. Improved ensemble mean forecasting of ENSO events by a zero mean stochastic error model of an intermediate coupled model. Clim. Dyn. 2016, 47, 3901–3915. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Evensen, G. Sampling strategies and square root analysis schemes for the EnKF. Ocean. Dyn. 2003, 54, 539–560. [Google Scholar] [CrossRef]
- Zebiak, S.E.; Cane, M.A. A model EI Niño-Southern Oscillation. Mon. Weather Rev. 1987, 115, 2262–2278. [Google Scholar] [CrossRef]
- Zhang, R.-H.; Zebiak, S.E.; Kleeman, R. A new intermediate coupled model for El Niño simulation and prediction. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Zhang, R.-H.; Kleeman, R.; Zebiak, S.E.; Keenlyside, N.; Raynaud, S. An empirical parameterization of subsurface entrainment temperature for improved SST simulations in an intermediate ocean model. J. Clim. 2005, 18, 350–371. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, G.; Zhang, R.-H.; Sun, Z. On the role of ocean entrainment temperature (Te) in decadal changes of El Niño/ Southern Oscillation. Ann. Geophys. 2011, 29, 529–540. [Google Scholar] [CrossRef][Green Version]
- Zhu, J.; Zhou, G.; Zhang, R.-H.; Sun, Z. Improving ENSO prediction in a hybrid coupled model with an embedded entrainment temperature parameterization. Int. J. Climatol. 2013, 33, 343–355. [Google Scholar] [CrossRef]
- Keenlyside, N.; Kleeman, R. Annual cycle of equatorial zonal currents in the Pacific. Geophys. Res. Lett. 2002, 107, 1–13. [Google Scholar] [CrossRef]
- McCreary, J.P. A linear stratified ocean model of the equatorial undercurrent. Philos. Trans. R. Soc. Lond. 1981, 298, 603–635. [Google Scholar]
- Gill, A.E. An estimation of sea-level and surface-currents during the 1972 EI Niño and consequenct thermal effects. J. Phys. Oceanogr. 1983, 13, 486–606. [Google Scholar] [CrossRef]
- Zhang, R.-H.; Busalacchi, A.J. The Roles of Atmospheric Stochastic Forcing (SF) and Oceanic Entrainment Temperature (Te) in Decadal Modulation of ENSO. J. Clim. 2007, 21, 674–704. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003; Volume 87, pp. 136–204. [Google Scholar]
- Li, X.; Pichel, W.; Maturi, E.; Clemente-Colon, P.; Sapper, J. Deriving the operational nonlinear multichannel sea surface temperature algorithm coefficients for NOAA-15 AVHRR/3. Int. J. Remote Sens. 2001, 22, 699–704. [Google Scholar] [CrossRef]
- Li, X.; Pichel, W.; Clemente-Colon, P.; Krasnopolsky, V.; Sapper, J. Validation of coastal sea and lake surface temperature measurements derived from NOAA/AVHRR data. Int. J. Remote. Sens. 2001, 22, 1285–1303. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M. Improved global sea surface temperature analyses. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W.; Peterson, T.C.; Lawrimore, J. Improvements NOAAs Historical Merged Land-Ocean Temp Analysis (1880–2006). J. Clim. 2008, 21, 2283–2296. [Google Scholar] [CrossRef]
- Xue, Y.; Smith, T.M.; Reynolds, R.W. Interdecadal Changes of 30-Yr SST Normals during 1871–2000. J. Clim. 2003, 16, 1601–1612. [Google Scholar] [CrossRef]
- Eric, F.; Elizabeth, C.K.; Philip, B.; Thomas, C.; Lydia, G.; Boyin, H.; Chunying, L.; Shawn, R.S.; Steven, J.W.; Zhang, H.-M. The International Comprehensive Ocean-Atmosphere Data Set— Meeting Users Needs and Future Priorities. Front. Mar. Sci. 2019, 23, 1–8. [Google Scholar]
- Liu, W.; Huang, B.; Thorne, P.W.; Banzon, V.F.; Zhang, H.M.; Freeman, E.; Lawrimore, J.; Peterson, T.C.; Smith, T.M.; Woodruff, S.D. Extended Reconstructed Sea Surface Temperature Version 4 (ERSST.v4): Part II. Parametric and Structural Uncertainty Estimations. J. Clim. 2015, 28, 931–951. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Busalacchi, A.J.; Anderson, D.L.T. A TOGA retrospective. Oceanography 2010, 23, 86–103. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Busalacchi, A.J.; Cheney, R.; Donguy, J.R.; Gage, K.S.; Halpern, D.; Ji, M.; Julian, P.; Meyers, G.; Mitchum, G.T.; et al. The Tropical Ocean-Global Atmosphere (TOGA) observing system: A decade of progress. J. Geophys. Res. 2020, 103, 14169–14240. [Google Scholar]
- Ji, M.; Leetmaa, A. Impact of Data Assimilation on Ocean Initialization and El Niño Prediction. Mon. Weather Rev. 1997, 125, 742–753. [Google Scholar] [CrossRef]
- Chen, D. Coupled data assimilation for enso prediction. Adv. Geosci. 2010, 18, 45–62. [Google Scholar]
- Oberhuber, J.M. Predicting the E1 Nifio event with a global climate model. Geophys. Res. Lett. 1998, 25, 2273–2276. [Google Scholar] [CrossRef]
- Gao, C.; Wu, X.; Zhang, R.H. Testing a Four-Dimensional Variational Data Assimilation Method Using an Improved Intermediate Coupled Model for ENSO Analysis and Prediction. Adv. Atmos. Sci. 2016, 33, 875–888. [Google Scholar] [CrossRef][Green Version]
- Gao, C.; Zhang, R.H.; Wu, X.; Sun, J. Idealized experiments for optimizing model parameters using a 4D-Variational method in an intermediate coupled model of ENSO. Adv. Atmos. Sci. 2018, 35, 410–422. [Google Scholar] [CrossRef]
- Injan, S.; Wangwongchai, A.; Humphries, U. Application of Data Assimilation and the Relationship between ENSO and Precipitation. Math. Comput. Appl. 2021, 26, 1–16. [Google Scholar]
- Zavala-Garay, J.; Moore, A.M.; Kleeman, R. Influence of stochastic forcing on ENSO prediction. J. Geophys. Res. Ocean. 2004, 109, 1–10. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, R.H.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D.; et al. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
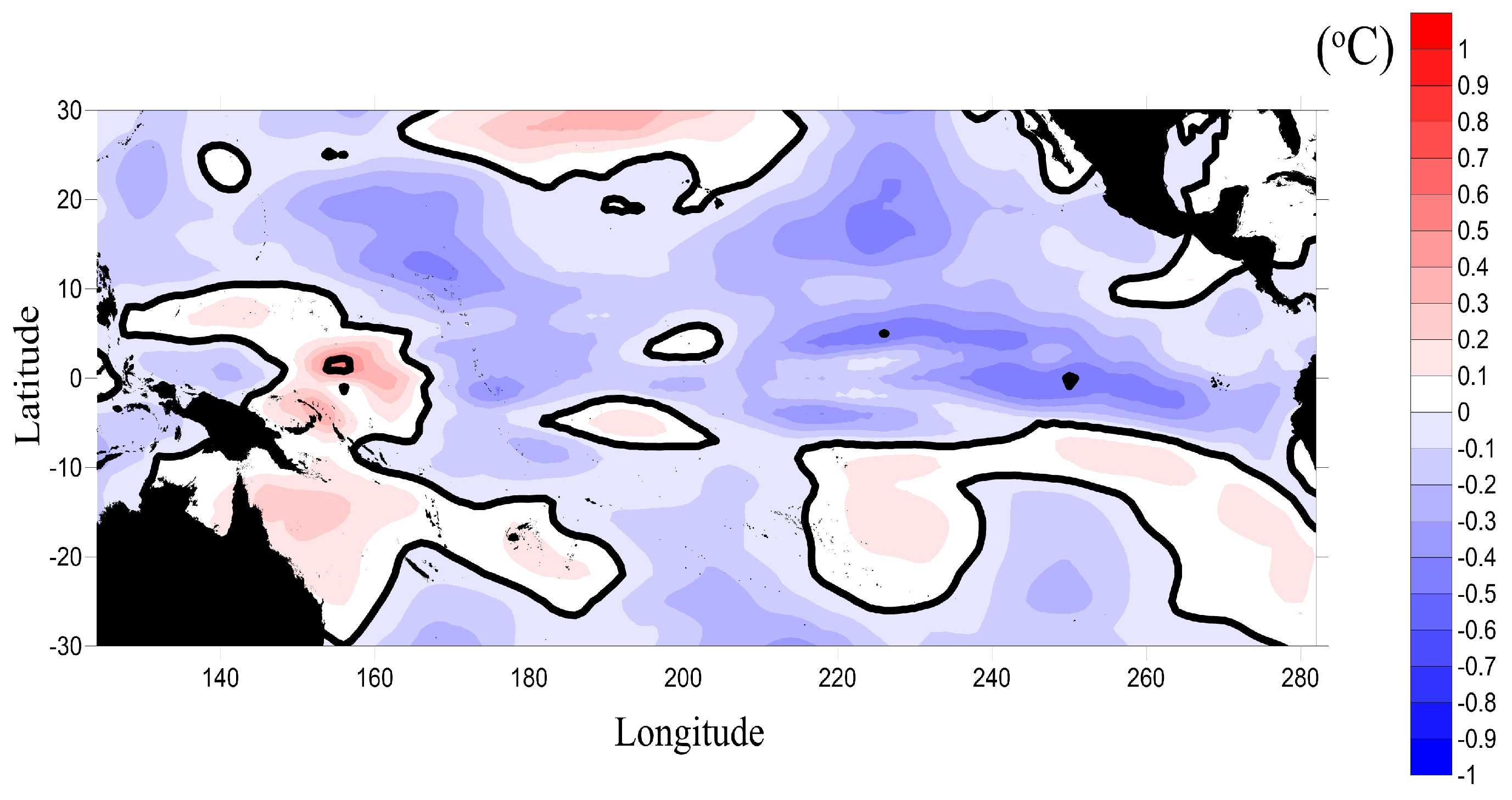
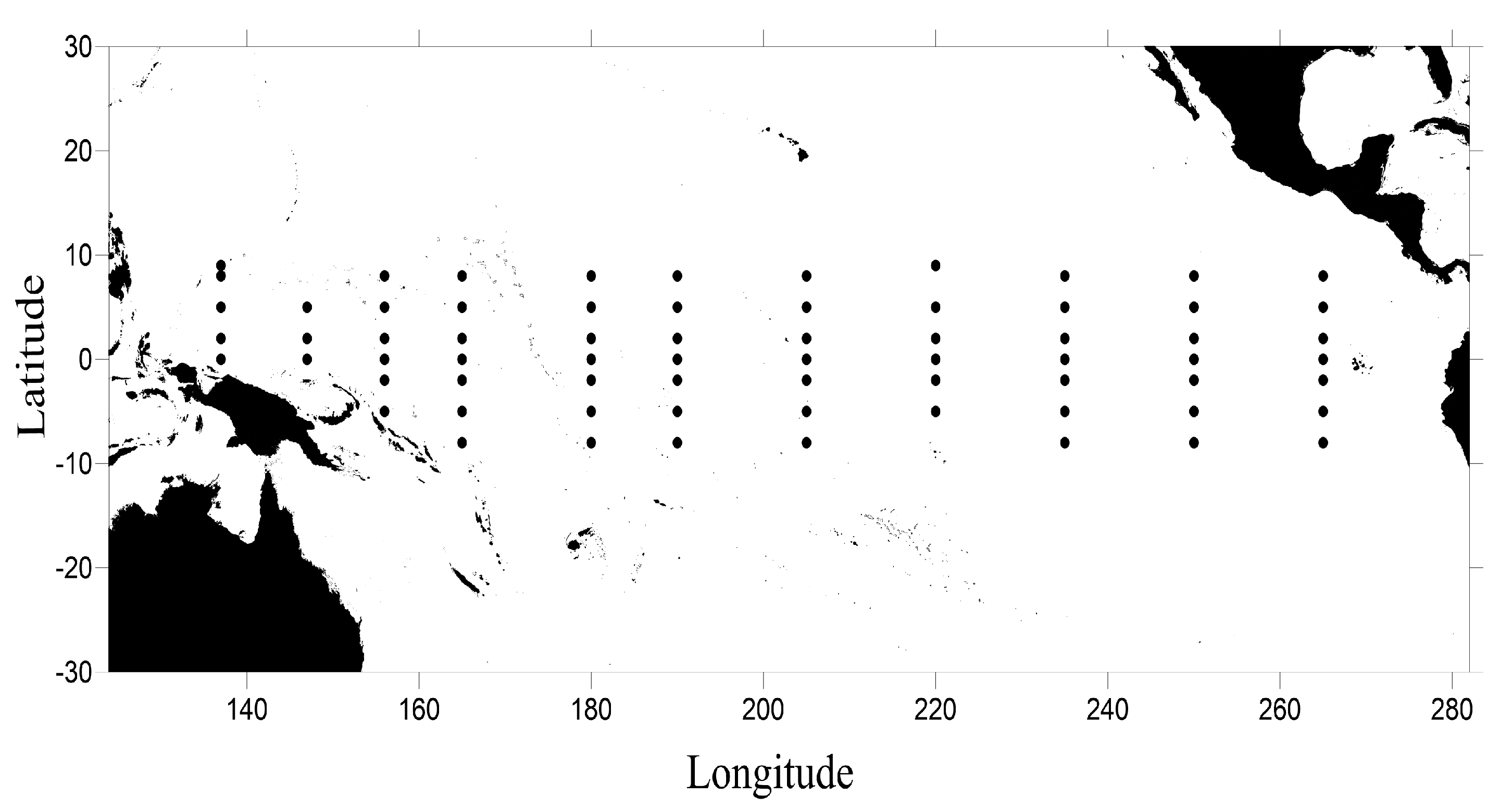
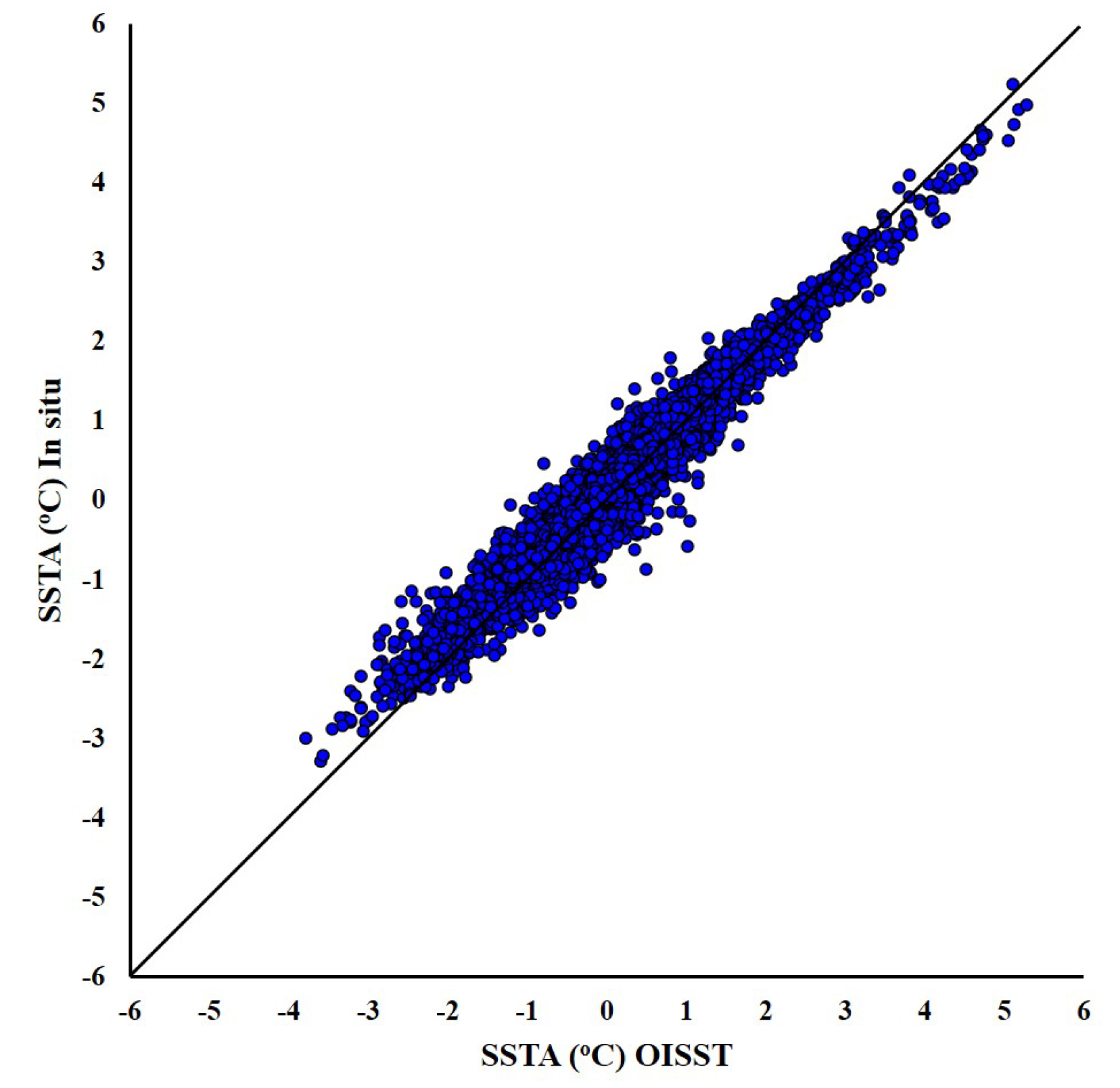
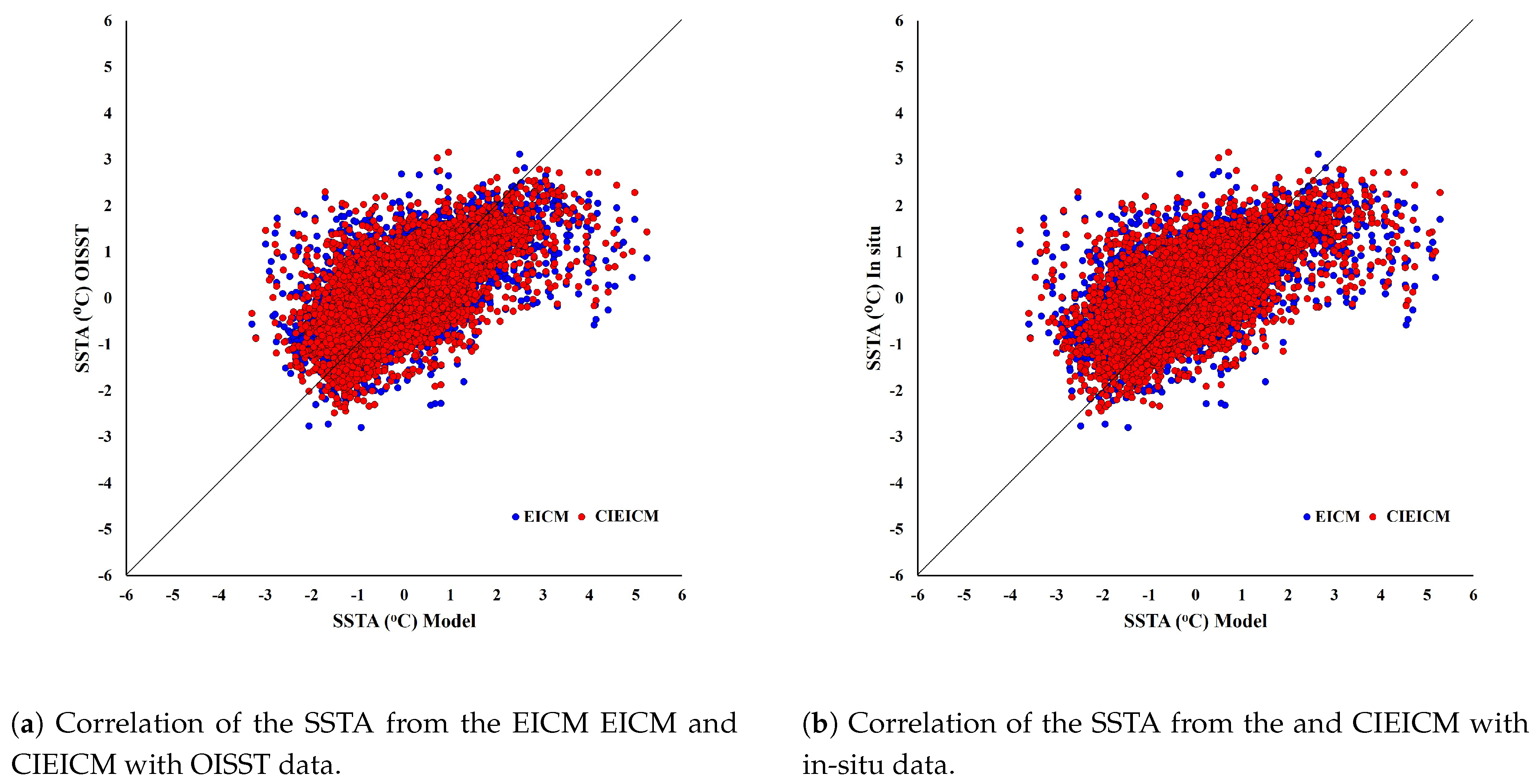

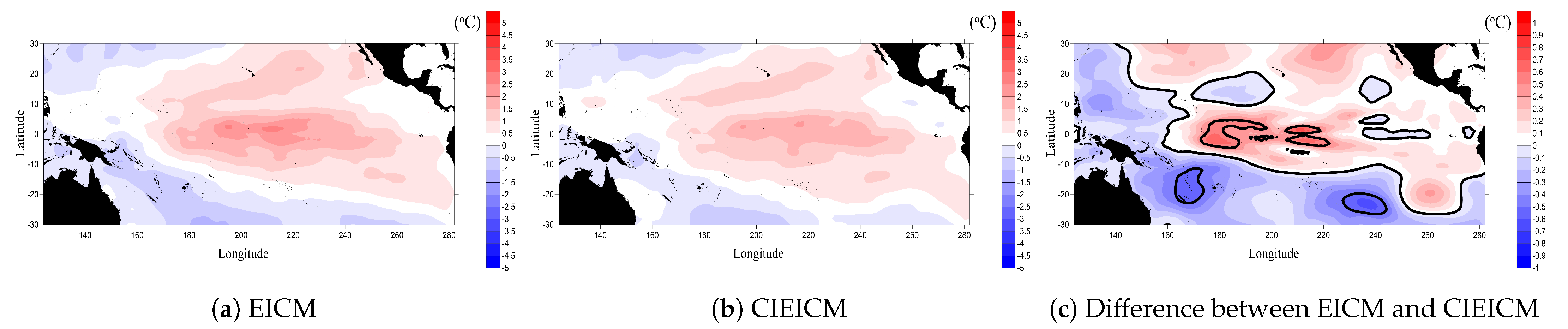

| Detail | ERSST | OISST | IN SITU |
|---|---|---|---|
| Source | National Oceanic and Atmospheric Administration (NOAA) | ||
| Name of data | Sea Surface Temperature Anomaly (SSTA) | ||
| Longitude | 0 E to 360 E | 0.125 E to 359.875 E | 137 E to 265 E |
| Latitude | −90 N to 90 N | −89.875 N to 89.875 N | −8 N to 9 N |
| Time | 1854-01 to Present | 1981-09 to Present | 1977-01 to Present |
| Resolution | 22 | 0.250.25 | Point |
| Search | https://www.ncdc.noaa.gov/data-access/marineocean-data/extended-reconstructed-sea-surface-temperature-ersst | https://www.ncdc.noaa.gov/oisst | https://www.pmel.noaa.gov/tao/drupal/disdel/index.html |
| [accessed on 5 August 2020] | [accessed on 22 December 2020] | [accessed on 27 February 2021] | |
| Model Type | Root Mean | Correlation | Standard | Significance of the Correlation |
|---|---|---|---|---|
| Square Deviation (C) | Coefficient (−) | Deviation (C) | Coefficient (p-Value) | |
| EICM | 0.616 | 0.535 | 0.896 | 0 |
| CIEICM | 0.605 | 0.548 | 0.869 | 0 |
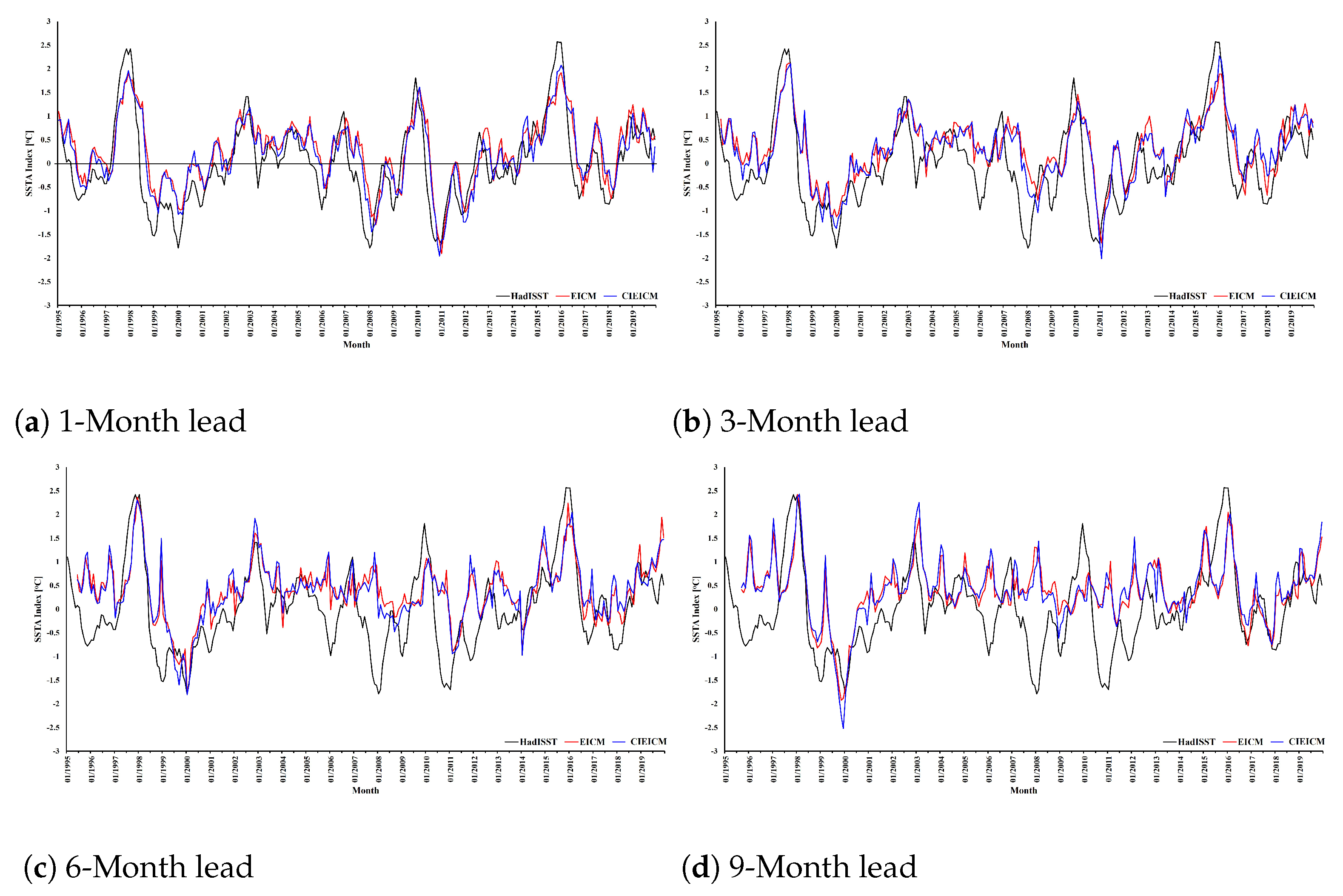
| Month Lead | Measurements | Root Mean Square Deviation | Correlation Coefficients | ||
|---|---|---|---|---|---|
| EICM | CIEICM | EICM | CIEICM | ||
| Jan | 1413 | 0.691 | 0.669 | 0.777 | 0.789 |
| Feb | 1402 | 0.559 | 0.535 | 0.766 | 0.778 |
| Mar | 1402 | 0.533 | 0.513 | 0.691 | 0.718 |
| Apr | 1391 | 0.55 | 0.521 | 0.606 | 0.629 |
| May | 1392 | 0.668 | 0.646 | 0.405 | 0.399 |
| Jun | 1369 | 0.772 | 0.743 | 0.318 | 0.336 |
| Jul | 1383 | 0.774 | 0.744 | 0.436 | 0.434 |
| Aug | 1389 | 0.767 | 0.733 | 0.419 | 0.476 |
| Sep | 1394 | 0.737 | 0.71 | 0.516 | 0.556 |
| Oct | 1384 | 0.691 | 0.652 | 0.723 | 0.746 |
| Nov | 1394 | 0.684 | 0.663 | 0.758 | 0.763 |
| Dec | 1396 | 0.710 | 0.665 | 0.770 | 0.788 |
| Mean | 0.676 | 0.652 | 0.600 | 0.616 | |
| Mann-Whitney U | Wilcoxon W | Z | Asymp. Sig (1-Tailed) | |
|---|---|---|---|---|
| 41,416.5 | 86,566.5 | −1.688 | 0.0455 |
| Month Lead | Measurements | Root Mean Square Deviation | Correlation Coefficients | ||
|---|---|---|---|---|---|
| EICM | CIEICM | EICM | CIEICM | ||
| 1-Month Lead | 300 | 0.555 | 0.51 | 0.827 | 0.842 |
| 2-Month Lead | 299 | 0.654 | 0.624 | 0.759 | 0.77 |
| 3-Month Lead | 298 | 0.673 | 0.651 | 0.744 | 0.749 |
| 4-Month Lead | 297 | 0.721 | 0.716 | 0.706 | 0.698 |
| 5-Month Lead | 296 | 0.76 | 0.754 | 0.659 | 0.676 |
| 6-Month Lead | 295 | 0.808 | 0.794 | 0.611 | 0.63 |
| 7-Month Lead | 294 | 0.861 | 0.843 | 0.55 | 0.563 |
| 8-Month Lead | 293 | 0.897 | 0.877 | 0.506 | 0.509 |
| 9-Month Lead | 292 | 0.904 | 0.89 | 0.494 | 0.481 |
| 10-Month Lead | 291 | 0.889 | 0.889 | 0.499 | 0.464 |
| 11-Month Lead | 290 | 0.881 | 0.871 | 0.45 | 0.499 |
| 12-Month Lead | 289 | 0.871 | 0.855 | 0.434 | 0.489 |
| Mean | 0.790 | 0.773 | 0.603 | 0.614 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Injan, S.; Wangwongchai, A.; Humphries, U.; Khan, A.; Yusuf, A. Reinitializing Sea Surface Temperature in the Ensemble Intermediate Coupled Model for Improved Forecasts. Axioms 2021, 10, 189. https://doi.org/10.3390/axioms10030189
Injan S, Wangwongchai A, Humphries U, Khan A, Yusuf A. Reinitializing Sea Surface Temperature in the Ensemble Intermediate Coupled Model for Improved Forecasts. Axioms. 2021; 10(3):189. https://doi.org/10.3390/axioms10030189
Chicago/Turabian StyleInjan, Sittisak, Angkool Wangwongchai, Usa Humphries, Amir Khan, and Abdullahi Yusuf. 2021. "Reinitializing Sea Surface Temperature in the Ensemble Intermediate Coupled Model for Improved Forecasts" Axioms 10, no. 3: 189. https://doi.org/10.3390/axioms10030189
APA StyleInjan, S., Wangwongchai, A., Humphries, U., Khan, A., & Yusuf, A. (2021). Reinitializing Sea Surface Temperature in the Ensemble Intermediate Coupled Model for Improved Forecasts. Axioms, 10(3), 189. https://doi.org/10.3390/axioms10030189








