Periodic Property and Instability of a Rotating Pendulum System
Abstract
1. Introduction
2. Problem’s Description
3. The Homotopy Perturbation Method
4. Method of Solution
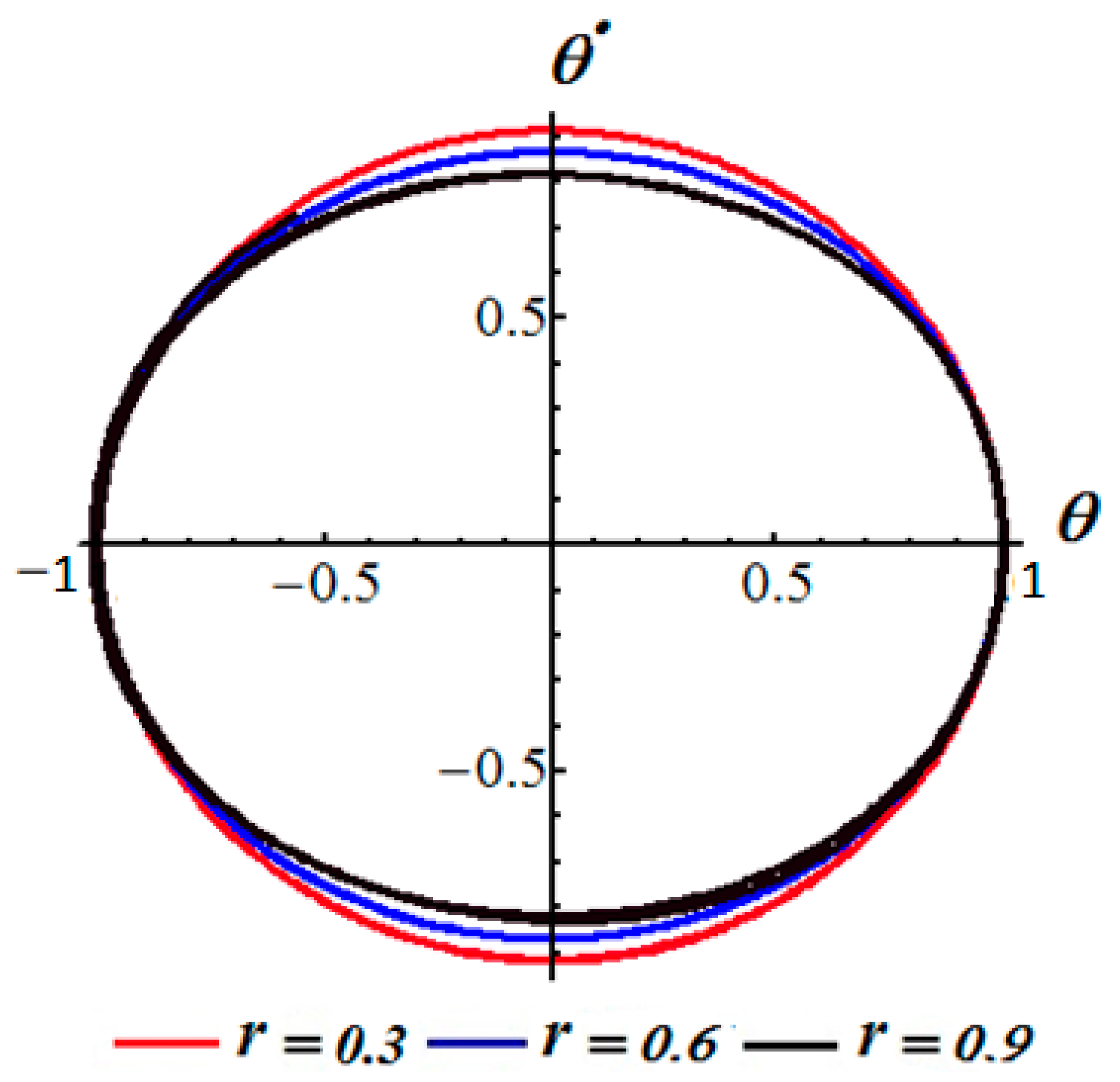
5. Stability Analysis
6. He’s Frequency Formulation
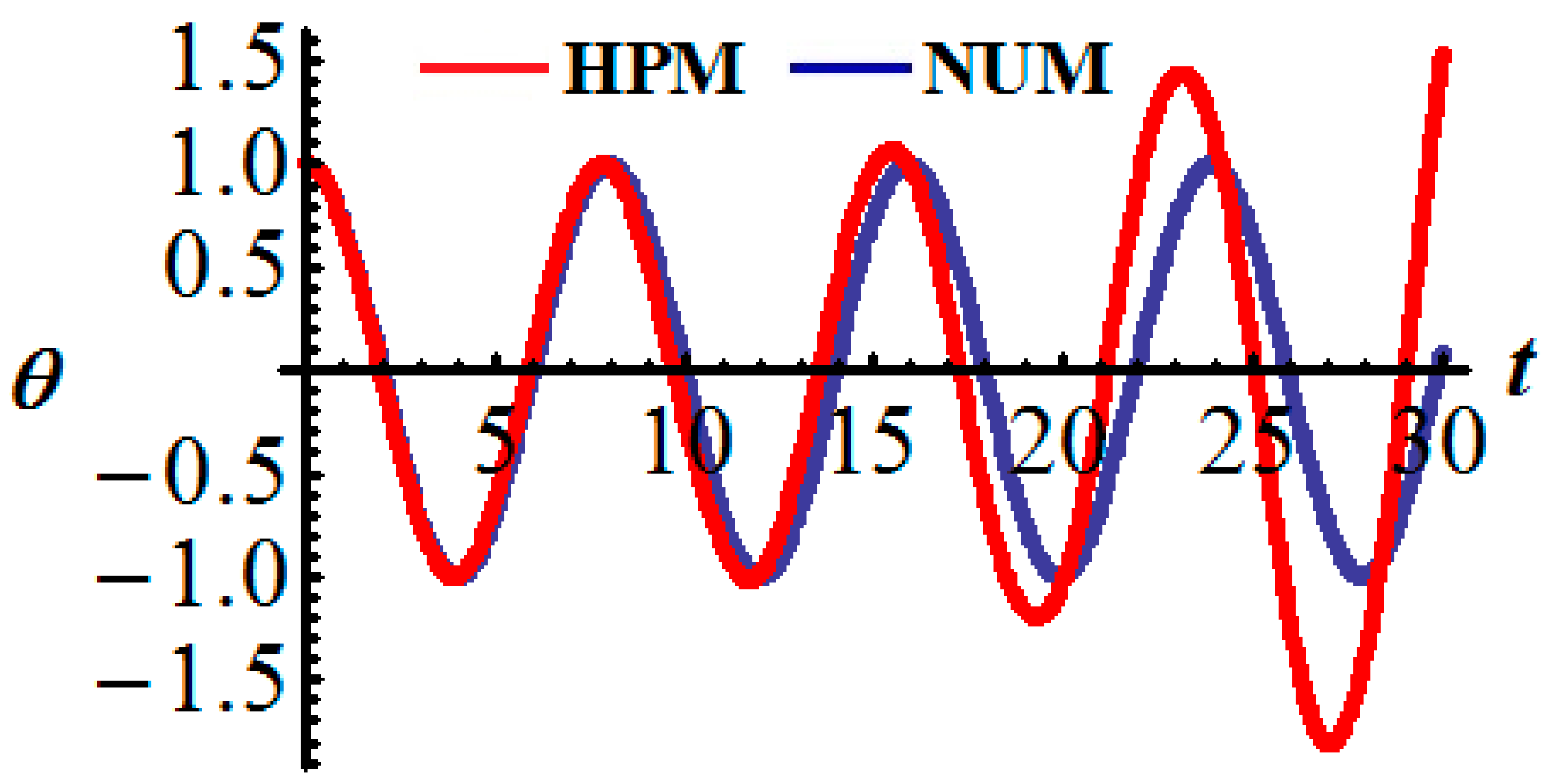
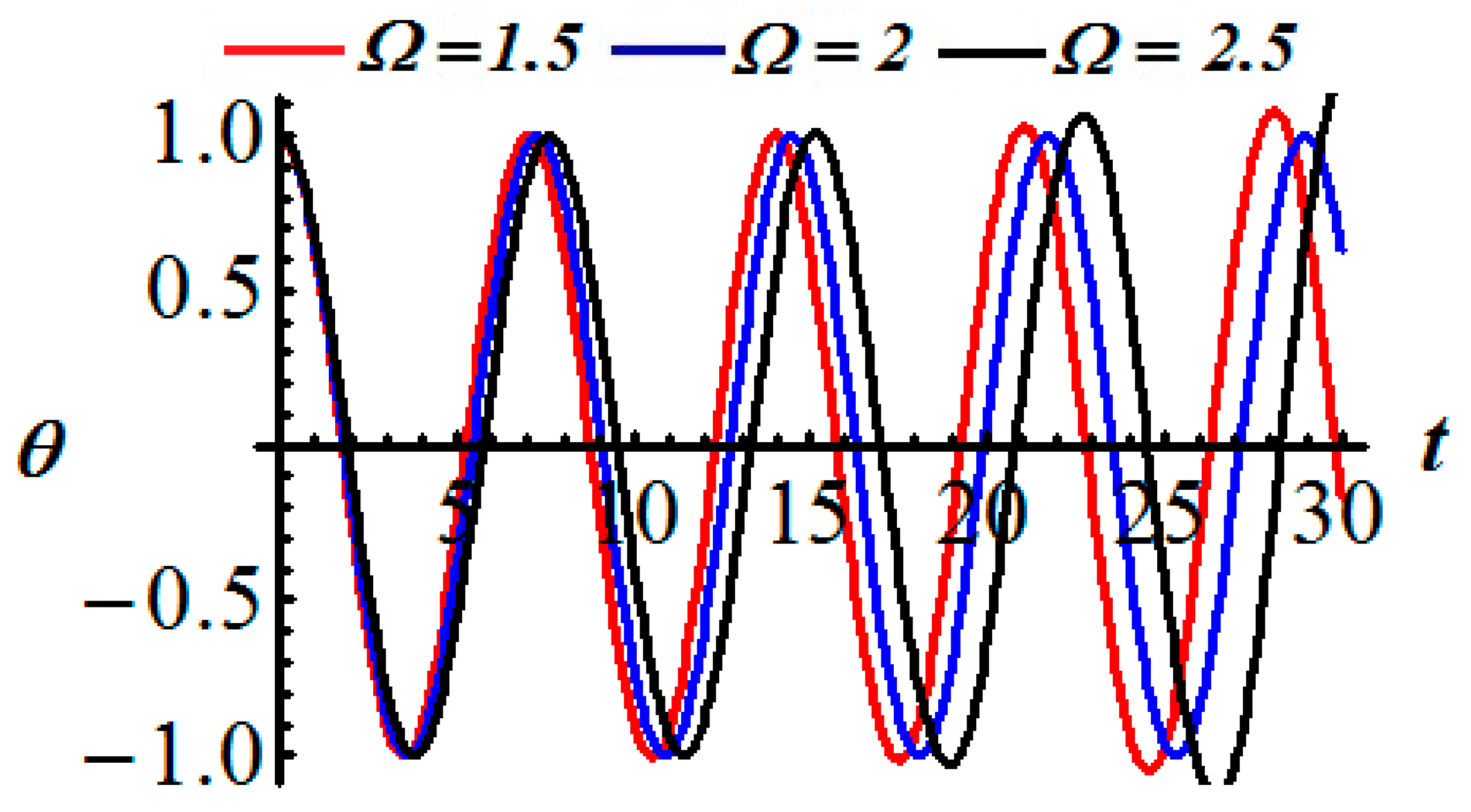
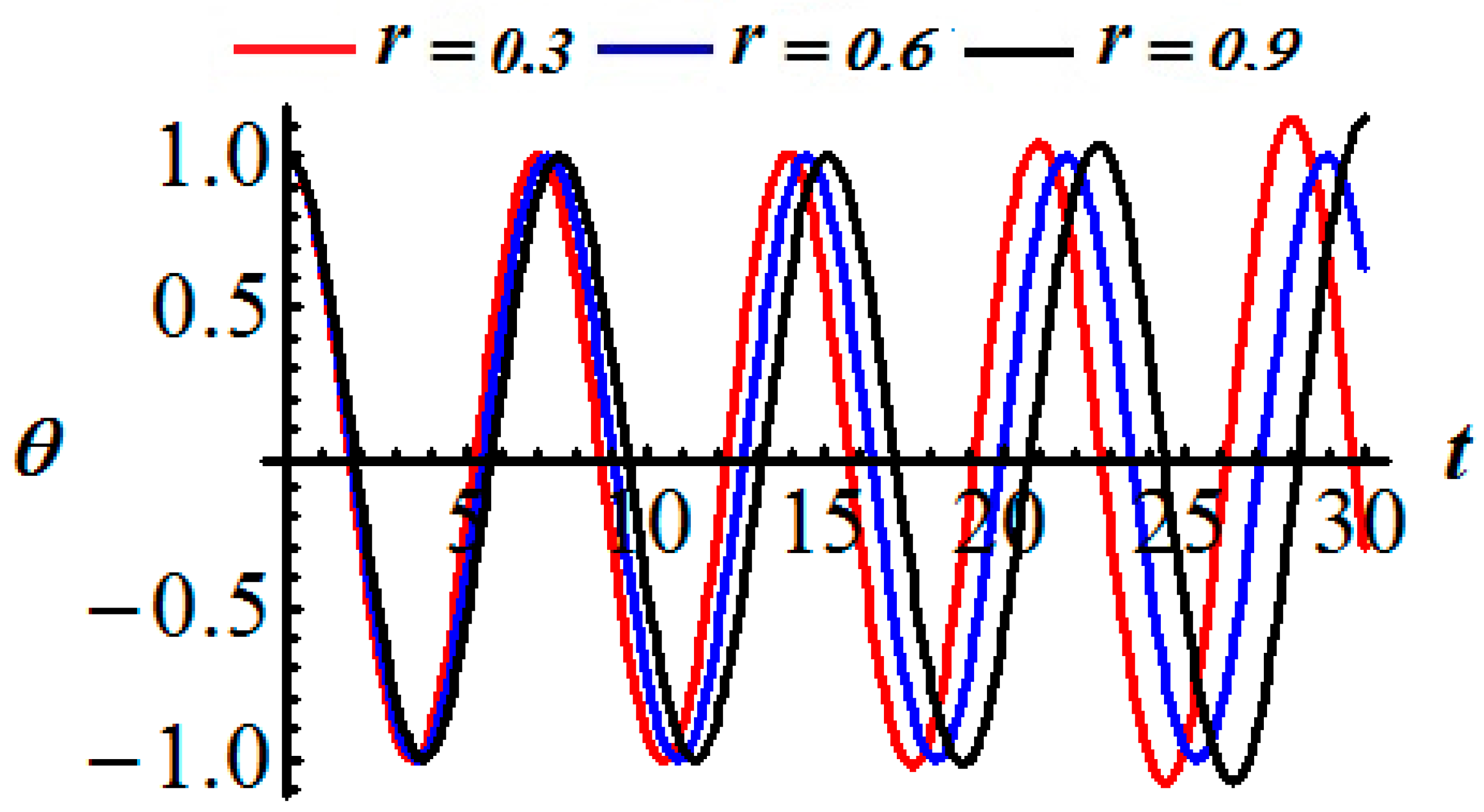
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, W.M.; Wang, H.; Liu, M. Dynamics analysis of an impulsive stochastic model for spruce budworm growth. Appl. Comput. Math. 2021, 19, 336–359. [Google Scholar]
- Janevski, G.; Kozic, P.; Pavlovic, R.; Posavljak, S. Moment Lyapunov exponents and stochastic stability of a thin-walled beam subjected to axial loads and end moments. Facta Univ. Ser. Mech. Eng. 2021, 19, 209–228. [Google Scholar] [CrossRef]
- Pavlovic, I.R.; Pavlovic, R.; Janevski, G.; Despenić, N.; Pajković, V. Dynamic behavior of two elastically connected nanobeams under a white noise process. Facta Univ. Ser. Mech. Eng. 2020, 18, 219–227. [Google Scholar] [CrossRef]
- Zuo, Y.-T. A gecko-like fractal receptor of a three-dimensional printing technology: A fractal oscillator. J. Math. Chem. 2021, 59, 735–744. [Google Scholar] [CrossRef]
- Yeasmin, I.A.; Rahman, M.S.; Alam, M.S. The modified Lindstedt-Poincare method for solving quadratic nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2020, 1461348420979758. [Google Scholar] [CrossRef]
- El-Sabaa, F.M.; Amer, T.S.; Gad, H.M.; Bek, M.A. On the motion of a damped rigid body near resonances under the influence of harmonically external force and moments. Results Phys. 2020, 19, 103352. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Meth. Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Anjum, N.; Ain, Q.T. Application of He’s fractional derivative and fractional complex transform for time fractional Camassa-Holm equation. Therm. Sci. 2020, 24, 3023–3030. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Homotopy perturbation for excited nonlinear equations. Sci. Eng. Appl. 2017, 2, 96–108. [Google Scholar] [CrossRef]
- Amer, T.S.; Galal, A.A.; Elnaggar, S. The vibrational motion of a dynamical system using homotopy perturbation technique. Appl. Math. 2020, 11, 1081–1099. [Google Scholar] [CrossRef]
- El-Dib, Y.O.; Moatimid, G.M. Stability configuration of a rocking rigid rod over a circular surface using the homotopy perturbation method and Laplace transform. Arab. J. Sci. Eng. 2019, 44, 6581–6591. [Google Scholar] [CrossRef]
- Ganji, S.S.; Ganji, D.D.; Babazadeh, H.; Karimpour, S. Variational approach method for nonlinear oscillations of the motion of a rigid rocking back and forth and cubic-quintic Duffing oscillators. Prog. Electromagn. Res. M 2008, 4, 23–32. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Periodic solution and stability behavior for nonlinear oscillator having a cubic nonlinearity time-delayed. Int. Annu. Sci. 2018, 5, 12–25. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Periodic solution of the cubic nonlinear Klein-Gordon equation and the stability criteria via the He-multiple-scales method. Pramana J. Phys. 2019, 92, 7. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Stability approach for periodic delay Mathieu equation by the He-multiple-scales method. Alex. Eng. J. 2018, 57, 4009–4020. [Google Scholar] [CrossRef]
- Hosen, M.A.; Chowdhury, M.S.H. Accurate approximations of the nonlinear vibration of couple-mass-springs systems with linear and nonlinear stiffnesses. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1072–1090. [Google Scholar] [CrossRef]
- Hosen, M.A. Analysis of nonlinear vibration of couple-mass–spring systems using iteration technique. Multidiscip. Modeling Mater. Struct. 2020, 16, 1539–1558. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Homotopy perturbation method for N/MEMS oscillators. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Tian, D.; Ain, Q.-T.; Anjum, N.; He, C.-H.; Cheng, B. Fractal N/MEMS: From pull-in instability to pull-in stability. Fractals 2021, 29, 2150030. [Google Scholar] [CrossRef]
- Meshki, H.; Rezaei, A.; Sadeghi, A. Homotopy Perturbation-Based Dynamic Analysis of Structural Systems. J. Eng. Mech. 2020, 146, 04020136. [Google Scholar] [CrossRef]
- Wang, K.L.; Yao, S.W. He’s fractiona; derivative for the evolution equation. Therm. Sci. 2020, 24, 2507–2513. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. The enhanced homotopy perturbation method for axial vibration of strings. Facta Univ. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- He, C.H.; Tian, D.; Moatimid, G.M.; Salman, H.F.; Zekry, M.H. Hybrid Rayleigh-Van der Pol-Duffing Oscillator (HRVD): Stability Analysis and Controller. J. Low Freq. Noise Vib. Act. Control 2021. [Google Scholar] [CrossRef]
- He, J.-H.; Galal, M.M.; Mostapha, D.R. Nonlinear Instability of Two Streaming-Superposed Magnetic Reiner-Rivlin Fluids by He-Laplace Method. J. Electroanal. Chem. 2021, 895, 115388. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H.; Ain, Q.T.; Tian, D. Li-He’s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Univ. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- El-Dib, Y.O.; Matoog, R.T. The Rank Upgrading Technique for a Harmonic Restoring Force of Nonlinear Oscillators. J. Appl. Comput. Mech. 2021, 7, 782–789. [Google Scholar] [CrossRef]
- Elgazery, N.S. A Periodic Solution of the Newell-Whitehead-Segel (NWS) Wave Equation via Fractional Calculus. J. Appl. Comput. Mech. 2020, 6, 1293–1300. [Google Scholar]
- Koochi, A.; Goharimanesh, M. Nonlinear Oscillations of CNT Nano-resonator Based on Nonlocal Elasticity: The Energy Balance Method. Rep. Mech. Eng. 2021, 2, 41–50. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Herrera-May, A.; Ambrosio, R.; Jimenez-Fernandez, V.M.; Sandoval-Hernandez, M.A.; Alvarez-Gasca, O.; Palma-Grayeb, B.E. The study of heat transfer phenomena by using modified homotopy perturbation method coupled by Laplace transform. Therm. Sci. 2020, 24, 1105–1115. [Google Scholar] [CrossRef]
- Li, X.X.; He, C.H. Homotopy perturbation method coupled with the enhanced perturbation method. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1399–1403. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Huseynov, I.T.; Aliev, N.A.; Aliev, F.A. Analytical approach to a class of Bagley-Torvik equations. TWMS J. Pure Appl. Math. 2020, 11, 238–258. [Google Scholar]
- Qalandarov, A.A.; Khaldjigitov, A.A. Mathematical and Numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Fikret, A.A.; Aliev, N.A.; Mutallimov, M.M.; Namazov, A.A. Algorithm for solving the identification problem for determining the fractional-order derivative of an oscillatory system. Appl. Comput. Math. 2020, 19, 435–442. [Google Scholar]
- Zhang, J.J.; Shen, Y.; He, J.H. Some analytical methods for singular boundary value problem in a fractal space: A review. Appl. Comput. Math. 2019, 18, 225–235. [Google Scholar]
- Song, H.Y. A thermodynamic model for a packing dynamic system. Therm. Sci. 2020, 24, 2331–2335. [Google Scholar] [CrossRef]
- Yao, S.W. Variational principle for non-linear fractional wave equation in a fractal space. Therm. Sci. 2021, 25, 1243–1247. [Google Scholar] [CrossRef]
- Liu, H.Y.; Li, Z.M.; Yao, S.W.; Yao, Y.J.; Liu, J. A variational principle for the photocatalytic Nox abatement. Therm. Sci. 2020, 24, 2515–2518. [Google Scholar] [CrossRef]
- He, J.H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1252–1260. [Google Scholar] [CrossRef]
- Qie, N.; Hou, W.F.; He, J.H. The fastest insight into the large amplitude vibration of a string. Rep. Mech. Eng. 2020, 2, 1–5. [Google Scholar] [CrossRef]
- Liu, C.X. Periodic solution of fractal Phi-4 equation. Therm. Sci. 2021, 25, 1345–1350. [Google Scholar] [CrossRef]
- Liu, C.X. A short remark on He’s frequency formulation. J. Low Freq. Noise Vib. Act. Control 2021, 40, 672–674. [Google Scholar] [CrossRef]
- Feng, G.Q.; Niu, J.Y. He’s frequency formulation for nonlinear vibration of a porous foundation with fractal derivative. Int. J. Geomath. 2021, 12, 14. [Google Scholar] [CrossRef]
- Feng, G.Q. He’s frequency formula to fractal undamped Duffing equation. J. Low Freq. Noise Vib. Act. Control 2021, 1461348421992608. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Palacios-Pineda, L.M.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Trejo, D.O. He’s frequency-amplitude formulation for nonlinear oscillators using Jacobi elliptic functions. J. Low Freq. Noise Vib. Act. Control 2020, 39, 1216–1223. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.P. Residual calculation in He’s frequency-amplitude formulation. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1040–1047. [Google Scholar] [CrossRef]
- Gilat, A. Numerical Methods for Engineers and Scientists; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Simos, T.E.; Tsitouras, C. 6th order Runge-Kutta pairs for scalar autonomous IVP. Appl. Comput. Math. 2020, 19, 412–421. [Google Scholar]
- Hussanan, A.; Khan, I.; Khan, W.A.; Chen, Z.M. Micropolar mixed convective flow Cattaneo-Christove heat flux: Non-Fourier Heat Conduction Analysis. Therm. Sci. 2020, 24, 1345–1356. [Google Scholar] [CrossRef]


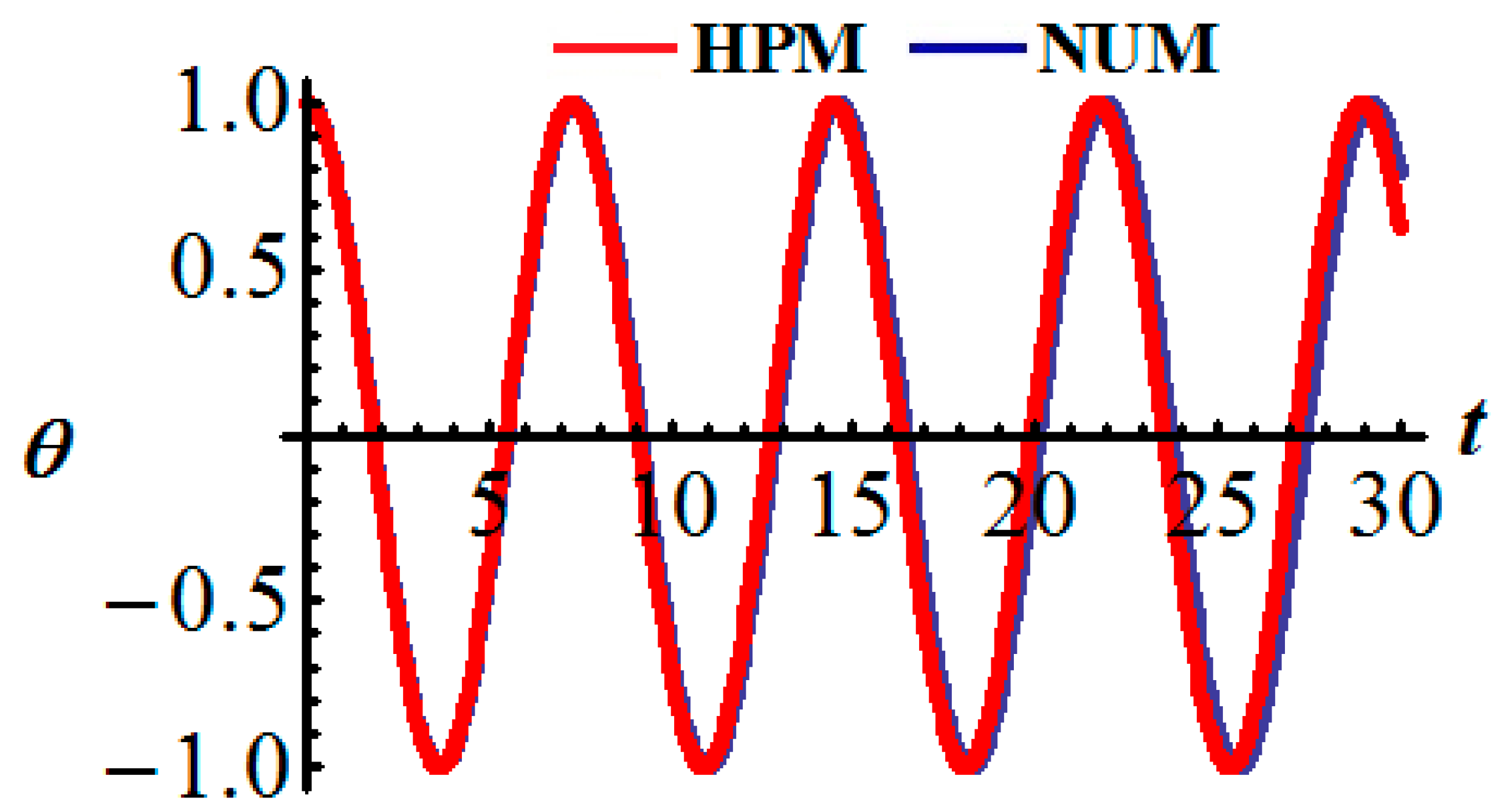
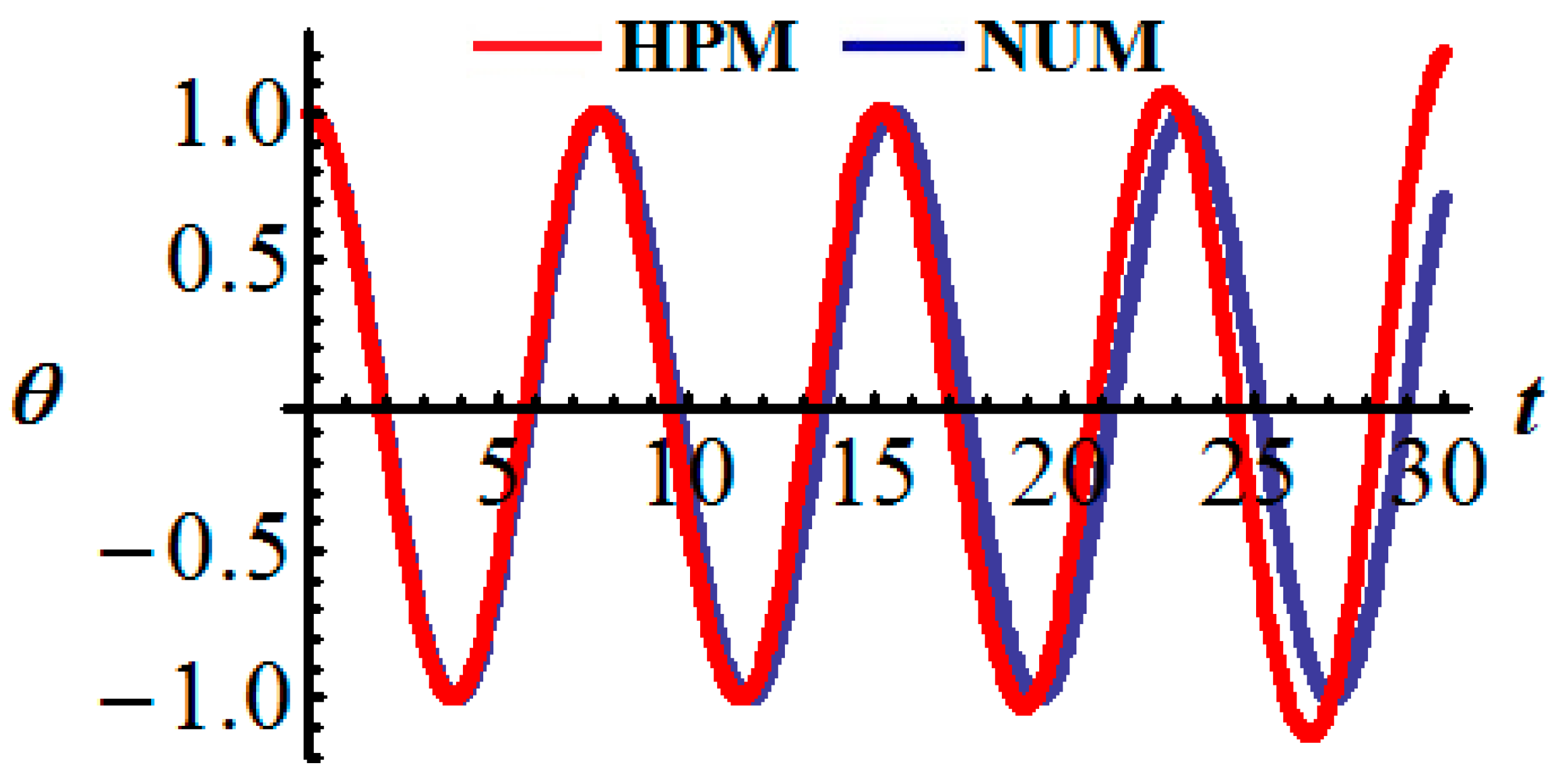
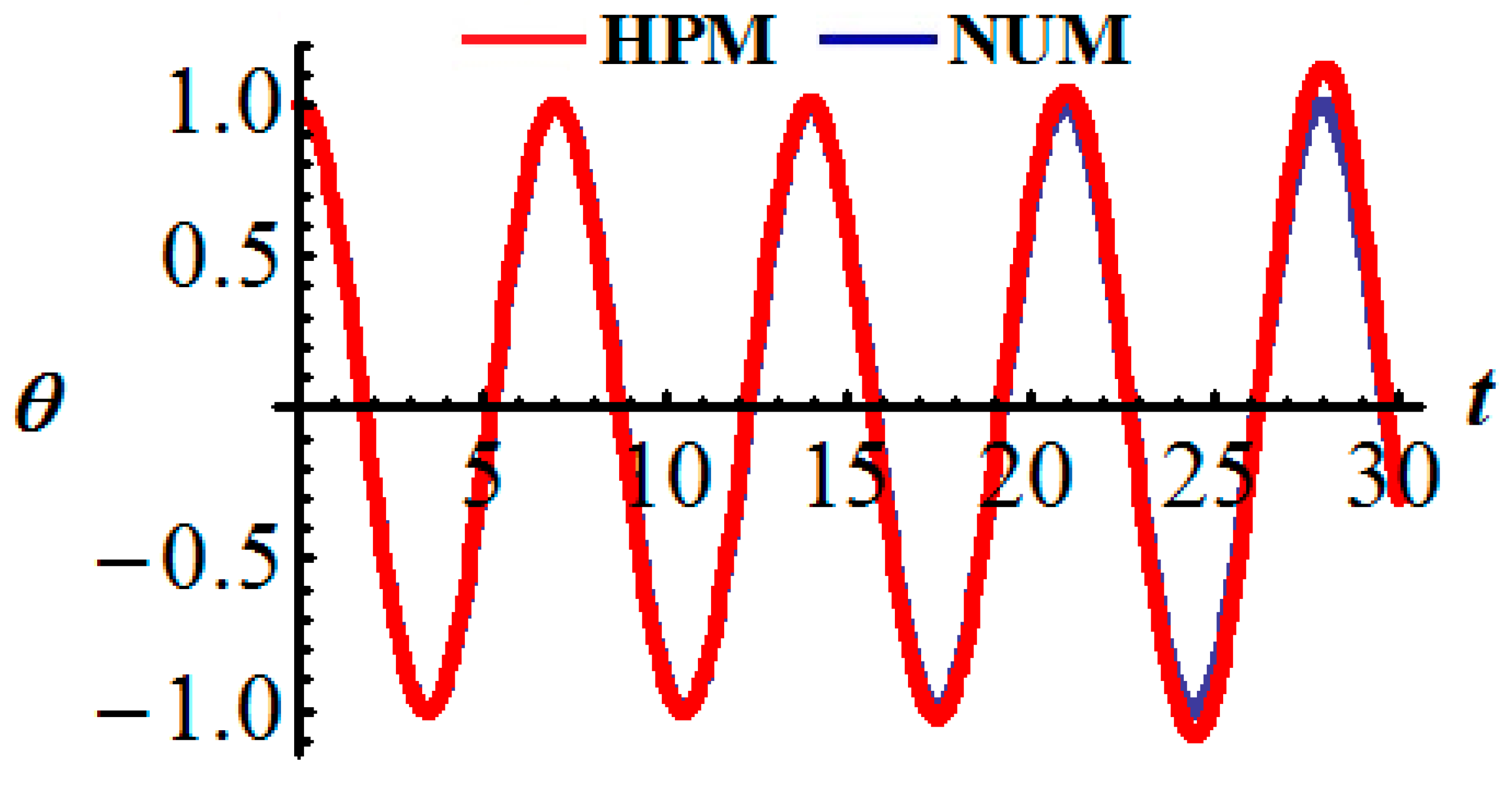
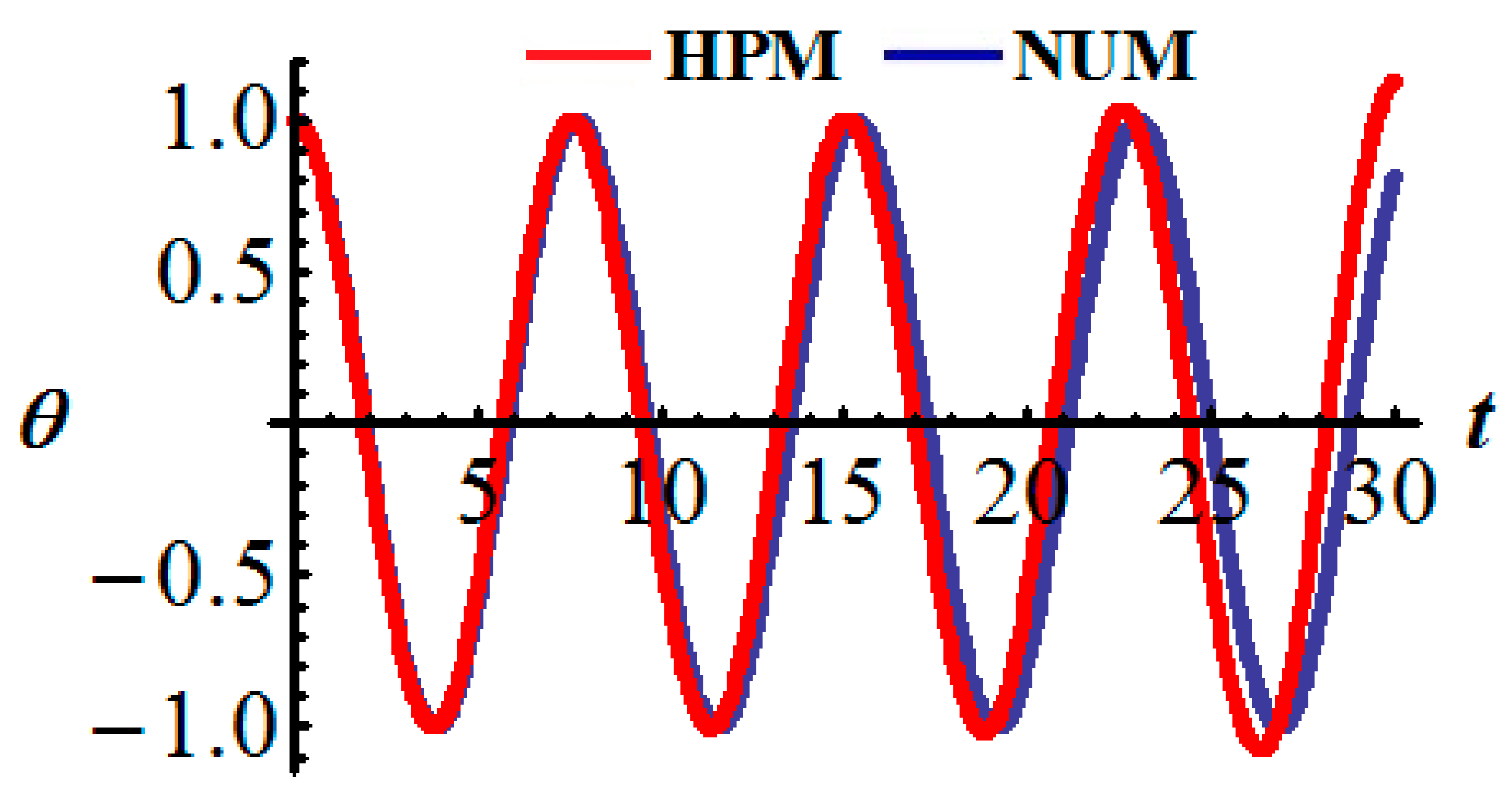

| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.630869 | 0.627776 | 0.0049026 |
| 2 | 0.21956 | −0.225384 | 0.0265278 |
| 3 | −0.899482 | −0.903169 | 0.00409939 |
| 4 | −0.908171 | −0.903095 | 0.00558896 |
| 5 | −0.239734 | −0.22469 | 0.0627527 |
| 6 | 0.614791 | 0.628734 | 0.02268 |
| 7 | 0.999796 | 1.00071 | 0.000911276 |
| 8 | 0.646672 | 0.630153 | 0.0255458 |
| 9 | −0.199286 | −0.225065 | 0.129353 |
| 10 | −0.890417 | −0.903541 | 0.0147397 |
| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.654764 | 0.64695 | 0.0119336 |
| 2 | −0.148467 | −0.16355 | 0.101592 |
| 3 | −0.847042 | −0.858298 | 0.013288 |
| 4 | −0.956805 | −0.946617 | 0.0106482 |
| 5 | −0.404543 | −0.366363 | 0.0943759 |
| 6 | 0.432158 | 0.473118 | 0.0947819 |
| 7 | 0.965135 | 0.977907 | 0.0132337 |
| 8 | 0.830583 | 0.792124 | 0.046304 |
| 9 | 0.118301 | 0.0465204 | 0.606763 |
| 10 | −0.677385 | −0.73201 | 0.0806414 |
| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.685404 | 0.671387 | 0.0204506 |
| 2 | 0.0527615 | −0.0808787 | 0.532912 |
| 3 | −0.758994 | 0.783883 | 0.0327925 |
| 4 | −0.99427 | −0.985533 | 0.00878713 |
| 5 | −0.604164 | 0.538474 | 0.108728 |
| 6 | 0.157724 | 0.242582 | 0.538009 |
| 7 | 0.824048 | 0.875886 | 0.0629072 |
| 8 | 0.977147 | 0.942131 | 0.0358349 |
| 9 | 0.51624 | 0.385223 | 0.253791 |
| 10 | −0.261008 | −0.404121 | 0.548309 |
| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.627452 | 0.625023 | 0.00387119 |
| 2 | −0.229458 | −0.23406 | 0.0200579 |
| 3 | −0.905921 | −0.908752 | 0.00312526 |
| 4 | 0.900042 | −0.896209 | 0.00425873 |
| 5 | 0.215822 | −0.204251 | 0.0536163 |
| 6 | 0.638176 | 0.648882 | 0.0167751 |
| 7 | 0.999907 | 1.00072 | 0.000812474 |
| 8 | 0.616603 | 0.605241 | 0.0184257 |
| 9 | −0.243047 | 0.262363 | 0.0794747 |
| 10 | 0.911628 | −0.921237 | 0.0105405 |
| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.682004 | 0.668681 | 0.0195354 |
| 2 | −0.0636153 | −0.0902769 | 0.419106 |
| 3 | 0.770003 | 0.793214 | 0.0301438 |
| 4 | 0.991721 | 0.982383 | 0.0094154 |
| 5 | −0.582943 | 0.520499 | 0.107117 |
| 6 | 0.189856 | 0.269191 | 0.417868 |
| 7 | 0.845418 | 0.891707 | 0.0547537 |
| 8 | 0.967025 | 0.929664 | 0.038635 |
| 9 | 0.474508 | 0.35122 | 0.259822 |
| 10 | −0.313132 | −0.443194 | 0.415355 |
| Time | Numerical Results (NR) | HPM Results (HPMR) | |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 0.700116 | 0.68309 | 0.0243185 |
| 2 | −0.00515091 | −0.0393558 | 6.64055 |
| 3 | −0.707562 | −0.739703 | 0.0454255 |
| 4 | −0.999944 | 0.995252 | 0.00469164 |
| 5 | −0.692595 | 0.611115 | 0.117644 |
| 6 | 0.0154523 | 0.129692 | 7.39304 |
| 7 | 0.714933 | 0.793976 | 0.11056 |
| 8 | 0.999775 | 0.983871 | 0.0159081 |
| 9 | 0.685001 | 0.518703 | 0.24277 |
| 10 | −0.0257521 | −0.252657 | 8.81111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.-H.; Amer, T.S.; Elnaggar, S.; Galal, A.A. Periodic Property and Instability of a Rotating Pendulum System. Axioms 2021, 10, 191. https://doi.org/10.3390/axioms10030191
He J-H, Amer TS, Elnaggar S, Galal AA. Periodic Property and Instability of a Rotating Pendulum System. Axioms. 2021; 10(3):191. https://doi.org/10.3390/axioms10030191
Chicago/Turabian StyleHe, Ji-Huan, Tarek S. Amer, Shimaa Elnaggar, and Abdallah A. Galal. 2021. "Periodic Property and Instability of a Rotating Pendulum System" Axioms 10, no. 3: 191. https://doi.org/10.3390/axioms10030191
APA StyleHe, J.-H., Amer, T. S., Elnaggar, S., & Galal, A. A. (2021). Periodic Property and Instability of a Rotating Pendulum System. Axioms, 10(3), 191. https://doi.org/10.3390/axioms10030191








