Unveiling the Dynamics of the European Entrepreneurial Framework Conditions over the Last Two Decades: A Cluster Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
- The adult population survey (APS), which provides standardized data on entrepreneurial activities and attitudes within each country—at least 2000 randomly selected adults (18–64 years of age)in each economy.
- The national expert survey (NES) investigates the national framework conditions for entrepreneurship by means of standardized questionnaires; national teams collect experts’ opinions about components of the entrepreneurship ecosystem through a national expert survey.
2.2. Methodology
- Optimization techniques—based on the early choice of a number of clusters, k, and a division of all cases is made by the pre-established k groups. Next, the optimization of the chosen criterion is performed. In general, it is intended that within each group, the elements are as similar as possible and as different as possible from elements in other groups;
- Hierarchical techniques—based on a matrix of similarities (or differences) in which each element of the matrix describes the degree of similarity (or difference) between each two cases, based on the chosen variables. These techniques can be agglomerative or divisive. In the first case, the procedure starts with n groups including one individual that are grouped successively until only one group is obtained including all n individuals. In the divisive, 0 the reverse process is applied: one starts from a group with all of the individuals and successive divisions are applied until obtaining n groups;
- Density or mode-seeking techniques—groups are formed by looking for regions that contain a relatively dense concentration of cases.
- Other techniques—these include those that allow groups to overlap (fuzzy clusters), additive partitive methods (kmeans and hill climbing), those that do not use a similarity matrix but that can be directly applied to the original data and others that are not included in the previous types;
- Euclidean distance between two cases (i and j) is the square root of the sum of the squares of the differences between values of i and j for all variables (), that is,
- Minkowski distance can be considered as a generalization of Euclidean distance (coincide when r = 2):
- Mahalanobis distance considers the covariance matrix for the calculation of distanceswhere and are the vectors of variable values for individuals i and j, respectively.
- Single linkage or criterion of the nearest neighbor, for which the similarity between two groups is the maximum similarity between any two cases belonging to those groups. That is, for the two groups (i, j) and (k), the distance between the two is given by Equation (5).In this case, the coefficients in recurrence Equation (4) are
- Complete linkage or the criterion of the furthest neighbor uses the process inverse to the previous one; that is, given two groups, the distance between the two is given by Equation (6).In this case, the coefficients in recurrence Equation (4) are
- Average defines the distance as the average of the distances between all pairs of individuals constituted by elements of the two groups. This strategy is, in a way, intermediate in relation to the first two described.In this case, the coefficients in recurrence Equation (4) are
- Centroid defines the distance between two groups as the distance between their centroids, points defined by the means of the variables that characterize the individuals in each group.In this case, the coefficients in recurrence Equation (4) are
- Ward method [20] is based on the loss of information resulting from the grouping of individuals and measured by adding the squares of the deviations from individual observations relative to the averages of the groups in which they are classified.In this case, the coefficients in recurrence Equation (4) are
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APS | adult population survey |
| EDL | economic development level |
| EFCs | Entrepreneurial Framework Conditions |
| GEM | Global Entrepreneurship Monitor |
| NES | national expert survey |
| TEA | total early-stage entrepreneurial activity |
Appendix A
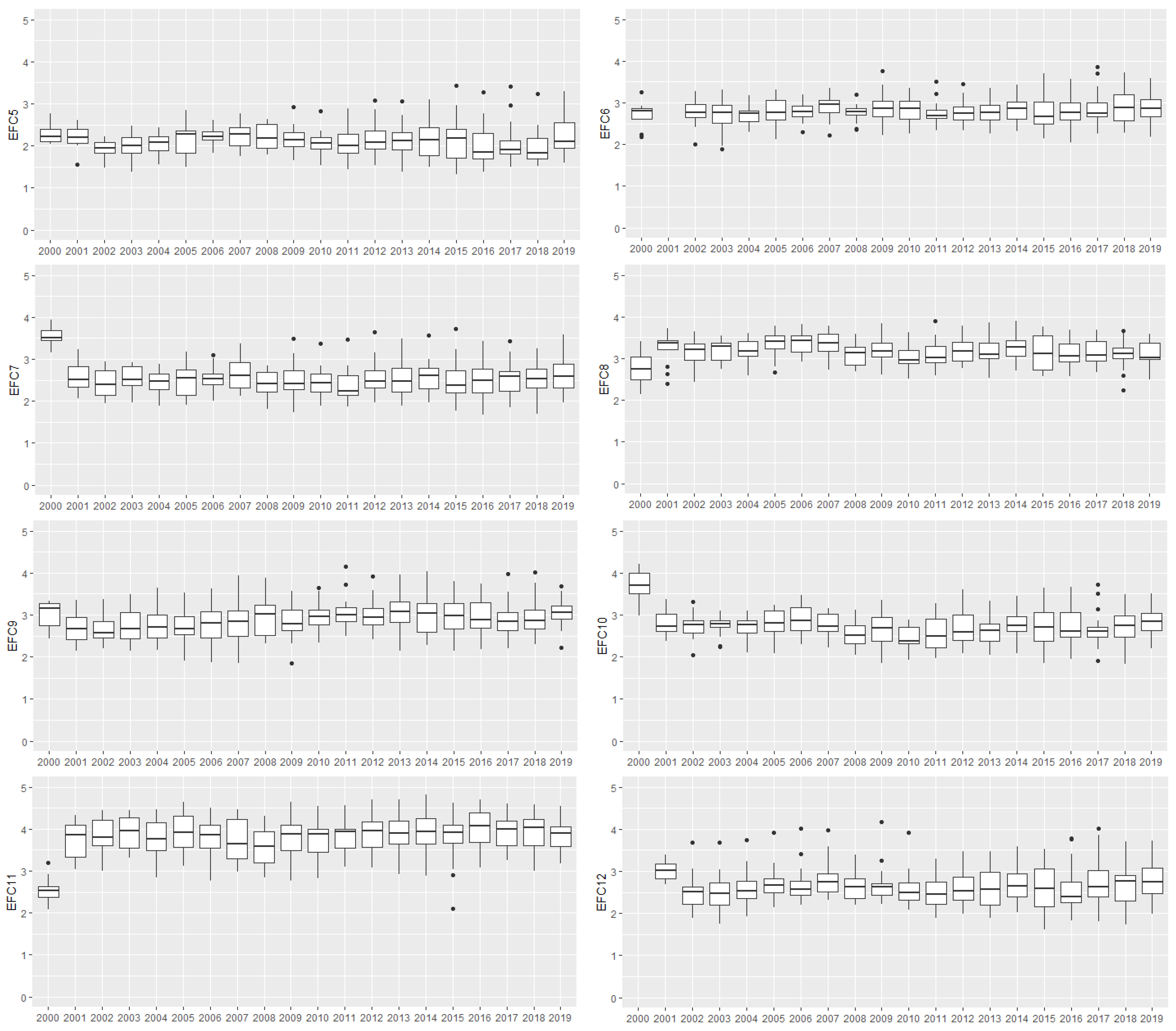
| EFC | Description | Indicator |
|---|---|---|
| 1 | The availability of financial resources—equity and debt—for small and medium enterprises (SMEs) (including grants and subsidies) | Financing for entrepreneurs |
| 2 | The extent to which public policies support entrepreneurship—entrepreneurship as a relevant economic issue | Governmental support and policies |
| 3 | The extent to which public policies support entrepreneurship—taxes or regulations are either size neutral or encourage new and SMEs | Taxes and bureaucracy |
| 4 | The presence and quality of programs directly assisting SMEs at all levels of government (national, regional, municipal) | Governmental programs |
| 5 | The extent to which training in creating or managing SMEs is incorporated within the education and training system at primary and secondary levels | Basic school entrepreneurial education and training |
| 6 | The extent to which training in creating or managing SMEs is incorporated within the education and training system in higher education, such as vocational education, college, business schools, etc. | Post-school entrepreneurial education and training |
| 7 | The extent to which national research and development will lead to new commercial opportunities and is available to SMEs | R&D transfer |
| 8 | The presence of property rights, commercial, accounting and other legal and assessment services and institutions that support or promote SMEs | Commercial and professional infrastructure |
| 9 | The level of change in markets from year to year | Internal market dynamics |
| 10 | The extent to which new firms are free to enter existing markets | Internal market openness |
| 11 | Ease of access to physical resources—communication, utilities, transportation, land or space—at a price that does not discriminate against SMEs | Physical and services infrastructure |
| 12 | The extent to which social and cultural norms encourage or allow actions leading to new business methods or activities that can potentially increase personal wealth and income | Cultural and social norms |
References
- Fernandes, A.J.; Ferreira, J.J. Entrepreneurial ecosystems and networks: A literature review and research agenda. Rev. Manag. Sci. 2021, 1–59. [Google Scholar] [CrossRef]
- Farinha, L.; Lopes, J.; Bagchi-Sen, S.; Sebastião, J.R.; Oliveira, J. Entrepreneurial dynamics and government policies to boost entrepreneurship performance. Socio Econ. Plan. Sci. 2020, 72, 100950. [Google Scholar] [CrossRef]
- De Brito, S.; Leitão, J. Mapping and defining entrepreneurial ecosystems: A systematic literature review. Knowl. Manag. Res. Pract. 2020, 19, 1–22. [Google Scholar] [CrossRef]
- Herrington, M.; Kew, P.K. Global Entrepreneurship Monitor: 2016/17 Global Report; Technical Report; Global Entrepreneurship Research Association (GERA): London, UK, 2017. [Google Scholar]
- Kelley, D.; Bosma, N.; Amorós, J.E. Global Entrepreneurship Monitor 2010 Global Report; Technical Report; Global Entrepreneurship Research Association (GERA): London, UK, 2011. [Google Scholar]
- Pilar, M.D.F.; Marques, M.; Correia, A. New and growing firms entrepreneurs’ perceptions and their discriminant power in edl countries. Glob. Bus. Econ. Rev. 2018, 21, 474–499. [Google Scholar] [CrossRef]
- Braga, V.; Queirós, M.; Correia, A.; Braga, A. High-Growth Business Creation and Management: A Multivariate Quantitative Approach Using GEM Data. J. Knowl. Econ. 2017, 9, 424–445. [Google Scholar] [CrossRef]
- Correia, A.; Costa e Silva, E.; Lopes, I.C.; Braga, A.; Braga, V. Experts’ perceptions on the entrepreneurial framework conditions. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2017; Volume 1906, p. 110004. [Google Scholar]
- Autio, E.; Kenney, M.; Mustar, P.; Siegel, D.; Wright, M. Entrepreneurial innovation: The importance of context. Res. Policy 2014, 43, 1097–1108. [Google Scholar] [CrossRef]
- Singer, S.; Herrington, M.; Menipaz, E. Global Entrepreneurship Monitor: Global Report 2017/18; Technical Report; Global Entrepreneurship Research Association (GERA): London, UK, 2018. [Google Scholar]
- Costa e Silva, E.; Correia, A.; Duarte, F. How Portuguese experts’ perceptions on the entrepreneurial framework conditions have changed over the years: A benchmarking analysis. In AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2018; Volume 2040, p. 110005. [Google Scholar]
- Sokal, R.R. The principles and practice of numerical taxonomy. Taxon 1963, 12, 190–199. [Google Scholar] [CrossRef]
- Driver, H.E. Survey of numerical classification in anthropology. In The Use of Computers in Anthropology; De Gruyter Mouton: Berlin, Germany, 2011; pp. 301–344. [Google Scholar]
- Johnson, M.E. Multivariate Statistical Simulation: A Guide to Selecting and Generating Continuous Multivariate Distributions; John Wiley & Sons: Hoboken, NJ, USA, 1987; Volume 192. [Google Scholar]
- Walter, G.A.; Barney, J.B. Management objectives in Mergers and Acquisitions. Strateg. Manag. J. II(I) 1990, 11, 79–86. [Google Scholar] [CrossRef]
- Doyle, P.; Saunders, J. Market segmentation and positioning in specialized industrial markets. J. Mark. 1985, 49, 24–32. [Google Scholar] [CrossRef]
- Green, P.E.; Schaffer, C.; Patterson, K. A reduced space approach to the clustering of categorical data in market segmentation. J. Mark. 1991, 55, 20–31. [Google Scholar] [CrossRef]
- Reis, E. Estatística Multivariada Aplicada, 2nd ed.; Edições Sílabo: Lisboa, Portugal, 2001; ISBN 972-618-247-6. [Google Scholar]
- Aldenderfer, M.S.; Blashfield, R.K. Cluster analysis software and the literature on clustering. In Cluster Analysis; SAGE Publications Inc.: Thousand Oaks, CA, USA, 1984; pp. 75–81. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Handl, J.; Knowles, J.; Kell, D.B. Computational cluster validation in post-genomic data analysis. Bioinformatics 2005, 21, 3201–3212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunn, J.C. Well-separated clusters and optimal fuzzy partitions. J. Cybern. 1974, 4, 95–104. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Brock, G.; Pihur, V.; Datta, S.; Datta, S. clValid, an R package for cluster validation. J. Stat. Softw. 2008, 5, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Bezdek, J.C.; Keller, J.; Krisnapuram, R.; Pal, N. Fuzzy Models and Algorithms for Pattern Recognition and Image Processing; Springer Science & Business Media: Berlin, Germany, 1999; Volume 4. [Google Scholar]
- Scitovski, R.; Sabo, K.; Martínez Álvarez, F.; Ungar, S. Cluster Analysis and Applications; Springer International Publishing: Berlin, Germany, 2021. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 4th ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Vendramin, L.; Campello, R.J.; Hruschka, E.R. On the comparison of relative clustering validity criteria. In Proceedings of the 2009 SIAM International Conference on Data Mining, SIAM, Sparks, NV, USA, 30 April–2 May 2009; pp. 733–744. [Google Scholar]
- Gajawada, S.; Toshniwal, D. Hybrid cluster validation techniques. In Advances in Computer Science, Engineering & Applications; Springer: Berlin, Germany, 2012; pp. 267–273. [Google Scholar]
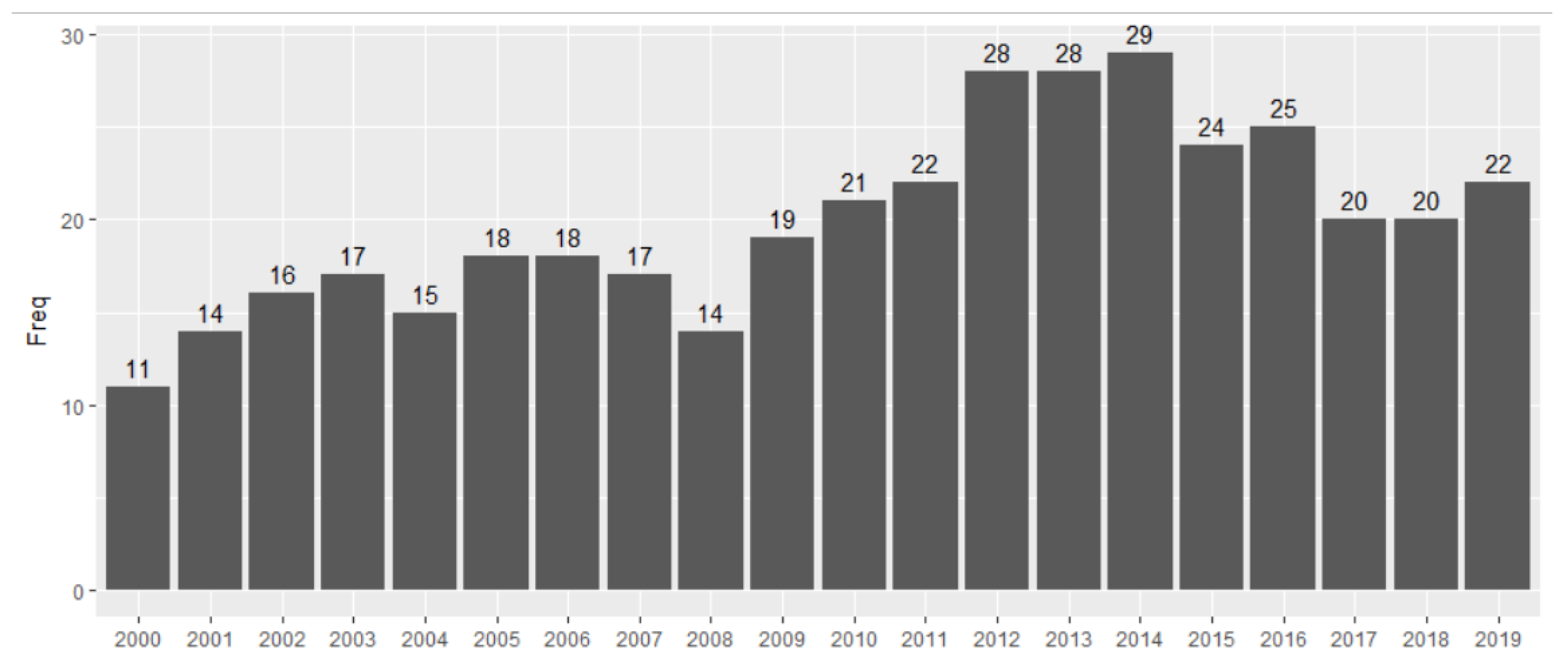


| Connectivity | Dunn Index | Silhouette Width | ||||
|---|---|---|---|---|---|---|
| Year | k | Method | k | Method | k | Method |
| 2000 | 2 | hierarchical | 5 | hierarchical | 2 | hierarchical |
| 2001 | 2 | hierarchical | 4 | pam | 2 | hierarchical |
| 2002 | 2 | hierarchical | 2 | hierarchical | 2 | hierarchical |
| 2003 | 2 | hierarchical | 5 | kmeans | 3 | hierarchical |
| 2004 | 2 | hierarchical | 3 | hierarchical | 2 | hierarchical |
| 2005 | 2 | hierarchical | 5 | hierarchical | 2 | hierarchical |
| 2006 | 2 | hierarchical | 4 | hierarchical | 2 | hierarchical |
| 2007 | 2 | hierarchical | 5 | pam | 2 | hierarchical |
| 2008 | 2 | pam | 5 | hierarchical | 2 | pam |
| 2009 | 2 | hierarchical | 4 | kmeans | 2 | hierarchical |
| 2010 | 2 | hierarchical | 4 | hierarchical | 2 | kmeans |
| 2011 | 2 | kmeans | 5 | pam | 2 | kmeans |
| 2012 | 2 | hierarchical | 4 | hierarchical | 2 | kmeans |
| 2013 | 2 | hierarchical | 5 | kmeans | 2 | kmeans |
| 2014 | 2 | hierarchical | 5 | pam | 2 | hierarchical |
| 2015 | 2 | hierarchical | 5 | pam | 2 | hierarchical |
| 2016 | 2 | fanny | 5 | kmeans | 2 | kmeans |
| 2017 | 2 | hierarchical | 3 | kmeans | 2 | hierarchical |
| 2018 | 2 | pam | 5 | hierarchical | 2 | pam |
| 2019 | 2 | pam | 5 | kmeans | 2 | pam |
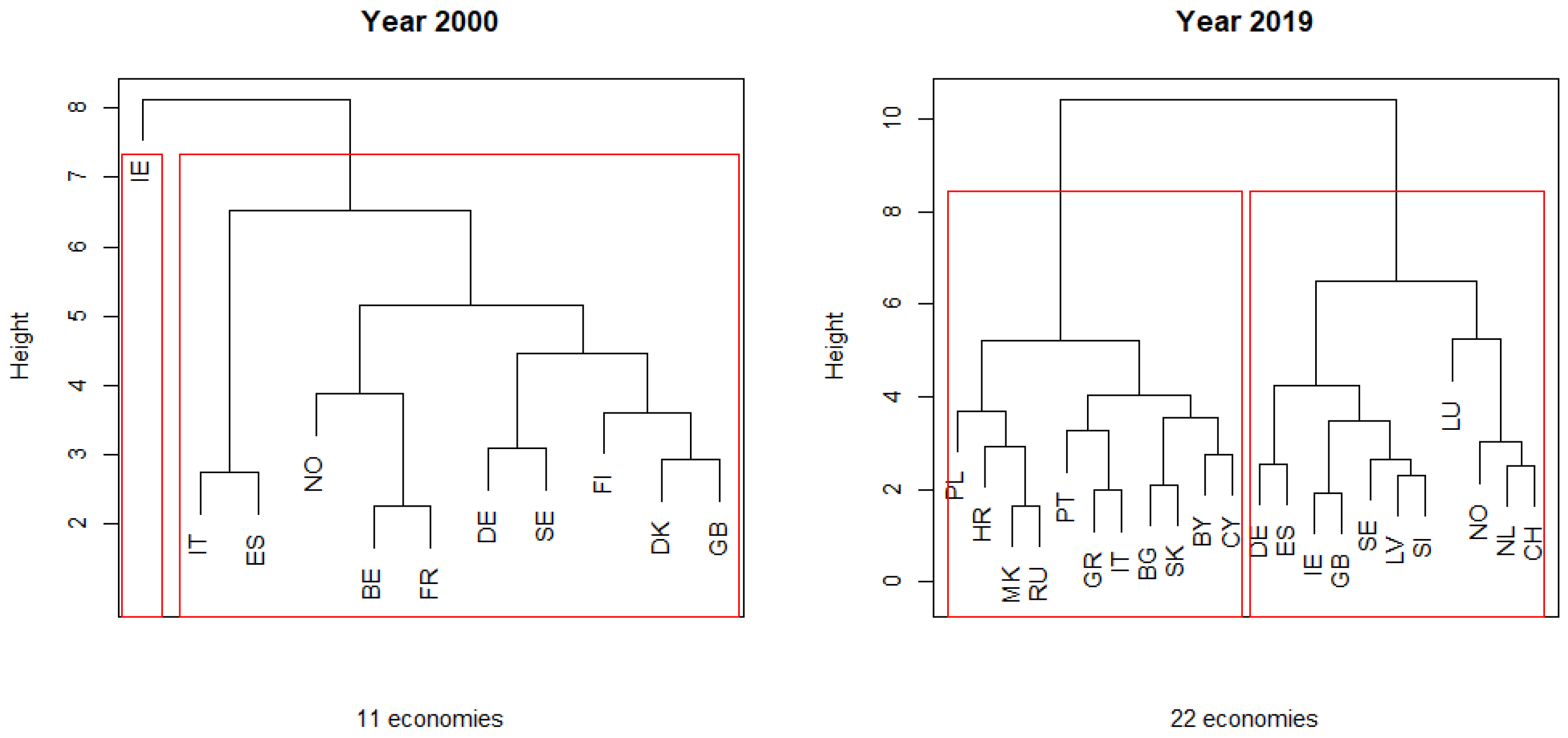
| Year | Cluster 1 | Cluster 2 | Year | Cluster 1 | Cluster 2 |
|---|---|---|---|---|---|
| 2000 (2.92) | BE, DK, FI, FR, DE, IT, NO, ES, SE, GB (2.88) | IE (3.34) | 2010 (2.67) | BA, HR, FR, GR, HU, IT, MK, ME, NO, PT, RU, SI, ES, SE, GB (2.55) | FI, DE, IS, IE, LV, CH (2.99) |
| 2001 (2.85) | HU, IT, NO, PT, ES, SE (2.61) | BE, DK, FI, FR, DE, IE, NL, GB (3.04) | 2011 (2.68) | BA, HR, CZ, FI, FR, DE, GR, HU, IE, LV, LT, NO, PL, PT, RU, SK, SI, ES, SE, GB (2.63) | NL, CH (3.24) |
| 2002 (2.72) | BE, HR, HU, NO, SI, SE (2.50) | DK, FI, FR, DE, IS, IE, NL, ES, CH, GB (2.85) | 2012 (2.76) | BA, HR, GR, HU, IT, LT, PL, PT, RO, RU, SK, SI, ES, SE (2.53) | AT, BE, CH, DK, EE, FI, FR, DE, IE, LV, MK, NL, NO, GB (2.99) |
| 2003 (2.71) | HR, GR, IT, NO, SI, SE (2.49) | BE, DK, FI, FR, DE, IS, IE, NL, ES, CH, GB (2.84) | 2013 (2.74) | BA, BE, CZ, DE, EE, ES, FR, GB, GR, HR, HU, IE, IT, LT, LU, MK, NO, PL, PT, RO, RU, SK, SE, SI (2.67) | CH, FI, LV, NL (3.18) |
| 2004 (2.70) | HR, HU, PL, SI (2.47) | BE, DK, FI, DE, GR, IS, IE, NL, NO, PT, ES (2.78) | 2014 (2.81) | BA, HR, GR, HU, IT, NA, PL, RO, RU, SK, SI, ES, GB (2.58) | AT, BE, DK, EE, FI, FR, DE, IE, LV, LT, LU, NL, NO, PT, SE, CH (3.00) |
| 2005 (2.79) | HR, HU, IT, SI (2.41) | AT, BE, DK, FI, DE, GR, IS, IE, LV, NL, NO, ES, CH, GB (2.90) | 2015 (2.76) | BG, ES, GR, HR, HU, IT, RO, SK, (2.37) | BE, CH, DE, EE, FI, GB, IE, LU, LV, MK, NL, NO, PL, PT, SE, SI (2.95) |
| 2006 (2.81) | HR, CZ, HU, IT, LV, RU, SI (2.60) | BE, DK, FI, DE, GR, IS, IE, NL, NO, ES, GB (2.94) | 2016 (2.73) | AT, FI, FR, DE, IE, LV, LU, PT, ES, BG, HR, CY, GR, HU, IT, MK, PL, RU, SK, SI, SE, GB (2.64) | CH, EE, NL (3.40) |
| 2007 (2.88) | HR, GR, IT, RO, RU, RS, SI, ES (2.64) | AT, BE, DK, FI, IS, IE, NO, CH, GB (3.09) | 2017 (2.78) | BA, BG, HR, CY, GR, IT, PL, SK, ES (2.52) | EE, NL, FR, DE, IE, LV, LU, SI, SE, CH, GB (2.99) |
| 2008 (2.73) | BA, HR, GR, IT, MK, RU, RS, SI, ES (2.59) | DK, FI, DE, IE, NO (2.98) | 2018 (2.78) | BG, HR, GR, IT, PL, RU, SK (2.46) | AT, CY, FR, DE, IE, LV, LU, NL, SI, ES, SE, CH, GB (2.96) |
| 2009 (2.73) | BA, HR, GR, HU, IT, LV, RU, RS, SI, ES, GB (2.52) | BE, DK, FI, DE, IS, NL, NO, CH (3.02) | 2019 (2.85) | BY, BG, HR, CY, GR, IT, MK, PL, PT, RU, SK (2.61) | DE, IE, LV, LU, NL, NO, SI, ES, SE, CH, GB (3.10) |
| Year | Cluster 1 | Cluster 2 | All Economies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Av. | StD | CV | # | Av. | StD | CV | # | Av. | StD | CV | |
| 2000 | 10 | 2.88 | 0.175 | 6.1 | 1 | 3.34 | — | — | 11 | 2.92 | 0.216 | 7.4 |
| 2001 | 6 | 2.61 | 0.153 | 5.9 | 8 | 3.04 | 0.07 | 2.3 | 14 | 2.85 | 0.244 | 8.6 |
| 2002 | 6 | 2.50 | 0.118 | 4.7 | 10 | 2.85 | 0.099 | 3.5 | 16 | 2.72 | 0.203 | 7.5 |
| 2003 | 5 | 2.49 | 0.065 | 2.6 | 11 | 2.84 | 0.123 | 4.3 | 16 | 2.71 | 0.203 | 7.5 |
| 2004 | 4 | 2.47 | 0.048 | 1.9 | 11 | 2.78 | 0.187 | 6.7 | 15 | 2.70 | 0.221 | 8.2 |
| 2005 | 4 | 2.41 | 0.057 | 2.4 | 14 | 2.90 | 0.156 | 5.4 | 18 | 2.79 | 0.250 | 9.0 |
| 2006 | 7 | 2.60 | 0.071 | 2.7 | 11 | 2.94 | 0.144 | 4.9 | 18 | 2.81 | 0.209 | 7.4 |
| 2007 | 8 | 2.64 | 0.088 | 3.3 | 9 | 3.09 | 0.074 | 2.4 | 17 | 2.88 | 0.243 | 8.4 |
| 2008 | 9 | 2.59 | 0.161 | 6.2 | 5 | 2.98 | 0.049 | 1.6 | 14 | 2.73 | 0.234 | 8.6 |
| 2009 | 11 | 2.52 | 0.131 | 5.2 | 8 | 3.02 | 0.173 | 5.7 | 19 | 2.73 | 0.294 | 10.8 |
| 2010 | 15 | 2.55 | 0.181 | 7.1 | 6 | 2.99 | 0.118 | 3.9 | 21 | 2.67 | 0.261 | 9.8 |
| 2011 | 20 | 2.63 | 0.210 | 8.8 | 2 | 3.24 | 0.061 | 1.9 | 22 | 2.68 | 0.272 | 10.1 |
| 2012 | 14 | 2.53 | 0.145 | 5.7 | 14 | 2.99 | 0.178 | 6.0 | 28 | 2.76 | 0.286 | 10.4 |
| 2013 | 24 | 2.67 | 0.229 | 8.6 | 4 | 3.18 | 0.133 | 4.2 | 28 | 2.74 | 0.283 | 10.3 |
| 2014 | 13 | 2.58 | 0.158 | 6.1 | 16 | 3.00 | 0.166 | 5.5 | 29 | 2.81 | 0.267 | 9.5 |
| 2015 | 8 | 2.37 | 0.126 | 5.3 | 16 | 2.95 | 0.253 | 8.6 | 24 | 2.76 | 0.352 | 12.8 |
| 2016 | 22 | 2.64 | 0.233 | 8.8 | 3 | 3.40 | 0.095 | 2.8 | 25 | 2.73 | 0.333 | 12.2 |
| 2017 | 9 | 2.52 | 0.137 | 5.4 | 11 | 2.99 | 0.278 | 9.3 | 20 | 2.78 | 0.322 | 11.6 |
| 2018 | 7 | 2.46 | 0.200 | 8.1 | 13 | 2.96 | 0.206 | 7.0 | 20 | 2.78 | 0.319 | 11.5 |
| 2019 | 11 | 2.61 | 0.115 | 4.4 | 11 | 3.10 | 0.202 | 7.1 | 22 | 2.85 | 0.298 | 10.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa e Silva, E.; Correia, A.; Borges, A. Unveiling the Dynamics of the European Entrepreneurial Framework Conditions over the Last Two Decades: A Cluster Analysis. Axioms 2021, 10, 149. https://doi.org/10.3390/axioms10030149
Costa e Silva E, Correia A, Borges A. Unveiling the Dynamics of the European Entrepreneurial Framework Conditions over the Last Two Decades: A Cluster Analysis. Axioms. 2021; 10(3):149. https://doi.org/10.3390/axioms10030149
Chicago/Turabian StyleCosta e Silva, Eliana, Aldina Correia, and Ana Borges. 2021. "Unveiling the Dynamics of the European Entrepreneurial Framework Conditions over the Last Two Decades: A Cluster Analysis" Axioms 10, no. 3: 149. https://doi.org/10.3390/axioms10030149
APA StyleCosta e Silva, E., Correia, A., & Borges, A. (2021). Unveiling the Dynamics of the European Entrepreneurial Framework Conditions over the Last Two Decades: A Cluster Analysis. Axioms, 10(3), 149. https://doi.org/10.3390/axioms10030149








