Null Darboux Curve Pairs in Minkowski 3-Space

Abstract

Based on the fundamental theories of null curves in Minkowski 3-space, the null Darboux mate curves of a null curve are defined which can be regarded as a kind of extension for Bertrand curves and Mannheim curves in Minkowski 3-space. The relationships of null Darboux curve pairs are explored and their expression forms are presented explicitly.

1. Introduction

The associated curves or the curve pairs, i.e., two curves related to each other at the corresponding points, play important roles in the curve theory of differential geometry. The most fascinating examples are Bertrand curves and Mannheim curves in three-dimensional space. Taking Euclidean 3-space as an example, a Bertrand curve shares its normal line with another curve and its curvature $\kappa$, torsion $\tau$ satisfy $\lambda \kappa +\mu \tau =1$ for some constants $\lambda$ and $\mu$ [1]; the principal normal line of a Mannheim curve coincides with the binormal line of another curve and its curvature $\kappa$, torsion $\tau$ satisfy $\kappa =\lambda ({\kappa }^2+{\tau }^2)$ for some constant $\lambda$ [2]. Over years, many mathematicians extended the notions of curve pairs, such as Bertrand curve, Mannheim curve, evolute and involute and so on from Euclidean space to Lorentz–Minkowski space [3,4,5].

The Darboux vector comes to mind naturally when we consider the fact that most curve pairs are proposed from the frame of a space curve. The Darboux vector of a space curve describes the direction of rotation axis of a Cartan frame. Explicitly, for a curve $r\left(s\right)$ framed by $\left\{T\right(s),N(s),B(s\left)\right\}$ in three-dimensional space, the Darboux vector $D\left(s\right)$ is the axis around which the Frenet frame rotates when $r\left(s\right)$ does real-time spirals, and $D\left(s\right)$ satisfies Darboux equations as follows

$$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)=D\left(s\right)\times T\left(s\right),\hfill \\ N^{\prime }\left(s\right)=D\left(s\right)\times N\left(s\right),\hfill \\ B^{\prime }\left(s\right)=D\left(s\right)\times B\left(s\right).\hfill \end{array}\right.$$

Motivated by the definitions of Bertrand curve and Mannheim curve, we can consider another kind of associated curve by setting a condition that two space curves share the same Darboux vector field at the corresponding points in Minkowski 3-space. It is well known that there are three kinds of typical vectors, i.e., space-like, time-like and null (light-like) vectors, and the curves are classified into space-like, time-like and null (light-like) curves according to the causal character of their tangent vectors, correspondingly. Among them, the null curve is quite different because the norm of its tangent vector vanishes everywhere [6,7,8].

One of the authors found a kind of representation form of null curves and some special null curves or curve pairs are discussed [5]. Based on previous works, the null Darboux curve pairs in three-dimensional Minkowski space are investigated. In Section 2, some basic facts for space-like, time-like and null (light-like) curves are recalled. Meanwhile, the null Darboux curve and its Darboux mate curve are defined explicitly. In Section 3, Section 4 and Section 5, the space-like Darboux mate curves, time-like Darboux mate curves and null Darboux mate curves of a null curve are studied, respectively.

All geometric objects are smooth and regular unless otherwise stated.

2. Preliminaries

Let ${\mathbb{E}}_1^3$ be a Minkowski 3-space with natural Lorentzian metric

$$\langle ·,·\rangle =d{x}_1^2+d{x}_2^2-d{x}_3^2$$

in terms of the natural coordinate system $(x_1,x_2,x_3)$. Let $a=(a_1,a_2,a_3)$ and $b=(b_1,b_2,b_3)$ be vectors in ${\mathbb{E}}_1^3$. Then their scalar product is given by

$$\langle a,b\rangle =a_1{b}_1+a_2{b}_2-a_3{b}_3$$

and the exterior product by

$$a\times b=\left|\begin{array}{ccc}{e}_1& e_2& e_3\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|=\left(\left|\begin{array}{cc}{a}_2& a_3\\ b_2& b_3\end{array}\right|,\left|\begin{array}{cc}{a}_3& a_1\\ b_3& b_1\end{array}\right|,-\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|\right),$$

where $\{e_1,e_2,e_3\}$ is an orthonormal basis in ${\mathbb{E}}_1^3$. One can have

$$\begin{array}{c}\hfill e_1\times e_2=-e_3,e_2\times e_3=e_1,e_3\times e_1=e_2.\end{array}$$

A vector $\upsilon$ ∈ ${\mathbb{E}}_1^3$ is said to be space-like if $\langle \upsilon ,\upsilon \rangle >0$ or $\upsilon =0$; time-like if $\langle \upsilon ,\upsilon \rangle <0$; null (light-like) if $\langle \upsilon ,\upsilon \rangle =0$ respectively, which is called the causal character of the vector. An arbitrary curve $r\left(t\right)$ is space-like, time-like or light-like if its velocity vector is space-like, time-like or light-like. At the same time, the space-like curves in ${\mathbb{E}}_1^3$ can be classified into the first kind space-like curve, the second kind space-like curve and the pseudo null curve according to the causal character of their principal normal vectors [6,9].

Proposition 1.

([5]) Let $r\left(s\right)$ be a non-null curve parameterized by arc length s and framed by $\{T,N,B\}$ in ${\mathbb{E}}_1^3$.

• If $\langle r^{″}\left(s\right),r^{″}\left(s\right)\rangle \ne 0$, the following Frenet equations are satisfied

  $$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)=\kappa \left(s\right)N\left(s\right),\hfill \\ N^{\prime }\left(s\right)=-{\epsilon }_1\kappa \left(s\right)T\left(s\right)+\tau \left(s\right)B\left(s\right),\hfill \\ B^{\prime }\left(s\right)={\epsilon }_2\tau \left(s\right)N\left(s\right),\hfill \end{array}\right.$$

  where $\langle T,T\rangle ={\epsilon }_2$, $\langle N,N\rangle ={\epsilon }_1{\epsilon }_2$, $\langle B,B\rangle =-{\epsilon }_1$, $\langle T,N\rangle =\langle T,B\rangle =\langle B,N\rangle =0$, ${\epsilon }_i=\pm 1,(i=1,2)$. When ${\epsilon }_1=1,{\epsilon }_2=1$, $r\left(s\right)$ is a first kind space-like curve; when ${\epsilon }_1=-1,{\epsilon }_2=1$, $r\left(s\right)$ is a second kind space-like curve; when ${\epsilon }_1=-1,{\epsilon }_2=-1$, $r\left(s\right)$ is a time-like curve. The functions $\kappa \left(s\right)$ and $\tau \left(s\right)$ are called the curvature and torsion functions of $r\left(s\right)$, respectively.
• If $\langle r^{″}\left(s\right),r^{″}\left(s\right)\rangle =0$, $r\left(s\right)$ is a pseudo null curve, the Frenet equations are given by

  $$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)=N\left(s\right),\hfill \\ N^{\prime }\left(s\right)=\kappa \left(s\right)N\left(s\right),\hfill \\ B^{\prime }\left(s\right)=-T\left(s\right)-\kappa \left(s\right)B\left(s\right),\hfill \end{array}\right.$$

  where $\langle T,T\rangle =\langle N,B\rangle =1$, $\langle N,N\rangle =\langle B,B\rangle =\langle T,N\rangle =\langle T,B\rangle =0$. The function $\kappa \left(s\right)$ is called the curvature function of $r\left(s\right)$.

Proposition 2.

([5]) Let $r\left(s\right)$ be a null curve parameterized by null arc length s, i.e., $\langle r^{″}\left(s\right), r^{″}\left(s\right)\rangle =1$, and framed by $\{T,N,B\}$ in ${\mathbb{E}}_1^3$. Then there exists a unique frame field $\{T,N,B\}$ such that

$$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)=N\left(s\right),\hfill \\ N^{\prime }\left(s\right)=\kappa \left(s\right)T\left(s\right)-B\left(s\right),\hfill \\ B^{\prime }\left(s\right)=-\kappa \left(s\right)N\left(s\right),\hfill \end{array}\right.$$

where the function $\kappa \left(s\right)$ is called the null curvature function of $r\left(s\right)$.

Remark 1.

Hereafter, a null geodesic in ${\mathbb{E}}_1^3$ is excluded.

Proposition 3.

([5]) Let $r\left(s\right)$ be a null curve parameterized by null arc length s in ${\mathbb{E}}_1^3$. Then $r\left(s\right)$ can be written as

$$r\left(s\right)=\int \frac{f}{2f^{\prime }}(f-f^{-1},2,f+f^{-1})ds,$$

where $f\left(s\right)$ is the structure function which satisfies

$$\kappa \left(s\right)=\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{\left[{(log{f}^{\prime })}^{\prime }\right]}^{\prime }.$$

Similar to the definitions of Bertrand curve and Mannheim curve, we can define a new kind of curve pair with the Darboux vector of a null curve as follows:

Definition 1.

Let $r\left(s\right)$ be a null curve with Darboux vector field $D\left(s\right)$, and $\tilde{r}\left(s\right)$ another space curve with Darboux vector field $\tilde{D}\left(s\right)$ in ${\mathbb{E}}_1^3$. If $\tilde{r}\left(s\right)$ shares the same Darboux vector field as $r\left(s\right)$, then $r\left(s\right)$ is called a null Darboux curve and $\tilde{r}\left(s\right)$ its Darboux mate curve.

Remark 2.

A null Darboux curve $r\left(s\right)$ and its Darboux mate curve $\tilde{r}\left(s\right)$ can be related by

$$\tilde{r}\left(s\right)=r\left(s\right)+\lambda \left(s\right)D\left(s\right)$$

for some non-zero function $\lambda \left(s\right),$ which is called the distance function between $r\left(s\right)$ and $\tilde{r}\left(s\right)$.

Remark 3.

For convenience, we recall the Darboux vector fields of space curves in ${\mathbb{E}}_1^3$ as follows:

• $D\left(s\right)=-\tau \left(s\right)T\left(s\right)+\kappa \left(s\right)B\left(s\right)$, if $r\left(s\right)$ is a first kind space-like curve;
• $D\left(s\right)=\tau \left(s\right)T\left(s\right)-\kappa \left(s\right)B\left(s\right)$, if $r\left(s\right)$ is a second kind space-like curve;
• $D\left(s\right)=\kappa \left(s\right)T\left(s\right)-N\left(s\right)$, if $r\left(s\right)$ is a pseudo null curve;
• $D\left(s\right)=\tau \left(s\right)T\left(s\right)+\kappa \left(s\right)B\left(s\right)$, if $r\left(s\right)$ is a time-like curve;
• $D\left(s\right)=-\kappa \left(s\right)T\left(s\right)-B\left(s\right)$, if $r\left(s\right)$ is a null curve.

3. Null Darboux Curve and Its Space-Like Darboux Mate Curves

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its space-like Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. From Remark 2, $\tilde{r}\left(s\right)$ can be expressed by

$$\tilde{r}\left(s\right)=r\left(s\right)+\lambda \left(s\right)D\left(s\right),$$

(1)

where $\lambda \left(s\right)$ is the distance function.

Taking derivative on both sides of (1) with respect to the null arc length s, we get

$$\tilde{T}\frac{d\tilde{s}}{ds}=[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B.$$

(2)

Taking the scalar product on both sides of (2), we have

$${\left(\frac{d\tilde{s}}{ds}\right)}^2=2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1].$$

(3)

This means that

$${ϵ}_1\frac{d\tilde{s}}{ds}=\sqrt{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]},({ϵ}_1=\pm 1).$$

(4)

Therefore, (2) can be simplified with the help of (4) as

$${ϵ}_1\tilde{T}=\frac{[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B}{\sqrt{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]}}.$$

(5)

3.1. The First Kind Space-Like Darboux Mate Curves

Let $\tilde{r}\left(s\right)$ be the first kind space-like Darboux mate curve of $r\left(s\right)$. From Definition 1 and Remark 3, we know $\tilde{D}={ϵ}_{0}D,({ϵ}_0=\pm 1)$, i.e.,

$$-\tilde{\tau }\tilde{T}+\tilde{\kappa }\tilde{B}={ϵ}_0(-\kappa T-B).$$

(6)

Taking the scalar product on both sides of (6), we obtain

$${\tilde{\tau }}^2-{\tilde{\kappa }}^2=2\kappa ,$$

(7)

where $\tilde{\kappa }$, $\tilde{\tau }$ are the curvature and torsion of $\tilde{r}\left(s\right)$, $\kappa$ is the null curvature of $r\left(s\right)$.

Taking the scalar product on both sides of (5) and (6) , we have

$${ϵ}_2\tilde{\tau }=\frac{1-2{\lambda }^{\prime }\kappa -\lambda {\kappa }^{\prime }}{\sqrt{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]}},({ϵ}_2={ϵ}_0{ϵ}_1=\pm 1).$$

(8)

From (7) and (8), we also have

$${ϵ}_3\tilde{\kappa }=\frac{1-\lambda {\kappa }^{\prime }}{\sqrt{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]}},({ϵ}_3=\pm 1).$$

(9)

Substituting (5), (8) and (9) into (6), then $\tilde{B}$ can be written as

$${ϵ}_4\tilde{B}=\frac{[1-{\left(\lambda \kappa \right)}^{\prime }]T+{\lambda }^{\prime }B}{\sqrt{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]}},({ϵ}_4={ϵ}_0{ϵ}_3=\pm 1).$$

(10)

Taking the exterior product on both sides of (5) and (10), we get

$$\tilde{N}={ϵ}_1{ϵ}_{4}N.$$

(11)

Differentiating (11) with respect to the null arc length s, we get

$$(-\tilde{\kappa }\tilde{T}+\tilde{\tau }\tilde{B})\frac{d\tilde{s}}{ds}={ϵ}_1{ϵ}_4(\kappa T-B).$$

(12)

From (12), we obtain ${\left(\frac{d\tilde{s}}{ds}\right)}^2=1$. Then from (3), we have

$$2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]=1.$$

(13)

Consequently, (5) can be simplified as

$${ϵ}_1\tilde{T}=[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B.$$

(14)

Differentiating (14) with respect to the null arc length s, we get

$$\tilde{\kappa }\tilde{N}={(-\lambda \kappa )}^{″}T+(1-\lambda {\kappa }^{\prime })N-{\lambda }^{″}B.$$

(15)

Considering (9), (11) and (15), we have ${ϵ}_0={ϵ}_1$, ${\lambda }^{″}=0$ and ${\left(\lambda \kappa \right)}^{″}=0$. Thus $\lambda \left(s\right)=as+b,(a\ne 0,b\in \mathbb{R}).$ Through appropriate transformation, we can let $b=0$. Then from (13), the null curvature $\kappa \left(s\right)$ can be written as

$$\kappa \left(s\right)=\frac{c}{s}+\frac{2a+1}{2a^2},(c\in \mathbb{R}).$$

From (8) and (9), the curvature and the torsion of $\tilde{r}\left(s\right)$ can be expressed as

$$\tilde{\kappa }\left(s\right)={ϵ}_3(\frac{ac}{s}+1);\tilde{\tau }\left(s\right)=-(\frac{ac}{s}+\frac{a+1}{a}).$$

Meanwhile, the frame $\{\tilde{T},\tilde{N},\tilde{B}\}$ can be expressed by $\{T,N,B\}$ as follows

$$\left\{\begin{array}{c}\tilde{T}=-{ϵ}_0(\frac{1}{2a}T+aB),\hfill \\ \tilde{N}={ϵ}_{3}N,\hfill \\ \tilde{B}=-{ϵ}_0{ϵ}_3(\frac{1}{2a}T-aB),\hfill \end{array}\right.$$

where ${ϵ}_0,{ϵ}_3=\pm 1.$

Based on the above discussions, we have the following conclusions.

Theorem 1.

The distance function $\lambda \left(s\right)$ between a null Darboux curve and its first kind space-like Darboux mate curve is a linear function of s, i.e.,

$$\lambda \left(s\right)=as+b,(a\ne 0,b\in \mathbb{R}).$$

Theorem 2.

Let $r\left(s\right)$ be a null Darboux curve with a first kind space-like Darboux mate curve. Then the null curvature $\kappa \left(s\right)$ of $r\left(s\right)$ can be expressed as

$$\kappa \left(s\right)=\frac{c}{s}+\frac{2a+1}{2a^2},(0\ne a={\lambda }^{\prime }\left(s\right),c\in \mathbb{R}).$$

Theorem 3.

Let $\tilde{r}\left(s\right)$ be a first kind space-like Darboux mate curve of a null Darboux curve. Then the curvature $\tilde{\kappa }\left(s\right)$ and the torsion $\tilde{\tau }\left(s\right)$ are

$$\tilde{\kappa }\left(s\right)={ϵ}_3(\frac{ac}{s}+1);\tilde{\tau }\left(s\right)=-(\frac{ac}{s}+\frac{a+1}{a}),$$

where $0\ne a={\lambda }^{\prime }\left(s\right),c\in \mathbb{R},$${ϵ}_3=\pm 1$.

Theorem 4.

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its first kind space-like Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. Then

$$\left(\begin{array}{c}\tilde{T}\\ \tilde{N}\\ \tilde{B}\end{array}\right)=\left(\begin{array}{ccc}-\frac{1}{2a}{ϵ}_0& 0& -a{ϵ}_0\\ 0& {ϵ}_3& 0\\ -\frac{1}{2a}{ϵ}_0{ϵ}_3& 0& a{ϵ}_0{ϵ}_3\end{array}\right)\left(\begin{array}{c}T\\ N\\ B\end{array}\right),$$

where $0\ne a={\lambda }^{\prime }\left(s\right)\in \mathbb{R},$${ϵ}_0,{ϵ}_3=\pm 1.$

In the following, we explore the explicit representations of a null Darboux curve and its first kind space-like Darboux mate curve.

Theorem 5.

Let $r\left(s\right)$ be a null Darboux curve with a first kind space-like Darboux mate curve. Then it can be represented as

$$r\left(s\right)=C_1\int u^2\left(s\right)ds+C_2\int u\left(s\right)v\left(s\right)ds+C_3\int v^2\left(s\right)ds,$$

where $C_1,C_2,C_3\in {\mathbb{E}}_1^3$, $u\left(s\right)$ and $v\left(s\right)$ are given by (17) and (18).

Proof. 

From Theorem 2, the null curvature is $\kappa \left(s\right)=\frac{c}{s}+\frac{2a+1}{2a^2}$. Up to translation, we can let $\kappa \left(s\right)=\frac{c}{s}$; then, from Proposition 2, the curve $r\left(s\right)$ satisfies

$$s^2{r}^{\left(4\right)}-2cs{r}^{″}+c{r}^{\prime }=0.$$

(16)

Solving Equation (16), we get

$$r\left(s\right)=C_1\int u^2\left(s\right)ds+C_2\int u\left(s\right)v\left(s\right)ds+C_3\int v^2\left(s\right)ds,$$

where $C_1,C_2,C_3\in {\mathbb{E}}_1^3$, some functions $u\left(s\right)$ and $v\left(s\right)$ are given by

• if $c<0$, then

  $$\left\{\begin{array}{c}u\left(s\right)=\sqrt{s}{J}_1\left(\sqrt{-2cs}\right),\hfill \\ v\left(s\right)=\sqrt{s}{Y}_1\left(\sqrt{-2cs}\right),\hfill \end{array}\right.$$

  (17)
• if $c>0$, then

  $$\left\{\begin{array}{c}u\left(s\right)=Re\left(\sqrt{s}{Z}_1\left(i\sqrt{-2cs}\right)\right),\hfill \\ v\left(s\right)=Im\left(\sqrt{s}{Z}_1\left(i\sqrt{-2cs}\right)\right),\hfill \end{array}\right.$$

  (18)

$Z_1\left(s\right)$ is the cylinder function, $J_1\left(s\right)$ is the Bessel function of the first kind and $Y_1\left(s\right)$ is the Bessel function of the second kind [10]. □

Corollary 1.

Let $\tilde{r}\left(s\right)$ be the first kind space-like Darboux mate curve of a null Darboux curve $r\left(s\right)$. Then it can be represented as

$$\begin{array}{cc}\hfill \tilde{r}\left(s\right)=& C_1(\int u^2\left(s\right)ds+2as{u}^{\prime 2}\left(s\right)+2asu\left(s\right)u^{\prime \prime }\left(s\right)-2ac{u}^2\left(s\right))+\hfill \\ & C_2(\int u\left(s\right)v\left(s\right)ds+2as{u}^{\prime }\left(s\right)v^{\prime }\left(s\right)+as{u}^{\prime \prime }\left(s\right)v\left(s\right)+asu\left(s\right)v^{\prime \prime }\left(s\right)-2acu\left(s\right)v\left(s\right))+\hfill \\ & C_3(\int v^2\left(s\right)ds+2as{v}^{\prime 2}\left(s\right)+2asv\left(s\right)v^{\prime \prime }\left(s\right)-2ac{v}^2\left(s\right)),\hfill \end{array}$$

where $0\ne a={\lambda }^{\prime }\left(s\right),c\in \mathbb{R}$, $C_1,C_2,C_3\in {\mathbb{E}}_1^3$, $u\left(s\right)$ and $v\left(s\right)$ are stated as Theorem 5.

Proof. 

From the expression form of the null Darboux curve $r\left(s\right)$ in Theorem 5, through calculations, the Darboux vector $D\left(s\right)$ of $r\left(s\right)$ is obtained as

$$\begin{array}{cc}\hfill D\left(s\right)=& C_1(2u\left(s\right)u^{\prime \prime }\left(s\right)+2u^{\prime 2}\left(s\right)-\frac{2c{u}^2\left(s\right)}{s})+\hfill \\ & C_2(2u^{\prime }\left(s\right)v^{\prime }\left(s\right)+u^{\prime \prime }\left(s\right)v\left(s\right)+u\left(s\right)v^{\prime \prime }\left(s\right)-\frac{2cu\left(s\right)v\left(s\right)}{s})+\hfill \\ & C_3(2v\left(s\right)v^{\prime \prime }\left(s\right)+2v^{\prime 2}\left(s\right)-\frac{2c{v}^2\left(s\right)}{s}).\hfill \end{array}$$

From Theorem 1 and Remark 2, the conclusion can be achieved easily. □

3.2. The Second Kind Space-Like Darboux Mate Curves

Let $\tilde{r}\left(s\right)$ be the second kind space-like Darboux mate curve of $r\left(s\right)$. From Definition 1 and Remark 3, we know $\tilde{D}={ϵ}_{0}D,({ϵ}_0=\pm 1)$, i.e.,

$$\tilde{\tau }\tilde{T}-\tilde{\kappa }\tilde{B}={ϵ}_0(-\kappa T-B),$$

(19)

where $\tilde{\kappa }$, $\tilde{\tau }$ are the curvature and torsion of $\tilde{r}\left(s\right)$, $\kappa$ is the null curvature of $r\left(s\right)$.

Taking the scalar product on both sides of (19), we obtain

$${\tilde{\tau }}^2+{\tilde{\kappa }}^2=2\kappa .$$

Furthermore, by taking the scalar product on both sides of (5) and (19), we obtain

$${\tilde{\tau }}^2=\frac{{(2{\lambda }^{\prime }\kappa +\lambda {\kappa }^{\prime }-1)}^2}{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]};{\tilde{\kappa }}^2=\frac{-{(1-\lambda {\kappa }^{\prime })}^2}{2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]}.$$

From Equation (3), $2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]$ must be positive, we get $\tilde{\kappa }=0$ identically. In this case, $\tilde{r}\left(s\right)$ is a straight line which has no meaning.

Theorem 6.

A second kind space-like curve can not be the Darboux mate curve of a null Darboux curve.

3.3. The Pseudo Null Darboux Mate Curves

Let $\tilde{r}\left(s\right)$ be the pseudo null Darboux mate curve of $r\left(s\right)$. From Definition 1 and Remark 3, we know $\tilde{D}={ϵ}_{0}D,({ϵ}_0=\pm 1)$, i.e.,

$$\tilde{\kappa }\tilde{T}-\tilde{N}={ϵ}_0(-\kappa T-B),$$

(20)

where $\tilde{\kappa }$ is the curvature of $\tilde{r}\left(s\right)$, $\kappa$ is the null curvature of $r\left(s\right)$.

Taking the scalar product on both sides of (20), we obtain

$${\tilde{\kappa }}^2=2\kappa .$$

(21)

By taking the scalar product on both sides of (5) and (20), we obtain

$$2{\tilde{\kappa }}^2{\lambda }^{\prime }[{\left(\lambda \kappa \right)}^{\prime }-1]={(2{\lambda }^{\prime }\kappa +\lambda {\kappa }^{\prime }-1)}^2.$$

(22)

Substituting (21) into (22), after calculations, we obtain $1-\lambda {\kappa }^{\prime }=0.$ Then, (5) can be simplified as

$${ϵ}_1\tilde{T}=\frac{\kappa T+B}{\sqrt{2\kappa }}.$$

(23)

Differentiating (23) with respect to the null arc length s, we obtain

$${ϵ}_1\tilde{N}=\frac{{\kappa }^{\prime }}{4{\lambda }^{\prime }{\kappa }^2}(\kappa T-B).$$

(24)

Taking scalar product on both sides of (24), we obtain $0=-\frac{{\kappa }^{\prime 2}}{8{\lambda }^{\prime 2}{\kappa }^3},$ which means ${\kappa }^{\prime }=0$. From $1-\lambda {\kappa }^{\prime }=0$, it is a contradiction.

Theorem 7.

A pseudo null curve can not be the Darboux mate curve of a null Darboux curve.

4. Null Darboux Curve and Its Time-Like Darboux Mate Curves

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its time-like Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. From Remark 2, $\tilde{r}\left(s\right)$ can be expressed by

$$\tilde{r}\left(s\right)=r\left(s\right)+\lambda \left(s\right)D\left(s\right),$$

(25)

where $\lambda \left(s\right)$ is the distance function.

Taking derivative on both sides of (25) with respect to the null arc length s, we get

$$\tilde{T}\frac{d\tilde{s}}{ds}=[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B.$$

(26)

Taking the scalar product on both sides of (26), we have

$${(\frac{d\tilde{s}}{ds})}^2=2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }].$$

(27)

It means that

$${ϵ}_1\frac{d\tilde{s}}{ds}=\sqrt{2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]},({ϵ}_1=\pm 1).$$

(28)

Therefore, (26) can be simplified with the help of (28) as

$${ϵ}_1\tilde{T}=\frac{[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B}{\sqrt{2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]}}.$$

(29)

From Definition 1 and Remark 3, we know $\tilde{D}={ϵ}_{0}D,({ϵ}_0=\pm 1)$, i.e.,

$$\tilde{\tau }\tilde{T}+\tilde{\kappa }\tilde{B}={ϵ}_0(-\kappa T-B).$$

(30)

Taking the scalar product on both sides of (30), we obtain

$${\tilde{\kappa }}^2-{\tilde{\tau }}^2=2\kappa ,$$

(31)

where $\tilde{\kappa }$, $\tilde{\tau }$ are the curvature and torsion of $\tilde{r}\left(s\right)$, $\kappa$ is the null curvature of $r\left(s\right)$.

Taking the scalar product on both sides of (29) and (30), we have

$${ϵ}_2\tilde{\tau }=\frac{1-2{\lambda }^{\prime }\kappa -\lambda {\kappa }^{\prime }}{\sqrt{2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]}},({ϵ}_2={ϵ}_0{ϵ}_1=\pm 1).$$

(32)

From (31) and (32), we also have

$${ϵ}_3\tilde{\kappa }=\frac{1-\lambda {\kappa }^{\prime }}{\sqrt{2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]}},({ϵ}_3=\pm 1).$$

(33)

Substituting (29), (32) and (33) into (30), then $\tilde{B}$ can be written as

$${ϵ}_4\tilde{B}=\frac{[1-{\left(\lambda \kappa \right)}^{\prime }]T+{\lambda }^{\prime }B}{\sqrt{2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]}},({ϵ}_4={ϵ}_0{ϵ}_3=\pm 1).$$

(34)

Taking the exterior product on both sides of (29) and (34), we get

$$\tilde{N}=-{ϵ}_1{ϵ}_{4}N.$$

(35)

Differentiating (35) with respect to the null arc length s, we get

$$(\tilde{\kappa }\tilde{T}+\tilde{\tau }\tilde{B})\frac{d\tilde{s}}{ds}=-{ϵ}_1{ϵ}_4(\kappa T-B).$$

(36)

Taking the scalar product on both sides of (36), we obtain ${(\frac{d\tilde{s}}{ds})}^2=1$. Then from (27), we have

$$2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]=1.$$

(37)

Consequently, (29) can be simplified as

$${ϵ}_1\tilde{T}=[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B.$$

(38)

Taking derivative on both sides of (38) with respect to the null arc length s, we get

$$\tilde{\kappa }\tilde{N}={(-\lambda \kappa )}^{″}T+(1-\lambda {\kappa }^{\prime })N-{\lambda }^{″}B.$$

(39)

Considering (33), (35) and (39), we have ${ϵ}_0=-{ϵ}_1$, ${\lambda }^{″}=0$ and ${\left(\lambda \kappa \right)}^{″}=0$. Thus $\lambda \left(s\right)=as+b,(a\ne 0,b\in \mathbb{R}).$ Through appropriate transformation, we can let $b=0$. Then from (37), the null curvature $\kappa \left(s\right)$ can be written as

$$\kappa \left(s\right)=\frac{c}{s}+\frac{2a-1}{2a^2},(c\in \mathbb{R}).$$

From (32) and (33), the curvature and the torsion of $\tilde{r}\left(s\right)$ can be expressed as

$$\tilde{\kappa }\left(s\right)={ϵ}_3(\frac{ac}{s}+1);\tilde{\tau }\left(s\right)=-(\frac{ac}{s}+\frac{a-1}{a}).$$

Meanwhile, the frame $\{\tilde{T},\tilde{N},\tilde{B}\}$ can be expressed by $\{T,N,B\}$ as follows

$$\left\{\begin{array}{c}\tilde{T}=-{ϵ}_0(\frac{1}{2a}T-aB),\hfill \\ \tilde{N}={ϵ}_{3}N,\hfill \\ \tilde{B}={ϵ}_0{ϵ}_3(\frac{1}{2a}T+aB),\hfill \end{array}\right.$$

where ${ϵ}_0,{ϵ}_3=\pm 1.$

Based on the above discussions, we have the following results.

Theorem 8.

The distance function $\lambda \left(s\right)$ between a null Darboux curve and its time-like Darboux mate curve is a linear function of s, i.e.,

$$\lambda \left(s\right)=as+b,(a\ne 0,b\in \mathbb{R}).$$

Theorem 9.

Let $r\left(s\right)$ be a null Darboux curve with a time-like Darboux mate curve. Then the null curvature $\kappa \left(s\right)$ of $r\left(s\right)$ can be expressed as

$$\kappa \left(s\right)=\frac{c}{s}+\frac{2a-1}{2a^2},(0\ne a={\lambda }^{\prime }\left(s\right),c\in \mathbb{R}).$$

Theorem 10.

Let $\tilde{r}\left(s\right)$ be a time-like Darboux mate curve of a null Darboux curve. Then the curvature $\tilde{\kappa }\left(s\right)$ and the torsion $\tilde{\tau }\left(s\right)$ are

$$\tilde{\kappa }\left(s\right)={ϵ}_3(\frac{ac}{s}+1);\tilde{\tau }\left(s\right)=-(\frac{ac}{s}+\frac{a-1}{a}),$$

where $0\ne a={\lambda }^{\prime }\left(s\right),c\in \mathbb{R},{ϵ}_3=\pm 1$.

Theorem 11.

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its time-like Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. Then

$$\left(\begin{array}{c}\tilde{T}\\ \tilde{N}\\ \tilde{B}\end{array}\right)=\left(\begin{array}{ccc}-\frac{1}{2a}{ϵ}_0& 0& a{ϵ}_0\\ 0& {ϵ}_3& 0\\ \frac{1}{2a}{ϵ}_0{ϵ}_3& 0& a{ϵ}_0{ϵ}_3\end{array}\right)\left(\begin{array}{c}T\\ N\\ B\end{array}\right),$$

where $0\ne a={\lambda }^{\prime }\left(s\right)\in \mathbb{R},{ϵ}_0,{ϵ}_3=\pm 1.$

Remark 4.

The explicit representations of a null Darboux curve and its time-like Darboux mate curve are same as those in Theorem 5 and Corollary 1, we omit the corresponding proofs here.

5. Null Darboux Curve and Its Null Darboux Mate Curves

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its null Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. From Definition 1 and Remark 3, we know $\tilde{D}={ϵ}_{0}D,({ϵ}_0=\pm 1)$, i.e.,

$$-\tilde{\kappa }\tilde{T}-\tilde{B}={ϵ}_0(-\kappa T-B).$$

(40)

Taking the scalar product on both sides of (40), we obtain $\tilde{\kappa }=\kappa ,$ where $\kappa$ and $\tilde{\kappa }$ are the null curvatures of $r\left(s\right)$ and $\tilde{r}\left(s\right)$, respectively.

Meanwhile, from Remark 2, $\tilde{r}\left(s\right)$ can be expressed by

$$\tilde{r}\left(s\right)=r\left(s\right)+\lambda \left(s\right)D\left(s\right),$$

(41)

where $\lambda \left(s\right)$ is the distance function.

Taking derivative on both sides of (41) with respect to the null arc length s, we get

$$\tilde{T}\frac{d\tilde{s}}{ds}=[1-{\left(\lambda \kappa \right)}^{\prime }]T-{\lambda }^{\prime }B.$$

(42)

Taking the scalar product on both sides of (42), we get $2{\lambda }^{\prime }[1-{\left(\lambda \kappa \right)}^{\prime }]=0.$

We now consider the open subset $\mathcal{O}=\{{\lambda }^{\prime }\ne 0\}$. Suppose that $\mathcal{O}$ is not empty. On $\mathcal{O}$, $1-{\left(\lambda \kappa \right)}^{\prime }=0$, then (42) can be written as

$$\tilde{T}\frac{d\tilde{s}}{ds}=-{\lambda }^{\prime }B.$$

(43)

Taking the scalar product on both sides of (40) and (43), we obtain $\frac{d\tilde{s}}{ds}=-{ϵ}_0{\lambda }^{\prime }\kappa$. Thus, $\tilde{T}$ can be expressed as

$$\tilde{T}=\frac{{ϵ}_0}{\kappa }B.$$

(44)

Differentiating (44) with respect to the null arc length s, we have

$$\tilde{N}=\frac{1}{{\lambda }^{\prime }\kappa }N+\frac{{\kappa }^{\prime }}{{\lambda }^{\prime }{\kappa }^3}B.$$

(45)

From (40), (44) and $\tilde{\kappa }=\kappa$, we obtain

$$\tilde{B}={ϵ}_0\kappa T.$$

(46)

Taking the exterior product on both sides of (44) and (46), we have

$$\tilde{N}=-N.$$

(47)

From (45) and (47), we know ${\kappa }^{\prime }=0$ and ${\lambda }^{\prime }\kappa =-1.$ Those follow that $1-{\left(\lambda \kappa \right)}^{\prime }=2,$ which contradicts with the condition $1-{\left(\lambda \kappa \right)}^{\prime }=0$. Thus, $\mathcal{O}$ is empty, i.e., ${\lambda }^{\prime }\equiv 0$, $\lambda$ is a non-zero constant. Then (42) can be simplified as

$$\tilde{T}\frac{d\tilde{s}}{ds}=(1-\lambda {\kappa }^{\prime })T.$$

(48)

By taking the scalar product on both sides of (40) and (48), we obtain ${ϵ}_0\frac{d\tilde{s}}{ds}=1-\lambda {\kappa }^{\prime }$. It follows that

$$\tilde{T}={ϵ}_{0}T.$$

(49)

Considering (40), (49) and $\tilde{\kappa }=\kappa$, we have

$$\tilde{B}={ϵ}_{0}B.$$

(50)

Taking the exterior product on both sides of (49) and (50), we obtain

$$\tilde{N}=N.$$

(51)

On the other hand, differentiating (49) with respect to the null arc length s, we have

$$(1-\lambda {\kappa }^{\prime })\tilde{N}=N.$$

(52)

From (51) and (52), we have $1-\lambda {\kappa }^{\prime }=1$. It implies that the null curvature $\kappa$ is a constant. Summarizing the above process, we have the following conclusions.

Theorem 12.

The distance function $\lambda \left(s\right)$ between a null Darboux curve $r\left(s\right)$ and its null Darboux mate curve $\tilde{r}\left(s\right)$ is a non-zero constant.

Theorem 13.

Let $r\left(s\right)$ be a null Darboux curve with a null Darboux mate curve $\tilde{r}\left(s\right)$. Then their null curvatures are constants.

Theorem 14.

Let $r\left(s\right)$ be a null Darboux curve framed by $\{T,N,B\}$ and $\tilde{r}\left(s\right)$ its null Darboux mate curve framed by $\{\tilde{T},\tilde{N},\tilde{B}\}$. Then

$$\left(\begin{array}{c}\tilde{T}\\ \tilde{N}\\ \tilde{B}\end{array}\right)=\left(\begin{array}{ccc}{ϵ}_0& 0& 0\\ 0& 1& 0\\ 0& 0& {ϵ}_0\end{array}\right)\left(\begin{array}{c}T\\ N\\ B\end{array}\right),({ϵ}_0=\pm 1).$$

In the following, we investigate the explicit representations of a null Darboux curve and its null Darboux mate curve.

Theorem 15.

Let $r\left(s\right)$ be a null Darboux curve and $\tilde{r}\left(s\right)$ its null Darboux mate curve. Then

• when $\kappa >0,$ they are

  $$\left\{\begin{array}{c}r\left(s\right)=C_{1}sinh\sqrt{2\kappa }s+C_{2}cosh\sqrt{2\kappa }s+C_{3}s;\hfill \\ \tilde{r}\left(s\right)=C_{1}sinh\sqrt{2\kappa }s+C_{2}cosh\sqrt{2\kappa }s+C_3(s-2\lambda \kappa );\hfill \end{array}\right.$$
• when $\kappa <0,$ they are

  $$\left\{\begin{array}{c}r\left(s\right)=C_{1}sin\sqrt{-2\kappa }s+C_{2}cos\sqrt{-2\kappa }s+C_{3}s;\hfill \\ \tilde{r}\left(s\right)=C_{1}sin\sqrt{-2\kappa }s+C_{2}cos\sqrt{-2\kappa }s+C_3(s-2\lambda \kappa ),\hfill \end{array}\right.$$

where $C_1,C_2,C_3\in {\mathbb{E}}_1^3$, λ is a non-zero constant.

Proof. 

From Theorem 13, the null curvatures $\kappa$ and $\tilde{\kappa }$ of the null Darboux curve pairs are equal constants denoted by $\tilde{\kappa }=\kappa =\mp \frac{c_0^2}{2}$. By Proposition 3, we have

$$\kappa =\frac{1}{2}{\left[{(log{f}^{\prime })}^{\prime }\right]}^2-{(log{f}^{\prime })}^{″}=\mp \frac{c_0^2}{2},(0<c_0\in \mathbb{R}).$$

Solving the above differential equation, the structure functions $f\left(s\right)$ of $r\left(s\right)$ are

(1)

$f\left(s\right)=\frac{2}{c_0}tan\left(\frac{c_{0}s}{2}\right)$ for $\kappa =-\frac{c_0^2}{2}<0$;

(2)

$f\left(s\right)=\frac{2}{c_0}tanh\left(\frac{c_{0}s}{2}\right)$ for $\kappa =\frac{c_0^2}{2}>0$.

According to Proposition 3, the expressions of $r\left(s\right)$ can be written as

$$\left\{\begin{array}{c}r\left(s\right)=C_{1}sinh\sqrt{2\kappa }s+C_{2}cosh\sqrt{2\kappa }s+C_{3}s,\kappa >0,\hfill \\ r\left(s\right)=C_{1}sin\sqrt{-2\kappa }s+C_{2}cos\sqrt{-2\kappa }s+C_{3}s,\kappa <0,\hfill \end{array}\right.$$

(53)

where $C_1,C_2,C_3\in {\mathbb{E}}_1^3$.

From (53), the Darboux vectors $D\left(s\right)$ of $r\left(s\right)$ are obtained as

$$D\left(s\right)=-2\kappa C_3,\kappa \ne 0.$$

According to Remark 2 and Theorem 12, the expression form of $\tilde{r}\left(s\right)$ are stated as

$$\left\{\begin{array}{c}\tilde{r}\left(s\right)=C_{1}sinh\sqrt{2\kappa }s+C_{2}cosh\sqrt{2\kappa }s+C_3(s-2\lambda \kappa ),\kappa >0,\hfill \\ \tilde{r}\left(s\right)=C_{1}sin\sqrt{-2\kappa }s+C_{2}cos\sqrt{-2\kappa }s+C_3(s-2\lambda \kappa ),\kappa <0,\hfill \end{array}\right.$$

where the distance function $\lambda$ is a non-zero constant. □

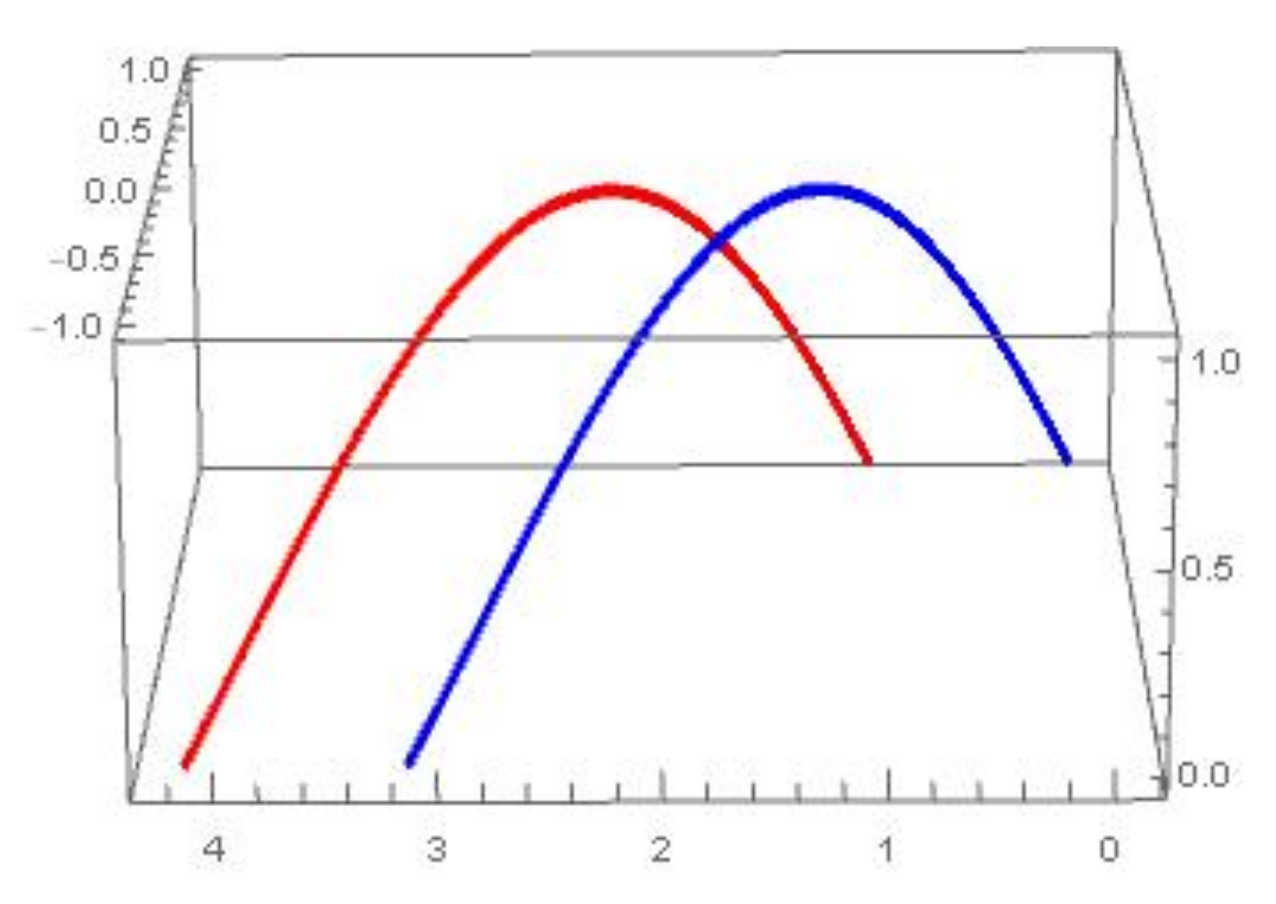
Example 1.

Let $r\left(s\right)=(sins,coss,s)$ be a null Darboux curve with null curvature $\kappa =-\frac{1}{2}$. When the distance function $\lambda \left(s\right)=1$, its null Darboux mate curve is $\tilde{r}\left(s\right)=(sins,coss,s+1)$ (Figure 1).