Symmetry Breaking of a Time-2D Space Fractional Wave Equation in a Complex Domain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Complex Fractional Differential Operator
2.2. Symmetric Fractional Differential Operator (SFDO)
2.3. Time-2D Space Wave Equation
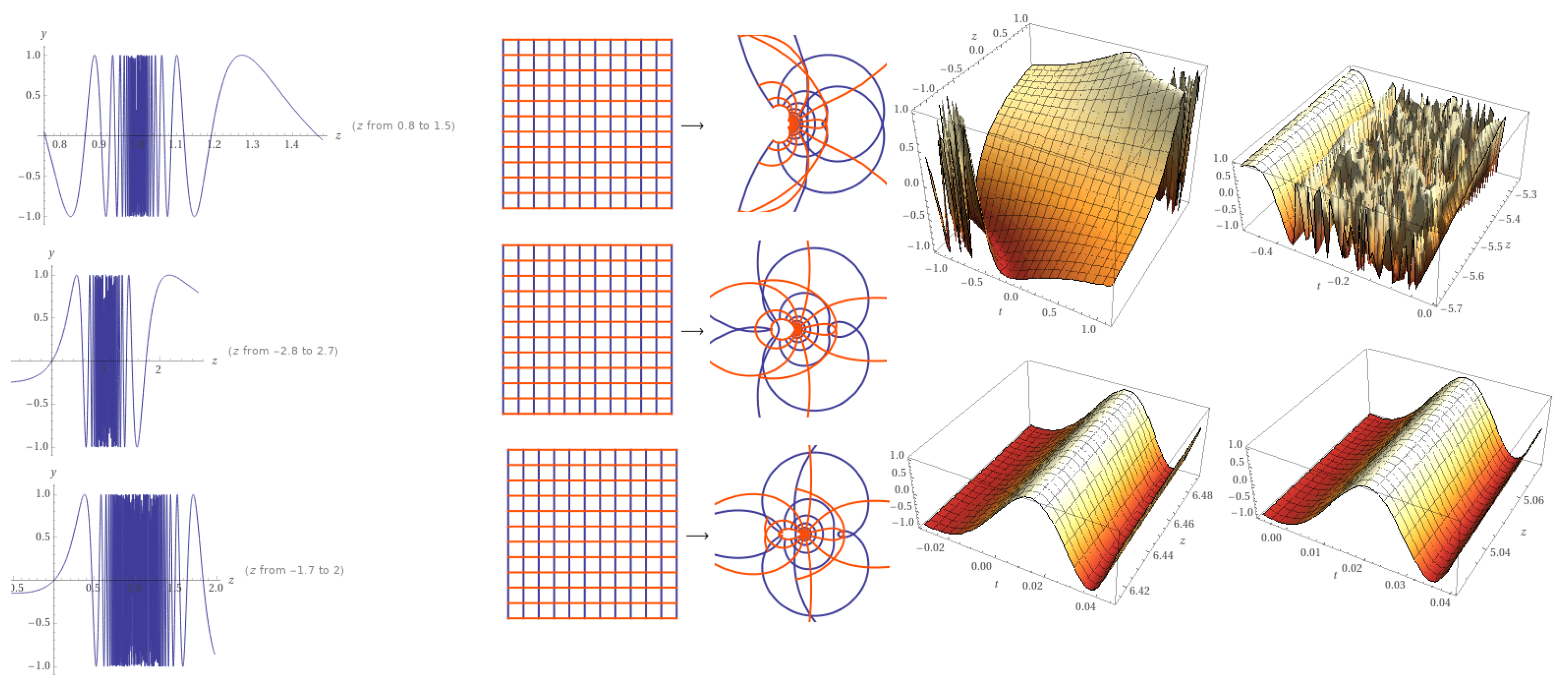
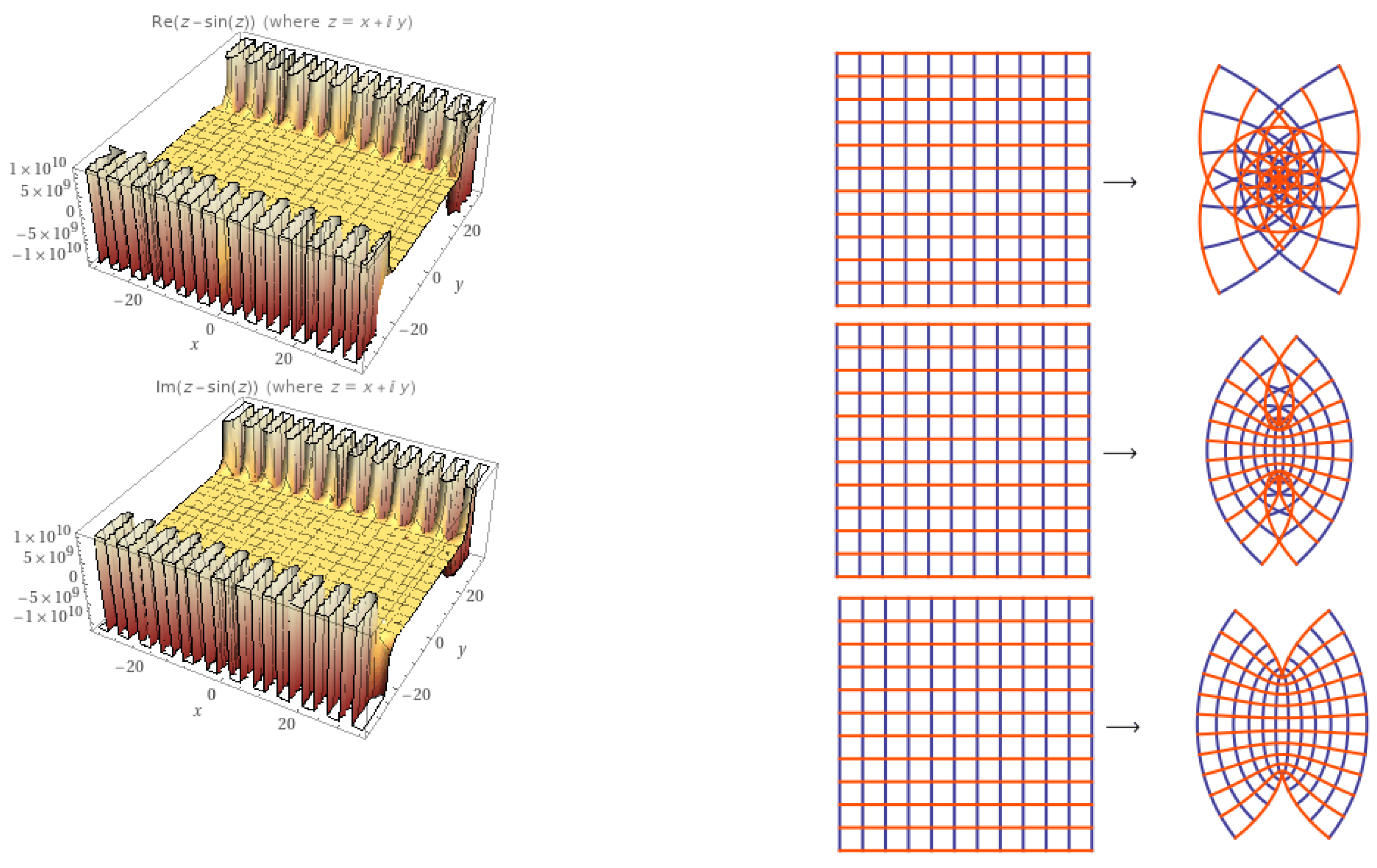
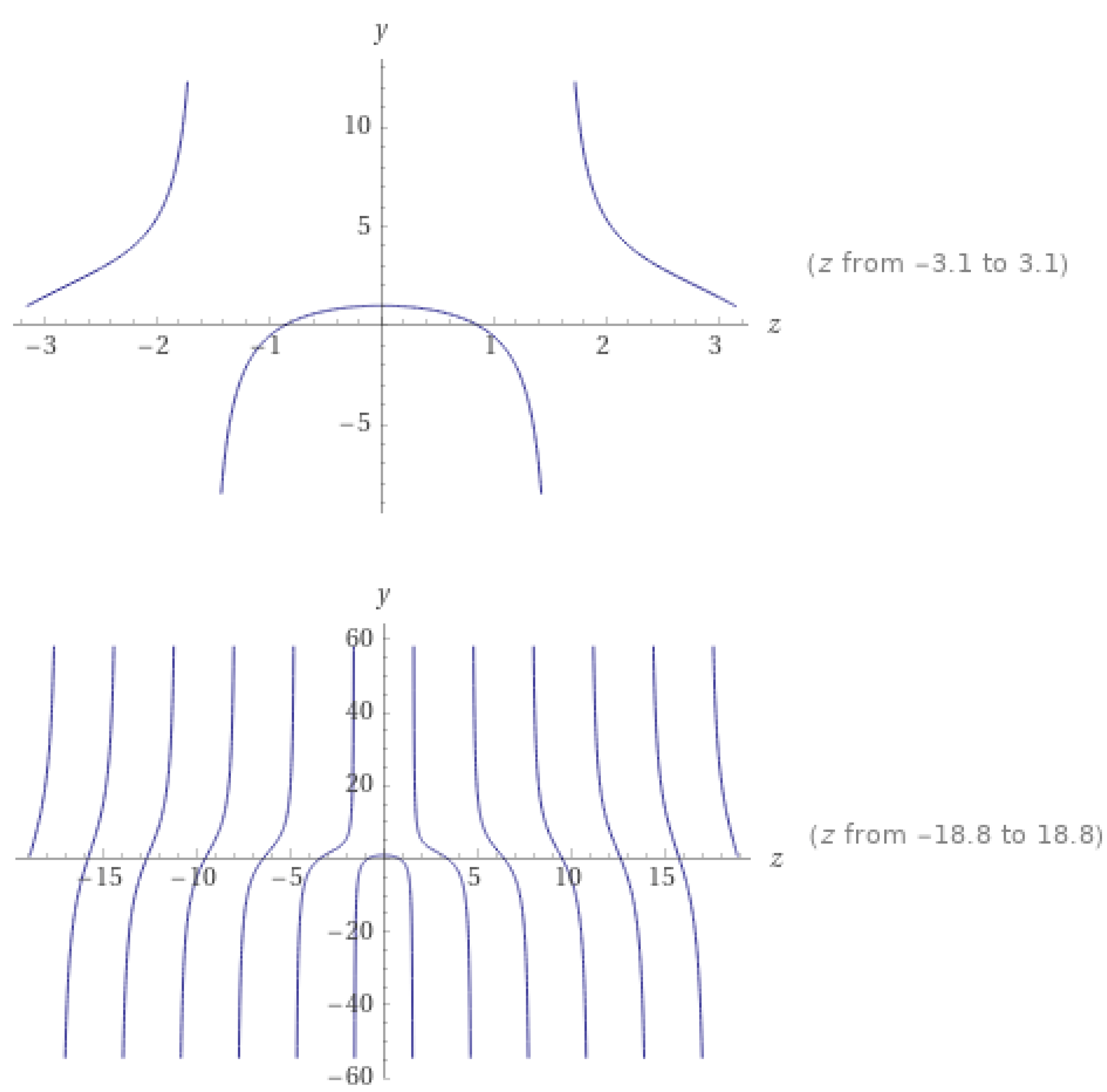
3. Results
3.1. Time-Fractional Wave Equation
3.2. Dominated Solutions by a Chaotic Function
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, P.; Malomed, B.A.; Mihalache, D. Symmetry breaking of spatial Kerr solitons in fractional dimension. Chaos Solitons Fractals 2020, 132, 109602. [Google Scholar] [CrossRef] [Green Version]
- Rusin, R.; Marangell, R.; Susanto, H. Symmetry breaking bifurcations in the NLS equation with an asymmetric delta potential. Nonlinear Dyn. 2020, 100, 3815–3824. [Google Scholar] [CrossRef]
- Yagasaki, K.; Yamazoe, S. Numerical analyses for spectral stability of solitary waves near bifurcation points. Jpn. J. Ind. Appl. Math. 2021, 38, 125–140. [Google Scholar] [CrossRef]
- Sa, L.; Ribeiro, P.; Prosen, T. Complex spacing ratios: A signature of dissipative quantum chaos. Phys. Rev. 2020, 10, 021019. [Google Scholar] [CrossRef]
- Miller, S.S.; Mocanu, P.T. Differential Subordinations: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- MacGregor, T.H. Majorization by univalent functions. Duke Math. J. 1967, 43, 95–102. [Google Scholar] [CrossRef]
- Fernandez, A. A complex analysis approach to Atangana-Baleanu fractional calculus. Math. Methods Appl. Sci. 2019, 44, 8070–8087. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.K.; Prajapati, J.C. On a generalization of Mittag-Leffler function and its properties. J. Math. Anal. Appl. 2007, 336, 797–811. [Google Scholar] [CrossRef] [Green Version]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef] [Green Version]
- Godula, J.; Starkov, V.V. Sharpness of certain Campbell and Pommerenke estimates. Math. Notes 1998, 63, 586–592. [Google Scholar] [CrossRef]
- Campbell, D.M. Majorization-subordination theorems for locally univalent functions, II. Can. J. Math. 1973, 25, 420–425. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Baleanu, D. On quantum hybrid fractional conformable differential and integral operators in a complex domain. In Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matemáticas; Springer: Berlin, Germany, 2021; Volume 115, pp. 1–13. [Google Scholar]
- Ibrahim, R.W.; Baleanu, D. On a combination of fractional differential and integral operators associated with a class of normalized functions. AIMS Math. 2021, 6, 4211–4226. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. Generalized Briot-Bouquet differential equation based on new differential operator with complex connections. Axioms 2020, 9, 42. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. On subclasses of analytic functions based on a quantum symmetric conformable differential operator with application. Adv. Differ. Equ. 2020, 2020, 325. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Baleanu, D. Analytic Solution of the Langevin Differential Equations Dominated by a Multibrot. Fractal Set. Fractal Fract. 2021, 5, 50. [Google Scholar] [CrossRef]
- Goodman, A.W. An invitation to the study of univalent and multivalent functions. Intr. Nat. J. Hath. Mh. Sci. 1979, 2, 163–186. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, R.W.; Baleanu, D. Symmetry Breaking of a Time-2D Space Fractional Wave Equation in a Complex Domain. Axioms 2021, 10, 141. https://doi.org/10.3390/axioms10030141
Ibrahim RW, Baleanu D. Symmetry Breaking of a Time-2D Space Fractional Wave Equation in a Complex Domain. Axioms. 2021; 10(3):141. https://doi.org/10.3390/axioms10030141
Chicago/Turabian StyleIbrahim, Rabha W., and Dumitru Baleanu. 2021. "Symmetry Breaking of a Time-2D Space Fractional Wave Equation in a Complex Domain" Axioms 10, no. 3: 141. https://doi.org/10.3390/axioms10030141
APA StyleIbrahim, R. W., & Baleanu, D. (2021). Symmetry Breaking of a Time-2D Space Fractional Wave Equation in a Complex Domain. Axioms, 10(3), 141. https://doi.org/10.3390/axioms10030141






