An Innovative Grey Approach for Group Multi-Criteria Decision Analysis Based on the Median of Ratings by Using Python

Abstract

Some decision-making problems, i.e., multi-criteria decision analysis (MCDA) problems, require taking into account the attitudes of a large number of decision-makers and/or respondents. Therefore, an approach to the transformation of crisp ratings, collected from respondents, in grey interval numbers form based on the median of collected scores, i.e., ratings, is considered in this article. In this way, the simplicity of collecting respondents’ attitudes using crisp values, i.e., by applying some form of Likert scale, is combined with the advantages that can be achieved by using grey interval numbers. In this way, a grey extension of MCDA methods is obtained. The application of the proposed approach was considered in the example of evaluating the websites of tourism organizations by using several MCDA methods. Additionally, an analysis of the application of the proposed approach in the case of a large number of respondents, done in Python, is presented. The advantages of the proposed method, as well as its possible limitations, are summarized.

1. Introduction

Multi-criteria decision-making (MCDM), or multi-criteria decision analysis (MCDA), has so far been used for solving a large number of numerous different decision-making problems [1,2,3,4]. Therefore, MCDA is dealing with solving complex real-world problems of the greatest interest to the organization that cannot be solved by conventional methods [5,6,7,8]. In due course of time, many multi-criteria analysis (MCA) methods were proposed, primarily due to the dynamic and rapid development of the field of operational research. The following can be mentioned as some of the most cited articles from this area: Hajkowicz and Collins [9], Hajkowicz and Higgins [10], Kaklauskas et al. [11], Kostreva et al. [12], and Belton and Vickers [13].

Besides this research, there are many studies in this area, such as: research and development project portfolio selection [14] (Mavrotas and Makryvelios, 2021), assessing national energy sustainability [15], energy consumption analysis of high-speed trains [16], evaluation of transport emissions reduction policies [17], planning renewable energy use and carbon saving [18], and so forth.

MCDA has also been used successfully for solving decision-making problems that are related to uncertainties or require a group decision-making approach for solving them [19,20,21,22,23,24,25]. As some examples of such approaches, the following can be mentioned: a grey absolute decision analysis [26], a multiple criteria decision analysis framework for the dispersed group [27], a fuzzy multi-criteria analysis [28,29,30], and collaborative decision-making in the multi-actor multi-criteria analysis [31].

From the aforestated, it is clear that some decision-making problems can be more adequately solved if a larger number of respondents take part in solving them. In such cases, the question that arises is how to transform the attitudes collected from respondents into group attitudes.

The approach based on the use of a five-point Liker’s scale, or similar, can be mentioned as one of the probably simplest approaches for collecting the respondents’ attitudes. So far, in numerous articles published in scientific journals, numerous approaches have been proposed for the transformation of individual attitudes acquired in this way into group attitudes. The results obtained, the advantages, as well as the weaknesses of these approaches, are also presented in these journals.

In this article, an approach to the transformation of crisp ratings, collected from respondents, as grey interval numbers form based on the median of collected scores, i.e., ratings, is considered. Therefore, the article proposes the transformation of individual ratings collected from respondents into grey intervals with the aim of performing MCDA with minimal loss of information in relation to cases when crisp ratings are transformed into crisp group ratings. The application of the proposed approach was considered on the example of evaluating the websites of tourism organizations by using several MCDA methods, and also an analysis of the application of the proposed approach in the case of a large number of respondents was done in Python and described. Additionally, the main idea of the article was to propose a simple procedure for gathering respondent’s attitudes instead of a complex procedure that is sometimes difficult to understand by ordinary respondents/decision-makers who are not familiar with MCDM and fuzzy logic.

Therefore, the rest of this article is organized as follows: In Section 2, some basic definitions about grey numbers are given, while a new approach is proposed in Section 3. In Section 4, a numerical illustration is presented in order to highlight the basic characteristics of the proposed approach, while in Section 5 an analysis of the obtained results is performed. Finally, conclusions are given at the end of the article.

2. Preliminaries

Definition 1.

Grey number [32]. A grey number$\otimes x$is such a number whose exact value is unknown, but the range in which value can lie is known.

Definition 2.

Interval grey number [32]. An interval grey number is a grey number with a known lower bound$\underset{\_}{x}$and upper bound$\overline{x}$, but with the unknown value of x, and it is shown as follows:

$$\otimes x\in \left[\underset{\_}{x},\overline{x}\right]=\left[\underset{\_}{x}\le x\le \overline{x}\right].$$

(1)

Definition 3.

The whitening function [33,34,35]. The whitening function transforms an interval grey number into a crisp number whose possible values lie between the bounds of the interval grey number. For the given interval grey number, the whitened value x_(λ) of interval grey number$\otimes x$is defined as

$$x_{\left(\lambda \right)}=\left(1-\mathsf{\lambda }\right)\underset{\_}{x}+\lambda \overline{x},$$

(2)

where$\in \left[0,1\right]$denotes the whitening coefficient.

In the particular case λ = 0.5, the whitened value becomes the mean of the interval grey number, as follows:

$$x_{\left(0.5\right)}=0.5(\underset{\_}{x}+\overline{x}).$$

(3)

3. The Newly Proposed Approach

Suppose that the decision matrix is presented in the form

$$D=[x_{ij}^k],$$

(4)

where: $x_{ij}^k$ denotes the evaluation of alternative i to criterion j stated by the decision-maker k; i = 1,…,m, and m denotes the number of alternatives; j = 1,…,n, and n denotes the number of criteria; k = 1… K, and K denotes the number of decision-makers.

Such a three-dimensional matrix can be transformed into a group two-dimensional matrix as follows:

$$D=[{x^{\prime }}_{ij}],$$

(5)

with

$${x^{\prime }}_{ij}=\left({\displaystyle \sum _{k=1}^K{x}_{ij}^k}\right)/K.$$

(6)

Essentially, ${x^{\prime }}_{ij}$ denotes rating of alternative i to criterion j. Such defined ${x^{\prime }}_{ij}$ is actually the mean value of all assessments of the alternative i in relation to the criterion j.

However, the matrix shown using Equation (4) can be also transformed into a grey group decision matrix, as follows:

$$D=([{\underset{\_}{x}}_{ij},{\overline{x}}_{ij}]),$$

(7)

with

$${\underset{\_}{x}}_{ij}=\left({\displaystyle \sum _{k\in k^{-}}{x}_{ij}^k}\right)/n^{-};$$

(8)

$${\overline{x}}_{ij}=\left({\displaystyle \sum _{k\in k^{+}}{x}_{ij}^k}\right)/n^{+}.$$

(9)

In (8), $k^{-}$ denotes the set of elements whose values are less than or equal to the median value of $x_{ij}^k$, and $n^{-}$ denotes the number of elements in this set. Similarly, $k^{+}$ in (9) denotes a set of elements whose values are greater than or equal to the median value of $x_{ij}^k$ and $n^{+}$ denotes the number of elements in this set.

Example

Let S be a sequence of 10 integers from interval [1, 5] and S = (1, 2, 3, 1, 5, 3, 3, 1, 4, 5).

Then, the mean and median of S are as follows: mean = 2.80 and median = 3.00. The mean value of a number which is less than or equal to the median (1, 2, 3, 1, 3, 3, 1) is x_l = 2.00 and the mean value of a number greater or equal to the median (3, 5, 3, 3, 4, 5) is x_u = 3.83.

The mean value of such interval [2.00, 3.83], determined using Equation (3), is 2.915, and the distance between it and the mean is 2.915 − 2.80 = 0.115, that is in percentages 4.11%.

The results obtained based on several sequences of randomly generated numbers from interval [1, 10] are shown in

Table 1. Difference between the mean value of the sequence of numbers and the value obtained by the proposed approach.

Sample	Mean	Median	xl	xu	xm = (xu − xl)/2	d = abs(Mean − xm)	d (%)
5	5.60	5.00	4.00	7.00	5.50	0.10	1.79
10	7.10	7.50	5.40	8.80	7.10	0.00	0.00
15	5.13	6.00	2.88	7.50	5.19	0.05	1.06
20	6.50	7.00	5.08	8.00	6.54	0.04	0.64
25	4.52	4.00	2.43	6.50	4.46	0.06	1.23
50	5.20	5.00	3.07	7.14	5.11	0.09	1.81
100	5.01	5.00	2.93	7.09	5.01	0.00	0.02
150	5.16	5.00	3.05	6.91	4.98	0.18	3.45

. The calculation was done in Python using the seed (1).

From Table 1, it can be seen that the difference between the mean value of the sequence of numbers and the value obtained by the proposed approach is not large.

4. A Numerical Illustration

In this section, the use of the proposed approach is presented in the case of evaluating websites of tourist organizations from Eastern Serbia. The evaluation was performed on the websites of 5 tourist organizations from the Timok frontier, or more precisely tourist organizations of the Municipalities of Boljevac, Bor, Majdanpek, Negotin and Kladovo (It is important to state that the order of municipalities does not correspond to the order of alternatives, because the aim of this article is not to favor any of the above-mentioned tourist organizations.). The evaluation is performed based on the following criteria: Visual design—C₁, Structure and navigability—C₂, Content—C₃, Innovation—C₄, Personalization—C₅.

The evaluation was performed using ARAS [36], WASPAS [37], CoCoSo [38] and WISP [39] methods. In the first case, the evaluation was performed using ordinary MCDA methods and the mean value of the collected ratings, while in the first case, the evaluation was performed using the proposed approach.

This illustration does not show all the possibilities that the proposed approach provides in terms of analysis. The main goal was to compare the results obtained by applying the mean value of all assessments and the proposed approach, where the transformation of grey numbers was performed using Equation (3) and λ = 0.5.

The rating obtained from 10 respondents is shown in

Table 2. Ratings of alternative A₁ in relation to the evaluation criteria obtained from 10 respondents.

A1	I	II	III	IV	V	VI	VII	VIII	IX	X
C1	1	2	3	3	5	3	3	4	3	2
C2	3	3	4	5	3	4	4	4	2	4
C3	3	3	4	3	3	4	4	5	5	4
C4	1	1	2	3	4	4	5	2	3	2
C5	2	1	2	2	1	2	3	4	3	2

,

Table 3. Ratings of alternative A₂ in relation to the evaluation criteria obtained from 10 respondents.

A2	I	II	III	IV	V	VI	VII	VIII	IX	X
C1	3	5	4	4	4	4	5	3	2	2
C2	5	5	4	5	4	5	5	4	3	4
C3	2	4	4	4	3	4	5	3	3	3
C4	4	4	5	4	2	2	5	3	5	3
C5	4	4	5	3	4	3	4	3	2	4

,

Table 4. Ratings of alternative A₃ in relation to the evaluation criteria obtained from 10 respondents.

A3	I	II	III	IV	V	VI	VII	VIII	IX	X
C1	1	2	2	2	2	2	2	3	2	1
C2	3	5	5	4	2	2	3	4	4	4
C3	1	4	4	2	2	2	4	3	2	2
C4	1	1	3	3	1	1	4	2	1	1
C5	3	5	5	3	4	4	3	4	4	4

,

Table 5. Ratings of alternative A₄ in relation to the evaluation criteria obtained from 10 respondents.

A4	I	II	III	IV	V	VI	VII	VIII	IX	X
C1	4	4	4	5	4	4	4	4	5	4
C2	5	5	4	5	3	3	4	5	5	3
C3	5	5	4	4	3	3	4	5	5	5
C4	4	4	5	5	5	3	5	5	4	3
C5	4	4	5	3	4	4	3	5	4	4

and

Table 6. Ratings of alternative A₅ in relation to the evaluation criteria obtained from 10 respondents.

A4	I	II	III	IV	V	VI	VII	VIII	IX	X
C1	4	3	5	5	5	3	5	3	4	3
C2	4	4	4	5	4	3	5	4	4	4
C3	5	4	4	4	3	3	4	4	3	5
C4	4	4	5	3	2	4	3	5	3	3
C5	3	4	4	4	4	3	4	5	4	4

.

The group decision matrix, formed on the basis of the responses of all respondents, is shown in

Table 7. Group decision-making matrix.

Criteria Alternatives	C1	C2	C3	C4	C5
A1	2.90	3.60	3.80	2.70	2.20
A2	3.60	4.40	3.50	3.70	3.60
A3	1.90	3.60	2.60	1.80	3.90
A4	4.20	4.20	4.30	4.30	4.00
A5	4.00	4.10	3.90	3.60	3.90

. The elements of this matrix represent the mean value of the ratings obtained from the respondents.

A similar decision matrix is shown in

Table 8. The median of ratings obtained from the respondents.

Criteria Alternatives	C1	C2	C3	C4	C5
A1	2.96	3.81	3.92	2.70	2.11
A2	3.79	4.40	3.50	3.82	3.81
A3	1.95	3.79	2.31	1.40	3.96
A4	4.10	4.20	4.30	4.30	4.00
A5	4.00	4.05	3.96	3.60	3.95

, where the elements of that matrix represent the median of ratings obtained from the respondents.

The results of the evaluation performed using ordinary ARAS, WASPAS, CoCoSo and WISP methods, weighting vector w_i = (0.25, 0.24, 0.22, 0.20, 0.10), and the data from Table 7, are shown in

Table 9. Ranking of alternatives using ordinary ARAS, WASPAS, CoCoSo and WISP methods.

	ARAS		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Si	Rank	Si	Rank	Si	Rank
A1	0.73	4	0.73	4	1.80	4	0.87	4
A2	0.88	3	0.88	3	2.17	3	0.95	3
A3	0.61	5	0.60	5	1.49	5	0.81	5
A4	0.99	1	0.99	1	2.43	1	1.00	1
A5	0.92	2	0.92	2	2.25	2	0.96	2

.

In the second case, based on data from Table 8 as well as ratings from Table 2, Table 3, Table 4, Table 5 and Table 6, a grey decision matrix was formed as shown in

Table 10. Grey group decision-making matrix.

Criteria Alternatives	C1	C2	C3	C4	C5
A1	[2.50, 3.43]	[3.44, 4.17]	[3.50, 4.33]	[1.60, 3.80]	[1.71, 2.50]
A2	[3.25, 4.33]	[3.80, 5.00]	[2.80, 4.20]	[3.14, 4.50]	[3.44, 4.17]
A3	[1.78, 2.13]	[3.25, 4.33]	[1.83, 2.78]	[1.00, 1.80]	[3.62, 4.29]
A4	[4.00, 4.20]	[3.40, 5.00]	[3.60, 5.00]	[3.60, 5.00]	[3.75, 4.25]
A5	[3.33, 4.67]	[3.88, 4.22]	[3.63, 4.29]	[2.80, 4.40]	[3.78, 4.13]

.

The evaluation results generated using the grey ARAS, WASPAS, CoCoSo and WISP methods, and the data from Table 10, are shown in

Table 11. Ranking of alternatives using grey WS, WP, WASPAS and CoCoSo methods.

	ARAS		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Si	Rank	Si	Rank	Si	Rank
A1	0.76	4	0.46	4	1.90	4	0.74	4
A2	0.91	3	0.55	3	2.29	3	0.89	3
A3	0.59	5	0.36	5	1.47	5	0.62	5
A4	0.99	1	0.60	1	2.48	1	0.99	1
A5	0.92	2	0.56	2	2.32	2	0.92	2

. It should be noted again that the grey numbers from Table 10 were transformed into crisp values, using Equation (3) and λ = 0.5, before the evaluation.

From Table 9 and Table 11, it can be seen that differences in ranking orders of alternatives achieved on the basis of the mean value of all assessments and the proposed approach were not observed. Of course, it should be reiterated here that the proposed approach provides significantly greater opportunities in terms of analyzing various scenarios, such as pessimistic or optimistic.

5. Analysis and Discussion

In order to verify the proposed approach, this section presents the results of the evaluation based on the assessments of a number of virtual respondents. For easier evaluation, the scores were generated as random numbers from the interval [1, 10], using a program written in the Python programming language, in which all calculations were also performed. In this analysis, random numbers are generated with the seed (1). The results obtained on the basis of series of 10, 50, 100 and 150 virtual respondents are shown in

Table 12. Ranking of alternatives on the basis of 10 virtual respondents and crisp approach.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Qi	Rank	Ki	Rank	Si	Rank
A1	0.83	5	0.75	5	0.75	5	1.77	5	0.59	5
A2	1.00	1	0.91	1	0.91	1	2.16	1	1.00	1
A3	0.98	2	0.87	2	0.88	2	2.09	2	0.88	2
A4	0.84	4	0.75	4	0.76	4	1.79	4	0.61	4
A5	0.89	3	0.80	3	0.81	3	1.91	3	0.71	3

,

Table 13. Ranking of alternatives on the basis of 10 virtual respondents and the proposed grey approach.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Qi	Rank	Ki	Rank	Si	Rank
A1	0.82	5	0.74	5	0.75	5	1.78	5	0.58	5
A2	1.00	1	0.92	1	0.92	1	2.18	1	1.00	1
A3	0.95	2	0.84	2	0.86	2	2.04	2	0.80	2
A4	0.83	4	0.75	4	0.75	4	1.79	4	0.59	4
A5	0.88	3	0.80	3	0.81	3	1.91	3	0.69	3

,

Table 14. Ranking of alternatives on the basis of 50 virtual respondents and crisp approach.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Si	Si	Ki	Rank	Si	Rank
A1	0.97	3	0.94	3	0.94	3	1.90	3	0.91	3
A2	0.92	4	0.89	4	0.89	4	1.80	4	0.78	4
A3	1.00	1	0.97	1	0.97	1	1.97	1	1.00	1
A4	0.91	5	0.88	5	0.89	5	1.79	5	0.77	5
A5	0.97	2	0.94	2	0.95	2	1.91	2	0.91	2

,

Table 15. Ranking of alternatives on the basis of 50 virtual respondents and the proposed grey approach.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Qi	Rank	Ki	Rank	Si	Rank
A1	0.98	2	0.94	2	0.94	2	1.90	2	0.94	2
A2	0.92	5	0.89	5	0.89	5	1.79	5	0.80	5
A3	1.00	1	0.96	1	0.96	1	1.94	1	1.00	1
A4	0.93	4	0.89	4	0.89	4	1.81	4	0.82	4
A5	0.97	3	0.93	3	0.93	3	1.87	3	0.90	3

,

Table 16. Ranking orders of alternatives obtained on the basis of 50 virtual respondents.

	Crisp					Grey Approach
Alternatives	WS	WP	WASPAS	CoCoSo	WISP	WS	WP	WASPAS	CoCoSo	WISP
A1	3	3	3	3	3	2	2	2	2	2
A2	4	4	4	4	4	5	5	5	5	5
A3	1	1	1	1	1	1	1	1	1	1
A4	5	5	5	5	5	4	4	4	4	4
A5	2	2	2	2	2	3	3	3	3	3

,

Table 17. Ranking orders of alternatives obtained on the basis of 100 virtual respondents.

	Crisp					Grey Approach
Alternatives	WS	WP	WASPAS	CoCoSo	WISP	WS	WP	WASPAS	CoCoSo	WISP
A1	4	4	4	4	4	4	4	4	4	4
A2	3	3	3	3	3	2	2	2	2	2
A3	2	2	2	2	2	3	3	3	3	3
A4	1	1	1	1	1	1	1	1	1	1
A5	5	5	5	5	5	5	5	5	5	5

,

Table 18. Ranking of alternatives on the basis of 150 virtual respondents and crisp methods.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Si	Si	Ki	Rank	Si	Rank
A1	0.993	2	0.960	2	0.961	2	1.840	2	0.977	2
A2	0.975	3	0.944	3	0.944	3	1.808	3	0.927	3
A3	0.971	5	0.938	5	0.939	5	1.799	5	0.914	5
A4	1.000	1	0.968	1	0.968	1	1.854	1	1.000	1
A5	0.973	4	0.942	4	0.942	4	1.805	4	0.923	4

,

Table 19. Ranking of alternatives on the basis of 150 virtual respondents and grey methods.

	WS		WP		WASPAS		CoCoSo		WISP
Alternatives	Si	Rank	Pi	Rank	Qi	Rank	Ki	Rank	Si	Rank
A1	0.988	2	0.954	2	0.955	2	1.806	2	0.965	2
A2	0.988	3	0.953	3	0.954	3	1.805	3	0.963	3
A3	0.987	4	0.952	4	0.953	4	1.804	4	0.960	4
A4	1.000	1	0.966	1	0.966	1	1.828	1	1.000	1
A5	0.985	5	0.952	5	0.952	5	1.801	5	0.958	5

and

Table 20. Ranking orders of alternatives obtained on the basis of 150 virtual respondents.

	Crisp					Grey Approach
Alternatives	WS	WP	WASPAS	CoCoSo	WISP	WS	WP	WASPAS	CoCoSo	WISP
A1	2	2	2	2	2	2	2	2	2	2
A2	3	3	3	3	3	3	3	3	3	3
A3	5	5	5	5	5	4	4	4	4	4
A4	1	1	1	1	1	1	1	1	1	1
A5	4	4	4	4	4	5	5	5	5	5

. The weighting vector w_i = (0.2, 0.2, 0.2, 0.2, 0.2) is used in this evaluation.

The calculation details obtained on the basis of 10 virtual respondents are shown in Table 12 and Table 13. As can be seen from Table 12 and Table 13, in this case, the same ranking orders are obtained by applying all methods and approaches.

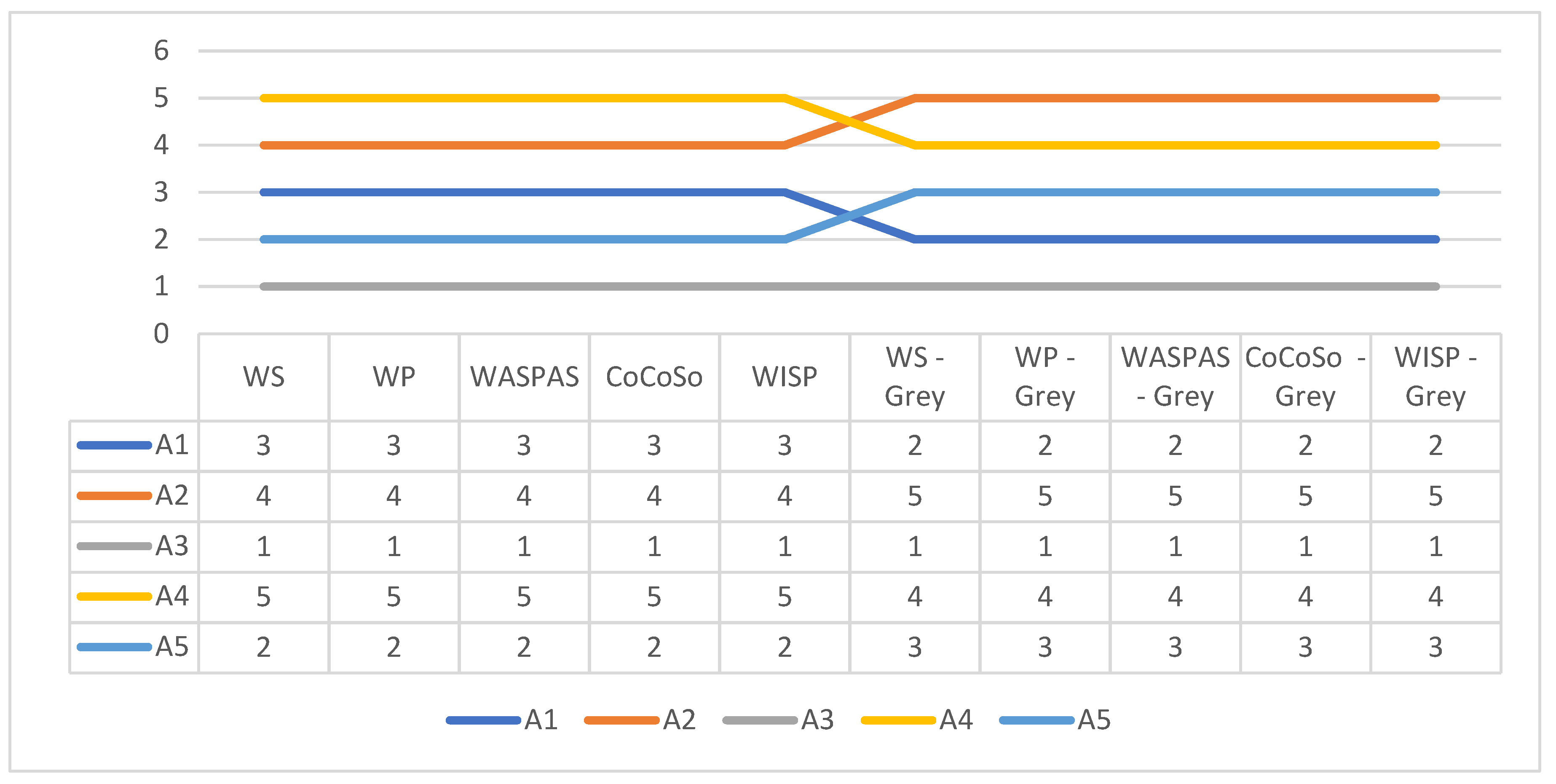
The calculation details obtained on the basis of 50 virtual respondents are shown in Table 14, Table 15 and Table 16. In this case, there were some discrepancies in the order of the second and third-placed alternatives, which can be clearly seen in Figure 1.

It can be seen from Table 14 and Table 15 that differences between second-placed and third-placed alternatives are not high, which is why it can be expected that the same ranking order of alternatives could be obtained by using another weight vector.

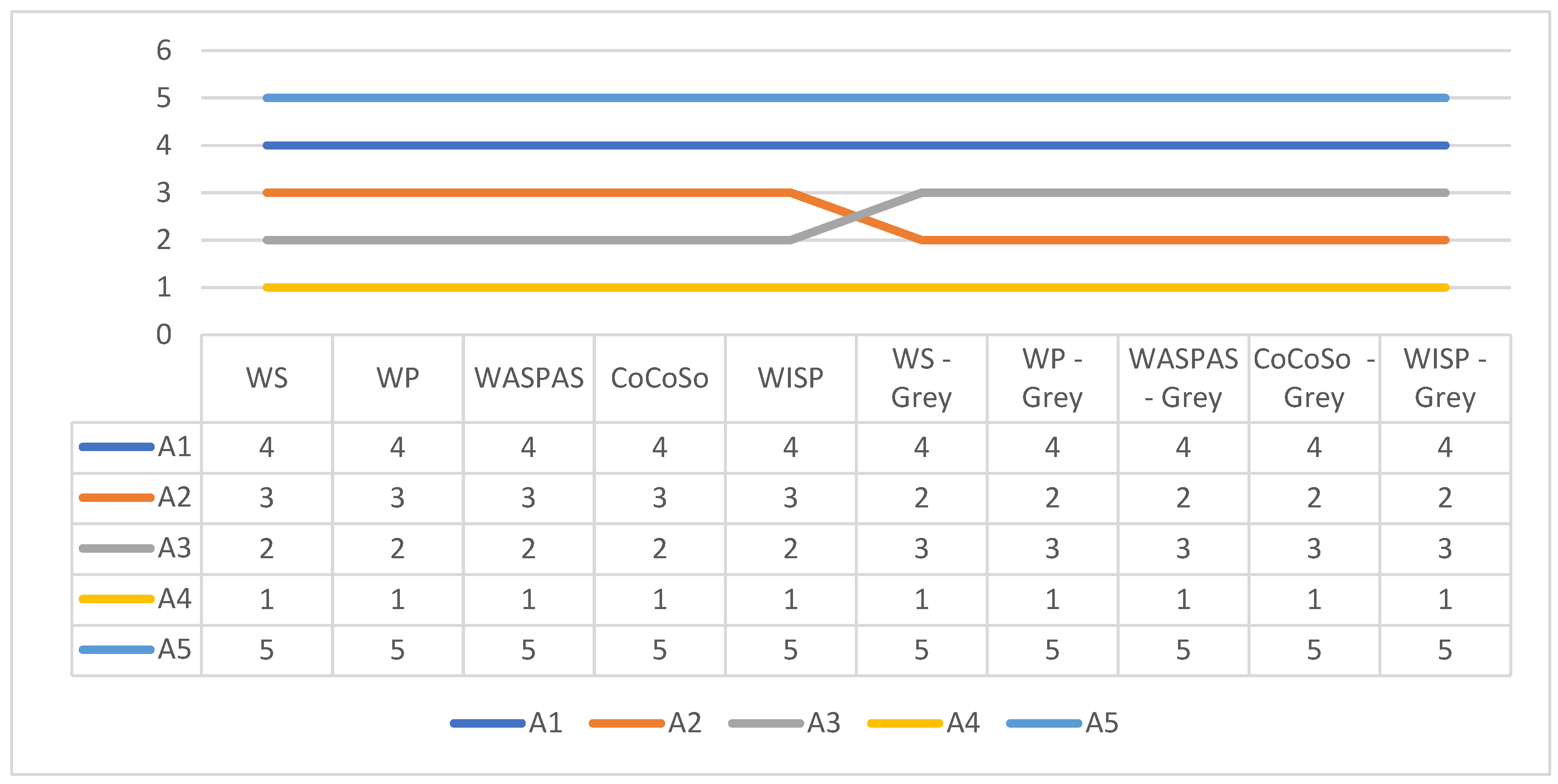
Ranking orders of alternatives, obtained on the basis of 100 virtual respondents, are shown in Tabe 17, and presented in Figure 2. This case is similar to the previous one.

From Table 17 and Figure 2 it can be observed that in this case, the differences occur only in the case of the second and third-placed alternatives.

Ranking orders of alternatives that arise from 150 virtual respondents are arranged in Table 18, Table 19 and Table 20 and presented in Figure 3.

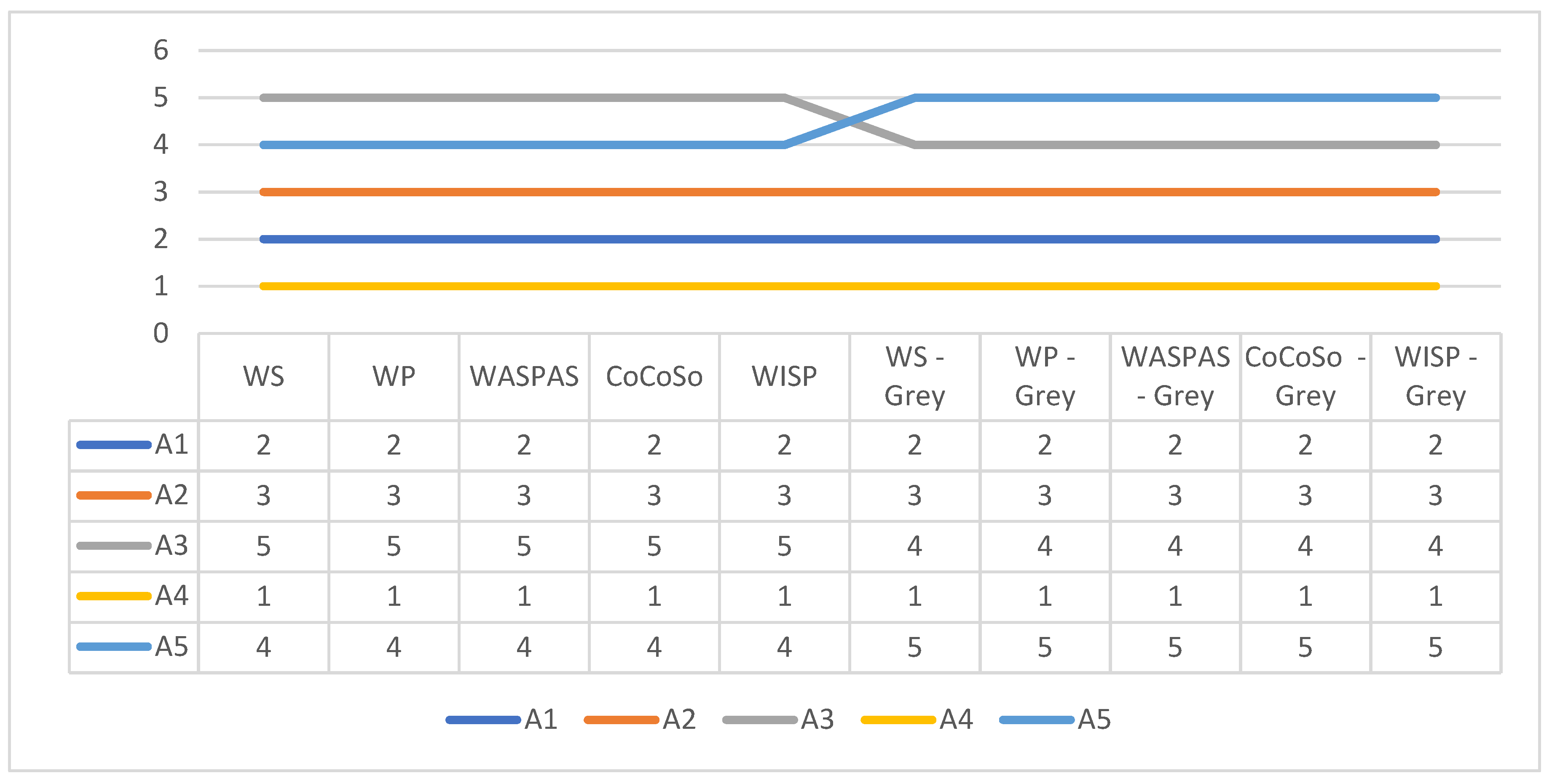
Table 20 and Figure 3 clearly show that the alternative A₄ is best ranked according to all methods, with all crisp methods gave the same order of ranking A_4, A₁, A₂, A₅, A₃, while the proposed grey approach gave the following rankings order A_4, A₁, A₂, A₃, A₅. However, from Table 20 it is observable that there are very small differences in overall performance between the second-placed, third-placed and fourth-placed alternatives, which is why it can be expected that different ranking orders of alternatives could be obtained by using another weighting vector.

6. Conclusions

The advantages of using grey instead of crisp numbers in multi-criteria decision analysis have been considered and proven in a number of previously published studies. One of the advantages which should be emphasized using grey numbers is the possibility of considering various scenarios, such as: pessimistic, realistic, and optimistic. The proposed approach allows the transformation of crisp ratings, collected by employing surveys based on the use of the Likert scale, into grey numbers and thus considering different scenarios. The proposed approach may be suitable when it is necessary to collect and analyze the realistic attitudes of a larger number of respondents. Moreover, the proposed transformation enables greater robustness and further possibility of analysis and consideration of different scenarios.

The results of the website evaluation based on the mean value of the ratings obtained from all respondents and the proposed approach did not indicate a difference in the ranking orders of alternatives. However, the results of the conducted analysis indicate that differences may arise between the two approaches, especially in the case of the lower-ranked alternatives.

Some differences in the results are expected because the proposed approach is not a substitute for applying the mean value of the scores obtained from all respondents, but an approach that further allows the possibility of analysis. Certain differences in the ranking results using the newly proposed approach and applying the mean of the scores obtained in all respondents can be cited as a weakness of this approach.

Finally, consideration of the transformation of a larger number of crisp ratings into corresponding triangular fuzzy numbers or interval-valued triangular fuzzy numbers can be mentioned as one of the possible directions for the further development of the proposed approach.