Abstract
In this paper, the Weibull extension distribution parameters are estimated under a progressive type-II censoring scheme with random removal. The parameters of the model are estimated using the maximum likelihood method, maximum product spacing, and Bayesian estimation methods. In classical estimation (maximum likelihood method and maximum product spacing), we did use the Newton–Raphson algorithm. The Bayesian estimation is done using the Metropolis–Hastings algorithm based on the square error loss function. The proposed estimation methods are compared using Monte Carlo simulations under a progressive type-II censoring scheme. An empirical study using a real data set of transformer insulation and a simulation study is performed to validate the introduced methods of inference. Based on the result of our study, it can be concluded that the Bayesian method outperforms the maximum likelihood and maximum product-spacing methods for estimating the Weibull extension parameters under a progressive type-II censoring scheme in both simulation and empirical studies.
1. Introduction
Several cases in life-testing and reliability experiments arise when units are withdrawn or lost from the test before failure. These data of such tests or studies are called censored samples. Right, left, interval censoring, single or multiple censoring, and type-I or type-II censoring are all examples of censoring schemes, but conventional type-I and type-II censoring schemes do not allow units to be withdrawn at any stage other than the end of the experiment. In type-II censoring, a total of n units are placed on the test but instead of continuing until all units fail, the test is terminated at the time of the th failure of units. Progressive type-II censoring is a generalization of this type of censorship. Increasingly, the type-II censoring scheme has recently sparked a lot of interest among statisticians. Under this case, units are placed under test at time zero, and failures are observed. In the first failure observed of surviving units are randomly selected, removed, and so on. In th failures are observed and the remaining are all removed, and the experiment terminates. For more information, see Balakrishnan and Aggarwala (2000) [1] Balakrishnan, N. (2007) [2].
Under progressive type-II censoring, Almetwally and Almongy (2019) [3] discussed the Bayesian approach to infer the parameter estimation of the distribution of generalized power of Weibull. Hashem and Alyami (2021) [4] discussed inference on an exponential doubly Poisson distribution for a parallel-series structure. Abu-Moussa et al. (2021) [5] estimated the reliability of the stress–strength parameter for the Rayleigh distribution. Chen and Gui (2021) [6] estimated the unknown parameters of truncated normal distribution. Mahto et al. (2021) [7] introduced statistical inference for progressive stress accelerated from the Burr X distribution. Almetwally et al. (2021) [8] discussed Bayesian and non-Bayesian estimation methods to estimate parameters of the Marshall–Olkin alpha power Weibull distribution.
Abd El-Raheem et al. (2021) [9] discussed accelerated life tests for modified Kies exponential lifetime distribution. Almongy et al. (2021) [10] discussed parameter estimation of the Weibull generalized exponential distribution. There are lots of other studies on this subject.
Sometimes, it is not acceptable to perform the test on some of the tested units, though these units have not failed. In this status, at each failure, the form of removal is random. It is proposed that any testing unit being withdrawn from the life test is independent of the others but with the same probability . To treat this problem, there are various types of distributions used in reliability and engineering fields to deal with this type of censoring. The most widely used are binomial and geometric distribution. Yuen and Tse (1996) [11] used binomial distribution and a distribution of probability for progressive removal (random removals). Tse et al. (2000) [12] analyzed Weibull distribution data under Type-II progressive censoring with binomial removals. Ashour et al. (2021) [13] estimated the Weibull parameters under progressive first-failure with binomial removals. Alshenawy et al. (2020) [14] discussed progressive type-II censored samples of extended odd Weibull exponential distribution with binomial removals. Ghahramani et al. (2020) [15] analyzed the progressive Type-II censored sample with dependent random removals.
Since the Weibull distribution lacks a bathtub or upside-down bathtub-shaped hazard rate feature, it cannot be used to model a system’s complex lifetime, according to Peng and Yan (2014) [16]. Hence, many extensions of the Weibull distribution are raised to overcome this deficiency. For instance, Mudholkar and Srivastava (1993) [17] introduced an exponential Weibull distribution. Several modified Weibull distributions with bathtub-shaped failure rate functions were proposed by Xie et al. (2002) [18]. Murthy et al. (2004) [19] and Pham and Lai (2007) [20] introduced detailed overviews of the different developments in extensions of the Weibull distribution. Bebbington et al. (2007) [21] presented a flexible Weibull extension. Nadarajah et al. (2011) [22] introduced a beta-generalized Weibull distribution. Singla et al. (2012) [23] presented a beta-generalized Weibull distribution. The Weibull extension (WE) distribution was introduced by Yong (2004) [24] for modeling data in various fields, such as engineering, medicine, and reliability.
It would be advantageous for models with bathtub-shaped failure rate functions to be an extension of Weibull distribution because the Weibull distribution is highly used. It is necessary to consider models with few parameters to obtain accurate estimates of the parameters in the case of a small data size. Even for a Weibull distribution with two parameters, parameter estimation is a difficult task. Maximum likelihood estimation is one of the techniques that can be used to estimate the parameters. Although the most widely used approach for model estimation is maximum likelihood estimation, it does not include a closed-form solution. As a consequence, many techniques, such as the maximum product of spacing (MPS) method and the Bayesian method, can be used to estimate the model parameters.
Cheng and Amin (1979) [25] proposed the MPS estimation method. Ranneby (1984) [26] discussed this method as an alternative to the maximum likelihood estimation (MLE) method for the estimation of parameters of continuous univariate distributions. It gives efficient estimators for more distributions, such as three-parameter Gamma–Log normal or Weibull distribution. Cheng and Amin (1983) [27] discuss the MPS consistency and asymptotic properties, as well as the fact that when they exit, the MPS is at least as effective as the MLEs.
The major objective of this paper is to address the estimation problem of the WE distribution parameters when the data are progressively type-II censored with binomial removals. Here, the MLE of the model parameters is derived. The MPS of this model is discussed. Moreover, the Bayesian estimation method is derived and the Markov Chain Monte Carlo (MCMC) method is used to find an approximate value of integrals of the posterior model parameters. The performance of the MLE, MPS and Bayesian estimation methods are investigated numerically for different sample sizes and parameter values.
The rest of this paper is organized as follows. The model description and notations are introduced in Section 2. MLE, MPS, and Bayesian estimation methods are given in Section 3. We provide a simulation study in Section 4. In Section 5, the transformer insulation application of real data is discussed. Finally, some remarks are offered in Section 6.
2. Model Description and Notations
Suppose a random variable has WE distribution with parameter vector . The reliability function of WE distribution is given by Yuen and Tse (1996) [11] as follows:
The corresponding hazard rate function of the WE model has the following form:
and the pdf is given by the following:
The cumulative distribution function for the new Weibull extended distribution is given by the following:
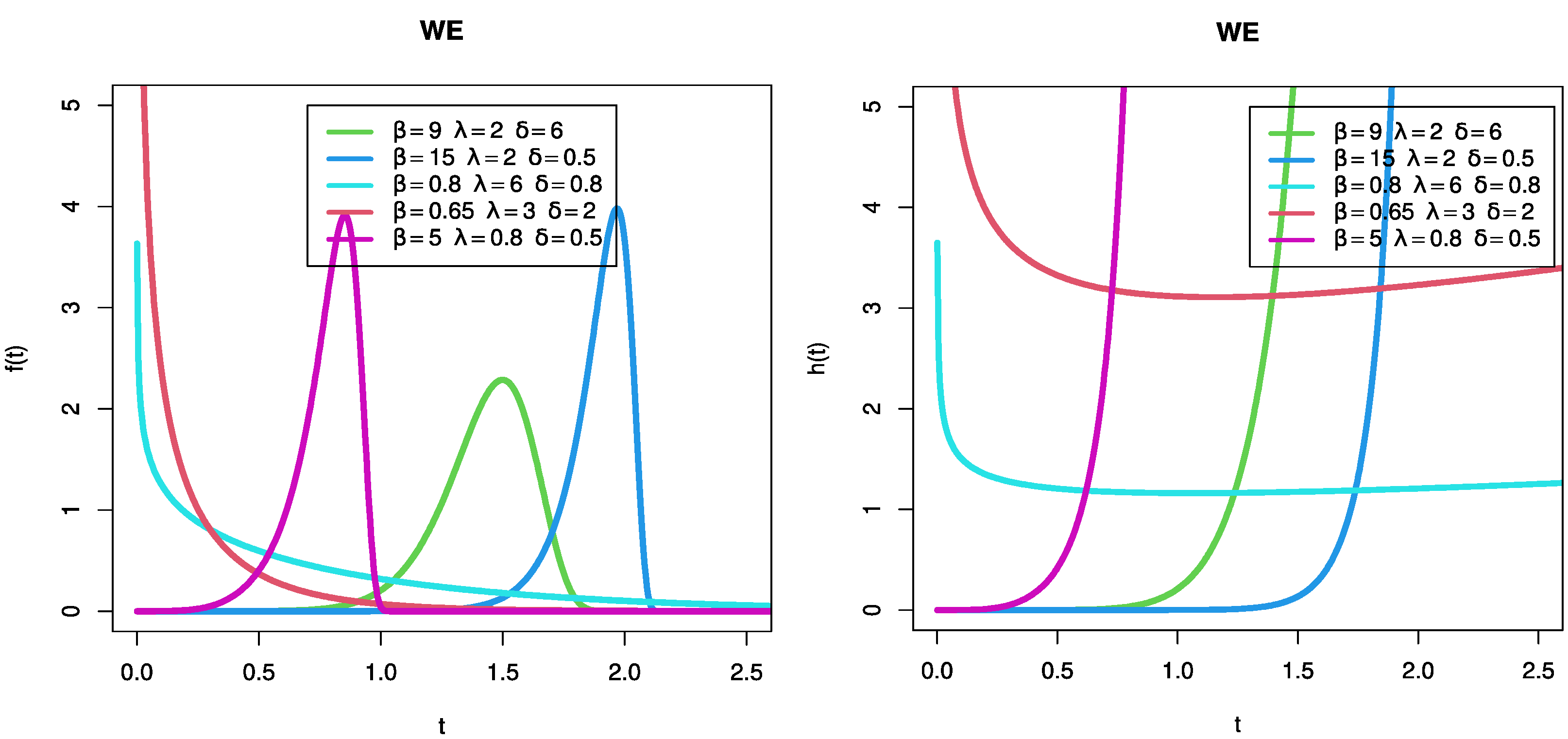
A versatile model that provides left-skewed, symmetrical, right-skewed, and reverse-J-shaped densities is the WE distribution (See
Figure 1
left). Its hazard rate (HR) feature can provide decreasing, steady, rising, upside down bathtub, bathtub, and reverse-J-shaped risk rates (see
Figure 1
right).
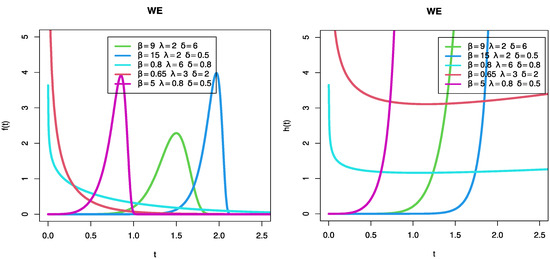
Figure 1.
Different possible shapes of the WE density and hazard function for several parametric values.
The quantile function of the WE distribution is as follows:
The progressive type-II censored scheme (PTIICS) can be described as follows:
Assume that independent observations have been set on life testing and the progressive censoring scheme . At the time of the first failure, , and units are randomly removed from the remaining surviving items. At the time of the second failure,
and units of the remaining
are randomly removed, and so on. The test continues until the th failure at which time, all the remaining
units are removed.
The experimenter determines the number of m failures and the removal probability
in PTIIC. Assume that each unit being excluded from the test is independent of the others but has the same removal probability as the others. Then, at each failure time, the number of units removed follows a binomial distribution, as follows: for and . The data form is as follows: .
The probability mass function for the number of units removed at each failure time, it’s a binomial distribution, is as follows:
while for i = 2, 3, …, m − 1.
where . Moreover, suppose that
is independent of for all i. Then the joint likelihood function can be derived as follows:
where i.e.,
𝔓’s MLE can be quickly calculated by maximizing Equation (8). As a result, the MLE of P can be found by solving the equation below.
Hence,
Since does not require the binomial parameter , then the likelihood function under PTIICS can be written as
In MPS, the joint MPS under PTIICS can be written in the same mode as follows:
where
where is a constant that does not depend on parameters and the following is true:
3. The MLE, MPS, and Bayesian Estimation Methods under PTIICS
The MLE, MPS, and Bayesian estimation methods of WE distribution parameters based on PTIICS data with binomial random removal are discussed in this section.
3.1. MLE Method
Using Equation (9), the likelihood function for WE distribution based on PTIICS can be written as follows:
where is a constant that does not depend on the parameters.
The natural logarithm of the likelihood function equation can be obtained as follows:
For convenience, , hence the partial derivatives of Equation (12) are given as follows:
and
The MLE has no tractable expression since the above Equations (13)–(15) are difficult to solve analytically. However, through the use of statistical tools, they can be approached by regular optimization algorithms, such as the Newton–Raphson, Nelder–Mead or quasi-Newton Broyden–Fletcher–Goldfarb–Shannon (BFGS) algorithms.
3.2. MPS Method
Using Equation (9), the MPS function of WE distribution based on PTIICS can be written as follows:
where is a constant which does not depend on the parameters. The natural logarithm of the product spacing function is as follows:
Let , then the partial derivatives by the MPS method of Equation (17) are given as follows:
and
where .
Using the Newton–Raphson algorithm, the MPS estimates of the WE distribution parameters can be obtained.
3.3. Bayesian Estimation
We consider the Bayesian approximation in this section for estimating the WE distribution parameters based on PTIICS under the assumption that the random variables have an independent prior distribution of gamma, assuming that , and . Then, the prior joint density of , and can be written as follows:
The posterior probability can be interpreted as a proportion to the probability equation product (11) and the densities of the joint prior to Equation (21):
Then, the posterior joint density of is as follows:
The squared error (SE) of the loss function, which is the symmetric loss function used, can be defined by . The Bayes method leads to the estimator , which, if the SE loss function is applied, is called the Bayes estimator. Under the SE loss function, the usual estimator of the parameters is the posterior mean. Therefore, the Bayesian estimators of the parameters under SE, say is obtained as the posterior mean, as follows:
where the conditional posterior densities are defined as follows:
and
It is very difficult, analytically, to solve these integrals, so the MCMC method will be used. Gibb’s sampling and more general Metropolis within Gibbs samplers are an important sub-class of the MCMC techniques. Such an algorithm was first developed by Metropolis et al. (1953) [28] and Hastings (1970) [29].
The Metropolis–Hastings (M–H) algorithm is one of the two most popular examples of the MCMC method, along with Gibb’s sampling. The M–H algorithm is similar to acceptance–rejection sampling in that it assumes that a candidate value can be derived from a proposal distribution as a normal distribution for each iteration of the algorithm.
4. Simulation Study
For estimating parameters of the WE distribution in a lifetime under PTIICS, the Monte Carlo simulation was used to compare MLE, MPS, and Bayesian estimation methods. The following data were developed from the WE distribution, using Equation (5), where is distributed as the WE distribution for different true parameters as follows:
- (1)
- Case I: . See Table 1.
 Table 1. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case I.
Table 1. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case I. - (2)
- Case II: . See Table 2.
 Table 2. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case II.
Table 2. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case II. - (3)
- Case III: . See Table 3.
 Table 3. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case III.
Table 3. The MLE, MPS, and Bayesian of the WE parameters under the PTIICS with random removal for Case III.
After generating a sample from the WE distribution with different sample sizes as 40, 80, and 150, we determine different probability as 0.35 and 0.85 and determine the different size of the censored sample by using the ratio of affected as as 0.7 and 0.9, then . We generate the random removal of progressive censoring from binomial removal as the following:
Balakrishnan and Sandhu [3] defined the algorithm to generate progressive censoring scheme as follows:
Generate independent Uniform (0, 1) observations .
- ▪
- We define set .
- ▪
- We set .
- ▪
- We generate WE distributed based on PTIICS as follows:
The MLE estimators are obtained by solving Equations (13)–(15). The MPS estimators are obtained by solving Equations (18)–(20). We can use the Newton–Raphson algorithm to find the optimal solution of MLE. Berndt et al. (1974) [30] discussed the Newton–Raphson algorithm. To find the root of a parameter’s estimators of WE distribution based on PTIICS by MLE and MPS method, we use the next algorithm:
- (1)
- Start with a near value of the true value as initial values satisfying .
- (2)
- Jacobian matrix defined over the function vector can be defined as:where is a first derivative.
- (3)
- The root can be found improved iteratively as the following:
- (4)
- Repeat these steps times as 10,000 to get an estimator of .
The Bayesian estimators are obtained by using the M–H algorithm to generate a sequence of draws from WE distribution parameters under PTIICS, as follows:
- (1)
- Start with any initial values satisfying .
- (2)
- Choose a candidate point based on the initial value from the proposal as normal with mean and variance is ).
- (3)
- Calculate the acceptance rate , for = 0 to N (a big number such as 10,000, for example), given the candidate point , .
- (4)
- Draw a value of u from the uniform (0, 1) distribution .
- (5)
- Steps 2–4 should be repeated times more until we have draws.
- (6)
- For the squared error loss function, the Bayes approximation of is used .
- (7)
- To get a Bayesian approximation of repeat these steps times.
To find the best efficiency of estimators, we use the bias and the mean squared error () of estimation. To compute the MLE, MPS, and Bayesian, 10,000 such iterations are made.
Concluding Remarks on the Simulation
- Table 1, Table 2 and Table 3 show the simulation effects. Based on these Tables, the following concluding remarks have been made: Case-I: (β = 0.5, λ = 0.5, δ = 0.5).
- ▪
- At fixed values of p and r, the bias decreases for three estimations as increases.
- ▪
- The most accurate method is MLE, as it has a minimum square error (MSE).
- Case II: (β = 0.5, λ = 3, δ = 0.5).
- ▪
- As increase, the bias decreases for MLE, MPS, and Bayesian measures.
- ▪
- The Bayesian estimation method represents the most accurate method because it has a MSE less than the others.
- Case III: (β = 1.5, λ = 3, δ = 2).
- ▪
- The bias decreases as the sample size increases and the most accurate method is the Bayesian measure.
- ▪
- We find that Bayesian estimators are more reliable than MLE and MPS estimators in the vast majority of cases.
5. Transformer Insulation Application
A real dataset is analyzed in this section to explain the proposed model and methods in the preceding sections. In addition, this dataset is used to demonstrate that the WE distribution based on the PTIICS sample can be a potential alternative to commonly known distributions, such as extended odd Weibull exponential (EOW) distribution, which is discussed under the PTIICS sample by Alshenawy et al. (2020) [14]; exponential Lomax(EL) distribution, introduced by El-Bassiouny et al. (2015) [31]; Weibull Lomax (WL) which was introduced by Tahir et al. (2015) [32]; and Odds Exponential-Pareto IV (OEPIV) which was introduced by Baharith et al. (2020) [33].
Chapter three of the book by Nelson (1990) [34], presents the results of an accelerated constant-stress based on the PTIICS life test of transformer insulation. The test consisted of a 42:4 kV constant voltage, where 14.4 kV is the standard voltage. These data are 0.6, 13.4, 15.2, 19.9, 25.0, 30.2, 32.8, 44.4, *, 56.2, where the sign “*” in these data refers to censored results when R progressives are 0, 0, 0, 0, 0, 0, 0, 1, 0.
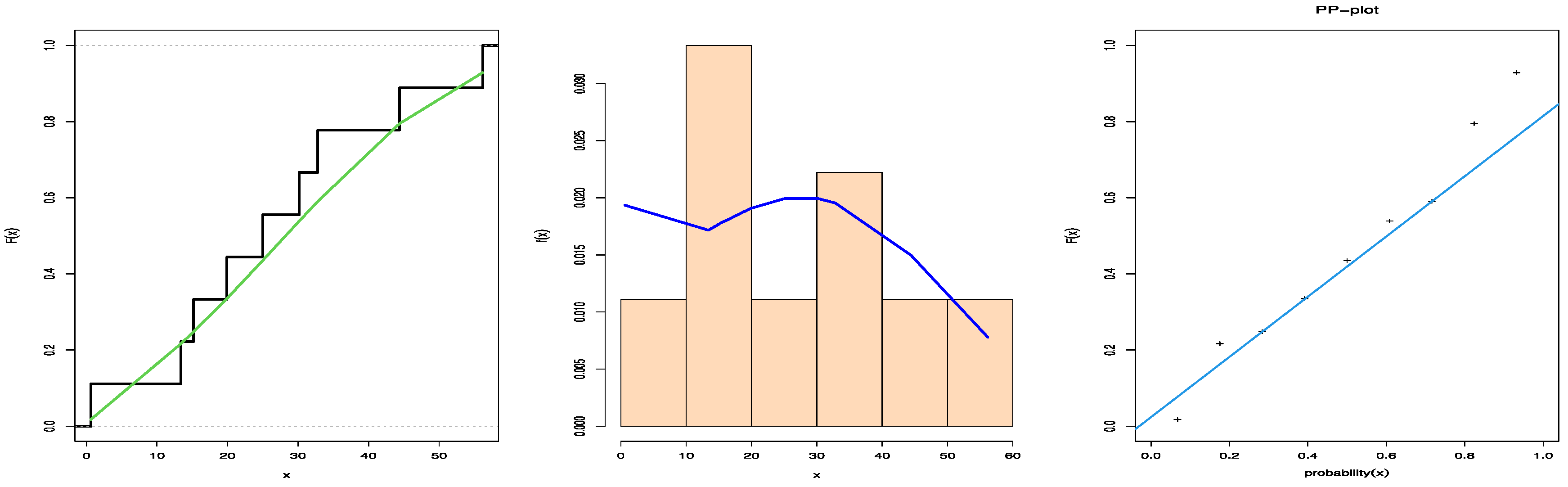
We explain how to conduct a goodness-of-fit test for the transformer insulation data and the proposed WE distribution based on PTIICS in the following subsection. The empirical cdf, the histogram of the pdf, and PP plots are displayed in Figure 2.
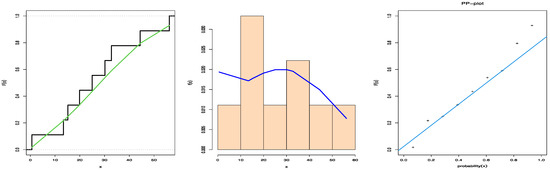
Figure 2.
Plots of empirical cdf, histogram, and PP plots for the WE distribution.
Modified Kolmogorov–Smirnov Algorithm for Censored Data Fitting
We have to use the modified Kolmogorov–Smirnov (KS) goodness-of-fit test if the data are PT-II censored data and not complete. Pakyari and Balakrishnanan (2012) [35] originally produced the modified KS (MKS) statistics for THE PTIICS data. This algorithm relies on a number of steps:
- (1)
- Estimate the parameters of WE distribution based on PTIICS.
- (2)
- Calculate the statistic of the MKS test as the following:where ,
- (3)
- By using the statistic of MKS test and sample size, we calculate the p-Value of this test.
The summary of the results of the MKS test for WE distribution and commonly known distributions, such as EOW, WL, EL, and OEPIV, are shown in Table 4 based on the results of MLE.

Table 4.
MLE for parameters of WE distribution and commonly known distributions under PTIICS for real data.
We conclude that the best model to fit the data of the transformer insulation is WE distribution based on PTIICS, according to the results of the MKS test with p-value, the Akaike information criterion (AIC), the corrected AIC (CAIC), and the Hannan–Quinn information criterion (HQIC). The WE distribution based on PTIICS has the smallest value of MKS, AIC, BIC, CAIC, and HQIC, and has the largest value of p-value.
Using the MLE, MPS, and Bayesian methods, Table 5 shows the parameter estimates and their standard errors (SEs) for the WE distribution based on PTIICS. We conclude that the Bayesian estimation method is the best.

Table 5.
MLE, MPS, and Bayesian estimation methods for parameters of WE distribution under PTIICS for real data.
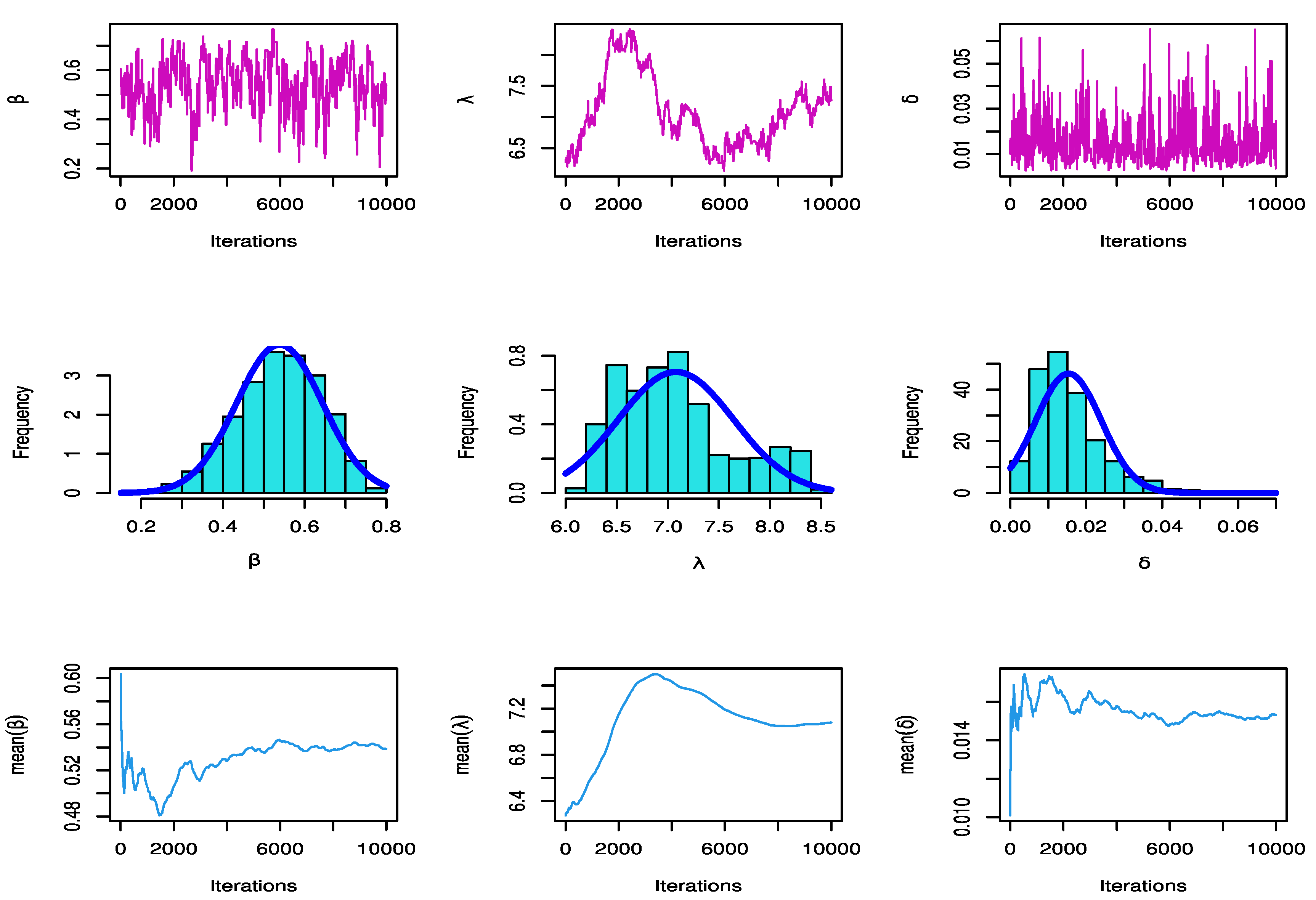
Figure 3 shows the history plots, estimated marginal posterior density, and MCMC convergence of , and .
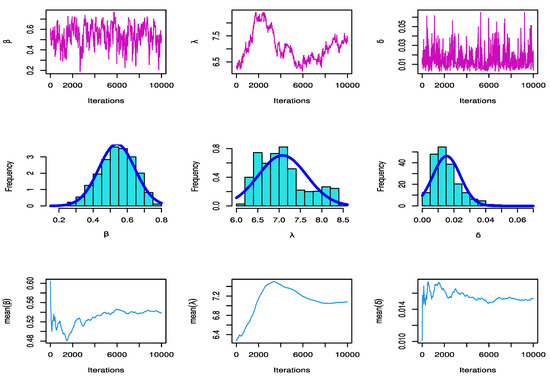
Figure 3.
The MCMC plots for data based on PTIICS.
6. Conclusions
In this article, the Bayesian estimation, MPS, and MLE methods were adopted for estimating the WE distribution parameters under a progressive type-II censored sample with binomial removals. Simulations were used to investigate the output of the three proposed estimators for various parameter values and sample sizes. The Newton–Raphson algorithm and Metropolis–Hastings algorithm were determined for the non-Bayesian and Bayesian estimation methods. Furthermore, the simulation results were used to investigate the effects of sample size, failure size, and removal probabilities on estimate accuracy. We may infer from our research that the Bayesian estimation method outperforms the MLE and MPS methods in estimating the WE parameters in PTIICS with random removal. Finally, to illustrate the methods of inference discussed in the paper, transformer insulation of real data from engineering fields was investigated.
Author Contributions
Methodology, H.M.A., E.M.A.; software, E.M.A.; formal analysis, D.A.A.; investigation, D.A.A.; data curation, H.M.A., F.Y.A.; writing—review and editing, F.Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
The author(s) received no specific funding for this study.
Data Availability Statement
Data is available in this paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest to report regarding the present study.
References
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Springer Science Business Media: Berlin/Heidelberg, Germany; Birkhauser Boston: Cambridge, MA, USA, 2000. [Google Scholar]
- Balakrishnan, N. Progressive censoring methodology: An appraisal. Test 2007, 16, 211. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Almongy, H.M. Maximum product spacing and Bayesian method for parameter estimation for generalized power Weibull distribution under censoring scheme. J. Data Sci. 2019, 17, 407–444. [Google Scholar] [CrossRef]
- Hashem, A.F.; Alyami, S.A. Inference on a New Lifetime Distribution under Progressive Type-II Censoring for a Parallel-Series Structure. Complexity 2021, 2021, 88–89. [Google Scholar] [CrossRef]
- Abu-Moussa, M.H.; Abd-Elfattah, A.M.; Hafez, E.H. Estimation of Stress-Strength Parameter for Rayleigh Distribution Based on Progressive Type-II Censoring. Inf. Sci. Lett. 2021, 10, 101–110. [Google Scholar]
- Chen, S.; Gui, W. Estimation of Unknown Parameters of Truncated Normal Distribution under Adaptive Progressive Type-II Censoring Scheme. Mathematics 2021, 9, 49. [Google Scholar]
- Mahto, A.K.; Tripathi, Y.M.; Wu, S.J. Statistical inference based on progressively type-II censored data from the Burr X distribution under progressive-stress accelerated life test. J. Stat. Comput. Simul. 2021, 91, 368–382. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Sabry, M.A.; Alharbi, R.; Alnagar, D.; Mubarak, S.A.; Hafez, E.H. Marshall-Olkin Alpha Power Weibull Distribution: Different Methods of Estimation Based on Type-I and Type-II Censoring. Complexity 2021, 2021, 440–445. [Google Scholar] [CrossRef]
- Abd El-Raheem, A.M.; Almetwally, E.M.; Mohamed, M.S.; Hafez, E.H. Accelerated life tests for modified Kies exponential lifetime distribution: Binomial removal, transformers turn insulation application and numerical results. AIMS Math. 2021, 6, 5222–5255. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Alharbi, R.; Alnagar, D.; Hafez, E.H.; El-Din, M.M.M. The Weibull Generalized Exponential Distribution with Censored Sample: Estimation and Application on Real Data. Complexity 2021, 2021, 73–85. [Google Scholar] [CrossRef]
- Yuen, H.K.; Tse, S.K. Parameters estimation for Weibull distributed lifetimes under progressive censoring with random removals. J. Stat. Comput. Simul. 1996, 55, 57–71. [Google Scholar] [CrossRef]
- Tse, S.K.; Yang, C.; Yuen, H.K. Statistical analysis of Weibull distributed lifetime data under Type II progressive censoring with binomial removals. J. Appl. Stat. 2000, 27, 1033–1043. [Google Scholar] [CrossRef]
- Ashour, S.K.; El-Sheikh, A.A.; Elshahhat, A. Inferences for Weibull parameters under progressively first-failure censored data with binomial random removals. Stat. Optim. Inf. Comput. 2021, 9, 47–60. [Google Scholar] [CrossRef]
- Alshenawy, R.; Al-Alwan, A.; Almetwally, E.M.; Afify, A.Z.; Almongy, H.M. Progressive type-II censoring schemes of extended odd Weibull exponential distribution with applications in medicine and engineering. Mathematics 2020, 8, 1679. [Google Scholar] [CrossRef]
- Ghahramani, M.; Sharafi, M.; Hashemi, R. Analysis of the progressively Type-II right censored data with dependent random removals. J. Stat. Comput. Simul. 2020, 90, 1001–1021. [Google Scholar] [CrossRef]
- Peng, X.; Yan, Z. Estimation and application for a new extended Weibull distribution. Reliab. Eng. Syst. Saf. 2014, 121, 34–42. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Xie, M.; Tang, Y.; Goh, T.N. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 505. [Google Scholar]
- Pham, H.; Lai, C.D. On recent generalizations of the Weibull distribution. IEEE Trans. Reliab. 2007, 56, 454–458. [Google Scholar] [CrossRef]
- Bebbington, M.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Saf. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M. General results for the beta-modified Weibull distribution. J. Stat. Comput. Simul. 2011, 81, 1211–1232. [Google Scholar] [CrossRef]
- Singla, N.; Jain, K.; Sharma, S.K. The beta generalized Weibull distribution: Properties and applications. Reliab. Eng. Syst. Saf. 2012, 102, 5–15. [Google Scholar] [CrossRef]
- Yong, T. Extended Weibull Distributions in Reliability Engineering. Bachelor’s Thesis, University of Science & Technology of China, Shenzhen, China, 2004. [Google Scholar]
- Cheng, R.; Amin, N. Maximum Product of Spacings Estimation with Application to the Lognormal Distribution; Mathematical Report 79-1; University of Wales IST: Cardiff, UK, 1979. [Google Scholar]
- Ranneby, B. The maximum spacing method. An estimation method related to the maximum likelihood method. Scand. J. Stat. 1984, 4, 93–112. [Google Scholar]
- Cheng, R.C.H.; Amin, N.A.K. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. Ser. B 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Berndt, E.R.; Hall, B.H.; Hall, R.E.; Hausman, J.A. Estimation and inference in nonlinear structural models. Ann. Econ. Soc. Meas. 1974, 3, 653–665. [Google Scholar]
- El-Bassiouny, A.H.; Abdo, N.F.; Shahen, H.S. Exponential lomax distribution. Int. J. Comput. Appl. 2015, 121, 24–29. [Google Scholar]
- Tahir, M.H.; Cordeiro, G.M.; Mansoor, M.; Zubair, M. The Weibull-Lomax distribution: Properties and applications. Hacet. J. Math. Stat. 2015, 44, 455–474. [Google Scholar] [CrossRef]
- Baharith, L.A.; Al-Beladi, K.M.; Klakattawi, H.S. The Odds Exponential-Pareto IV Distribution: Regression Model and Application. Entropy 2020, 22, 497. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans and Data Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Pakyari, R.; Balakrishnan, N. A general-purpose approximate goodness-of-fit test for progressively type-II censored data. IEEE Trans. Reliab. 2012, 61, 238–244. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).