Thermal Equation of State of Fe3C to 327 GPa and Carbon in the Core
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. In Situ XRD Experiments at the BL10XU Beamline at Spring-8
3. Results
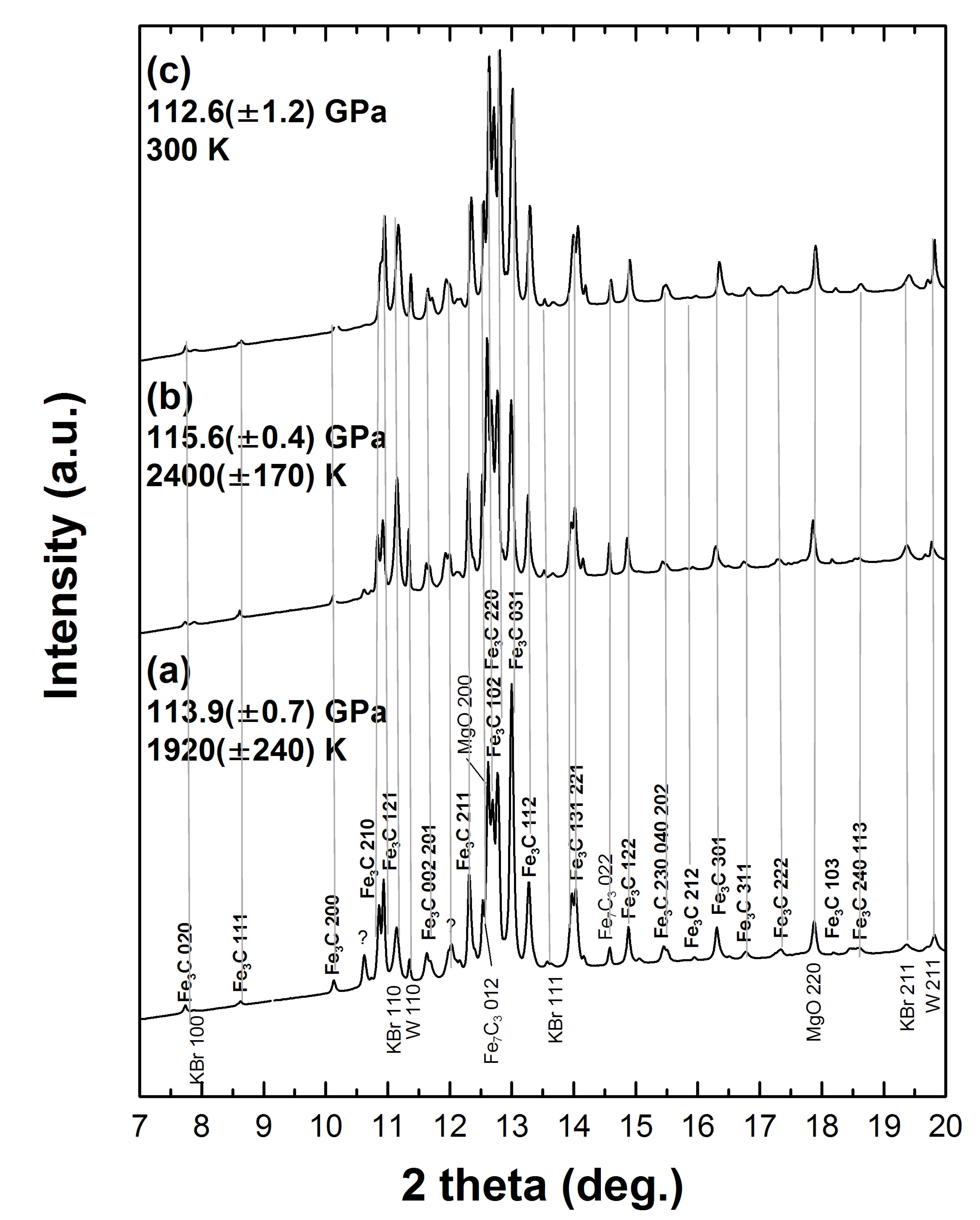
3.1. X-ray Diffraction Patterns of Fe3C
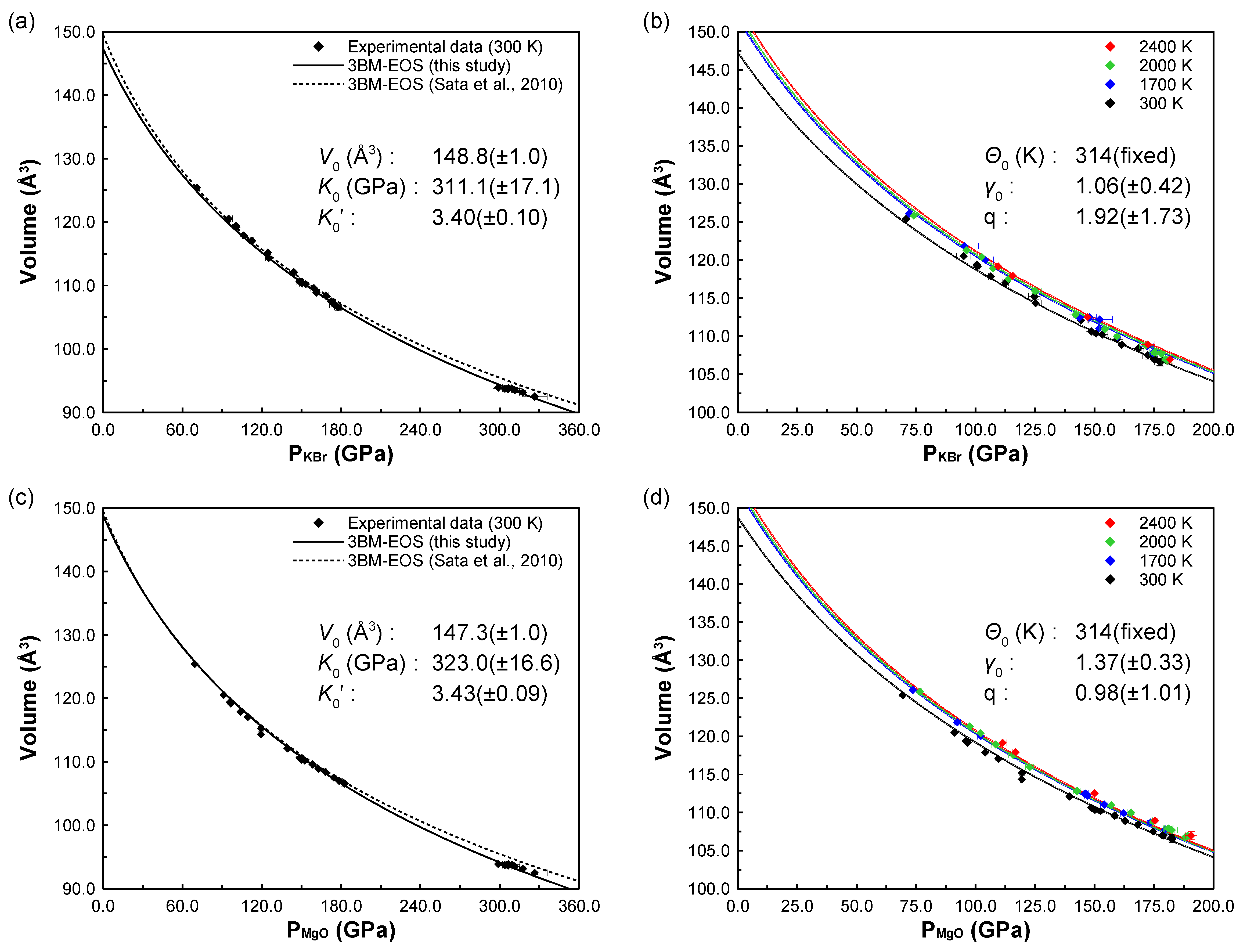
3.2. Compression Behavior and the Thermal Equation of State of Fe3C
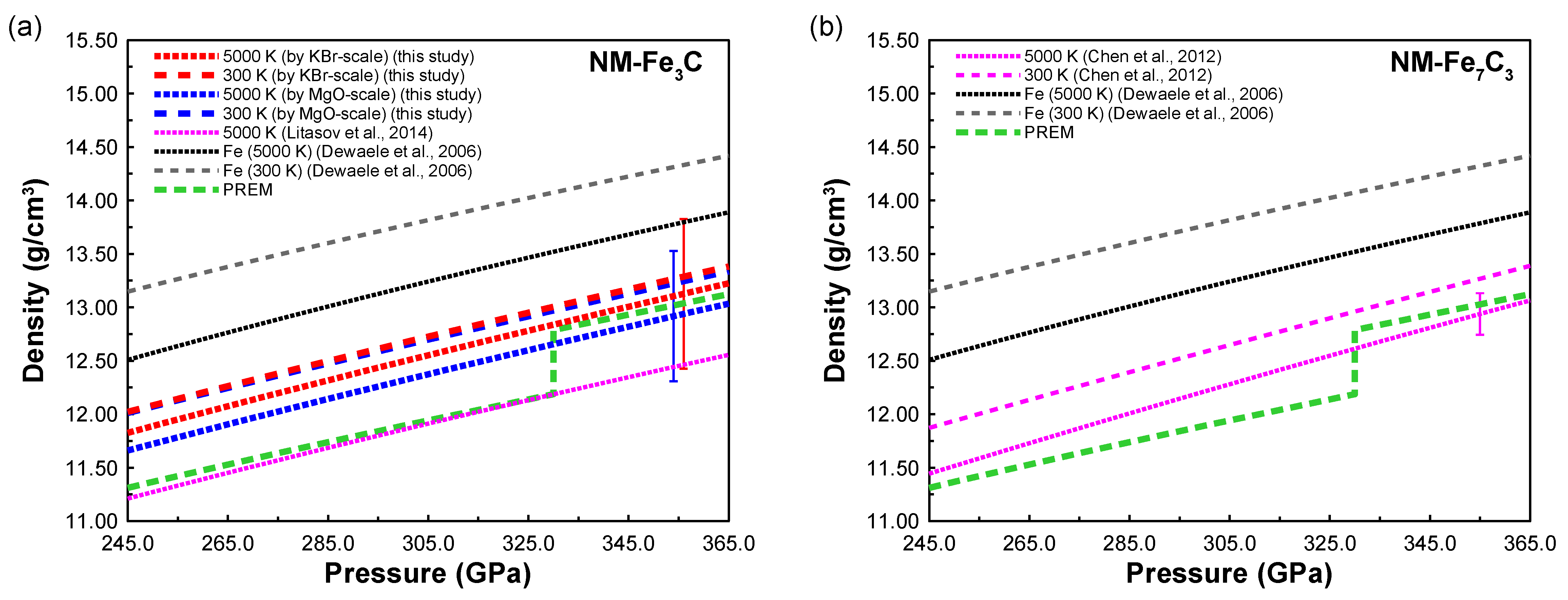
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Dubrovinskaia, N.; Narygina, O.; Kantor, I.; Kuznetzov, A.; Prakapenka, A.B.; Vitos, L.; Johansson, B.; Mikhaylushkin, A.S.; Simak, S.I.; et al. Body-centered cubic iron-nickel alloy in Earth’s core. Science 2007, 316, 1880–1883. [Google Scholar] [CrossRef] [PubMed]
- Vočadlo, L.; Alfe, D.; Gillan, M.J.; Price, G.D. The properties of iron under core conditions from first principles calculations. Phys. Earth Planet. Inter. 2003, 140, 101–125. [Google Scholar] [CrossRef]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 2199–2224. [Google Scholar] [CrossRef]
- Birch, F. Density and composition of mantle and core. J. Geophys. Res. 1964, 69, 4377–4388. [Google Scholar] [CrossRef]
- Brown, J.M.; McQueen, R.G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 1986, 91, 7485–7494. [Google Scholar] [CrossRef]
- Anderson, W.W.; Ahrens, T.J. An equation of state for liquid iron and implications for the Earth’s core. J. Geophys. Res. 1994, 99, 4273–4284. [Google Scholar] [CrossRef]
- Mao, H.K.; Wu, Y.; Chen, L.C.; Shu, J.F. Static compression of iron to 300 GPa and Fe0.8Ni0.2 alloy to 260 GPa: Implications for composition of the core. J. Geophys. Res. 1990, 95, 21737–21742. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Saxena, S.K.; Tutti, F.; Rekhi, S.; LeBehan, T. In-situ X-ray study of thermal expansion and phase transition of iron at multimegabar pressure. Phys. Rev. Lett. 2000, 84, 1720–1723. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.I.; Torrent, M. Quasihydrostatic equation of state of iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504–215507. [Google Scholar] [CrossRef]
- Sakai, T.; Takahashi, S.; Naoya Nishitani, N.; Mashino, I.; Ohtani, E.; Hirao, N. Equation of state of pure iron and Fe0.9Ni0.1 alloy up to 3 Mbar. Phys. Earth Planet. Inter. 2014, 228, 114–126. [Google Scholar] [CrossRef]
- Wood, B.J. Carbon in the core. Earth Planet. Sci. Lett. 1993, 117, 593–607. [Google Scholar] [CrossRef]
- Liu, J.; Lin, J.F.; Prakapenka, V.B.; Prescher, C.; Yoshino, T. Phase relations of Fe3C and Fe7C3 up to 185 GPa and 5200 K: Implication for the stability of iron carbide in the Earth’s core. Geophys. Res. Lett. 2016, 43, 12415–12422. [Google Scholar] [CrossRef]
- Mashino, I.; Miozzi, F.; Hirose, K.; Morard, G.; Sinmyo, R. Melting experiments on the Fe-C binary system up to 255 GPa: Constraints on the carbon content in the Earth’s core. Earth Planet. Sci. Lett. 2019, 515, 135–144. [Google Scholar] [CrossRef]
- Takahashi, S.; Ohtani, E.; Sakai, T.; Kamada, S.; Ozawa, S.; Sakamaki, T.; Ito, Y.; Hirao, N.; Ohishi, Y. Phase and melting relations of Fe3C to 300 GPa and carbon in the core. In Carbon in Earth’s Interior; AGU Monograph Volume; Manning, C.E., Lin, J.-F., Mao, W., Eds.; American Geophysical Union: Washington, DC, USA, 2019; Chapter 3; pp. 25–36. [Google Scholar]
- Hu, X.; Fei, Y.; Yang, J.; Cai, Y.; Ye, S.; Qi, M.; Liu, F.; Zhang, M. Phase stability and thermal equation of state of iron carbide Fe3C to 245 GPa. Geophys. Res. Lett. 2019. [Google Scholar] [CrossRef]
- Vočadlo, L.; Brodholt, J.; Dobson, D.P.; Knight, K.; Marshall, W.; Price, G.D.; Wood, I.G. The effect of ferromagnetism on the equation of state of Fe3C studied by first-principles calculations. Earth Planet. Sci. Lett. 2002, 203, 567–575. [Google Scholar] [CrossRef]
- Lin, J.F.; Struzhkin, V.V.; Mao, H.K.; Hemley, R.J.; Chow, P.; Hu, M.Y.; Li, J. Magnetic transition in compressed Fe3C from X-ray emission spectroscopy. Phys. Rev. B 2004, 70, 212405. [Google Scholar] [CrossRef]
- Prescher, C.; Dubrovinsky, L.; McCammon, C.; Glazyrin, K.; Nakajima, Y.; Kantor, A.; Merlini, M.; Hanfland, M. Structurally hidden magnetic transitions in Fe3C at high pressures. Phys. Rev. B 2012, 85, 10402. [Google Scholar] [CrossRef]
- Sata, N.; Hirose, K.; Shen, G.; Nakajima, Y.; Ohishi, Y.; Hirao, N. Compression of FeSi, Fe3C, Fe0.95O, and FeS under the core pressures and implication for light element in the Earth’s core. J. Geophys. Res. 2010, 115, B09204. [Google Scholar] [CrossRef]
- Litasov, K.D.; Sharygin, I.S.; Dorogokupets, P.I.; Shatskiy, A.; Gavryushkin, P.N.; Sokolova, T.S.; Ohtani, E.; Li, J.; Funakoshi, K. Thermal equation of state and thermodynamic properties of iron carbide Fe3C to 31 GPa and 1473 K. J. Geophys. Res. 2013, 118, 5274–5284. [Google Scholar] [CrossRef]
- Dewaele, A.; Belonoshko, A.B.; Garbarino, G.; Occelli, F.; Bouvier, P.; Hanfland, M.; Mezouar, M. High-pressure–high-temperature equation of state of KCl and KBr. Phys. Rev. B 2012, 85, 214105. [Google Scholar] [CrossRef]
- Kono, Y.; Irifune, T.; Higo, Y.; Inoue, T.; Barnhoon, A. P–V–T relation of MgO derived by simultaneous elastic wave velocity and in situ X-ray measurements: A new pressure scale for the mantle transition region. Phys. Earth Planet. Inter. 2010, 183, 196–211. [Google Scholar] [CrossRef]
- Ohishi, Y.; Hirao, N.; Sata, N.; Hirose, K.; Takata, M. Highly intense monochromatic X-ray diffraction facility for high-pressure research at SPring-8. High Press. Res. 2008, 28, 163–173. [Google Scholar] [CrossRef]
- Shen, G.; Mao, H.K.; Hemley, R.J. Laser-heated Diamond Anvil Cell Technique: Double-sided Heating with Multimode Nd:YAG Laser, in Advanced Materials ’96. In Proceedings of the 3rd NIRIM International Symposium on Advanced Materials, Tsukuba, Japan, 4–8 March 1996; pp. 149–152. [Google Scholar]
- Seto, Y.; Nishio-Hamane, D.; Nagai, T.; Sata, N. Development of a software suite on X-ray diffraction experiments. Rev. High Press. Sci. Technol. 2010, 20, 269–276. [Google Scholar] [CrossRef]
- Kuwayama, Y.; Hirose, K.; Sata, N.; Ohishi, Y. Pressure-induced structural evolution of pyrite-type SiO2. Phys. Chem. Miner. 2011, 38, 591–597. [Google Scholar] [CrossRef]
- Rainey, E.S.G.; Hernlund, J.W.; Kavner, A. Temperature distributions in the laser-heated diamond anvil cell from 3-D numerical modeling. J. Appl. Phys. 2013, 114, 204905. [Google Scholar] [CrossRef]
- Jackson, I.; Rigden, S.M. Analysis of P–V–T data: Constraints on the thermoelastic properties of high-pressure minerals. Phys. Earth Planet. Inter. 1996, 96, 85–112. [Google Scholar] [CrossRef]
- Li, J.; Mao, H.K.; Fei, Y.; Gregoryanz, E.; Eremets, M.; Zha, C.S. Compression of Fe3C to 30 GPa at room temperature. Phys. Chem. Miner. 2002, 29, 166–169. [Google Scholar] [CrossRef]
- Scott, H.P.; Williams, Q.; Knittle, E. Stability and equation of state of Fe3C to 73 GPa: Implications for carbon in the Earth’s core. Geophys. Res. Lett. 2001, 28, 1875–1878. [Google Scholar] [CrossRef]
- Ono, S.; Mibe, K. Magnetic transition of iron carbide at high pressures. Phys. Earth Planet. Inter. 2010, 180, 1–6. [Google Scholar] [CrossRef]
- Terasaki, H.; Kamada, S.; Sakai, T.; Ohtani, E.; Hirao, N.; Ohishi, Y. Liquidus and solidus temperature of a Fe-O-S alloy up to the pressures of the outer core: Implication for the thermal structure of the Earth’s core. Earth Planet. Sci. Lett. 2011, 232, 379–392. [Google Scholar] [CrossRef]
- Chen, B.; Gao, L.; Lavina, B.; Dera, P.; Alp, E.E.; Zhao, J.; Li, J. Magneto-elastic coupling in compressed Fe7C3 supports carbon in Earth’s inner core. Geophys. Res. Lett. 2012, 39, L18301. [Google Scholar] [CrossRef]
- Nakajima, Y.; Takahashi, E.; Sata, N.; Nishihara, Y.; Hirose, K.; Funakoshi, K.; Ohishi, Y. Thermoelastic property and high-pressure stability of Fe7C3: Implication for iron-carbide in the Earth’s core. Am. Mineral. 2011, 96, 1158–1165. [Google Scholar] [CrossRef]
| V0 (Å3) | K0 (GPa) | K0′ | EOS | Phase | Reference |
|---|---|---|---|---|---|
| 148.8 ± 1.0 | 311.1 ± 17.1 | 3.40 ± 0.10 | 3BM | NM | Model 1 (based on KBr EOS) |
| 147.3 ± 1.0 | 323 ± 16.6 | 3.43 ± 0.09 | 3BM | NM | Model 2 (based on MgO EOS) |
| 149.46 | 290 | 3.76 | 3BM | NM | Sata et al. [20] |
| 148.9 | 317 | 4.3 | 3BM | NM | Vočadlo et al. [17] |
| 155.3 | 174 | 4.8 | 3BM | - | Li et al. [30] |
| 155.2 | 175 | 5 | Vinet | PM | Litasov et al. [21] |
| 154.42 | 194 | 4.6 | Vinet | PM | Litasov et al., MGD [21] |
| 155.26 | 175.4 | 5.1 | 3BM | FM | Scott et al. [31] |
| 155.4 | 167 | 6.7 | Vinet | FM | Ono and Mibe [32] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, S.; Ohtani, E.; Ikuta, D.; Kamada, S.; Sakamaki, T.; Hirao, N.; Ohishi, Y. Thermal Equation of State of Fe3C to 327 GPa and Carbon in the Core. Minerals 2019, 9, 744. https://doi.org/10.3390/min9120744
Takahashi S, Ohtani E, Ikuta D, Kamada S, Sakamaki T, Hirao N, Ohishi Y. Thermal Equation of State of Fe3C to 327 GPa and Carbon in the Core. Minerals. 2019; 9(12):744. https://doi.org/10.3390/min9120744
Chicago/Turabian StyleTakahashi, Suguru, Eiji Ohtani, Daijo Ikuta, Seiji Kamada, Tatsuya Sakamaki, Naohisa Hirao, and Yasuo Ohishi. 2019. "Thermal Equation of State of Fe3C to 327 GPa and Carbon in the Core" Minerals 9, no. 12: 744. https://doi.org/10.3390/min9120744
APA StyleTakahashi, S., Ohtani, E., Ikuta, D., Kamada, S., Sakamaki, T., Hirao, N., & Ohishi, Y. (2019). Thermal Equation of State of Fe3C to 327 GPa and Carbon in the Core. Minerals, 9(12), 744. https://doi.org/10.3390/min9120744





