The Study on Numerical Simulation and Experiments of Four Product Hydrocyclone with Double Vortex Finders
Abstract
:1. Introduction
2. Mathematical Model of Turbulent Flow Field of Hydrocyclones
3. Numerical Simulation
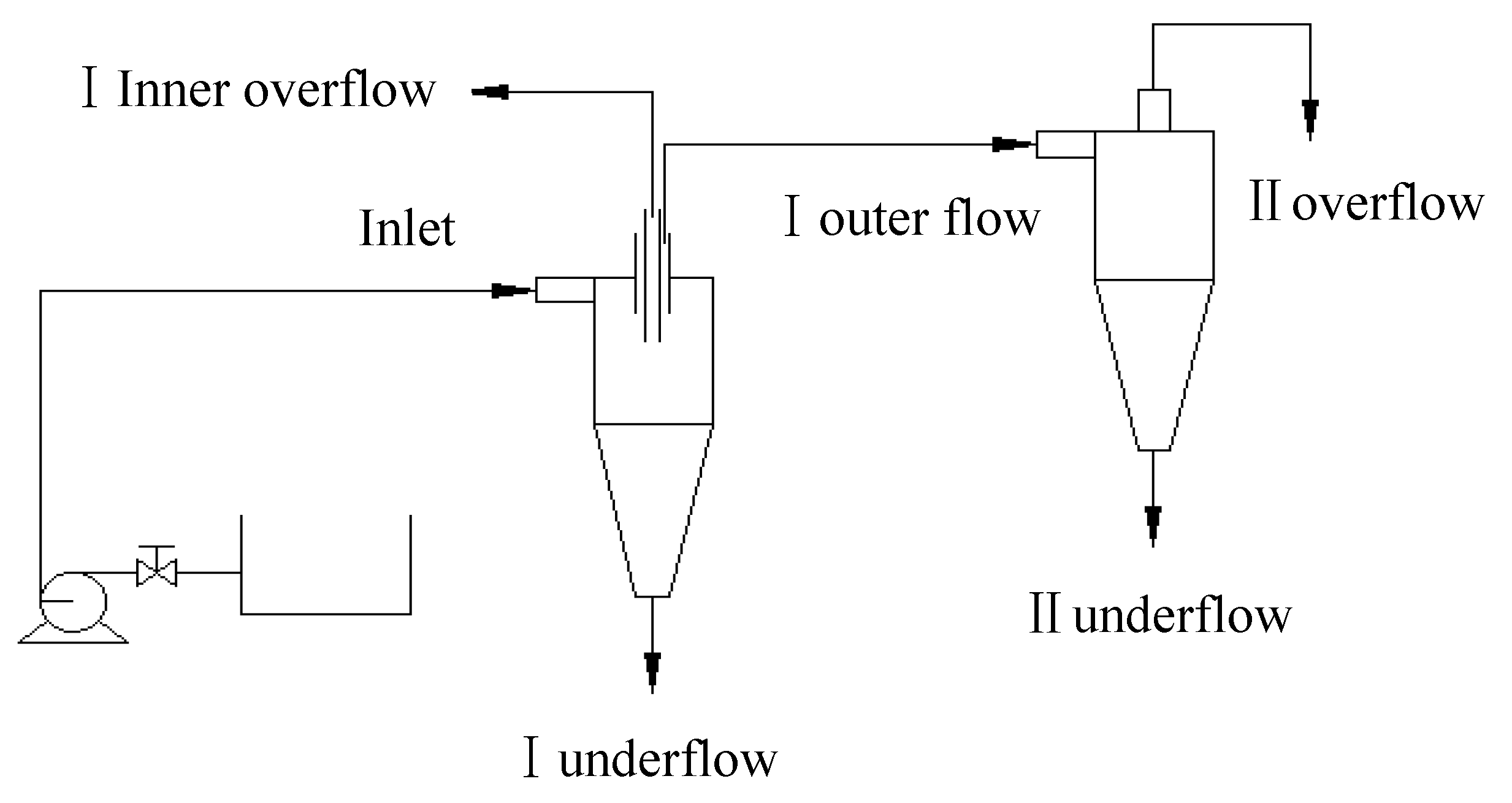
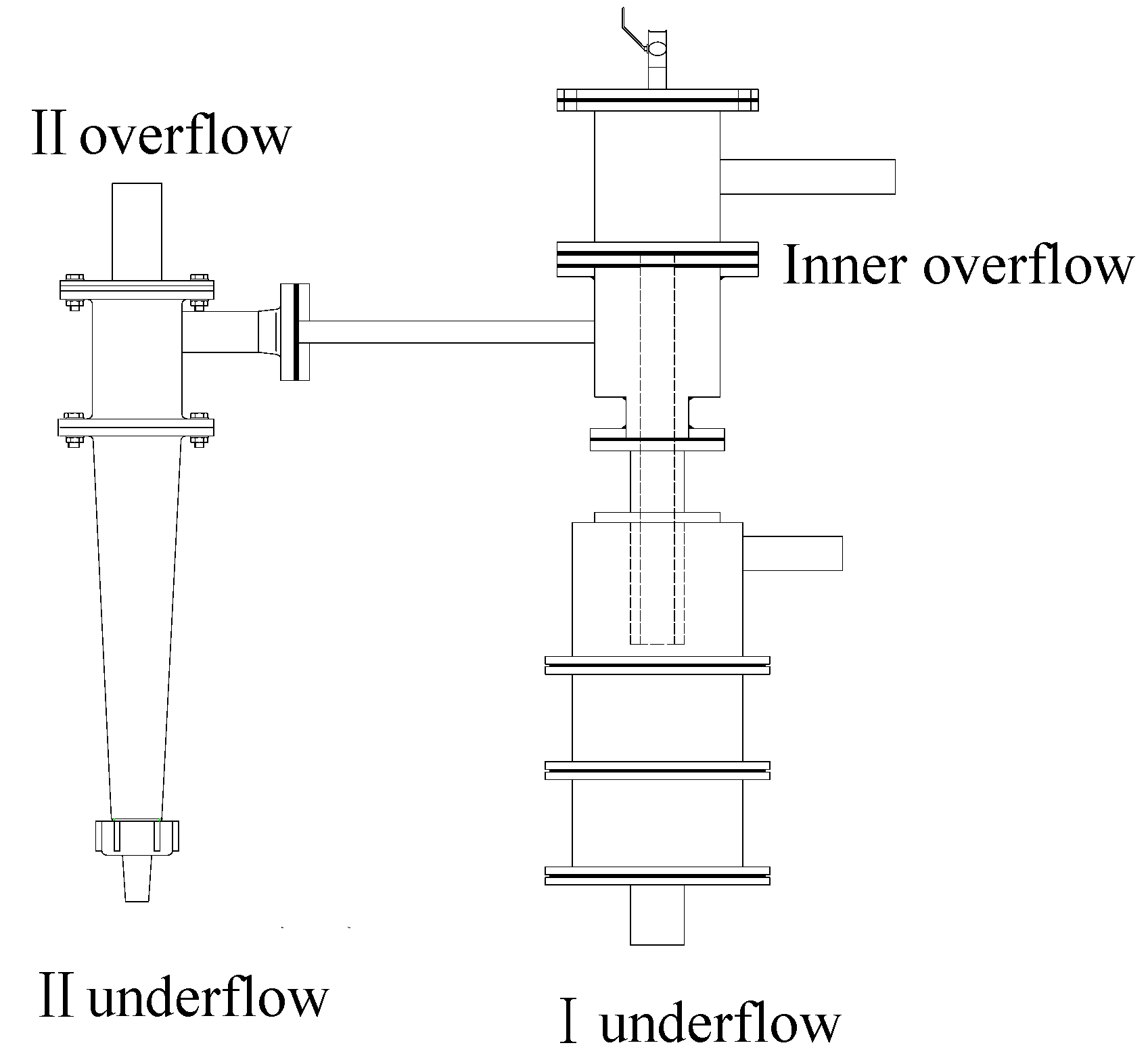
3.1. Modelling of Four Product Hydrocyclone
3.2. Numerical Simulation
3.2.1. Selection of Turbulence Model and Multi-Phase Flow Model
3.2.2. Boundary Condition and Calculation Scheme
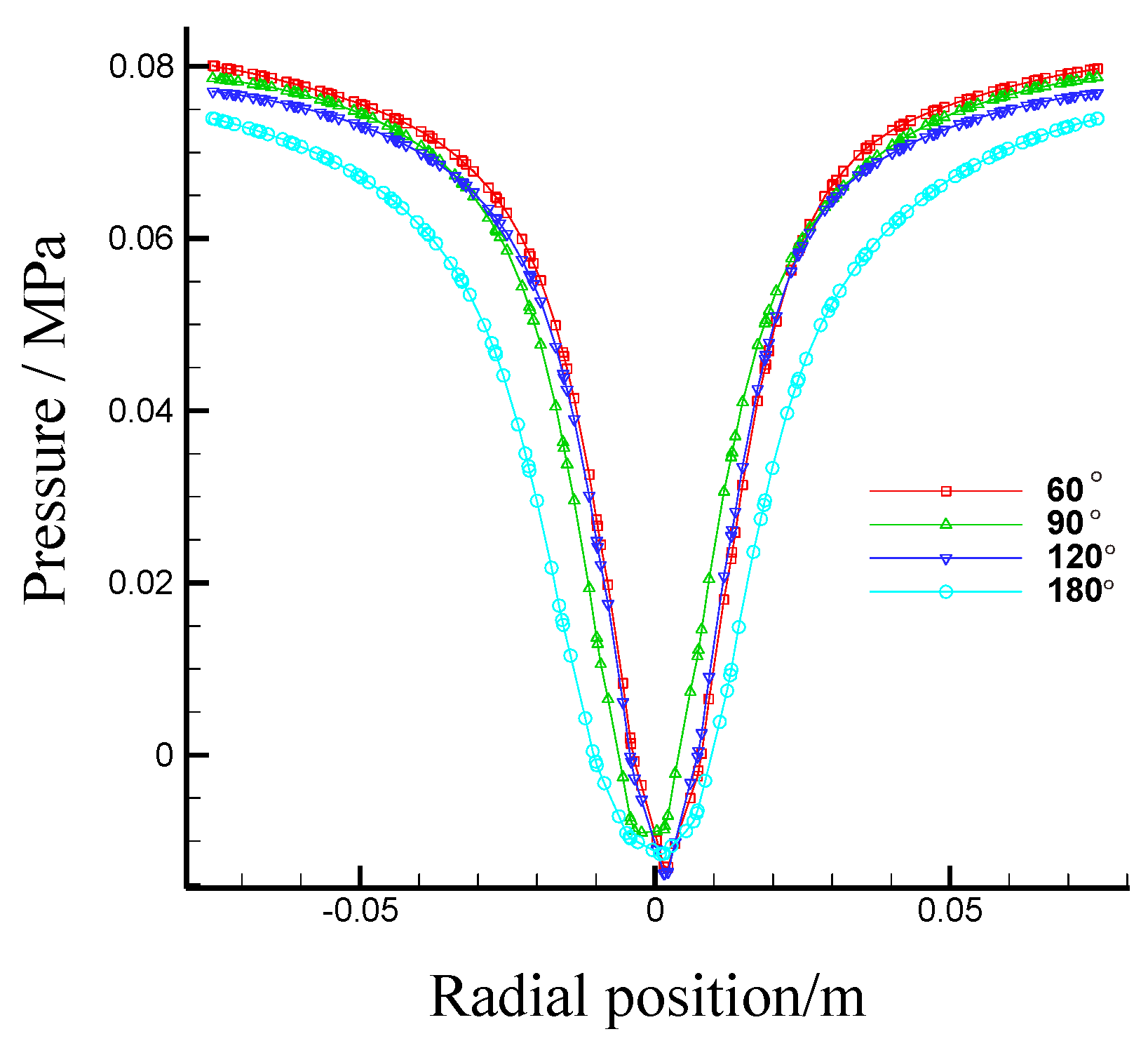
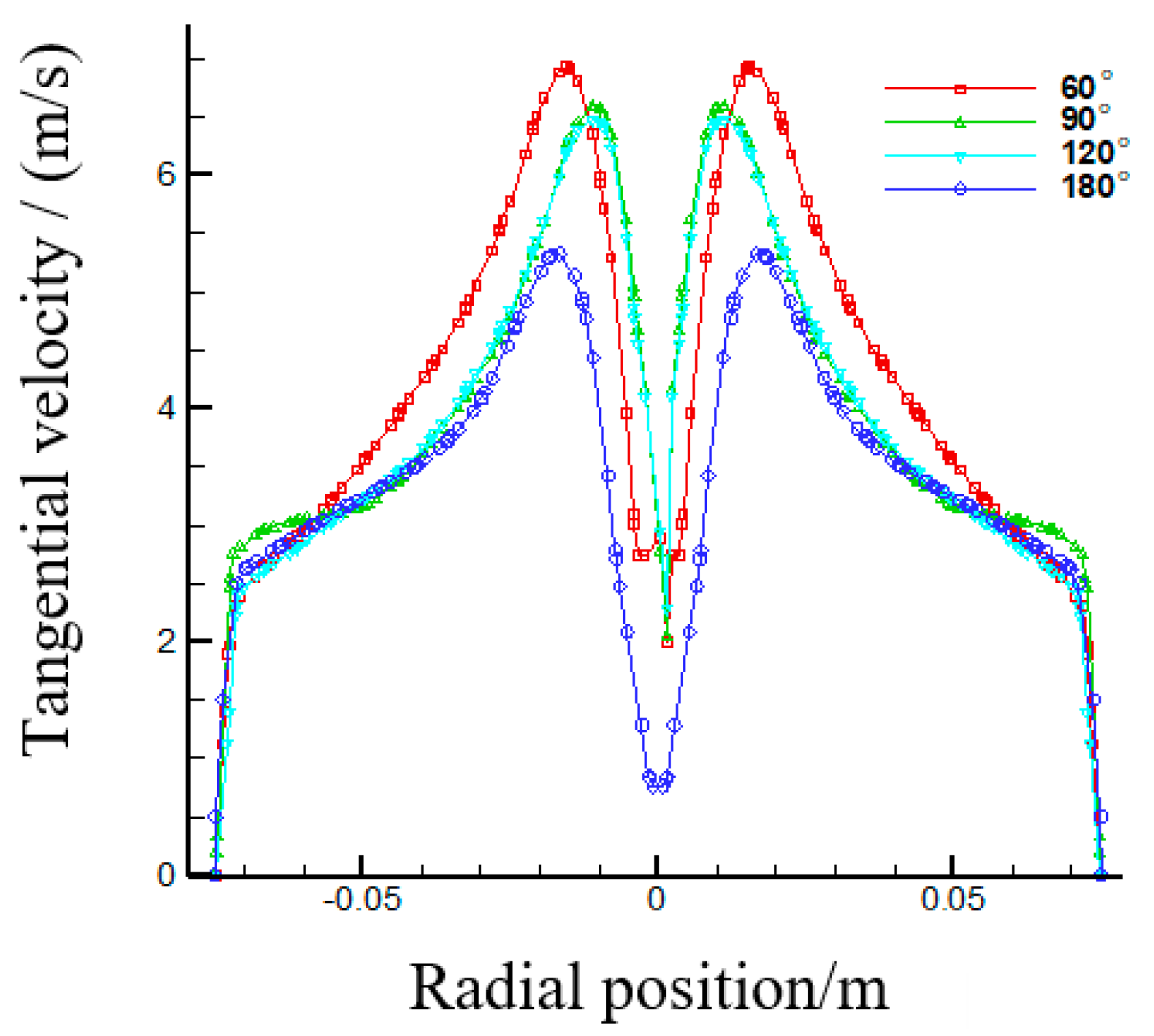
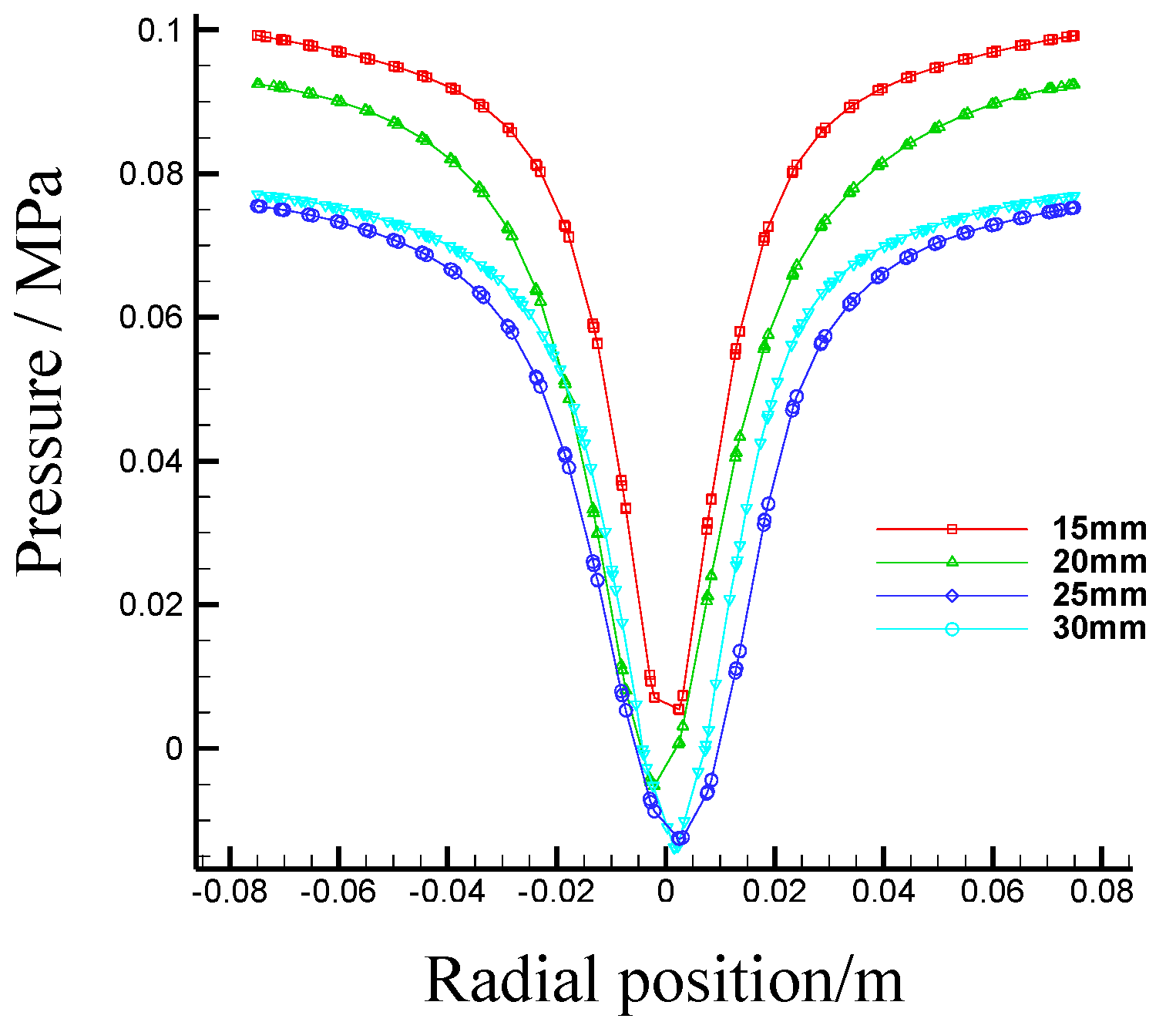
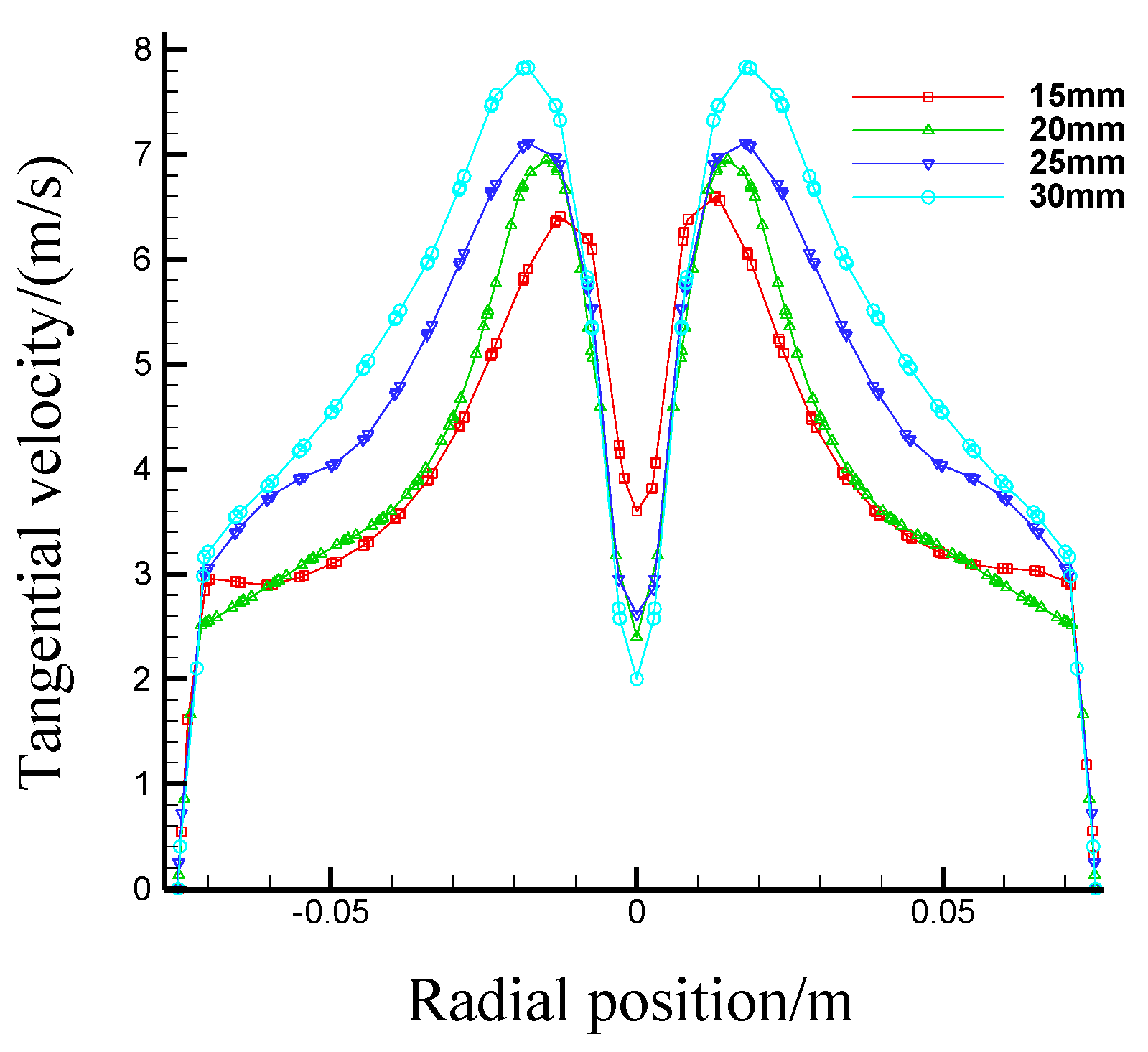
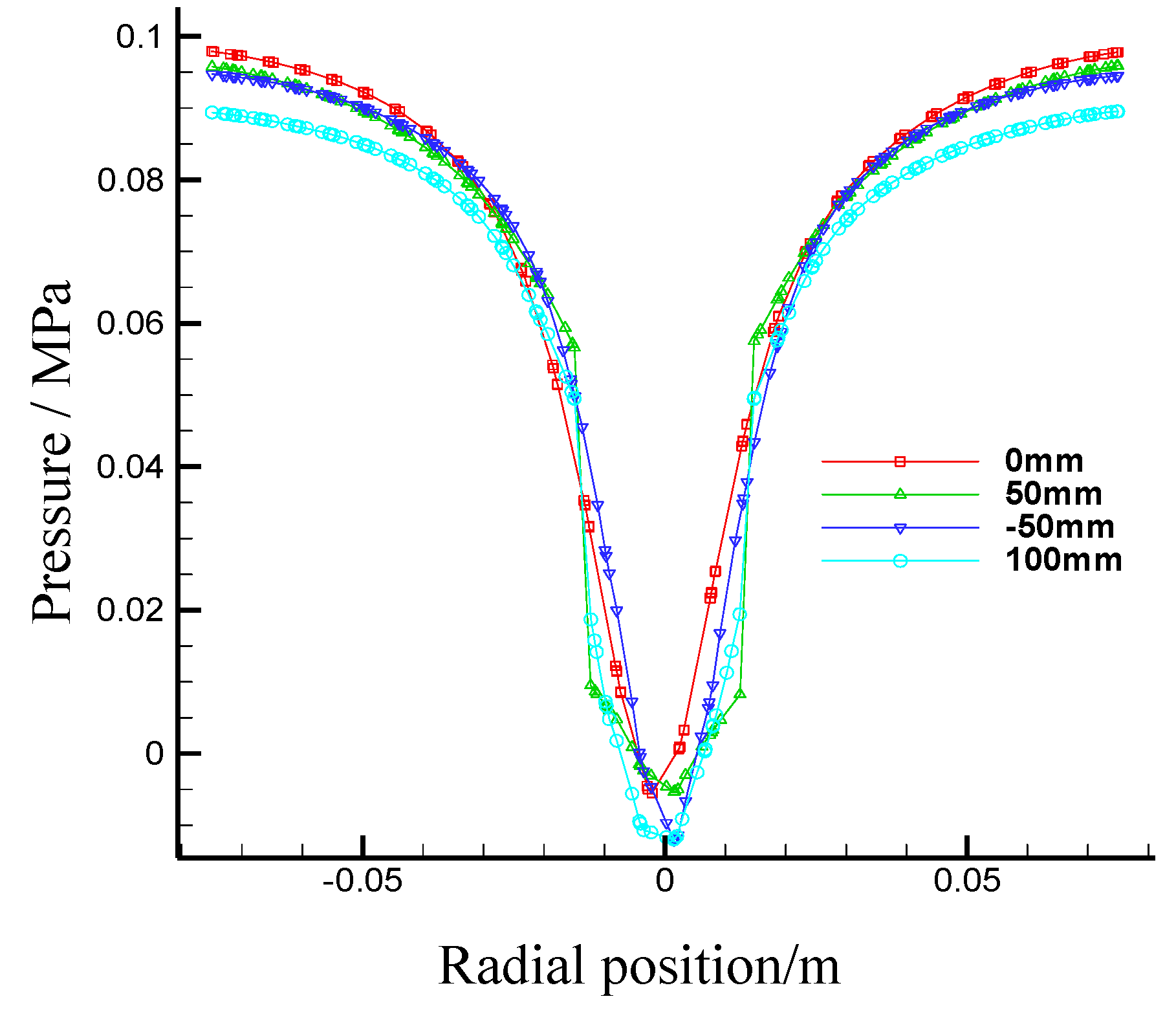
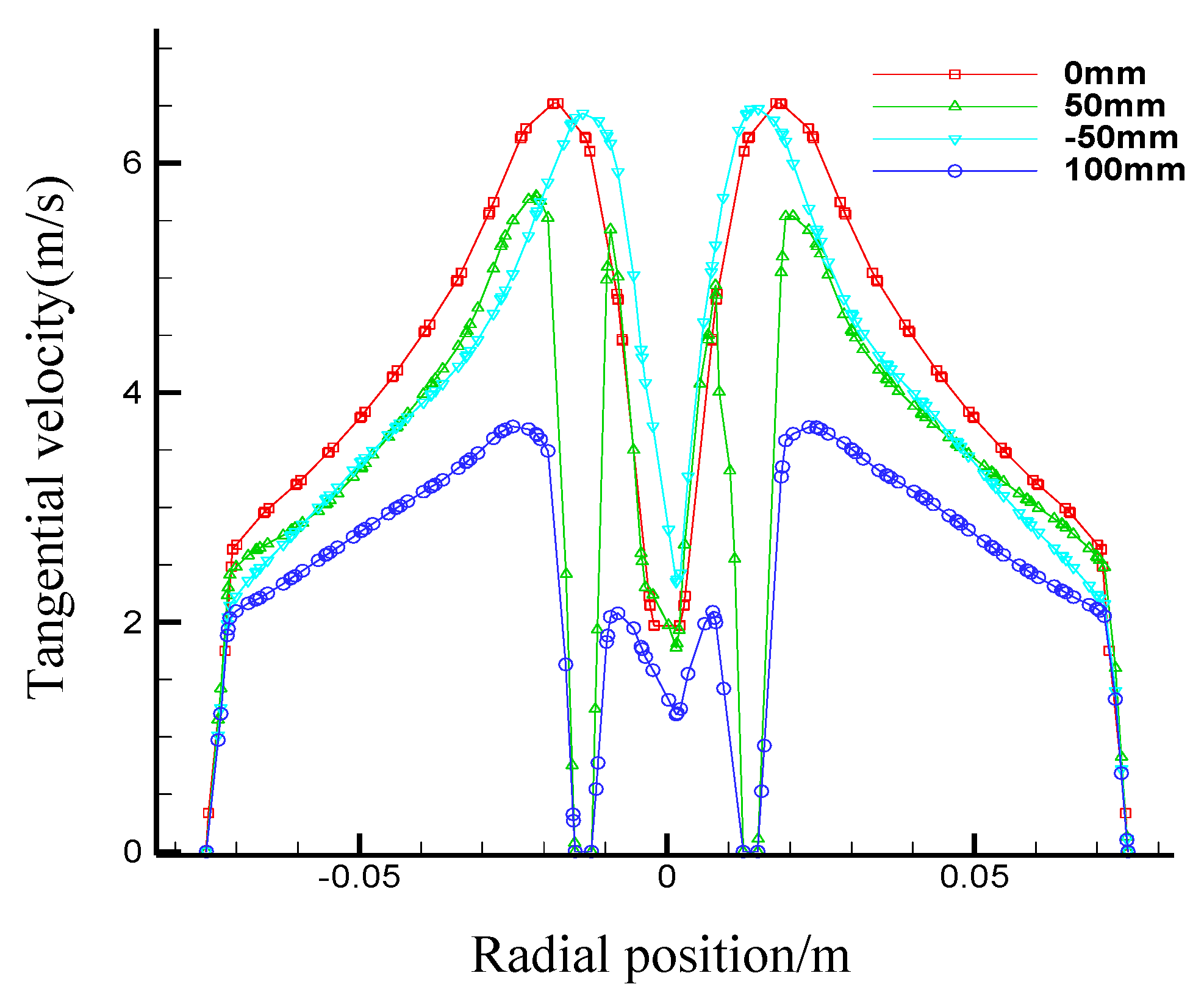
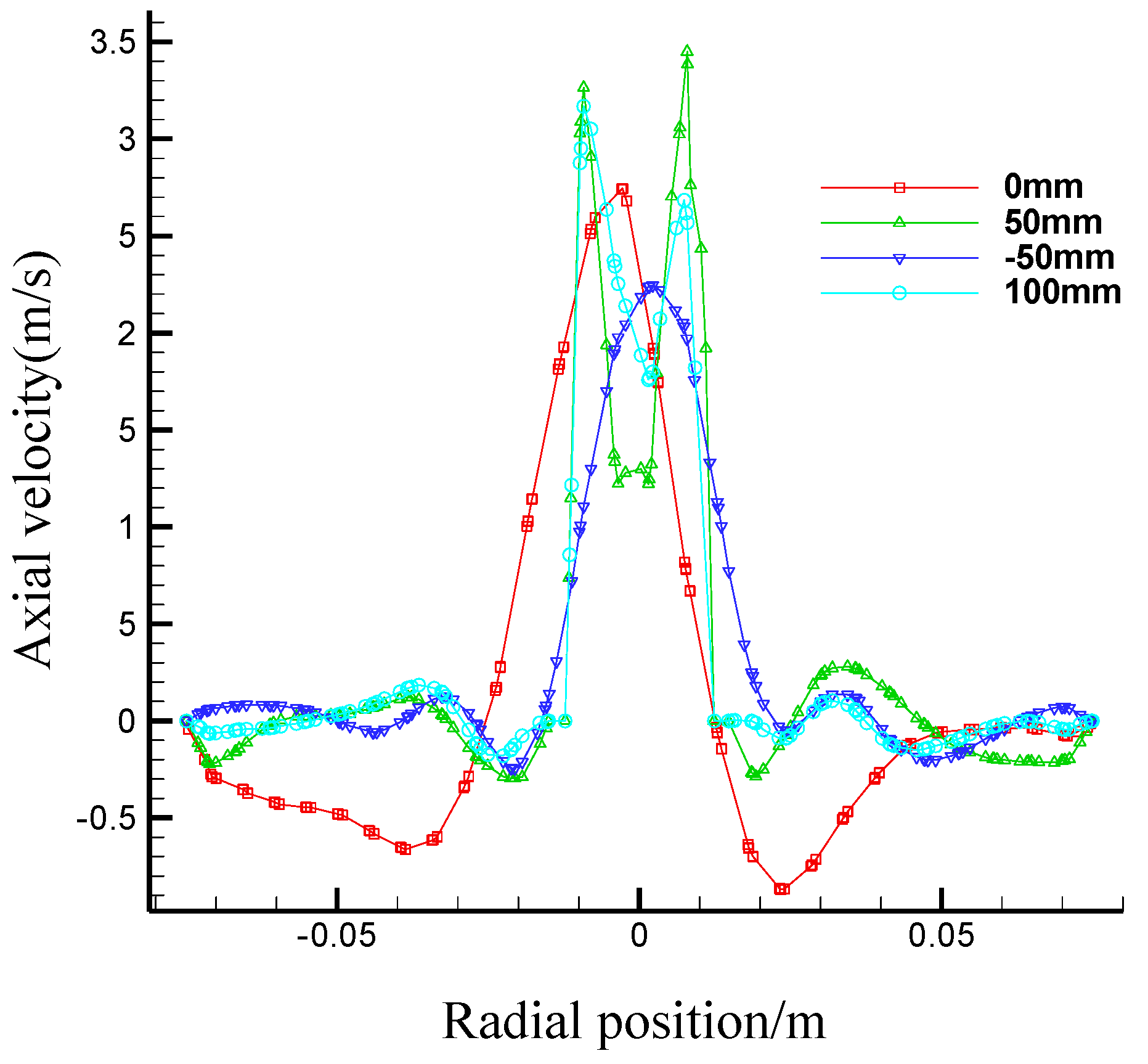
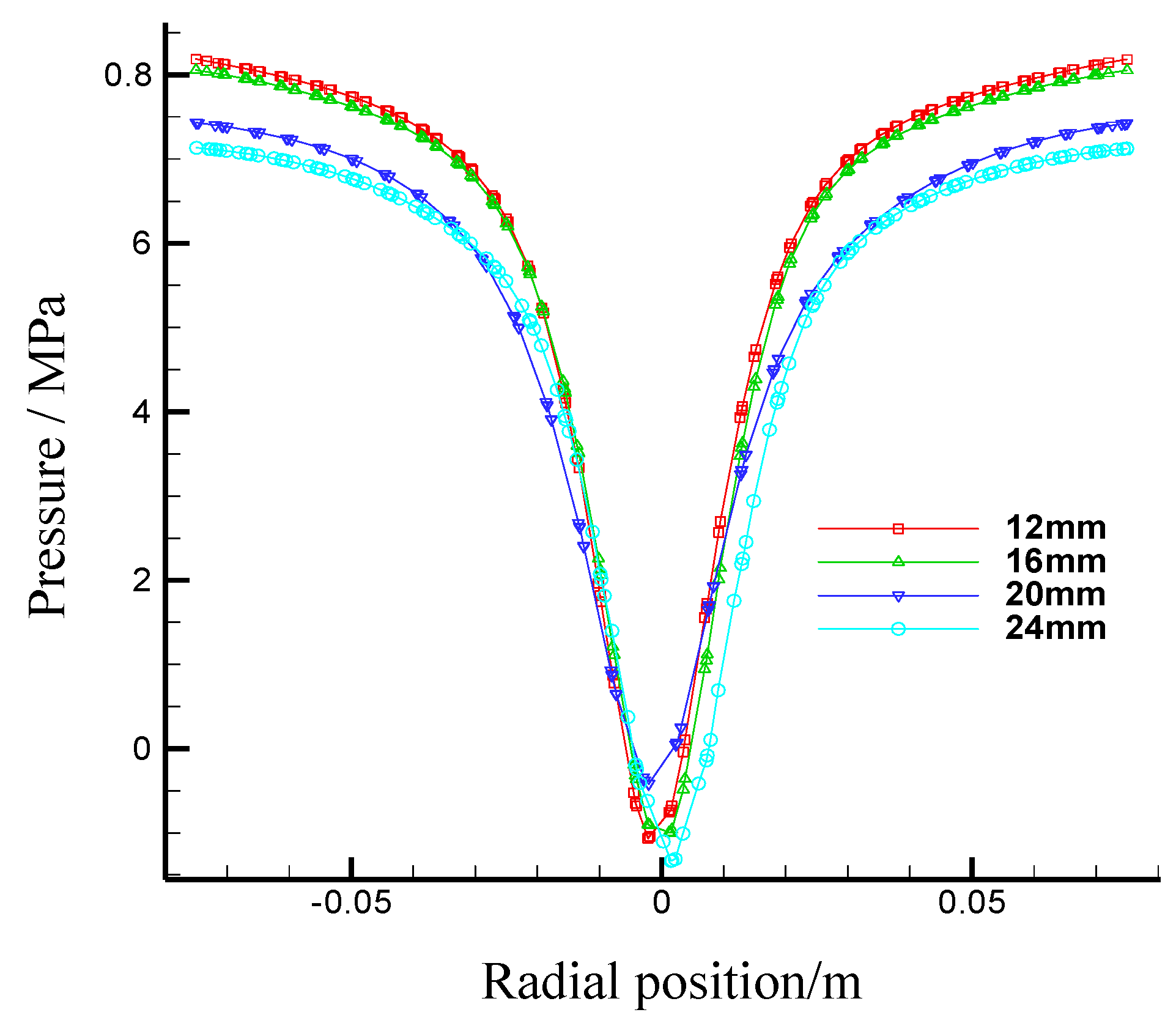
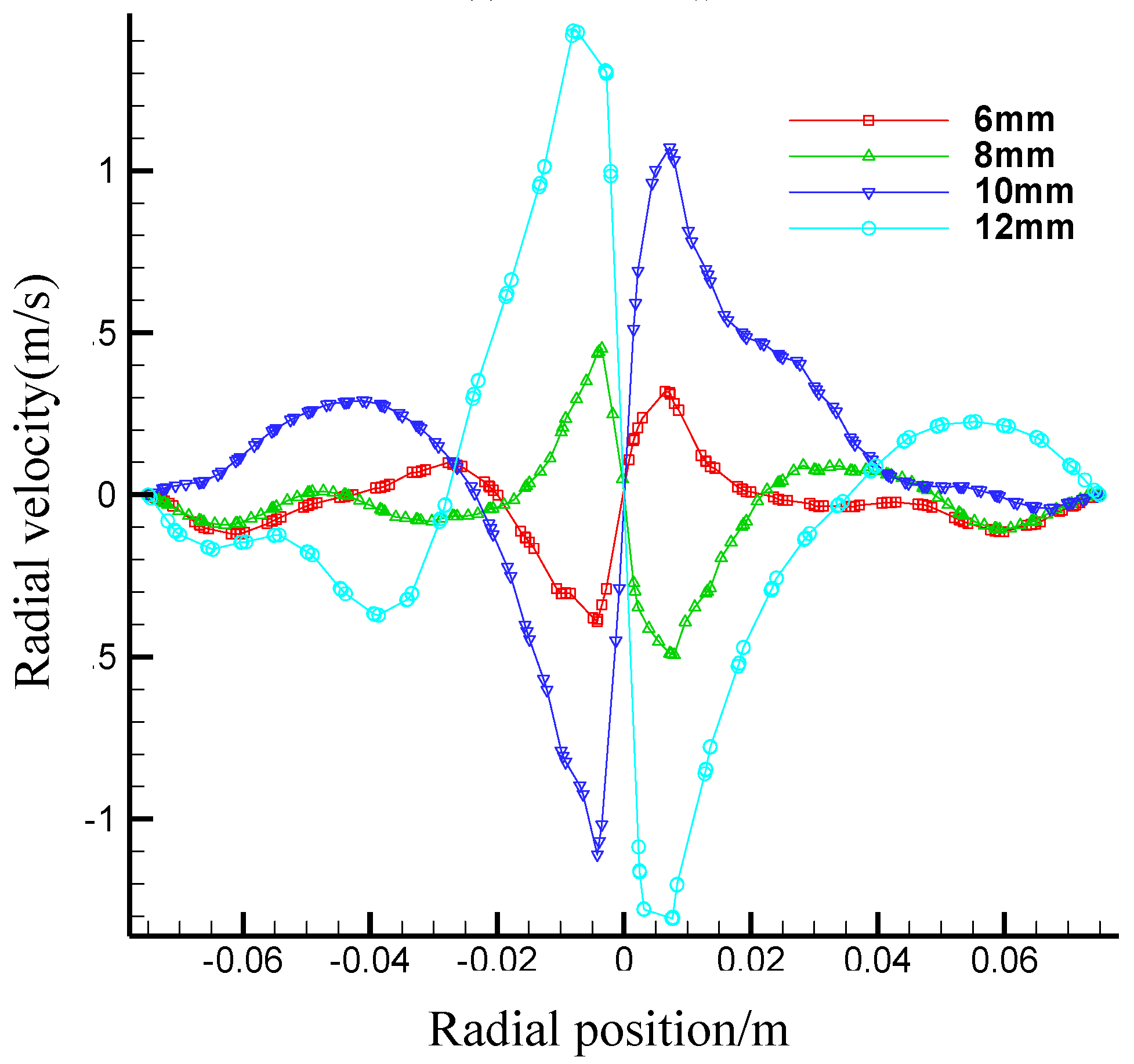
3.2.3. Simulation and Results Analysis
- Effects of the first section cone angle on the flow fields in the first section hydrocyclone
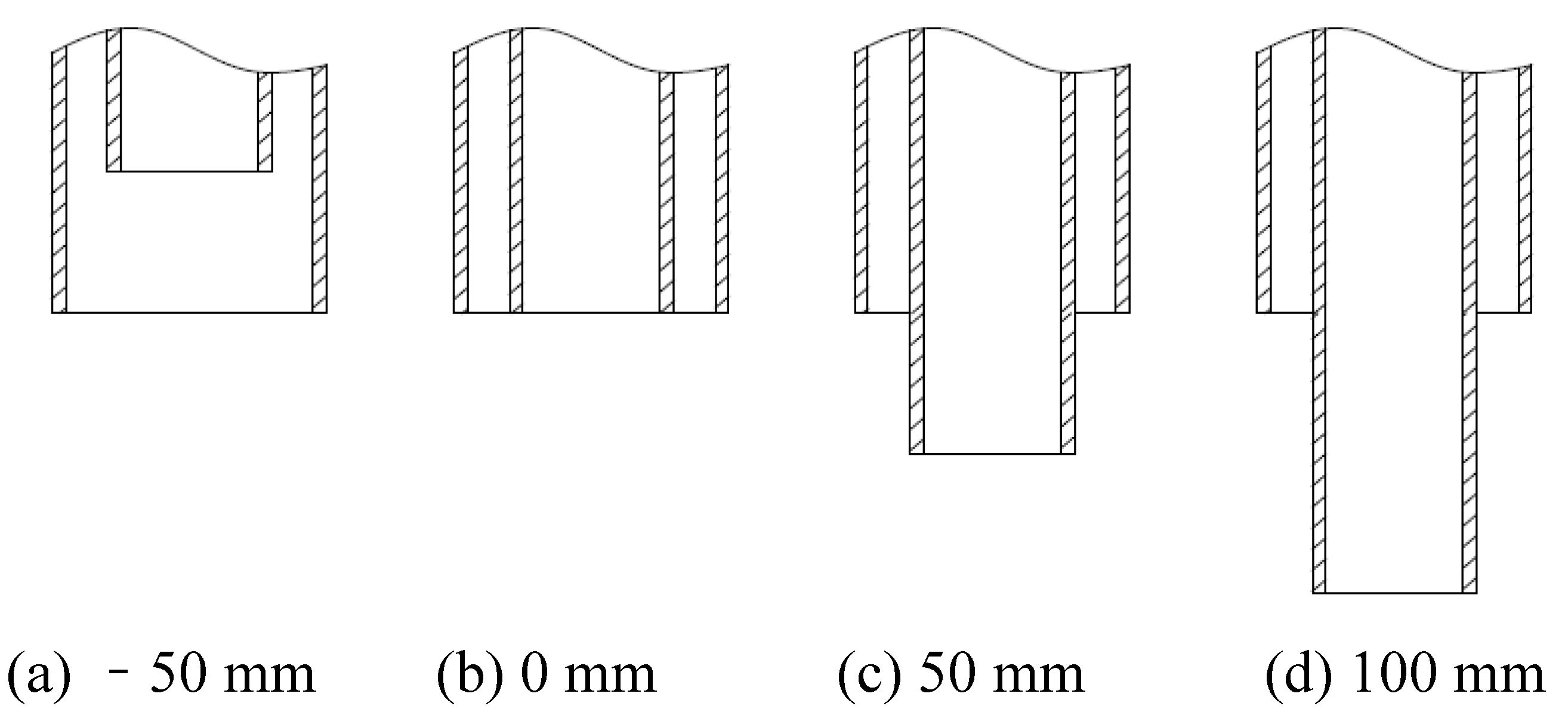
- Effects of the first section internal overflow pipe diameter on flow fields in the first section hydrocyclone
- Effects of the first section internal overflow pipe insertion depth on flow fields in the first section hydrocyclone
- Effects of the first section underflow outlet diameter on flow fields in the first section hydrocyclone
- Effects of the second section underflow outlet diameter on the first section hydrocyclone
4. Experimental Tests and Results
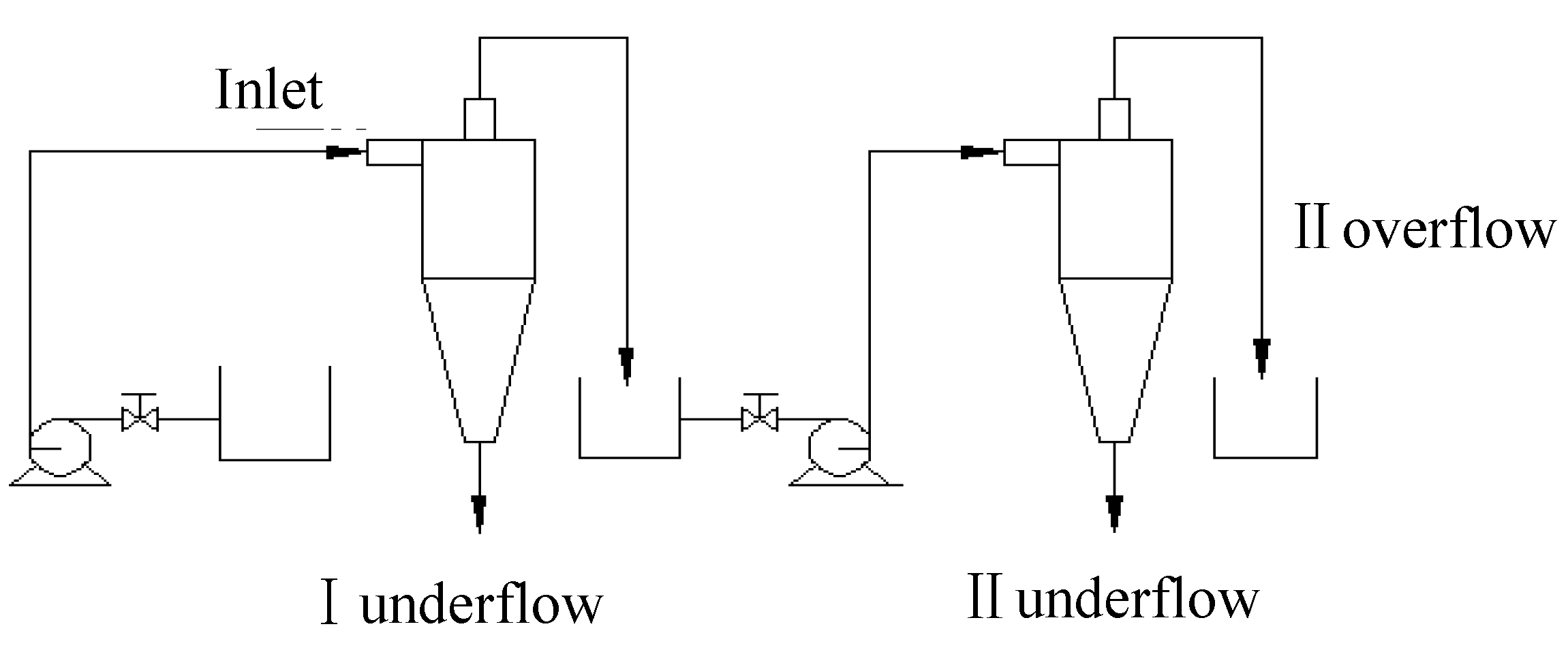
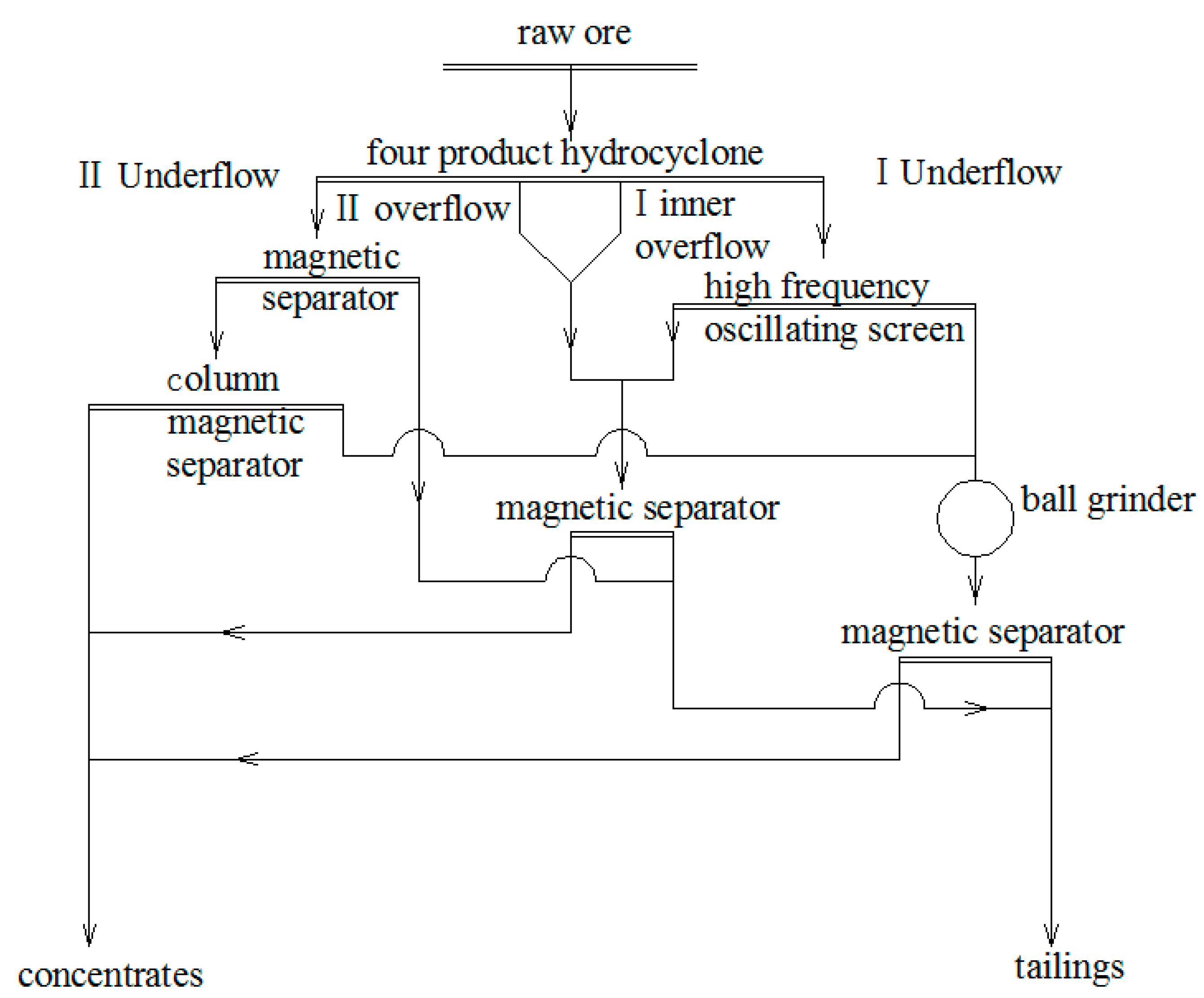
4.1. Procedure Design
4.2. Properties of Raw Ore
4.3. Hydrocyclone Design
4.4. Result Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vakamalla, T.R.; Kumbhar, K.S.; Ravi Gujjula, N.M. Computational and experimental study of the effect of inclination on hydrocyclone performance. Sep. Purif. Technol. 2014, 138, 104–117. [Google Scholar] [CrossRef]
- Svarovsky, L. Hydrocyclones; Technomic Publishing Co.: London, UK, 1984. [Google Scholar]
- Banerjee, C.; Chaudhury, K.; Majumder, A.K.; Chakraborty, S. Swirling flow hydrodynamics in hydrocyclone. Ind. Eng. Chem. Res. 2015, 54, 522–528. [Google Scholar] [CrossRef]
- Ni, L.; Tian, J.; Song, T.; Jong, Y.; Zhao, J. Optimizing Geometric Parameters in Hydrocyclones for Enhanced Separations: A Review and Perspective. Sep. Purif. Technol. 2018, 48, 30–51. [Google Scholar] [CrossRef]
- Vega, D.; Brito-Parada, P.R.; Cilliers, J.J. Optimising small hydrocyclone design using 3D printing and CFD simulations. Chem. Eng. J. 2018, 350, 653–659. [Google Scholar] [CrossRef]
- Hwang, K.; Chou, S. Designing vortex finder structure for improving the particle separation efficiency of a hydrocyclone. Sep. Purif. Technol. 2017, 172, 76–84. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, P.; Yang, X.; Zhang, Y. Short-Circuit Flow in Hydrocyclones with Arc-Shaped Vortex Finders. Chem. Eng. Technol. 2018, 41, 1783–1792. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, C. CFD modeling of particle behavior in supersonic flows with strong swirls for gas separation. Sep. Purif. Technol. 2017, 174, 22–28. [Google Scholar] [CrossRef]
- Hsiao, T.; Huang, S.; Hsu, C.; Chen, C.; Chang, P. Effects of the geometric configuration on cyclone performance. J. Aerosol Sci. 2015, 86, 1–12. [Google Scholar] [CrossRef]
- Krokhina, A.V.; Lvov, V.A.; Pavlikhin, G.P. A Probabilistic-Statistical Model of the Particle Classification Process in Small Hydrocyclone Classifiers. Chem. Eng. Technol. 2017, 40, 967–972. [Google Scholar] [CrossRef]
- Liu, P.; Chu, L.; Wang, J.; Yu, Y. Enhancement of Hydrocyclone Classification Efficiency for Fine Particles by Introducing a Volute Chamber with a Pre-Sedimentation. Chem. Eng. Technol. 2008, 31, 474–478. [Google Scholar] [CrossRef]
- Gonçalves, S.M.; Barrozo, M.A.S.; Vieira, L.G.M. Effects of solids concentration and underflow diameter on the performance of a newly designed hydrocyclone. Chem. Eng. Technol. 2017, 40. [Google Scholar] [CrossRef]
- Surmen, A.; Avci, A.; Karamangil, M.I. Prediction of the maximum-efficiency cyclone length for a cyclone with a tangential entry. Powder Technol. 2011, 207, 1–8. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Ibrahim, G.A.; Farghaly, M.G. Performance of a three-product hydrocyclone. Int. J. Miner. Process. 2009, 91, 34–40. [Google Scholar] [CrossRef]
- Obeng, D.P.; Morrell, S. The JK three-product cyclone-performance and potential applications. Int. J. Miner. Process. 2003, 69, 129–142. [Google Scholar] [CrossRef]
- Obeng, D.P.; Morrell, S.; Napier-Munn, T.J. Application of central composite rotatable design to modeling the effect of some operating variables on the performance of the three-product cyclone. Int. J. Miner. Process. 2005, 76, 181–192. [Google Scholar] [CrossRef]
- Mainza, A.; Narasimha, M.; Powell, M.S.; Holtham, P.N.; Brennan, M. Study of flow behavior in a three-product cyclone using computational fluid dynamics. Miner. Eng. 2006, 19, 1048–1058. [Google Scholar] [CrossRef]
- Mainza, A.; Powell, M.S.; Knopjes, B. Differential classification of dense material in a three-product cyclone. Miner. Eng. 2004, 17, 573–579. [Google Scholar] [CrossRef]
- Bhasker, C. Flow simulation in industrial cyclone separator. Adv. Eng. Soft. 2010, 41, 220–228. [Google Scholar] [CrossRef]
- Chen, J.; Chu, K.; Zou, R.; Yu, A.B.; Vince, A.; Barnett, G.D.; Barnett, P.J. Systematic study of the effect of particle density distribution on the flow and performance of a dense medium cyclone. Powder Technol. 2017, 314, 510–523. [Google Scholar] [CrossRef]
- Vakamalla, T.R.; Korprolu, V.B.R.; Arugonda, R.; Mangadoddy, A. Development of novel hydrocyclone designs for improved fines classification using multiphase CFD model. Sep. Purif. Technol. 2017, 175, 481–497. [Google Scholar] [CrossRef]
- Slack, M.D.; Prasad, R.O.; Bakker, A.; Boysan, F. Advances in cyclone modeling using unstructured grids. Chem. Eng. Res. 2000, 78, 1098–1104. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Hu, C.; Fan, J. CFD-DEM study of the effect of cyclone arrangements on the gas-solid flow dynamics in the full-loop circulating fluidized bed. Chem. Eng. Sci. 2017, 172, 199–215. [Google Scholar] [CrossRef]
- Siadaty, M.; Kheradmand, S.; Ghadiri, F. Improvement of the cyclone separation efficiency with a magnetic field. J. Aerosol Sci. 2017, 114, 219–232. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. Impacts of the vortex finder eccentricity on the flow pattern and performance of a gas cyclone. Sep. Purif. Technol. 2017, 187, 1–13. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, C.; Wei, D.; Lu, S.; Feng, Y. Effects of feed size distribution on separation performance of hydrocyclones with differdent vortex finder diameters. Powder Technol. 2017, 322, 114–123. [Google Scholar] [CrossRef]
- Patra, G.; Velpuri, B.; Chakraborty, S.; Meikap, B.C. Performance evaluation of a hydrocyclone with a spiral rib for separation of particles. Adv. Powder Technol. 2017, 28, 3222–3232. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, P.; Jiang, F.; Dong, K.; Jiang, Y.; Wang, B. Understanding the separation of particles in a hydrocyclone by force analysis. Powder Technol. 2017, 322, 471–489. [Google Scholar] [CrossRef]
- Ji, L.; Kuang, S.; Qi, Z.; Wang, Y.; Chen, J.; Yu, A. Computational analysis and optimization of hydrocyclone size to mitigate adverse effect of particle density. Sep. Purif. Technol. 2017, 174, 251–263. [Google Scholar] [CrossRef]
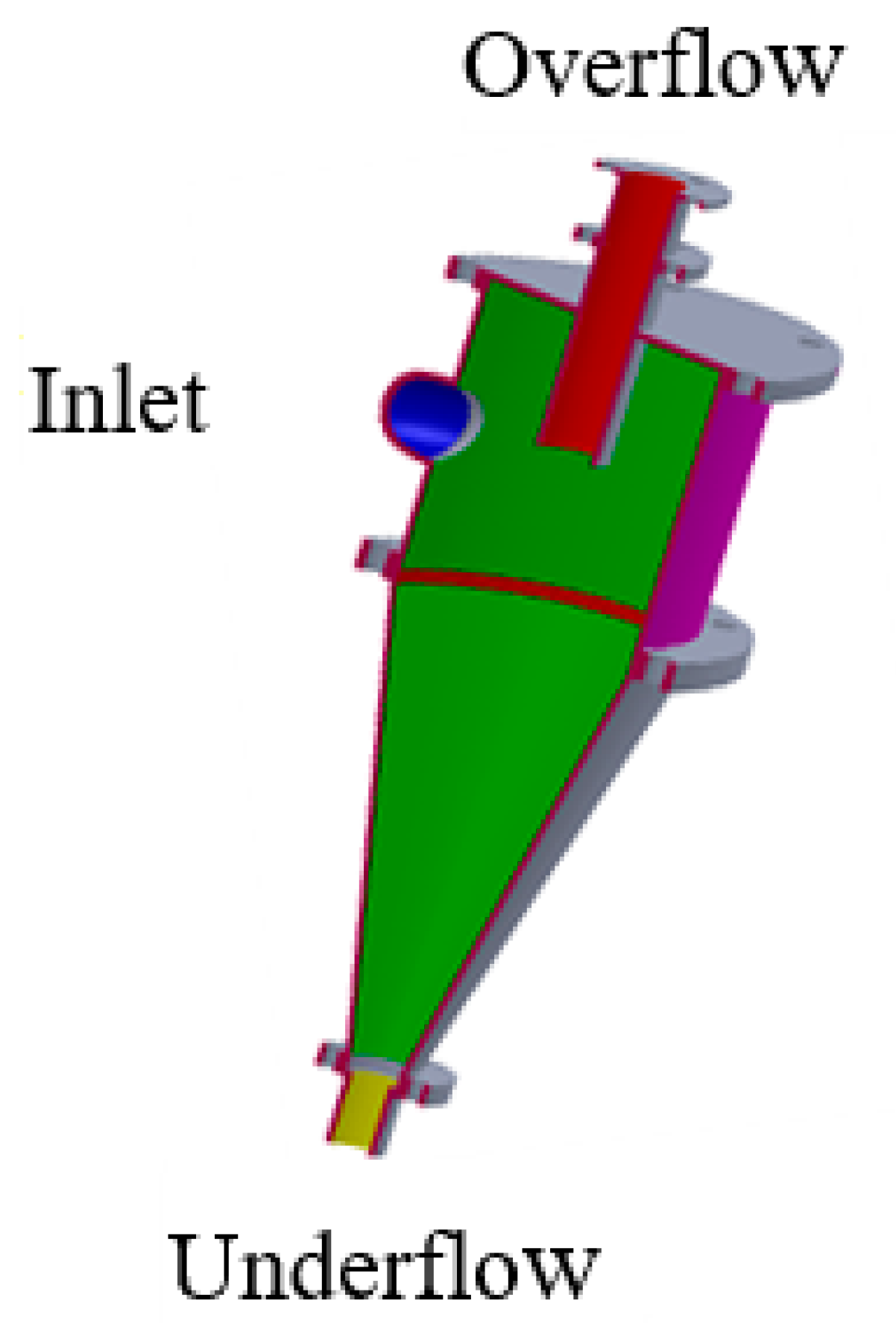
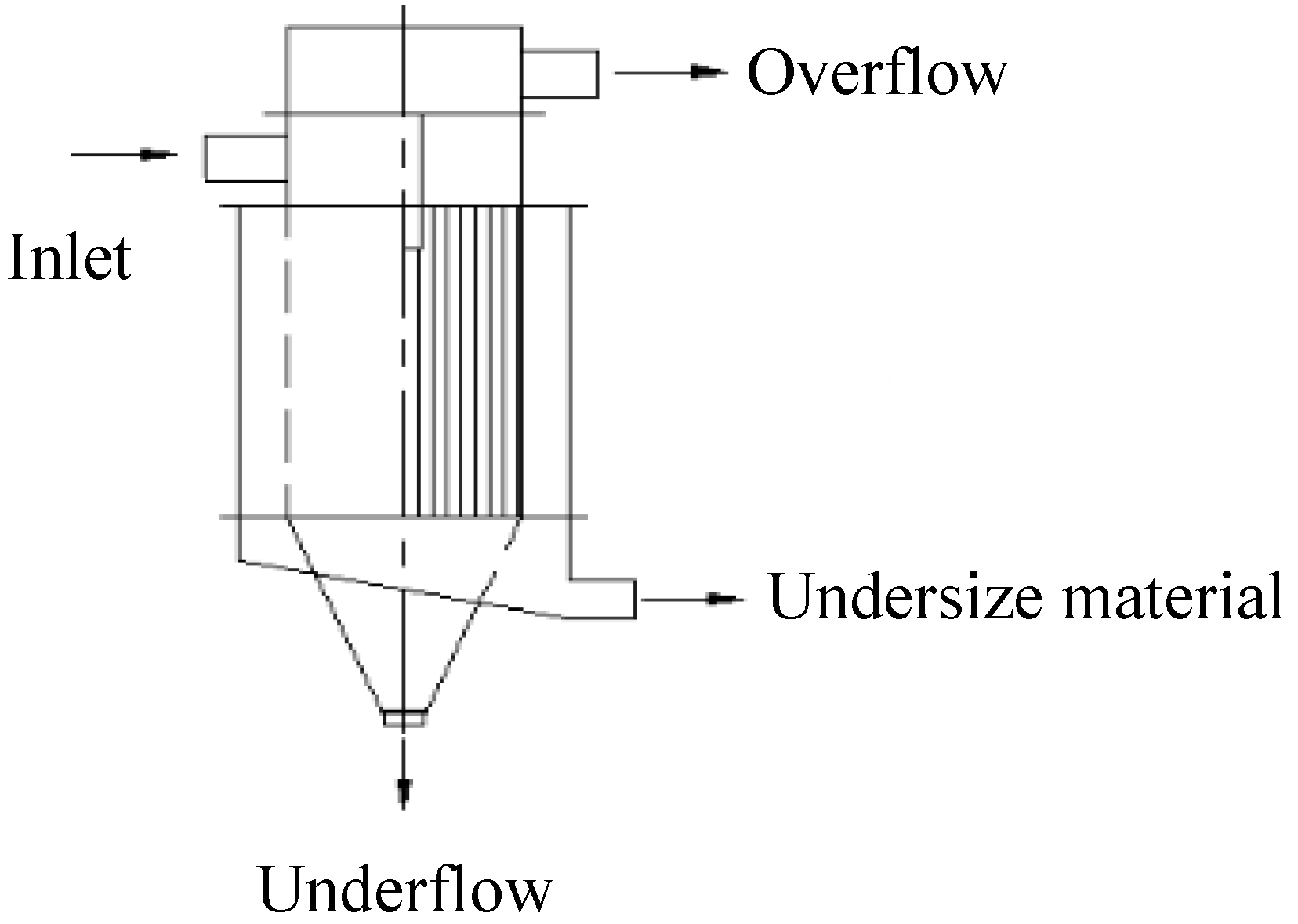
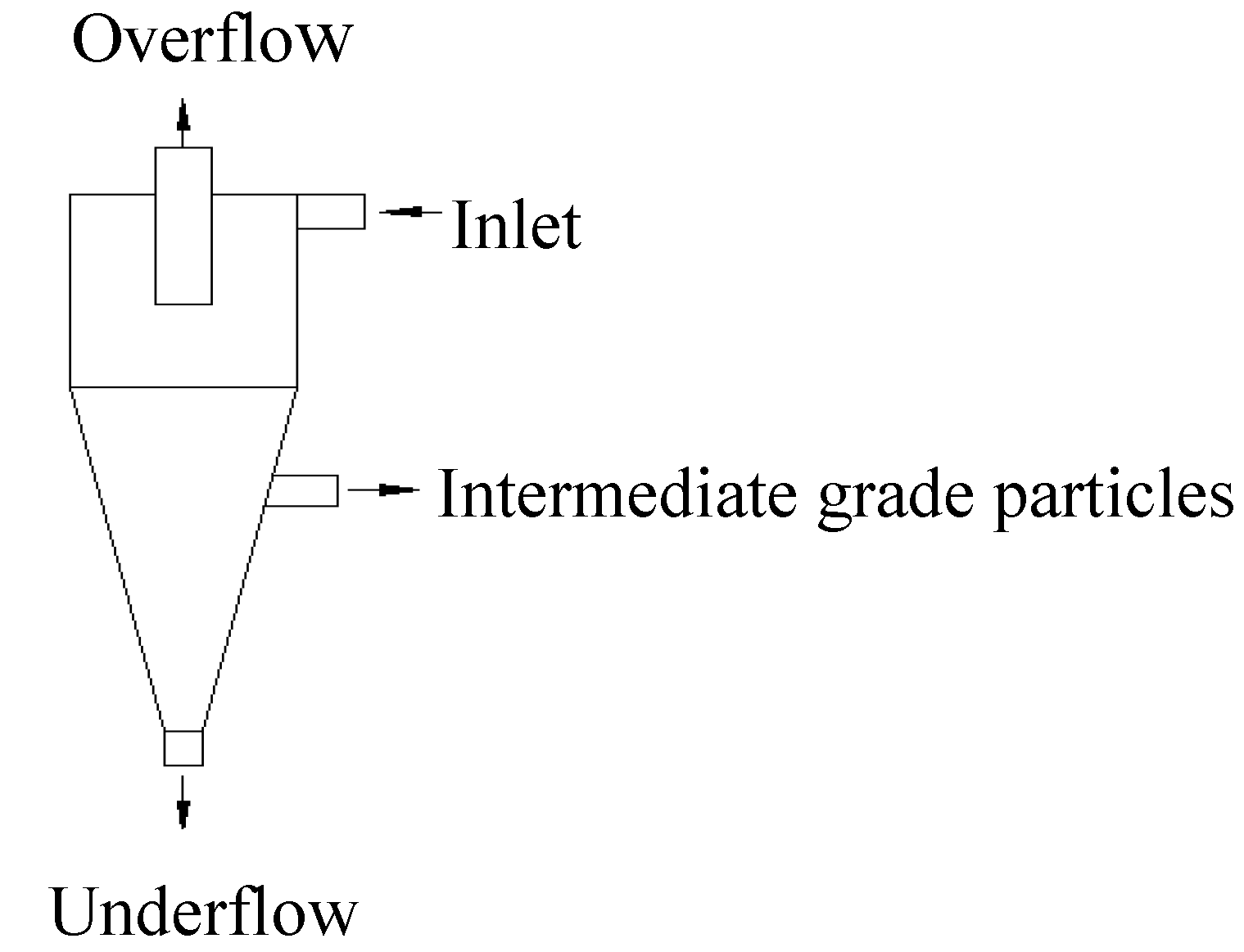

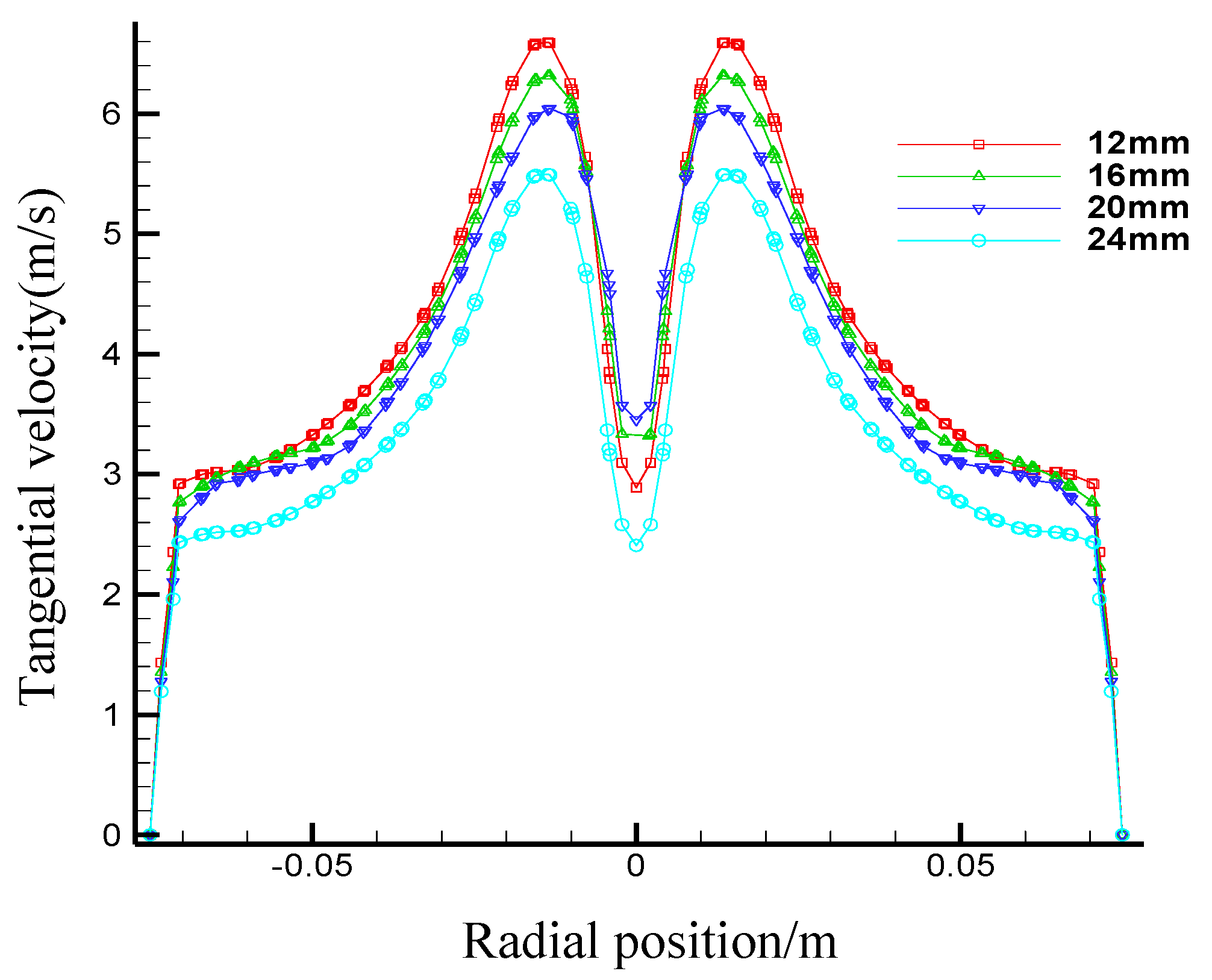
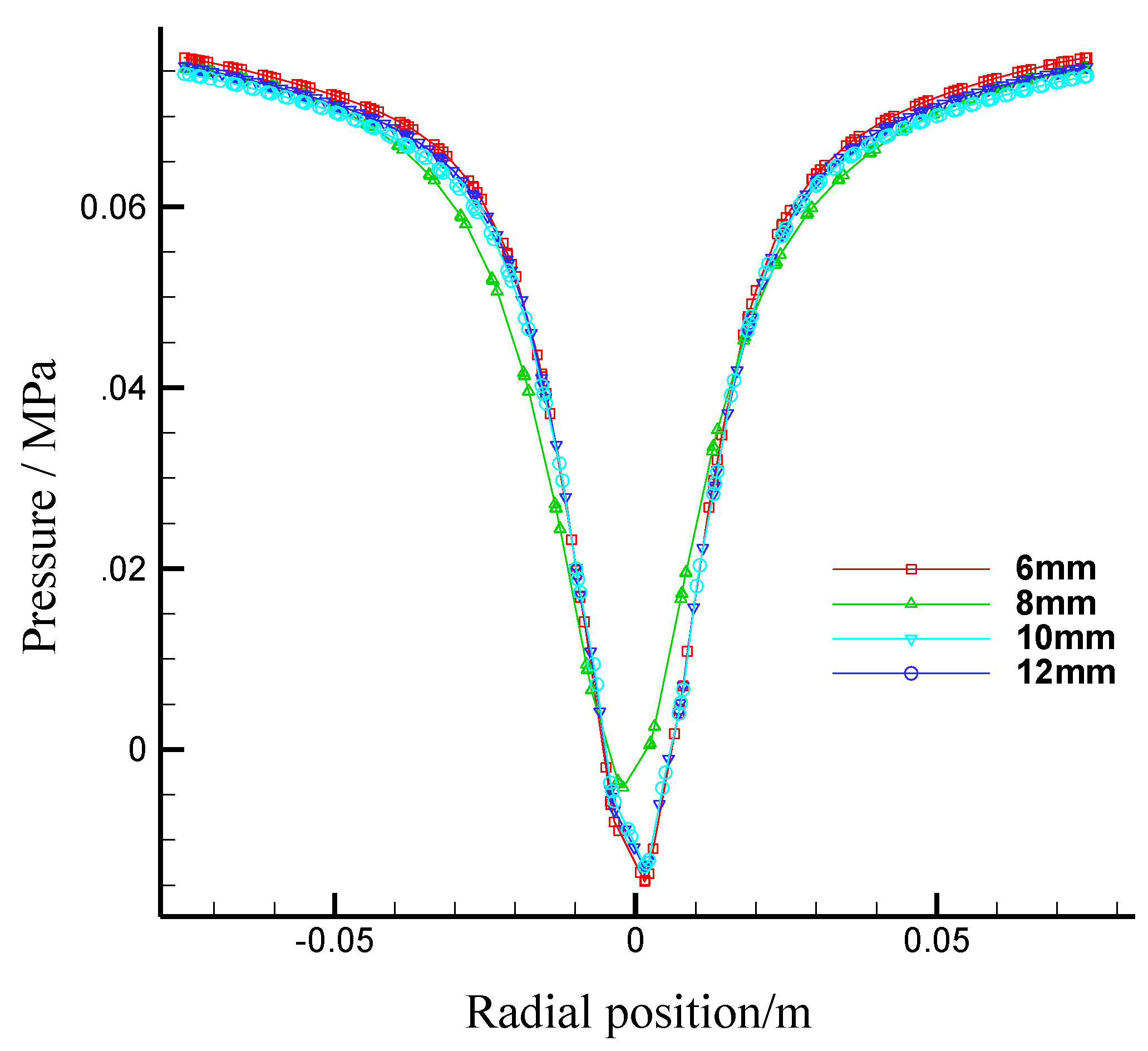
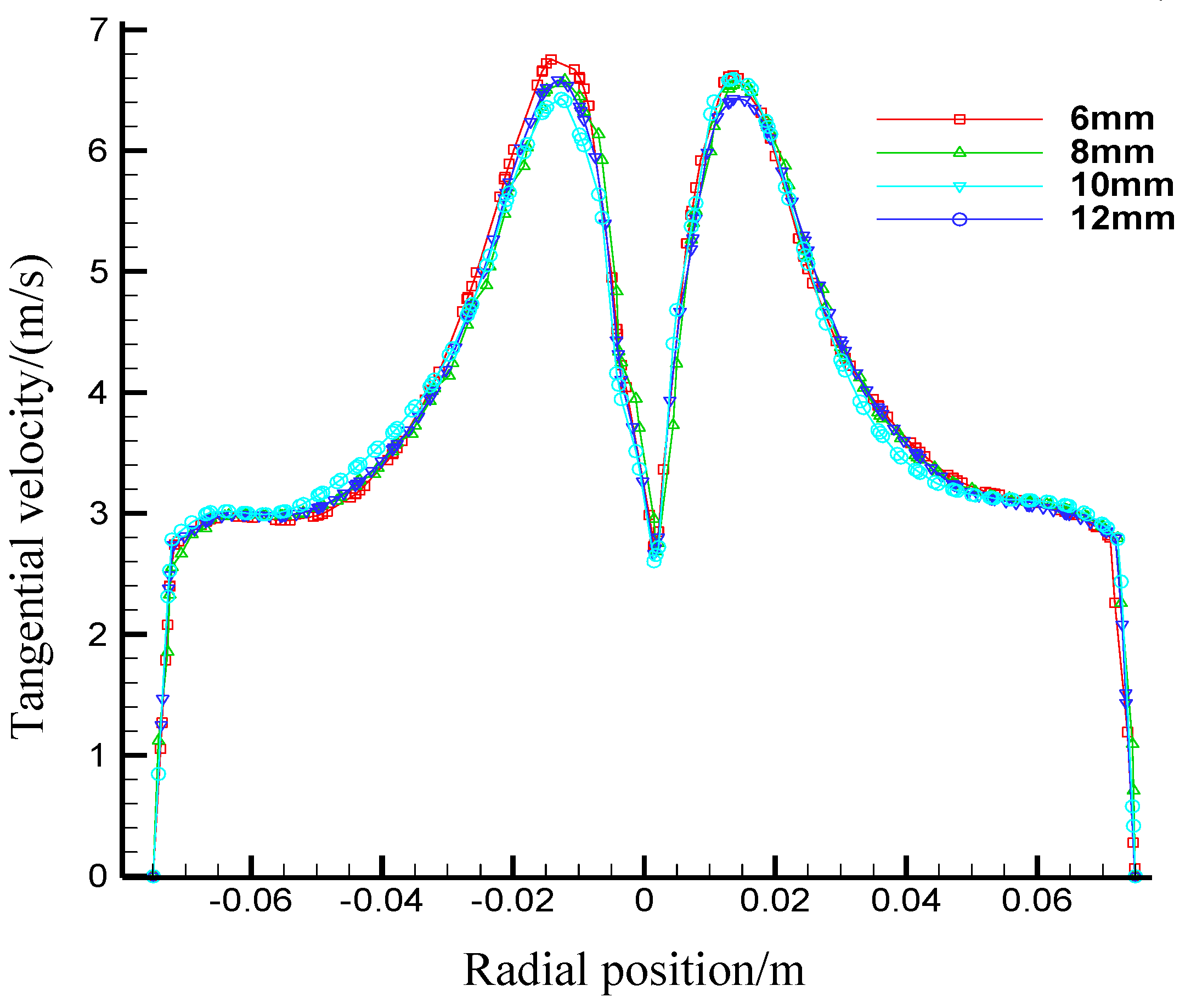
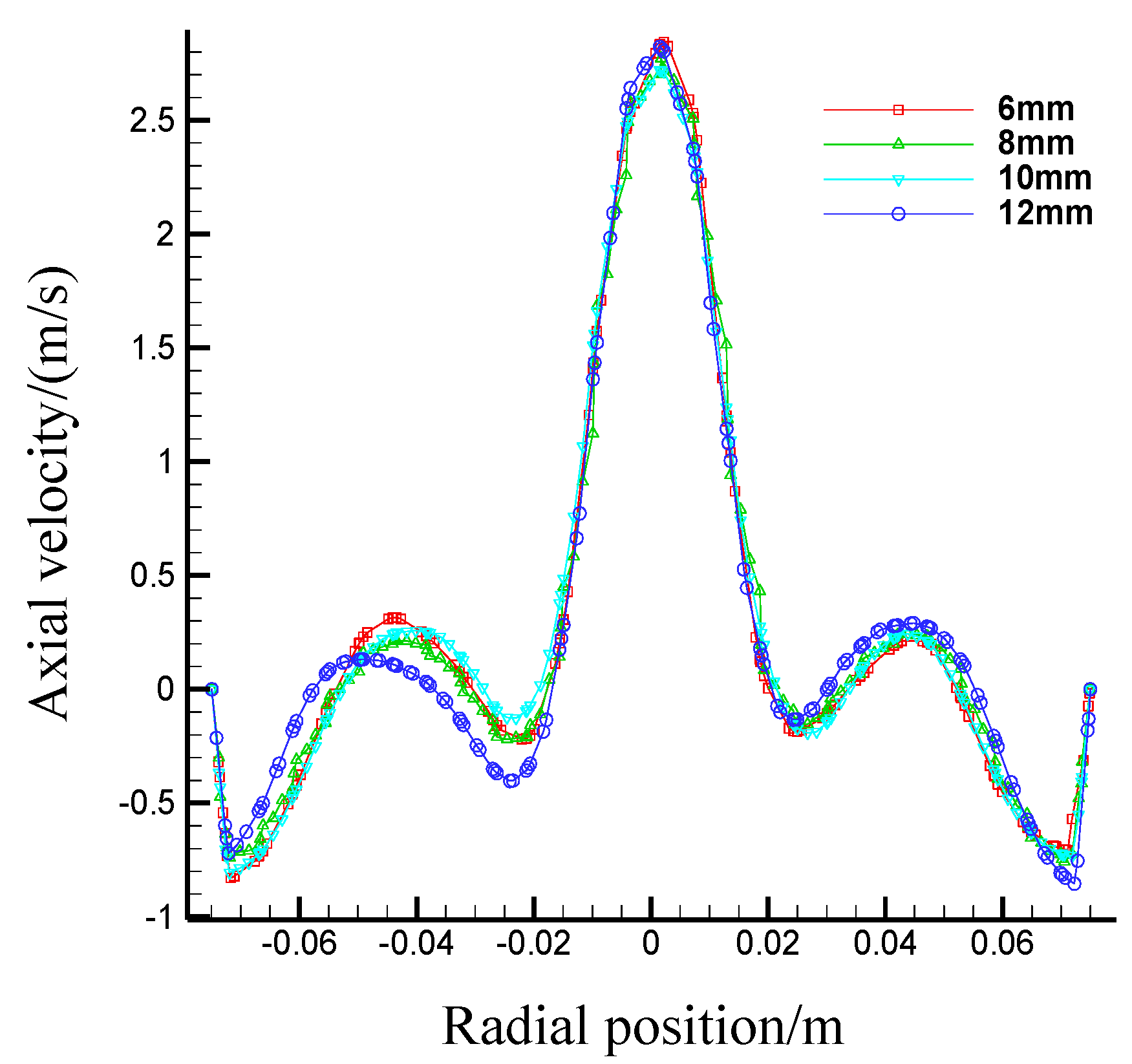

| Parameters | I Underflow | II Underflow | Inner Overflow | II Overflow |
|---|---|---|---|---|
| Turbulence intensities/% | 4.3 | 4.7 | 4.5 | 4.3 |
| hydraulic diameter/mm | 20 | 8 | 25 | 20 |
| Particle Size/mm | Yield/% | Cumulative Yield/% | Iron Grade/% | Iron Content/% | Distribution Rate/% | Cumulative Distribution Rate/% |
|---|---|---|---|---|---|---|
| +0.1 | 15.10 | 100 | 26.18 | 3.95 | 7.42 | 100 |
| −0.1 + 0.076 | 10.72 | 84.90 | 37.93 | 4.07 | 7.65 | 92.58 |
| −0.076 + 0.055 | 10.70 | 74.18 | 50.18 | 5.37 | 10.09 | 84.93 |
| −0.055 + 0.043 | 13.28 | 63.48 | 58.51 | 7.77 | 14.60 | 74.84 |
| −0.043 + 0.038 | 13.06 | 50.2 | 60.73 | 7.93 | 14.9 | 60.24 |
| −0.038 + 0.030 | 6.53 | 37.14 | 61.07 | 3.99 | 7.50 | 45.34 |
| −0.030 | 30.61 | 30.61 | 65.8 | 20.14 | 37.84 | 37.84 |
| total | 100.00 | 52.96 | 53.22 | 100.00 |
| Mass Concentration/% | Pressure/MPa | Angle of Cone/° | Diameter of I Underflow Pipe/mm | Diameter of II Underflow Pipe/mm | Diameter of Outer Overflow Pipe/mm | Diameter of Inner Overflow Pipe/mm |
|---|---|---|---|---|---|---|
| 30 | 0.11 | 180 | 8 | 4 | 15 | 9 |
| Results | Iron Grade/% | Iron Recovery Rate/% | |
|---|---|---|---|
| I underflow | Concentrates after magnetic separation | 66.24 | 49.22 |
| Tailings after magnetic separation | 22.46 | ||
| merged overflow | Concentrates after magnetic separation | 62.53 | 12.86 |
| Tailings after magnetic separation | 28.71 | ||
| II underflow | Concentrates after magnetic separation | 61.14 | 24.06 |
| Tailings after magnetic separation | 24.42 | ||
| composite result | Concentrates after magnetic separation | 65.08 | 86.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, P.; Jiang, L.; Yang, X. The Study on Numerical Simulation and Experiments of Four Product Hydrocyclone with Double Vortex Finders. Minerals 2019, 9, 23. https://doi.org/10.3390/min9010023
Zhang Y, Liu P, Jiang L, Yang X. The Study on Numerical Simulation and Experiments of Four Product Hydrocyclone with Double Vortex Finders. Minerals. 2019; 9(1):23. https://doi.org/10.3390/min9010023
Chicago/Turabian StyleZhang, Yuekan, Peikun Liu, Lanyue Jiang, and Xinghua Yang. 2019. "The Study on Numerical Simulation and Experiments of Four Product Hydrocyclone with Double Vortex Finders" Minerals 9, no. 1: 23. https://doi.org/10.3390/min9010023
APA StyleZhang, Y., Liu, P., Jiang, L., & Yang, X. (2019). The Study on Numerical Simulation and Experiments of Four Product Hydrocyclone with Double Vortex Finders. Minerals, 9(1), 23. https://doi.org/10.3390/min9010023





