Stability of AuCl2− from 25 to 1000 °C at Pressures to 5000 bar and Consequences for Hydrothermal Gold Mobilization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental
2.1.1. Reduced Conditions
2.1.2. Oxidized Conditions
2.2. Thermodynamic Calculations
3. Results
3.1. Experimental Au Solubility Determination
3.2. Au Solubility Constant at 25–1000 °C and Pressures up to 5 kbar
4. Discussion
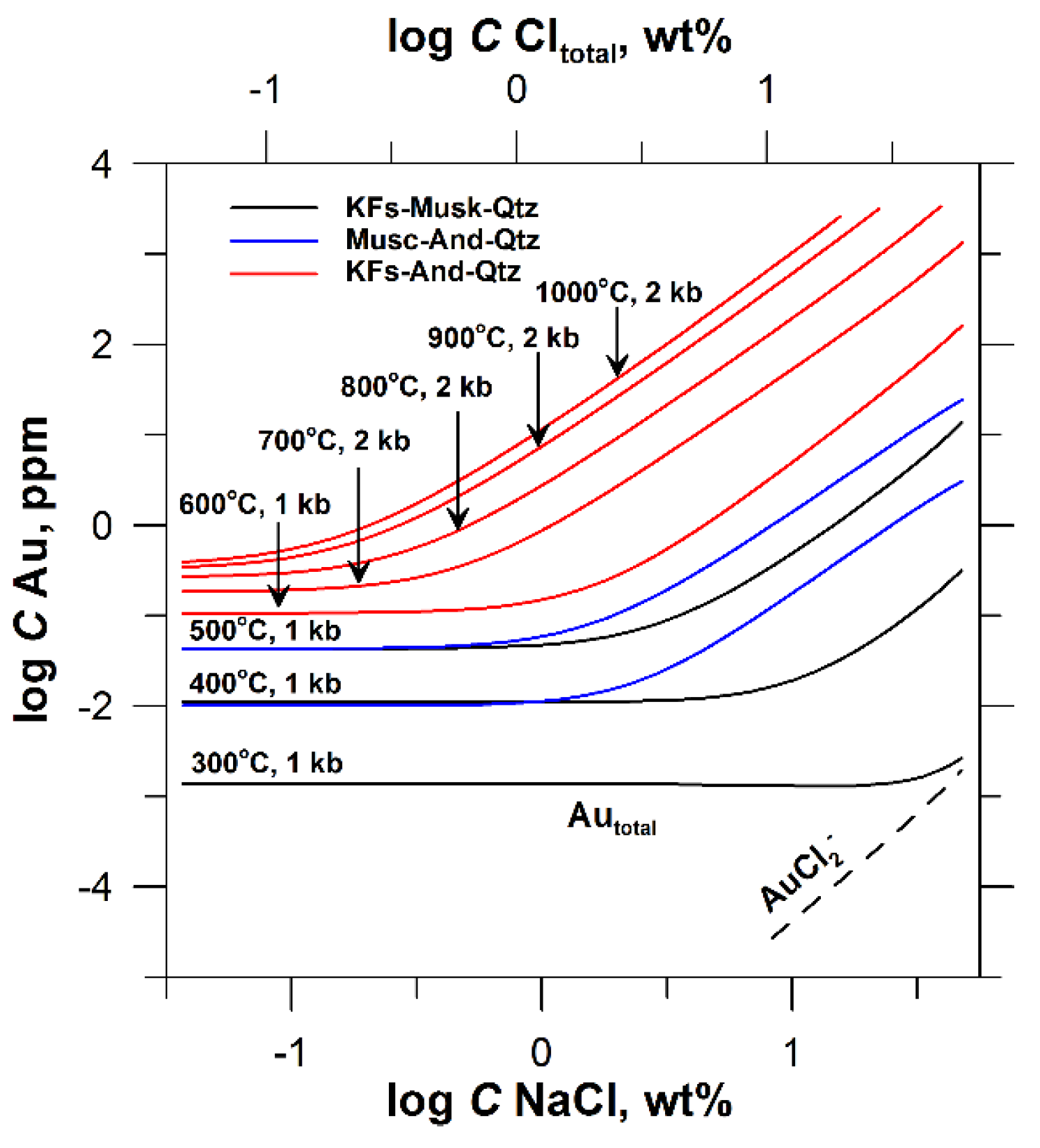
4.1. Effect of Temperature, pH, and Chlorinity on Au Solubility
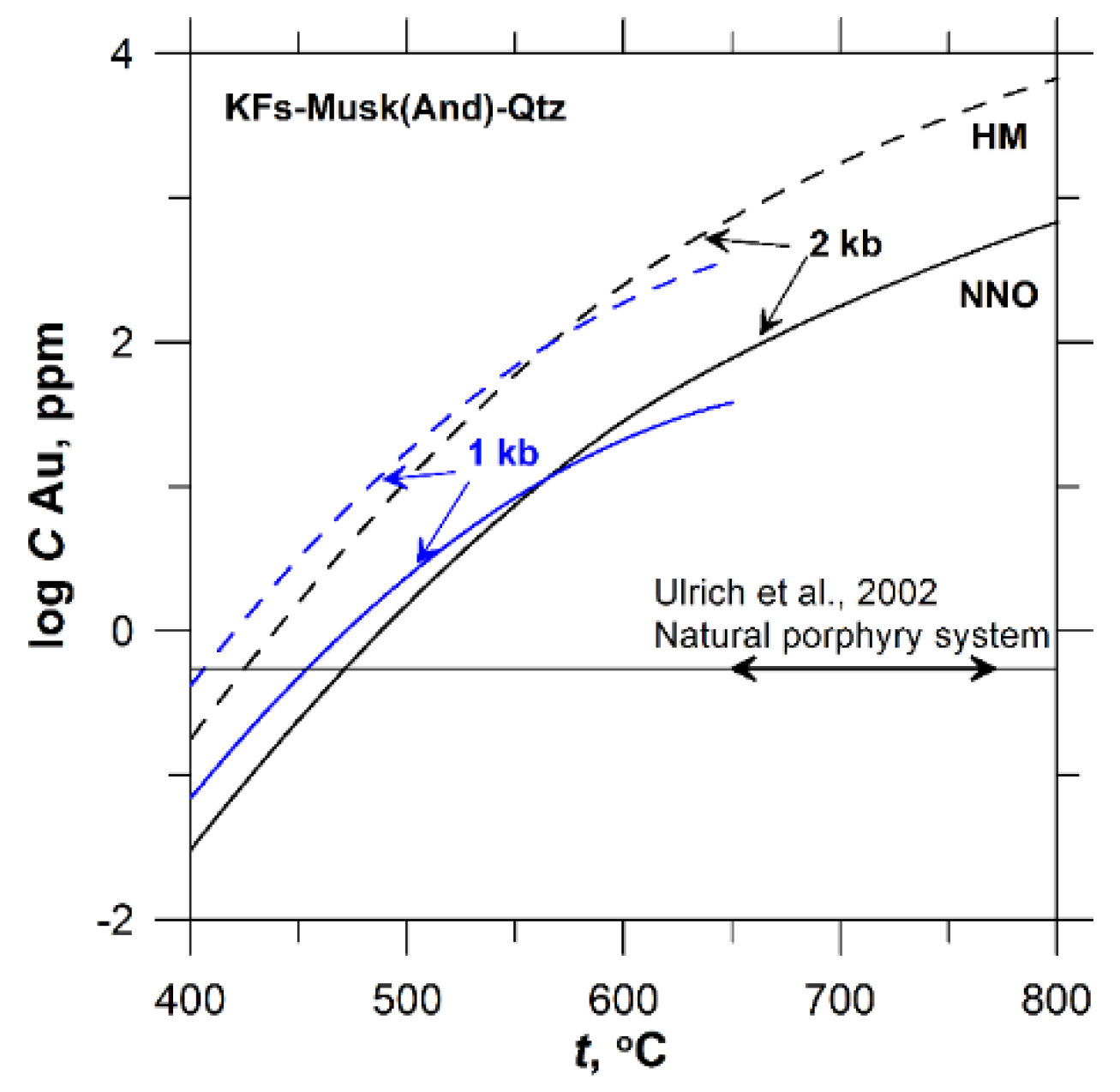
4.2. Gold Concentration in Natural Fluids
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seward, T.M.; Williams-Jones, A.E.; Migdisov, A.A. The chemistry of metal transport and deposition by ore-forming hydrothermal fluids. In Treatise on Geochemistry, 2nd ed.; Turekian, K., Holland, H., Eds.; Elsevier: New York, NY, USA, 2014; Volume 13, pp. 29–57. [Google Scholar]
- Ulrich, T.; Günther, D.; Heinrich, C.A. The Evolution of a porphyry Cu-Au deposit, based on LA-ICP-MS analysis of fluid inclusions: Bajo de la Alumbrera, Argentina. Econ. Geol. 2001, 96, 1743–1774. [Google Scholar] [CrossRef]
- Nikolaeva, N.M.; Erenburg, A.M.; Antipina, V.A. About the temperature dependence of standard potentials of halide complexes of gold. Izvestiya Sibirskogo Otdeleniya Akademii Nauk SSSR Seriya Khimicheskih Nauk 1972, 4, 126–128. (In Russian) [Google Scholar]
- Gammons, C.H.; Williams-Jones, A.E. The solubility of Au-Ag alloy + AgCl in HCl/NaCl solutions at 300 °C: New data on the stability of Au(I) chloride complexes in hydrothermal fluids. Geochim. Cosmochim. Acta 1995, 59, 3453–3468. [Google Scholar] [CrossRef]
- Zotov, A.V.; Kudrin, A.V.; Levin, K.A.; Shikina, N.D.; Var’yash, L.N. Experimental studies of the solubility and complexing of selected ore elements (Au, Ag, Cu, Mo, As, Sb, Hg) in aqueous solutions. In Fluids in the Crust. Equilibrium and Transport Properties; Shmulovich, K.I., Yardley, B.W.D., Gonchar, G.G., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 95–137. [Google Scholar]
- Stefánsson, A.; Seward, T.M. Stability of chloridogold(I) complexes in aqueous solutions from 300 to 600 °C and from 500 to 1800 bar. Geochim. Cosmochim. Acta 2003, 67, 4559–4576. [Google Scholar] [CrossRef]
- Ryabchikov, I.D.; Orlova, G.P. Gold in magmatic fluids. In Phizico-khimicheskie Modeli Petrogeneza i Rudoobrazovaniya; Nauka Press: Novosibirsk, Russia, 1984; pp. 103–111. (In Russian) [Google Scholar]
- Zajacz, Z.; Seo, J.H.; Candela, P.A.; Piccoli, P.M.; Heinrich, C.A.; Guillong, M. Alkali metals control the release of gold from volatile-rich magmas. Earth Planet. Sci. Lett. 2010, 297, 50–56. [Google Scholar] [CrossRef]
- Guo, H.; Audétat, A.; Dolejš, D. Solubility of gold in oxidized, sulfur-bearing fluids at 500–850 °C and 200–230 MPa: A synthetic fluid inclusion study. Geochim. Cosmochim. Acta 2018, 222, 655–670. [Google Scholar] [CrossRef]
- Pokrovski, G.S.; Tagirov, B.R.; Schott, J.; Bazarkina, E.F.; Hazemann, J.-L.; Proux, O. An in situ X-ray absorption spectroscopy study of gold-chloride complexing in hydrothermal fluids. Chem. Geol. 2009, 259, 17–29. [Google Scholar] [CrossRef]
- Mei, Y.; Liu, W.; Sherman, D.M.; Brugger, J. Metal complexing and ion hydration in low density hydrothermal fluids: Ab initio molecular dynamics simulation of Cu(I) and Au(I) in chloride solutions (25–1000 °C, 1–5000 bar). Geochim. Cosmochim. Acta 2014, 131, 196–212. [Google Scholar] [CrossRef]
- Archibald, S.M.; Migdisov, A.A.; Williams-Jones, A.E. The stability of Au-chloride complexes in water vapor at elevated temperatures and pressures. Geochim. Cosmochim. Acta 2001, 65, 4413–4423. [Google Scholar] [CrossRef]
- Kudrin, A.V. Behaviour of Mo in aqueous NaCl and KCl solutions at 300–450 °C. Geochem. Int. 1989, 26, 87–99. [Google Scholar]
- Driesner, T. The system H2O-NaCl. II. Correlations for molar volume, enthalpy, and isobaric heat capacity from 0 to 1000 °C, 1 to 5000 bar, and 0 to 1 XNaCl. Geochim. Cosmochim. Acta 2007, 71, 4902–4919. [Google Scholar] [CrossRef]
- Driesner, T.; Heinrich, C.A. The system H2O-NaCl. I. Correlation formulae for phase relations in temperature-pressure-composition space from 0 to 1000 °C, 0 to 5000 bar, and 0 to 1 XNaCl. Geochim. Cosmochim. Acta 2007, 71, 4880–4901. [Google Scholar] [CrossRef]
- Zotov, A.V.; Baranova, N.N. Thermodynamic properties of the aurochloride solute complex AuCl2− at temperatures of 350–500 °C and pressures of 500–1500 bars. Sciences Géologiques Bulletins Mémoires 1989, 42, 335–342. [Google Scholar] [CrossRef]
- Shvarov, Y.V. HCh: New potentialities for the thermodynamic simulation of geochemical systems offered by Windows. Geochem. Int. 2008, 46, 834–839. [Google Scholar] [CrossRef]
- Johnson, J.W.; Oelkers, E.H.; Helgeson, H.C. SUPCRT92: A software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000 °C. Comput. Geosci. 1992, 18, 899–947. [Google Scholar] [CrossRef]
- Wagner, W.; Pruss, A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Tagirov, B.R.; Zotov, A.V.; Akinfiev, N.N. Experimental study of dissociation of HCl from 350 to 500 °C and from 500 to 2500 bars: Thermodynamic properties of HCl(aq). Geochim. Cosmochim. Acta 1997, 61, 4267–4280. [Google Scholar] [CrossRef]
- Ho, P.C.; Palmer, D.A.; Mesmer, R.E. Electrical conductivity measurements of aqueous sodium chloride solutions to 600 °C and 300 MPa. J. Solut. Chem. 1994, 23, 997–1018. [Google Scholar] [CrossRef]
- Bandura, A.V.; Lvov, S.N. The ionization constant of water over wide ranges of temperature and density. J. Phys. Chem. Ref. Data 2006, 35, 15–30. [Google Scholar] [CrossRef]
- Akinfiev, N.N.; Diamond, L.W. Thermodynamic description of aqueous nonelectrolytes at infinite dilution over a wide range of state parameters. Geochim. Cosmochim. Acta 2003, 67, 613–627. [Google Scholar] [CrossRef]
- Robie, R.A.; Hemingway, B.S. Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 bar (105 Pascals) Pressure and at Higher Temperatures, U.S. Geological Survey Bulletin 2131; U.S. Government Printing Office: Washington, DC, USA, 1995.
- Berman, R.G. Internally consistent thermodynamic data for minerals in the system Na2O-K2O-CaO-MgO-FeO-Fe2O3-Al2O3-SiO2-TiO2-H2O-CO2. J. Petrol. 1988, 29, 445–522. [Google Scholar] [CrossRef]
- Sverjensky, D.A.; Hemley, J.J.; D’Angelo, M.D. Thermodynamic assessment of hydrothermal alkali feldspar-mica-aluminosilicate equilibria. Geochim. Cosmochim. Acta 1991, 55, 989–1004. [Google Scholar] [CrossRef]
- Shvarov, Y. A suite of programs, OptimA, OptimB, OptimC, and OptimS compatible with the Unitherm database, for deriving the thermodynamic properties of aqueous species from solubility, potentiometry and spectroscopy measurements. Appl. Geochem. 2015, 55, 17–27. [Google Scholar] [CrossRef]
- Anderson, G.M.; Castet, S.; Schott, J.; Mesmer, R.E. The density model for estimation of thermodynamic parameters of reactions at high temperatures and pressures. Geochim. Cosmochim. Acta 1991, 55, 1769–1779. [Google Scholar] [CrossRef]
- Tagirov, B.R.; Trigub, A.L.; Filimonova, O.N.; Kvashnina, K.O.; Nickolsky, M.S.; Lafuerza, S.; Chareev, D.A. Gold speciation and solubility in chloride fluids and melts: Insights from X-ray absorption spectroscopy, Ab initio molecular dynamics and thermodynamic modeling. Geochim. Cosmochim. Acta 2018. under review. [Google Scholar]
- Bortnikov, N.S.; Simonov, V.A.; Bogdanov, Y.A. Fluid inclusions in minerals from modern sulfide edifices: Physicochemical conditions of formation and evolution of fluids. Geol. Ore Depos. 2004, 46, 64–75. [Google Scholar]
- Hannington, M.D.; de Ronde, C.D.J.; Petersen, S. Sea-floor tectonics and submarine hydrothermal systems. In Economic Geology 100th Anniversary Volume; Henderquist, J.W., Thompson, J.F.H., Goldfarb, R.J., Richards, J.P., Eds.; Society of Economic Geologists: Littelton, CO, USA, 2005; pp. 111–141. [Google Scholar]
- Blundy, J.; Mavrogenes, J.; Tattitch, B.; Sparks, S.; Gilmer, A. Generation of porphyry copper deposits by gas–brine reaction in volcanic arcs. Nat. Geosci. 2015, 8, 235–240. [Google Scholar] [CrossRef]
- Aranovich, L.Y.; Newton, R.C.; Manning, C.E. Brine-assisted anatexis: Experimental melting in the system haplogranite–H2O–NaCl–KCl at deep-crustal conditions. Earth Plan. Sci. Lett. 2013, 374, 111–120. [Google Scholar] [CrossRef]
- Trigub, A.L.; Tagirov, B.R.; Kvashnina, K.O.; Lafuerza, S.; Filimonova, O.N.; Nickolsky, M.S. Experimental determination of gold speciation in sulfide-rich hydrothermal fluids under a wide range of redox conditions. Chem. Geol. 2017, 471, 52–64. [Google Scholar] [CrossRef]
- Akinfiev, N.N.; Zotov, A.V. Thermodynamic description of aqueous species in the system Cu-Ag-Au-S-O-H at temperatures of 0–600 °C and pressures of 1–3000 bar. Geochem. Int. 2010, 48, 714–720. [Google Scholar] [CrossRef]
- Tagirov, B.R.; Trigub, A.L.; Kvashnina, K.O.; Shiryaev, A.A.; Chareev, D.A.; Nickolsky, M.S.; Abramova, V.D.; Kovalchuk, E.V. Covellite CuS as a matrix for “invisible” gold: X-ray spectroscopic study of the chemical state of Cu and Au in synthetic minerals. Geochim. Cosmochim. Acta 2016, 191, 58–69. [Google Scholar] [CrossRef]
- Trigub, A.L.; Tagirov, B.R.; Kvashnina, K.O.; Chareev, D.A.; Nickolsky, M.S.; Shiryaev, A.A.; Baranova, N.N.; Kovalchuk, E.V.; Mokhov, A.V. X-ray spectroscopy study of the chemical state of “invisible” Au in synthetic minerals in the Fe-As-S system. Am. Mineral. 2017, 102, 1057–1065. [Google Scholar]
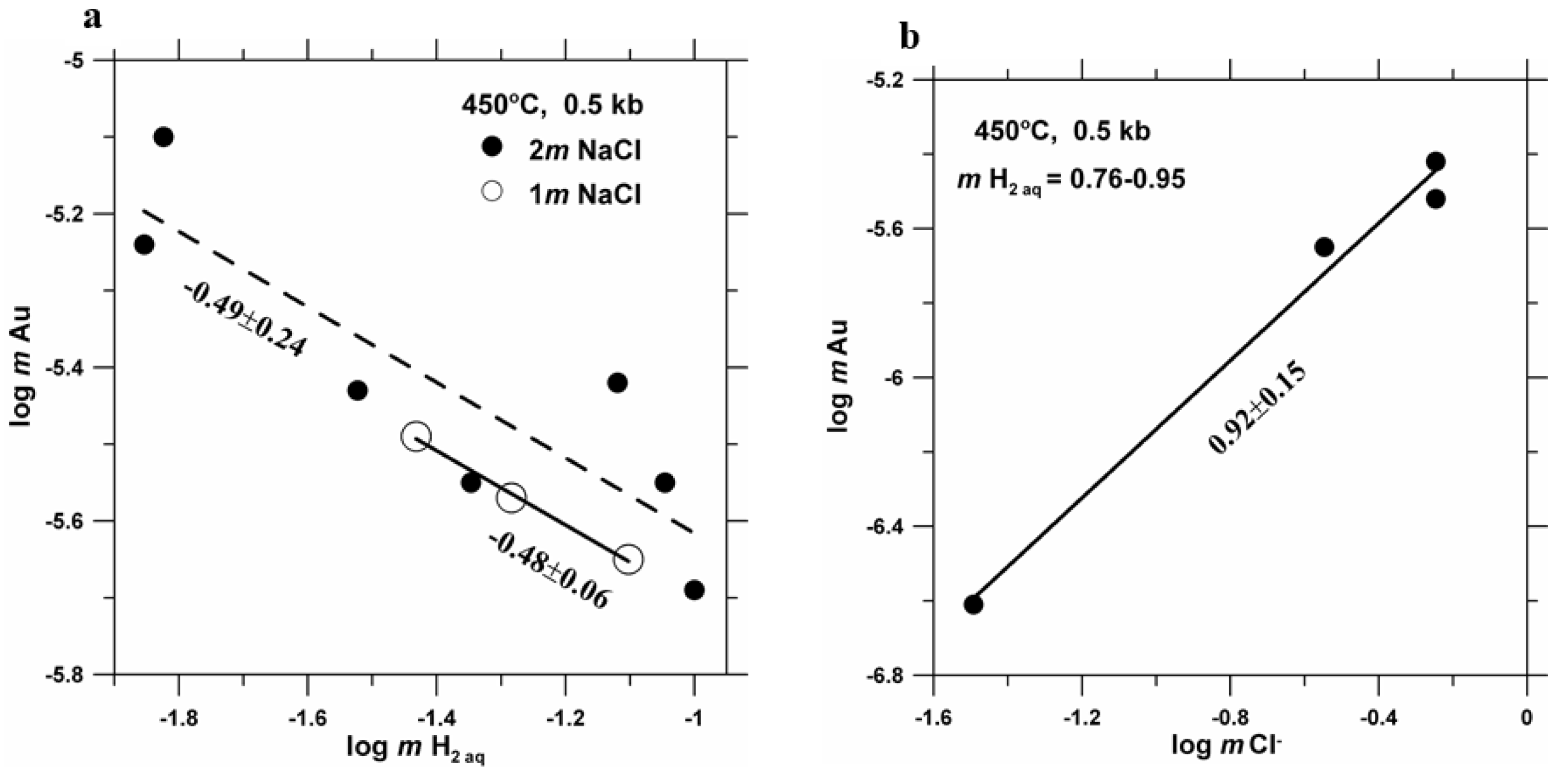
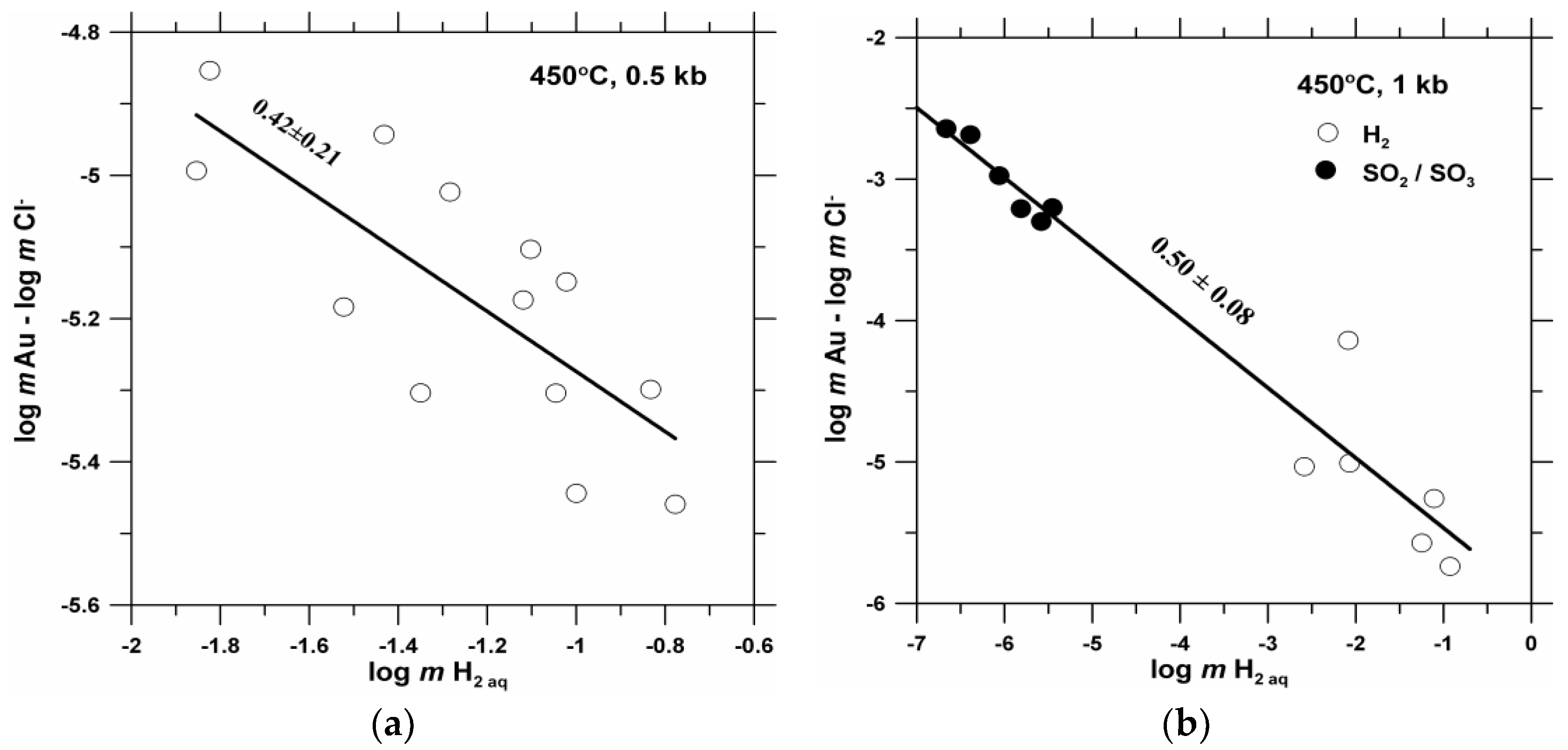
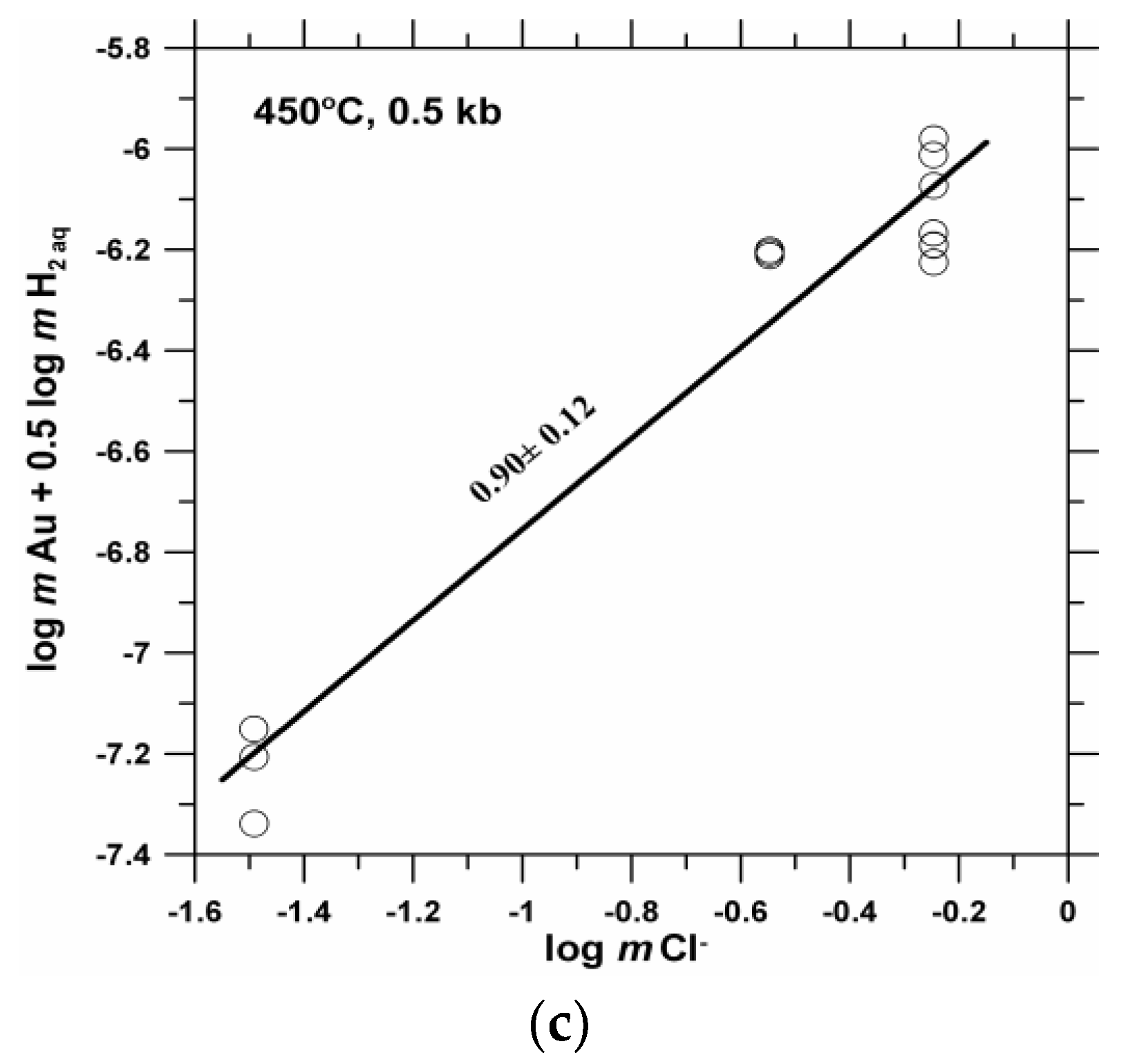
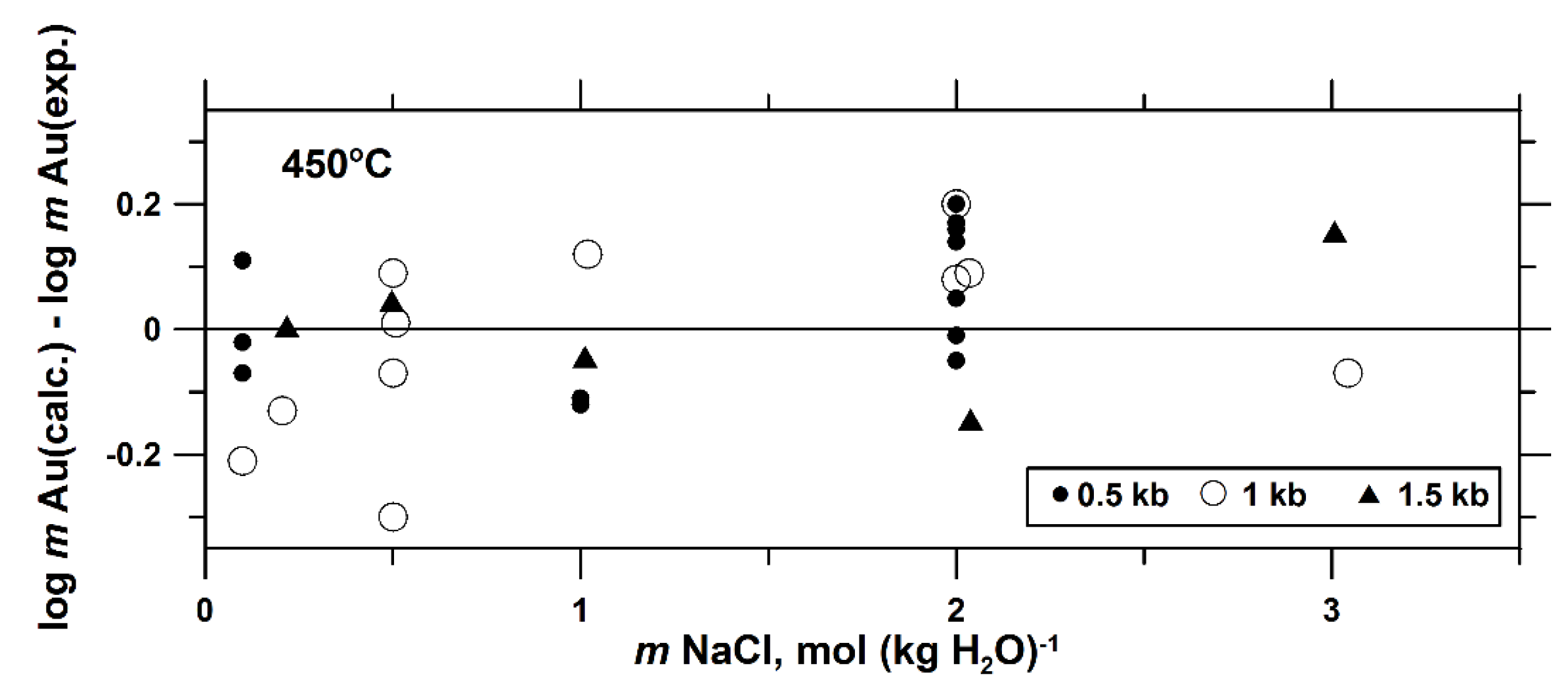
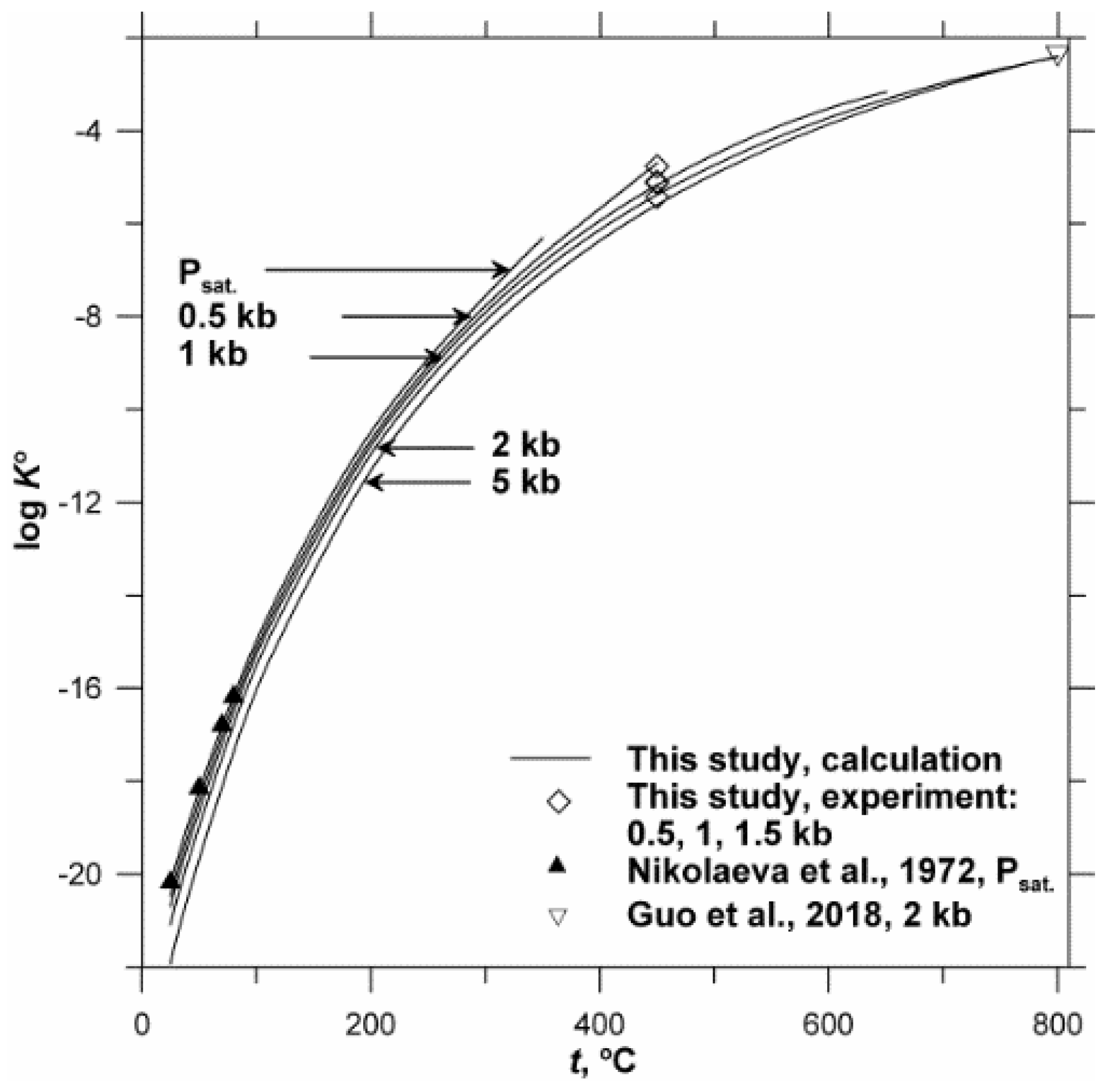
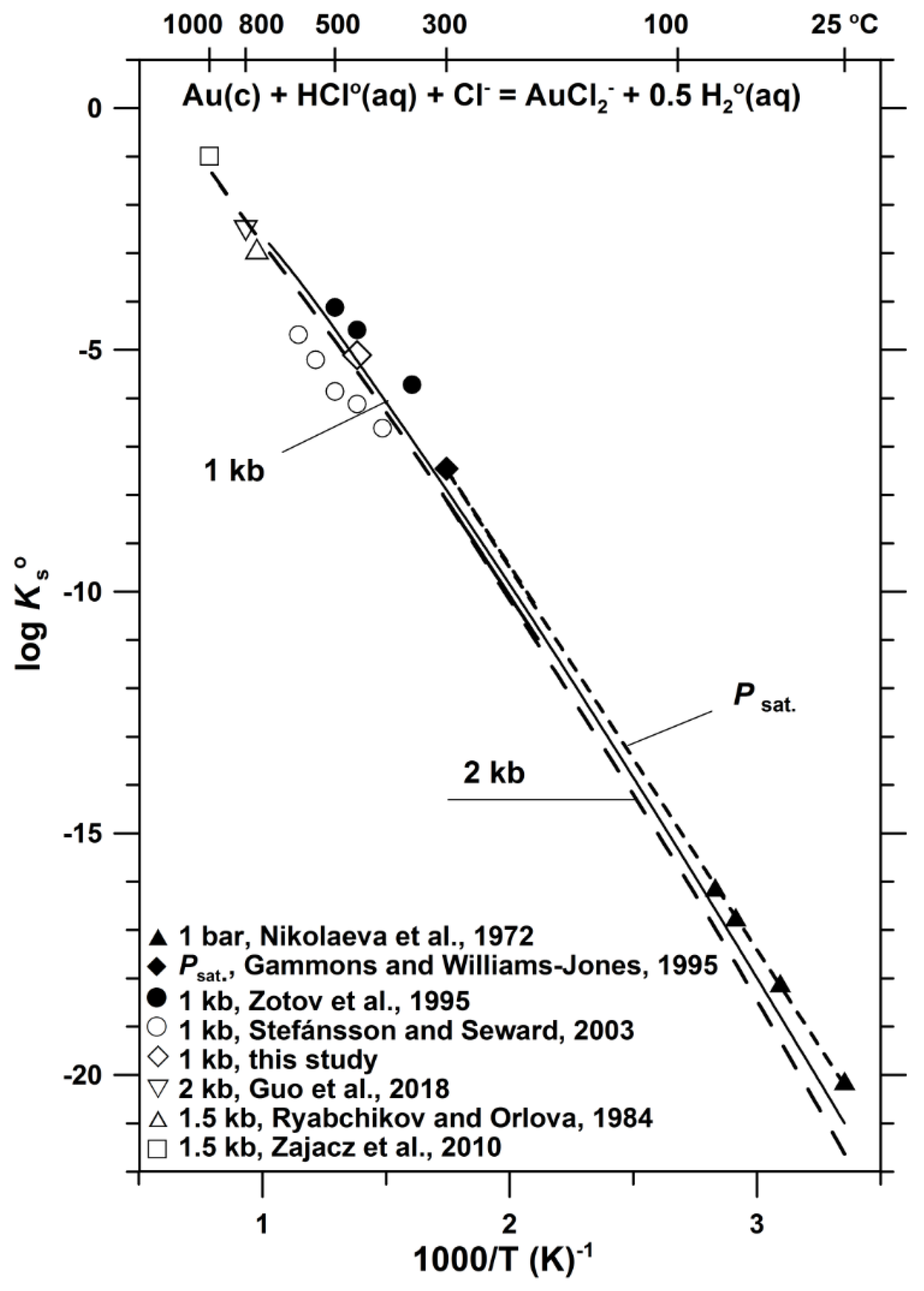
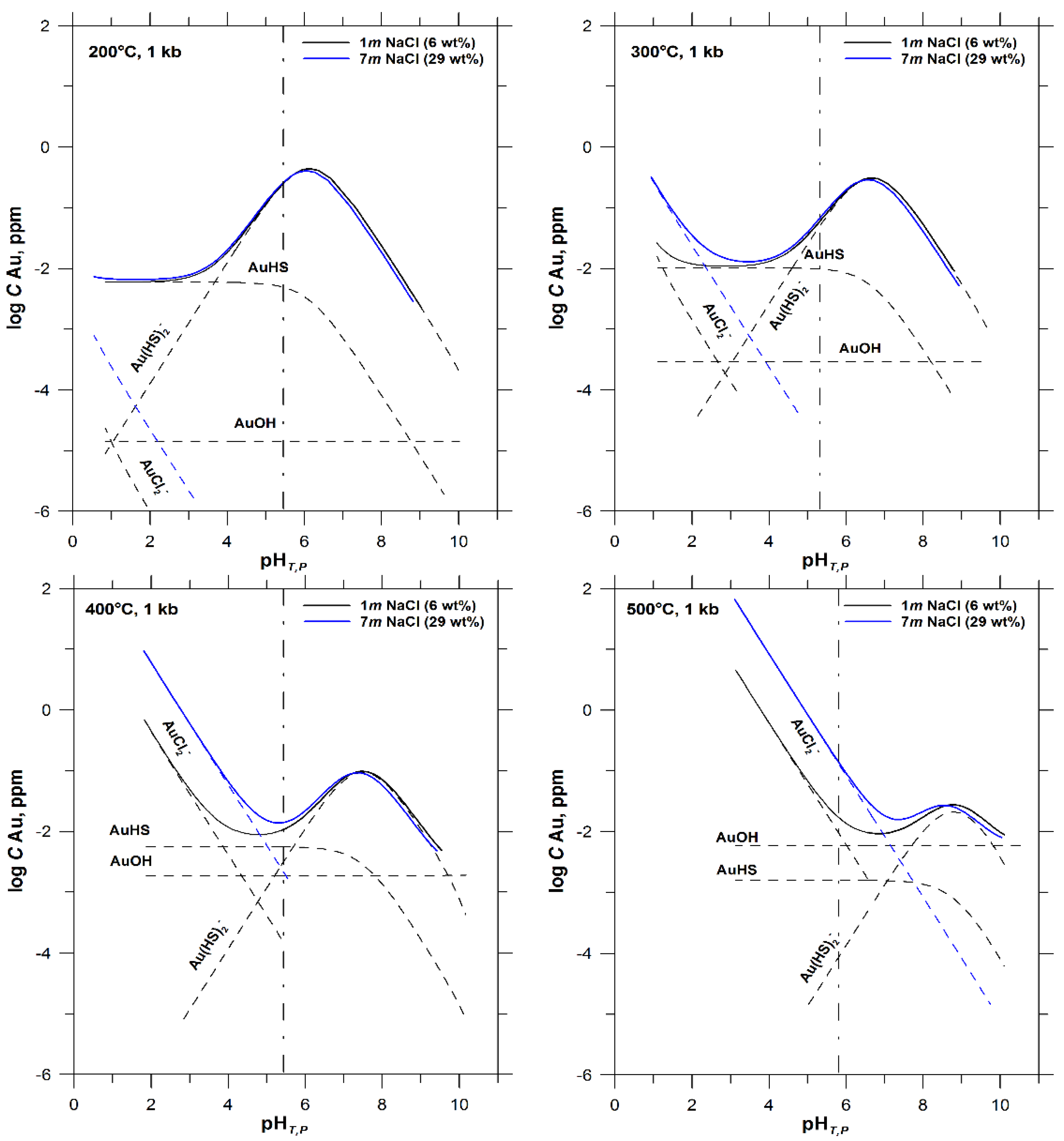
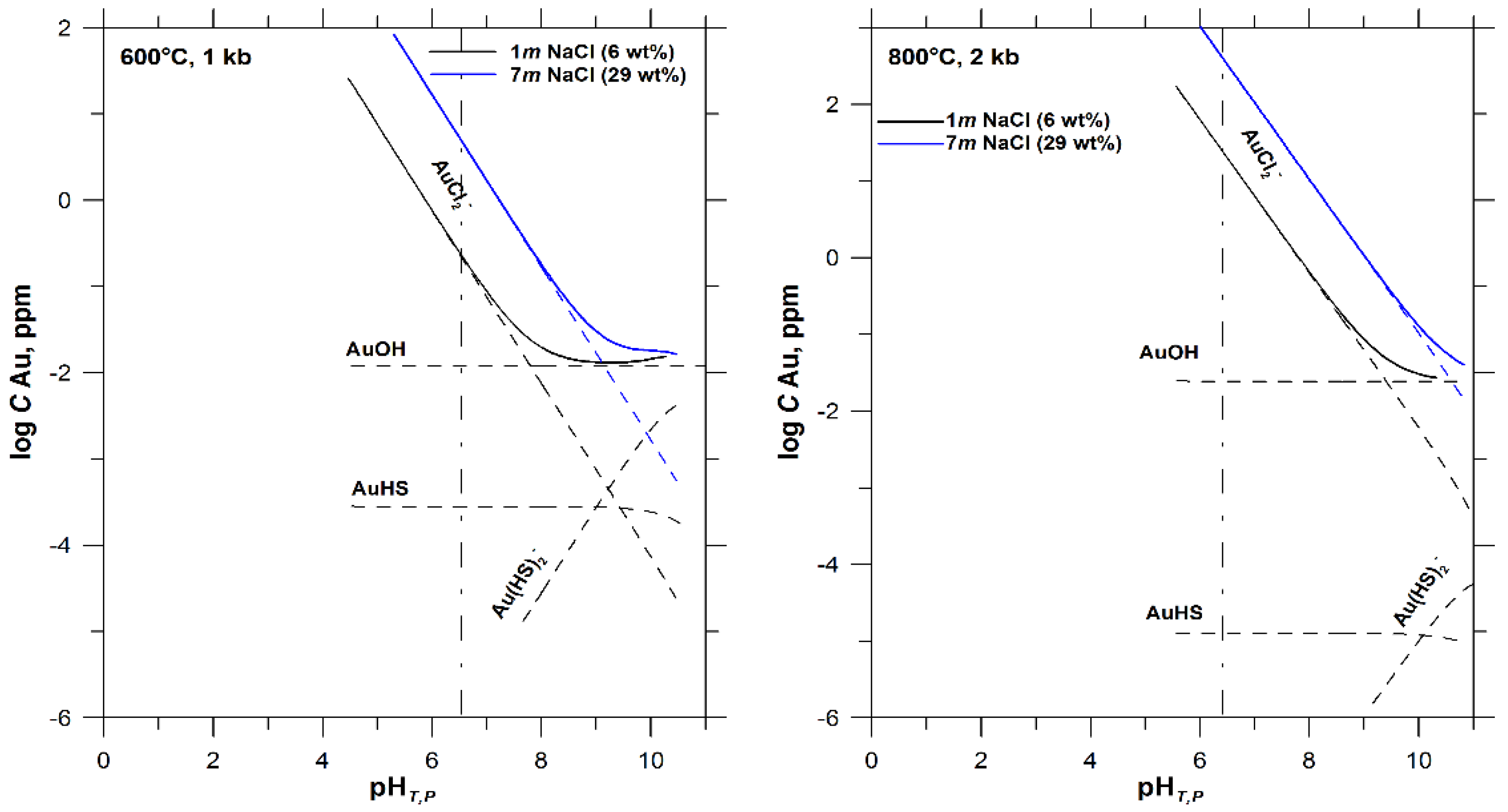
| m NaCl | m HCl | m H2SO4 | m SO2 | m H2(aq) | log m Au | Δlog m Au ** |
|---|---|---|---|---|---|---|
| 500 bar | ||||||
| 2 | 0.1 | 0.014 | −5.24 | 0.14 | ||
| 2 | 0.1 | 0.03 | −5.43 | 0.17 | ||
| 2 | 0.1 | 0.076 | −5.42 | −0.05 | ||
| 2 | 0.1 | 0.09 | −5.55 | 0.05 | ||
| 2 | 0.1 | 0.015 | −5.1 | −0.01 | ||
| 2 | 0.1 | 0.1 | −5.69 | 0.16 | ||
| 2 | 0.1 | 0.045 | −5.55 | 0.20 | ||
| 1 | 0.1 | 0.037 | −5.49 | −0.11 | ||
| 1 | 0.1 | 0.079 | −5.65 | −0.12 | ||
| 1 | 0.1 | 0.052 | −5.57 | −0.11 | ||
| 0.1 | 0.1 | 0.147 | −6.79 | −0.02 | ||
| 0.1 | 0.1 | 0.095 | −6.64 | −0.07 | ||
| 0.1 | 0.1 | 0.167 | −6.95 | 0.11 | ||
| 1000 bar | ||||||
| 2 | 0.1 | 0.0026 | −5.16 | 0.20 | ||
| 2 | 0.1 | 0.057 | −5.7 | 0.08 | ||
| 0.5 | 0.1 | 0.078 | −5.86 | −0.30 | ||
| 0.5 | 0.1 | 0.118 | −6.34 | 0.09 | ||
| 0.5 | 0.1 | 0.0085 | −5.61 | −0.07 | ||
| 0.5 | 0.1 | 0.0082 | −5.6 | −0.07 | ||
| 0.1 | 0.1 | 0.0003 | −5.28 | −0.21 | ||
| 0.206 | 0.119 | 0.0478 | 0.0987 | 5.86 × 10−7 * | −3.69 | −0.13 |
| 0.508 | 0.119 | 0.0478 | 0.0987 | 1.26 × 10−6 * | −3.62 | 0.01 |
| 1.018 | 0.119 | 0.0478 | 0.0987 | 2.22 × 10−6 * | −3.60 | 0.12 |
| 2.035 | 0.119 | 0.0478 | 0.0987 | 3.78 × 10−6 * | −3.44 | 0.09 |
| 3.043 | 0.119 | 0.0478 | 0.0987 | 5.07 × 10−6 * | −3.21 | −0.07 |
| 1500 bar | ||||||
| 0.218 | 0.119 | 0.0478 | 0.0987 | 8.05 × 10−7 * | −4.10 | −0.001 |
| 0.497 | 0.119 | 0.0478 | 0.0987 | 1.62 × 10−6 * | −3.93 | 0.04 |
| 1.012 | 0.119 | 0.0478 | 0.0987 | 2.94 × 10−6 * | −3.68 | −0.05 |
| 2.038 | 0.119 | 0.0478 | 0.0987 | 5.04 × 10−6 * | −3.42 | −0.15 |
| 3.007 | 0.119 | 0.0478 | 0.0987 | 6.55 × 10−6 * | −3.64 | 0.15 |
| t, °C | P, bar | log Ks° (exp.) | log Ks° (calc.) | Δlog Ks° (calc. − exp.) | Reference |
|---|---|---|---|---|---|
| 450 | 500 | −4.77 ± 0.07 | −4.72 | 0.05 | This study |
| 450 | 1000 | −5.10 ± 0.09 * | −5.22 | −0.12 | lbid. |
| 450 | 1000 | −5.12 ± 0.06 ** | −5.22 | −0.10 | lbid. |
| 450 | 1500 | −5.43 ± 0.09 | −5.36 | 0.07 | lbid. |
| 25 | 1 | −20.12 ± 0.08 | −20.14 | −0.02 | Nikolaeva et al. [3] |
| 50 | 1 | −18.09 ± 0.08 | −18.11 | −0.02 | lbid. |
| 70 | 1 | −16.74 ± 0.07 | −16.68 | 0.06 | lbid. |
| 80 | 1 | −16.12 ± 0.07 | −16.02 | 0.10 | lbid. |
| 300 | Psat. | −7.46 ± 0.40 | −7.47 | −0.01 | Gammons and Williams-Jones [4] |
| 750 | 1500 | −2.91 ± 0.30 | −2.59 | 0.32 | Ryabchikov and Orlova [7] |
| 800 | 2000 | −2.54 ± 0.20 | −2.33 | 0.21 | Guo et al. [9] |
| 1000 | 1500 | −0.99 ± 0.20 | −1.23 | −0.24 | Zajacz et al. [8] |
| t, °C | Pressure, bar | |||||
|---|---|---|---|---|---|---|
| Psat. | 500 | 1000 | 1500 | 2000 | 5000 | |
| 25 | −20.14 | −20.56 | −20.93 | −21.27 | −21.57 | −22.96 |
| 100 | −14.83 | −15.06 | −15.27 | −15.46 | −15.63 | −16.41 |
| 200 | −10.33 | −10.55 | −10.71 | −10.84 | −10.95 | −11.42 |
| 250 | −8.79 | −8.99 | −9.15 | −9.27 | −9.37 | −9.76 |
| 300 | −7.47 | −7.72 | −7.89 | −8.00 | −8.09 | −8.43 |
| 350 | −6.25 | −6.65 | −6.85 | −6.97 | −7.05 | −7.34 |
| 400 | −5.69 | −5.97 | −6.10 | −6.18 | −6.44 | |
| 450 | −4.72 | −5.22 | −5.36 | −5.45 | −5.68 | |
| 500 | −3.94 | −4.58 | −4.73 | −4.82 | −5.02 | |
| 550 | −4.02 | −4.19 | −4.27 | −4.45 | ||
| 600 | −3.56 | −3.71 | −3.79 | −3.95 | ||
| 650 | −3.16 | −3.30 | −3.37 | −3.51 | ||
| 700 | −2.81 | −2.93 | −2.99 | −3.11 | ||
| 750 | −2.59 | −2.64 | −2.76 | |||
| 800 | −2.28 | −2.33 | −2.43 | |||
| 850 | −2.00 | −2.04 | −2.13 | |||
| 900 | −1.73 | −1.77 | −1.85 | |||
| 950 | −1.47 | −1.51 | −1.60 | |||
| 1000 | −1.23 | −1.27 | −1.36 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zotov, A.V.; Kuzmin, N.N.; Reukov, V.L.; Tagirov, B.R. Stability of AuCl2− from 25 to 1000 °C at Pressures to 5000 bar and Consequences for Hydrothermal Gold Mobilization. Minerals 2018, 8, 286. https://doi.org/10.3390/min8070286
Zotov AV, Kuzmin NN, Reukov VL, Tagirov BR. Stability of AuCl2− from 25 to 1000 °C at Pressures to 5000 bar and Consequences for Hydrothermal Gold Mobilization. Minerals. 2018; 8(7):286. https://doi.org/10.3390/min8070286
Chicago/Turabian StyleZotov, Alexander V., Nikolai N. Kuzmin, Vladimir L. Reukov, and Boris R. Tagirov. 2018. "Stability of AuCl2− from 25 to 1000 °C at Pressures to 5000 bar and Consequences for Hydrothermal Gold Mobilization" Minerals 8, no. 7: 286. https://doi.org/10.3390/min8070286
APA StyleZotov, A. V., Kuzmin, N. N., Reukov, V. L., & Tagirov, B. R. (2018). Stability of AuCl2− from 25 to 1000 °C at Pressures to 5000 bar and Consequences for Hydrothermal Gold Mobilization. Minerals, 8(7), 286. https://doi.org/10.3390/min8070286





