The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Carbonation Experiments
2.3. Dissolution Experiments
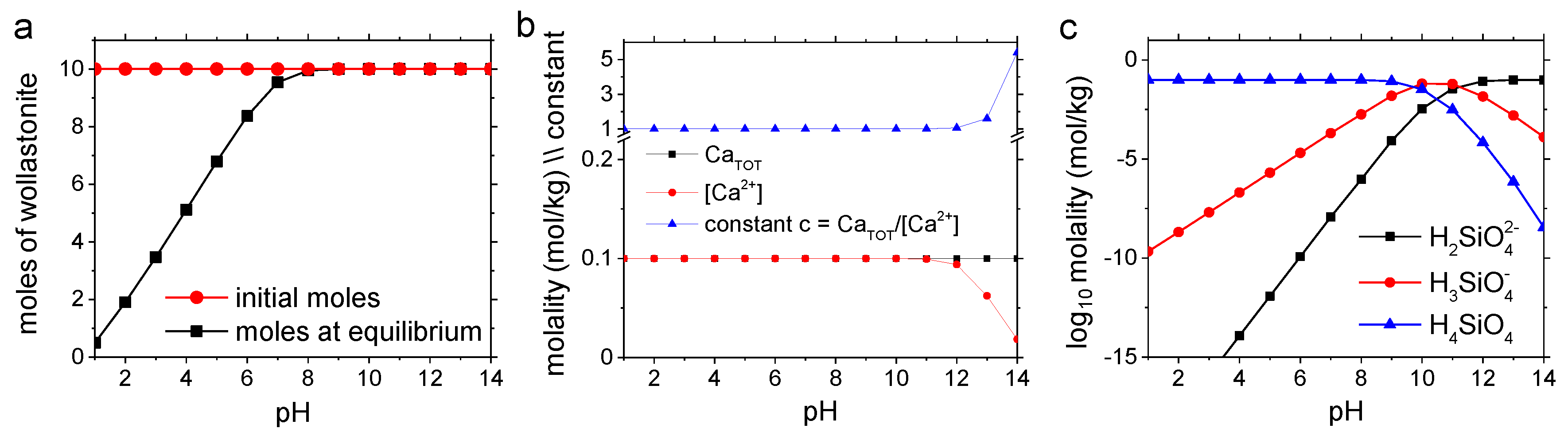
2.4. Characterization of Reactant/Product Phases and Geochemical Modeling
3. Results
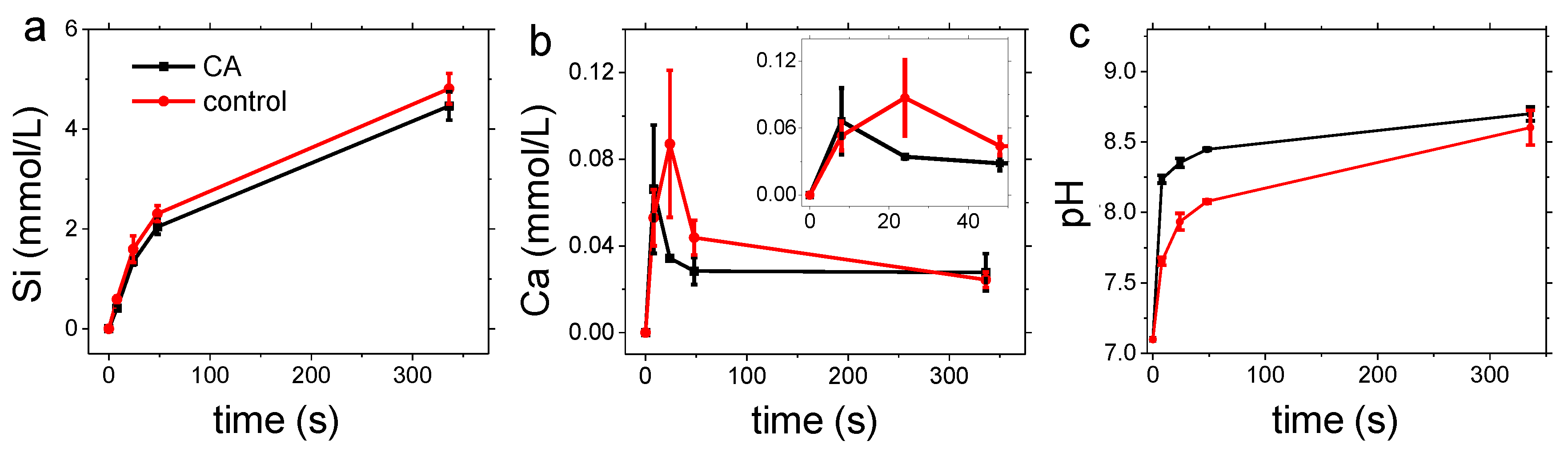
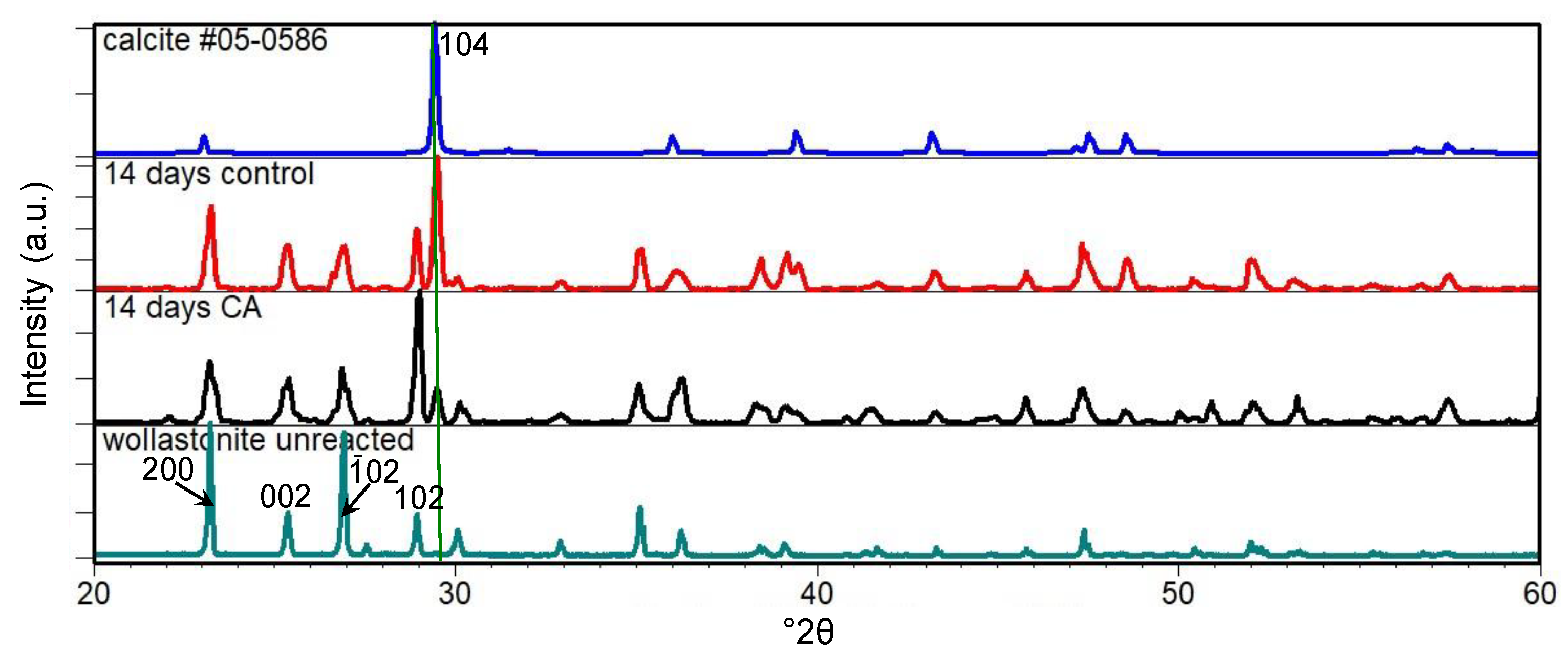
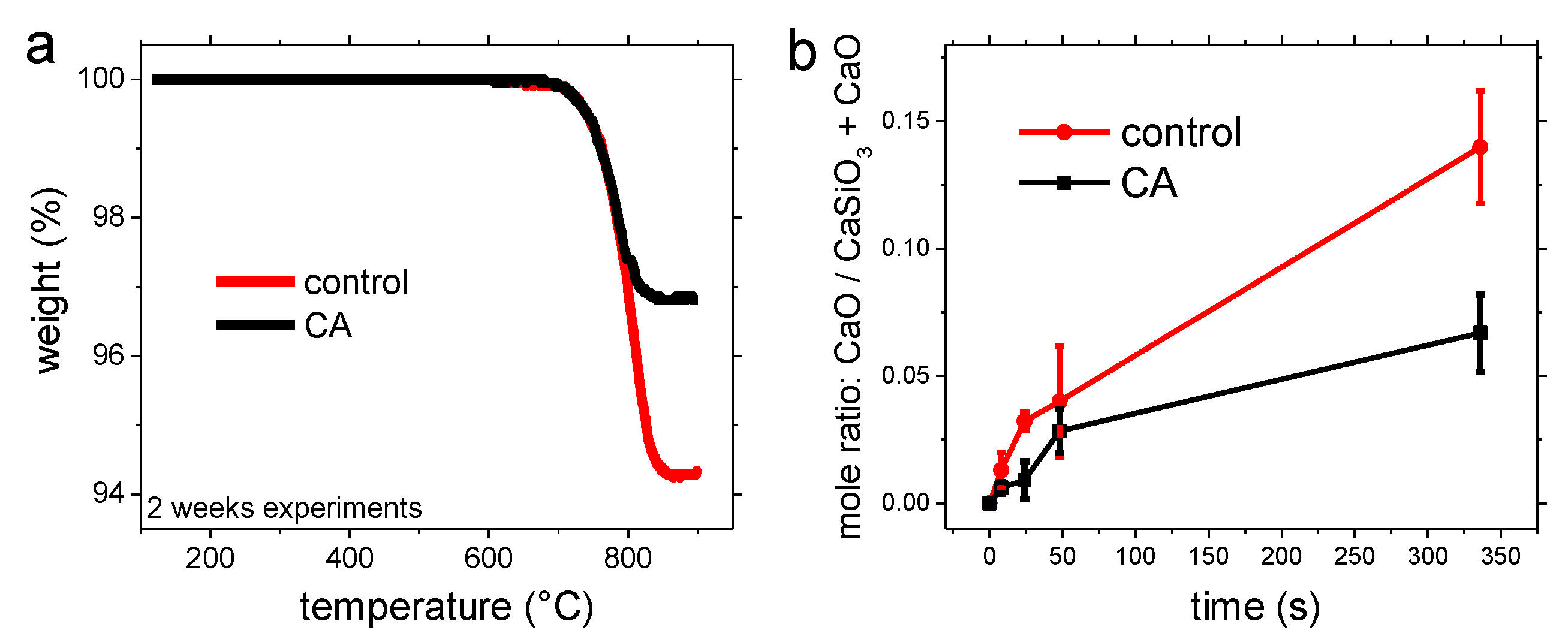
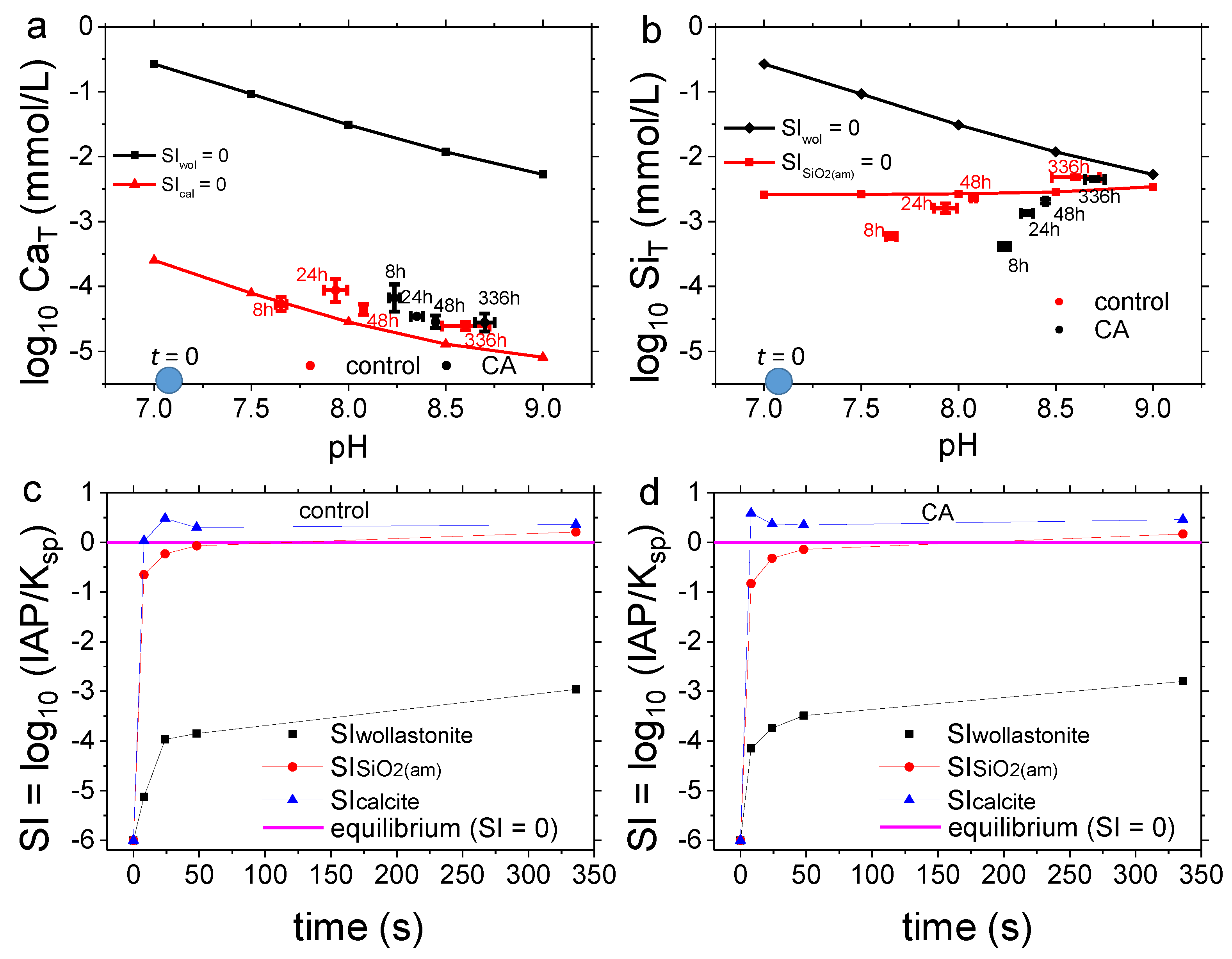
3.1. Carbonation of Wollastonite in the Presence of CA
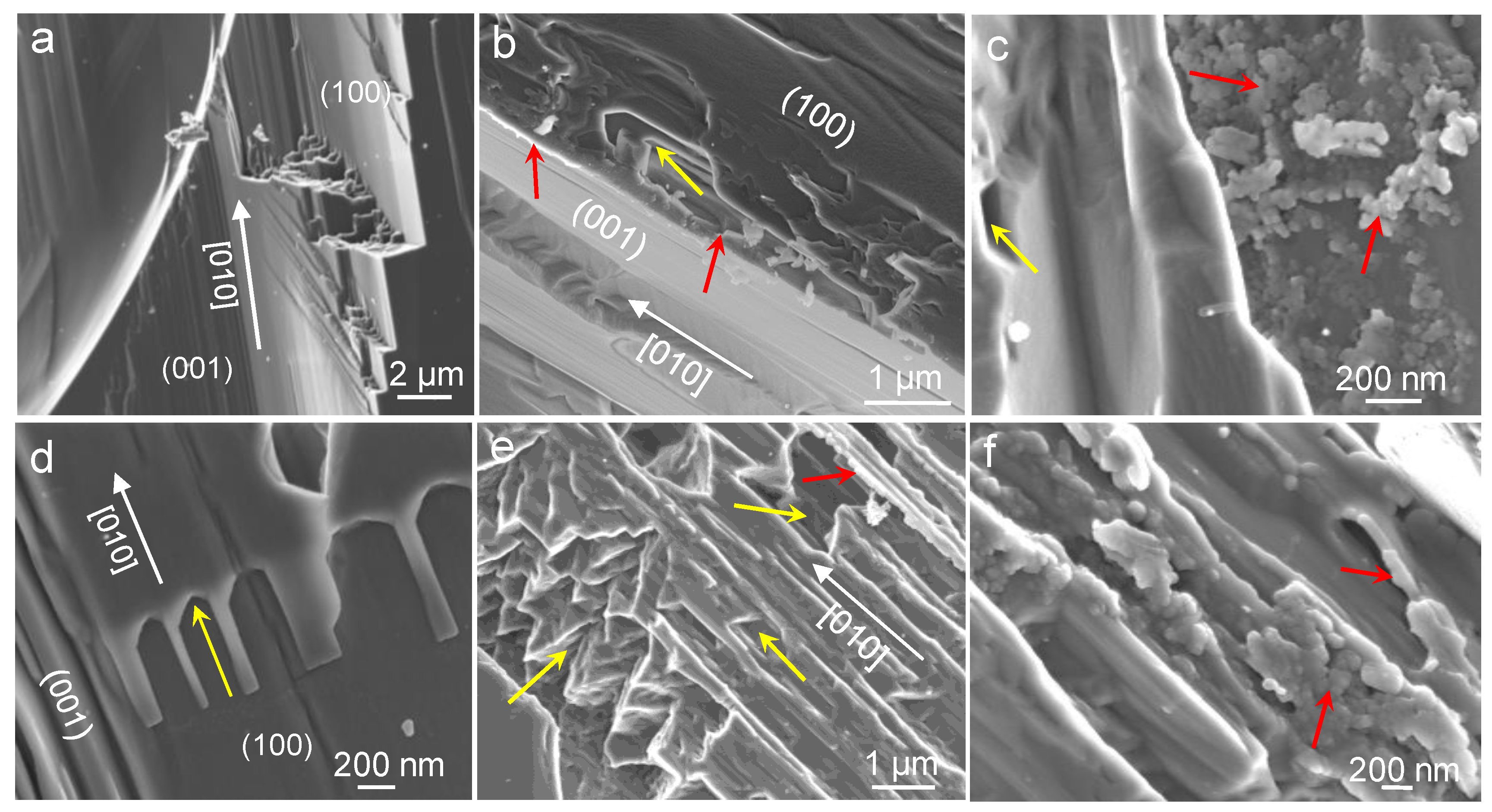
3.2. Dissolution Experiments
4. Discussion
4.1. Carbonation of Wollastonite
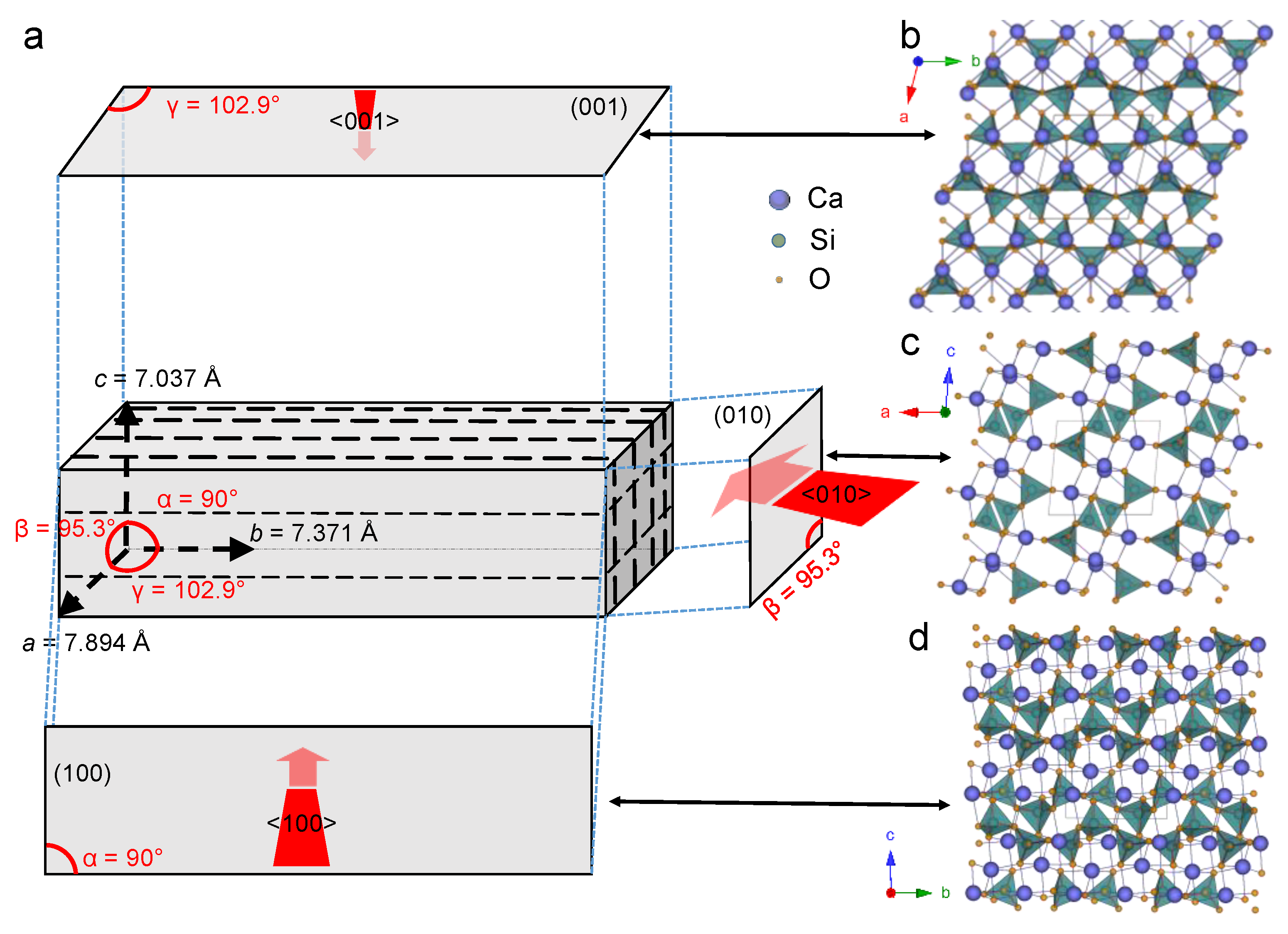
4.2. Dissolution Experiments
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Falkowski, P.; Scholes, R.J.; Boyle, E.E.A.; Canadell, J.; Canfield, D.; Elser, J.; Gruber, N.; Hibbard, K.; Högberg, P.; Linder, S.; et al. The global carbon cycle: A test of our knowledge of Earth as a system. Science 2000, 290, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Lackner, K.S. A guide for CO2 sequestration. Science 2003, 300, 1677–1678. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2014. Synthesis Report: Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Oelkers, E.H.; Gislason, S.R.; Matter, J. Mineral carbonation of CO2. Elements 2008, 4, 333–337. [Google Scholar] [CrossRef]
- Cole, D.R.; Oelkers, E.H. Carbon dioxide sequestration. Elements 2008, 4, 287–362. [Google Scholar]
- Sanna, A.; Uibu, M.; Caramanna, G.; Kuusik, R.; Maroto-Valer, M.M. A review of mineral carbonation technologies to sequester CO2. Chem. Soc. Rev. 2014, 43, 8049–8080. [Google Scholar] [CrossRef] [PubMed]
- Urey, H.C. The Planets: Their Origin and Development; Yale University Press: New Haven, CT, USA, 1952; 245p. [Google Scholar]
- Siefritz, W. CO2 disposal by means of silicates. Nature 1990, 345, 486. [Google Scholar] [CrossRef]
- Lackner, K.S.; Wendt, C.H.; Butt, D.P.; Joyce, E.L.; Sharp, D.H. Carbon dioxide disposal in carbonate minerals. Energy 1995, 20, 1153–1170. [Google Scholar] [CrossRef]
- Brantley, S.L. Kinetics of mineral dissolution. In Kinetics of Water-Rock Interaction; Brantley, S.L., Kubicki, J.D., White, A.F., Eds.; Springer: New York, NY, USA, 2008; pp. 151–210. [Google Scholar]
- Walker, J.C.G.; Hays, P.B.; Kasting, J.F. A negative feedback mechanism for the long-term stabilization of Earth’s surface temperature. J. Geophys. Res. 1981, 86, 9776–9782. [Google Scholar] [CrossRef]
- Berner, R.A.; Lasaga, A.; Garrels, R.M. The carbonate-silicate geochemical cycle and its effect on atmospheric carbon dioxide over the past 100 million years. Am. J. Sci. 1983, 283, 641–683. [Google Scholar] [CrossRef]
- Brady, P.V. The effect of silicate weathering on global temperature and atmospheric CO2. J. Geophys. Res. Solid Earth 1991, 96, 18101–18106. [Google Scholar] [CrossRef]
- Berner, R.A. The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 2003, 426, 323–326. [Google Scholar] [CrossRef] [PubMed]
- Houghton, R.A. Balancing the global carbon budget. Annu. Rev. Earth Planet. Sci. 2007, 35, 313–347. [Google Scholar] [CrossRef]
- Power, I.M.; Harrison, A.L.; Dipple, G.M.; Wilson, S.A.; Kelemen, P.B.; Hitch, M.; Southam, G. Carbon mineralization: From natural analogues to engineered systems. Rev. Miner. Geochem. 2013, 77, 305–360. [Google Scholar] [CrossRef]
- Azdarpour, A.; Asadullah, M.; Mohammadian, E.; Hamidi, H.; Junin, R.; Karaei, M.A. A review on carbon dioxide mineral carbonation through pH-swing process. Chem. Eng. J. 2015, 279, 615–630. [Google Scholar] [CrossRef]
- Gerdemann, S.J.; O’Connor, W.K.; Dahlin, D.C.; Penner, L.R.; Rush, H. Ex situ aqueous mineral carbonation. Environ. Sci. Technol. 2007, 41, 2587–2593. [Google Scholar] [CrossRef] [PubMed]
- Park, A.H.A.; Jadhav, R.; Fan, L.S. CO2 mineral sequestration: Chemically enhanced aqueous carbonation of serpentine. Can. J. Chem. Eng. 2003, 81, 885–890. [Google Scholar] [CrossRef]
- Park, A.A.; Fan, L. CO2 mineral sequestration: Physically activated dissolution of serpentine and pH swing process. Chem. Eng. Sci. 2004, 59, 5241–5247. [Google Scholar] [CrossRef]
- Krevor, S.C.; Lackner, K.S. Enhancing process kinetics for mineral carbon sequestration. Energ. Procedia 2009, 1, 4867–4871. [Google Scholar] [CrossRef]
- Zhao, H.; Park, Y.; Lee, D.H.; Park, A.H.A. Tuning the dissolution kinetics of wollastonite via chelating agents for CO2 sequestration with integrated synthesis of precipitated calcium carbonates. Phys. Chem. Chem. Phys. 2013, 15, 15185–15192. [Google Scholar] [CrossRef] [PubMed]
- Ghoorah, M.; Dlugogorski, B.Z.; Balucan, R.D.; Kennedy, E.M. Selection of acid for weak acid processing of wollastonite for mineralisation of CO2. Fuel 2014, 122, 277–286. [Google Scholar] [CrossRef]
- Matter, J.M.; Stute, M.; Snæbjörnsdottir, S.Ó.; Oelkers, E.H.; Gislason, S.R.; Aradottir, E.S.; Sigfusson, B.; Gunnarsson, I.; Sigurdardottir, H.; Gunnlaugsson, E.; et al. Rapid carbon mineralization for permanent disposal of anthropogenic carbon dioxide emissions. Science 2016, 352, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Gislason, S.R.; Oelkers, E.H. Carbon storage in basalt. Science 2014, 344, 373–374. [Google Scholar] [CrossRef] [PubMed]
- Daval, D.; Martinez, I.; Guigner, J.M.; Hellmann, R.; Corvisier, J.; Findling, N.; Dominici, C.; Goffé, B.; Guyot, F. Mechanism of wollastonite carbonation deduced from micro-to nanometer length scale observations. Am. Miner. 2009, 94, 1707–1726. [Google Scholar] [CrossRef]
- Daval, D.; Martinez, I.; Corvisier, J.; Findling, N.; Goffé, B.; Guyot, F. Carbonation of Ca-bearing silicates, the case of wollastonite: Experimental investigations and kinetic modeling. Chem. Geol. 2009, 265, 63–78. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Putnis, C.V.; Di Lorenzo, F.; Ruiz-Agudo, C.; Rodriguez-Navarro, C. Interfacial and surface controls on wollastonite carbonation: Insights from texture observations and geochemical modeling. Am. J. Sci. under review.
- Huijgen, W.J.; Witkamp, G.J.; Comans, R.N. Mechanisms of aqueous wollastonite carbonation as a possible CO2 sequestration process. Chem. Eng. Sci. 2006, 61, 4242–4251. [Google Scholar] [CrossRef]
- Dreybrodt, W.; Eisenlohr, L.; Madry, B.; Ringer, S. Precipitation kinetics of calcite in the system CaCO3-H2O-CO2: The conversion to CO2 by the slow process H+ + HCO3− → CO2 + H2O as a rate limiting step. Geochim. Cosmochim. Acta 1997, 61, 3897–3904. [Google Scholar] [CrossRef]
- Cizer, Ö.; Ruiz-Agudo, E.; Rodriguez-Navarro, C. Kinetic effect of carbonic anhydrase enzyme on the carbonation reaction of lime mortar. Int. J. Archit. Heritage 2018. [Google Scholar] [CrossRef]
- Bond, G.M.; Stringer, J.; Brandvold, D.K.; Simsek, F.A.; Medina, M.G.; Egeland, G. Development of integrated system for biomimetic CO2 sequestration using the enzyme carbonic anhydrase. Energy Fuels 2001, 15, 309–316. [Google Scholar] [CrossRef]
- Vinoba, M.; Bhagiyalakshmi, M.; Jeong, S.K.; Nam, S.C.; Yoon, Y. Carbonic anhydrase immobilized on encapsulated magnetic nanoparticles for CO2 sequestration. Chem. Eur. J. 2012, 18, 12028–12034. [Google Scholar] [CrossRef] [PubMed]
- Power, I.M.; Harrison, A.L.; Dipple, G.M. Accelerating mineral carbonation using carbonic anhydrase. Environ. Sci. Technol. 2016, 50, 2610–2618. [Google Scholar] [CrossRef] [PubMed]
- Silverman, D.N.; Lindskog, S. The catalytic mechanism of carbonic anhydrase: Implications of a rate-limiting protolysis of water. Acc. Chem. Res. 1988, 21, 30–36. [Google Scholar] [CrossRef]
- Frost, S.C.; McKenna, R. (Eds.) Carbonic Anhydrase: Mechanism, Regulation, Links to Disease and Industrial Applications; Springer: London, UK, 2014; Volume 75, 429p. [Google Scholar]
- Miyamoto, H.; Miyashita, T.; Okushima, M.; Nakano, S.; Morita, T.; Matsushiro, A. A carbonic anhydrase from the nacreous layer in oyster pearls. Proc. Natl. Acad. Sci. USA 1996, 93, 9657–9660. [Google Scholar] [CrossRef] [PubMed]
- Pierre, A.C. Enzymatic carbon dioxide capture. ISRN Chem. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Molva, M.; Kilic, S.; Ozdemir, E. Effect of carbonic anhydrase on CaCO3 crystallization in alkaline solution. Energy Fuels 2016, 30, 10686–10695. [Google Scholar] [CrossRef]
- Patel, T.N.; Park, A.H.A.; Banta, S. Periplasmic expression of carbonic anhydrase in Escherichia coli: A new biocatalyst for CO2 hydration. Biotechnol. Bioeng. 2013, 110, 1865–1873. [Google Scholar] [CrossRef] [PubMed]
- Gadikota, G.; Park, A.H.A. Accelerated carbonation of Ca-and Mg-bearing minerals and industrial wastes using CO2. In Carbon Dioxide Utilisation; Styring, P., Quadrelli, E.A., Armstrong, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 15–137. [Google Scholar]
- Ruiz-Agudo, E.; Putnis, C.V.; Rodriguez-Navarro, C.; Putnis, A. The mechanism of leached layer formation during chemical weathering of silicate minerals. Geology 2012, 40, 947–950. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; King, H.E.; Patiño-López, L.D.; Putnis, C.V.; Geisler, T.; Rodriguez-Navarro, C.; Putnis, A. Control of silicate weathering by interface-coupled dissolution–precipitation processes at the mineral-solution interface. Geology 2016, 44, 567–570. [Google Scholar] [CrossRef]
- Béarat, H.; McKelvy, M.J.; Chizmeshya, A.V.; Gormley, D.; Nunez, R.; Carpenter, R.W.; Squires, K.; Wolf, G.H. Carbon sequestration via aqueous olivine mineral carbonation: Role of passivating layer formation. Environ. Sci. Technol. 2006, 40, 4802–4808. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, P.S.; Mitchell, L.D. In situ laboratory X-ray powder diffraction study of wollastonite carbonation using a high-pressure stage. Appl. Geochem. 2009, 24, 1635–1639. [Google Scholar] [CrossRef]
- King, H.E.; Plümper, O.; Putnis, A. Effect of secondary phase formation on the carbonation of olivine. Environ. Sci. Technol. 2010, 44, 6503–6509. [Google Scholar] [CrossRef] [PubMed]
- Daval, D.; Sissmann, O.; Menguy, N.; Saldi, G.D.; Guyot, F.; Martinez, I.; Corvisier, J.; García, B.; Machouk, I.; Knauss, K.G.; Hellmann, R. Influence of amorphous silica layer formation on the dissolution rate of olivine at 90 °C and elevated pCO2. Chem. Geol. 2011, 284, 193–209. [Google Scholar] [CrossRef]
- Miller, Q.R.S.; Thompson, C.J.; Loring, J.S.; Windisch, C.F.; Bowden, M.E.; Hoyt, D.W.; Hu, J.Z.; Arey, B.W.; Rosso, K.M.; Schaef, H.T. Insights into silicate carbonation processes in water-bearing supercritical CO2 fluids. Int. J. Greenhouse Gas Control 2013, 15, 104–118. [Google Scholar] [CrossRef]
- Min, Y.; Li, Q.; Voltolini, M.; Kneafsey, T.; Jun, Y.S. Wollastonite carbonation in water-bearing supercritical CO2: Effects of particle size. Environ. Sci. Technol. 2017, 51, 13044–13053. [Google Scholar] [CrossRef] [PubMed]
- Schröder, H.C.; Krasko, A.; Le Pennec, G.; Adell, T.; Wiens, M.; Hassanein, H.; Müller, I.M.; Müller, W.E.G. Silicon Biomineralization; Springer: Berlin, Germany, 2003; 341p. [Google Scholar]
- Ehrlich, H.; Demadis, K.D.; Pokrovsky, O.S.; Koutsoukos, P.G. Modern views on desilicification: Biosilica and abiotic silica dissolution in natural and artificial environments. Chem. Rev. 2010, 110, 4656–4689. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Lian, B.; Hao, J.; Liu, C.; Wang, S. Effect of carbonic anhydrase on silicate weathering and carbonate formation at present day CO2 concentrations compared to primordial values. Sci. Rep. 2015, 5, 7733. [Google Scholar] [CrossRef] [PubMed]
- Nakata, K.; Shimomura, N.; Shiina, N.; Izumi, M.; Ichikawa, K.; Shiro, M. Kinetic study of catalytic CO2 hydration by water-soluble model compound of carbonic anhydrase and anion inhibition effect on CO2 hydration. J. Biochem. 2002, 89, 255–266. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Shaban, S.Y.; Ichikawa, K. A promising structural zinc enzyme model for CO2 fixation and calcification. Tetrahedron Lett. 2008, 49, 7303–7306. [Google Scholar] [CrossRef]
- Zastrow, M.L.; Peacock, A.F.; Stuckey, J.A.; Pecoraro, V.L. Hydrolytic catalysis and structural stabilization in a designed metalloprotein. Nat. Chem. 2012, 4, 118–123. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, G.A.; Šiller, L. Nickel nanoparticles catalyse reversible hydration of carbon dioxide for mineralization carbon capture and storage. Catal. Sci. Technol. 2013, 3, 1234–1239. [Google Scholar] [CrossRef]
- Sabouni, R.; Kazemian, H.; Rohani, S. Carbon dioxide capturing technologies: A review focusing on metal organic framework materials (MOFs). Environ. Sci. Pollut. Res. 2014, 21, 5427–5449. [Google Scholar] [CrossRef] [PubMed]
- Nath, I.; Chakraborty, J.; Verpoort, F. Metal organic frameworks mimicking natural enzymes: A structural and functional analogy. Chem. Soc. Rev. 2016, 45, 4127–4170. [Google Scholar] [CrossRef] [PubMed]
- D’Alessandro, D.M.; Smit, B.; Long, J.R. Carbon dioxide capture: Prospects for new materials. Angew. Chem. Int. Ed. 2010, 49, 6058–6082. [Google Scholar] [CrossRef] [PubMed]
- Cavka, J.H.; Jakobsen, S.; Olsbye, U.; Guillou, N.; Lamberti, C.; Bordiga, S.; Lillerud, K.P. A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability. J. Am. Chem. Soc. 2008, 130, 13850–13851. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, H.; Gándara, F.; Zhang, Y.B.; Jiang, J.; Queen, W.L.; Hudson, M.R.; Yaghi, O.M. Water adsorption in porous metal–organic frameworks and related materials. J. Am. Chem. Soc. 2014, 136, 4369–4381. [Google Scholar] [CrossRef] [PubMed]
- Gil-San Millan, R.; Lopez-Maya, E.; Ryo, S.G.; Kim, M.K.; Navarro, J.A.R. Improved soman and VX nerve agents degradation by magnesium hydroxide doped metal-organic frameworks. J. Mater. Chem. A. under review.
- López-Maya, E.; Montoro, C.; Rodríguez-Albelo, L.M.; Aznar Cervantes, S.D.; Lozano-Pérez, A.A.; Cenís, J.L.; Barea, E.; Navarro, J.A.R. Textile/metal–organic-framework composites as self-detoxifying filters for chemical-warfare agents. Angew. Chem. Int. Ed. 2015, 54, 6790–6794. [Google Scholar] [CrossRef] [PubMed]
- Valenzano, L.; Civalleri, B.; Chavan, S.; Bordiga, S.; Nilsen, M.H.; Jakobsen, S.; Lillerud, K.P.; Lamberti, C. Disclosing the complex structure of UiO-66 metal organic framework: A synergic combination of experiment and theory. Chem. Mater. 2011, 23, 1700–1718. [Google Scholar] [CrossRef]
- Deer, W.A.; Howie, R.A.; Zussman, J. Rock-Forming Minerals: Single-Chain Silicates; The Geological Society: London, UK, 1997; 668p. [Google Scholar]
- Bailey, A.; Reesman, A.L. A survey study of the kinetics of wollastonite dissolution in H2O-CO2 and buffered systems at 25 degrees C. Am. J. Sci. 1971, 271, 464–472. [Google Scholar] [CrossRef]
- Rimstidt, J.D.; Dove, P.M. Mineral/solution reaction rates in a mixed flow reactor: Wollastonite hydrolysis. Geochim. Cosmochim. Acta 1986, 50, 2509–2516. [Google Scholar] [CrossRef]
- Murphy, W.M.; Helgeson, H.C. Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. III. Activated complexes and the pH-dependence of the rates of feldspar, pyroxene, wollastonite, and olivine hydrolysis. Geochim. Cosmochim. Acta 1987, 51, 3137–3153. [Google Scholar] [CrossRef]
- Casey, W.H.; Westrich, H.R.; Banfield, J.F.; Ferruzzi, G.; Arnold, G.W. Leaching and reconstruction at the surfaces of dissolving chain-silicate minerals. Nature 1993, 366, 253–256. [Google Scholar] [CrossRef]
- Xie, Z.; Walther, J.V. Dissolution stoichiometry and adsorption of alkali and alkaline earth elements to the acid-reacted wollastonite surface at 25 °C. Geochim. Cosmochim. Acta 1994, 58, 2587–2598. [Google Scholar] [CrossRef]
- Kojima, T.; Nagamine, A.; Ueno, N.; Uemiya, S. Absorption and fixation of carbon dioxide by rock weathering. Energy Convers. Manag. 1997, 38, S461–S466. [Google Scholar] [CrossRef]
- Weissbart, E.J.; Rimstidt, J.D. Wollastonite: Incongruent dissolution and leached layer formation. Geochim. Cosmochim. Acta 2000, 64, 4007–4016. [Google Scholar] [CrossRef]
- Wu, J.C.S.; Sheen, J.D.; Chen, S.Y.; Fan, Y.C. Feasibility of CO2 fixation via artificial rock weathering. Ind. Eng. Chem. Res. 2001, 40, 3902–3905. [Google Scholar] [CrossRef]
- Golubev, S.V.; Pokrovsky, O.S.; Schott, J. Experimental determination of the effect of dissolved CO2 on the dissolution kinetics of Mg and Ca silicates at 25 °C. Chem. Geol. 2005, 217, 227–238. [Google Scholar] [CrossRef]
- Green, E.; Luttge, A. Incongruent dissolution of wollastonite measured with vertical scanning interferometry. Am. Miner. 2006, 91, 430–434. [Google Scholar] [CrossRef]
- Tai, C.Y.; Chen, W.R.; Shih, S.M. Factors affecting wollastonite carbonation under CO2 supercritical conditions. AIChE J. 2006, 52, 292–299. [Google Scholar] [CrossRef]
- Daval, D.; Bernard, S.; Rémusat, L.; Wild, B.; Guyot, F.; Micha, J.S.; Rieutord, F.; Magnin, V.; Fernandez-Martinez, A. Dynamics of altered surface layer formation on dissolving silicates. Geochim. Cosmochim. Acta 2017, 209, 51–69. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Shirokova, L.S.; Bénézeth, P.; Schott, J.; Golubev, S.V. Effect of organic ligands and heterotrophic bacteria on wollastonite dissolution kinetics. Am. J. Sci. 2009, 309, 731–772. [Google Scholar] [CrossRef]
- Schott, J.; Pokrovsky, O.S.; Spalla, O.; Devreux, F.; Gloter, A.; Mielczarski, J.A. Formation, growth and transformation of leached layers during silicate minerals dissolution: The example of wollastonite. Geochim. Cosmochim. Acta 2012, 98, 259–281. [Google Scholar] [CrossRef]
- Ding, W.; Fu, L.; Ouyang, J.; Yang, H. CO2 mineral sequestration by wollastonite carbonation. Phys. Chem. Miner. 2014, 41, 489–496. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for Phreeqc Version 3. A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey: Denver, VA, USA, 2013. Available online: http://pubs.usgs.gov/tm/06/a43 (accessed on 9 May 2018).
- Rodriguez-Navarro, C.; Ruiz-Agudo, E.; Luque, A.; Rodriguez-Navarro, A.B.; Ortega-Huertas, M. Thermal decomposition of calcite: Mechanisms of formation and textural evolution of CaO nanocrystals. Am. Miner. 2009, 94, 578–593. [Google Scholar] [CrossRef]
- Teng, H.H.; Dove, P.M.; De Yoreo, J.J. Kinetics of calcite growth: Surface processes and relationships to macroscopic rate laws. Geochim. Cosmochim. Acta 2000, 64, 2255–2266. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Burgos Cara, A.; Elert, K.; Putnis, C.V.; Ruiz-Agudo, E. Direct nanoscale imaging reveals the growth of calcite crystals via amorphous nanoparticles. Cryst. Growth Des. 2016, 16, 1850–1860. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Ruiz-Agudo, E.; Harris, J.; Wolf, S.E. Nonclassical crystallization in vivo et in vitro (II): Nanogranular features in biomimetic minerals disclose a general colloid-mediated crystal growth mechanism. J. Struct. Biol. 2016, 196, 260–287. [Google Scholar] [CrossRef] [PubMed]
- Turpault, M.P.; Trotignon, L. The dissolution of biotite single crystals in dilute HNO3 at 24 °C: Evidence of an anisotropic corrosion process of micas in acidic solutions. Geochim. Cosmochim. Acta 1994, 58, 2761–2775. [Google Scholar] [CrossRef]
- Awad, A.; Van Groos, A.K.; Guggenheim, S. Forsteritic olivine: Effect of crystallographic direction on dissolution kinetics. Geochim. Cosmochim. Acta 2000, 64, 1765–1772. [Google Scholar] [CrossRef]
- Daval, D.; Hellmann, R.; Saldi, G.D.; Wirth, R.; Knauss, K.G. Linking nm-scale measurements of the anisotropy of silicate surface reactivity to macroscopic dissolution rate laws: New insights based on diopside. Geochim. Cosmochim. Acta 2013, 107, 121–134. [Google Scholar] [CrossRef]
- Lasaga, A.C.; Luttge, A. Variation of crystal dissolution rate based on a dissolution stepwave model. Science 2001, 291, 2400–2404. [Google Scholar] [CrossRef] [PubMed]
- Dove, P.M.; Han, N.; De Yoreo, J.J. Mechanisms of classical crystal growth theory explain quartz and silicate dissolution behavior. Proc. Natl. Acad. Sci. USA 2005, 102, 15357–15362. [Google Scholar] [CrossRef] [PubMed]
- Pollet-Villard, M.; Daval, D.; Ackerer, P.; Saldi, G.D.; Wild, B.; Knauss, K.G.; Fritz, B. Does crystallographic anisotropy prevent the conventional treatment of aqueous mineral reactivity? A case study based on K-feldspar dissolution kinetics. Geochim. Cosmochim. Acta 2016, 190, 294–308. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Putnis, C.V.; Pel, L.; Rodriguez-Navarro, C. Template-assisted crystallization of sulfates onto calcite: Implications for the prevention of salt damage. Cryst. Growth Des. 2012, 13, 40–51. [Google Scholar] [CrossRef]
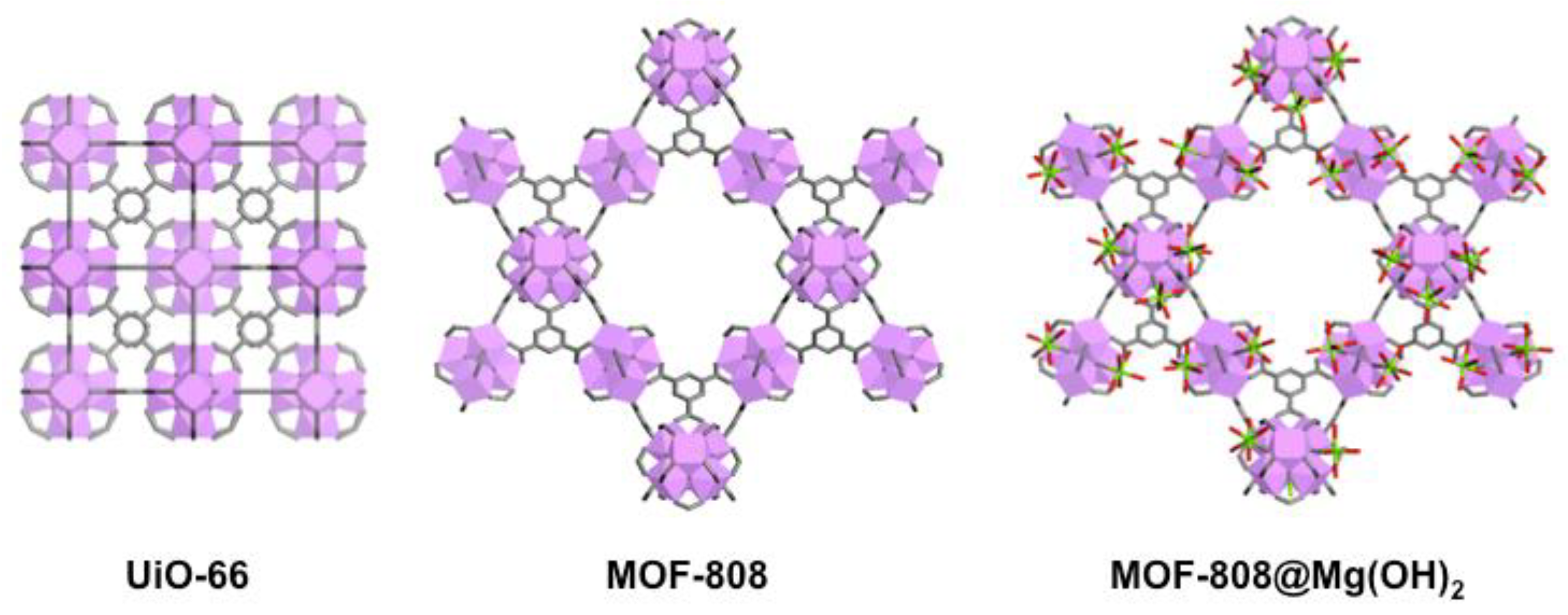



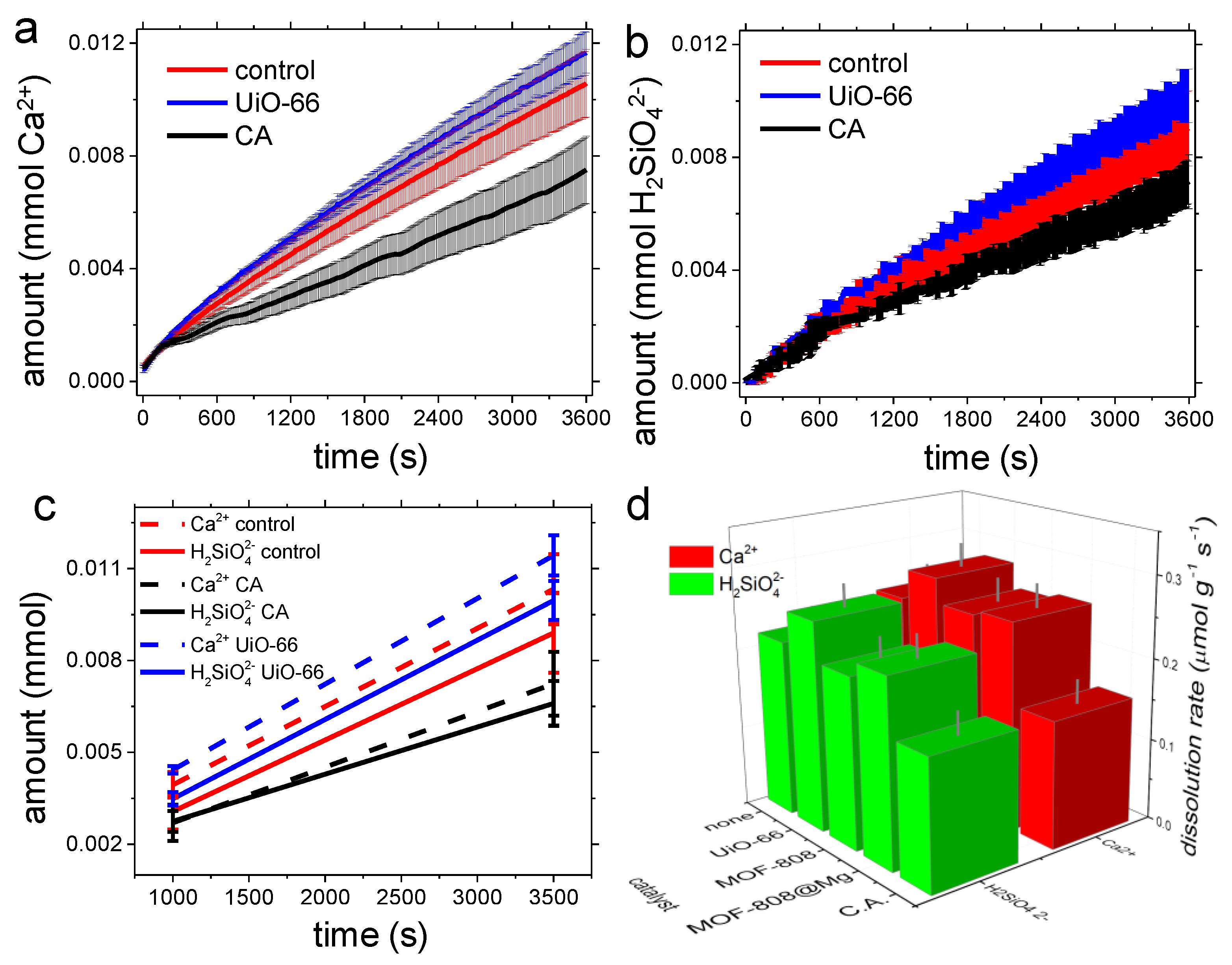
| Control | CA | UiO-66 | MOF-808 | MOF-808@Mg(OH)2 | |
|---|---|---|---|---|---|
| 1.28 ± 0.14 × 10−8 | 0.96 ± 0.11 × 10−8 | 1.47 ± 0.11 × 10−8 | 1.34 ± 0.16 × 10−8 | 1.31 ± 0.13 × 10−8 | |
| 1.19 ± 0.11 × 10−8 | 0.86 ± 0.09 ×10−8 | 1.32 ± 0.12 × 10−8 | 1.19 ± 0.15 × 10−8 | 1.19 ± 0.12 × 10−8 |
| ΔGdissolution wollastonite | ΔGprecipitation calcite | ΔGprecipitation Sio2 nH2O | ||||
|---|---|---|---|---|---|---|
| Time | No CA | CA | No CA | CA | No CA | CA |
| 8 h | −30.7 ± 1.1 | −25.1 ±1.1 | 0.1 ± 0.7 | 3.3 ± 1.3 | −3.9 ± 0.3 | −5.0 ± 0.3 |
| 24 h | −23.9 ± 0.7 | −22.4 ± 0.1 | 2.7 ± 0.9 | 2.2 ± 0.1 | −1.4 ± 0.4 | −1.9 ± 0.1 |
| 48 h | −23.1 ± 0.5 | −21.0 ± 0.3 | 1.7 ± 0.5 | 2.0 ± 0.5 | −0.4 ± 0.1 | −0.9 ± 0.2 |
| 336 h | −17.8 ± 1.2 | −16.9 ± 0.3 | 2.1 ± 0.5 | 2.7 ± 0.7 | 1.2 ± 0.1 | 1.0 ± 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Lorenzo, F.; Ruiz-Agudo, C.; Ibañez-Velasco, A.; Gil-San Millán, R.; Navarro, J.A.R.; Ruiz-Agudo, E.; Rodriguez-Navarro, C. The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration. Minerals 2018, 8, 209. https://doi.org/10.3390/min8050209
Di Lorenzo F, Ruiz-Agudo C, Ibañez-Velasco A, Gil-San Millán R, Navarro JAR, Ruiz-Agudo E, Rodriguez-Navarro C. The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration. Minerals. 2018; 8(5):209. https://doi.org/10.3390/min8050209
Chicago/Turabian StyleDi Lorenzo, Fulvio, Cristina Ruiz-Agudo, Aurelia Ibañez-Velasco, Rodrigo Gil-San Millán, Jorge A. R. Navarro, Encarnacion Ruiz-Agudo, and Carlos Rodriguez-Navarro. 2018. "The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration" Minerals 8, no. 5: 209. https://doi.org/10.3390/min8050209
APA StyleDi Lorenzo, F., Ruiz-Agudo, C., Ibañez-Velasco, A., Gil-San Millán, R., Navarro, J. A. R., Ruiz-Agudo, E., & Rodriguez-Navarro, C. (2018). The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration. Minerals, 8(5), 209. https://doi.org/10.3390/min8050209







