Classical Polarizable Force Field to Study Hydrated Hectorite: Optimization on DFT Calculations and Validation against XRD Data
Abstract
1. Introduction
2. Parametrization of PIM Force Field
2.1. Characteristics of the Polarizable Ion Model
2.2. Optimization Procedure
- Generation of a series of representative configurations using classical molecular dynamics (MD)
- DFT calculations on each of these configurations
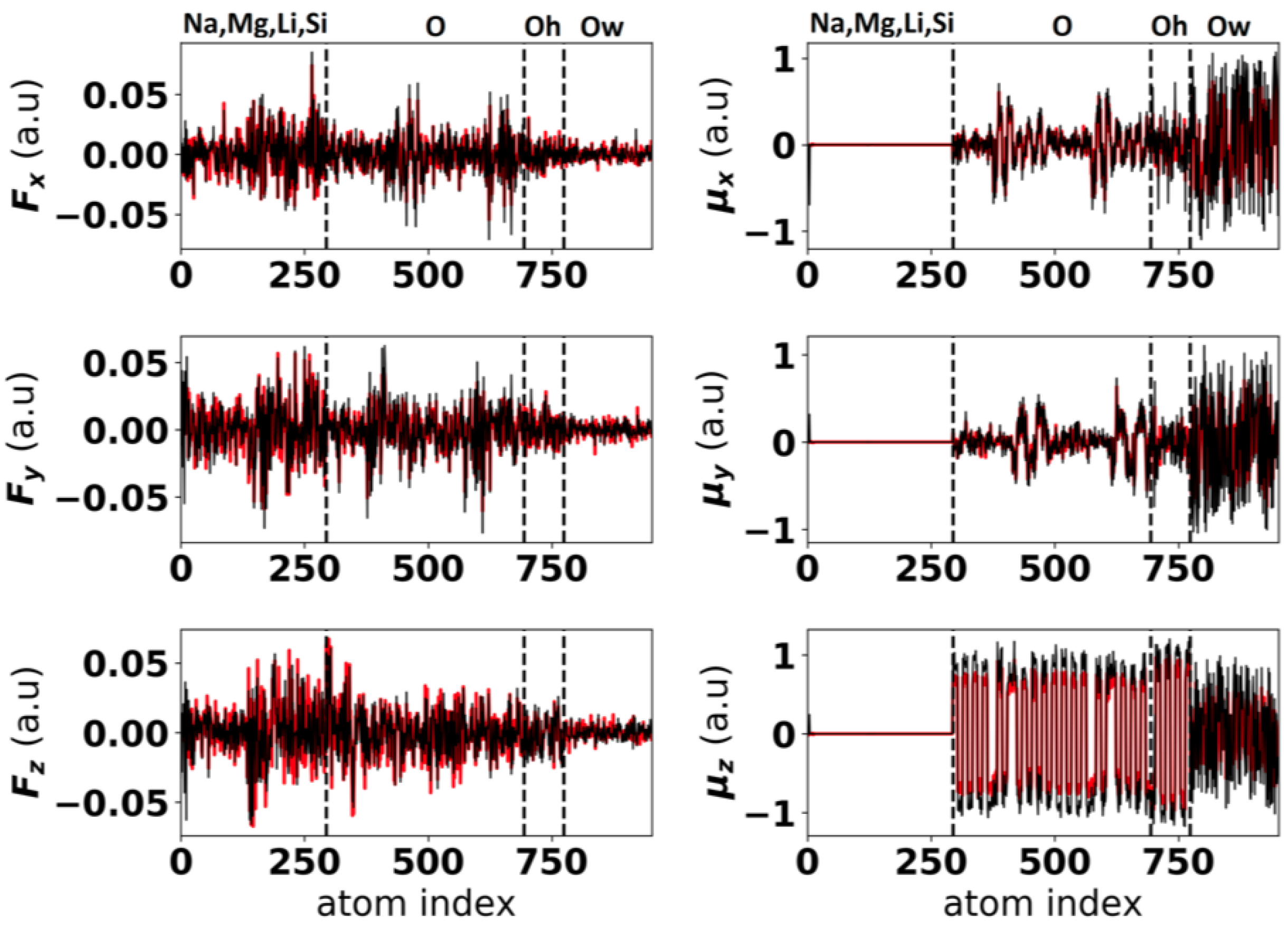
- Minimization of the error function on the dipoles with respect to the parameters of the polarization term (V) and of with respect to the repulsion term (V):where is the number of configurations on which DFT calculations are performed, is the number of atoms per configuration, are the dipoles obtained by classical molecular dynamics using a given set of parameters. are the forces obtained by classical molecular dynamics.
2.3. Simulation Details
2.3.1. Dry Hectorites
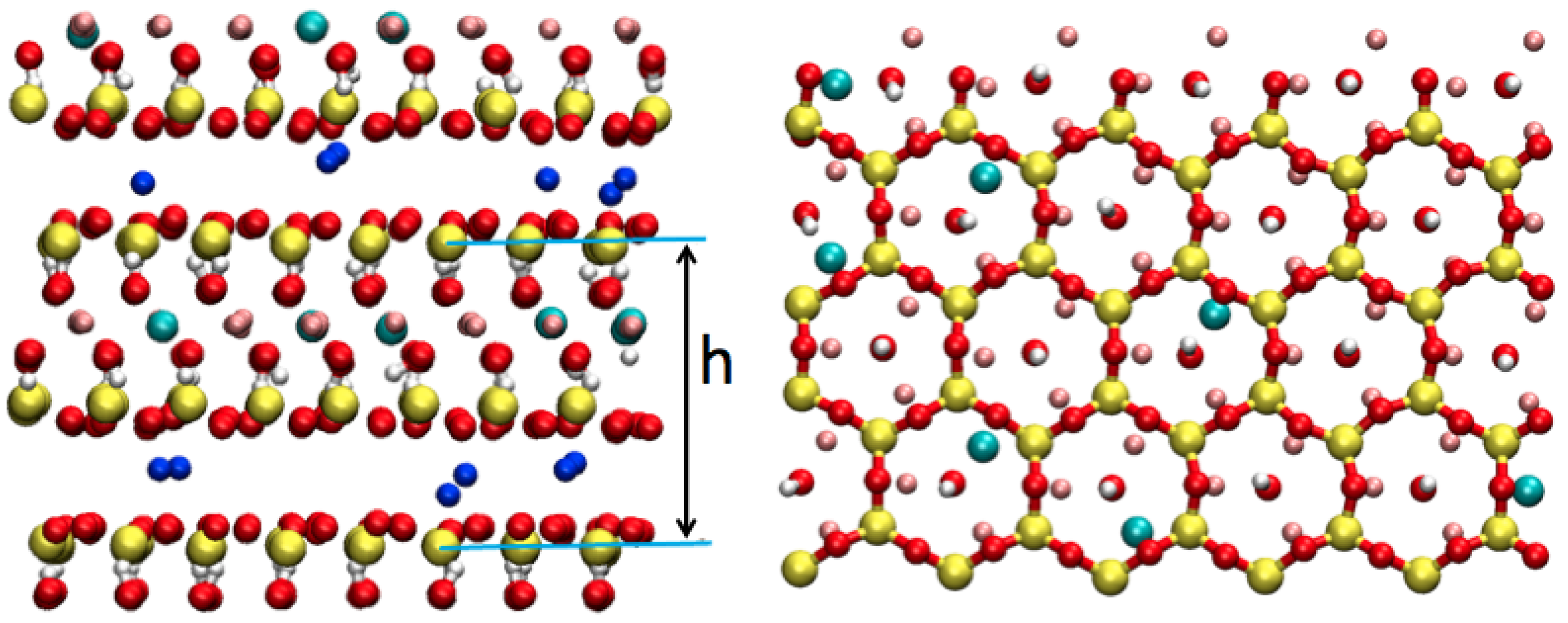
2.3.2. Hydrated Na-Hectorite
2.4. Force Field Parameters
3. Validation of the Force Field
3.1. Simulations Details
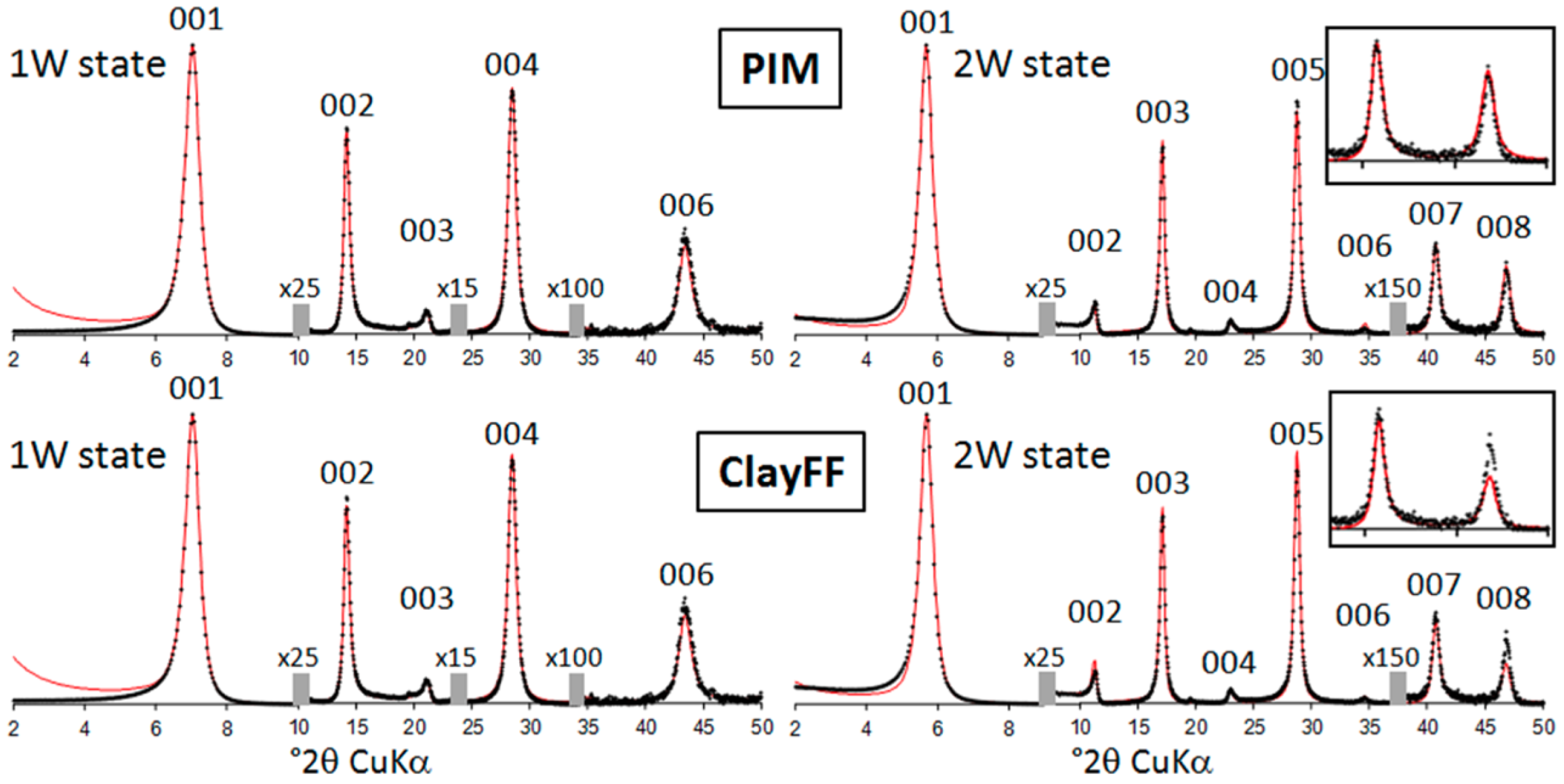
3.2. XRD Materials and Methods
3.3. Results and Discussion
3.3.1. Dry Hectorites
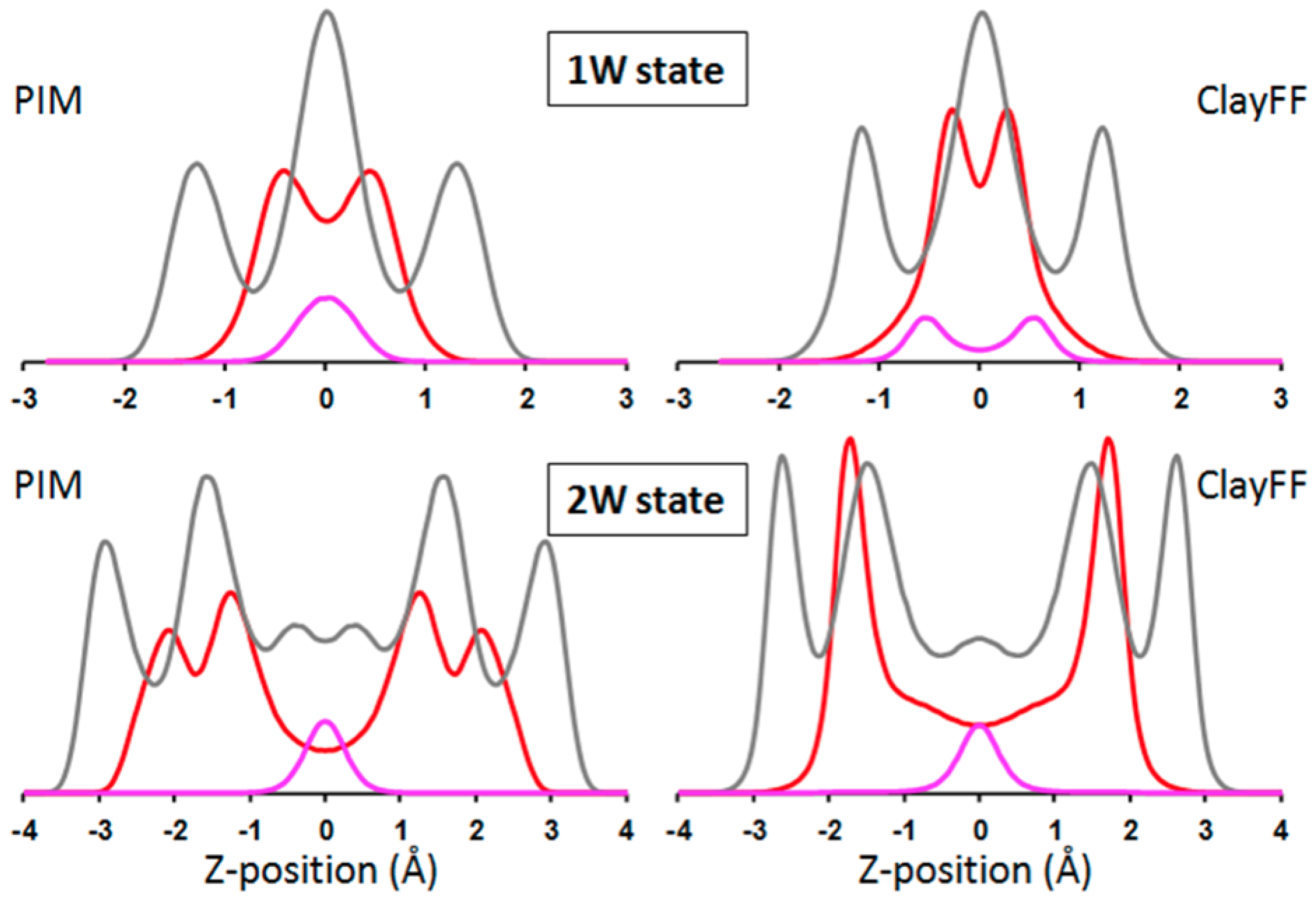
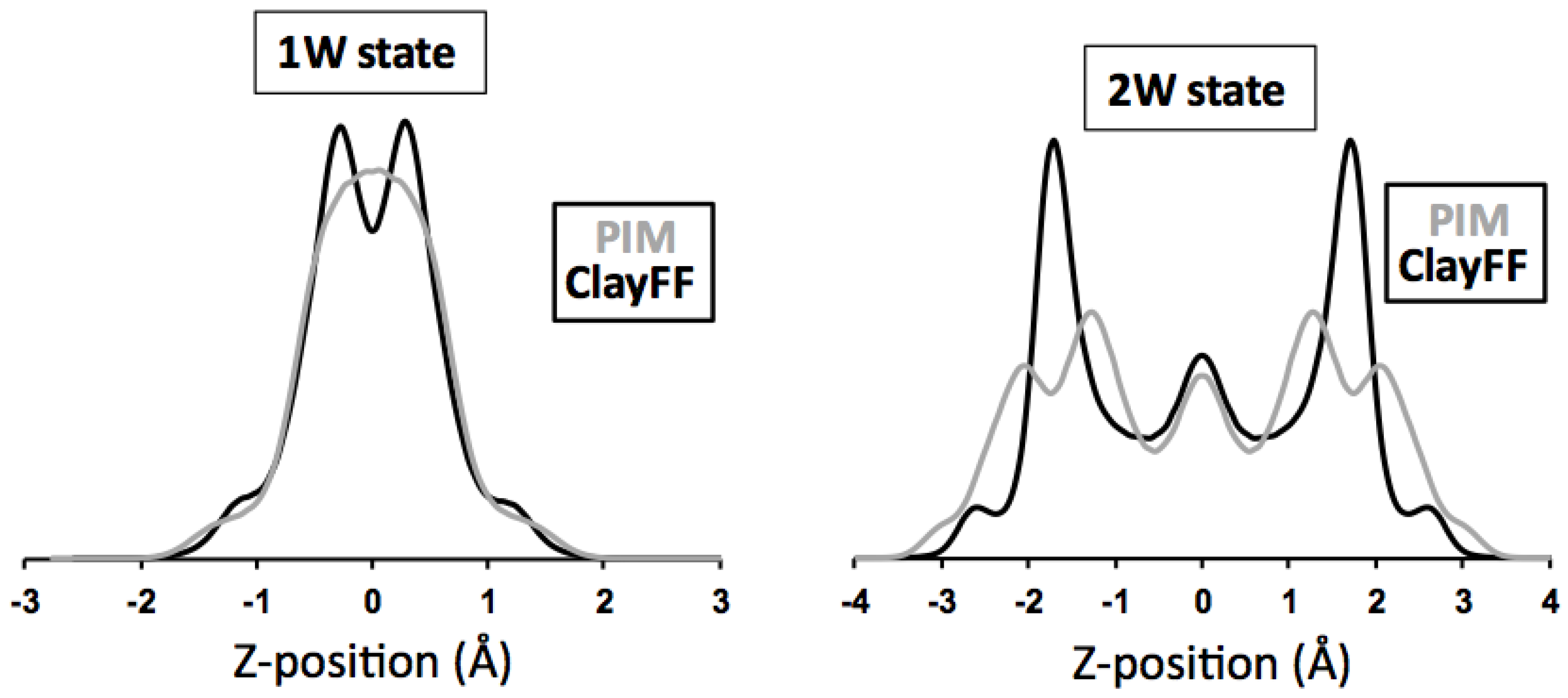
3.3.2. Hydrated Hectorites
3.4. Beyond Validation: Dynamics
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Greathouse, J.A.; Stellalevinsohn, H.R.; Denecke, M.A.; Bauer, A.; Pabalan, R.T. Uranyl surface complexes in a mixed-charge montmorillonite: Monte Carlo computer simulation and polarized XAFS results. Clays Clay Miner. 2005, 53, 278–286. [Google Scholar] [CrossRef]
- Tambach, T.J.; Bolhuis, P.G.; Hensen, E.J.M.; Smit, B. Hysteresis in clay swelling induced by hydrogen bonding: Accurate prediction of swelling states. Langmuir 2006, 22, 1223–1234. [Google Scholar] [CrossRef] [PubMed]
- Rotenberg, B.; Morel, J.-P.; Marry, V.; Turq, P.; Morel-Desrosiers, N. On the driving force of cation exchange in clays: Insights from combined microcalorimetry experimnets and molecular simulation. Geochim. Cosmochim. Acta 2009, 73, 4034–4044. [Google Scholar] [CrossRef]
- Malikova, N.; Dubois, E.; Marry, V.; Rotenberg, B.; Turq, P. Dynamics in clays—Combining neutron scattering and microscopic simulation. Z. Phys. Chem. 2010, 224, 153–181. [Google Scholar] [CrossRef]
- Anderson, R.L.; Ratcliffe, I.; Greenwell, H.C.; Williams, P.A.; Cliffe, S.; Coveney, P.V. Clay swelling—A challenge in the oilfield. Earth Sci. Rev. 2010, 98, 201–216. [Google Scholar] [CrossRef]
- Rotenberg, B.; Patel, A.J.; Chandler, D. Molecular explanation for why talc surfaces can be both hydrophilic and hydrophobic. J. Am. Chem. Soc. 2011, 133, 20521–20527. [Google Scholar] [CrossRef] [PubMed]
- Ferrage, E.; Sakharov, B.A.; Michot, L.J.; Delville, A.; Bauer, A.; Lanson, B.; Grangeon, S.; Frapper, G.; Jiménez-Ruiz, M.; Cuello, G.J. Hydration properties and interlayer organization of water and ions in synthetic Na-smectite with tetrahedral layer charge. Part 2. Toward a precise coupling between molecular simulations and diffraction data. J. Phys. Chem. C 2011, 115, 1867–1881. [Google Scholar] [CrossRef]
- Michot, L.J.; Ferrage, E.; Jiménez-Ruiz, M.; Boehm, M.; Delville, A. Anisotropic features of water and ion dynamics in synthetic Na- and Ca-smectites with tetrahedral layer charge. A combined quasi-elastic neutron-scattering and molecular dynamics simulations study. J. Phys. Chem. C 2012, 116, 16619–16633. [Google Scholar] [CrossRef]
- Marry, V.; Dubois, E.; Malikova, N.; Breu, J.; Haussler, W. Anisotropy of water dynamics in clays: Insights from molecular simulations for experimental QENS analysis. J. Phys. Chem. C 2013, 117, 15106–15115. [Google Scholar] [CrossRef]
- Morrow, C.P.; Yazaydin, A.Ö.; Krishnan, M.; Bowers, G.M.; Kalinichev, A.G.; Kirkpatrick, R.J. Structure, energetics and dynamics of smectite clay interlayer hydration: Molecular dynamics and metadynamics investigation of Na-hectorite. J. Phys. Chem. C 2013, 117, 5172–5187. [Google Scholar] [CrossRef]
- Churakov, S.V.; Gimmi, T.; Unruh, T.; Van Loon, L.R.; Juranyi, F. Resolving diffusion in clay minerals at different time scales: Combination of experimental and modeling approach. Appl. Clay Sci. 2014, 96, 36–44. [Google Scholar] [CrossRef]
- Porion, P.; Warmont, F.; Faugère, A.-M.; Rollet, A.-L.; Dubois, E.; Marry, V.; Michot, L.J.; Delville, A. 133Cs nuclear magnetic resonance relaxometry as a probe of the mobility of cesium cations confined within dense clay sediments. J. Phys. Chem. C 2015, 119, 15360–15372. [Google Scholar] [CrossRef]
- Rotenberg, B.; Marry, V.; Dufrêche, J.-F.; Malikova, N.; Giffaut, E.; Turq, P. Modelling water and ion diffusion in clays: A multiscale approach. C. R. Chim. 2007, 10, 1108–1116. [Google Scholar] [CrossRef]
- Tournassat, C.; Chapron, Y.; Leroy, P.; Bizi, M.; Boulahya, F. Comparison of molecular dynamics simulations with triple layer and modified Gouy-Chapman models in a 0.1 M NaCl-montmorillonite system. J. Colloid Interface Sci. 2009, 339, 533–541. [Google Scholar] [CrossRef] [PubMed]
- Jardat, M.; Dufrêche, J.-F.; Rotenberg, B.; Marry, V.; Rotenberg, B.; Turq, B. Salt exclusion in charged porous media: A coarse-graining strategy in the case of montmorillonite clays. Phys. Chem. Chem. Phys. 2009, 11, 2023–2033. [Google Scholar] [CrossRef] [PubMed]
- Bourg, I.C.; Sposito, G. Connecting the molecular scale to the continuum scale for diffusion processes in smectite-rich porous media. Environ. Sci. Technol. 2010, 44, 2085–2091. [Google Scholar] [CrossRef] [PubMed]
- Hedström, M.; Karnland, O. Donnan equilibrium in Na-montmorillonite from a molecular dynamics perspective. Geochim. Cosmochim. Acta 2012, 77, 266–274. [Google Scholar] [CrossRef]
- Boţan, A.; Marry, V.; Rotenberg, B.; Turq, P.; Noetinger, B. How electrostatics influences hydrodynamic boundary conditions: Poiseuille and electro-osmostic flows in clay nanopores. J. Phys. Chem. C 2013, 117, 978–985. [Google Scholar] [CrossRef]
- Ebrahimi, D.; Whittle, A.J.; Pellenq, R.J.M. Mesoscale properties of clay aggregates from potential of mean force representation of interactions between nanoplatelets. J. Chem. Phys. 2014, 140, 154309. [Google Scholar] [CrossRef]
- Tinnacher, R.M.; Holmboe, M.; Tournassat, C.; Bourg, I.C.; Davis, J.A. Ion adsorption and diffusion in smectite: Molecular, pore, and continuum scale views. Geochim. Cosmochim. Acta 2016, 177, 130–149. [Google Scholar] [CrossRef]
- Bacle, P.; Dufrêche, J.-F.; Rotenberg, B.; Bourg, I.C.; Marry, V. Modeling the transport of water and ionic tracers in a micrometric clay sample. Appl. Clay Sci. 2016, 123, 18–28. [Google Scholar] [CrossRef]
- Skipper, N.T.; Refson, K.; McConnell, J.D.C. Computer calculation of water-clay interactions using atomic pair potentials. Clay Miner. 1989, 24, 411–425. [Google Scholar] [CrossRef]
- Delville, A. Structure and properties of confined liquids: A molecular model of the clay-water interface. J. Phys. Chem. 1993, 97, 9703–9712. [Google Scholar] [CrossRef]
- Skipper, N.T.; Chang, F.-R.C.; Sposito, G. Monte Carlo simulation of interlayer molecular structure in swelling clay minerals. I: Methodology. Clays Clay Miner. 1995, 43, 285–293. [Google Scholar] [CrossRef]
- Teppen, B.J.; Rasmussen, K.; Bertsch, P.M.; Miller, D.M.; Schäfer, L. Molecular dynamics modeling of clay minerals: 1. Gibbsite, kaolinite, pyrophyllite and beidellite. J. Phys. Chem. B 1997, 101, 1579–1587. [Google Scholar] [CrossRef]
- Sainz-Diaz, C.I.; Hernández-Laguna, A.; Dove, M.T. Modeling of dioctahedral 2:1 phyllosilicates by means of transferable empirical potentials. Phys. Chem. Miner. 2001, 28, 130–141. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Reddy, U.V.; Bowers, G.M.; Loganathan, N.; Bowden, M. Water structure and dynamics in smectites: X-ray diffraction and 2H NMR spectroscopy of Mg-, Ca-, Sr-, Na-, Cs-, and Pb-hectorite. J. Phys. Chem. C 2016, 120, 8863–8876. [Google Scholar] [CrossRef]
- Lopes, P.E.M.; Roux, B.; MacKerell, A.D. Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability: Theory and applications. Theor. Chem. Acc. 2009, 124, 11–28. [Google Scholar] [CrossRef] [PubMed]
- Cieplak, P.; Dupradeau, F.-Y.; Duan, Y.; Wang, J. Polarization effects in molecular mechanical force fields. J. Phys. Condens. Matter 2009, 21, 333102. [Google Scholar] [CrossRef] [PubMed]
- Dazas, B.; Lanson, B.; Breu, J.; Robert, J.-L.; Pelletier, M.; Ferrage, E. Smectite fluorination and its impact on interlayer water content and structure: A way to fine tune the hydrophilicity of clay surfaces? Microporous Mesoporous Mater. 2013, 181, 233–247. [Google Scholar] [CrossRef]
- Marry, V.; Dubois, E.; Malikova, N.; Durand-Vidal, S.; Longeville, S.; Breu, J. Water dynamics in hectorite clays: Influence of temperature studied by coupling neutron spin echo and molecular dynamics. Environ. Sci. Technol. 2011, 45, 2850–2855. [Google Scholar] [CrossRef] [PubMed]
- Aguado, A.; Bernasconi, L.; Jahn, S.; Madden, P.A. Multipoles and interaction potentials in ionic materials from planewave-DFT calculations. Faraday Discuss. 2003, 124, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Jahn, S.; Madden, P.A. Modeling earth materials from crustal to lower mantle conditions: A transferable set of interaction potentials for the CMAS system. Phys. Earth Planet. Inter. 2007, 162, 129–139. [Google Scholar] [CrossRef]
- Tesson, S.; Salanne, M.; Rotenberg, B.; Tazi, S.; Marry, V. A classical polarizable force field for clays: Pyrophyllite and talc. J. Phys. Chem. C 2016, 120, 3749–3758. [Google Scholar] [CrossRef]
- Tesson, S.; Louisfrema, W.; Salanne, M.; Boutin, A.; Rotenberg, B.; Marry, V. Classical polarizable force field to study dry charged clays and zeolites. J. Phys. Chem. C 2017, 121, 9833–9846. [Google Scholar] [CrossRef]
- Michot, L.J.; Villieras, F.; François, M.; Yvon, F.; Le Dred, R.; Cases, J.M. The structural microscopic hydrophilicity of talc. Langmuir 1994, 10, 3765–3773. [Google Scholar] [CrossRef]
- Brigatti, M.F.; Galan, E.; Theng, B.K.G. Handbook of clay science—Structures and Mineralogy of Clay Minerals. Dev. Clay Sci. 2006, 2, 19–86. [Google Scholar]
- Ferrage, E. Investigation of the interlayer organization of water and ions in smectite from the combined use of diffraction experiments and molecular simulations. A review of methodology, applications and perspectives. Clays Clay Miner. 2016, 64, 346–371. [Google Scholar] [CrossRef]
- Ferrage, E.; Lanson, B.; Malikova, N.; Plançon, A.; Sakharov, B.; Drits, V.A. New insights on the distribution of interlayer water in bi-hydrated smectite from x-ray diffraction profile modeling of 00l reflections. Chem. Mater. 2005, 17, 3499–3512. [Google Scholar] [CrossRef]
- Dazas, B.; Ferrage, E.; Delville, A.; Lanson, B. Interlayer structure model of tri-hydrated low-charge smectite by X-ray diffraction and Monte Carlo modeling in the grand canonical ensemble. Am. Miner. 2014, 99, 1724–1735. [Google Scholar] [CrossRef]
- Szczerba, M.; Kalinichev, A.G. Intercalation of ethylene glycol in smectites: Several molecular simulation models verified by X-ray diffraction data. Clays Clay Miner. 2016, 64, 488–502. [Google Scholar] [CrossRef]
- Szczerba, M.; Ufer, K. New model of ethylene glycol intercalate in smectites for XRD modeling. Appl. Clay Sci. 2018, 153, 113–123. [Google Scholar] [CrossRef]
- Greathouse, J.; Sposito, G. Monte Carlo and Molecular Dynamics Studies of Interlayer Structure in Li(H2O)3-Smectites. J. Phys. Chem. B 1998, 102, 2406–2414. [Google Scholar] [CrossRef]
- Sutton, R.; Sposito, G. Molecular Simulation of Interlayer Structure and Dynamics in 12.4 Å Cs-Smectite Hydrates. J. Colloid Interface Sci. 2001, 237, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.; Sposito, G. Animated molecular dynamics simulations of hydrated caesium-smectite interlayers. Geochem. Trans. 2002, 3, 73–80. [Google Scholar] [CrossRef]
- Greathouse, J.A.; Hart, D.B.; Bowers, G.M.; Kirkpatrick, R.J.; Cygan, R.T. Molecular Simulation of Structure and Diffusion at Smectite?Water Interfaces: Using Expanded Clay Interlayers as Model Nanopores. J. Phys. Chem. C 2015, 119, 17126–17136. [Google Scholar] [CrossRef]
- Loganathan, N.; Yazaydin, A.Ö.; Bowers, G.M.; Kalinichev, A.G.; Kirkpatrick, R.J. Cation and Water Structure, Dynamics, and Energetics in Smectite Clays: A Molecular Dynamics Study of Ca-Hectorite. J. Phys. Chem. C 2016, 120, 12429–12439. [Google Scholar] [CrossRef]
- Loganathan, N.; Yazaydin, A.Ö.; Bowers, G.M.; Kalinichev, A.G.; Kirkpatrick, R.J. Structure, Energetics, and Dynamics of Cs+ and H2O in Hectorite: Molecular Dynamics Simulations with an Unconstrained Substrate Surface. J. Phys. Chem. C 2016, 120, 10298–10310. [Google Scholar] [CrossRef]
- Fumi, F.G.; Tosi, M.P. Ionic sizes and born repulsive parameters in the nacl-type alkali halides—I: The huggins-mayer and pauling forms. J. Phys. Chem. Solids 1964, 25, 31–43. [Google Scholar] [CrossRef]
- Tosi, M.P.; Fumi, F.G. Ionic sizes and born repulsive parameters in the nacl-type alkali halides—II: The generalized huggins-mayer form. J. Phys. Chem. Solids 1964, 25, 45–52. [Google Scholar] [CrossRef]
- Wang, B.; Truhlar, D.G. Including charge penetration effects in molecular modeling. J. Chem. Theory Comput. 2010, 6, 3330–3342. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.T.; Toennies, J.P. An improved simple model for the van der waals potential based on universal damping functions for the dispersion coefficients. J. Chem. Phys. 1984, 80, 3726–3741. [Google Scholar] [CrossRef]
- Tazi, S.; Molina, J.J.; Rotenberg, B.; Turq, P.; Vuilleumier, R.; Salanne, M. A transferable ab initio based force field for aqueous ions. J. Chem. Phys. 2012, 136, 114507. [Google Scholar] [CrossRef] [PubMed]
- Tesson, S.; Louisfrema, W.; Ferrage, E.; Rotenberg, B.; Salanne, M.; Boutin, A.; Marry, V. Classical polarizable force field to study hydrated charged clays and zeolites. 2018; submitted. [Google Scholar]
- Silvestrelli, P.L.; Parrinello, M. Water molecule dipole in the gas and in the liquid phase. Phys. Rev. Lett. 1999, 82, 3308–3311. [Google Scholar] [CrossRef]
- Bernasconi, L.; Wilson, M.; Madden, P.A. Cation polarizability from first-principles: Sn2+. Comput. Mater. Sci. 2001, 22, 94–98. [Google Scholar] [CrossRef]
- Bernasconi, L.; Madden, P.A.; Wilson, M. Ionic to molecular transition in AlCl3: An examination of the electronic structure. PhysChemComm 2002, 5, 1–11. [Google Scholar] [CrossRef]
- Souza, I.; Wilkens, T.; Martin, R.T. Polarization and localization in insulators: Generating function approach. Phys. Rev. B 2000, 62, 1666–1683. [Google Scholar] [CrossRef]
- Bérend, I.; Cases, J.M.; François, M.; Uriot, J.P.; Michot, L.J.; Masion, A.; Thomas, F. Mechanism of adsorption and desorption of water vapor by homoionic montmorillonites: 2. The Li+, Na+, K+, Rb+, and Cs+ exchanged forms. Clay Clay Miner. 1995, 43, 324–336. [Google Scholar] [CrossRef]
- Besson, G.; Glaeser, R.; Tchoubar, C. Le cesium, révélateur de structure des smectites. Clay Miner. 1983, 18, 11–19. [Google Scholar] [CrossRef]
- Cases, J.M.; Berend, I.; Francois, M.; Uriot, J.P.; Michot, L.J.; Thomas, F. Mechanism of adsorption and desorption of water vapor by homoionic montmorillonite. 3. The Mg2+, Ca2+, Sr2+ and Ba2+ exchanged forms. Clays Clay Miner. 1997, 45, 8–22. [Google Scholar] [CrossRef]
- Ferrage, E.; Lanson, B.; Sakharov, B.; Drits, V.A. Investigation of smectite hydration properties by modeling experimental x-ray diffraction patterns: Part I. Montmorillonite hydration properties. Am. Mineral. 2005, 90, 1358–1374. [Google Scholar] [CrossRef]
- Bowers, G.M.; Singer, J.W.; Bish, D.L.; Kirkpatrick, R.J. Alkali metal and H2O dynamics at the smectite/water interface. J. Phys. Chem. C 2011, 115, 23395–23407. [Google Scholar] [CrossRef]
- CP2K Developers Group. Available online: http://cp2k.berlios.de (accessed on 19 November 2016).
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé-Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Laino, T.; Hutter, J. Notes on “Ewald summation of electrostatic multipole interactions up to quadrupolar level” [J. Chem. Phys.119, 7471 (2003)]. J. Chem. Phys. 2008, 129, 074102. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space gaussian pseudopotentials from h to rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Krack, M. Pseudopotentials for h to kr optimized for gradient-corrected exchange-correlation functionals. Theor. Chem. Acc. 2005, 114, 145–152. [Google Scholar] [CrossRef]
- Silvestrelli, P.L. Maximally localized wannier functions for simulations with supercells of general symmetry. Phys. Rev. B 1999, 59, 9703–9706. [Google Scholar] [CrossRef]
- Marzari, N.; Souza, I.; Vanderbilt, D. An introduction to maximally-localized wannier functions. Psi-K Newsl. 2003, 57, 129–166. [Google Scholar]
- James, F.; Roos, M. Minuit—A system for function minimization and analysis of the parameter errors and correlations. Comput. Phys. Commun. 1975, 10, 343–367. [Google Scholar] [CrossRef]
- Dang, L.X.; Chang, T.-M. Molecular dynamics study of water clusters, liquid, and liquid-vapor interface of water with many-body potentials. J. Chem. Phys. 1997, 106, 8149–8159. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–334. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Sinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 134103. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; Taylor & Francis: New York, NY, USA, 1988; ISBN-13: 9780852743928. [Google Scholar]
- Robert, J.-L.; Beny, J.-M.; Della Ventura, G.; Hardy, M. Fluorine in micas: Crystal-chemical control of the OH-F distribution between trioctahedral and dioctahedral sites. Eur. J. Mineral. 1993, 5, 7–18. [Google Scholar] [CrossRef]
- Sakharov, B.A.; Naumov, A.S.; Drits, V.A. X-ray diffraction by mixed-layer structures with random distribution of stacking faults. Dokl. Akad. Nauk 1982, 265, 339–343. [Google Scholar]
- Sakharov, B.A.; Naumov, A.S.; Drits, V.A. X-ray intensities scattered by layer structure with short range ordering parameters S>1 and G>1. Dokl. Akad. Nauk 1982, 265, 871–874. [Google Scholar]
- Moore, D.M.; Reynolds, R.C., Jr. X-ray Diffraction and the Identification and Analysis of Clay Minerals; Oxford University Press: New York, NY, USA, 1997; ISBN-13: 9780195087130. [Google Scholar]
- Drits, V.A.; Srodon, J.; Eberl, D.D. XRD measurement of mean crystallite thickness of illite and illite/smectite: Reappraisal of the kubler index and the scherrer equation. Clays Clay Miner. 1997, 45, 461–475. [Google Scholar] [CrossRef]
- Seidl, W.; Breu, J. Single crystal structure refinement of tetramethylammonium-hectorite. Z. Kristallogr. 2005, 220, 169–176. [Google Scholar] [CrossRef]
- Rayner, J.H. The crystal structure of talc. Clays Clay Miner. 1973, 21, 103–114. [Google Scholar] [CrossRef]
- Dzene, L.; Verron, H.; Delville, A.; Michot, L. J.; Robert, J.L.; Tertre, E.; Hubert, F.; Ferrage, E. Influence of tetrahedral layer charge on the fixation of cesium in synthetic smectite. J. Phys. Chem. C 2017, 121, 23422–23435. [Google Scholar] [CrossRef]
- Malikova, N.; Cadéne, A.; Marry, V.; Dubois, E.; Turq, P.; Zanotti, J.M.; Longeville, S. Diffusion of water in clays—Microscopic simulation and neutron scattering. Chem. Phys. 2005, 317, 226–235. [Google Scholar] [CrossRef]
- Malikova, N.; Cadéne, A.; Dubois, E.; Marry, V.; Durand-Vidal, S.; Turq, P.; Breu, J.; Longeville, S.; Zanotti, J.M. Water diffusion in a synthetic hectorite clay studied by quasi-elastic neutron scattering. J. Phys. Chem. C 2007, 111, 17603–17611. [Google Scholar] [CrossRef]
| (Å) | (Å) | Angle () | (kcal/mol) | (Å) | (Å) | |
|---|---|---|---|---|---|---|
| 0.9752 | 0.215 | 104.52 | 0.1825 | 3.2340 | 0.5190 | 1.444 |
| Systems | ||
|---|---|---|
| Dry hectorite | 0.123 | 0.561 |
| Wet hectorite | 0.170 | 3.025 |
| Damping Interaction between and | |||||||
|---|---|---|---|---|---|---|---|
| Ion Pair (ij) | (Ha) | (Å−1) | (Ha·Å6) | (Ha·Å8) | (Å−1) | (Å−1) | |
| Li-O | 9.68 | 2.78 | 0.0477 | 0.156 | 4.17 | 1.19 | 2.79 |
| Li-O | 24.6 | 3.82 | 0.0477 | 0.156 | 4.17 | 1.16 | 2.78 |
| Li-OW | 0.427 | 3.50 | 0.0477 | 0.156 | 4.17 | - | - |
| Li-MW | - | - | - | - | - | 3.75 | 1.24 |
| Li-Na | - | - | - | - | - | 0.587 | 4.64 |
| Li-Cs | - | - | - | - | - | 0.0423 | 4.99 |
| Li-Ca | - | - | - | - | - | 3.87 | 3.64 |
| Li-Sr | - | - | - | - | - | 0.895 | 4.69 |
| System | Super Cell Dimensions | A (Å) | B (Å) | h (Å) | Number of HO per Unit Cell |
|---|---|---|---|---|---|
| monohydrated (1W) | 5 × 2 × 2 | 26.3 | 18.2 | 12.53 | 4.2 |
| bihydrated (2W) | 5 × 2 × 2 | 26.3 | 18.2 | 15.51 | 8.9 |
| Counterion | a (Å) | b (Å) | c (Å) | h (Å) | (deg) | (deg) | (deg) |
|---|---|---|---|---|---|---|---|
| Na | 5.235 (1) | 9.108 (4) | 9.813 (7) | 9.711 (1) | 91.8 (2) | 96.4 (2) | 90.02 (5) |
| Cs | 5.258 (5) | 9.106 (7) | 10.674 (7) | 10.524 (5) | 89.90 (6) | 99.53 (7) | 89.95 (4) |
| Ca | 5.255 (9) | 9.15 (2) | 10.23 (1) | 9.676 (1) | 90.1 (1) | 108.1 (2) | 90.2 (1) |
| Sr | 5.231 (6) | 9.11 (2) | 10.28 (2) | 9.767 (5) | 90.1 (2) | 106.9 (2) | 90.1 (1) |
| talc (exp) [87] | 5.293 | 9.179 | 9.469 | 9.381 | 90.57 | 98.91 | 90.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hånde, R.; Ramothe, V.; Tesson, S.; Dazas, B.; Ferrage, E.; Lanson, B.; Salanne, M.; Rotenberg, B.; Marry, V. Classical Polarizable Force Field to Study Hydrated Hectorite: Optimization on DFT Calculations and Validation against XRD Data. Minerals 2018, 8, 205. https://doi.org/10.3390/min8050205
Hånde R, Ramothe V, Tesson S, Dazas B, Ferrage E, Lanson B, Salanne M, Rotenberg B, Marry V. Classical Polarizable Force Field to Study Hydrated Hectorite: Optimization on DFT Calculations and Validation against XRD Data. Minerals. 2018; 8(5):205. https://doi.org/10.3390/min8050205
Chicago/Turabian StyleHånde, Ragnhild, Vivien Ramothe, Stéphane Tesson, Baptiste Dazas, Eric Ferrage, Bruno Lanson, Mathieu Salanne, Benjamin Rotenberg, and Virginie Marry. 2018. "Classical Polarizable Force Field to Study Hydrated Hectorite: Optimization on DFT Calculations and Validation against XRD Data" Minerals 8, no. 5: 205. https://doi.org/10.3390/min8050205
APA StyleHånde, R., Ramothe, V., Tesson, S., Dazas, B., Ferrage, E., Lanson, B., Salanne, M., Rotenberg, B., & Marry, V. (2018). Classical Polarizable Force Field to Study Hydrated Hectorite: Optimization on DFT Calculations and Validation against XRD Data. Minerals, 8(5), 205. https://doi.org/10.3390/min8050205






