A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses
Abstract
1. Introduction
2. Analytical Models for Heap Leaching
2.1. Mellado Model
2.2. Uncertainty Analysis
2.3. Sensitivity Analysis
2.4. Regionalization of Input Variables
3. Results and Discussion
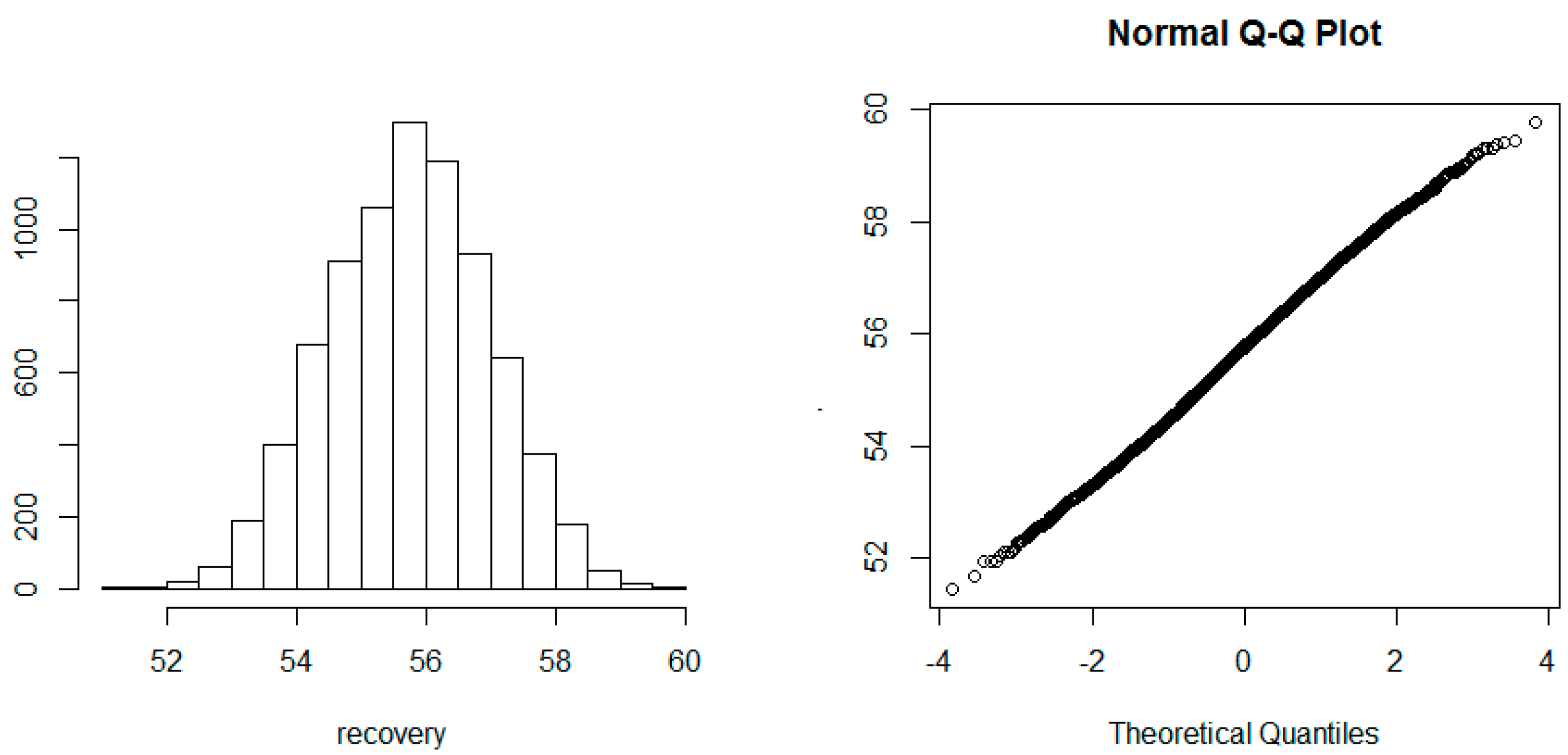
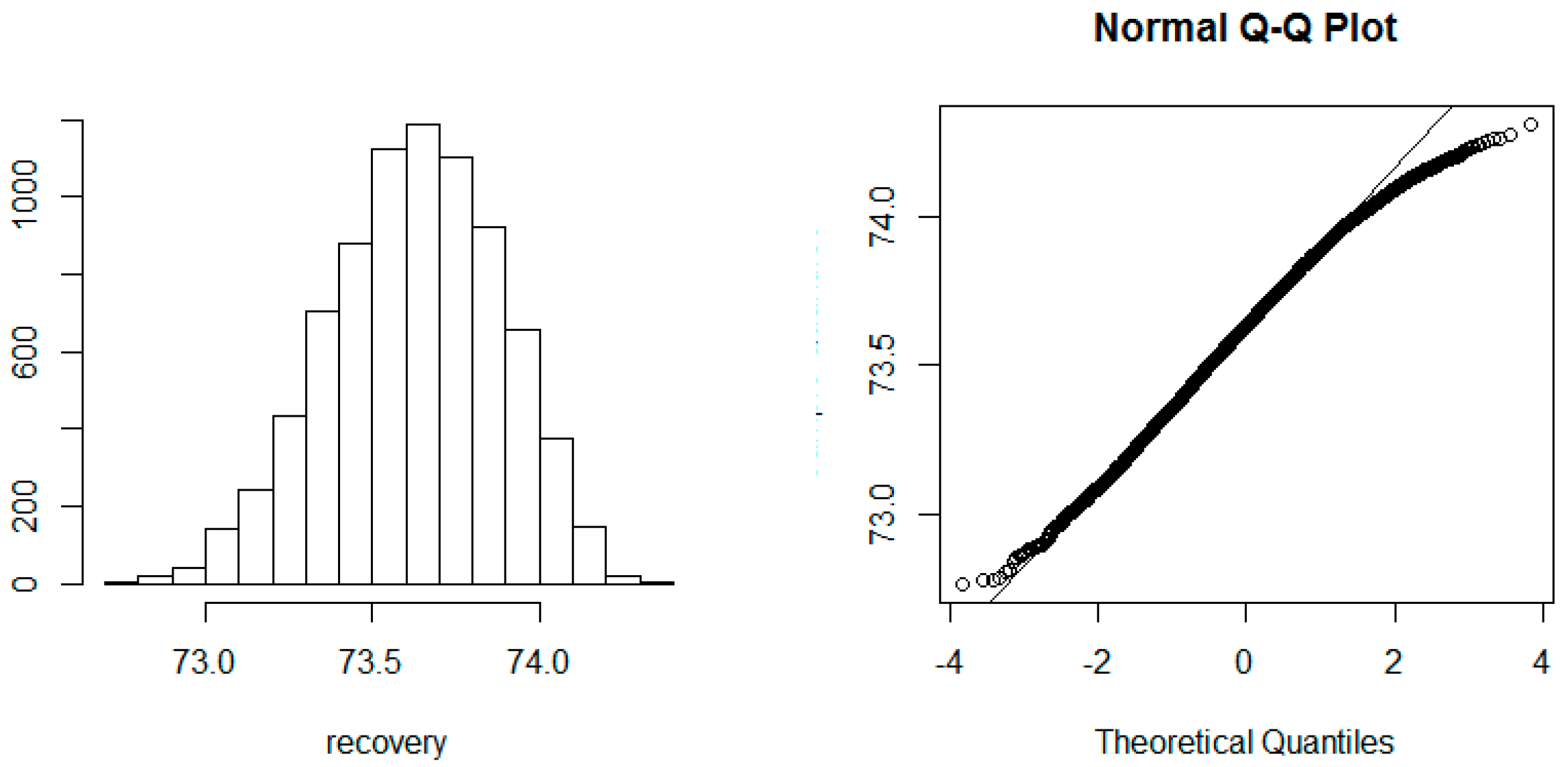
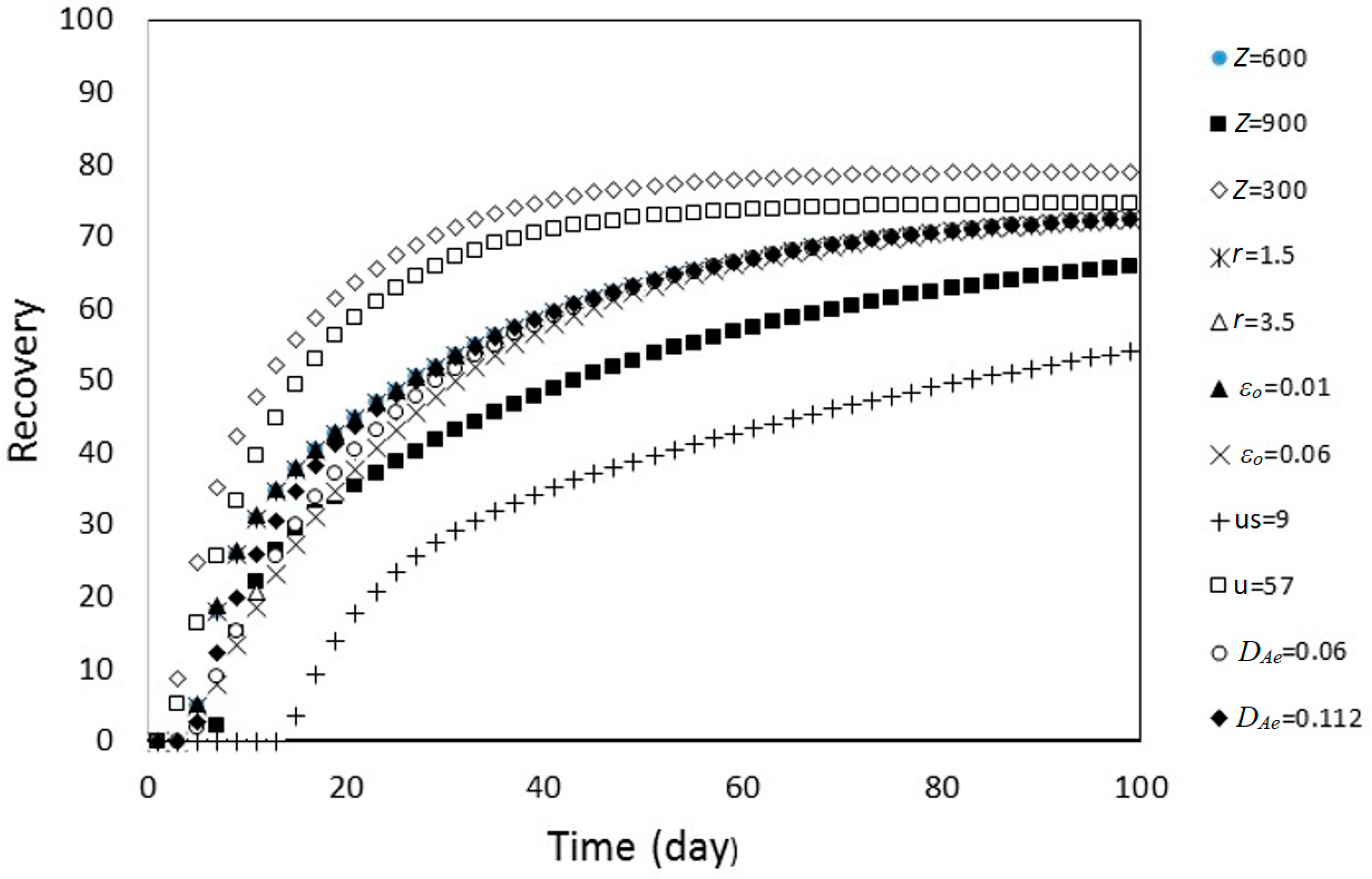
3.1. Uncertainty Analysis
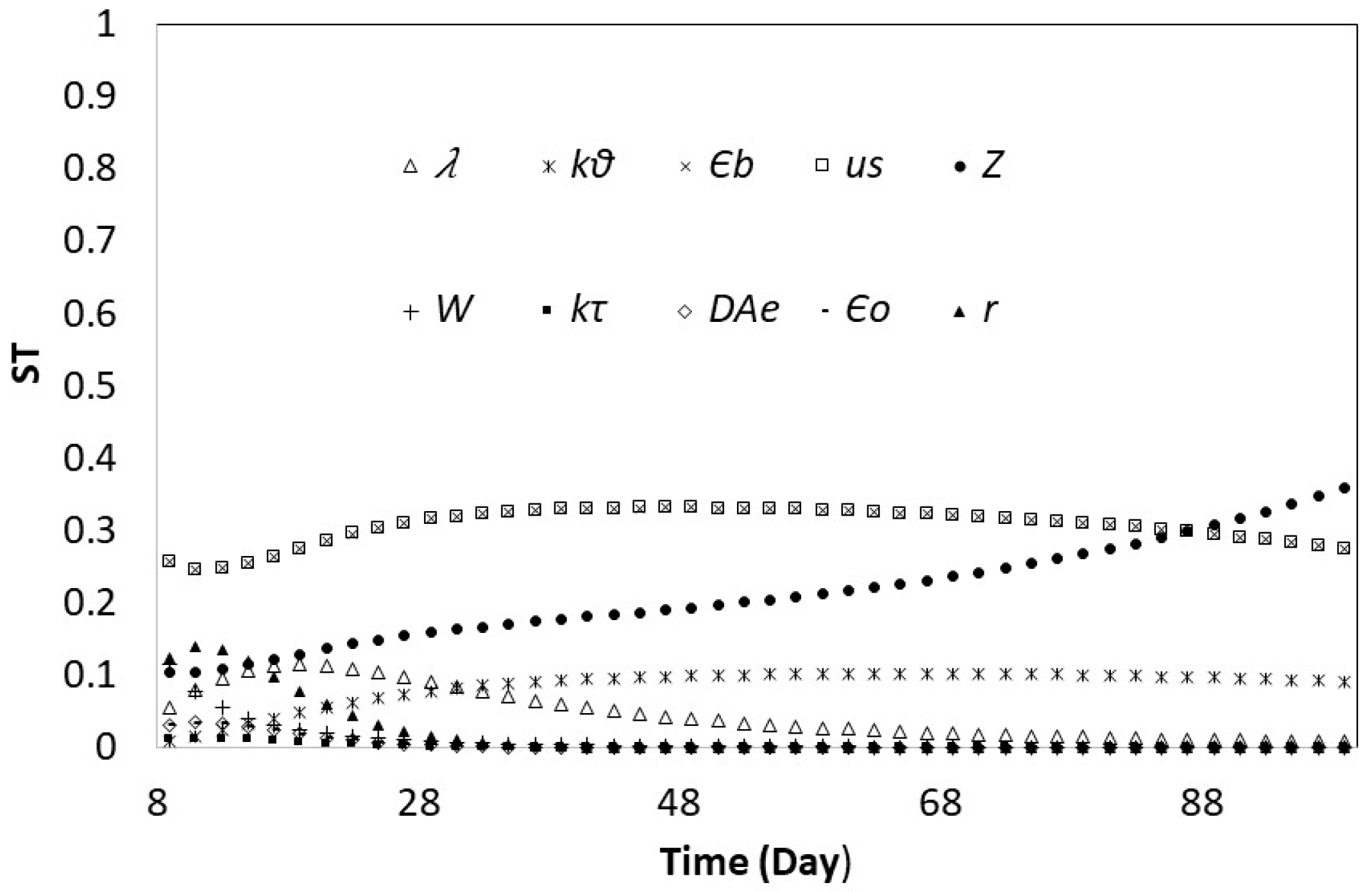
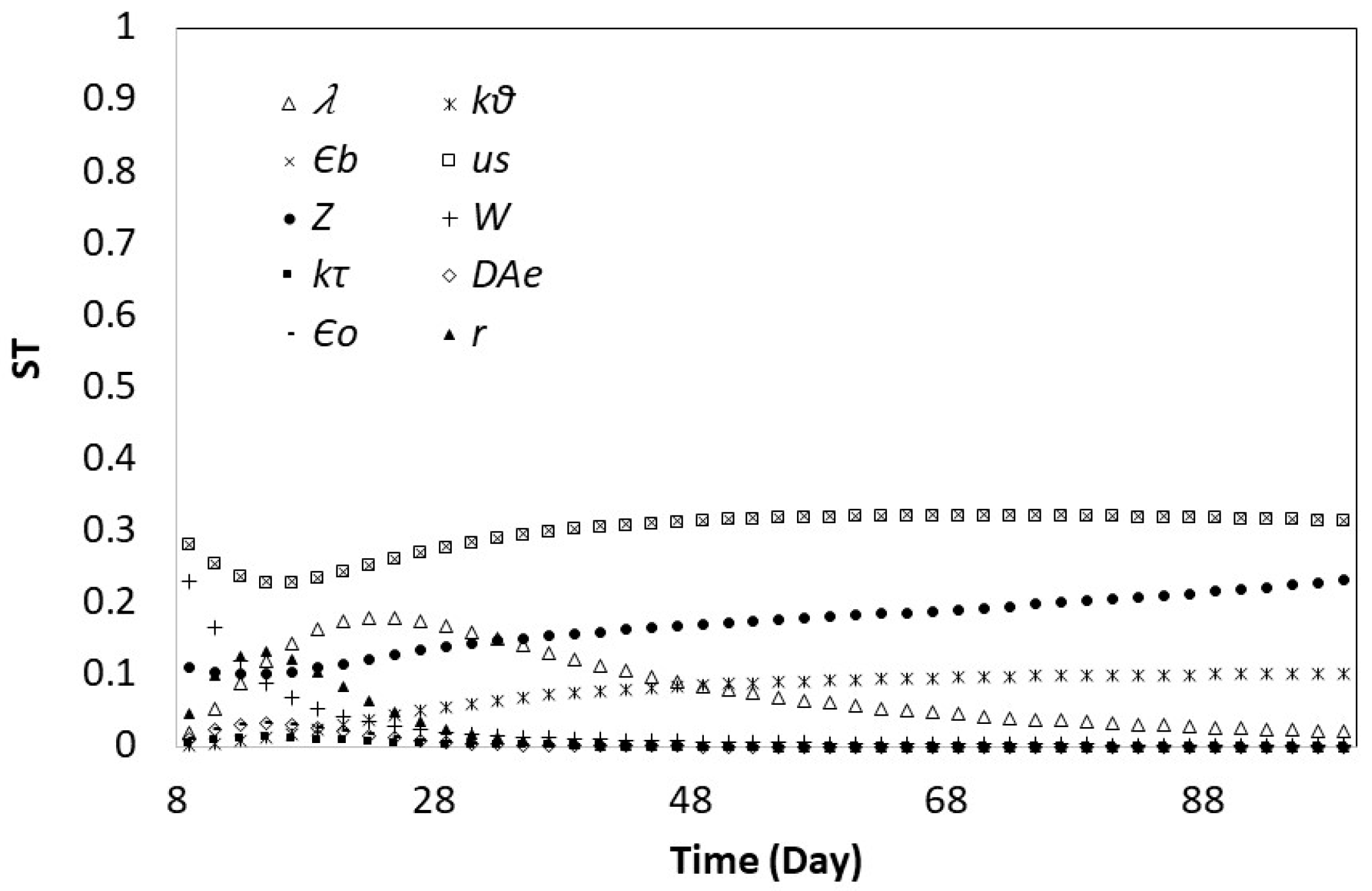
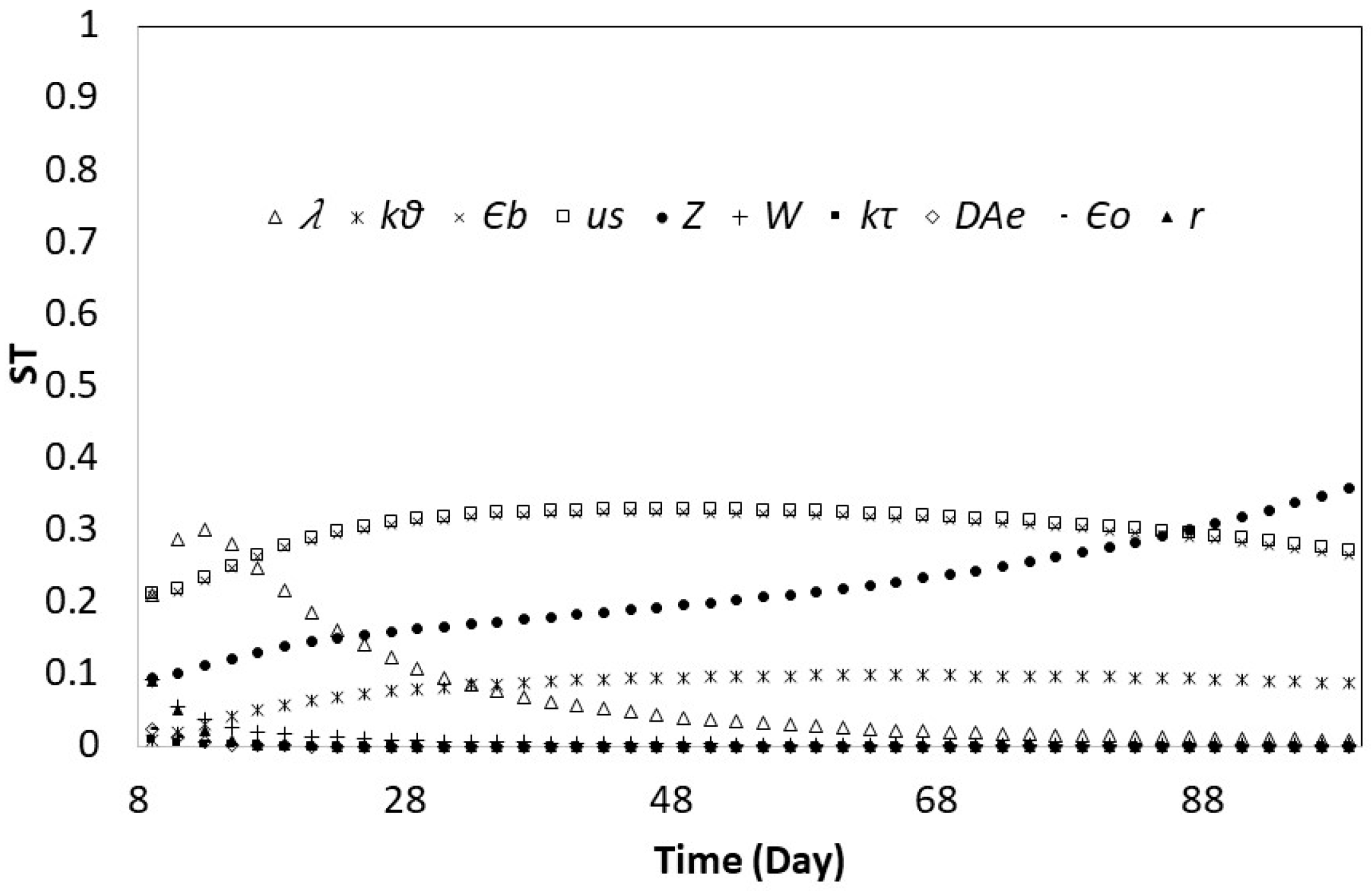
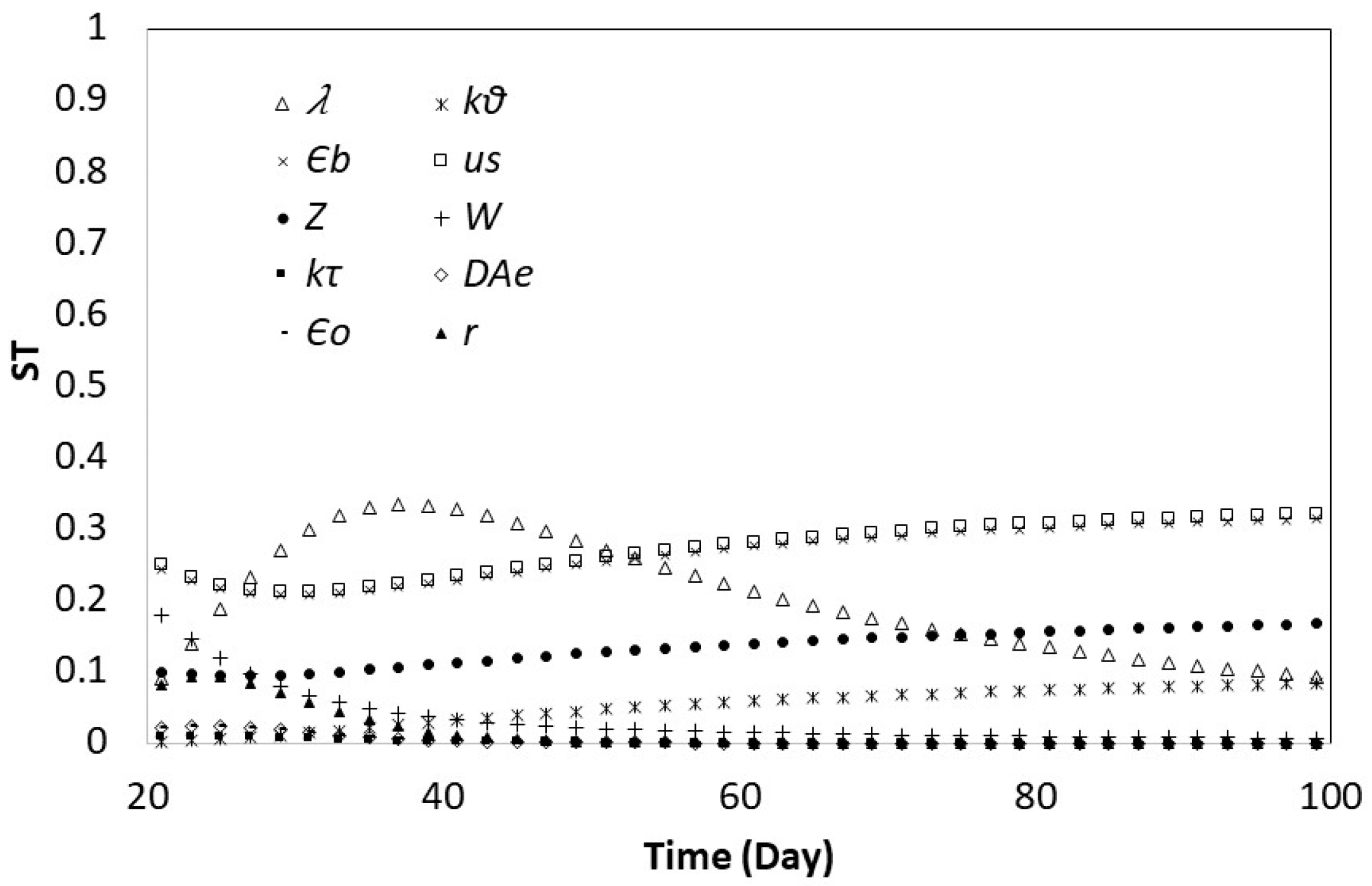
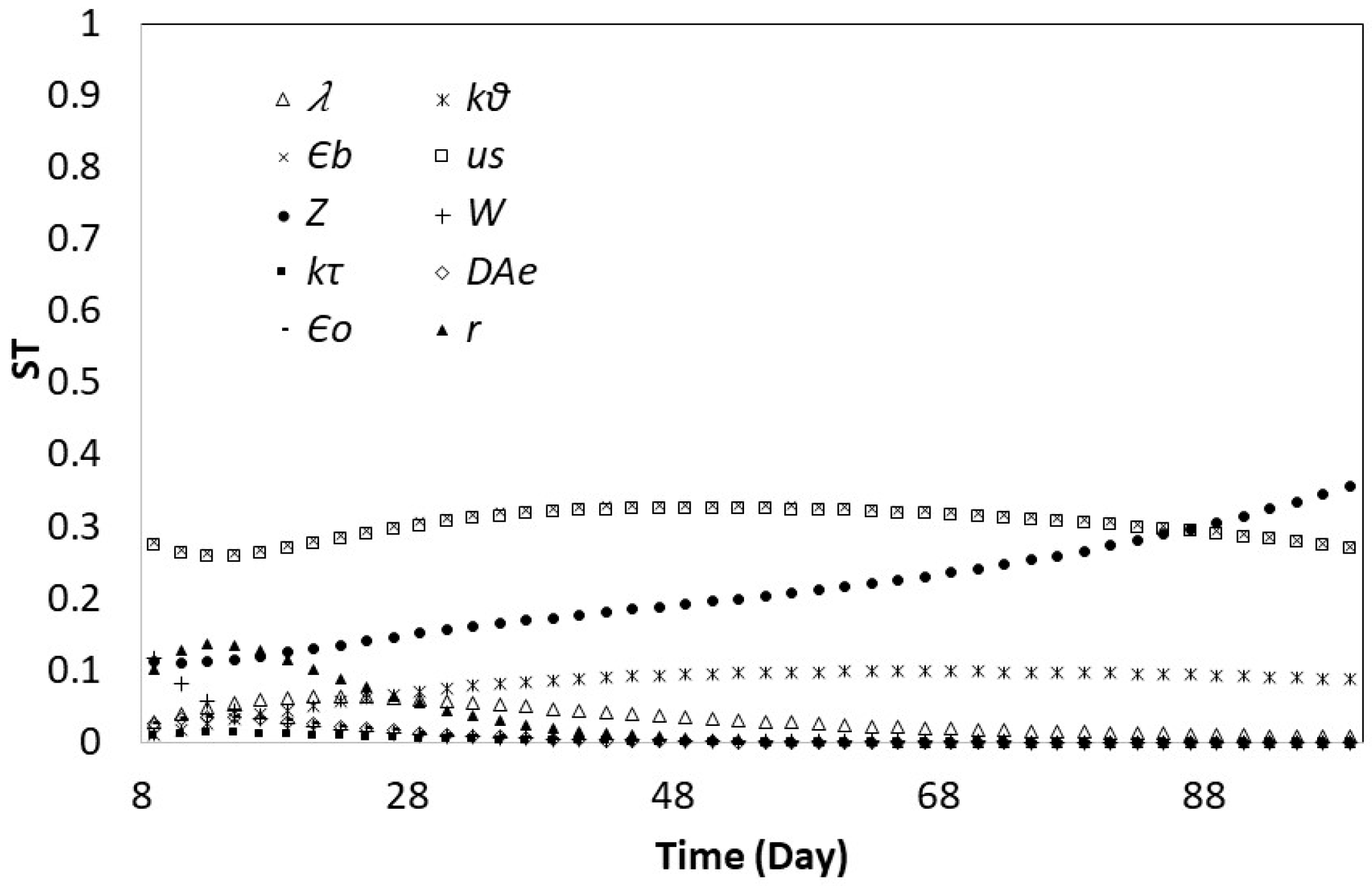
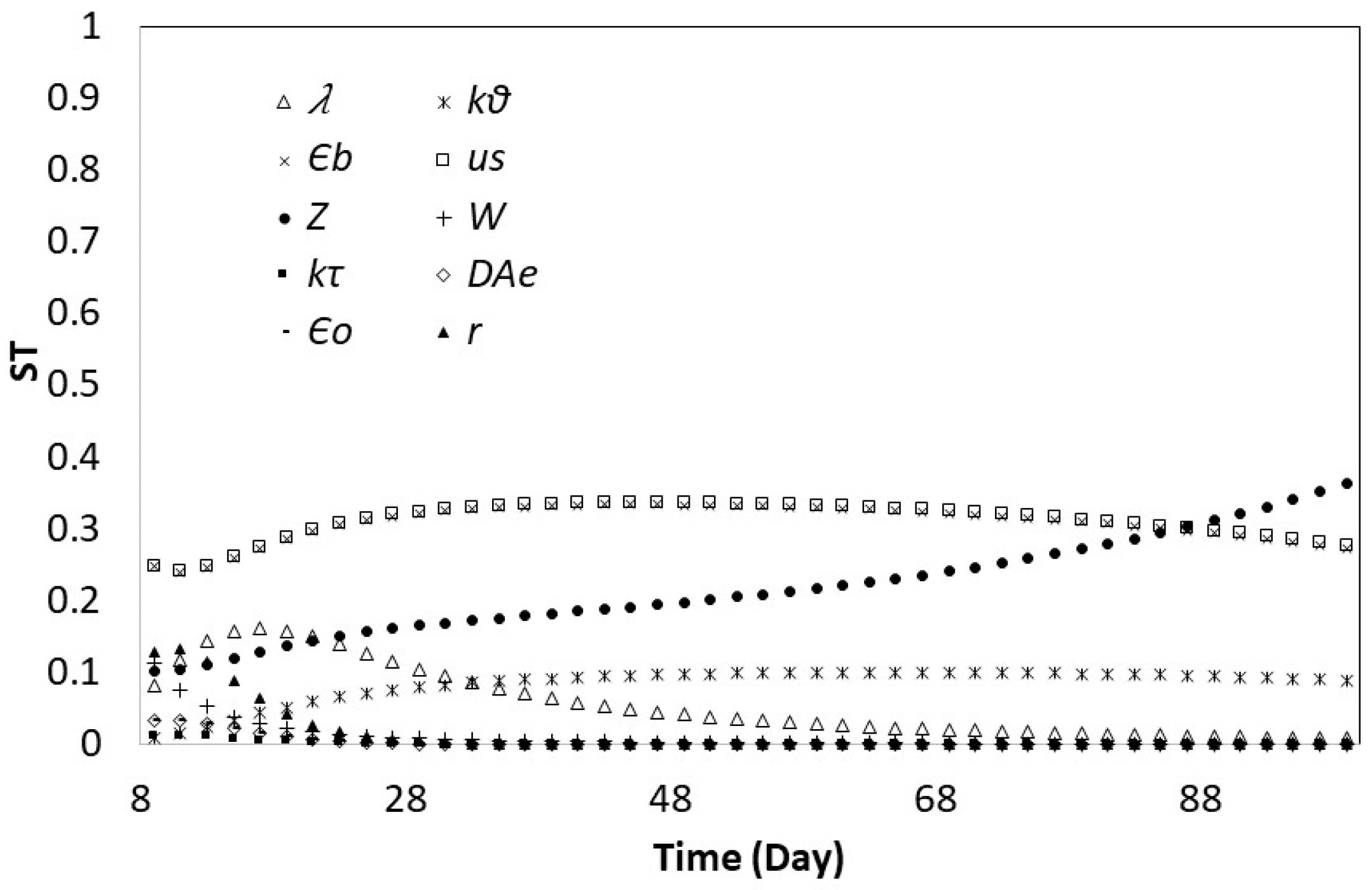
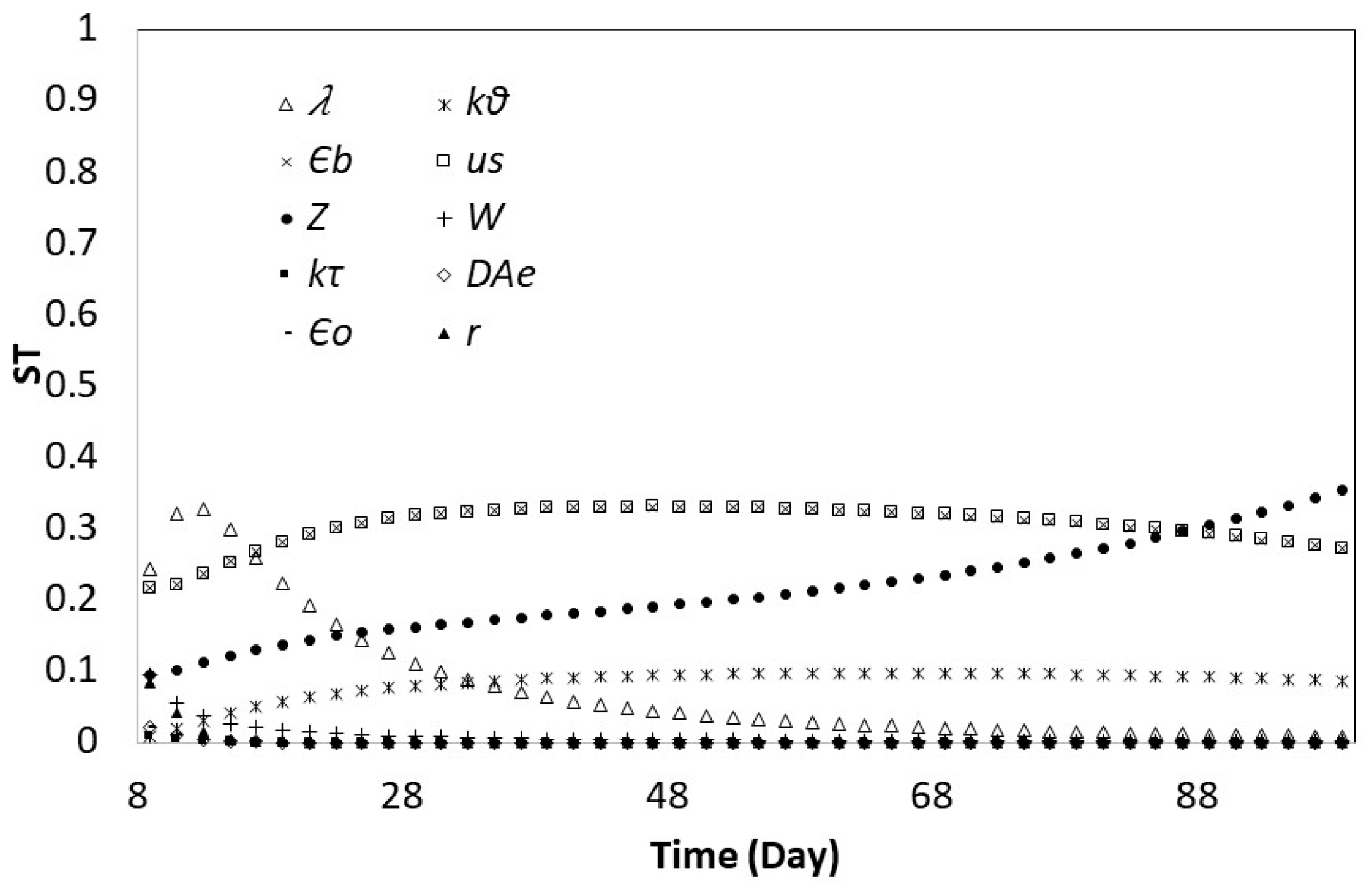
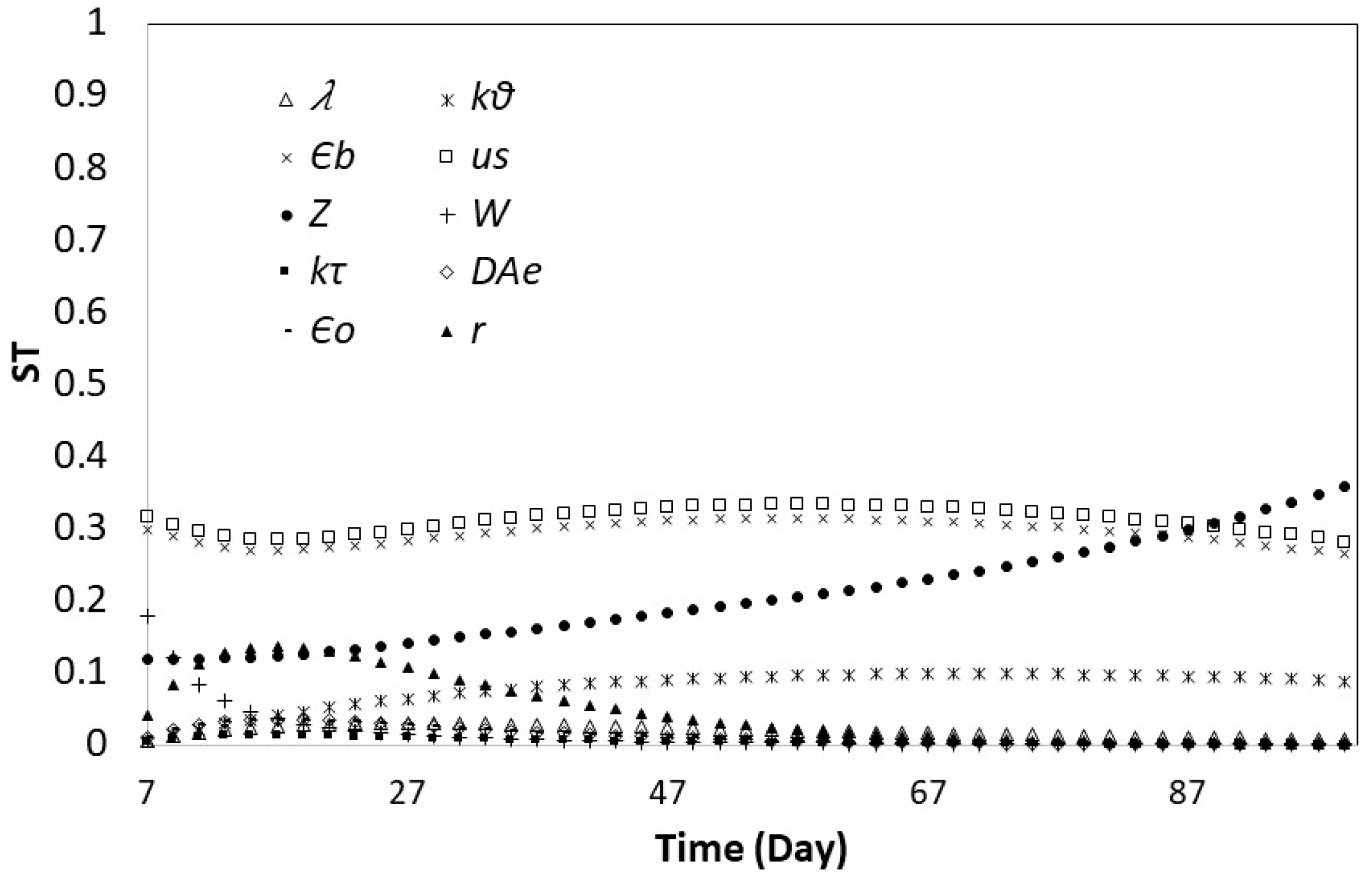
3.2. Global Sensitivity Analysis
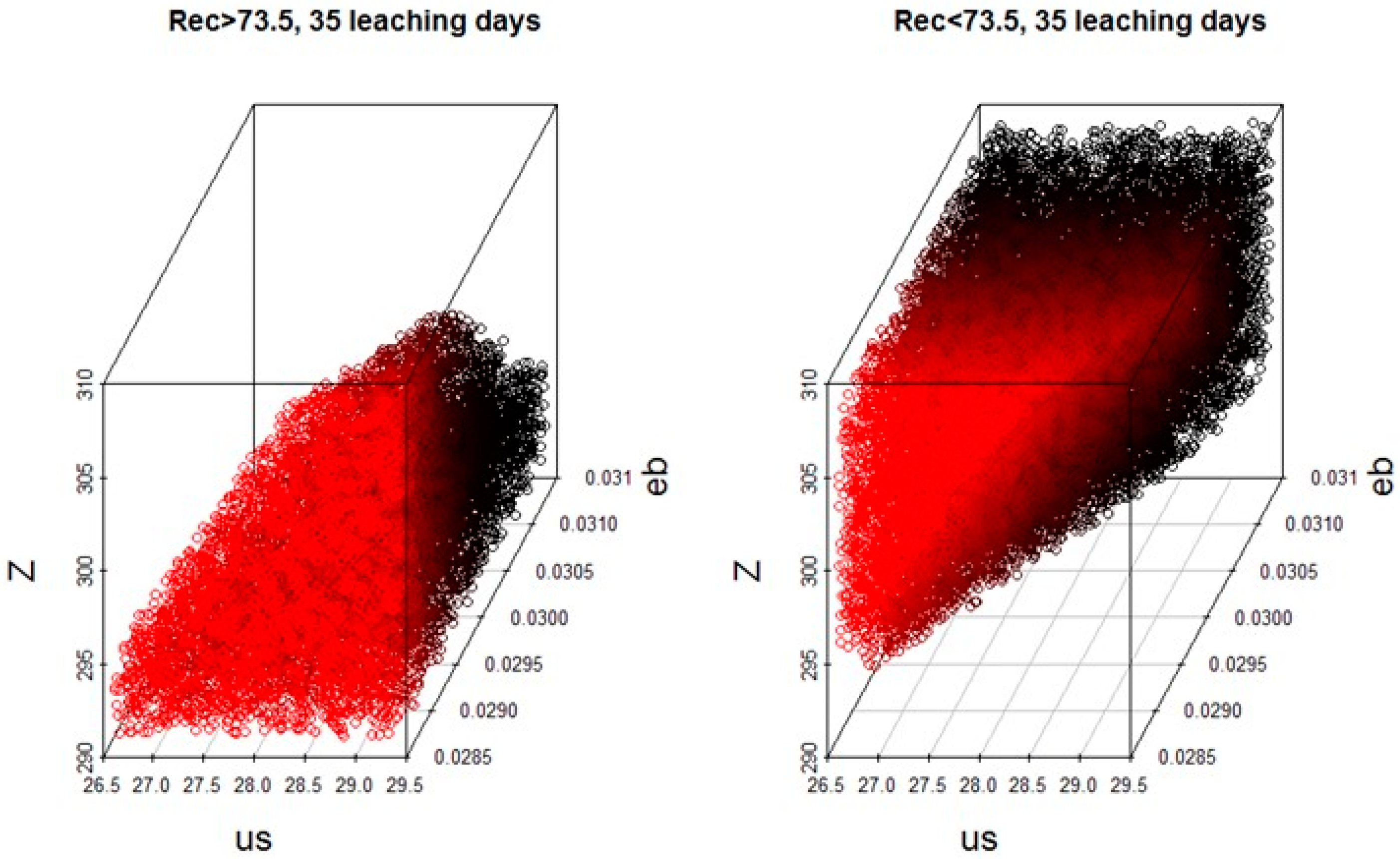
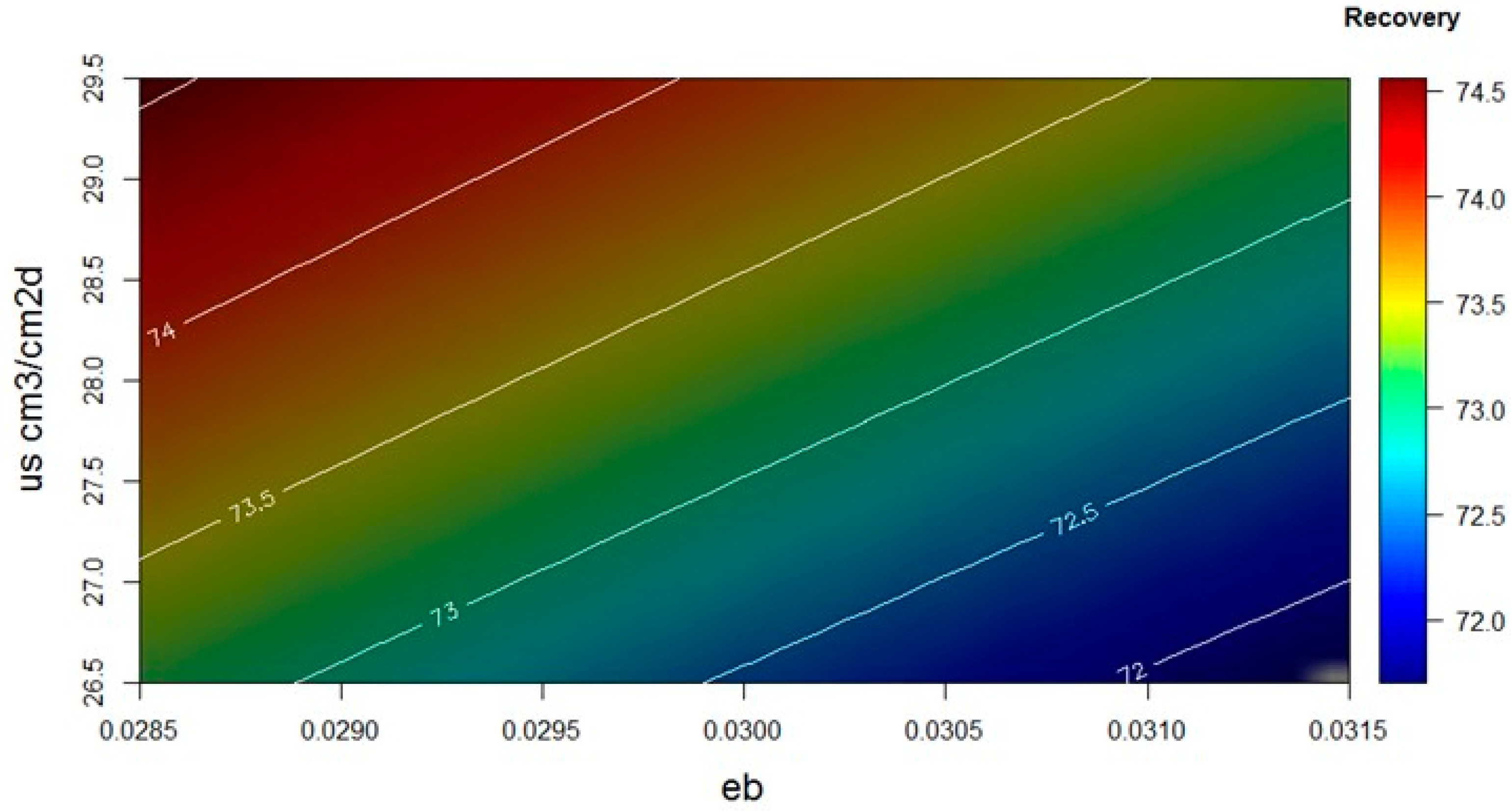
3.3. Regionalization
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Watling, H.R.; Elliot, A.D.; Maley, M.; van Bronswijk, W.; Hunter, C. Leaching of a low-grade, copper–nickel sulfide ore. 1. Key parameters impacting on Cu recovery during column bioleaching. Hydrometallurgy 2009, 97, 204–212. [Google Scholar] [CrossRef]
- Parbhakar-Fox, A. Geoenvironmental Characterisation of Heap Leach Materials at Abandoned Mines: Croydon Au-Mines, QLD, Australia. Minerals 2016, 6, 52. [Google Scholar] [CrossRef]
- Valencia, J.A.; Méndez, D.A.; Cueto, J.Y.; Cisternas, L.A. Saltpeter extraction and modelling of caliche mineral heap leaching. Hydrometallurgy 2008, 90, 103–114. [Google Scholar]
- Moreno, L.; Ordóñez, J.I.; Cisternas, L.A. Dissolution Model of Multiple Species: Leaching of Highly Soluble Minerals. Metall. Mater. Trans. B 2017, 48, 1817–1826. [Google Scholar] [CrossRef]
- Negron, L.; Pingitore, N.; Gorski, D. Porosity and Permeability of Round Top Mountain Rhyolite (Texas, USA) Favor Coarse Crush Size for Rare Earth Element Heap Leach. Minerals 2016, 6, 16. [Google Scholar] [CrossRef]
- McBride, D.; Gebhardt, J.E.; Croft, T.N.; Cross, M. Modeling the hydrodynamics of heap leaching in sub-zero temperatures. Miner. Eng. 2016, 90, 77–88. [Google Scholar] [CrossRef]
- Petersen, J. Heap leaching as a key technology for recovery of values from low-grade ores—A brief overview. Hydrometallurgy 2016, 165, 206–212. [Google Scholar] [CrossRef]
- Watling, H. Review of Biohydrometallurgical Metals Extraction from Polymetallic Mineral Resources. Minerals 2014, 5, 1–60. [Google Scholar] [CrossRef]
- Marsden, J.O.; Botz, M.M. Heap leach modeling—A review of approaches to metal production forecasting. Miner. Metall. Process. 2017, 34, 53–64. [Google Scholar] [CrossRef]
- Ghorbani, Y.; Franzidis, J.-P.; Petersen, J. Heap leaching technology—Current state, innovations and future directions: A review. Miner. Process. Extr. Metall. Rev. 2015, 37, 73–119. [Google Scholar] [CrossRef]
- Thiel, R.; Smith, M.E. State of the practice review of heap leach pad design issues. Geotext. Geomembr. 2004, 22, 555–568. [Google Scholar] [CrossRef]
- De Andrade Lima, L.R.P. A mathematical model for isothermal heap and column leaching. Braz. J. Chem. Eng. 2004, 21, 435–447. [Google Scholar] [CrossRef]
- Bouffard, S.C.; Dixon, D.G. Investigative study into the hydrodynamics of heap leaching processes. Metall. Mater. Trans. B 2001, 32, 763–776. [Google Scholar] [CrossRef]
- Bouffard, S.C.; Dixon, D.G. Evaluation of kinetic and diffusion phenomena in cyanide leaching of crushed and run-of-mine gold ores. Hydrometallurgy 2007, 86, 63–71. [Google Scholar] [CrossRef]
- Cross, M.; Bennett, C.R.; Croft, T.N.; McBride, D.; Gebhardt, J.E. Computational modeling of reactive multi-phase flows in porous media: Applications to metals extraction and environmental recovery processes. Miner. Eng. 2006, 19, 1098–1108. [Google Scholar] [CrossRef]
- Sheikhzadeh, G.A.; Mehrabian, M.A.; Mansouri, S.H.; Sarrafi, A. Computational modelling of unsaturated flow of liquid in heap leaching—Using the results of column tests to calibrate the model. Int. J. Heat Mass Transf. 2005, 48, 279–292. [Google Scholar] [CrossRef]
- Gálvez, E.D.; Moreno, L.; Mellado, M.E.; Ordóñez, J.I.; Cisternas, L.A. Heap leaching of caliche minerals: Phenomenological and analytical models—Some comparisons. Miner. Eng. 2012, 33, 46–53. [Google Scholar] [CrossRef]
- Mellado, M.E.; Cisternas, L.A. An analytical-numerical method for solving a heap leaching problem of one or more solid reactants from porous pellets. Comput. Aided Chem. Eng. 2008, 25, 877–882. [Google Scholar]
- Bouffard, S.C.; Dixon, D.G. Heap biooxidation of refractory gold ores: Current state of the art. Miner. Process. Extr. Metall. Rev. 2004, 25, 159–192. [Google Scholar] [CrossRef]
- Bennett, C.R.; McBride, D.; Cross, M.; Gebhardt, J.E. A comprehensive model for copper sulphide heap leaching. Hydrometallurgy 2012, 127–128, 150–161. [Google Scholar] [CrossRef]
- McBride, D.; Croft, T.N.; Cross, M.; Bennett, C.; Gebhardt, J.E. Optimization of a CFD—Heap leach model and sensitivity analysis of process operation. Miner. Eng. 2014, 63, 57–64. [Google Scholar] [CrossRef]
- Hoseinian, F.S.; Abdollahzade, A.; Mohamadi, S.S.; Hashemzadeh, M. Recovery prediction of copper oxide ore column leaching by hybrid neural genetic algorithm. Trans. Nonferrous Met. Soc. China 2017, 27, 686–693. [Google Scholar] [CrossRef]
- Lane, W.A.; Ryan, E.M. Verification, validation, and uncertainty quantification of a sub-grid model for heat transfer in gas-particle flows with immersed horizontal cylinders. Chem. Eng. Sci. 2018, 176, 409–420. [Google Scholar] [CrossRef]
- Ordóñez, J.I.; Moreno, L.; Mellado, M.E.; Cisternas, L.A. Modeling validation of caliche ore leaching using seawater. Int. J. Miner. Process. 2014, 126, 10–17. [Google Scholar] [CrossRef]
- Ordóñez, J.; Condori, A.; Moreno, L.; Cisternas, L. Heap Leaching of Caliche Ore. Modeling of a Multicomponent System with Particle Size Distribution. Minerals 2017, 7, 180. [Google Scholar] [CrossRef]
- Liddell, K.C. Shrinking core models in hydrometallurgy: What students are not being told about the pseudo-steady approximation. Hydrometallurgy 2005, 79, 62–68. [Google Scholar] [CrossRef]
- Mellado, M.E.; Cisternas, L.A.; Gálvez, E.D. An analytical model approach to heap leaching. Hydrometallurgy 2009, 95, 33–38. [Google Scholar] [CrossRef]
- Mellado, M.E.; Casanova, M.P.; Cisternas, L.A.; Gálvez, E.D. On scalable analytical models for heap leaching. Comput. Chem. Eng. 2011, 35, 220–225. [Google Scholar] [CrossRef]
- Ding, D.; Song, J.; Ye, Y.; Li, G.; Fu, H.; Hu, N.; Wang, Y. A kinetic model for heap leaching of uranium ore considering variation of model parameters with depth of heap. J. Radioanal. Nucl. Chem. 2013, 298, 1477–1482. [Google Scholar] [CrossRef]
- Dixon, D.G.; Hendrix, J.L. A general model for leaching of one or more solid reactants from porous ore particles. Metall. Trans. B 1993, 24, 157–169. [Google Scholar] [CrossRef]
- Dixon, D.G.; Hendrix, J.L. A mathematical model for heap leaching of one or more solid reactants from porous ore pellets. Metall. Trans. B 1993, 24, 1087–1102. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar]
- Lilburne, L.; Tarantola, S. Sensitivity analysis of spatial models. Int. J. Geogr. Inf. Sci. 2009, 23, 151–168. [Google Scholar] [CrossRef]
- Gálvez, E.D.; Capuz-Rizo, S.F. Assessment of global sensitivity analysis methods for project scheduling. Comput. Ind. Eng. 2016, 93, 110–120. [Google Scholar] [CrossRef]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. A posteriori analysis of analytical models for heap leaching. Miner. Metall. Process. 2012, 29, 103. [Google Scholar]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. On the optimization of flow rates on copper heap leaching operations. Int. J. Miner. Process. 2011, 101, 75–80. [Google Scholar] [CrossRef]
- Ordóñez, J.I.; Moreno, L.; Gálvez, E.D.; Cisternas, L.A. Seawater leaching of caliche mineral in column experiments. Hydrometallurgy 2013, 139, 79–87. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Reuter, U.; Liebscher, M. Global Sensitivity Analysis in View of Nonlinear Structural Behavior; LS-DYNA Anwenderforum: Bamberg, Germany, 2008; Volume 56. [Google Scholar]
- Iooss, B.; Lemaître, P. A Review on Global Sensitivity Analysis Methods. Uncertain. Manag. Simul.-Optim. Complex Syst. 2015, 59, 101–122. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity analysis for non-linear mathematical models. Math. Comput. Simul. 1993, 1, 407–414. [Google Scholar]
- Spear, R.; Hornberger, G.M. Eutrophication in peel inlet—II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Lucay, F.; Cisternas, L.A.; Gálvez, E.D. Global sensitivity analysis for identifying critical process design decisions. Chem. Eng. Res. Des. 2015, 103, 74–83. [Google Scholar] [CrossRef]
- Jansen, M.J.W. Analysis of variance designs for model output. Comput. Phys. Commun. 1999, 117, 35–43. [Google Scholar] [CrossRef]
- Pujol, G.; Iooss, B.; Janon, A. Global Sensitivity Analysis of Model Output, version 1.15.0; R Package; 2017. Available online: https://CRAN.R-project.org/package=sensitivity (accessed on 26 January 2018).
- R: A Language and Environment for Statistical Computing; R Core Team (2013); R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www. R-project.org (accessed on 26 January 2018).



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mellado, M.E.; Cisternas, L.A.; Lucay, F.A.; Gálvez, E.D.; Sepúlveda, F.D. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals 2018, 8, 44. https://doi.org/10.3390/min8020044
Mellado ME, Cisternas LA, Lucay FA, Gálvez ED, Sepúlveda FD. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals. 2018; 8(2):44. https://doi.org/10.3390/min8020044
Chicago/Turabian StyleMellado, Mario E., Luis A. Cisternas, Freddy A. Lucay, Edelmira D. Gálvez, and Felipe D. Sepúlveda. 2018. "A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses" Minerals 8, no. 2: 44. https://doi.org/10.3390/min8020044
APA StyleMellado, M. E., Cisternas, L. A., Lucay, F. A., Gálvez, E. D., & Sepúlveda, F. D. (2018). A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals, 8(2), 44. https://doi.org/10.3390/min8020044







