Abstract
Fluorite (CaF2), a halogen elemental mineral, always co-exists with other minerals. The Ca element in fluorite is often replaced by rare earth elements (REEs), such as cerium (Ce) and yttrium (Y). In this work, the electronic structures of fluorite crystals containing REE (Ce, Th, U, and Y) impurities were studied by density functional theory (DFT). The calculated results showed that the presence of impurities increased the lattice parameter of fluorite. The impurities caused the Fermi level to shift towards the high energy direction, making the fluorite accept electrons more easily. The impurities except Y led to the occurrence of an impurities state in the valence band. The Mullinken population values of F–REE bonds were larger than that of F–Ca and F–F bonds, and F–Y bonds had the largest population value. Analysis of the frontier molecular orbital showed that the impurities contributed greatly to the lowest unoccupied molecular orbital (LUMO). The interaction between oleic acid and impurities-bearing fluorite were discussed. The results suggested that the incorporation of impurities would enhanced the reactivity of fluorite with oleic acid.
1. Introduction
Fluorite (CaF2) is an important ore of fluorine, and becomes a strategic resource reserve in many countries. Crystalline fluorite has a very low index of refraction and an unusual ability to transmit ultraviolet light. It is widely used in many industries, such as aluminum fluoride manufacturing, glass manufacturing, primary aluminum production, ceramic, enamels, and hydrofluoric acid. China, Mexico, Namibia, Kenya, and South Africa are the major producing and exporting countries [1].
Fluorite often coexists with other calcium-containing minerals such as calcite, gypsum, and francolite due to the similarity in their formation characteristics [2,3,4]. Separation of fluorite from its associated gangue minerals is commonly carried out by flotation [5,6]. The conventional collectors used in the flotation of fluorite ores are fatty acids (oleic acid, for example) and their salts [7].
Fluorite crystals exist in a variety of colors, ranging from colorless through white, yellow, green, and purple to blue, but purple is the most common [1]. The various colors of fluorite may be attributable to the different impurities in the fluorite crystal [8]. It is reported that REE, such as cerium (Ce) and yttrium (Y), can replace the calcium (Ca) in fluorite in a form of isomorphism [9]. When the amount of substitution reaches a certain value, the replaced fluorite is called yttrofluorite and cerfluorite. In addition, the ion radius of calcium (1.06 Å) in fluorite (CaF2) crystal is very close to 1.10 Å of thorium (Th) and especially 1.05 Å of tetravalent uranium (U) [8,10]. It can be found that U and Th replace Ca in fluorite crystal in some scenarios. Lattice defects may change the Fermi energy, frontier orbital, and electronic structure of minerals which exert a considerable influence on the surface properties of minerals [11,12]. It is tenable to infer that, the incorporation of impurities such as Ce, Th, U, and Y in the fluorite crystal may lead to the different floatability of fluorite.
So far, the study about the impact of impurity defects on the flotation performance has been mainly focused on sulfide ores by density functional theory (DFT) calculations. Ye et al. investigated the effect of three typical impurities (iron, copper, and cadmium) on the flotation behavior of sphalerite [13]. They also studied the electronic structures of bulk sphalerite containing 14 typical kinds of impurities by [14]. Li et al. calculated the electronic property of pyrite crystals containing As, Se, Te, Co, or Ni atoms. The results showed that pyrite containing As, Co, or Ni was easier to oxidize by oxygen than pyrite containing Se or Te, and pyrite containing Co or Ni had greater interaction with xanthate [15]. Chen et al. investigated the adsorption of oxygen molecules (O2) on galena (100) surfaces containing Ag, Cu, Bi, and Mn impurities and found that the impurities could change the semiconductor electronic structure of galena surface and influence the adsorption of oxygen molecules [16].
However, few theoretical studies concerning the influence of impurities on the surface properties of fluorite crystals have been published. In this study, the electronic structures of fluorite bearing Ce, Th, U, and Y impurities were studied by DFT calculations, and the influence of impurities on the reactivity of fluorite was predicted. The findings in the effect of these impurities on the electronic structure and reactivity of fluorite would help solve some encountered problems in fluorite flotation practice.
2. Computational Details
The lattice parameter of fluorite crystal was obtained from the literature [17]. The symmetry group of fluorite crystal is FM-3M. The unit cell consists of eight F atoms and four Ca atoms, and the cell parameters are a = b = c = 5.4631 Å and α = β = γ = 90°. By replacing one Ca atom by an impurity REE atom, a crystal structure of impurity-bearing CaF2 was produced. The models of the fluorite supercells are shown in Figure 1.
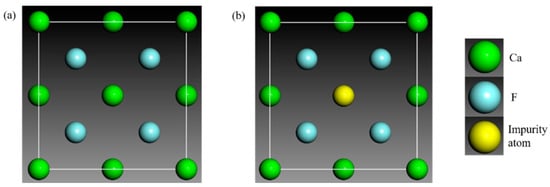
Figure 1.
Models of (a) perfect and (b) impurity-bearing fluorite crystals.
All of calculations in this work were carried out by the Material Studio (MS) 7.0 package. Geometry optimization, a first-principle pseudopotential method based on DFT, was performed using the CASTEP module [18]. Plane wave (PW) basis sets and ultrasoft pseudopotentials were employed for the DFT calculations [19,20]. Based on the test results, GGA-PBESOL [21,22] was set as the exchange correlation functional and 330 eV was used as the cut-off energy. The Brillouin zone was sampled with Monkhorst and Pack special k-points of a 4 × 4 × 4 grid for all structure calculations [23,24,25,26]. Only valence electrons were considered explicitly using ultrasoft pseudopotentials [27,28,29], and pseudo atomic calculations were performed for Ca 3s23p64s2, F 2s22p5, Ce 4f15s25p65d16s2, Th 6s26p66d27s2, U 5f36s26p66d17s2, Y 4s24p64d15s2. The convergence tolerances for geometry optimization calculations were set to the maximum displacement of 0.001 Å, the maximum force of 0.03 eV/Å, the maximum energy change of 1.0 × 10−5 eV/atom, and the maximum stress of 0.05 GP, and the self-consistent field (SCF) convergence tolerance was set to 1.0 × 10−6 eV/atom. Other parameters were default settings.
After geometry optimization, the density of state and the Mullilken population of fluorite supercells were calculated with a single-point energy method using CASTEP module. The Fermi energy and the frontier orbital were calculated also by a single-point energy method using DMol3 module with the same setting parameters as CASTEP. Both structure optimization and frontier orbital calculations of oleic acid were performed by Dmol3 with GGA-PBESOL functional, DNP basis set, all electron core potentials, basis file of 3.5, multipolar expansion of Hexadecapole, global orbital cutoff of 3.7 Å, occupation of fermi and SCF tolerance of 1.0 × 10−6 eV/atom. Other parameters were default settings.
3. Results and Discussion
3.1. Lattice Parameter
The unit cell parameters of impurity-bearing fluorite crystals are shown in Table 1. The lattice parameters of CaF2 bearing Ce, Th, U, and Y impurities are slightly larger than that of the perfect CaF2, and the Th-bearing fluorite has the maximum parameter. The lattice dilatation might lead to the distortion of the lattice which would change the electronic structure of fluorite [14].

Table 1.
Lattice parameter of impurity-bearing and perfect fluorite crystals.
3.2. Fermi Level
Fermi level (EF) [13,30,31,32], synonymous with Fermi energy, is widely used in semiconductor physics. If the electrons in fluorite crystals can be considered as a thermodynamic system, Fermi level is the chemical potential of the system based on statistical theory. From band structure theory, the Fermi level can be considered as a hypothetical energy level of an electron, such that in thermodynamic equilibrium, this energy level would have a 50% probability of being occupied at any given time. The Fermi level of the perfect and impurity-bearing CaF2 is shown in Table 2.

Table 2.
Fermi energies of perfect and impurity-bearing fluorite crystals.
Table 2 shows that the Fermi level of a perfect CaF2 crystal is −5.698 eV. For impurity-bearing CaF2, the Fermi level increases, indicating that the probability of the quantum state being occupied by electrons increases. The incorporation of these impurities causes fluorite crystal to be easier to accept electrons [33], which favors the adsorption of oleic acid on fluorite.
3.3. Density of States
Figure 2 shows the density of state (DOS) diagram of perfect and impurity-bearing fluorite crystals. The appearance of impurity atoms causes the total density peak to shift towards the lower energy and Fermi level to move towards higher energy. This indicates that the presence of impurities makes fluorite accept electrons more easily, and hence enhances the oxidation ability of fluorite crystals (consistent with the Fermi level study) [34,35], which facilitates the reaction of fluorite with reductive collectors (oleic acid).
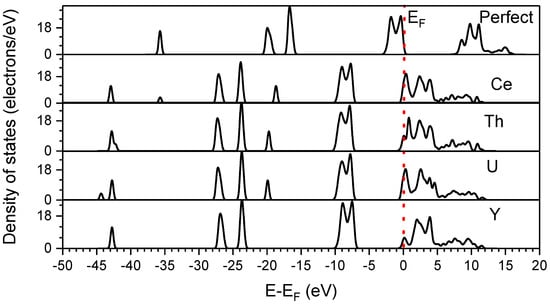
Figure 2.
Density of state (DOS) of perfect and impurity-bearing fluorite crystals.
Figure 3 shows the partial density of state (PDOS) of impurity-bearing fluorite crystals. Impurity atom has an impurity energy level near the Fermi level. The impurity levels of Ce, Th, and U are mainly composed of f orbitals, while the impurity level of Y is mainly contributed by the d orbital. The impurity atoms Ce, Th, and U have the energy level in the valence band except Y.
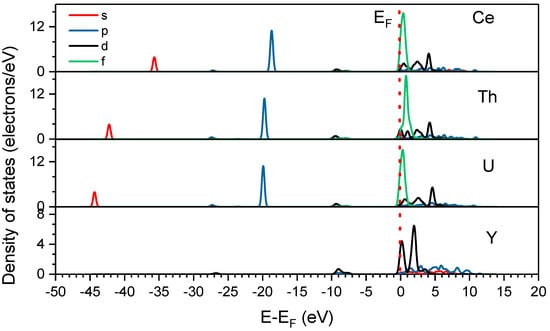
Figure 3.
Partial density of state (PDOS) of impurity atoms in fluorite crystal.
Figure 4 and Figure 5 show the PDOS of the Ca and F atoms adjacent to the impurity atom. The presence of impurity atoms causes the PDOS peaks of Ca and F atoms to move towards the lower energy. The state density near the Fermi level in the perfect fluorite crystal is mainly provided by the F atom. But, the presence of the impurity atoms causes the peak to shift to the left direction, and the peak near the Fermi level is provided by the impurity atom, indicating that impurity atoms play a dominant role in determining the chemical properties of impurity-bearing fluorite.
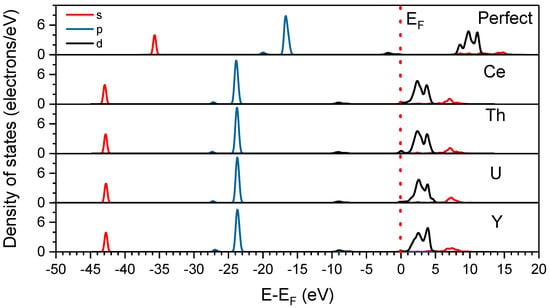
Figure 4.
PDOS of a single Ca atom adjacent to the impurity atom in fluorite crystals.
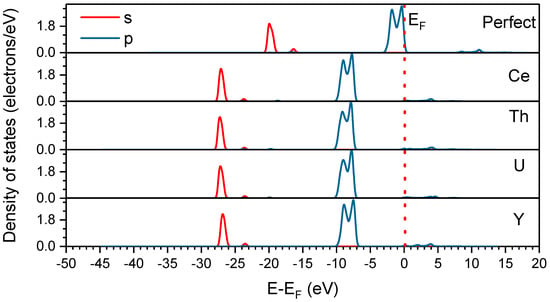
Figure 5.
PDOS of a single F atom adjacent to the impurity atom in fluorite crystals.
3.4. Analysis of the Mulliken Population
According to Mulliken population of a chemical bond [36,37,38], the covalency and ionic strength of the bond can be estimated. A high population value indicates a covalent bond, while a low value implies an ion-interacting bond. Substituted impurity atom mainly affects the atoms closed to it, so the Mulliken population analysis was carried out on the atoms and bonds adjacent to the impurity atom. The results are shown in Table 3.

Table 3.
Mulliken population of impurity atom and the atoms adjacent to impurity atom in impurity-bearing fluorite crystals.
Table 3 shows the p orbital of the Ca atom in the perfect fluorite crystal is not involved in bonding. Ca atoms can donor electrons, the main loss of electrons comes from the d orbital. F atoms can accept electrons, the main gain of electrons happens in the p orbital. The occurrence of impurity atoms gives rise to the redistribution of atomic valence and charge in fluorite crystals. The presence of Ce, Th, U, and Y increases the charge value of the F atom and decreases the charge value of the Ca atom. But, the impurity atoms are positively charged. The increase of positive charge in fluorite crystal enhances the adsorption of oleic acid anions onto the fluorite, which is beneficial for fluorite flotation.
Table 4 shows the Mulliken population values of the bonds formed between the impurity atom and adjacent atoms in impurity-bearing fluorite crystals. The presence of impurity atoms reduces the population value of F–Ca bonds and the covalency, but increases the bond length. It increases the population value of F–F bonds and the covalency, decreases the bond length. The population values of F–REE bonds are larger than that of F–Ca and F–F bonds, indicating that the covalency of F–REE bond is larger and hence the covalency of fluorite crystal is improved. It is wide accepted that the atoms on the commonly exposed surfaces of fluorite present unsaturated bonds [39,40,41]. Accordingly, the exposed REE atoms on the fluorite surface with unsaturated bonds have a stronger interaction with oleate ions, i.e., the interaction between oleic acid and fluorite becomes stronger. Therefore, the stronger the covalency is, the stronger the adsorption of oleic acid is [42]. The existence of impurity defects is favorable for the fluorite flotation.

Table 4.
Mulliken population of bonds formed between the impurity atom and the atoms adjacent to the impurity atoms in impurity-bearing fluorite crystals.
3.5. Effect of Impurity on the Reactivity of Fluorite
It is well established that oleic acid (OA) reacted with the Ca atoms on the surface of fluorite to form calcium oleate by chemical reaction [43,44,45]. During the reaction, the OA loses electrons and is oxidized while the fluorite accepts electrons and is reduced. As discussed above, impurities in the crystal can change the electronic structures of the fluorite, such as the Fermi energy, density of states, and the Mulliken population. Since the surface reactivity of fluorite is mainly dependent on these properties mentioned, the interaction of fluorite with flotation reagent (especially collector) would be changed.
The extent of the interaction of minerals with organics can be described by frontier molecular orbital theory was proposed by Fukui in 1952 [46]. The central idea of the theory is that the mineral with highest occupation molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is the most reactive in its interaction with organics. The HOMO energy is the highest, the most active and most likely to donate electrons. The LUMO energy is the lowest in all unoccupied orbitals and most likely to accept electrons.
HOMO and LUMO energies determine the ability of electron gain, loss and transfer of a molecule, and hence determines its main chemical properties. According to the linear combination principle of molecular orbitals, the molecular orbital consists of many atomic orbitals:
where is the molecular orbital; is the atomic orbital; is the atomic orbital coefficient. The magnitude of the atomic orbital coefficient of HOMO and LUMO represents the contribution of the constituent atom to the molecular orbital. The positive and negative sign of atomic orbital coefficient represent bonding and antibonding between the atoms, respectively. But, only the absolute value of the coefficient was concerned in this study. The greater the coefficient is, the stronger the effect of the atom exerts on orbital reactivity.
The fluorite acquires electrons and is reduced when reacted with oleic acid, so the LUMO of fluorite is considered here. Table 5 shows the frontier orbital coefficients of perfect and impurity-bearing CaF2 crystals. The impurity atoms in the fluorite lattice leads to smaller orbital coefficients for Ca and F and larger ones for the impurity atoms. The effect of impurity atoms on the fluorite LUMO follows the order, Th > Y > Ce > U. The greater the orbital coefficient is, the greater its contribution to LUMO is. The largest atomic orbital coefficient of impurity compared to those of Ca and F, is indicative of the decisive role of impurity atoms in determining the reactivity of fluorite.

Table 5.
Frontier orbital coefficients of perfect and impurity-bearing fluorites.
The reaction between OA and fluorite happens between the HOMO of OA as electron donor and the LUMO of fluorite as electron acceptor. According to the frontier orbital theory, the extent of their interaction can be defined by the following Equation:
where is the HOMO level of the OA, and is the LUMO level of CaF2. Based on frontier orbital theory, the smaller the value of is, the stronger the interaction between OA and fluorite is [14]. The HOMO and LUMO values of perfect CaF2, the impurity-bearing CaF2, and values are shown in Table 6.

Table 6.
Frontier orbital energies of the impurity-bearing fluorite crystals and oleic acid.
Table 6 shows that the between perfect CaF2 and OA is 3.424 eV. For CaF2 bearing Ce, Th, U, and Y impurities, the is much smaller, suggesting that the incorporation of these impurities can benefit the interaction between OA and fluorite. Among these impurity-bearing fluorite crystals, for the Th-bearing fluorite is smallest (2.376 eV), indicating that the interaction between the Th-bearing fluorite and OA is the strongest.
4. Conclusions
The electronic structures of bulk fluorite bearing Ce, Th, U, and Y impurities were calculated using DFT. The results showed that the impurities changed the structure and electronic properties of fluorite, including the Fermi level, density of states, and the Mulliken population. The presence of impurities increased the lattice parameters of fluorite, and made the Fermi level shift towards the direction of high energy, causing the fluorite to accept electrons more easily. The results of DOS and Mulliken population indicated that the incorporation of impurity atoms made oleic acid more easily adsorb on fluorite. The frontier molecular orbital calculations suggested that the incorporation of impurities of Ce, Th, U, and Y can enhance the reactivity of fluorite with oleic acid.
Supplementary Materials
The following are available online at http://www.mdpi.com/2075-163X/7/9/160/s1, Table S1: The unit cell parameters of fluorite under different exchange correlation functional; Table S2: The unit cell parameters of fluorite under different cut-off energy values.
Acknowledgments
The authors acknowledge financial support from the National Natural Science Foundation of China (51774328, 51404300), the Innovation-driven Program of Central South University of China (2017CX007), the National 111 Project (B14034), and the Innovation Program for Postgraduate Students of Central South University (2017zzts192).
Author Contributions
Wei Jiang and Zhiyong Gao conceived and designed the experiments, and wrote the paper; Wei Jiang and Jiande Gao performed the experiments; Wei Sun and Yuehua Hu analyzed the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- El-Nadi, Y.A. Solvent extraction and recovery of Y(III) and Yb(III) from fluorspar mineral. Int. J. Miner. Metall. Mater. 2013, 20, 713–719. [Google Scholar] [CrossRef]
- Somasundaran, P.; Amankonah, J.O.; Ananthapadmabhan, K.P. Mineral–solution equilibria in sparingly soluble mineral systems. Colloids Surf. 1985, 15, 309–333. [Google Scholar] [CrossRef]
- Marinakis, K.I.; Shergold, H.L. The mechanism of fatty acid adsorption in the presence of fluorite, calcite and barite. Int. J. Miner. Process. 1985, 14, 161–176. [Google Scholar] [CrossRef]
- Pugh, R.; Stenius, P. Solution chemistry studies and flotation behaviour of apatite, calcite and fluorite minerals with sodium oleate collector. Int. J. Miner. Process. 1985, 15, 193–218. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, Z.; Sun, W.; Hu, Y. Selective flotation of scheelite from calcite: A novel reagent scheme. Int. J. Miner. Process. 2016, 154, 10–15. [Google Scholar] [CrossRef]
- Gao, Z.; Bai, D.; Sun, W.; Cao, X.; Hu, Y. Selective flotation of scheelite from calcite and fluorite using a collector mixture. Miner. Eng. 2015, 72, 23–26. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Z. Interactions of amphoteric amino phosphoric acids with calcium-containing minerals and selective flotation. Int. J. Miner. Process. 2003, 72, 87–94. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Y.; Li, X. Preliminary Study of the Relationship between Irradiation Damage and Fluorite Colour. Acta Mineral. Sin. 1983, 4, 10. [Google Scholar]
- Peng, J.; Hu, R.; Qi, L.; Jiang, G. REE geochemistry of fluorite from the Qinglong antimony deposit and its geological implications. Sci. Geol. Sin. 2002, 37, 277–287. [Google Scholar]
- Gabelman, J.W. Migration of Uranium and Thorium: Exploration Significance; GSW Books: McLean, VA, USA, 1977. [Google Scholar]
- Catlow, C.R.A. Defect Structures in fluorite crystals. Acta Crystallogr. 1973, 32, 1944–1947. [Google Scholar]
- Hayes, W. Crystals with the Fluorite Structure: Electronic, Vibrational, and Defect Properties; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- Chen, Y.; Chen, J.; Lan, L.; Yang, M. The influence of the impurities on the flotation behaviors of synthetic ZnS. Miner. Eng. 2012, 27–28, 65–71. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, J.; Guo, J. A DFT study on the effect of lattice impurities on the electronic structures and floatability of sphalerite. Miner. Eng. 2010, 23, 1120–1130. [Google Scholar] [CrossRef]
- Yu-Qiong, L.I.; Chen, J.H.; Chen, Y.; Guo, J. Density functional theory study of influence of impurity on electronic properties and reactivity of pyrite. Trans. Nonferr. Met. Soc. China 2011, 21, 1887–1895. [Google Scholar]
- Chen, J.; Ke, B.; Lan, L.; Li, Y. DFT and experimental studies of oxygen adsorption on galena surface bearing Ag, Mn, Bi and Cu impurities. Miner. Eng. 2015, 71, 170–179. [Google Scholar]
- Speziale, S.; Duffy, T.S. Single-crystal elastic constants of fluorite (CaF2) to 9.3 GPa. Phys. Chem. Miner. 2002, 29, 465–472. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B Condens. Matter 1992, 45, 13244. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Condens. Matter 1990, 41, 7892. [Google Scholar] [CrossRef] [PubMed]
- Vilaplana, R.; Santamaríapérez, D.; Gomis, O.; Manjόn, F.J.; González, J.; Segura, A.; Muñoz, A.; Rodríguez-Hernández, P.; Pérez-González, E.; Marín-Borráa, V.; et al. Structural and vibrational study of Bi2Se3 under high pressure. Phys. Rev. B 2011, 84, 1160–1164. [Google Scholar]
- Bilal, M.; Ahmad, I.; Aliabad, H.A.R.; Asadabadi, S.J. Detailed DFT studies of the band profiles and optical properties of antiperovskites SbNCa 3, and BiNCa 3. Comput. Mater. Sci. 2014, 85, 310–315. [Google Scholar] [CrossRef]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B Condens. Matter 1977, 16, 5188–5192. [Google Scholar] [CrossRef]
- Macdonald, A.H. Comment on special points for Brillouin-zone integrations. Phys. Rev. B Condens. Matter 1978, 18, 5897–5899. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Smirnov, V.P. Modification of the Monkhorst-Pack special points meshes in the Brillouin zone for density functional theory and Hartree-Fock calculations. Phys. Rev. B 2004, 70, 155–163. [Google Scholar] [CrossRef]
- Ramíarez, R.; Böhm, M.C. Simple geometric generation of special points in brillouin-zone integrations. Two-dimensional bravais lattices. Int. J. Quantum Chem. 1986, 30, 391–411. [Google Scholar] [CrossRef]
- Laasonen, K.; Pasquarello, A.; Car, R.; Lee, C.; Vanderbilt, D. Car-Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials. Phys. Rev. B Condens. Matter 1993, 47, 10142. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Kresse, G.; Furthmüller, J.; Hafner, J. Chemisorption of H on Pd(111): An ab initio approach with ultrasoft pseudopotentials. Phys. Rev. B Condens. Matter 1996, 54, 2157–2166. [Google Scholar] [CrossRef] [PubMed]
- Furthmüller, J.; Hafner, J.; Kresse, G. Ab initio calculation of the structural and electronic properties of carbon and boron nitride using ultrasoft pseudopotentials. Phys. Rev. B Condens. Matter 1994, 50, 15606–15622. [Google Scholar] [CrossRef] [PubMed]
- Wood, A.; Giersig, M.; Mulvaney, P. Fermi Level Equilibration in Quantum Dot-Metal Nanojunctions. J. Phys. Chem. B 2001, 105, 8810–8815. [Google Scholar] [CrossRef]
- Himpsel, F.J.; Hollinger, G.; Pollak, R.A. Determination of the Fermi-level pinning position at Si(111) surfaces. Phys. Rev. B Condens. Matter 1983, 28, 7014–7018. [Google Scholar] [CrossRef]
- Tengstedt, C.; Osikowicz, W.; Salaneck, W.R.; Parker, L.D.; Jsu, C.-H.; Fahlman, M. Fermi-level pinning at conjugated polymer interfaces. Appl. Phys. Lett. 2006, 88, 121. [Google Scholar] [CrossRef]
- Chen, J.H.; Wang, L.; Chen, Y.; Li, Y.Q.; Guo, J. Density functional theory of effects of vacancy defects on electronic structure and flotation of galena. Chin. J. Nonferr. Met. 2010, 20, 1815–1821. [Google Scholar]
- Imai, Y.; Mukaida, M.; Tsunoda, T. Calculation of electronic energy and density of state of iron-disilicides using a total-energy pseudopotential method, CASTEP. Thin Solid Films 2001, 381, 176–182. [Google Scholar] [CrossRef]
- Völkel, A.R.; Street, R.A.; Knipp, D. Carrier transport and density of state distributions in pentacene transistors. Phys. Rev. B 2002, 66, 248. [Google Scholar] [CrossRef]
- Roy, R.K.; Hirao, K.; Krishnamurty, S.; Pal, S. Mulliken population analysis based evaluation of condensed Fukui function indices using fractional molecular charge. J. Chem. Phys. 2001, 115, 2901–2907. [Google Scholar]
- Carbó-Dorca, R.; Bultinck, P. Quantum Mechanical Basis for Mulliken Population Analysis. J. Math. Chem. 2004, 36, 231–239. [Google Scholar] [CrossRef]
- Huzinaga, S.; Narita, S. Mulliken Population Analysis and Point Charge Model of Molecules. Isr. J. Chem. 2013, 19, 242–254. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Li, C.W.; Sun, W.; Hu, Y.H. Anisotropic surface properties of calcite: A consideration of surface broken bonds. Colloid Surface A 2017, 520, 53–61. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Sun, W.; Hu, Y.H. Mineral cleavage nature and surface energy: Anisotropic surface broken bonds consideration. Trans. Nonferr. Met. Soc. China 2014, 24, 2930–2937. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Hu, Y.H.; Sun, W.; Drelich, J.W. Surface-charge anisotropy of scheelite crystals. Langmuir 2016, 32, 6282–6288. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Q.; Chen, J.H.; Chen, Y. Electronic Structures and Flotation Behavior of Pyrite Containing Vacancy Defects. Acta Phys. Chim. Sin. 2010, 26, 1435–1441. [Google Scholar]
- Free, M.L.; Miller, J.D. The significance of collector colloid adsorption phenomena in the fluorite/oleate flotation system as revealed by FTIR/IRS and solution chemistry analysis. Int. J. Miner. Process. 1996, 48, 197–216. [Google Scholar] [CrossRef]
- Jańczuk, B.; González-Martín, M.L.; Bruque, J.M.; del Pozo, J.M. The influence of oleate adsorption at the fluorite/water interface on fluorite surface free energy. Appl. Surf. Sci. 1993, 72, 201–207. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Sun, W.; Hu, Y.H.; Liu, X.W. Anisotropic surface broken bond properties and wettability of calcite and fluorite crystals. Nonferr. Met. Soc. China 2012, 22, 1203–1208. [Google Scholar] [CrossRef]
- Yamabe, S.; Minato, T. Frontier Orbital Theory. Chem. Educ. 1992, 40, 450–454. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).