Optimal Location of Vanadium in Muscovite and Its Geometrical and Electronic Properties by DFT Calculation
Abstract
:1. Introduction
2. Methods
2.1. Structure and Models
2.2. DFT Calculations
3. Results and Discussion
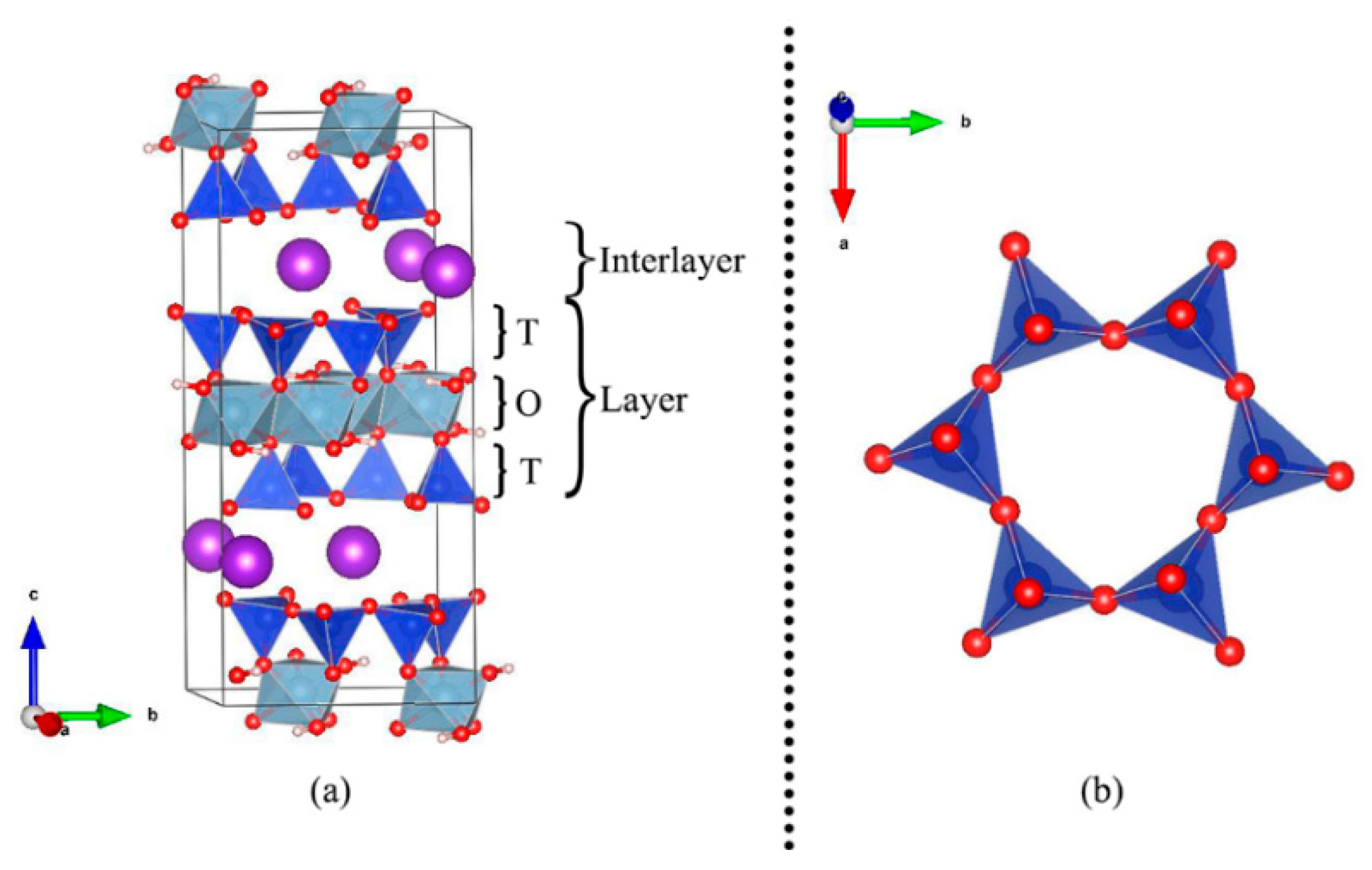
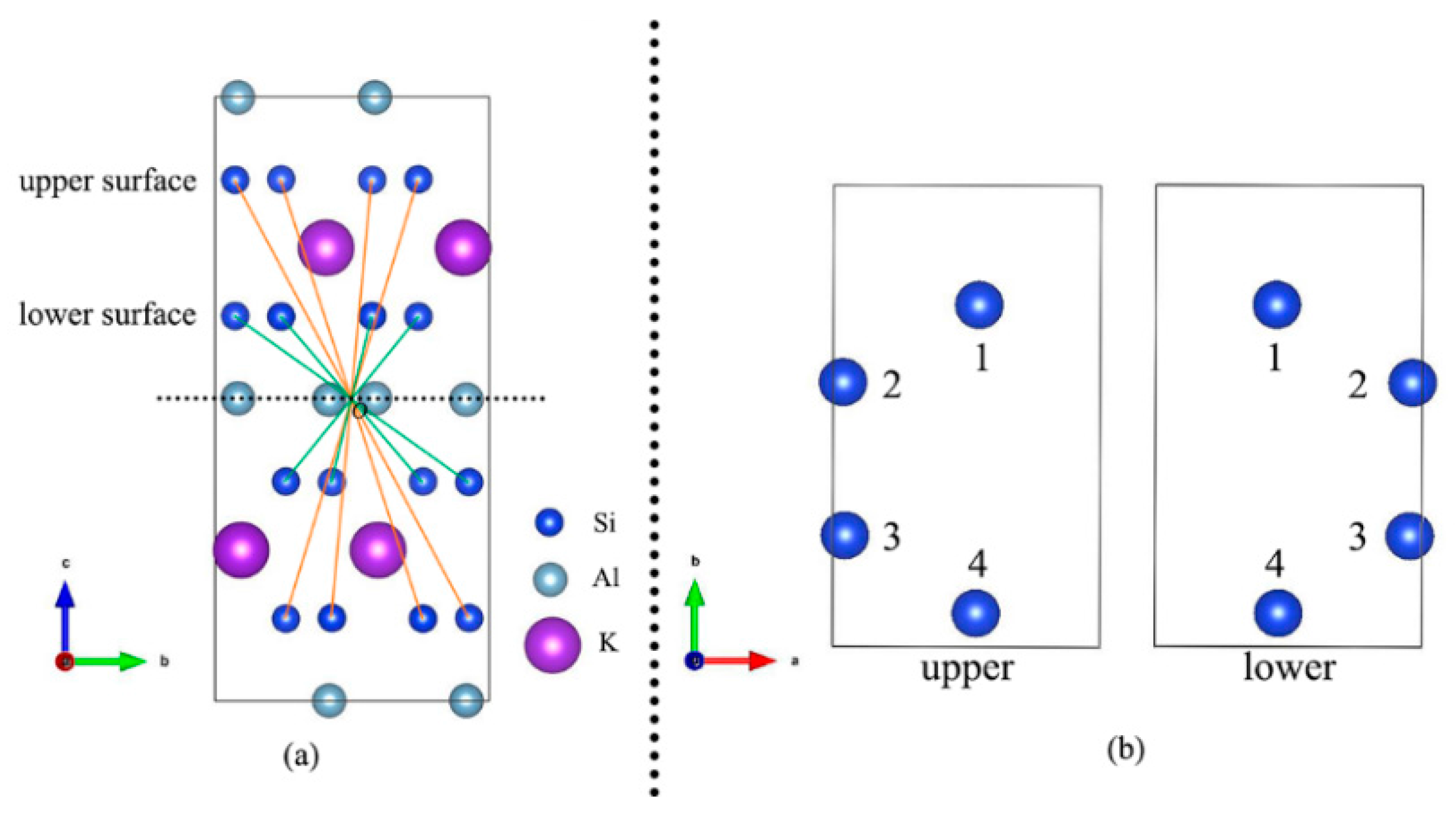
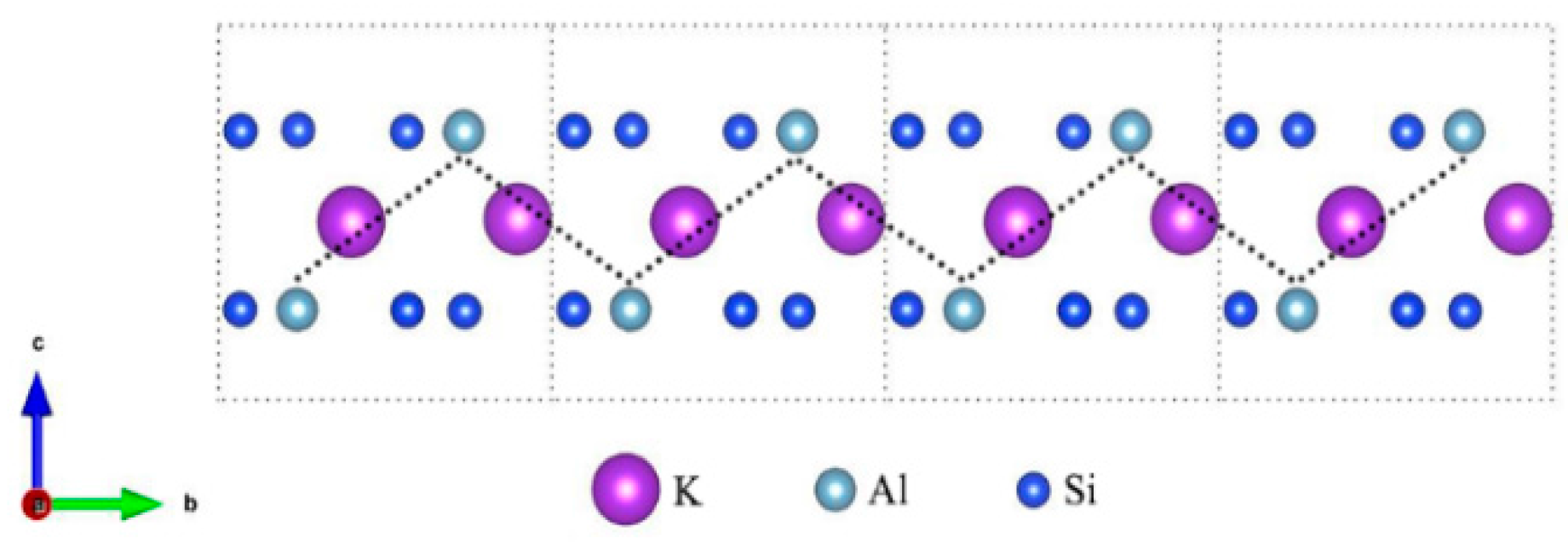
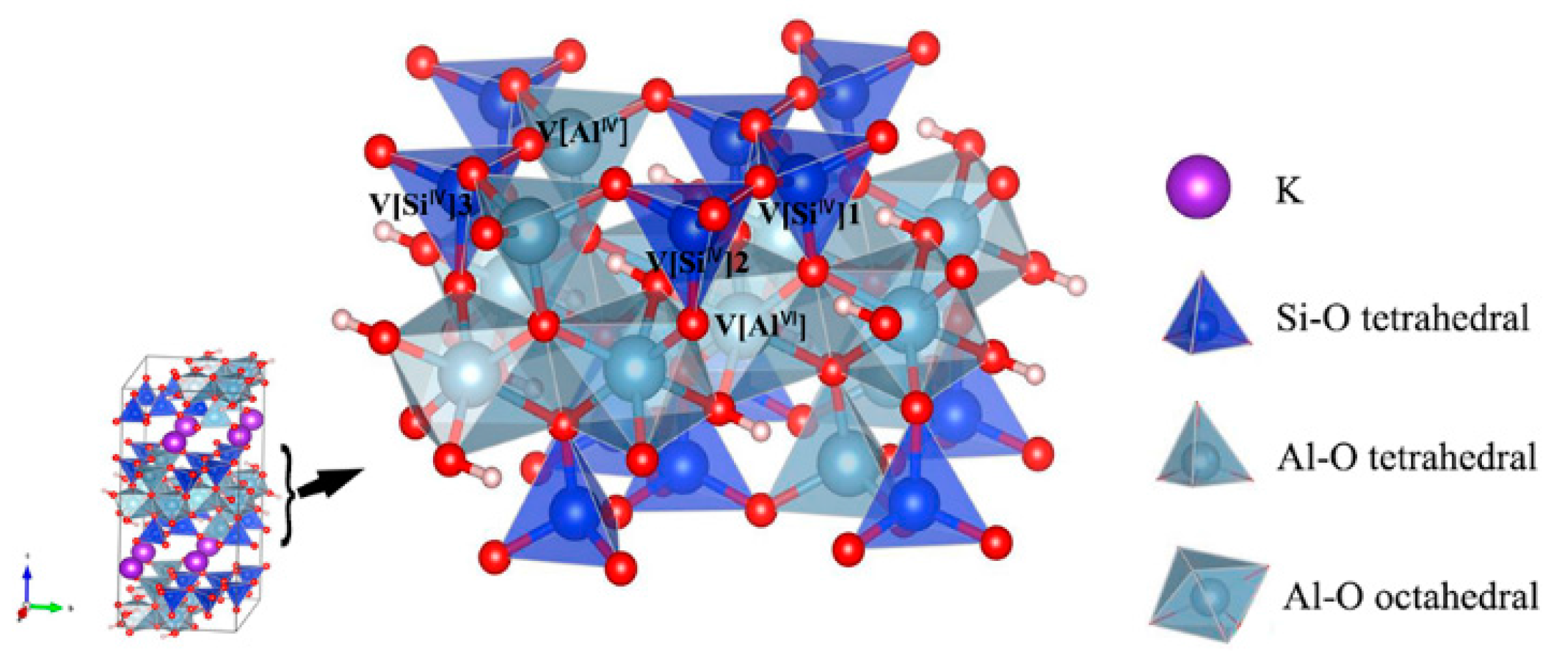
3.1. Muscovite Model
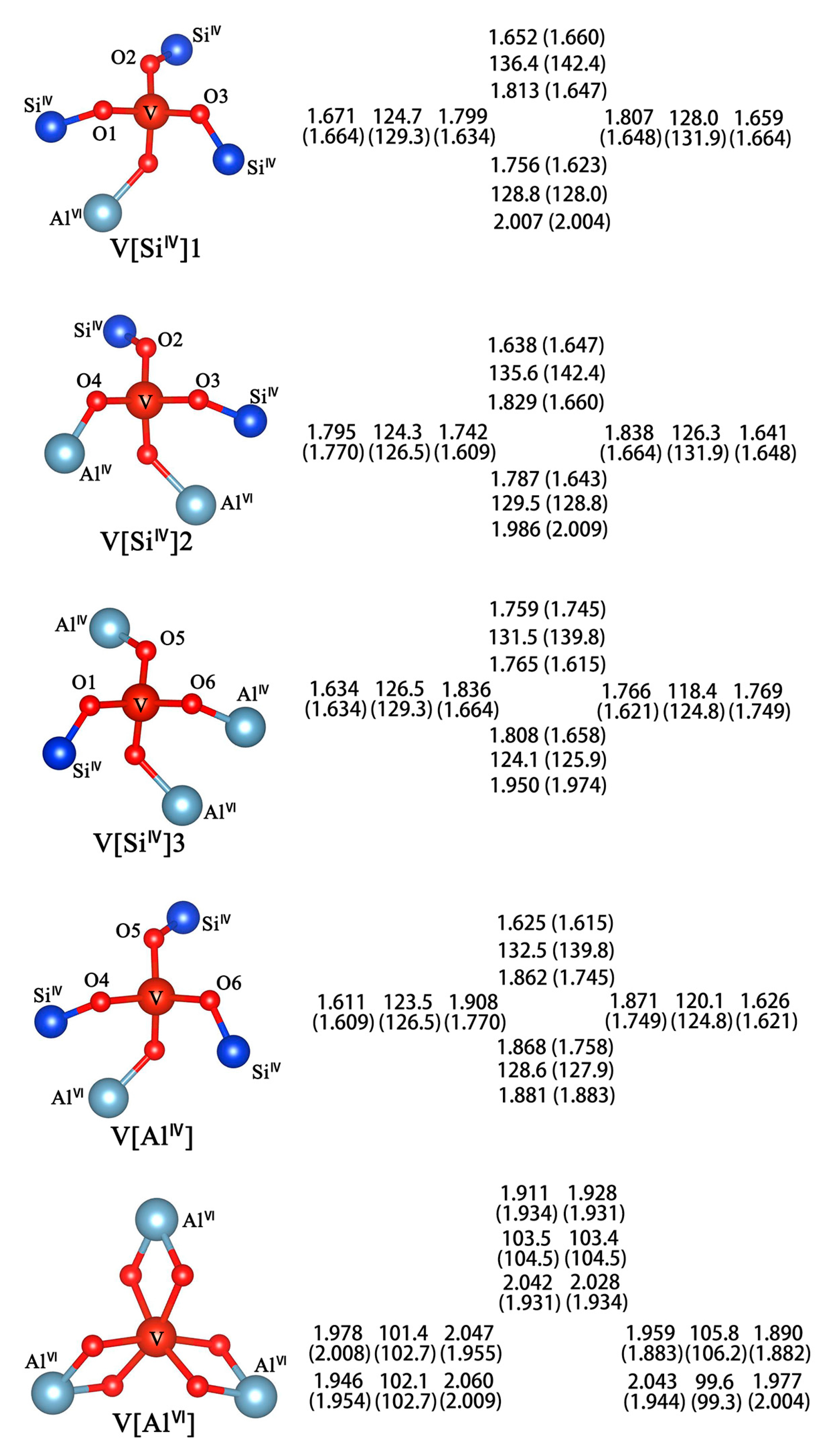
3.2. Optimal Location of Vanadium and Local Geometry
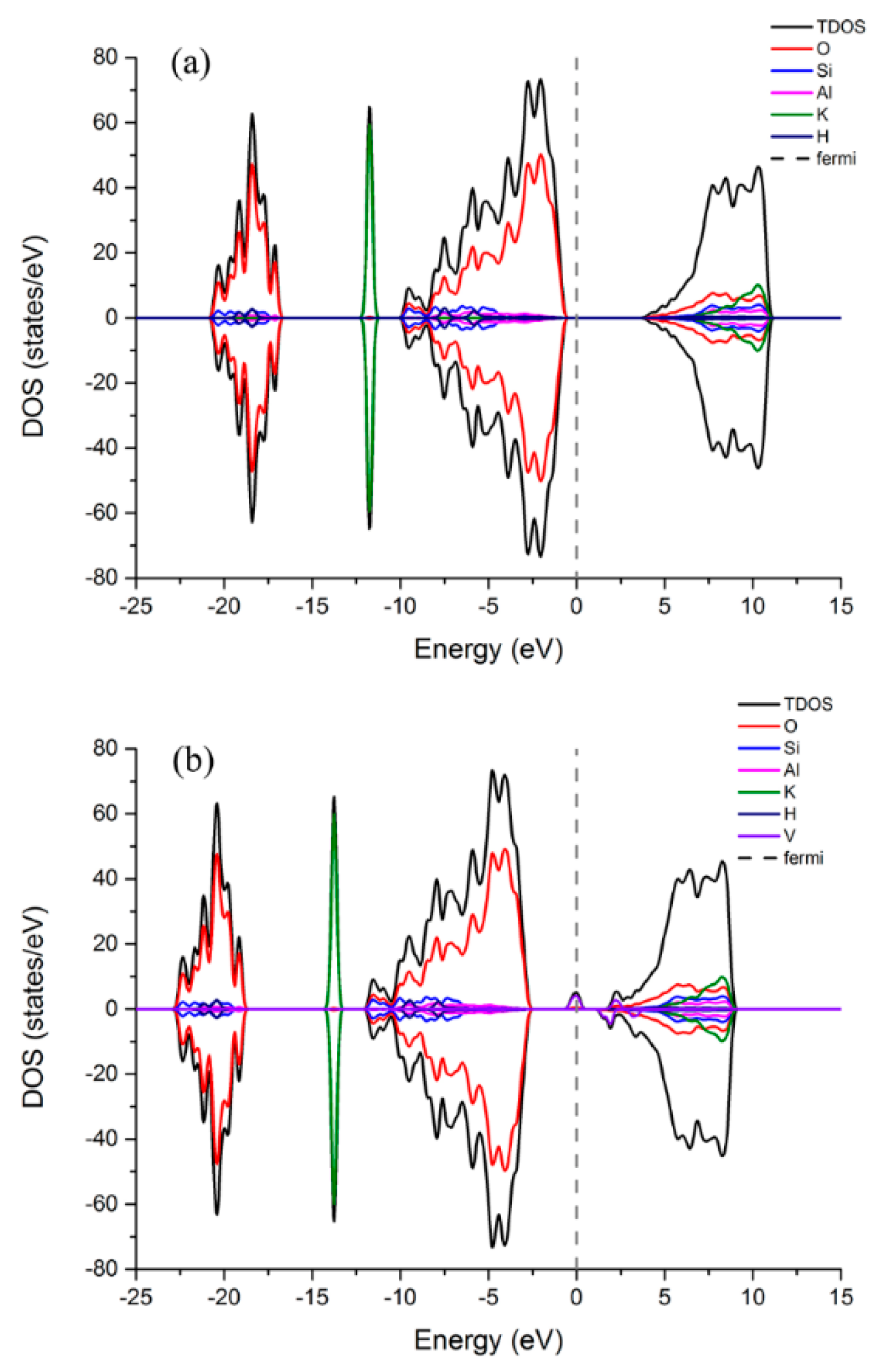
3.3. Electronic Properties of Vanadium-Bearing Muscovite
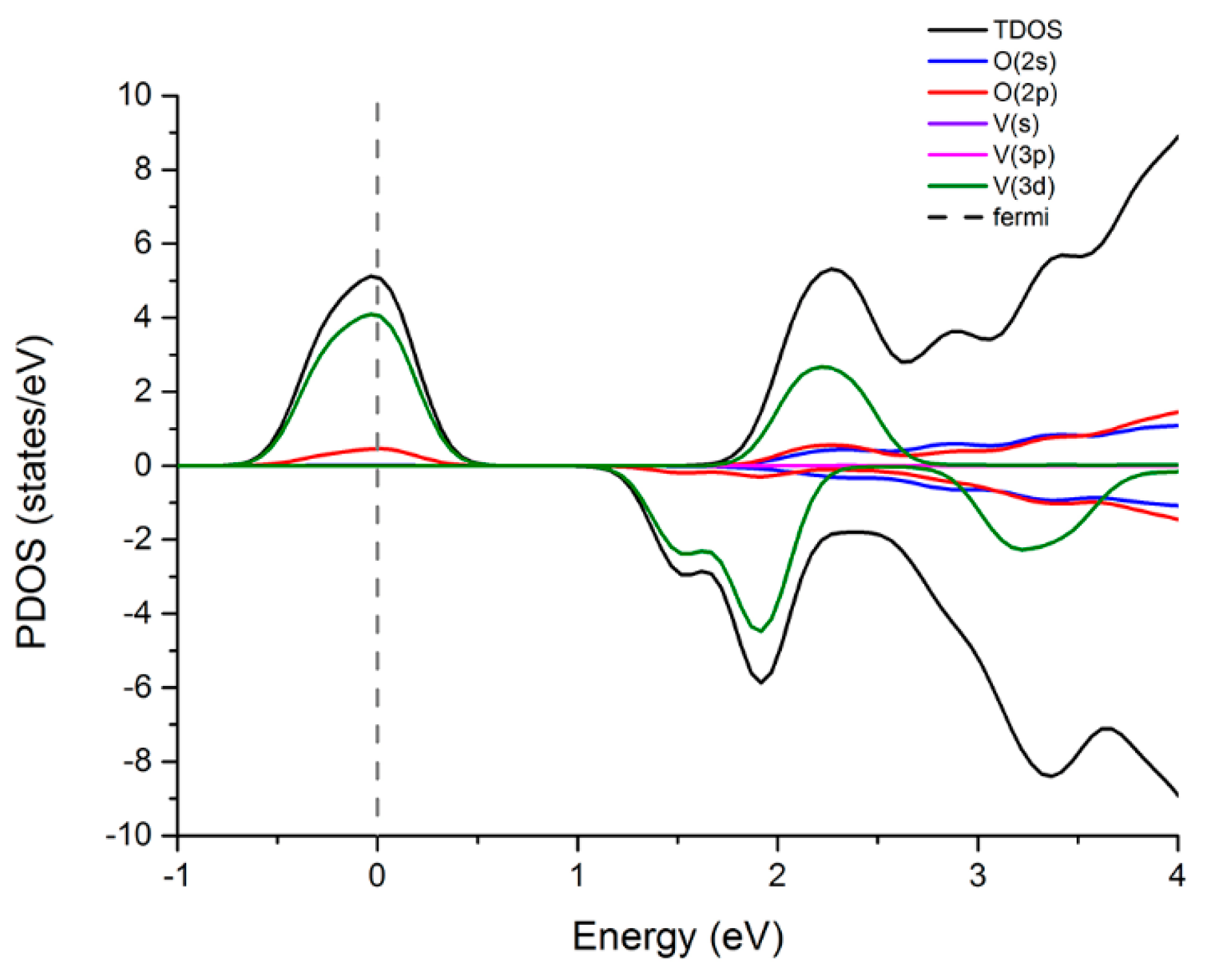
3.3.1. Density of States (DOS) and Magnetism
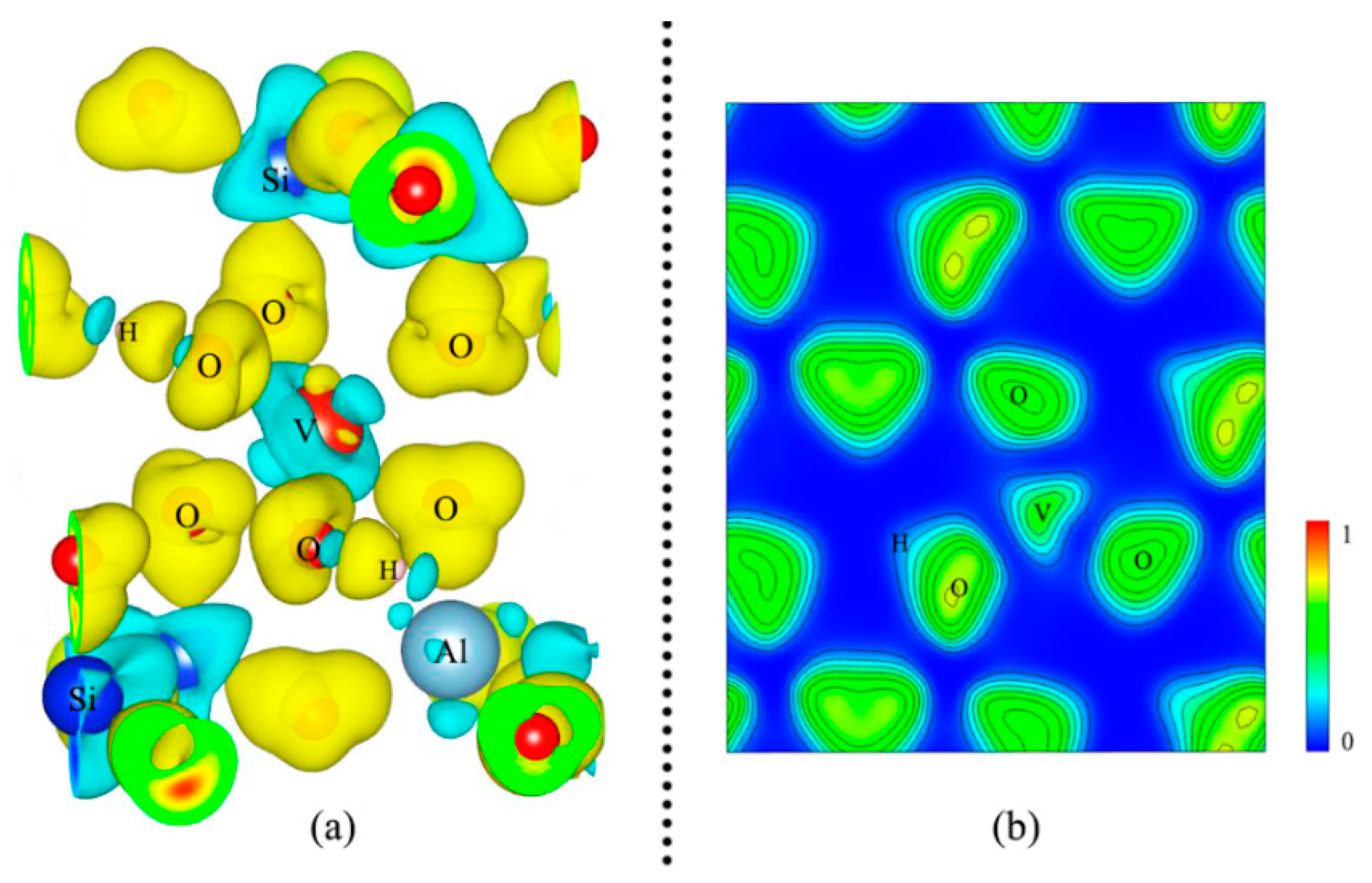
3.3.2. Charge Transfer and Bond Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, Y.M.; Bao, S.X.; Liu, T.; Chen, T.J.; Huang, J. The technology of extracting vanadium from stone coal in China: History, current status and future prospects. Hydrometallurgy 2011, 109, 116–124. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Li, L.Y.; Graff, G.; Liu, J.; Zhang, H.M.; Yang, Z.G.; Hu, J.Z. Towards understanding the poor thermal stability of V5+ electrolyte solution in vanadium redox flow batteries. J. Power Sources 2011, 196, 3669–3672. [Google Scholar] [CrossRef]
- Yamamura, T.; Wu, X.W.; Ohta, S.; Shirasaki, K.; Sakuraba, H.; Satoh, I.; Shikama, T. Vanadium solid-salt battery: Solid state with two redox couples. J. Power Sources 2011, 196, 4003–4011. [Google Scholar] [CrossRef]
- Dai, S.; Yan, X.; Ward, C.R.; Hower, J.C.; Zhao, L.; Wang, X.; Zhao, L.; Ren, D.; Finkelman, R.B. Valuable elements in Chinese coals: A review. Int. Geol. Rev. 2016, 1–31. [Google Scholar] [CrossRef]
- Xue, N.N.; Zhang, Y.M.; Liu, T.; Huang, J.; Liu, H.; Chen, F. Mechanism of vanadium extraction from stone coal via hydrating and hardening of anhydrous calcium sulfate. Hydrometallurgy 2016, 166, 48–56. [Google Scholar] [CrossRef]
- Cai, Z.L.; Zhang, Y.M.; Liu, T.; Huang, J. Vanadium extraction from refractory stone coal using novel composite additive. JOM 2015, 67, 2629–2634. [Google Scholar] [CrossRef]
- Zhu, X.B.; Zhang, Y.M.; Huang, J.; Liu, T.; Wang, Y. A kinetics study of multi-stage counter-current circulation acid leaching of vanadium from stone coal. Int. J. Miner. Process. 2012, 114–117, 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, Y.M.; Liu, T.; Chen, T.J.; Bian, Y.; Bao, S.X. Pre-concentration of vanadium from stone coal by gravity separation. Int. J. Miner. Process. 2013, 121, 1–5. [Google Scholar]
- Chae, J.U.; Kwon, K.D. Effects of Fe substitution on lithium incorporation into muscovite. J. Miner. Soc. Korea 2015, 28, 127–133. [Google Scholar] [CrossRef]
- Ortega-Castro, J.; Hernández-Haro, N.; Hernández-Laguna, A.; Sainz-Díaz, C.I. DFT calculation of crystallographic properties of dioctahedral 2:1 phyllosilicates. Clay Miner. 2008, 43, 351–361. [Google Scholar] [CrossRef]
- Hernández-Haro, N.; Ortega-Castro, J.; Valle, C.P.D.; Muñoz-Santiburcio, D.; Sainz-Díaz, C.I.; Hernández-Laguna, A. Computational study of the elastic behavior of the 2M1 muscovite-paragonite series. Am. Mineral. 2013, 98, 651–664. [Google Scholar] [CrossRef]
- Ulian, G.; Valdrè, G. Density functional investigation of the thermo-physical and thermo-chemical properties of 2M1 muscovite. Am. Mineral. 2015, 100, 935–944. [Google Scholar] [CrossRef]
- Wang, J.W.; Kalinichev, A.G.; James-Kirkpatrick, R.; Cygan, R.T. Structure, Energetics, and Dynamics of water adsorbed on the muscovite (001) surface: A molecular dynamics simulation. J. Phys. Chem. B 2005, 109, 15893–15905. [Google Scholar] [CrossRef] [PubMed]
- Mignon, P.; Ugliengo, P.; Sodupe, M.; Hernandez, E.R. Ab initio molecular dynamics study of the hydration of Li+, Na+ and K+ in a montmorillonite model. Influence of isomorphic substitution. Phys. Chem. Chem. Phys. 2010, 12, 688–697. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, H.; Suehara, S. Interlayer bonding energy of layered minerals: Implication for the relationship with friction coefficient. J. Geophys. Res. 2015, 120, 2212–2219. [Google Scholar] [CrossRef]
- Catti, M.; Ferraris, G.; Hull, S.; Pavese, A. Powder neutron diffraction study of 2M1 muscovite at room pressure and at 2 GPa. Eur. J. Mineral. 1994, 6, 171–178. [Google Scholar]
- Herrero, C.P.; Sanz, J. Short-range order of the Si, Al distribution in layer silicates. J. Phys. Chem. Solids 1991, 52, 1129–1135. [Google Scholar] [CrossRef]
- Palin, E.J.; Dove, M.T.; Redfern, S.A.T.; Ortega-Castro, J.; Sainz-Díaz, C.I.; Hernández-Laguna, A. Computer simulations of cations order-disorder in 2:1 dioctahedral phyllosilicates using cation-exchange potentials and Monte Carlo methods. Int. J. Quantum Chem. 2014, 114, 1257–1286. [Google Scholar] [CrossRef]
- Loewenstein, W.; Loewenstein, M.C.; Paulo, S. The distribution of aluminum in the tetrahedra of silicates and aluminates. Am. Mineral. 1954, 39, 92–96. [Google Scholar]
- Warren, M.C.; Dove, M.T.; Myers, E.R.; Bosenick, A.; Palin, E.J.; Sainz-Díaz, C.I.; Guiton, B.S.; Redfern, S.A.T. Monte Carlo methods for the study of cation ordering in minerals. Mineral. Mag. 2001, 65, 221–248. [Google Scholar] [CrossRef]
- Winkler, B.; Pickard, C.; Milman, V. Applicability of a quantum mechanical ‘virtual crystal approximation’ to study Al/Si-disorder. Chem. Phys. Lett. 2002, 362, 266–270. [Google Scholar] [CrossRef]
- Palin, E.J.; Dove, M.T.; Redfern, S.A.T.; Bosenick, A.; Sainz-Díaz, C.I.; Warren, M.C. Computational study of tetrahedral Al-Si ordering in muscovite. Phys. Chem. Miner. 2001, 28, 534–544. [Google Scholar] [CrossRef]
- Bosenick, A.; Dove, M.T.; Myers, E.R.; Palin, E.J.; Sainz-Díaz, C.I.; Guiton, B.S.; Warren, M.C.; Craig, M.S.; Redfern, S.A.T. Computational methods for the study of energies of cation distributions: applications to cation-ordering phase transitions and solid solutions. Mineral. Mag. 2001, 65, 193–219. [Google Scholar] [CrossRef]
- Rosso, K.M.; Rustad, J.R.; Bylaska, E.J. The Cs/K Exchange in Muscovite Interlayers: An Ab Initio Treatment. Clays Clay Miner. 2001, 49, 500–513. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Berghout, A.; Tunega, D.; Zaoui, A. Density Functional Theory (DFT) study of the hydration steps of Na+/Mg2+/Ca2+/Sr2+/Ba2+-exchanged montmorillonites. Clays Clay Miner. 2010, 58, 174–187. [Google Scholar] [CrossRef]
- Liao, T.; Sasaki, T.; Sun, Z.Q. The oxygen migration in the apatite-type lanthanum silicate with the cation substitution. Phys. Chem. Chem. Phys. 2013, 15, 17553–17559. [Google Scholar] [CrossRef] [PubMed]
- Kalita, J.M.; Wary, G. Estimation of band gap of muscovite mineral using thermoluminescence (TL) analysis. Phys. B Condens. Matter 2016, 485, 53–59. [Google Scholar] [CrossRef]
- Sham, L.J.; Schlüter, M. Density-Functional Theory of the Band Gap. Phys. Rev. B 1985, 32, 3883–3889. [Google Scholar] [CrossRef]
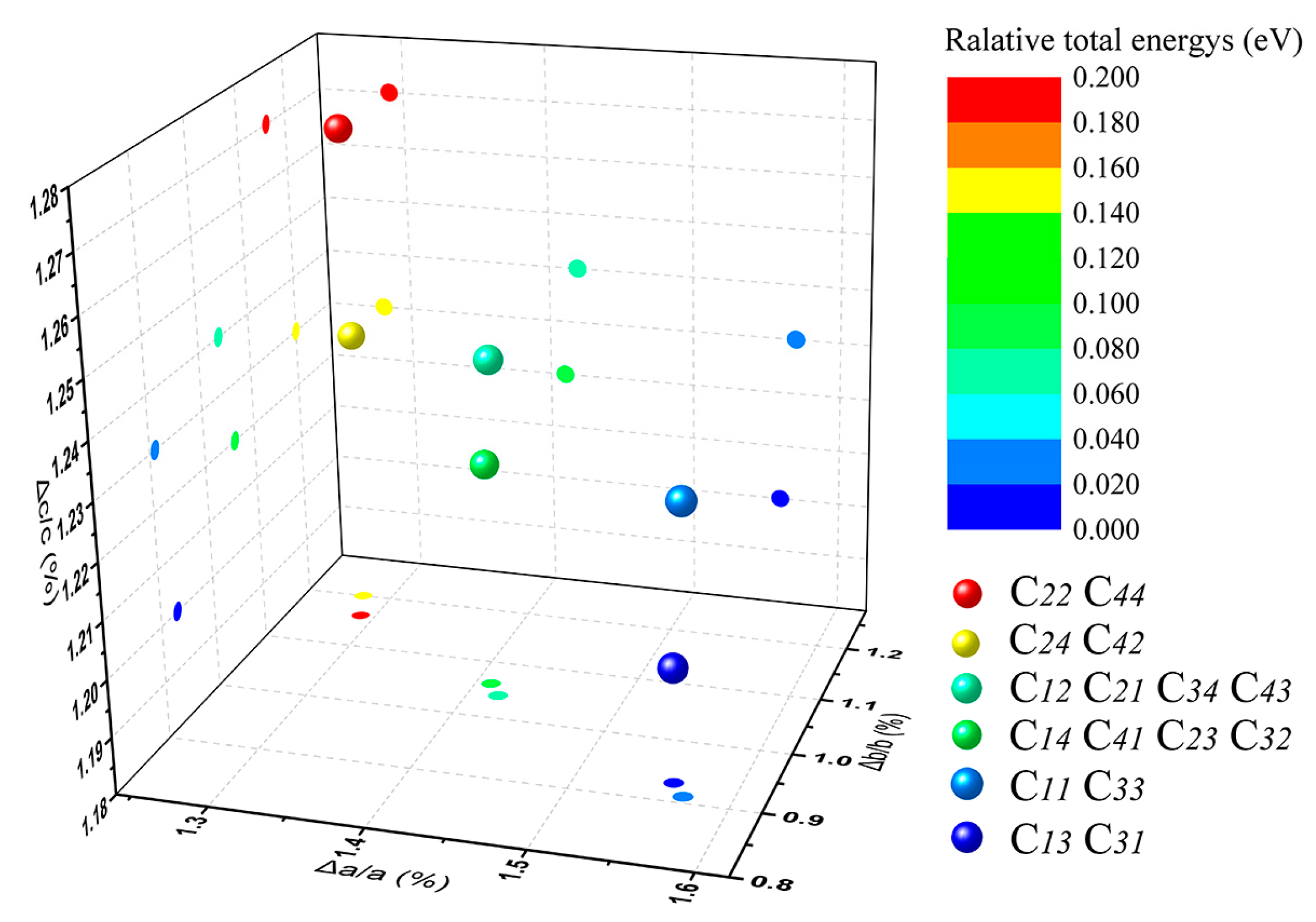
| CUL | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | E (eV) |
|---|---|---|---|---|---|---|---|
| Exp | 5.211 | 9.040 | 20.021 | 90.00 | 95.76 | 90.00 | - |
| C11 | 5.293 | 9.122 | 20.267 | 90.00 | 95.83 | 90.00 | 0.025 |
| C12 | 5.285 | 9.134 | 20.270 | 89.90 | 95.88 | 90.09 | 0.072 |
| C13 | 5.292 | 9.124 | 20.261 | 90.00 | 95.83 | 90.00 | 0 |
| C14 | 5.284 | 9.136 | 20.266 | 89.95 | 95.88 | 90.09 | 0.089 |
| C21 | 5.285 | 9.134 | 20.270 | 90.10 | 95.88 | 89.91 | 0.077 |
| C22 | 5.278 | 9.145 | 20.275 | 90.00 | 95.94 | 90.00 | 0.187 |
| C23 | 5.284 | 9.136 | 20.266 | 90.05 | 95.88 | 89.91 | 0.091 |
| C24 | 5.278 | 9.148 | 20.267 | 90.00 | 95.94 | 90.00 | 0.148 |
| C31 | 5.292 | 9.124 | 20.261 | 90.00 | 95.83 | 90.00 | 0 |
| C32 | 5.284 | 9.136 | 20.266 | 89.95 | 95.88 | 90.09 | 0.093 |
| C33 | 5.293 | 9.122 | 20.267 | 90.00 | 95.83 | 90.00 | 0.027 |
| C34 | 5.285 | 9.134 | 20.270 | 89.90 | 95.88 | 90.09 | 0.072 |
| C41 | 5.284 | 9.136 | 20.266 | 90.05 | 95.88 | 89.91 | 0.091 |
| C42 | 5.278 | 9.148 | 20.267 | 90.00 | 95.94 | 90.00 | 0.147 |
| C43 | 5.285 | 9.134 | 20.270 | 90.10 | 95.88 | 89.91 | 0.078 |
| C44 | 5.278 | 9.145 | 20.275 | 90.00 | 95.94 | 90.00 | 0.186 |
| Config | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | ES (eV) |
|---|---|---|---|---|---|---|---|
| Model | 10.584 | 9.124 | 20.261 | 90.00 | 95.83 | 90.00 | - |
| V[AlVI] | 10.543 | 9.124 | 20.358 | 90.01 | 95.73 | 90.00 | −1.228 |
| V[AlVI] | 10.553 | 9.130 | 20.376 | 90.01 | 95.73 | 90.00 | −0.344 |
| V[SiIV]1 | 10.576 | 9.143 | 20.416 | 90.00 | 95.74 | 90.00 | −0.434 |
| V[SiIV]2 | 10.571 | 9.145 | 20.417 | 90.00 | 95.77 | 90.01 | −0.519 |
| V[SiIV]3 | 10.570 | 9.147 | 20.415 | 89.97 | 95.73 | 90.03 | −0.340 |
| Site | V[SiIV]1 | V[SiIV]2 | V[SiIV]3 | V[AlIV] |
|---|---|---|---|---|
| O1 | 0.158 * | 0.090 | 0.184 * | 0.063 |
| O2 | 0.152 * | 0.189 * | 0.077 | 0.057 |
| O3 | 0.187 * | 0.197 * | 0.060 | 0.056 |
| O4 | 0.031 | 0.180 * | 0.054 | 0.115 * |
| O5 | −0.008 | 0.074 | 0.102 * | 0.157 * |
| O6 | 0.081 | 0.073 | 0.232 * | 0.131 * |
| (S*)2 | 2.34 × 10−4 | 4.82 × 10−5 | 2.88 × 10−3 | 3.00 × 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Q.; Zhang, Y.; Liu, T.; Huang, J.; Xue, N.; Shi, Q. Optimal Location of Vanadium in Muscovite and Its Geometrical and Electronic Properties by DFT Calculation. Minerals 2017, 7, 32. https://doi.org/10.3390/min7030032
Zheng Q, Zhang Y, Liu T, Huang J, Xue N, Shi Q. Optimal Location of Vanadium in Muscovite and Its Geometrical and Electronic Properties by DFT Calculation. Minerals. 2017; 7(3):32. https://doi.org/10.3390/min7030032
Chicago/Turabian StyleZheng, Qiushi, Yimin Zhang, Tao Liu, Jing Huang, Nannan Xue, and Qihua Shi. 2017. "Optimal Location of Vanadium in Muscovite and Its Geometrical and Electronic Properties by DFT Calculation" Minerals 7, no. 3: 32. https://doi.org/10.3390/min7030032
APA StyleZheng, Q., Zhang, Y., Liu, T., Huang, J., Xue, N., & Shi, Q. (2017). Optimal Location of Vanadium in Muscovite and Its Geometrical and Electronic Properties by DFT Calculation. Minerals, 7(3), 32. https://doi.org/10.3390/min7030032






