Strength Reduction of Coal Pillar after CO2 Sequestration in Abandoned Coal Mines
Abstract
:1. Introduction
2. Theoretical Model
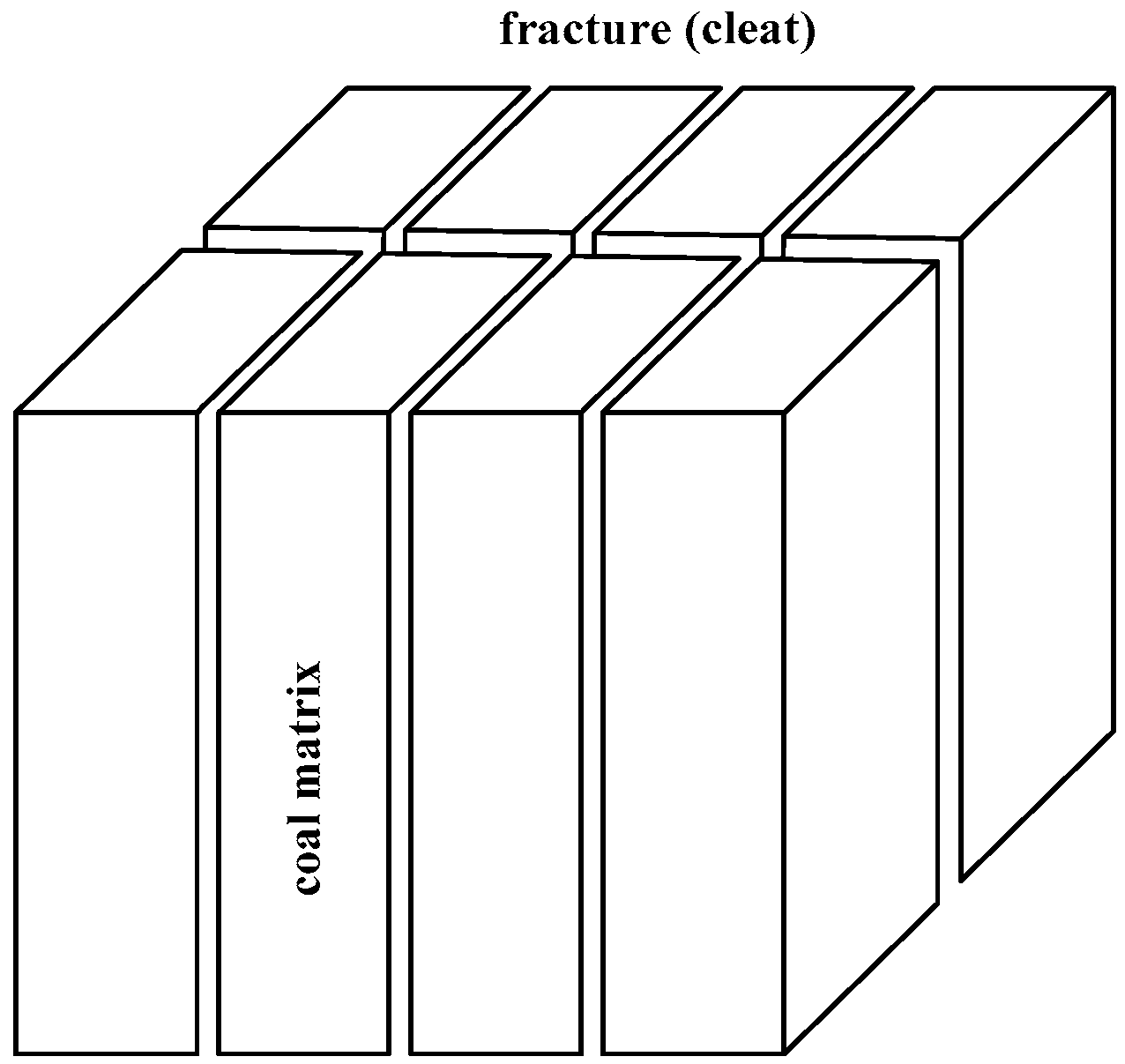
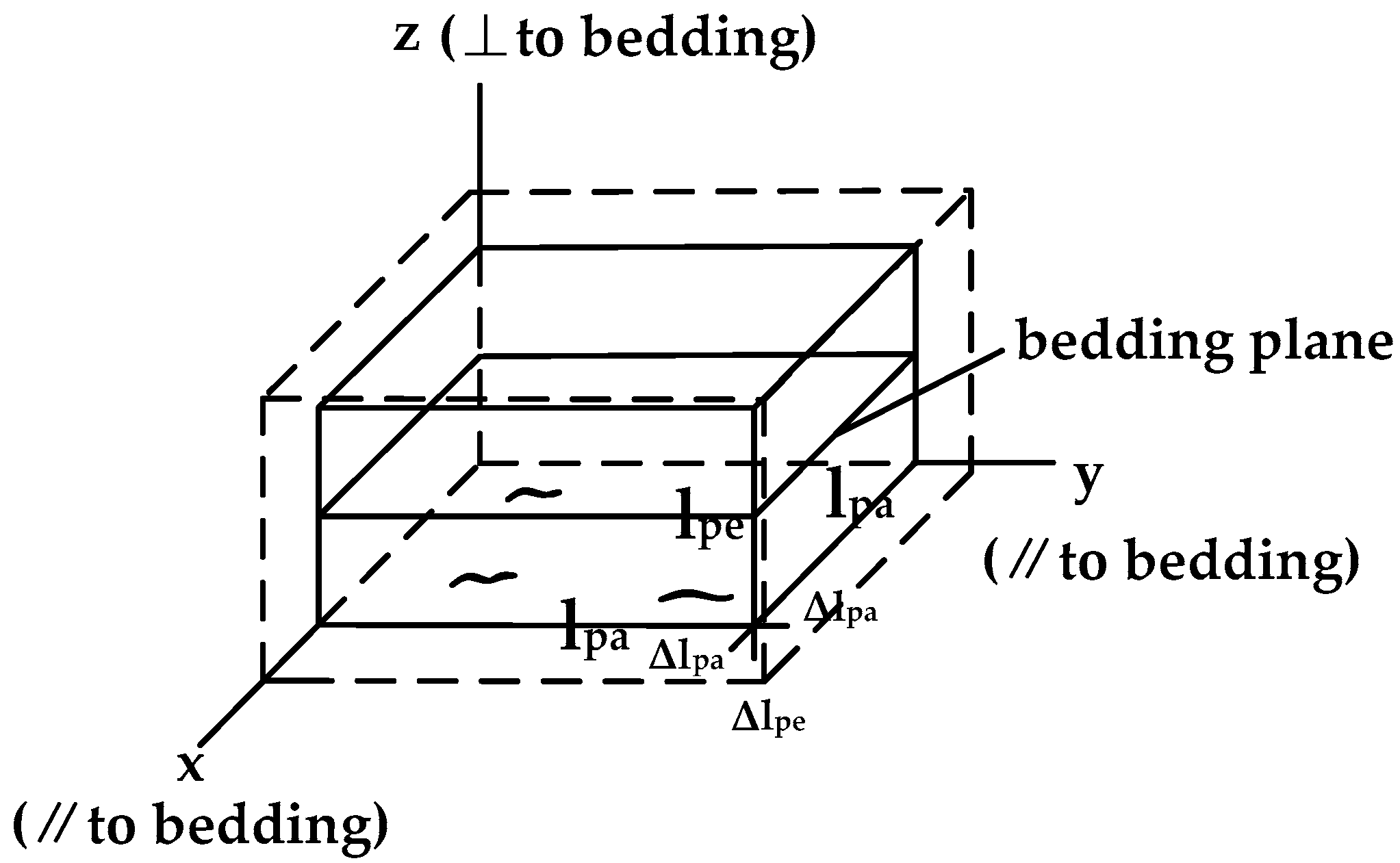
2.1. Adsorption-Induced Swelling Strain
2.2. Adsorption-Induced Stress under Uniaxial Conditions
2.3. Mechanical Strength Change after Gas Adsorption
3. Discussion
3.1. Swelling Strain and Swelling Stress
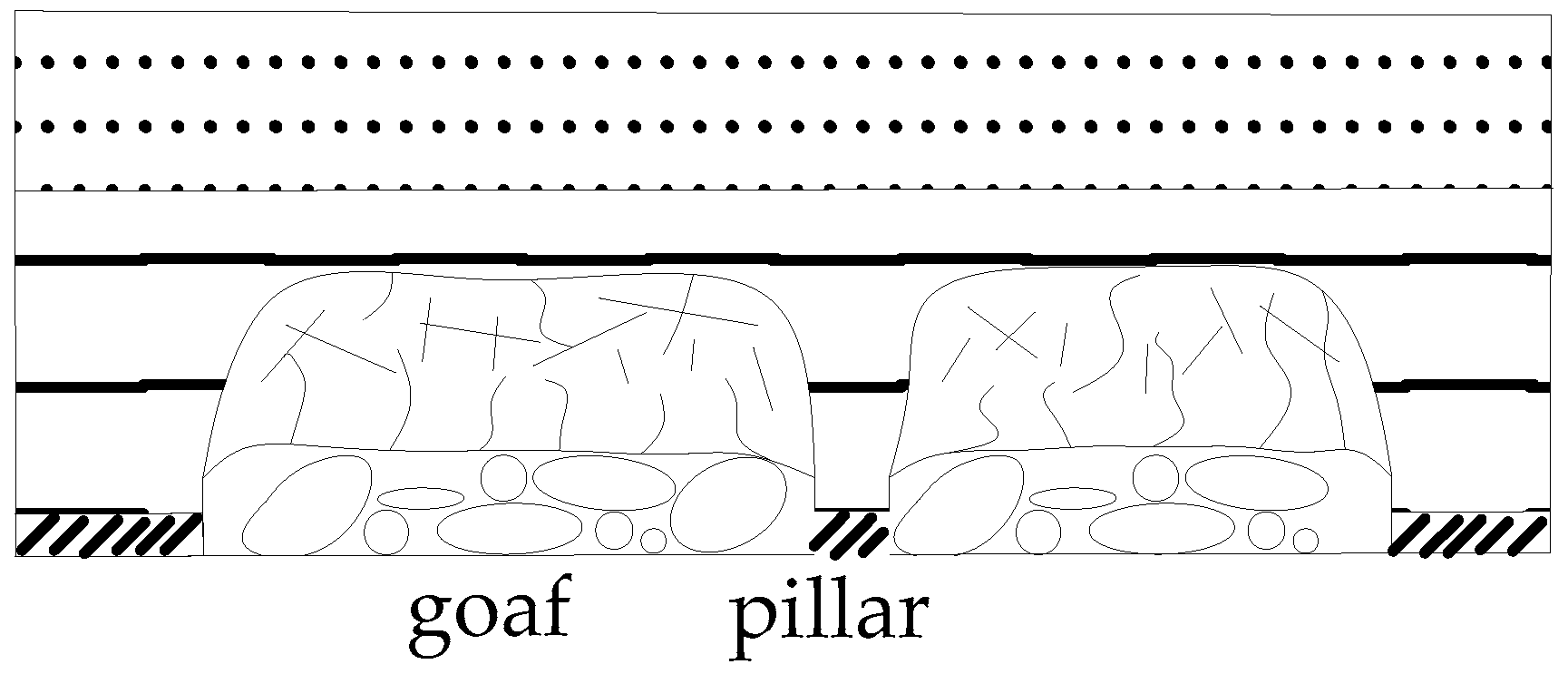
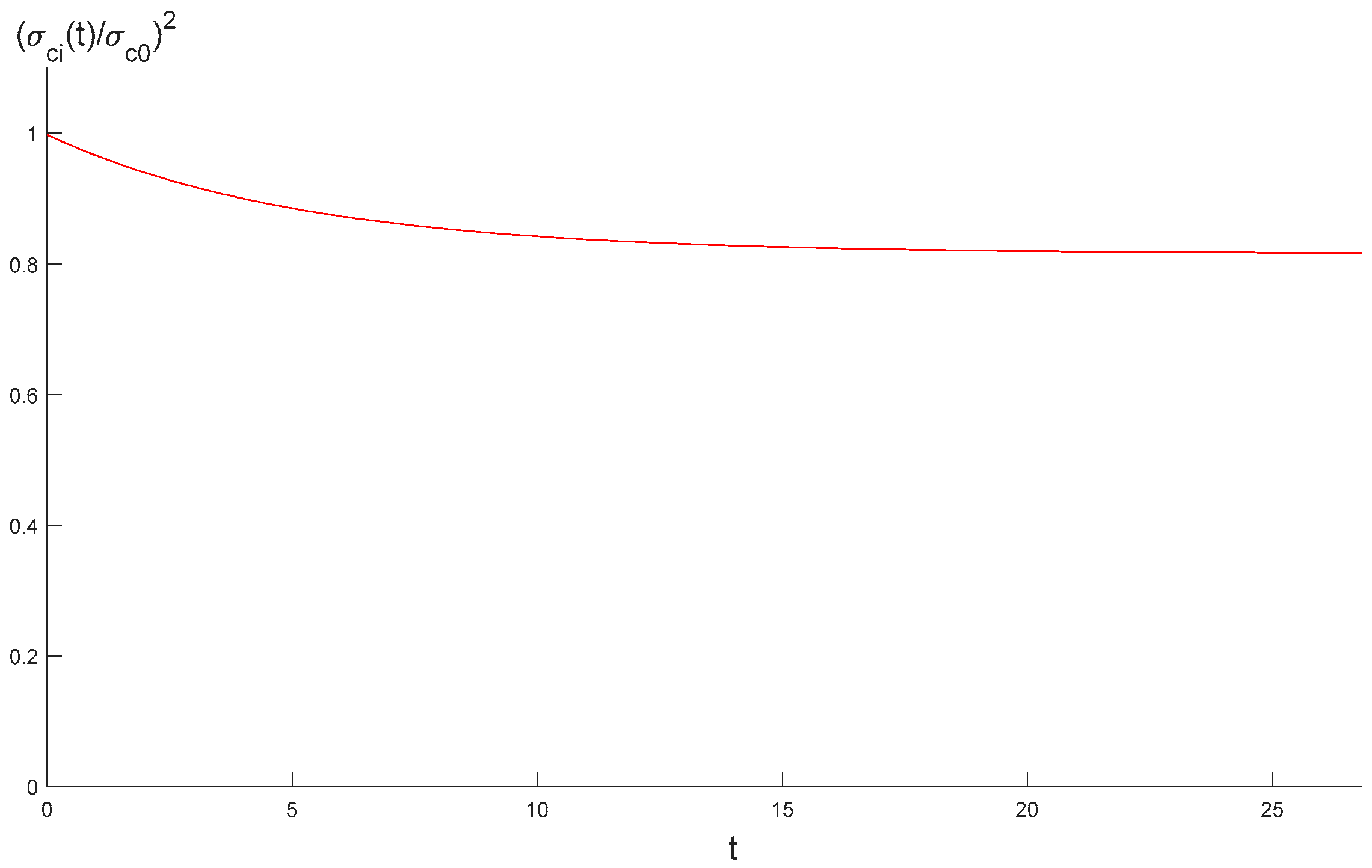
3.2. Stress and Strength Reduction
4. Conclusions
- There are a large number of coal mines that will be closed and some of them are located in deep formations in China. CO2 storage in abandoned coal mines could be a potential option for greenhouse gas disposal.
- The volume strain and swelling stress, as a function of time, and different loading pressure steps are deduced. Equation (15) is used to describe swelling stress considering coal has already had prior swelling deformation under the condition of step-by-step non-linear loading and a non-Langmuir isothermal model. The model presented in this paper is different from other models, in which only the initial state and the final equilibrium state are considered, and the incremental swelling process is neglected.
- A theoretical model based on linear swelling stress–strain work is proposed to calculate the reduction ratio of coal pillar strength under uniaxial conditions. This theoretical model can be used to describe strength reduction during adsorption under adsorption pressure loading step-by-step.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, F.; Zhou, H.; Lu, T.; Hu, D.W.; Sheng, Q.; Hu, Q.Z. Analysis of reservoir deformation and fluid transportation induced by injection of CO2 into saline aquifer: (I) Two-phase flow-reservoir coupling model. Rock Soil Mech. 2014, 35, 2549–2554. (In Chinese) [Google Scholar]
- Edenhofer, O. Mitigation of climate change IA models and WGIII: Lessons from IPCC AR5. In Proceedings of the 7th IAMC Meeting, Valencia, Spain, 23–25 October 2014.
- International Energy Agency (IEA). Four Energy Policies Can Keep the 2 °C Climate Goal Alive; International Energy Agency (IEA): Paris, France, 2013. [Google Scholar]
- Seomoon, H.; Lee, M.; Sung, W. Analysis of methane recovery through CO2-N2 mixed gas injection considering gas diffusion phenomenon in coal seam. Energy Explor. Exploit. 2016, 34, 661–675. [Google Scholar] [CrossRef]
- He, L.; Shen, P.; Liao, X.; Li, F.; Gao, Q.; Wang, Z. Potential evaluation of CO2 EOR and sequestration in Yanchang oilfield. J. Energy Inst. 2016, 89, 215–221. [Google Scholar] [CrossRef]
- Chareonsuppanimit, P.; Mohammad, S.A.; Robinson, R.L.; Gasem, K.A.M. High-pressure adsorption of gases on shales: Measurements and modeling. Int. J. Coal Geol. 2012, 95, 34–46. [Google Scholar] [CrossRef]
- Lu, Y.; Ao, X.; Tang, J.; Jia, Y.; Zhang, X.; Chen, Y. Swelling of shale in supercritical carbon dioxide. J. Nat. Gas Sci. Eng. 2016, 30, 268–275. [Google Scholar] [CrossRef]
- Day, S.; Fry, R.; Sakurovs, R.; Weir, S. Swelling of coals by supercritical gases and its relationship to sorption. Energy Fuels 2010, 24, 2777–2783. [Google Scholar] [CrossRef]
- Piessens, K.; Dusar, M. Feasibility of CO2 sequestration in abandoned coal mines in Belgium. Geol. Belg. 2004, 7, 168–180. [Google Scholar]
- Piessens, K.; Dusar, M. Integration of CO2 sequestration and CO2 geothermics in energy systems for abandoned coal mines. Geol. Belg. 2004, 7, 181–189. [Google Scholar]
- Van Tongeren, P.; Dreesen, R. Residual space volumes in abandoned coal mines of the Belgian Campine basin and possibilities for use. Geol. Belg. 2004, 7, 157–164. [Google Scholar]
- Jalili, P.; Saydam, S.; Cinar, Y. CO2 storage in abandoned coal mines. In Proceedings of the 2011 Underground Coal Operators’ Conference, Beijing, China, 8–9 January 2011.
- Van Krevelen, D.W. Coal-Typology, Chemistry, Physics, Constitution; Elsevier: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Sanada, Y.; Honda, H. Swelling equilibrium of coal by pyridine at 25 degrees C. Fuel 1966, 45, 295. [Google Scholar]
- Solomon, P.R.; Fletcher, T.H. Impact of coal pyrolysis on combustion. Symp. (Int.) Combust. 1994, 25, 463–474. [Google Scholar]
- Walker, P.L.; Verma, S.K.; Rivera-Utrilla, J.; Khan, M.R. A direct measurement of expansion in coals and macerais induced by carbon dioxide and methanol. Fuel 1988, 67, 719–726. [Google Scholar] [CrossRef]
- Karacan, C.Ö. Swelling-induced volumetric strains internal to a stressed coal associated with CO2 sorption. Int. J. Coal Geol. 2007, 72, 209–220. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Modelling of anisotropic coal swelling and its impact on permeability behaviour for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 2011, 85, 257–267. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, D.; Zhao, Y.; Cai, T. Study on microstructural changes of coal after methane adsorption. J. Nat. Gas Sci. Eng. 2016, 30, 28–37. [Google Scholar] [CrossRef]
- Shovkun, I.; Espinoza, D.N.; Ramos, M.J. Coupled reservoir simulation of geomechanics and fluid flow in organic-rich rocks: Impact of gas desorption and stress changes on permeability during depletion. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TE, USA, 26–29 June 2016.
- Heller, R.; Zoback, M. Adsorption of methane and carbon dioxide on gas shale and pure mineral samples. J. Unconv. Oil Gas Resour. 2014, 8, 14–24. [Google Scholar] [CrossRef]
- Hol, S.; Spiers, C.J. Competition between adsorption-induced swelling and elastic compression of coal at CO2 pressures up to 100 MPa. J. Mech. Phys. Solids 2012, 60, 1862–1882. [Google Scholar] [CrossRef]
- Zang, J.; Wang, K. Gas sorption-induced coal swelling kinetics and its effects on coal permeability evolution: Model development and analysis. Fuel 2017, 189, 164–177. [Google Scholar] [CrossRef]
- Feng, R.; Harpalani, S.; Pandey, R. Laboratory measurement of stress-dependent coal permeability using pulse-decay technique and flow modeling with gas depletion. Fuel 2016, 177, 76–86. [Google Scholar] [CrossRef]
- Connell, L.D. A new interpretation of the response of coal permeability to changes in pore pressure, stress and matrix shrinkage. Int. J. Coal Geol. 2016, 162, 169–182. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Tu, S.; Tu, H.; Wang, C. A study of directional permeability and gas injection to flush coal seam gas testing apparatus and method. Transp. Porous Media 2016, 111, 573–589. [Google Scholar] [CrossRef]
- Connell, L.D.; Mazumder, S.; Sander, R.; Camilleri, M.; Pan, Z.; Heryanto, D. Laboratory characterisation of coal matrix shrinkage, cleat compressibility and the geomechanical properties determining reservoir permeability. Fuel 2016, 165, 499–512. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Pan, Z.; Connell, L.D.; Chen, Z.; Qu, H. Impact of coal matrix strains on the evolution of permeability. Fuel 2017, 189, 270–283. [Google Scholar] [CrossRef]
- Jasinge, D.; Ranjith, P.G.; Choi, X.; Fernando, J. Investigation of the influence of coal swelling on permeability characteristics using natural brown coal and reconstituted brown coal specimens. Energy 2012, 39, 303–309. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Perera, M.S.A. A new triaxial apparatus to study the mechanical and fluid flow aspects of carbon dioxide sequestration in geological formations. Fuel 2011, 90, 2751–2759. [Google Scholar] [CrossRef]
- Verma, A.K.; Sirvaiya, A. Comparative analysis of intelligent models for prediction of Langmuir constants for CO2 adsorption of Gondwana coals in India. Geomech. Geophys. Geo Energy Geo Resour. 2016, 2, 97–109. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Jasinge, D.; Choi, S.K.; Mehic, M.; Shannon, B. The effect of CO2 saturation on mechanical properties of Australian black coal using acoustic emission. Fuel 2010, 89, 2110–2117. [Google Scholar] [CrossRef]
- Viete, D.R.; Ranjith, P.G. The mechanical behaviour of coal with respect to CO2 sequestration in deep coal seams. Fuel 2007, 86, 2667–2671. [Google Scholar] [CrossRef]
- Vishal, V.; Ranjith, P.G.; Singh, T.N. An experimental investigation on behaviour of coal under fluid saturation, using acoustic emission. J. Nat. Gas Sci. Eng. 2015, 22, 428–436. [Google Scholar] [CrossRef]
- Myers, A.L. Thermodynamics of adsorption in porous materials. AIChE J. 2002, 48, 145–160. [Google Scholar] [CrossRef]
- Myers, A.L.; Monson, P.A. Adsorption in porous materials at high pressure: Theory and experiment. Langmuir 2002, 18, 10261–10273. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. A theoretical model for gas adsorption-induced coal swelling. Int. J. Coal Geol. 2007, 69, 243–252. [Google Scholar] [CrossRef]
- Hol, S.; Peach, C.J.; Spiers, C.J. Effect of 3-D stress state on adsorption of CO2 by coal. Int. J. Coal Geol. 2012, 93, 1–15. [Google Scholar] [CrossRef]
- Liu, J.; Spiers, C.J.; Peach, C.J.; Vidal-Gilbert, S. Effect of lithostatic stress on methane sorption by coal: Theory vs. experiment and implications for predicting in-situ coalbed methane content. Int. J. Coal Geol. 2016, 167, 48–64. [Google Scholar] [CrossRef]
- Hol, S.; Gensterblum, Y.; Massarotto, P. Sorption and changes in bulk modulus of coal—Experimental evidence and governing mechanisms for CBM and ECBM applications. Int. J. Coal Geol. 2014, 128, 119–133. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Perera, M.S.A. Effects of cleat performance on strength reduction of coal in CO2 sequestration. Energy 2012, 45, 1069–1075. [Google Scholar] [CrossRef]
- Perera, M.S.A.; Ranjith, P.G.; Viete, D.R. Effects of gaseous and super-critical carbon dioxide saturation on the mechanical properties of bituminous coal from the Southern Sydney Basin. Appl. Energy 2013, 110, 73–81. [Google Scholar] [CrossRef]
- Wang, S.; Hou, G.; Zhang, M.; Sun, Q. Analysis of the visible fracture system of coalseam in Chengzhuang Coalmine of Jincheng City, Shanxi Province. Chin. Sci. Bull. 2005, 50, 45–51. [Google Scholar] [CrossRef]
- Liu, S.; Sang, S.; Liu, H.; Zhu, Q. Growth characteristics and genetic types of pores and fractures in a high-rank coal reservoir of the southern Qinshui basin. Ore Geol. Rev. 2015, 64, 140–151. [Google Scholar] [CrossRef]
- Staib, G.; Sakurovs, R.; Gray, E.M.A. Kinetics of coal swelling in gases: Influence of gas pressure, gas type and coal type. Int. J. Coal Geol. 2014, 132, 117–122. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics; John Wiley & Sons: Hoboken, NY, USA, 1980. [Google Scholar]
- Scherer, G.W. Dilatation of porous glass. J. Am. Ceram. Soc. 1986, 69, 473–480. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J.; Quenard, D.A. Modelling drying shrinkage in reconstructed porous materials: Application to porous Vycor glass. Model. Simul. Mater. Sci. Eng. 1998, 6, 211. [Google Scholar] [CrossRef]
- Hu, S.; Wang, E.; Li, X.; Bai, B. Effects of gas adsorption on mechanical properties and erosion mechanism of coal. J. Nat. Gas Sci. Eng. 2016, 30, 531–538. [Google Scholar] [CrossRef]
- Hagin, P.N.; Zoback, M.D. Laboratory studies of the compressibility and permeability of low-rank coal samples from the Powder River Basin, Wyoming, USA. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010.
- Yang, Y.; Zoback, M.D. The effects of gas adsorption on swelling, visco-plastic creep and permeability of sub-bituminous coal. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011.
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces; Science Press: Beijing, China, 1984. (In Chinese) [Google Scholar]
- Hol, S.; Spiers, C.J.; Peach, C.J. Microfracturing of coal due to interaction with CO2 under unconfined conditions. Fuel 2012, 97, 569–584. [Google Scholar] [CrossRef]
- Wang, G.X.; Massarotto, P.; Rudolph, V. An improved permeability model of coal for coalbed methane recovery and CO2 geosequestration. Int. J. Coal Geol. 2009, 77, 127–136. [Google Scholar] [CrossRef]
- Wu, S.Y.; Zhao, W. Analysis of effective stress in adsorbed methane-coal system. Chin. J. Rock Mech. Eng. 2005, 24, 1674–1678. (In Chinese) [Google Scholar]
- Bai, B.; Li, X.C.; Liu, Y.F.; Fang, Z.M.; Wang, W. Preliminary theoretical study on impact on coal caused by interactions between CO2 and coal. Rock Soil Mech. 2007, 28, 823–826. (In Chinese) [Google Scholar]
- Lin, W. Gas Sorption and the Consequent Volumetric and Permeability Change of Coal. Ph.D. Thesis, Stanford University, Stanford, CA, USA, March 2010. [Google Scholar]
- Yu, W.; Al-Shalabi, E.W.; Sepehrnoori, K. A sensitivity study of potential CO2 injection for enhanced gas recovery in Barnett shale reservoirs. In Proceedings of the SPE Unconventional Resources Conference, The Woodlands, TX, USA, 1–3 April 2014.
- Chikatamarla, L.; Cui, X.; Bustin, R.M. Implications of volumetric swelling/shrinkage of coal in sequestration of acid gases. In Proceedings of the International Coalbed Methane Symposium, Tuscaloosa, AL, USA, 3–7 May 2004.
- Robertson, E.P.; Christiansen, R.L. Modeling laboratory permeability in coal using sorption-induced strain data. SPE Reserv. Eval. Eng. 2007, 10, 260–269. [Google Scholar] [CrossRef]
- Sing, K.S.W. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Vandamme, M.; Pereira, J.M.; Dangla, P.; Vidal-Gilbert, S. Measurement and modeling of adsorptive-poromechanical properties of bituminous coal cores exposed to CO2: Adsorption, swelling strains, swelling stresses and impact on fracture permeability. Int. J. Coal Geol. 2014, 134, 80–95. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Vandamme, M.; Dangla, P.; Pereira, J.M.; Vidal-Gilbert, S. Adsorptive-mechanical properties of reconstituted granular coal: Experimental characterization and poromechanical modeling. Int. J. Coal Geol. 2016, 162, 158–168. [Google Scholar] [CrossRef]
- Liu, H.H.; Rutqvist, J. A new coal-permeability model: Internal swelling stress and fracture-matrix interaction. Transp. Porous Media 2010, 82, 157–171. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Pereira, J.M.; Vandamme, M.; Dangla, P.; Vidal-Gilbert, S. Desorption-induced shear failure of coal bed seams during gas depletion. Int. J. Coal Geol. 2015, 137, 142–151. [Google Scholar] [CrossRef]
- Wang, S.; Elsworth, D.; Liu, J. Permeability evolution during progressive deformation of intact coal and implications for instability in underground coal seams. Int. J. Rock Mech. Min. Sci. 2013, 58, 34–45. [Google Scholar] [CrossRef]
- Melnichenko, Y.B.; He, L.; Sakurovs, R.; Kholodenko, A.L.; Blach, T.; Mastalerz, M.; Andrzej, P.; Radliński, A.; Cheng, G.; Mildner, D.F.R. Accessibility of pores in coal to methane and carbon dioxide. Fuel 2012, 91, 200–208. [Google Scholar] [CrossRef]

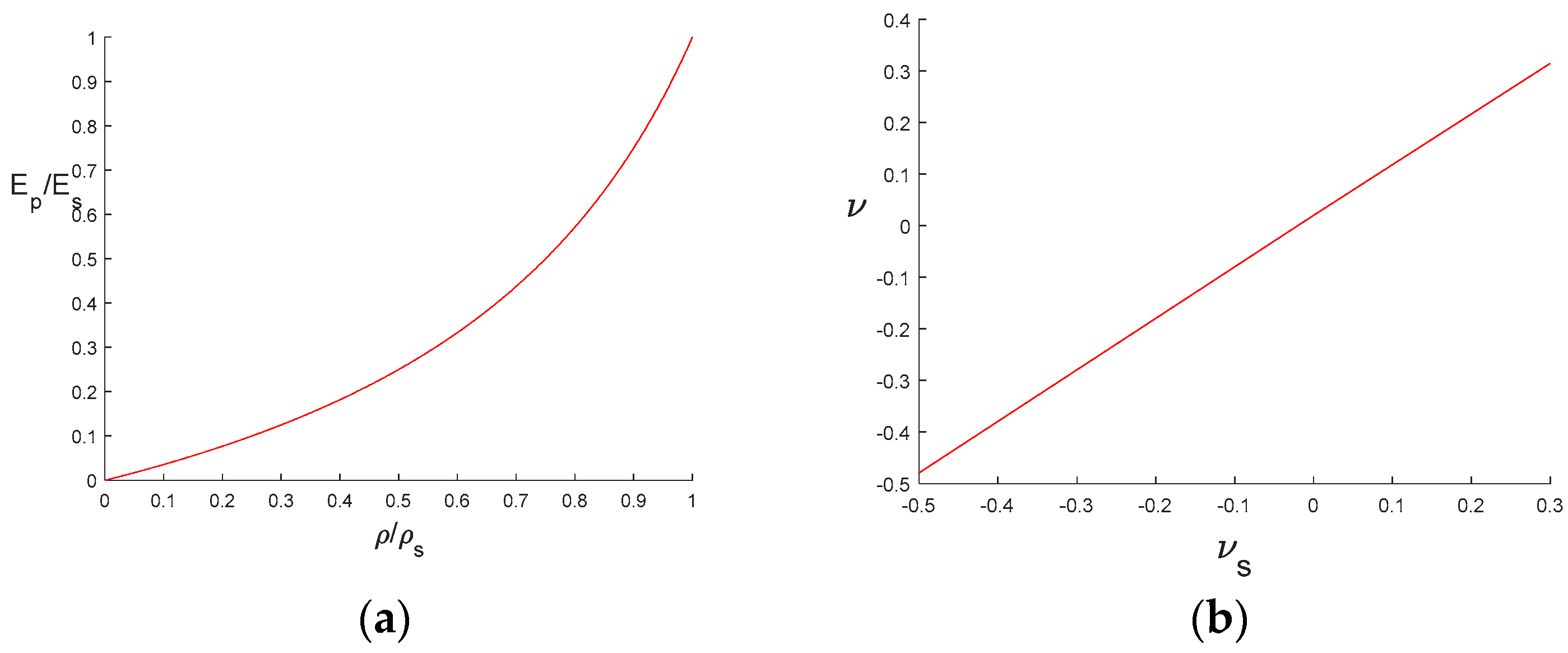


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Q.; Liu, X.; Wang, E.; Wang, S. Strength Reduction of Coal Pillar after CO2 Sequestration in Abandoned Coal Mines. Minerals 2017, 7, 26. https://doi.org/10.3390/min7020026
Du Q, Liu X, Wang E, Wang S. Strength Reduction of Coal Pillar after CO2 Sequestration in Abandoned Coal Mines. Minerals. 2017; 7(2):26. https://doi.org/10.3390/min7020026
Chicago/Turabian StyleDu, Qiuhao, Xiaoli Liu, Enzhi Wang, and Sijing Wang. 2017. "Strength Reduction of Coal Pillar after CO2 Sequestration in Abandoned Coal Mines" Minerals 7, no. 2: 26. https://doi.org/10.3390/min7020026
APA StyleDu, Q., Liu, X., Wang, E., & Wang, S. (2017). Strength Reduction of Coal Pillar after CO2 Sequestration in Abandoned Coal Mines. Minerals, 7(2), 26. https://doi.org/10.3390/min7020026






