Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data
Abstract
:1. Introduction
2. Principle of CT Scanning
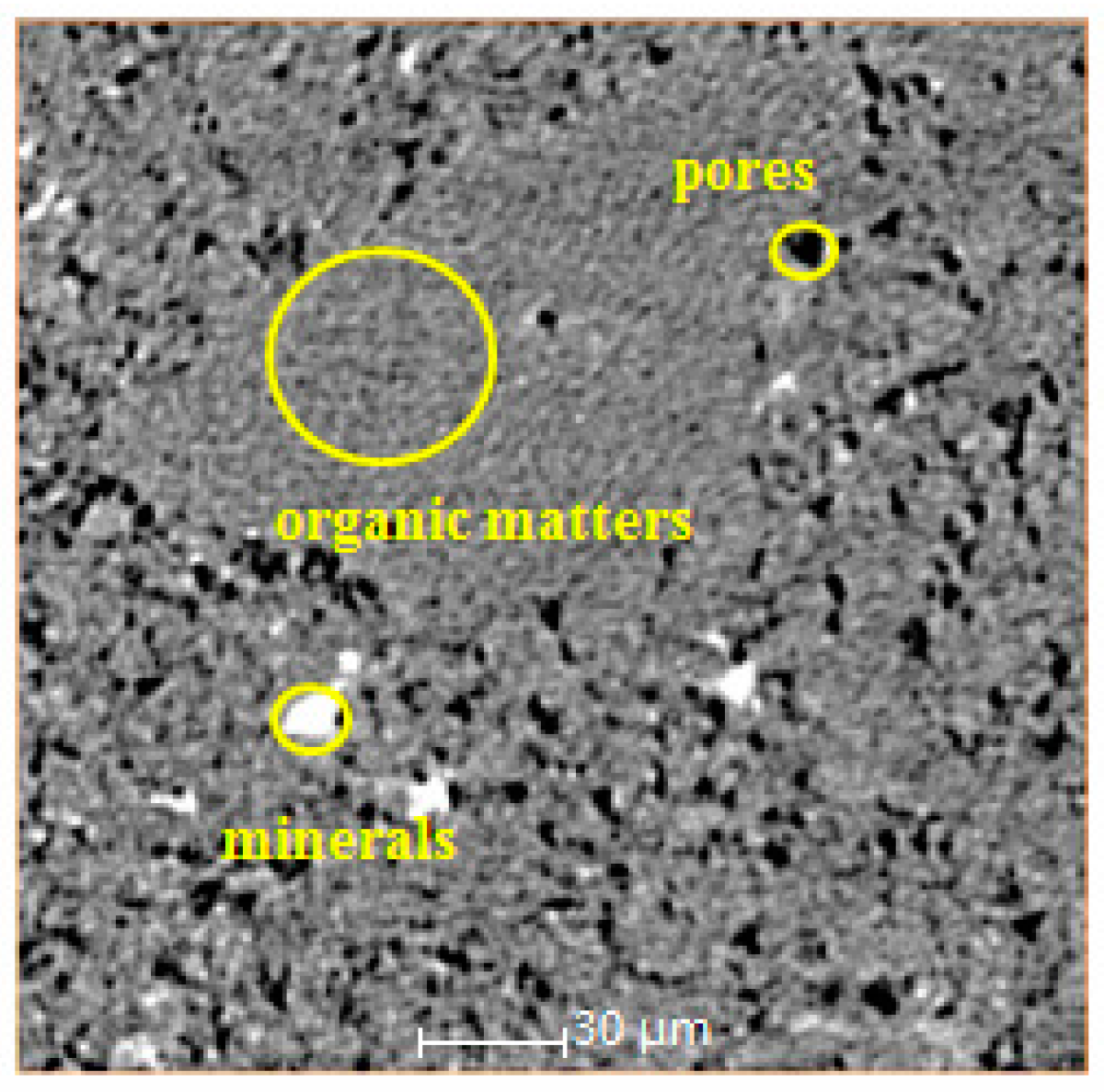
3. Coal Sample Processing and CT Scanning
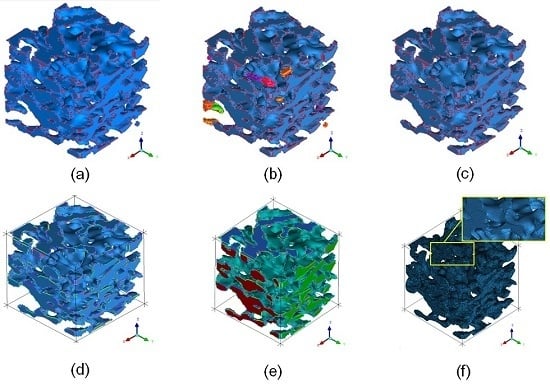
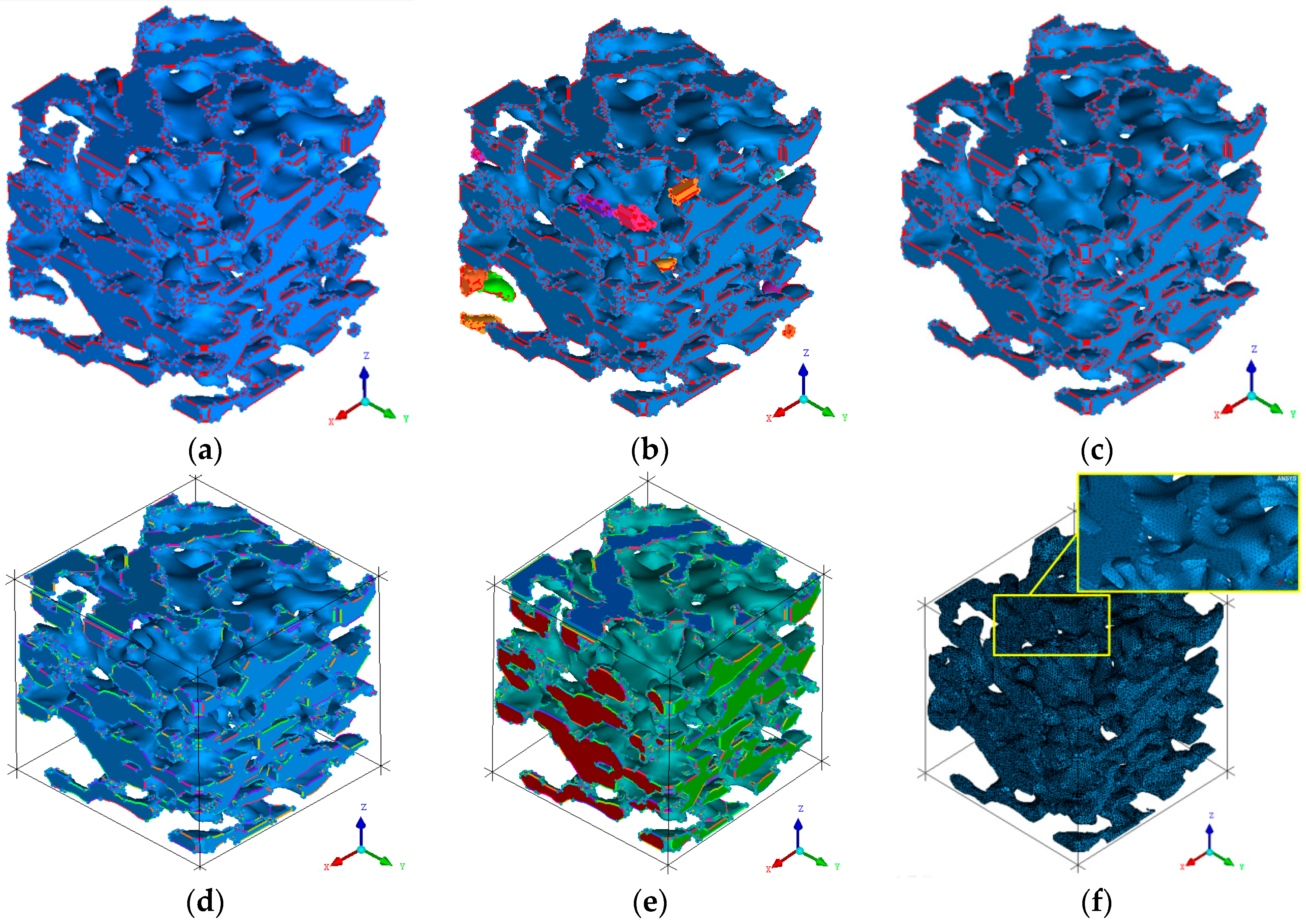
4. Visualization of the 3D Reconstruction of Coal Sample
5. Construction and Optimization of the Model of Micro-Pore Structure of Coal
6. Simulation on the Seepage Characteristics of Low-Pressure Water in Coal Micro-Pore Structure Model
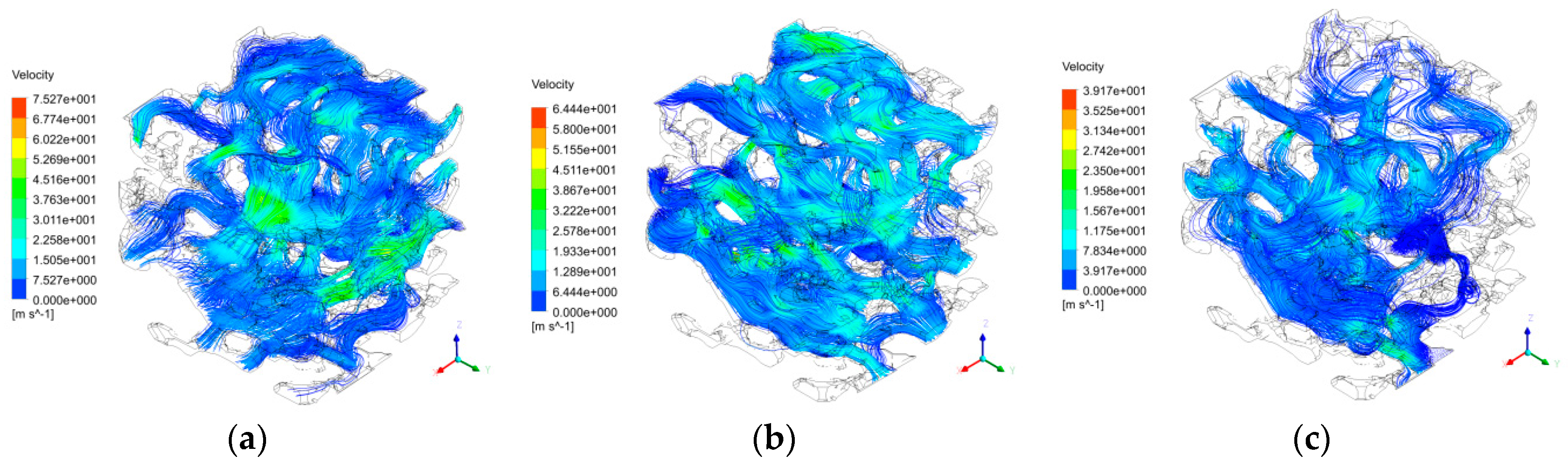
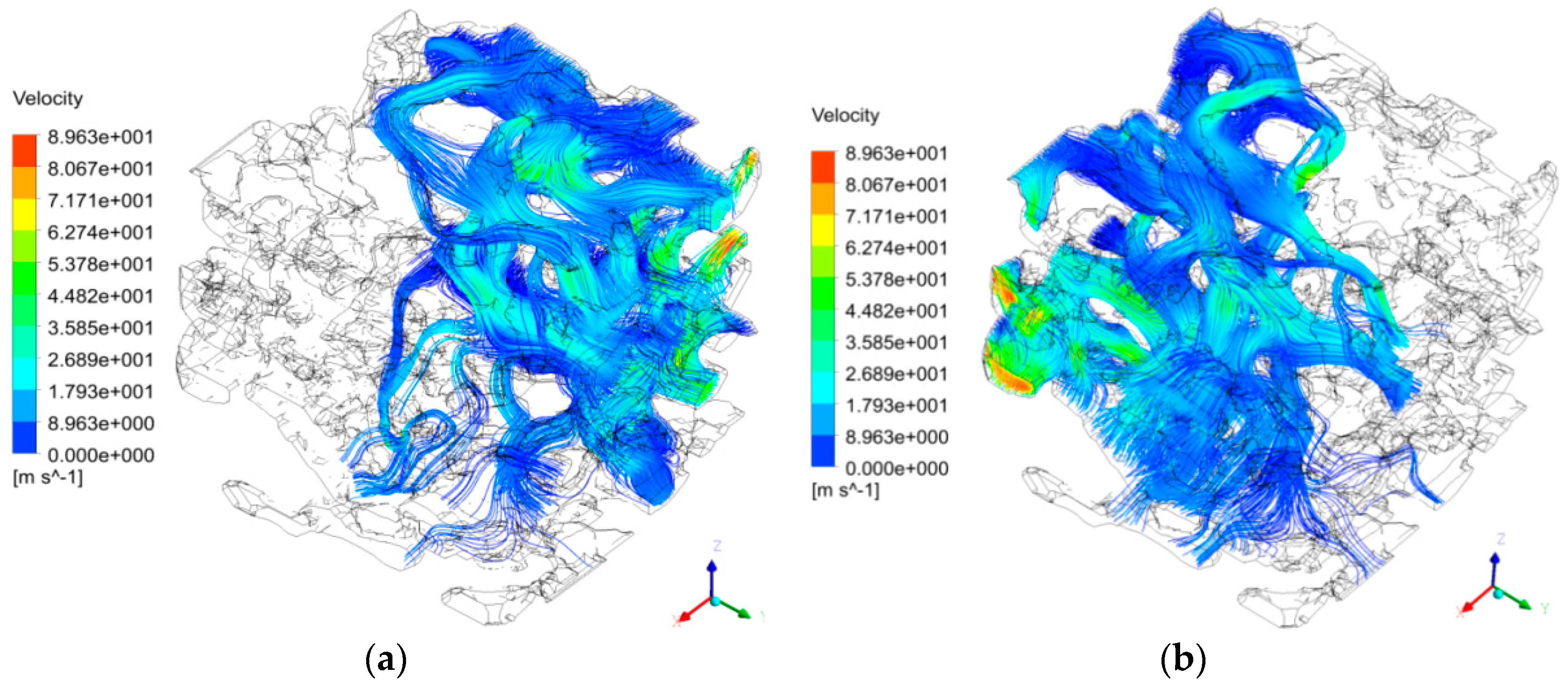
6.1. Numerical Simulations on Single-Channel Seepage Characteristics Along the X, Y, and Z Directions
- (1)
- In the maximum pore-connected cluster, although all the pores were connected with each other, the seepage of low-pressure water was observed in only a few pores. The seepage of low-pressure water firstly selected the paths with large pore radii, short paths, and shorter distances from the outlet.
- (2)
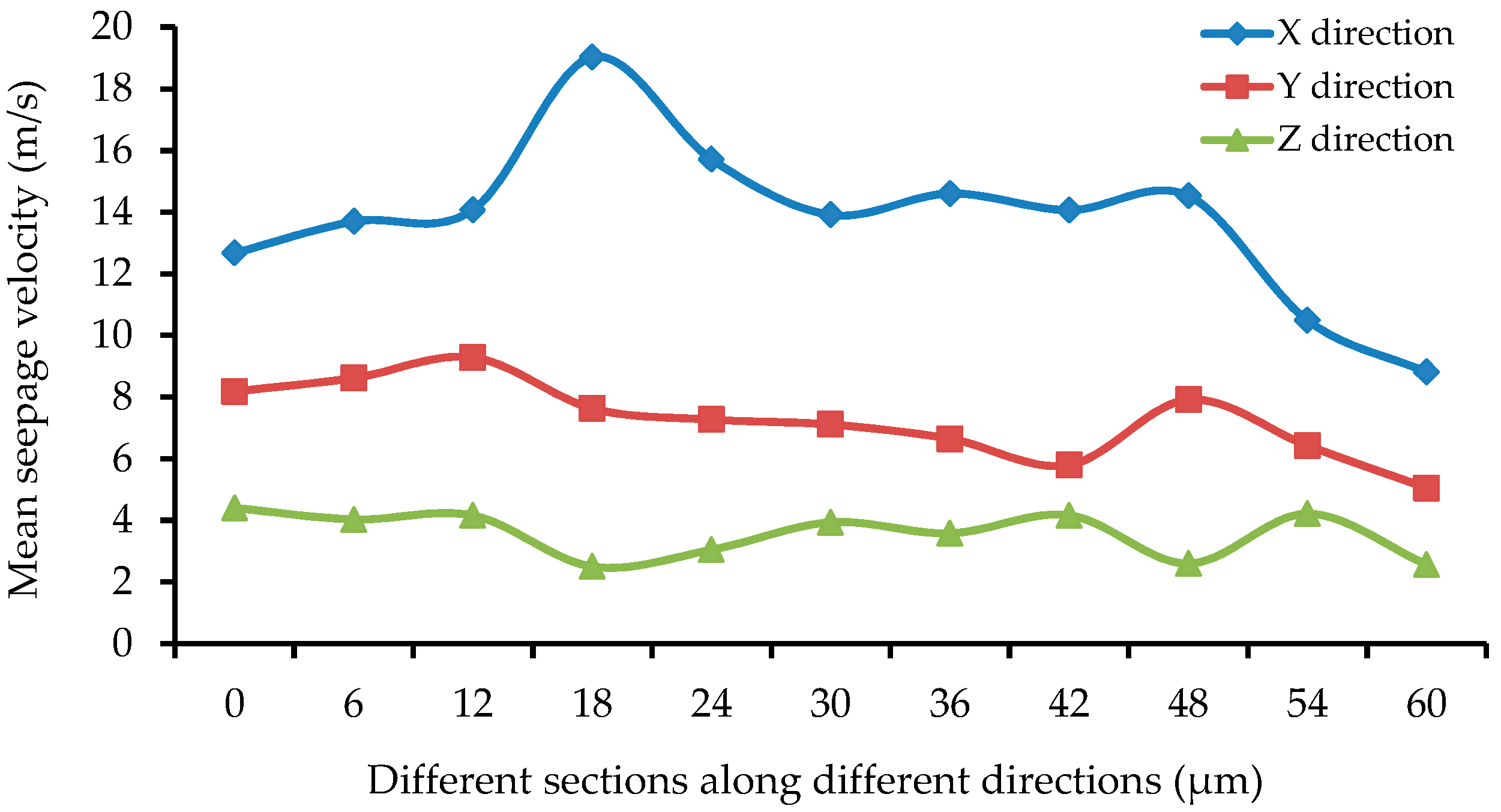
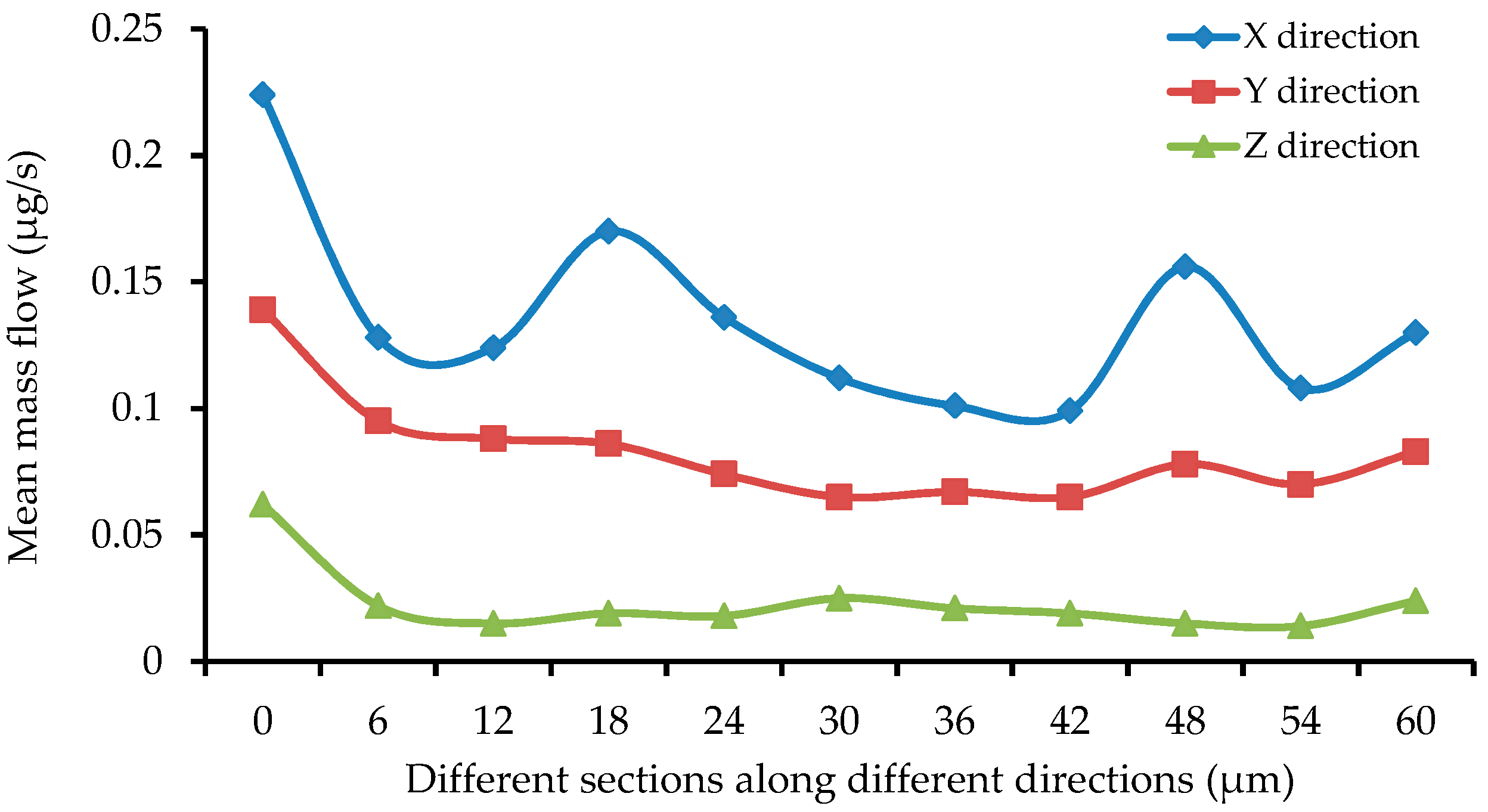
- In terms of the seepage in a single pore channel, the seepage velocity of low-pressure water decreased in the direction from the pore center to pore wall until it became zero. In terms of the whole micro-pore structure, the maximum seepage velocity appeared in the center region where water seepage was fully developed. The maximum velocities of the single-channel water seepage in the X and Y directions were up to 75.3 and 64.4 m/s, respectively; in the Z direction, in spite of the gravity effect, the maximum seepage velocity still reached 39.2 m/s. Overall, at the micro-scale, the seepage velocity of low-pressure water in a single-channel was relatively large, with the minimum value near the pore wall where the low-pressure water passed through.
- (3)
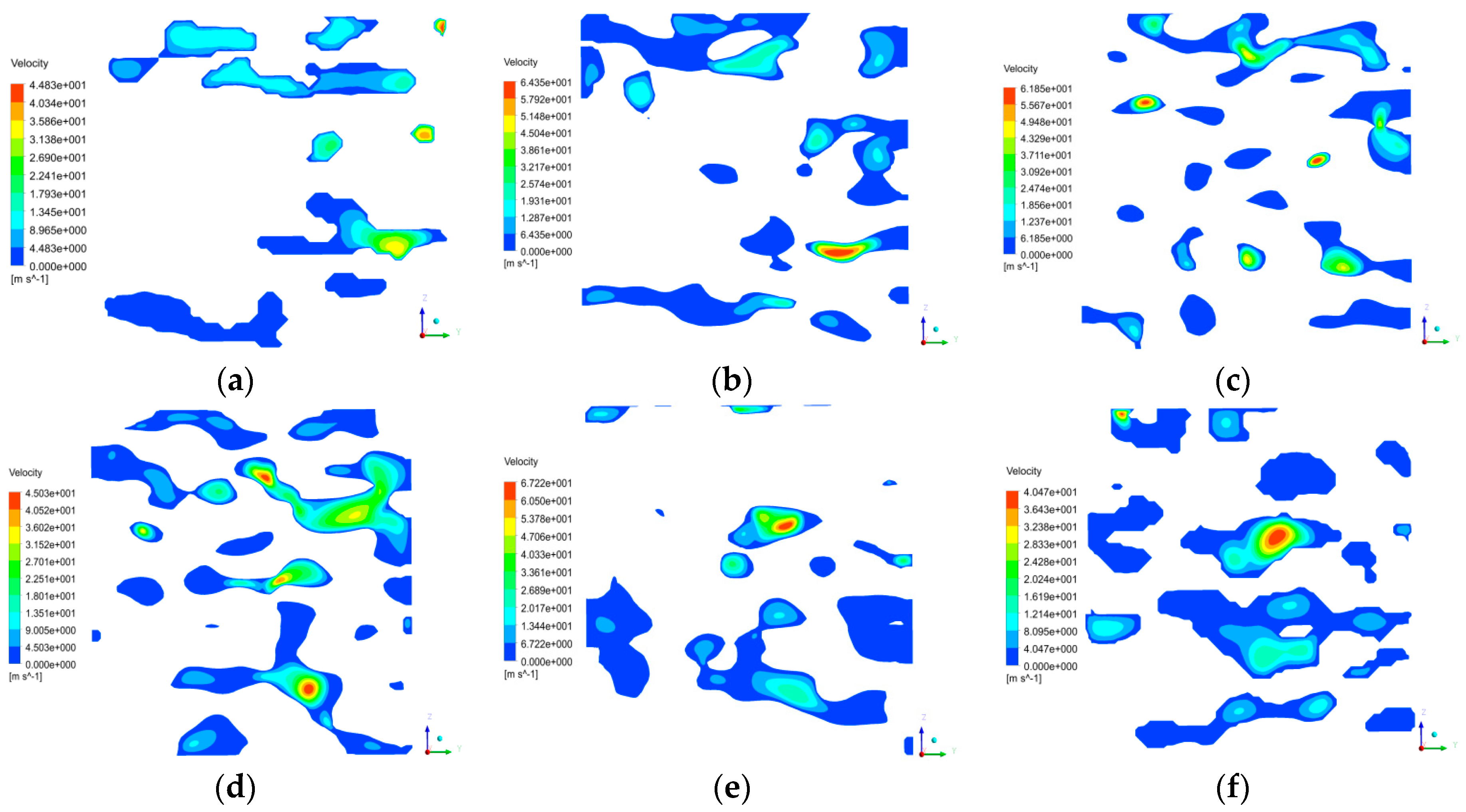
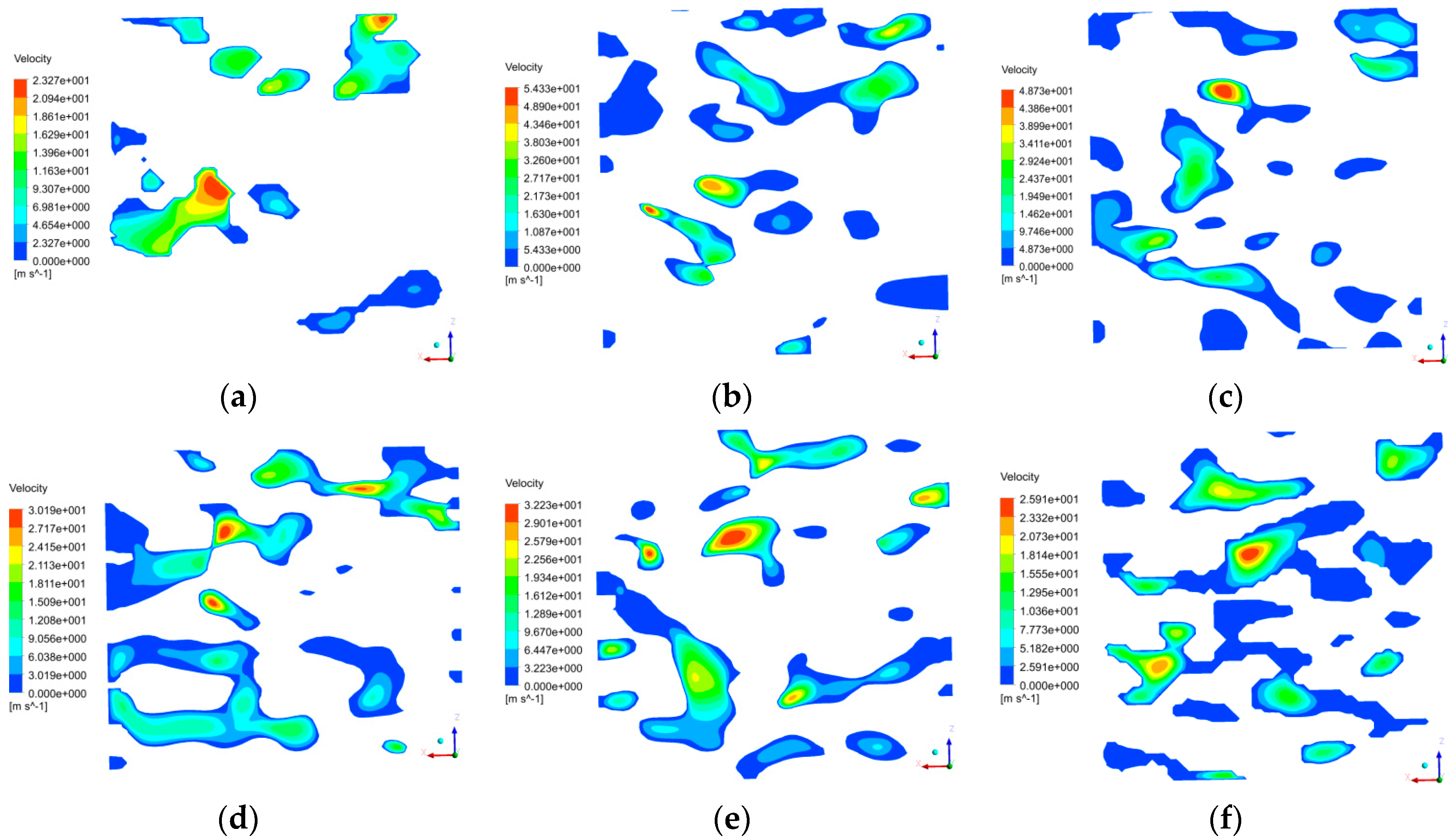
- At different sections, the maximum seepage velocity appeared at the center of the small pore channel of the section where the water flowed. Moreover, the water seepage velocity increased as the pore radius and bending degree decreased.
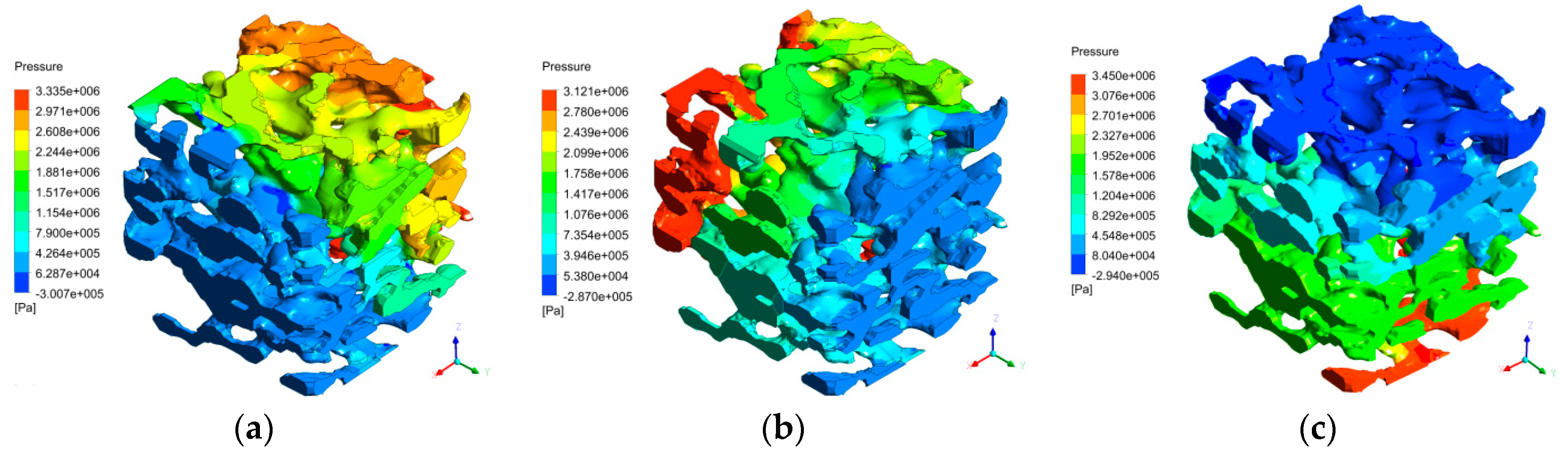
6.2. Pressure, Seepage Velocity, and Mass Flow Rate of Single-Channel Seepage at Different Sections
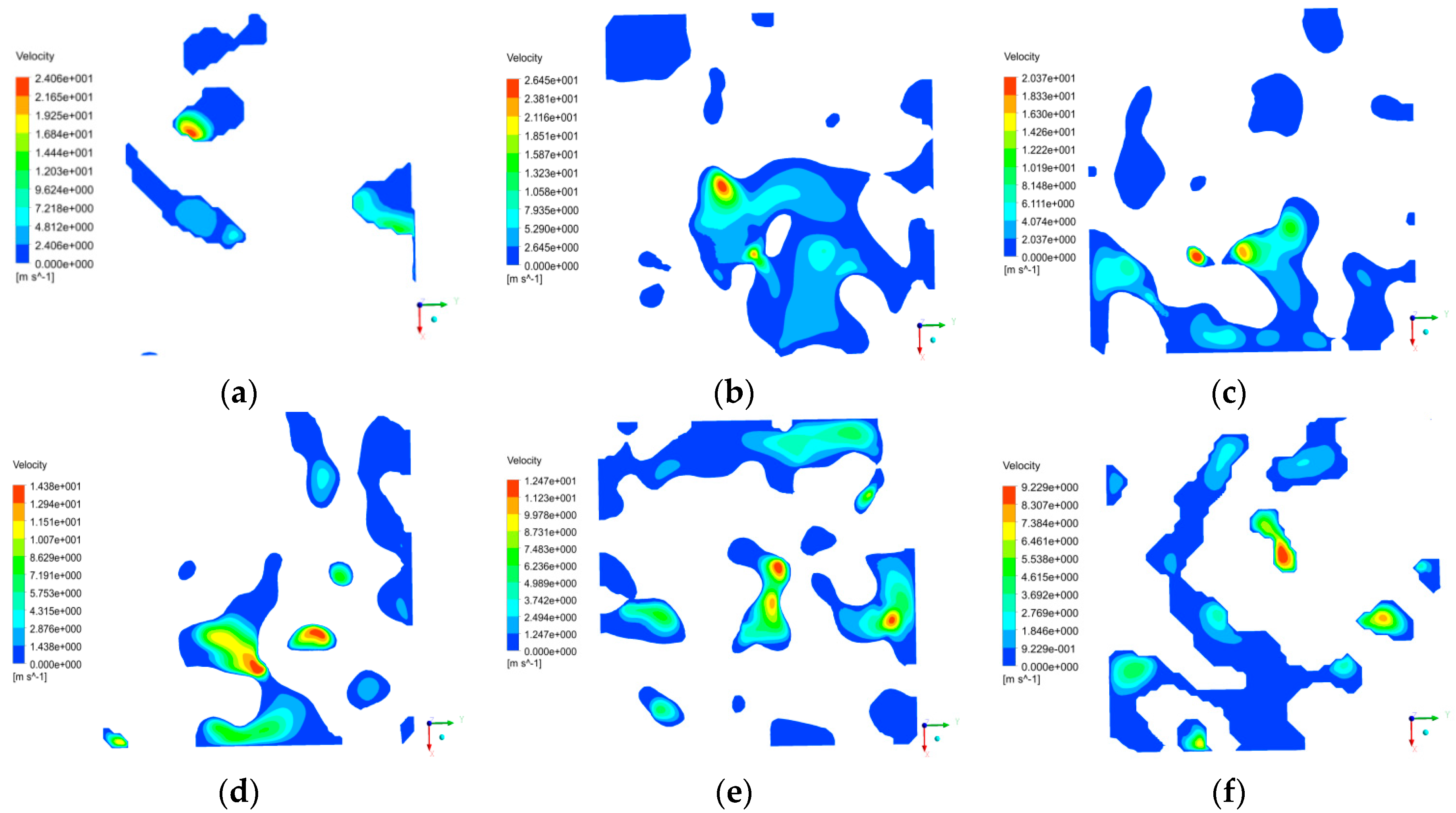
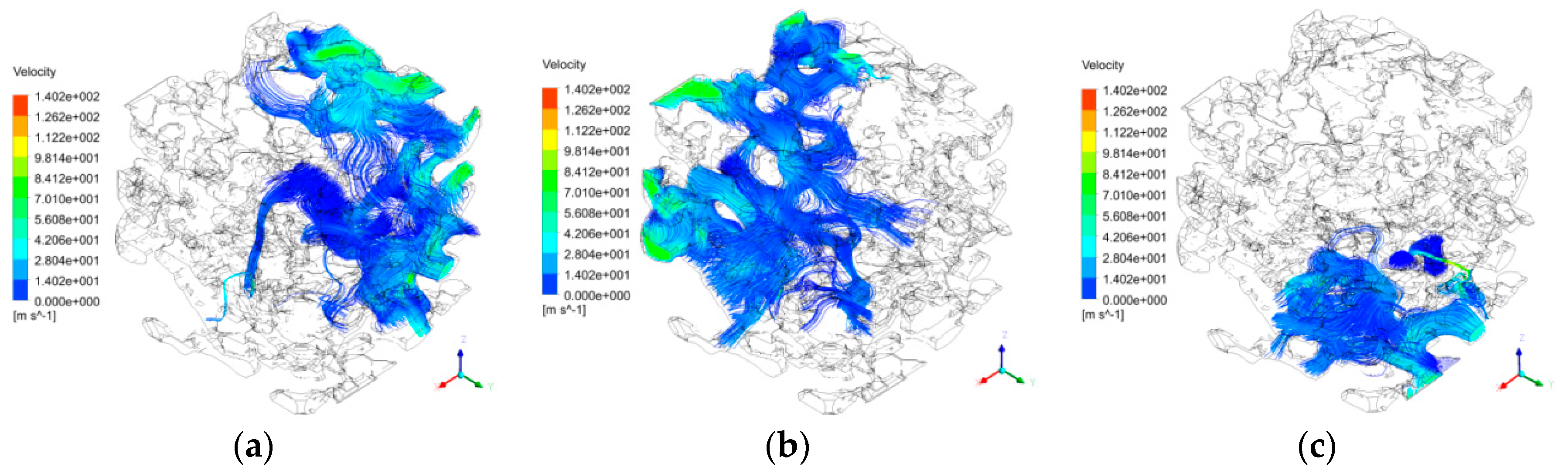
6.3. Numerical Simulation on Seepage Characteristics of Dual-Channel and Multi-Channel Seepage
7. Conclusions
- (1)
- The micro-pore structure model of the digital coal body in the present study had the actual size of 60 μm × 60 μm × 60 μm and contained a total of 219 pores in it. The micro-pore model of the coal had a maximum pore radius of 4.36 μm, a maximum pore volume of 3336 μm3, a mean pore radius of 1.17 μm, a mean pore volume of 124.23 μm3, a bulk porosity of 15.47%, a throat number of 311, a maximum throat radius of 2.77 μm, a mean throat radius of 0.62 μm, a maximum throat length of 13.89 μm, a mean throat length of 2.32 μm, a maximum pore-to-throat ratio of 20.50, a mean pore-to-throat ratio of 2.08, a maximum throat volume of 518 μm3, and a mean throat volume of 14.67 μm3.
- (2)
- During the seepage process of low-pressure water, the water flow did not pass through each path uniformly, but preferentially passed through the paths with large pore radii, short paths, and short distances from the outlet. In terms of a single pore channel, the seepage velocity of low-pressure water decreased gradually along the direction from the pore center to pore wall; in terms of the overall micro-pore structure, the maximum seepage velocity appeared at the center of small pore channel in the coal center region where the water flow was fully developed. For single-channel seepage in different directions, the seepage pressure decreased gradually along the direction of water seepage; moreover, the mean seepage velocity and mass flow rate of the seepage in the X direction were the largest, followed by those in the Y direction, and the mean seepage velocity and mass flow rate of the seepage in the Z direction were the smallest. At the micro-scale, the seepage velocities of low-pressure water in the dual-channel seepage in the direction of (X + Y) and the multi-channel seepage in the direction of (X + Y + Z) were greatly enhanced compared with the velocity in single-channel seepage. Due to the effects of the seepage water pressure and different numbers of channels in different directions, the dual-channel and multi-channel seepage characteristics of low-pressure water exhibited great changes and complex variation rules compared with the characteristics of single-channel seepage.
- (3)
- Using the software of Avizo, the related pore and throat data of the coal micro-pore structure model were extracted, and the coal micro-pore structure model could be converted into a geometric model in CAD format. The geometric model was then imported to many types of finite element and discrete element software, such as CFX, COMSOL, and EDEM for numerical simulations. Meanwhile, using 3D printing technology, we can use the coal powders to prepare the samples that can reflect the coal’s actual micro-pore structure for experimental investigation. The present study provides a new idea and a novel way to investigate the seepage rules in the micro-pore structure of coal. It also casts light on exploring the stress and strain analysis, as well as discrete element analysis of the micro-structure of coal.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CT | Computerized Tomography |
| FEI | Field Electron and Ion Co. |
| CFX | ANSYS CFX Software |
| X-CT | X-Ray Computed Tomography |
| SOD | the Distance between the X-Ray Source and the Detector |
| ODD | the Distance between the Stage Sample and the Detector |
| MRT | Magnetic Resonance Tomography |
| ICEM CFD | ANSYS ICEM CFD Software |
| CFD | Computational Fluid Dynamics |
| CAD | Computer Aided Design |
| LBM | Lattice Boltzmann Method |
| SDUST | Shandong University of Science and Technology |
Nomenclature
| μ | linear attenuation coefficient |
| I0 | incident intensity |
| I | intensity of ray attenuated by the object |
| ∆x | distance(m) |
| a | mass percentage |
| p | logarithm of the ratio of input intensity to output intensity |
References
- Yang, Z.; Yao, W.L.; Ma, L.Z.; Wise, L. Pore structure characteristics of the relative water-resisting layer on the top of the ordovician in longgu coal mine. Int. J. Min. Sci. Technol. 2014, 24, 657–661. [Google Scholar]
- Geet, M.V.; Swennen, R.; David, P. Quantitative coal characterisation by means of microfocus X-ray computer tomography, colour image analysis and back-scattered scanning electron microscopy. Int. J. Coal Geol. 2001, 46, 11–25. [Google Scholar] [CrossRef]
- Simons, F.J.; Verhelst, F. Quantitative characterization of coal by means of micro focal X-ray computed microtomography (CMT) and color image analysis (CIA). Int. J. Coal Geol. 1997, 34, 69–88. [Google Scholar] [CrossRef]
- Mazumder, S.; Wolf, K.H.A.A.; Elewaut, K.; Ephraim, R. Application of X-ray computed tomography for analyzing cleat spacing and cleat aperture in coal samples. Int. J. Coal Geol. 2006, 65, 205–222. [Google Scholar] [CrossRef]
- Golab, A.; Ward, C.R.; Permana, A.; Lennox, P.; Botha, P. High-resolution three-dimensional imaging of coal using microfocus X-ray computed tomography, with special reference to modes of mineral occurrence. Int. J. Coal Geol. 2013, 113, 97–108. [Google Scholar] [CrossRef]
- Karacan, C.O.; Okandan, E. Adsorption and gas transport in coal microstructure: Investigation and evaluation by quantitative X-ray CT imaging. Fuel 2001, 80, 509–520. [Google Scholar] [CrossRef]
- Mathews, J.P.; Pone, J.D.N.; Mitchell, G.D.; Halleck, P. High-resolution X-ray computed tomography observations of the thermal drying of lump-sized subbituminous coal. Fuel Process. Technol. 2011, 92, 58–64. [Google Scholar] [CrossRef]
- Meng, Q.R.; Zhao, Y.S.; Hu, Y.Q.; Feng, Z.C.; Yu, Y.M. Experimental study on pore structure and pore shape of coking coal. J. China Coal Soc. 2011, 36, 487–490. [Google Scholar]
- Yao, Y.B.; Liu, D.M.; Cai, Y.D.; Li, J.Q. Advanced characterization of pores and fractures in coals by nuclear magnetic resonance and X-ray computed tomography. Sci. China Earth Sci. 2010, 53, 854–862. [Google Scholar] [CrossRef]
- Song, X.X.; Tang, Y.G.; Li, W.; Feng, Z.C.; Kang, Z.Q.; Li, Y.J.; Xiang, J.H. Advanced characterization of seepage pores in deformed coals based on micro-CT. J. China Coal Soc. 2013, 38, 435–440. [Google Scholar]
- Coles, M.E.; Hazlett, R.D.; Spanne, P.; Jones, K.W. Pore level imaging of fluid transport using synchrotron X-ray microtomography. J. Pet. Sci. Eng. 1998, 19, 55–63. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis Press: London, UK, 1994. [Google Scholar]
- Teng, G.R.; Tan, Y.L.; Gao, M. Simulation of gas seepage in fissured coal based on lattice boltzmann method. Chin. J. Rock Mech. Eng. 2007, 36, 3503–3508. [Google Scholar]
- Jin, Y.; Zhu, Y.B.; Wu, Y.; Zheng, J.L.; Dong, J.B.; Li, X. Numerical investigation of migration mechanism for coal-bed methane flow through cleats with rough surfaces in coal reservoir. J. China Coal Soc. 2014, 39, 1826–1834. [Google Scholar]
- Liu, Y.; Li, S.H.; Liu, X.Y. Coupled fluid flow and stress computation model of dual media based on continuum-medium distinct element method. Chin. J. Rock Mech. Eng. 2011, 30, 951. [Google Scholar]
- Perera, M.S.A.; Ranjith, P.G.; Choi, S.K.; Bouazza, A.; Kodikara, J.; Airey, D. A review of coal properties pertinent to carbon dioxide sequestration in coal seams: With special reference to victorian brown coals. Environ. Earth Sci. 2011, 64, 223–235. [Google Scholar] [CrossRef]
- Ritman, E.L. Molecular imaging in small animals-roles for micro-CT. J. Cell. Biochem. 2002, 87, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Badea, C.T.; Drangova, M.; Holdsworth, D.W.; Johnson, G.A. In vivo small-animal imaging using micro-CT and digital subtraction angiography. Phys. Med. Biol. 2008, 53, 319–350. [Google Scholar] [CrossRef] [PubMed]
- Ritman, E.L. Micro-computed tomography—Current status and developments. Annu. Rev. Biomed. Eng. 2004, 6, 185–208. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, D.S.; Bao, S.L. The technology and application in biomedicine micro-CT. Mod. Instrum. 2009, 15, 19–23. [Google Scholar]
- Xu, Y.; Zou, J.; Yao, S.Y. 3D X-ray microscope and its typical applications. CT Theory Appl. 2014, 23, 967–977. [Google Scholar]
- Rong, H.R.; Bai, H.B. Concealed fault analysis based on the CT projection matrix. Int. J. Min. Sci. Technol. 2016, 26, 361–367. [Google Scholar]








| Detector | SOD/ODD (mm/mm) | Voltage (kV) | Electric Current (μA) | Scanning Frame | Time (h) | Exposure Time (s) | Penetration Rate (%) |
|---|---|---|---|---|---|---|---|
| 20× | 35/13 | 41 | 240 | 900 | 19 | 65 | 57 |
| Number of Throats | Maximum Throat Radius (μm) | Mean Throat Radius (μm) | Maximum Throat Length (μm) | Mean Throat Length (μm) | Maximum Pore-Throat Ratio | Mean Pore-Throat Ratio | Maximum Throat Volume (μm3) | Mean Throat Volume (μm3) |
|---|---|---|---|---|---|---|---|---|
| 311 | 2.77 | 0.62 | 13.89 | 2.32 | 20.50 | 2.08 | 518 | 14.67 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Zhang, Q.; Bai, R.; Ni, G. Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data. Minerals 2016, 6, 78. https://doi.org/10.3390/min6030078
Zhou G, Zhang Q, Bai R, Ni G. Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data. Minerals. 2016; 6(3):78. https://doi.org/10.3390/min6030078
Chicago/Turabian StyleZhou, Gang, Qi Zhang, Ruonan Bai, and Guanhua Ni. 2016. "Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data" Minerals 6, no. 3: 78. https://doi.org/10.3390/min6030078
APA StyleZhou, G., Zhang, Q., Bai, R., & Ni, G. (2016). Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data. Minerals, 6(3), 78. https://doi.org/10.3390/min6030078