The Growth of Gypsum in the Presence of Hexavalent Chromium: A Multiscale Study
Abstract
:1. Introduction
2. Material and Methods
2.1. In Situ AFM Observations
2.2. Precipitation Experiments
3. Results
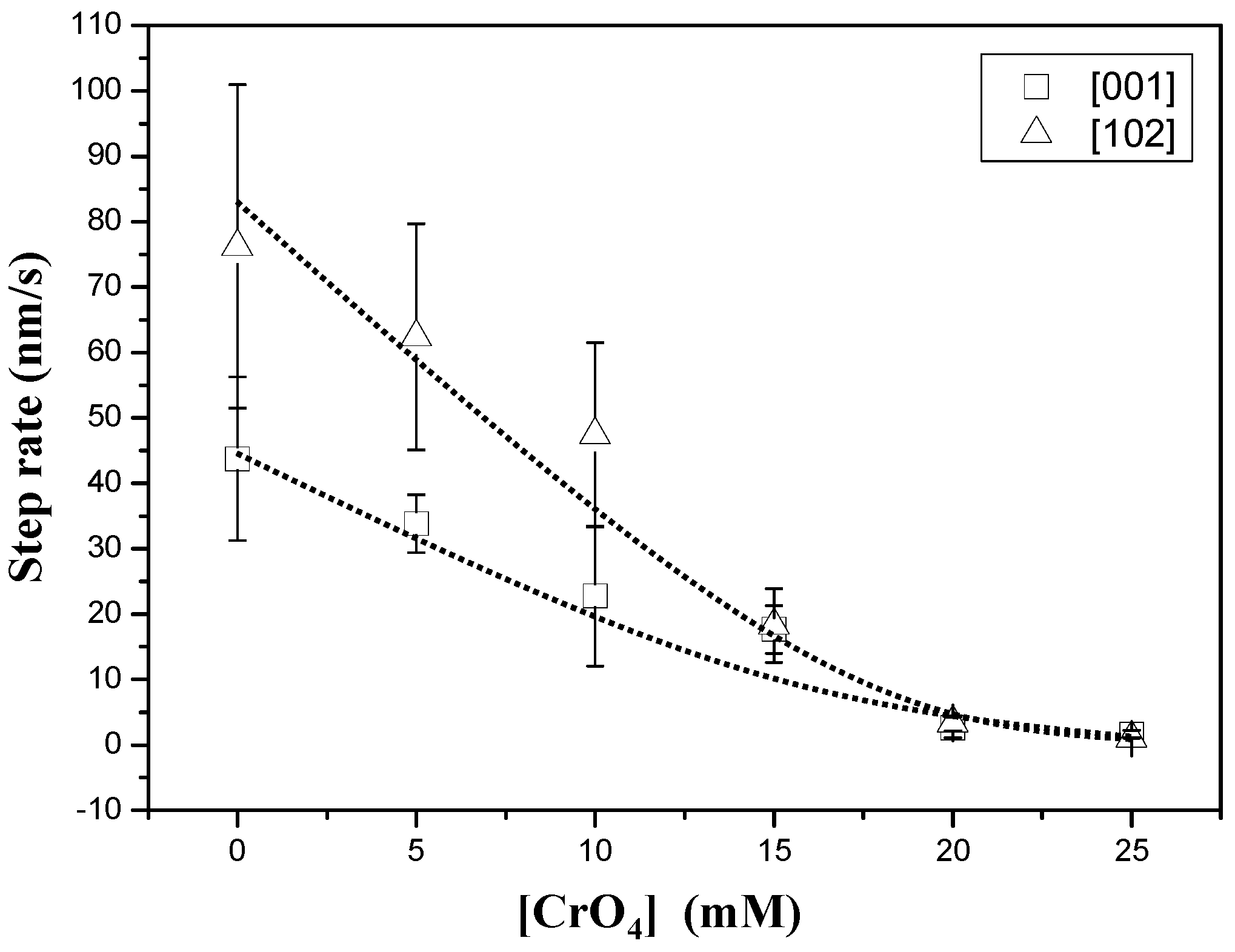
3.1. AFM Observations
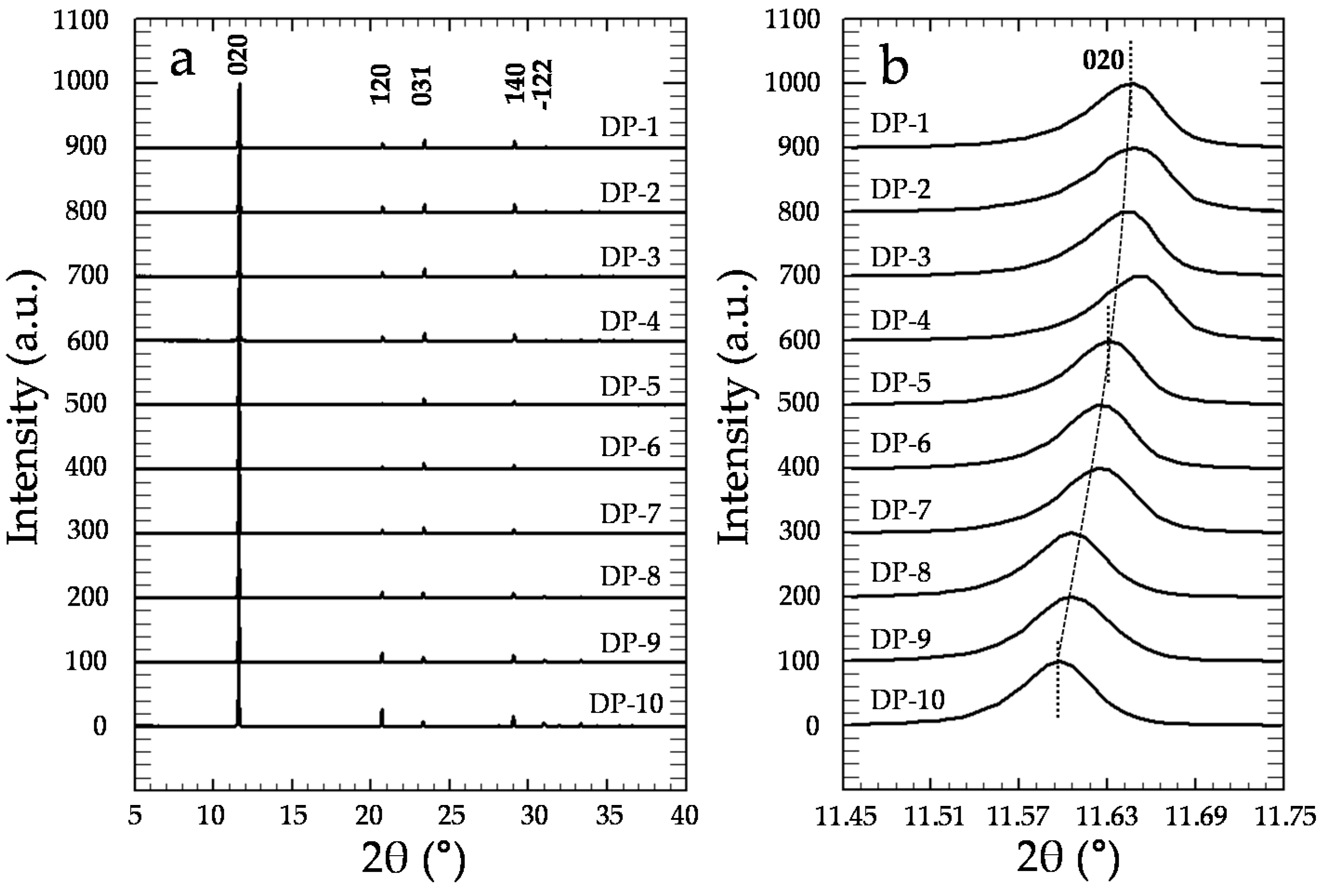
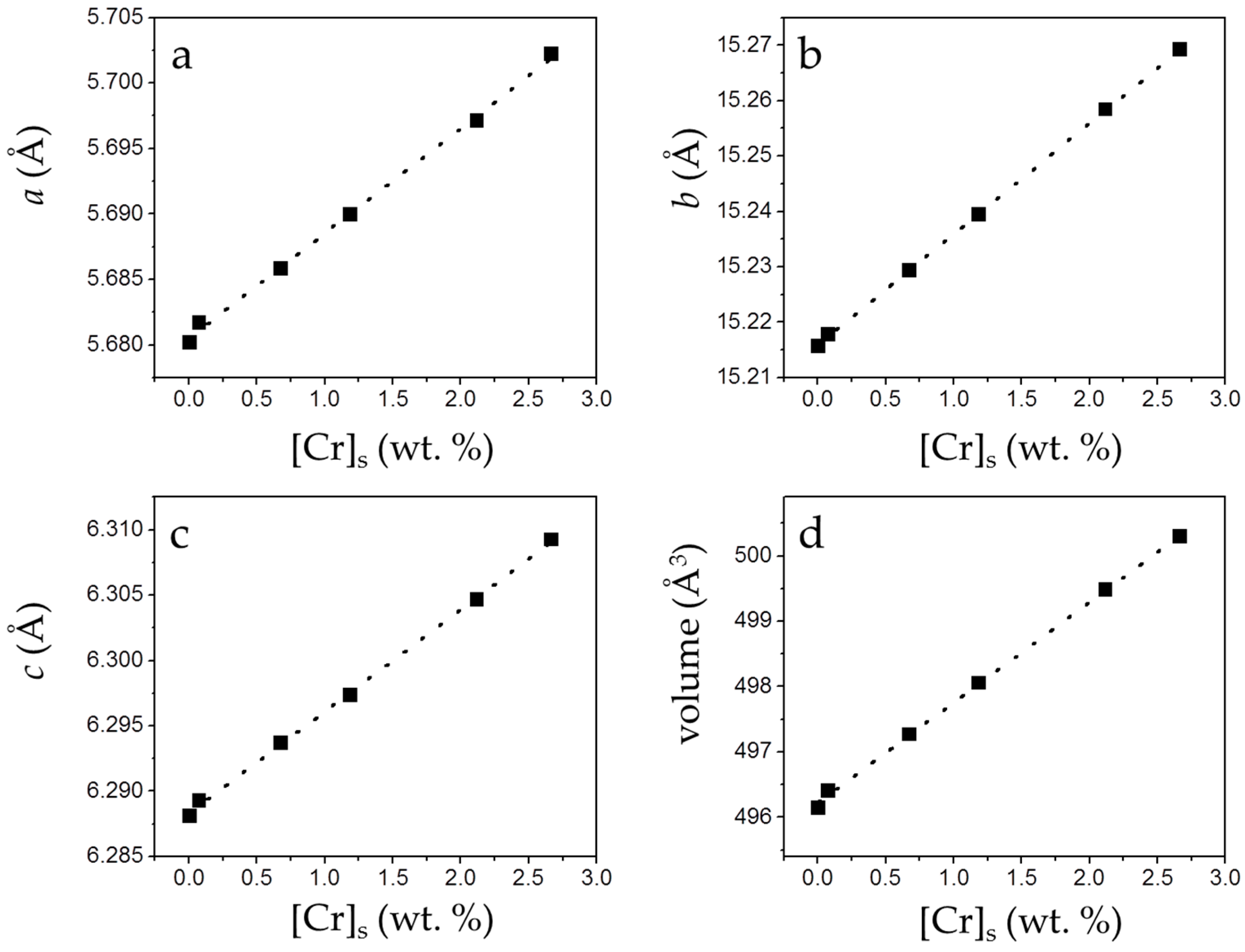
3.2. Precipitation of Gypsum in the Presence of CrO42−
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davis, K.J.; Dove, P.M.; de Yoreo, J.J. The role of Mg2+ as an impurity in calcite growth. Science 2000, 290, 1134–1137. [Google Scholar] [CrossRef] [PubMed]
- Astilleros, J.M.; Pina, M.; Fernández-Díaz, L.; Putnis, A. Nanoscale growth of solids crystallising from multicomponent aqueous solutions. Surf. Sci. 2003, 545, L767–L773. [Google Scholar] [CrossRef]
- Shtukenberg, A.G.; Astilleros, J.M.; Putnis, A. Nanoscale observations of epitaxial growth of hashemite on barite (001). Surf. Sci. 2005, 590, 212–223. [Google Scholar] [CrossRef]
- Astilleros, J.M.; Pina, M.; Fernández-Díaz, L.; Prieto, M.; Putnis, A. Nanoscale phenomena during the growth of solid solutions on calcite {104} surfaces. Chem. Geol. 2006, 225, 322–335. [Google Scholar] [CrossRef]
- Vavouraki, A.I.; Putnis, C.V.; Putnis, A.; Koutsoukos, P.G. An Atomic Force Microscopy study of the growth of calcite in the presence of sodium sulfate. Chem. Geol. 2008, 253, 243–251. [Google Scholar] [CrossRef]
- Sethmann, I.; Wang, J.; Becker, U.; Putnis, A. Strain-induced segmentation of magnesian calcite thin films growing on a calcite substrate. Cryst. Growth Des. 2010, 10, 4319–4326. [Google Scholar] [CrossRef]
- Nielsen, L.C.; de Yoreo, J.J.; de Paolo, D.J. General model for calcite growth kinetics in the presence of impurity ions. Geochim. Cosmochim. Acta 2013, 115, 100–114. [Google Scholar] [CrossRef]
- Astilleros, J.M. Estudio Integrado de la Cristalización de Soluciones Sólidas no Ideales: (Ca,M)CO3 (M = Ba, Sr, Mn). Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2001. [Google Scholar]
- Astilleros, J.M.; Pina, C.M.; Fernández-Díaz, L.; Putnis, A. Molecular scale surface processes during the growth of calcite in the presence of manganese. Geochim. Cosmochim. Acta 2002, 66, 3177–3189. [Google Scholar] [CrossRef]
- Astilleros, J.M.; Pina, C.M.; Fernández-Díaz, L.; Putnis, A. Metastable phenomena on calcite {104} surfaces growing from Sr2+-Ca2+-CO32− aqueous solutions. Chem. Geol. 2003, 193, 93–107. [Google Scholar] [CrossRef]
- Astilleros, J.M.; Fernández-Díaz, L.; Putnis, A. The role of magnesium in the growth of calcite: An AFM study. Chem. Geol. 2010, 271, 52–58. [Google Scholar] [CrossRef]
- Freij, S.J.; Putnis, A.; Astilleros, J.M. Nanoscale observations of the effect of cobalt on calcite growth and dissolution. J. Cryst. Growth 2004, 267, 288–300. [Google Scholar] [CrossRef]
- Sánchez-Pastor, N.; Pina, C.M.; Fernández-Díaz, L.; Astilleros, J.M. The effect of CO32− on the growth of barite {001} and {210} surfaces: An AFM study. Surf. Sci. 2006, 600, 1369–1381. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Putnis, C.V.; Kowacz, M.; Ortega-Huertas, M.; Putnis, A. Boron incorporation into calcite during growth: Implications for the use of boron in carbonates as a pH proxy. Earth Planet. Sci. Lett. 2012, 345–348, 9–17. [Google Scholar] [CrossRef]
- Nriagu, J.O.; Nieboer, E. Chromium in the Natural and Human Environments; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. User’s Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport and Inverse Geochemical Calculations: U.S. Geological Survey Water Resources Investigations Report 99-4259; U.S. Geological Survey: Denver, CO, USA, 1999.
- Perkins, R.B.; Palmer, C.D. Solubility of Ca6[Al(OH)6]2(CrO4)3·26H2O, the chromate analogue of ettringite; 5–75 °C. Appl. Geochem. 2000, 15, 1203–1218. [Google Scholar] [CrossRef]
- Kostov, L.; Kostov, R.I. Crystal Habits of Minerals; Bulgarian Academic Monographs; Pensoft Publishers: Sofia, Bulgaria, 1999; pp. 308–310. [Google Scholar]
- Morales, J.; Astilleros, J.M.; Fernández-Díaz, L. Nanoscopic characteristics of anhydrite (100) growth. Cryst. Growth Des. 2012, 12, 414–421. [Google Scholar] [CrossRef]
- Söhnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Colloid Interface Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- Söhnel, O.; Mullin, J.W. A method for the determination of precipitation induction periods. J. Cryst. Growth 1978, 44, 377–382. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Comodi, P.; Nazzareni, S.; Zanazzi, P.F.; Speziale, S. High-pressure behavior of gypsum: A single-crystal X-ray study. Am. Mineral. 2008, 93, 1530–1537. [Google Scholar] [CrossRef]
- Thompson, P.; Cox, D.E.; Hastings, J.B. Rietveld refinement of Debye-Scherrer synchrotron X-ray data from Al2O3. J. Appl. Crystallogr. 1987, 20, 79–83. [Google Scholar] [CrossRef]
- Finger, L.W.; Cox, D.E.; Jephcoat, A.P. A correction for powder diffraction peak asymmetry due to axial divergence. J. Appl. Cryst. 1994, 27, 892–900. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; García-Ruiz, J.M.; Delgado-López, J.M.; Sazaki, G. In situ observation of step dynamics on gypsum crystals. Cryst. Growth Des. 2010, 10, 3909–3916. [Google Scholar] [CrossRef]
- Hawthorne, F.C.; Krivovichev, S.V.; Burns, P.C. The crystal chemistry of sulfate minerals. In Sulfate Minerals Crystallography, Geochemistry, and Environmental Significance. Reviews in Mineralogy & Geochemistry; Alpers, C.N., Jambor, J.L., Nordstrom, D.K., Eds.; Mineralogical Society of America and Geochemical Society: Washington, DC, USA, 2000; Volume 40, pp. 1–112. [Google Scholar]
- Casari, B.M.; Eriksson, A.K.; Langer, V. Synthesis methods for Ce(CrO4)2·xH2O and crystal structures of K2CrSO7, (NH4)2Cr2O7 and Na2Cr2O7·2H2O. Z. Naturforsch. B 2007, 62, 771–777. [Google Scholar] [CrossRef]
- Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Z. Phys. 1921, 5, 17–26. (In German) [Google Scholar] [CrossRef]
- Glynn, P.D.; Reardon, E.J.; Plummer, L.N.; Busenberg, E. Reaction paths and equilibrium end-points in solid-solution aqueous-solution systems. Geochim. Cosmochim. Acta 1990, 54, 267–282. [Google Scholar] [CrossRef]
- Fernández-González, A.; Martín-Díaz, R.; Prieto, M. Crystallisation of Ba(SO4, CrO4) solid solutions from aqueous solutions. J. Crys. Growth 1999, 200, 227–235. [Google Scholar] [CrossRef]
- Leisinger, S.M.; Lothenbach, B.; Saout, G.L.; Kägi, R.; Wehrli, B.; Johnson, C.A. Solid solutions between CrO4- and SO4-ettringite Ca6(Al(OH)6)2[(CrO4)x(SO4)1−x]3·26H2O. Environ. Sci. Technol. 2010, 44, 8983–8988. [Google Scholar] [CrossRef] [PubMed]
- Baron, D.; Palmer, C.D. Solid-solution aqueous-solution reactions between jarosite (KFe3(SO4)2(OH)6) and its chromate analogue. Geochim. Cosmochim. Acta 2002, 66, 2841–2853. [Google Scholar] [CrossRef]
- Prieto, M.; Fernández-González, A.; Putnis, A.; Fernández-Díaz, L. Nucleation, growth, and zoning phenomena in crystallizing (Ba,Sr)CO3, Ba(SO4,CrO4), (Ba,Sr)SO4, and (Cd,Ca)CO3 solid solutions from aqueous solutions. Geochim. Cosmochim. Acta 1997, 61, 3383–3397. [Google Scholar] [CrossRef]
- Prieto, M.; Fernández-González, A.; Martín-Díaz, R. Sorption of chromate ions diffusing through barite-hydrogel composites: Implications for the fate and transport of chromium in the environment. Geochim. Cosmochim. Acta 2002, 66, 783–795. [Google Scholar] [CrossRef]
- Prieto, M.; Astilleros, J.M.; Fernández-Díaz, L. Environmental remediation by crystallization of solid solutions. Elements 2013, 9, 195–201. [Google Scholar] [CrossRef]





| Exp. Id. | [CrO42−] (mol/L) | [SO42−] (mol/L) | [Ca2+] (mol/L) | [Cl−] (mol/L) | [Na+] (mol/L) | βGp |
|---|---|---|---|---|---|---|
| AFM-1 | 0.000 | 0.024 | 0.024 | 0.049 | 0.049 | 1.363 |
| AFM-2 | 0.005 | 0.025 | 0.025 | 0.050 | 0.060 | 1.356 |
| AFM-3 | 0.010 | 0.026 | 0.026 | 0.052 | 0.072 | 1.357 |
| AFM-4 | 0.015 | 0.027 | 0.027 | 0.053 | 0.083 | 1.364 |
| AFM-5 | 0.020 | 0.027 | 0.027 | 0.054 | 0.094 | 1.362 |
| AFM-6 | 0.025 | 0.028 | 0.028 | 0.055 | 0.105 | 1.364 |
| Exp. Id. | [CrO42−] (mol/L) | [SO42−] (mol/L) | [Ca2+] (mol/L) | [Cl−] (mol/L) | [Na+] (mol/L) | βGp | tw (s) | Weight (g) |
|---|---|---|---|---|---|---|---|---|
| DP-1 | 0.00 | 0.26 | 0.26 | 0.52 | 0.52 | 47.6 | 8.7 ± 2.3 | 4.08 ± 0.02 |
| DP-2 | 0.01 | 0.26 | 0.26 | 0.52 | 0.54 | 47.6 | 9.3 ± 2.5 | 4.04 ± 0.05 |
| DP-3 | 0.03 | 0.26 | 0.26 | 0.52 | 0.58 | 47.6 | 10.3 ± 3.2 | 4.05 ± 0.03 |
| DP-4 | 0.06 | 0.26 | 0.26 | 0.52 | 0.64 | 47.6 | 12.0 ± 2.6 | 4.03 ± 0.07 |
| DP-5 | 0.10 | 0.26 | 0.26 | 0.52 | 0.72 | 47.3 | 16.3 ± 3.0 | 3.99 ± 0.07 |
| DP-6 | 0.20 | 0.26 | 0.26 | 0.52 | 0.92 | 47.3 | 25.0 ± 3.6 | 3.81 ± 0.04 |
| DP-7 | 0.40 | 0.25 | 0.25 | 0.51 | 1.31 | 46.2 | 40.7 ± 6.0 | 3.47 ± 0.05 |
| DP-8 | 0.60 | 0.25 | 0.25 | 0.50 | 1.70 | 47.3 | 60.0 ± 5.0 | 3.27 ± 0.04 |
| DP-9 | 0.80 | 0.25 | 0.25 | 0.49 | 2.09 | 47.6 | 92.0 ± 3.0 | 2.85 ± 0.13 |
| DP-10 | 1.00 | 0.24 | 0.24 | 0.48 | 2.48 | 47.6 | 150.0 ± 8.2 | 2.44 ± 0.08 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, J.; Astilleros, J.M.; Matesanz, E.; Fernández-Díaz, L. The Growth of Gypsum in the Presence of Hexavalent Chromium: A Multiscale Study. Minerals 2016, 6, 22. https://doi.org/10.3390/min6010022
Morales J, Astilleros JM, Matesanz E, Fernández-Díaz L. The Growth of Gypsum in the Presence of Hexavalent Chromium: A Multiscale Study. Minerals. 2016; 6(1):22. https://doi.org/10.3390/min6010022
Chicago/Turabian StyleMorales, Juan, José Manuel Astilleros, Emilio Matesanz, and Lurdes Fernández-Díaz. 2016. "The Growth of Gypsum in the Presence of Hexavalent Chromium: A Multiscale Study" Minerals 6, no. 1: 22. https://doi.org/10.3390/min6010022
APA StyleMorales, J., Astilleros, J. M., Matesanz, E., & Fernández-Díaz, L. (2016). The Growth of Gypsum in the Presence of Hexavalent Chromium: A Multiscale Study. Minerals, 6(1), 22. https://doi.org/10.3390/min6010022






