Applicability Analysis with the Improved Spectral Unmixing Models Based on the Measured Hyperspectral Data of Mixed Minerals
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and Data Acquisition
2.2. Linear Spectrum Mixing Model and Evaluation Index
2.3. Improved Linearized Spectral Unmixing Model
2.3.1. CR-FCLSM
- (1)
- All maximum points on the spectral curve are obtained after the spectrum is derived and the maximum point is found.
- (2)
- Take the maximum point as the starting point, calculate the slope of the line between the maximum point and each subsequent maximum point in the long-wave direction. The point with the most significant slope is the following endpoint of the envelope and is calculated according to the method used for the last point.
- (3)
- Repeat step (2) in the short-wave direction;
- (4)
- Connect all endpoints to get the envelope of the curve. Envelope removal is the division of the reflectance values on each band of the spectral curve by the reflectance values on the envelope. After the envelope is removed, the reflectance of the peak point on the spectral curve becomes 1, and the reflectance of the non-peak point will be less than 1. The formula for envelope removal is as follows [29]:
2.3.2. NL-FCLSM
2.3.3. RDM
3. Results and Discussion
3.1. Change Analysis of Spectral Characteristics of Mixed Minerals
3.2. Analysis of Unmixing Accuracy for Three Linearized Spectral Models
3.3. Comparison Between the Traditional Linear Spectral Unmixing Model and the Improved Linear Unmixing Model
3.4. Validation of the Applicability of the Improved Spectral Unmixing Model in Mineral Mixing Scenarios
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FCLSM | Fully Constrained Linear Spectral Mode |
| CR-FCLSM | Continuum Removal—Fully Constrained Linear Spectral Model |
| NL-FCLSM | Natural Logarithm—Fully Constrained Linear Spectral Model |
| RDM | Ratio Derivative Model |
| AE | Abundance Error |
References
- Smith, M.O.; Johnson, P.E.; Adams, J.B. Quantitative determination of mineral types and abundances from reflectance spectra using principal components analysis. J. Geophys Res. Solid Earth. 1985, 90, 797–804. [Google Scholar] [CrossRef]
- Celik, B. QLSU (QGIS Linear Spectral Unmixing) Plugin: An open source linear spectral unmixing tool for hyperspectral & multispectral remote sensing imagery. Environ. Model. Softw. 2023, 168, 105782. [Google Scholar]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Ramakrishnan, D.; Bharti, R. Hyperspectral remote sensing and geological applications. Curr. Sci. 2015, 108, 879–891. [Google Scholar]
- Moghadam, H.J.; Oskouei, M.M.; Nouri, T. Unmixing of hyperspectral data for mineral detection using a hybrid method, Sar Chah-e Shur, Iran. Arab. J. Geosci. 2020, 13, 1–17. [Google Scholar] [CrossRef]
- Kopačková, V.; Hladíková, L. Applying spectral unmixing to determine surface water parameters in a mining environment. Remote Sens. 2014, 6, 11204–11224. [Google Scholar] [CrossRef]
- Ertürk, A.; Erten, E. Unmixing of pollution-associated sea snot in the near surface after its outbreak in the Sea of Marmara using hyperspectral PRISMA data. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X. Retrieving the hydrous minerals on Mars by sparse unmixing and the Hapke model using MRO/CRISM data. Icarus 2017, 288, 160–171. [Google Scholar] [CrossRef]
- Wang, Y.; Lyu, S.; Ning, B.; Yan, D.; Hou, M.; Sun, P.; Li, L. Spectral Unmixing of Pigments on Surface of Painted Artefacts Considering Spectral Variability. ISPRS Annals of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2024, 10, 403–409. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Mustard, J.F.; Murchie, S.L.; Pelkey, S.M.; Ehlmann, B.L.; Milliken, R.E.; Gendrin, A.; LeMoigne, J. Martian clay minerals formed by evaporitic processes. Nat. Geosci. 2012, 5, 398–402. [Google Scholar]
- Shipman, H.; Adams, J.B. Feasibility of detecting minerals in desert alluvial fans using reflection spectra. J. Geophys. Res. 1987, 92, 10391–10392. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef]
- Keshava, N. A survey of spectral unmixing algorithms. Linc. Lab. J. 2003, 14, 55–78. [Google Scholar]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.M.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Wan, L.; Chen, T.; Plaza, A.; Cai, H. Hyperspectral unmixing based on spectral and sparse deep convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11669–11682. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Faul, U.H. Permeability of partially molten upper mantle rocks from experiments and percolation theory. J. Geophys. Res. Solid Earth 1997, 102, 10299–10311. [Google Scholar] [CrossRef]
- Chen, K.; Bowler, J.M.; Magee, J.W. Hydrological evolution of the Lop Nur basin (China) during the Late Quaternary inferred from evaporite mineralogy and sedimentology. Quat. Sci. Rev. 2018, 199, 134–150. [Google Scholar]
- Li, M.; Zhang, X.; Liu, C. Origin of the Late Triassic evaporite deposits in the Sichuan Basin, China: Constraints from boron isotopes. Sediment. Geol. 2020, 406, 105725. [Google Scholar]
- Gu, X.; Zhang, Y.; Li, B. Fluid inclusion and stable isotope constraints on the genesis of fluorite deposits in southern Hunan, China. Ore Geol. Rev. 2019, 115, 103181. [Google Scholar]
- Beretka, J.; Crook, D.N.; King, G.A. Physico-chemical properties of by-product gypsum. J. Chem. Technol. Biotechnol. 1981, 31, 151–162. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, J.; He, Z. A laboratory-created dataset with ground truth for hyperspectral unmixing evaluation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2170–2183. [Google Scholar] [CrossRef]
- Thouvenin, P.A.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral unmixing with spectral variability using a perturbed linear mixing model. IEEE Trans. Signal Process. 2015, 64, 525–538. [Google Scholar] [CrossRef]
- Poulet, F.; Erard, S. Nonlinear spectral mixing: Quantitative analysis of laboratory mineral mixtures. J. Geophys. Res. Planets 2004, 109, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.R.; Chen, H. Linear estimation with transformed measurement for nonlinear estimation. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 221–236. [Google Scholar] [CrossRef]
- Miranker, W.L.; Van Veldhuizen, M. The method of envelopes. Math. Comput. 1978, 32, 453–496. [Google Scholar] [CrossRef][Green Version]
- Fernández-González, A.; Montejo-Bernardo, J.M. Natural Logarithm Derivative Method: A novel and easy methodology for finding maximums in overlapping experimental peaks. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2009, 74, 714–718. [Google Scholar] [CrossRef]
- Zhao, H.Q.; Zhang, L.F.; Wu, T.X.; Huang, C.P. Research on the model of spectral unmixing for minerals based on derivative of ratio spectroscopy. Spectrosc. Spectr. Anal. 2013, 33, 172–176. [Google Scholar]
- Yu, X.; Lin, W.; Wang, D.; Li, Y.; Sun, Y. Identification and characteristic analysis of urban vegetation spectra under different dust deposition. Environ. Sci. Pollut. Res. 2023, 30, 21299–21312. [Google Scholar] [CrossRef]
- Wu, B.; Wang, J.; Zhang, B.; Dong, Y. Influencing Factor Analysis of Spectral Unmixing Model for Solid Particle Mixtures. J. Mater. Sci. Eng. 2021, 39, 814–819. [Google Scholar]
- Zhang, H.; Yu, L.; Li, D. Characteristic band selection of hyperspectral unmixing based on pixel simulation experiment. Spectrosc. Lett. 2025, 2, 1–13. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Klein, A.J. USGS Spectral Library Version 7; USGS: Reston, VA, USA, 2017; p. 1035. [Google Scholar]
- Deville, Y.; Faury, G. Hyperspectral unmixing with spectral variability: Reducing sensitivity to learning parameters, by combining linear and nonlinear NMF algorithms. Digit. Signal Process. 2025, 163, 105241. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Mendoza-Chavarría, J.N.; Gutierrez-Navarro, O.; Quintana-Quintana, L.; Leon, R.; Ortega, S.; Callico, G.M. Robust and Unified Semi-Supervised Unmixing of Hyperspectral Imaging for Linear and Multilinear Models. IEEE Access. 2025, 13, 53140–53158. [Google Scholar] [CrossRef]
- Grillini, F.; Thomas, J.-B.; George, S. Comparison of Imaging Models for Spectral Unmixing in Oil Painting. Sensors 2021, 21, 2471. [Google Scholar] [CrossRef] [PubMed]
- Valero, E.M.; Martínez-Domingo, M.A.; López-Baldomero, A.B.; López-Montes, A.; Abad-Muñoz, D.; Vílchez-Quero, J.L. Unmixing and pigment identification using visible and short-wavelength infrared: Reflectance vs logarithm reflectance hyperspaces. J. Cult. Heritage. 2023, 64, 290–300. [Google Scholar] [CrossRef]
- Du, R.; Chen, J.; Xiang, Y.; Xiang, R.; Yang, X.; Wang, T.; Chen, Y. Timely monitoring of soil water-salt dynamics within cropland by hybrid spectral unmixing and machine learning models. Int. Soil Water Conserv. Res. 2024, 12, 726–740. [Google Scholar] [CrossRef]
- Jeong, S.W.; Lee, I.H.; Kim, Y.G.; Kang, K.S.; Shim, D.; Hurry, V.; Park, Y.I. Spectral unmixing of hyperspectral images revealed pine wilt disease sensitive endmembers. Physiol. Plant. 2025, 177, e70090. [Google Scholar] [CrossRef]



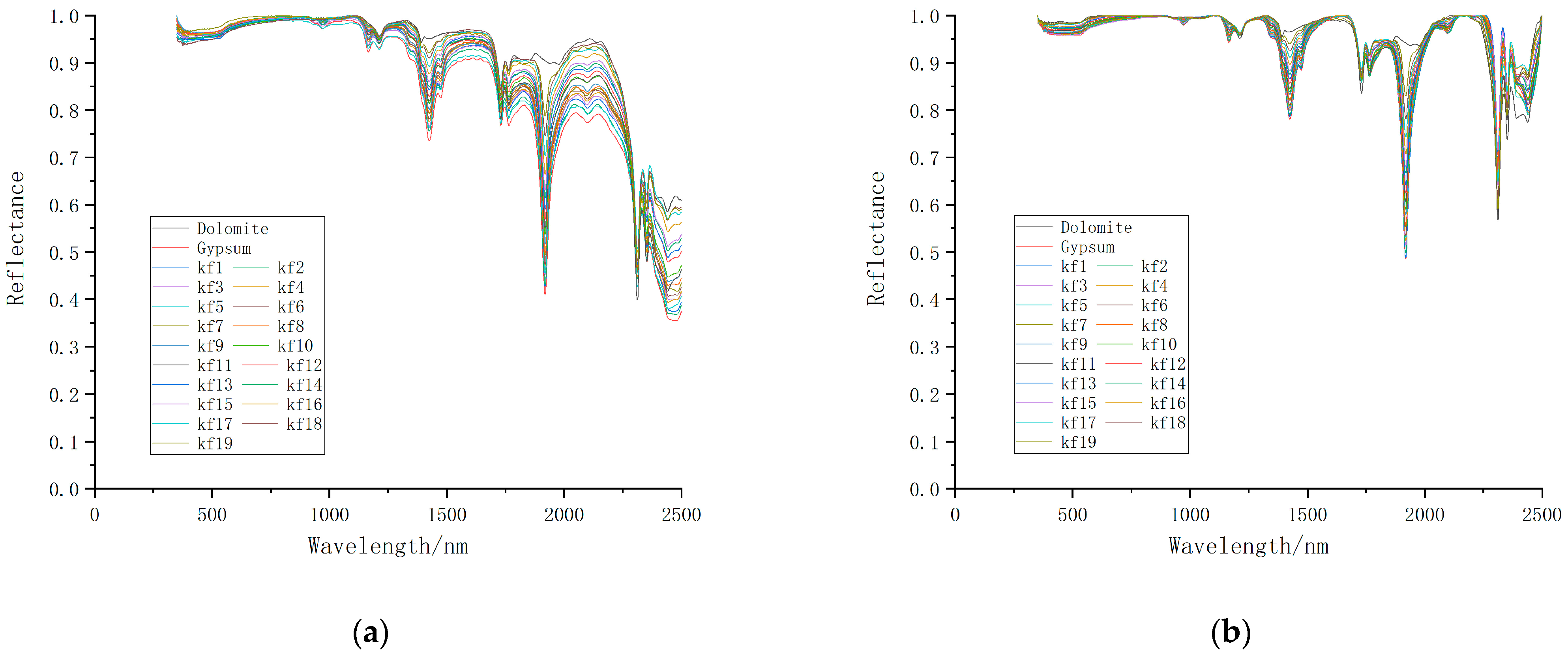
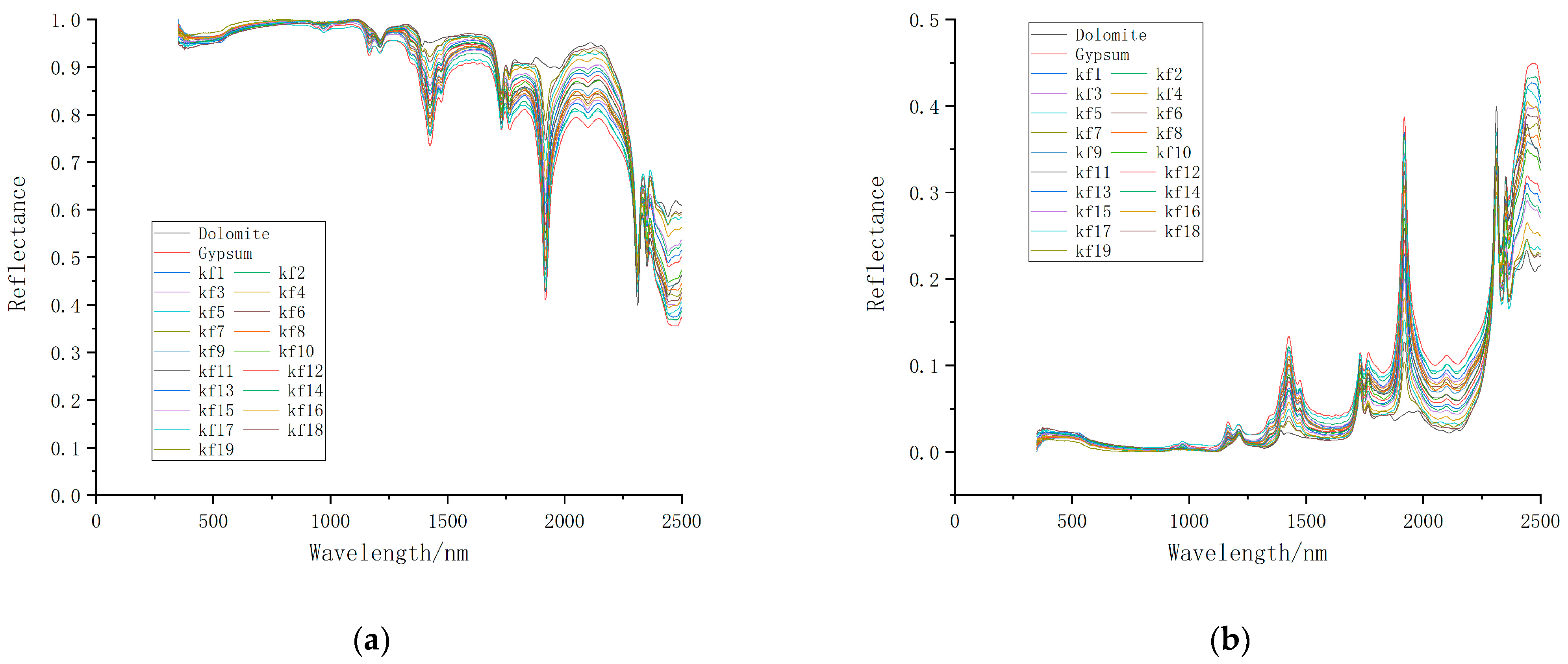
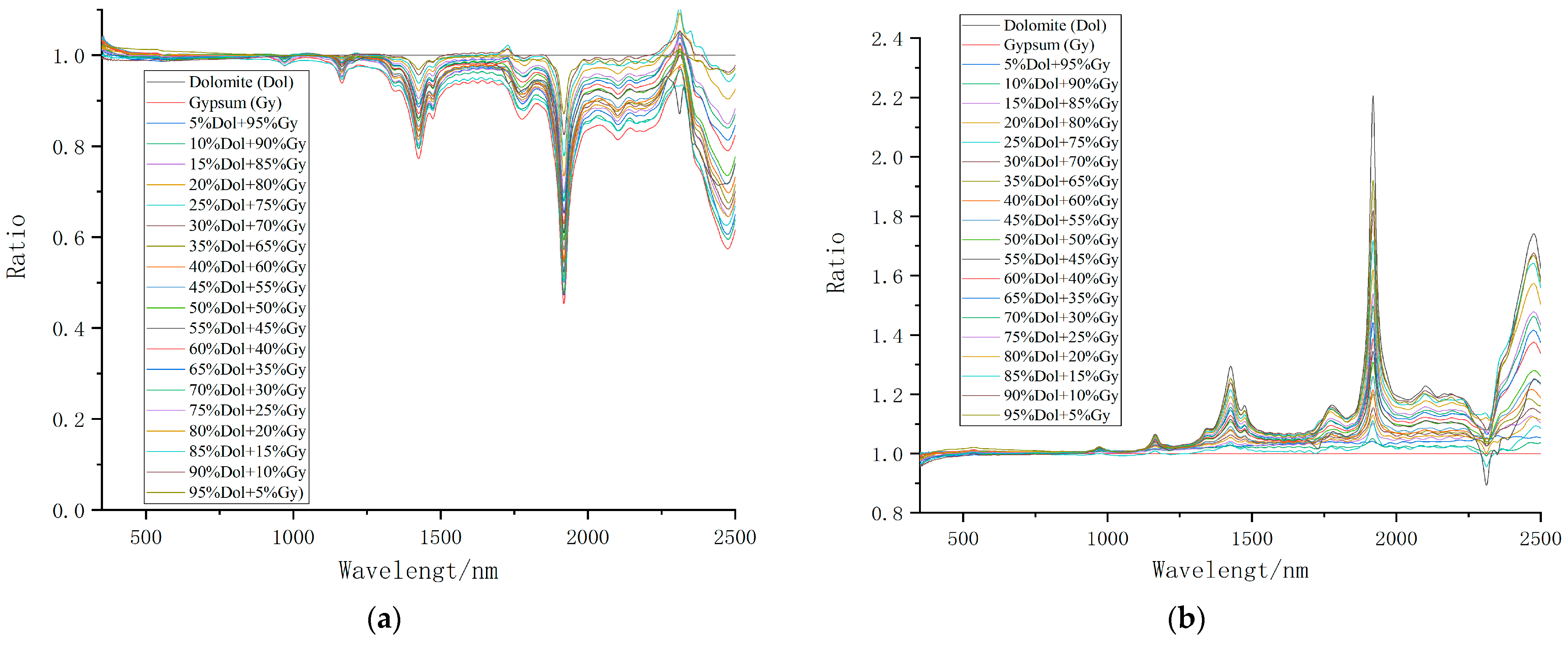
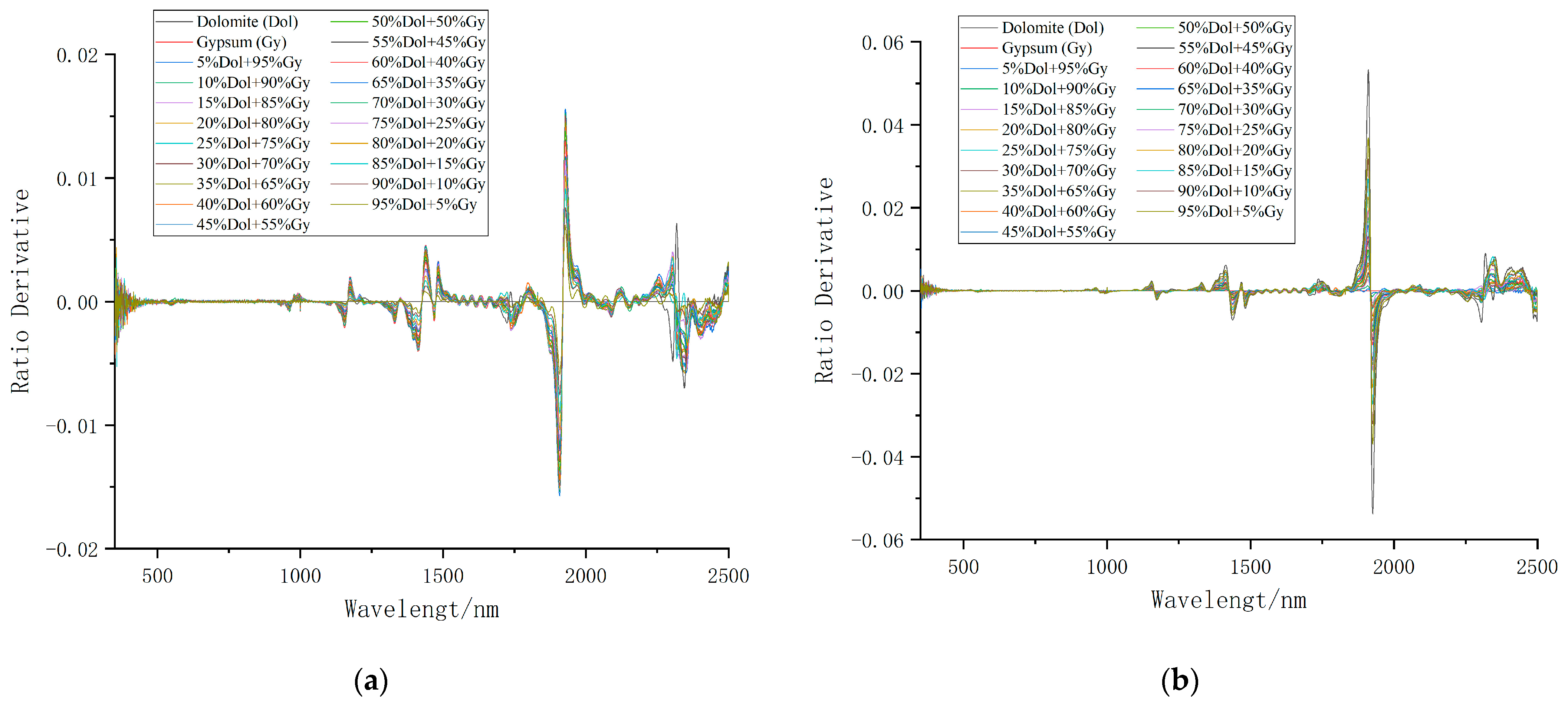
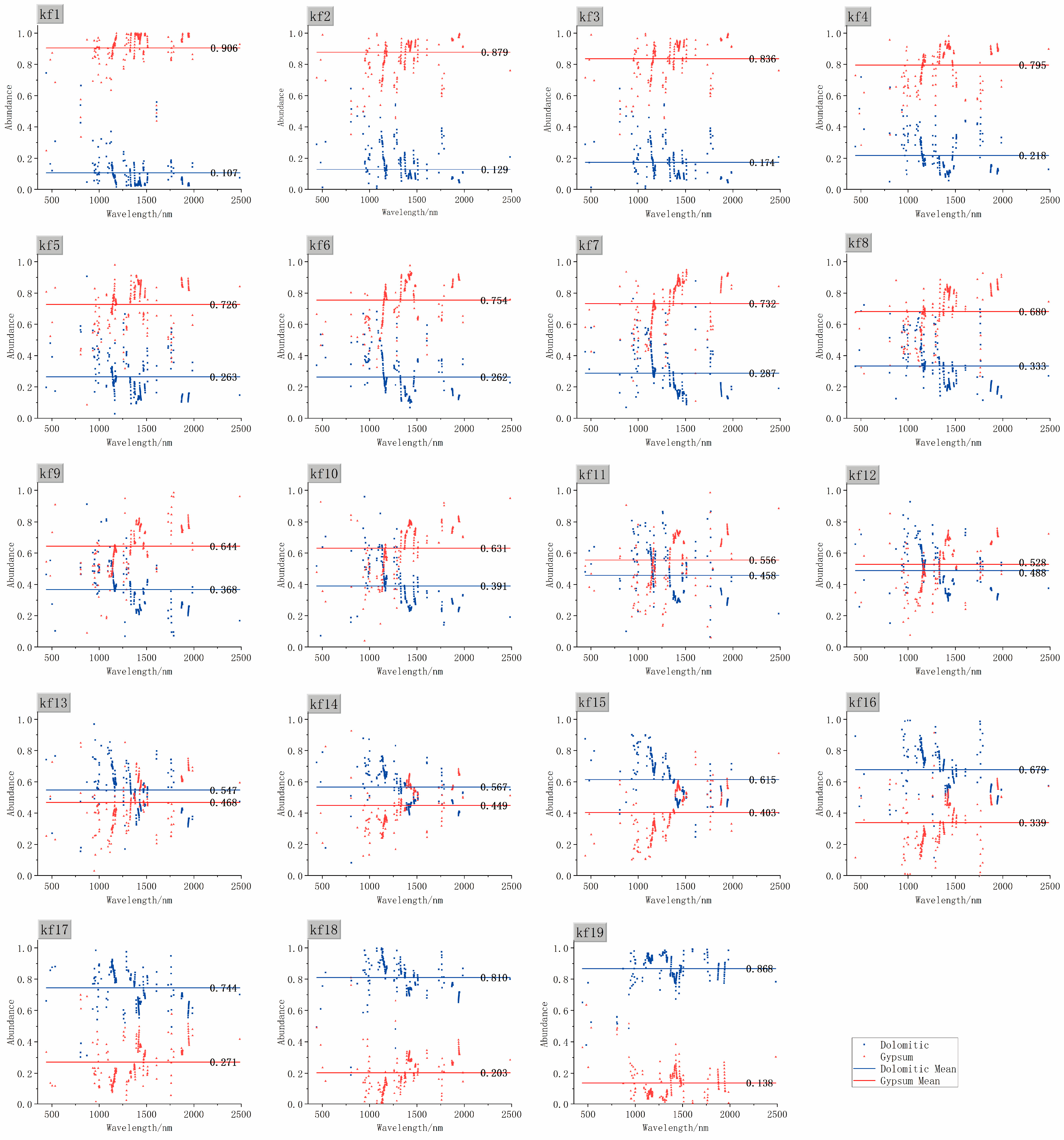
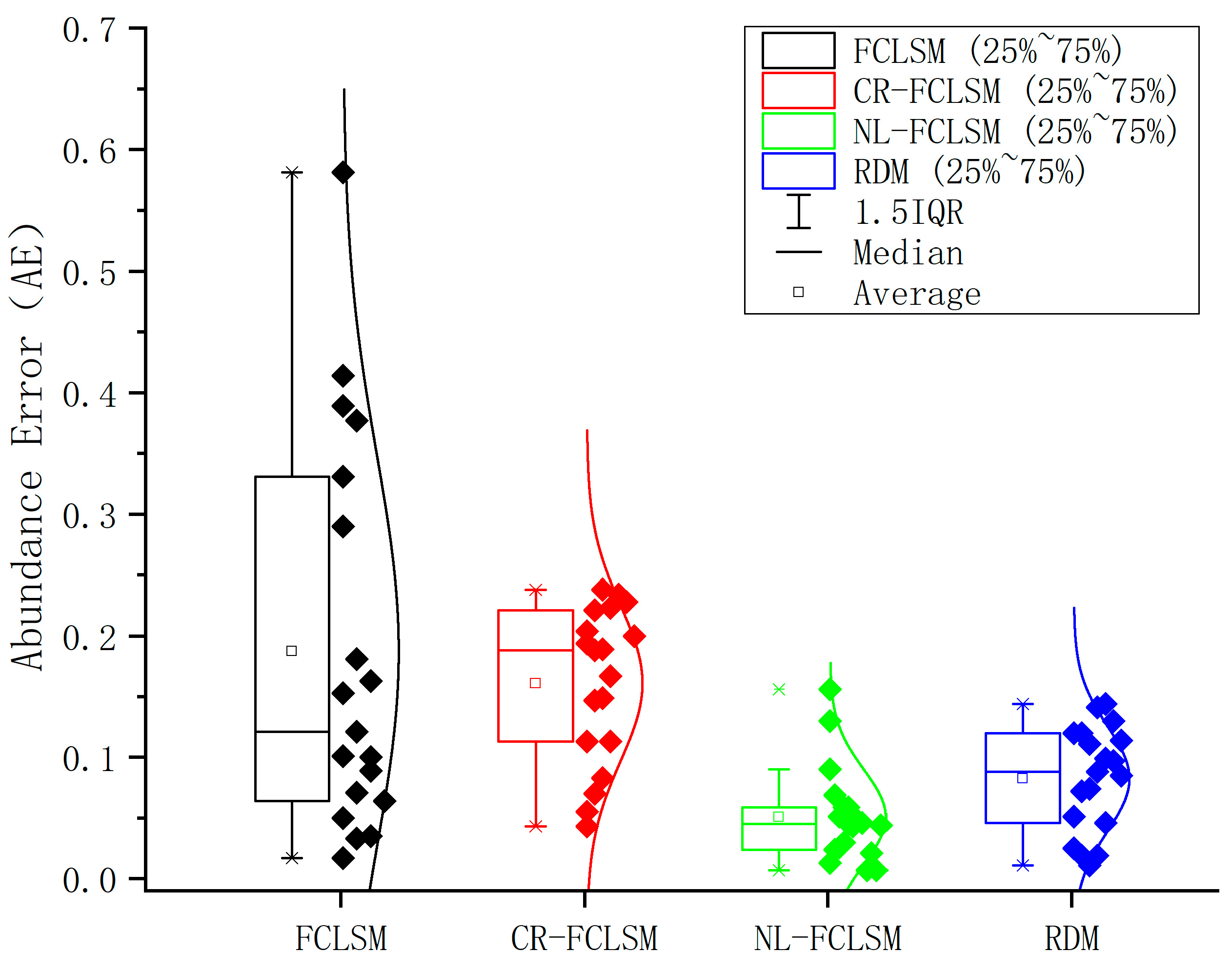
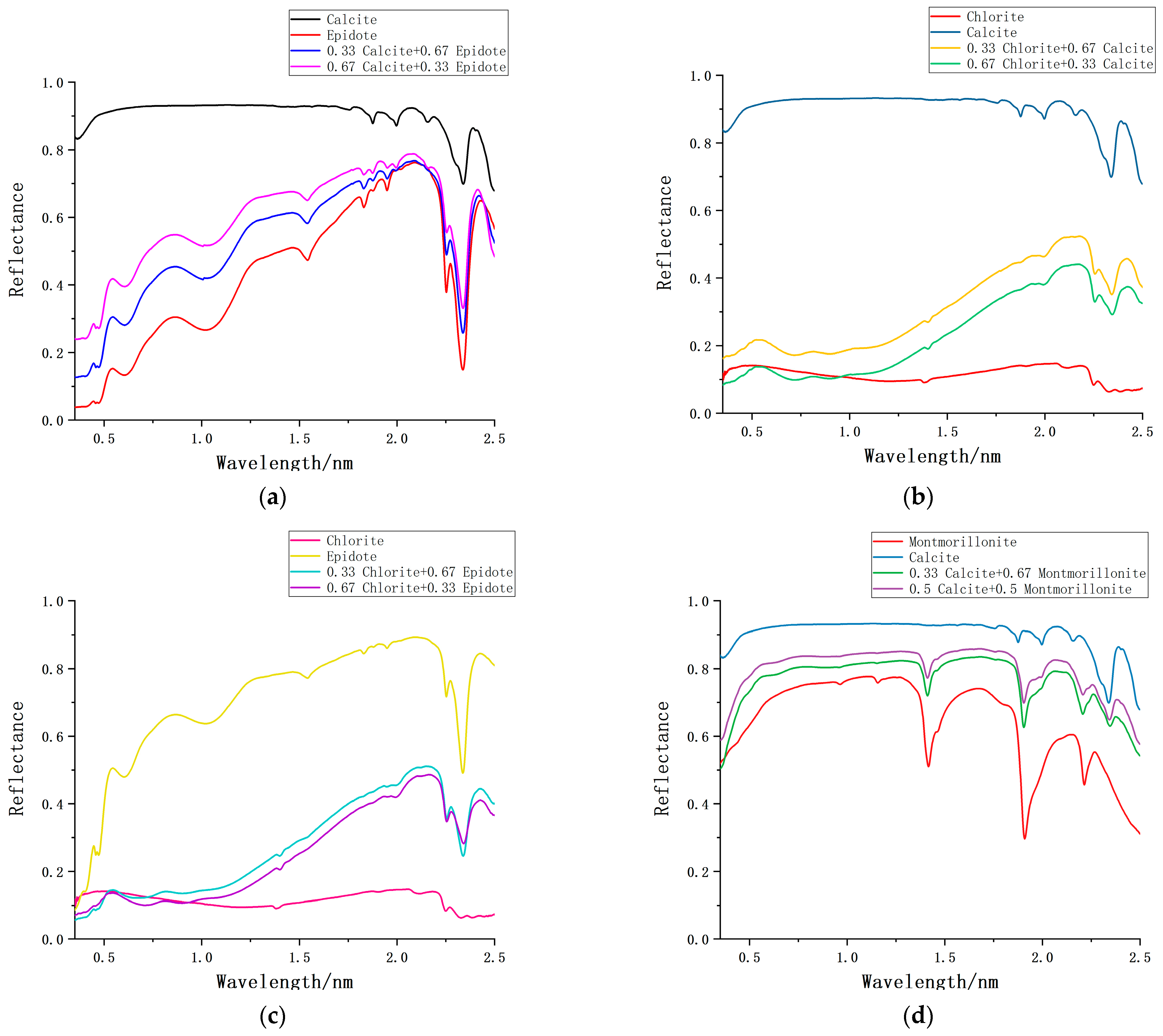
| Sample Number | Mixing Ratio | Weight of Dolomite (g) | Weight of Gypsum (g) |
|---|---|---|---|
| kf1 | 5% Dolomite, 95% Gypsum | 2.00 | 32.87 |
| kf2 | 10% Dolomite, 90% Gypsum | 4.00 | 31.14 |
| kf3 | 15% Dolomite, 85% Gypsum | 6.00 | 29.41 |
| kf4 | 20% Dolomite, 80% Gypsum | 8.00 | 27.68 |
| kf5 | 25% Dolomite, 75% Gypsum | 10.00 | 25.95 |
| kf6 | 30% Dolomite, 70% Gypsum | 12.00 | 24.22 |
| kf7 | 35% Dolomite, 65% Gypsum | 14.00 | 22.49 |
| kf8 | 40% Dolomite, 60% Gypsum | 16.00 | 20.76 |
| kf9 | 45% Dolomite, 55% Gypsum | 18.00 | 19.03 |
| kf10 | 50% Dolomite, 50% Gypsum | 20.00 | 17.38 |
| kf11 | 55% Dolomite, 45% Gypsum | 22.00 | 15.57 |
| kf12 | 60% Dolomite, 40% Gypsum | 24.00 | 13.84 |
| kf13 | 65% Dolomite, 35% Gypsum | 26.00 | 12.11 |
| kf14 | 70% Dolomite, 30% Gypsum | 28.00 | 10.38 |
| kf15 | 75% Dolomite, 25% Gypsum | 30.00 | 8.65 |
| kf16 | 80% Dolomite, 20% Gypsum | 32.00 | 6.92 |
| kf17 | 85% Dolomite, 15% Gypsum | 34.00 | 5.19 |
| kf18 | 90% Dolomite, 10% Gypsum | 36.00 | 3.46 |
| kf19 | 95% Dolomite, 5% Gypsum | 38.00 | 1.73 |
| Sample | Actual Abundance | CR-FCLSM | NL-FCLSM | RDM | |||
|---|---|---|---|---|---|---|---|
| Unmixing Abundance | AE | Unmixing Abundance | AE | Unmixing Abundance | AE | ||
| kf1 | 0.05 | 0.007 | 0.043 | 0.140 | 0.090 | 0.107 | 0.057 |
| kf2 | 0.1 | 0.045 | 0.055 | 0.087 | 0.013 | 0.129 | 0.029 |
| kf3 | 0.15 | 0.080 | 0.070 | 0.219 | 0.069 | 0.174 | 0.024 |
| kf4 | 0.2 | 0.117 | 0.083 | 0.224 | 0.024 | 0.218 | 0.018 |
| kf5 | 0.25 | 0.137 | 0.113 | 0.120 | 0.130 | 0.263 | 0.013 |
| kf6 | 0.3 | 0.153 | 0.147 | 0.274 | 0.026 | 0.262 | 0.038 |
| kf7 | 0.35 | 0.202 | 0.149 | 0.319 | 0.030 | 0.287 | 0.063 |
| kf8 | 0.4 | 0.206 | 0.194 | 0.349 | 0.051 | 0.333 | 0.067 |
| kf9 | 0.45 | 0.262 | 0.188 | 0.391 | 0.059 | 0.368 | 0.082 |
| kf10 | 0.5 | 0.297 | 0.204 | 0.455 | 0.045 | 0.391 | 0.109 |
| kf11 | 0.55 | 0.361 | 0.189 | 0.394 | 0.156 | 0.458 | 0.092 |
| kf12 | 0.6 | 0.379 | 0.221 | 0.557 | 0.043 | 0.488 | 0.112 |
| kf13 | 0.65 | 0.412 | 0.238 | 0.602 | 0.048 | 0.547 | 0.103 |
| kf14 | 0.7 | 0.477 | 0.223 | 0.654 | 0.046 | 0.567 | 0.133 |
| kf15 | 0.75 | 0.516 | 0.234 | 0.691 | 0.059 | 0.615 | 0.135 |
| kf16 | 0.8 | 0.572 | 0.228 | 0.793 | 0.007 | 0.679 | 0.121 |
| kf17 | 0.85 | 0.650 | 0.200 | 0.871 | 0.021 | 0.744 | 0.106 |
| kf18 | 0.9 | 0.733 | 0.167 | 0.907 | 0.007 | 0.810 | 0.090 |
| kf19 | 0.95 | 0.837 | 0.113 | 0.906 | 0.044 | 0.868 | 0.082 |
| Mean | / | / | 0.161 | / | 0.051 | / | 0.078 |
| Sample | Actual Abundance | CR-FCLSM | NL-FCLSM | RDM | |||
|---|---|---|---|---|---|---|---|
| Unmixing Abundance | AE | Unmixing Abundance | AE | Unmixing Abundance | AE | ||
| kf1 | 0.95 | 0.993 | 0.043 | 0.860 | 0.090 | 0.906 | 0.044 |
| kf2 | 0.9 | 0.955 | 0.055 | 0.913 | 0.013 | 0.879 | 0.021 |
| kf3 | 0.85 | 0.920 | 0.070 | 0.781 | 0.069 | 0.836 | 0.014 |
| kf4 | 0.8 | 0.883 | 0.083 | 0.777 | 0.024 | 0.795 | 0.005 |
| kf5 | 0.75 | 0.863 | 0.113 | 0.880 | 0.130 | 0.726 | 0.024 |
| kf6 | 0.7 | 0.847 | 0.147 | 0.726 | 0.026 | 0.754 | 0.054 |
| kf7 | 0.65 | 0.799 | 0.149 | 0.680 | 0.030 | 0.732 | 0.082 |
| kf8 | 0.6 | 0.794 | 0.194 | 0.651 | 0.051 | 0.680 | 0.080 |
| kf9 | 0.55 | 0.738 | 0.188 | 0.609 | 0.059 | 0.644 | 0.094 |
| kf10 | 0.5 | 0.704 | 0.204 | 0.545 | 0.045 | 0.631 | 0.131 |
| kf11 | 0.45 | 0.639 | 0.189 | 0.606 | 0.156 | 0.556 | 0.106 |
| kf12 | 0.4 | 0.621 | 0.221 | 0.443 | 0.043 | 0.528 | 0.128 |
| kf13 | 0.35 | 0.588 | 0.238 | 0.398 | 0.048 | 0.468 | 0.118 |
| kf14 | 0.3 | 0.523 | 0.223 | 0.346 | 0.046 | 0.449 | 0.149 |
| kf15 | 0.25 | 0.484 | 0.234 | 0.309 | 0.059 | 0.403 | 0.153 |
| kf16 | 0.2 | 0.428 | 0.228 | 0.207 | 0.007 | 0.339 | 0.139 |
| kf17 | 0.15 | 0.350 | 0.200 | 0.129 | 0.021 | 0.271 | 0.121 |
| kf18 | 0.1 | 0.267 | 0.167 | 0.093 | 0.007 | 0.203 | 0.103 |
| kf19 | 0.05 | 0.163 | 0.113 | 0.094 | 0.044 | 0.138 | 0.088 |
| Mean | / | / | 0.161 | / | 0.051 | / | 0.087 |
| Mixed Minerals | FCLSM | NL-FCLSM | ||||
|---|---|---|---|---|---|---|
| Unmixing Abundance/a1 | Unmixing Abundance/a2 | AE | Unmixing Abundance/a1 | Unmixing Abundance/a2 | AE | |
| 0.33 Calcite + 0.67 Epidote | 0.202 | 0.798 | 0.128 | 0.369 | 0.631 | 0.039 |
| 0.67 Calcite + 0.33 Epidote | 0.346 | 0.654 | 0.324 | 0.550 | 0.445 | 0.115 |
| 0.33 Chlorite + 0.67 Calcite | 0.245 | 0.755 | 0.085 | 0.545 | 0.455 | 0.215 |
| 0.67 Chlorite + 0.33 Calcite | 0.146 | 0.854 | 0.524 | 0.713 | 0.287 | 0.043 |
| 0.33 Chlorite + 0.67 Epidote | 0.698 | 0.302 | 0.368 | 0.539 | 0.462 | 0.209 |
| 0.67 Chlorite + 0.33 Epidote | 0.742 | 0.258 | 0.072 | 0.602 | 0.398 | 0.068 |
| 0.33 Calcite + 0.67 Montmorillonite | 0.495 | 0.505 | 0.165 | 0.421 | 0.580 | 0.091 |
| 0.5 Calcite + 0.5 Montmorillonite | 0.623 | 0.377 | 0.123 | 0.304 | 0.696 | 0.196 |
| Mean | \ | \ | 0.224 | \ | \ | 0.122 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Duan, L.; Zhang, Y.; Li, H.; Li, D.; Li, Y. Applicability Analysis with the Improved Spectral Unmixing Models Based on the Measured Hyperspectral Data of Mixed Minerals. Minerals 2025, 15, 715. https://doi.org/10.3390/min15070715
Zhang H, Duan L, Zhang Y, Li H, Li D, Li Y. Applicability Analysis with the Improved Spectral Unmixing Models Based on the Measured Hyperspectral Data of Mixed Minerals. Minerals. 2025; 15(7):715. https://doi.org/10.3390/min15070715
Chicago/Turabian StyleZhang, Haonan, Lizeng Duan, Yang Zhang, Huayu Li, Donglin Li, and Yan Li. 2025. "Applicability Analysis with the Improved Spectral Unmixing Models Based on the Measured Hyperspectral Data of Mixed Minerals" Minerals 15, no. 7: 715. https://doi.org/10.3390/min15070715
APA StyleZhang, H., Duan, L., Zhang, Y., Li, H., Li, D., & Li, Y. (2025). Applicability Analysis with the Improved Spectral Unmixing Models Based on the Measured Hyperspectral Data of Mixed Minerals. Minerals, 15(7), 715. https://doi.org/10.3390/min15070715






