Controlling Parameters of Acoustic Velocity in Organic-Rich Mudstones (Vaca Muerta Formation, Argentina)
Abstract
1. Introduction
2. Geologic Setting
3. Dataset
4. Experimental Setup
5. Results
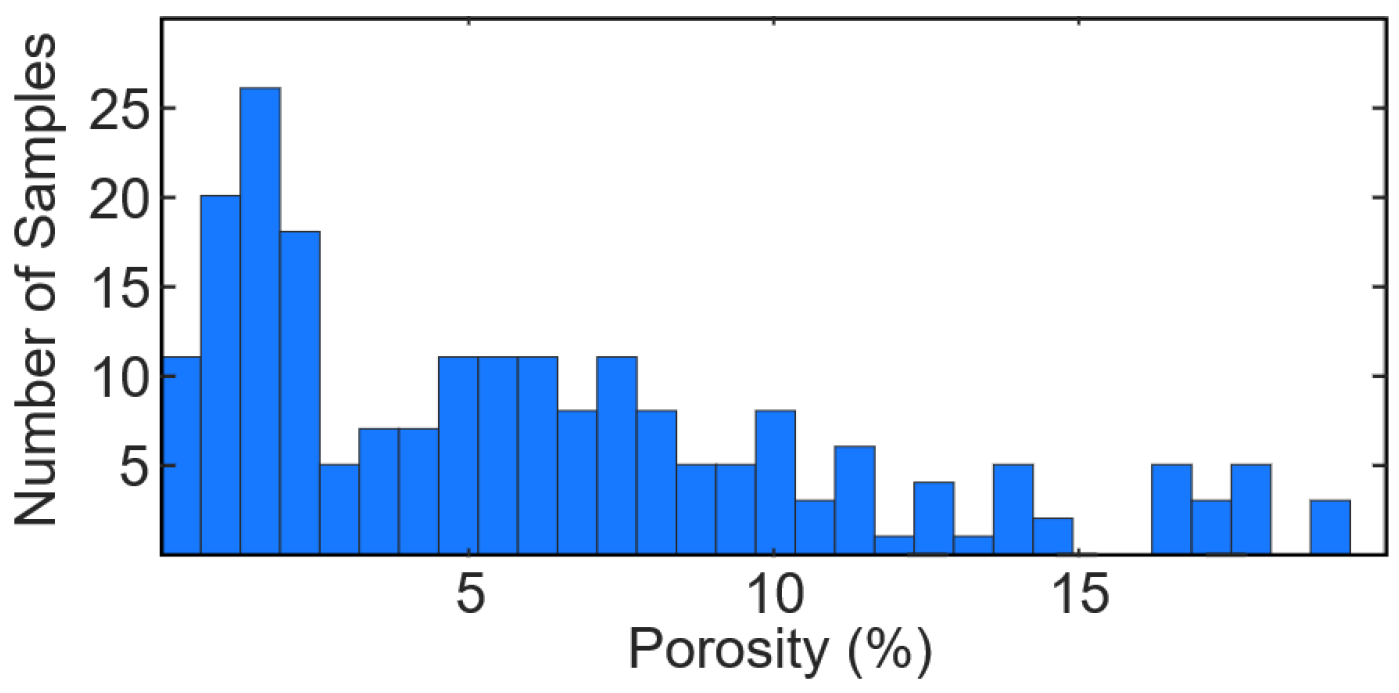
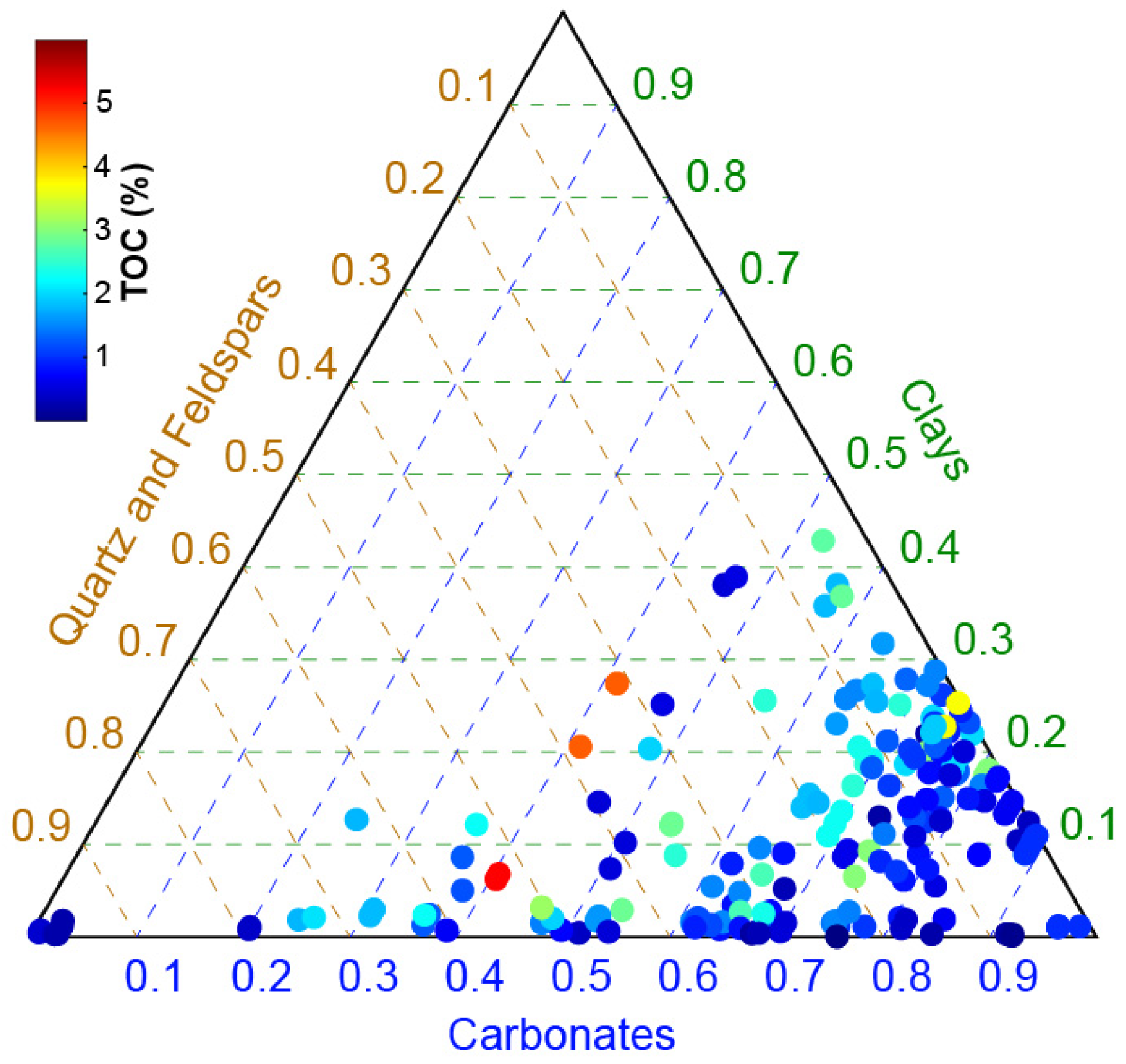
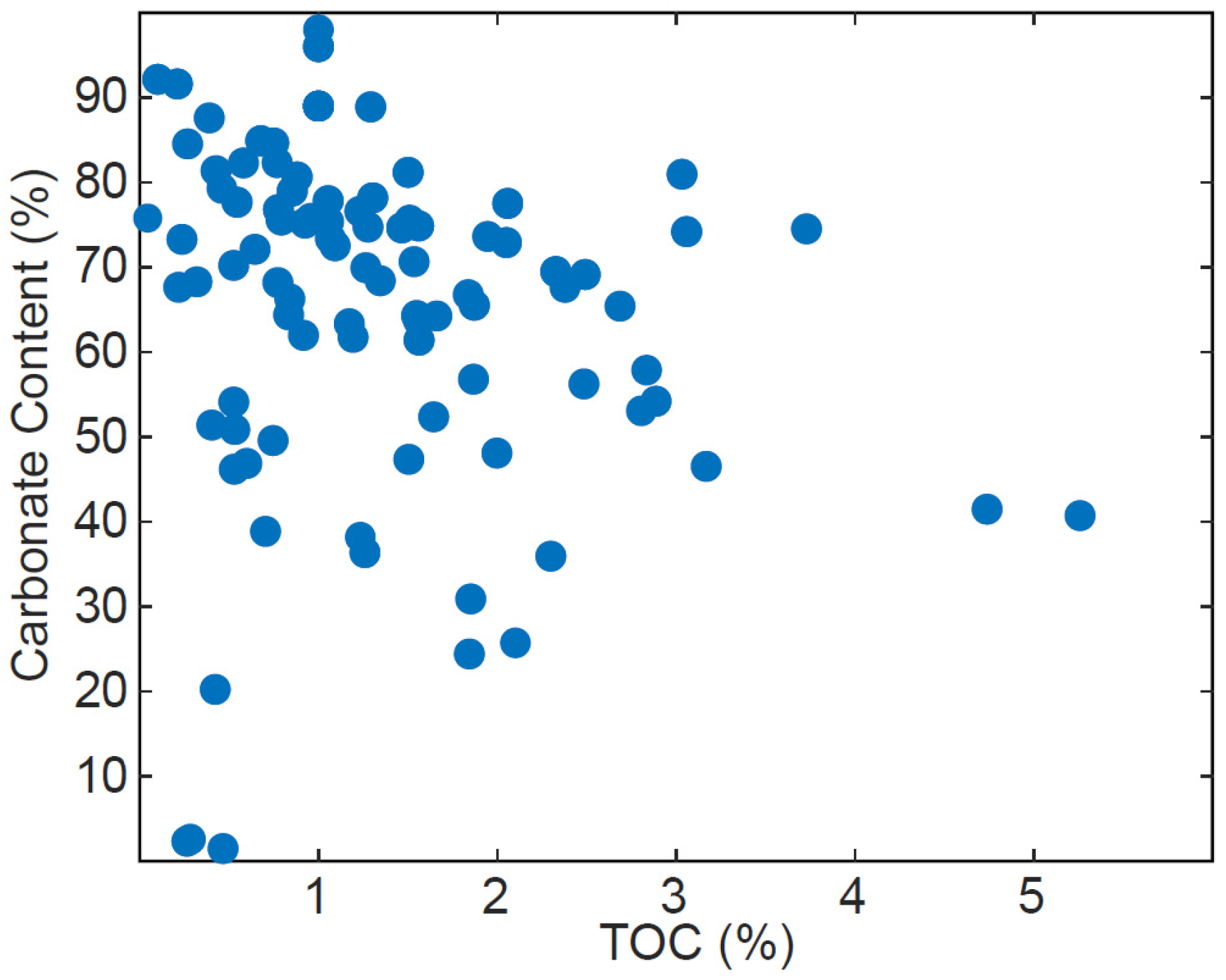
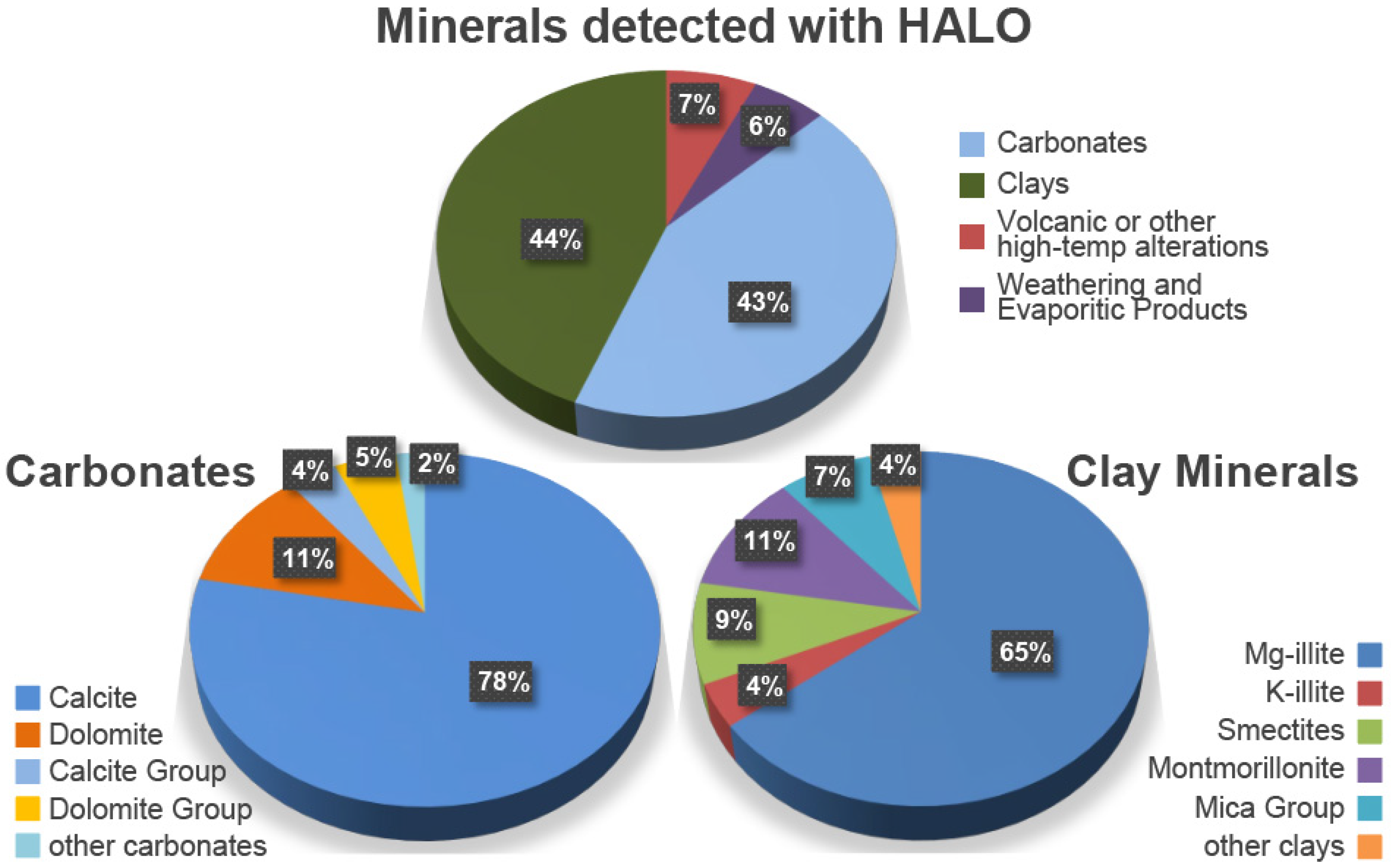
5.1. Porosity, Carbonate, TOC, and Mineral Composition
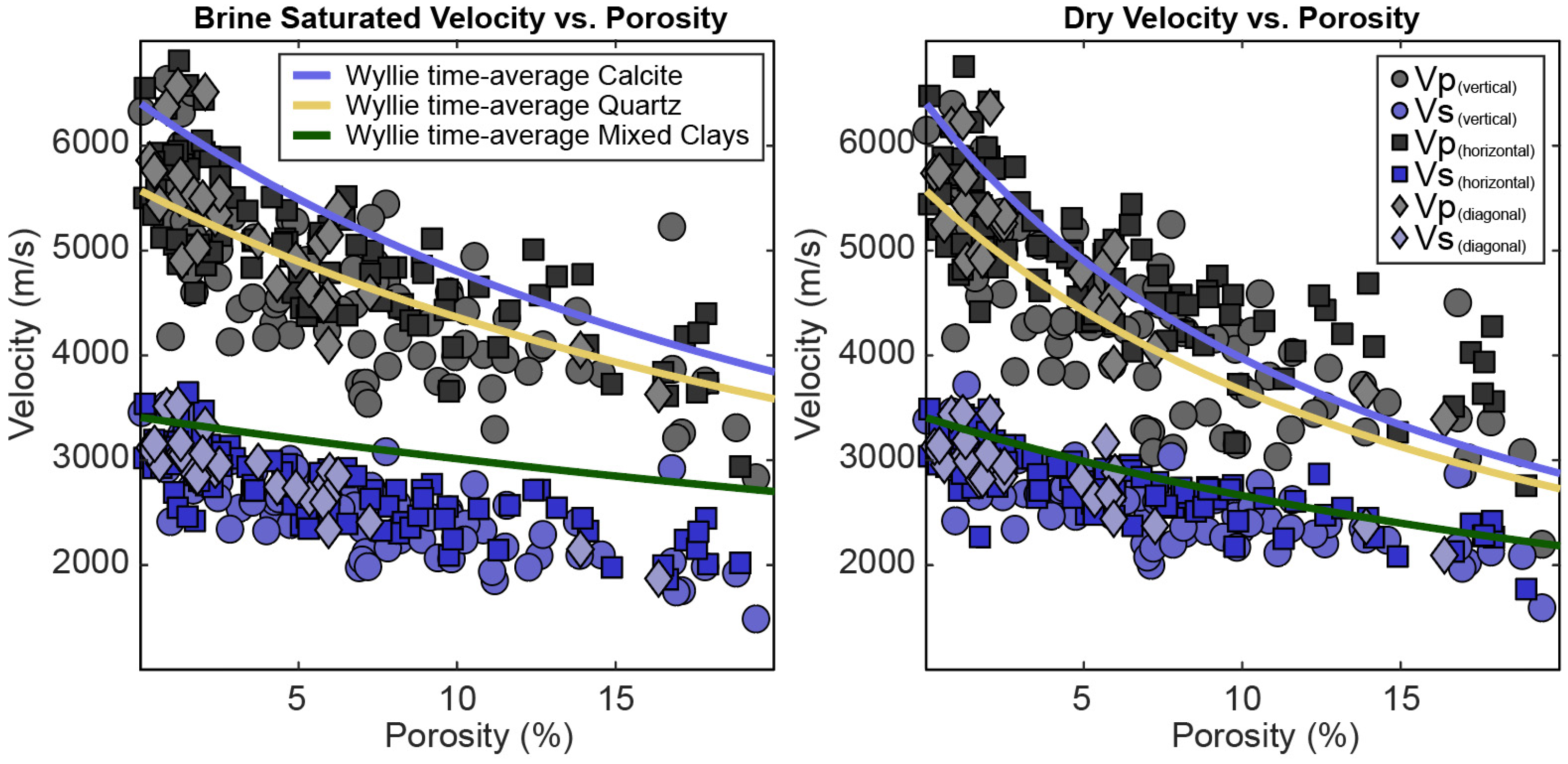
5.2. Compressional and Shear Wave Velocity
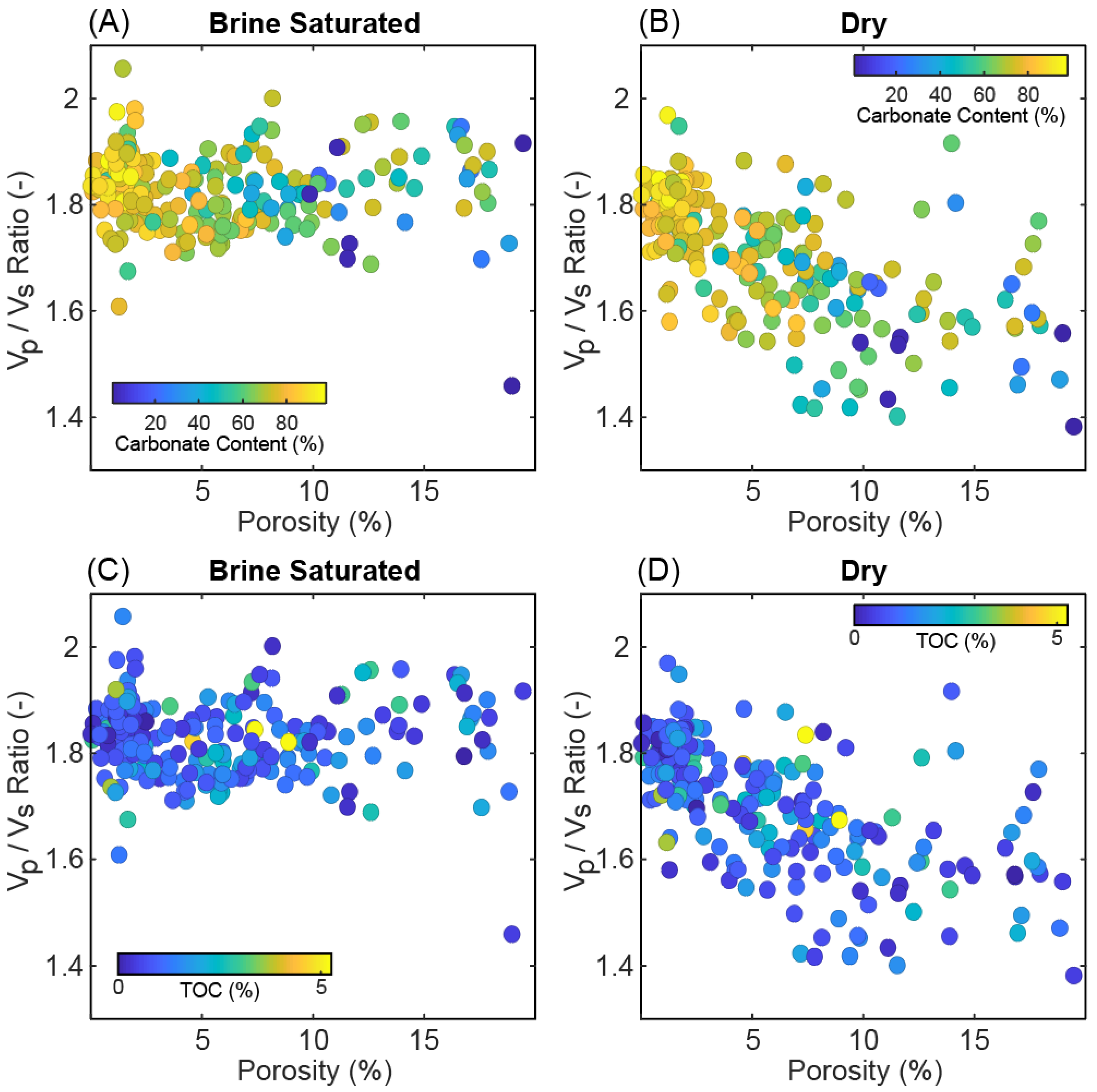
5.3. VP/VS Ratios
5.4. Pressure Sensitivity of Compressional and Shear Wave Velocity
6. Discussion
6.1. Mineralogy
6.2. Factors Controlling Velocity
6.3. VP/VS Ratio
6.4. Pressure Sensitivity of Compressional and Shear Velocity
7. Conclusions
8. Declaration of Generative AI in Scientific Writing
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sayers, C.M.; Dasgupta, S. A predictive anisotropic rock-physics model for estimating elastic rock properties of unconventional shale reservoirs. Lead. Edge 2019, 38, 358–365. [Google Scholar] [CrossRef]
- Massaro, A.S.; Espinoza, D.N.; Frydman, M.; Barredo, S.; Cuervo, S. Analyzing a suitable elastic geomechanical model for Vaca Muerta Formation. J. South Am. Earth Sci. 2017, 79, 472–488. [Google Scholar] [CrossRef]
- Wyllie, M.; Gregory, A.; Gardner, L. Elastic wave velocities in heterogeneous and porous media. Geophysics 1956, 21, 41–70. [Google Scholar] [CrossRef]
- Wyllie, M.; Gregory, A.; Gardner, G. An experimental investigation of factors affecting elastic wave velocities in porous media. Geophysics 1958, 23, 459–493. [Google Scholar] [CrossRef]
- Wyllie, M.; Gardner, G.; Gregory, A. Studies of elastic wave attenuation in porous media. Geophysics 1962, 27, 569–589. [Google Scholar] [CrossRef]
- Raymer, L.; Hunt, E.; Gardner, J.S. An Improved Sonic Transit Time-to-Porosity Transform. In Proceedings of the SPWLA 21st Annual Logging Symposium, Lafayette, LA, USA, 8–11 July 1980. [Google Scholar]
- Pickett, G.R. Acoustic character logs and their applications in formation evaluation. J. Pet. Technol. 1963, 15, 659–667. [Google Scholar] [CrossRef]
- Gardner, G.; Gardner, L.; Gregory, A. Formation velocity and density—The diagnostic basics for stratigraphic traps. Geophysics 1974, 39, 770–780. [Google Scholar] [CrossRef]
- EIA. Shale Oil and Shale Gas Resources are Globally Abundant. 2014. Available online: www.eia.gov/todayinenergy/detail.php?id=14431 (accessed on 25 June 2025).
- Tenaglia, M.; Eberli, G.P.; Weger, R.J.; Blanco, L.R.; Sánchez, L.E.R.; Swart, P.K. Total organic carbon quantification from wireline logging techniques: A case study in the Vaca Muerta Formation, Argentina. J. Pet. Sci. Eng. 2020, 194, 107489. [Google Scholar] [CrossRef]
- Santana, T.; Alimonti, L.; Marino, J. Seismic Reservoir Characterization to Delineate Areas for Early Development, Vaca Muerta Formation, Argentina. In Proceedings of the AAPG Annual Convention and Exhibition, San Antonio, TX, USA, 19–22 May 2019. [Google Scholar]
- Zeller, M.; Reid, S.B.; Eberli, G.P.; Weger, R.J.; Massaferro, J.L. Sequence architecture and heterogeneities of a field–scale Vaca Muerta analog (Neuquén Basin, Argentina)–From outcrop to synthetic seismic. Mar. Pet. Geol. 2015, 66, 829–847. [Google Scholar] [CrossRef]
- Acevedo, H.; Bande, A. Characterization of lower Vaca Muerta at Fortín de Piedra in Neuquén Basin, Argentina. Lead. Edge 2018, 37, 255–260. [Google Scholar] [CrossRef]
- Ravazzoli, C.L.; Blanco, G. A rock physics analysis based on inversion of poroelastic Brown and Korringa parameters in Vaca Muerta shale: Theoretical aspects and applications. J. Pet. Sci. Eng. 2021, 203, 108615. [Google Scholar] [CrossRef]
- Cuervo, S.; Lombardo, E.; Vallejo, D.; Crousse, L.; Hernandez, C.; Mosse, L. Towards a Simplified Petrophysical Model for the Vaca Muerta Formation. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; pp. 778–796. [Google Scholar]
- Yüksek, M.K.; Eberli, G.P.; Rueda, L.E.; Rodriguez-Blanco, L.; McNeill, D.F.; Weger, R.J. Mineralogical influences on acoustic velocities in the Vaca Muerta Formation, Neuquén Basin, Argentina: Insights from ultrasonic measurements. In Proceedings of the Asian Seismological Commission–15th General Assembly of the Asian Seismological Commission, Antalya, Turkey, 3–7 November 2024. [Google Scholar]
- Eberli, G.P.; Baechle, G.T.; Anselmetti, F.S.; Incze, M.L. Factors controlling elastic properties in carbonate sediments and rocks. Lead. Edge 2003, 22, 654–660. [Google Scholar] [CrossRef]
- Weger, R.J.; Eberli, G.P.; Baechle, G.T.; Massaferro, J.L.; Sun, Y.-F. Quantification of pore structure and its effect on sonic velocity and permeability in carbonates. AAPG Bull. 2009, 93, 1297–1317. [Google Scholar] [CrossRef]
- Kenter, J.A.; Podladchikov, F.; Reinders, M.; Van der Gaast, S.J.; Fouke, B.W.; Sonnenfeld, M.D. Parameters controlling sonic velocities in a mixed carbonate-siliciclastics Permian shelf-margin (upper San Andres formation, Last Chance Canyon, New Mexico). Geophysics 1997, 62, 505–520. [Google Scholar] [CrossRef]
- Baechle, G.T.; Eberli, G.P.; Weger, R.J.; Massaferro, J.L. Changes in dynamic shear moduli of carbonate rocks with fluid substitution. Geophysics 2009, 74, E135–E147. [Google Scholar] [CrossRef]
- Yrigoyen, M. Hydrocarbon Resources of Argentina. In Proceedings of the World Petroleum Congress, Buenos Aires, Petrotecnia, 20–25 October 1991; pp. 38–54. [Google Scholar]
- Howell, J.A.; Schwarz, E.; Spalletti, L.A.; Veiga, G.D. The Neuquén Basin: An Overview. Geol. Soc. Lond. Spec. Publ. 2005, 252, 1–14. [Google Scholar] [CrossRef]
- Di Benedetto, M.; Biscayart, P.; Zunino, J.; Soldo, J. Geological Setting of the Vaca Muerta Fm, Neuquen Basin-A World class Shale Play. In Proceedings of the 76th EAGE Conference and Exhibition-Workshops, Amsterdam, The Netherlands, 16–19 June 2014; p. cp–401-00051. [Google Scholar]
- Kietzmann, D.A.; Palma, R.M.; Riccardi, A.C.; Martín-Chivelet, J.; López-Gómez, J. Sedimentology and sequence stratigraphy of a Tithonian–Valanginian carbonate ramp (Vaca Muerta Formation): A misunderstood exceptional source rock in the Southern Mendoza area of the Neuquén Basin, Argentina. Sediment. Geol. 2014, 302, 64–86. [Google Scholar] [CrossRef]
- Wang, H.; Feng, M.; Xiaoguang, T.; Zuodong, L.; Zhang, X.; Zhenzhen, W.; Denghua, L.; Bo, W.; Yinfu, X.; Liuyan, Y. Assessment of global unconventional oil and gas resources. Pet. Explor. Dev. 2016, 43, 925–940. [Google Scholar] [CrossRef]
- Fantin, M.; Crousse, L.; Cuervo, S.; Vallejo, D.; Gonzalez Tomassini, F.; Reijenstein, H.; Lipinski, C. Vaca Muerta Stratigraphy in central Neuquén Basin: Impact on emergent unconventional project. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014; p. URTEC–1923793-MS. [Google Scholar]
- Garcia, M.N.; Sorenson, F.; Bonapace, J.C.; Motta, F.; Bajuk, C.; Stockman, H. Vaca Muerta Shale Reservoir Characterization and Description: The Starting Point for Development of a Shale Play with very Good Possibilities for a Successful Project. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August, 2013. [Google Scholar]
- Weger, R.J.; Murray, S.T.; McNeill, D.F.; Swart, P.K.; Eberli, G.P.; Blanco, L.R.; Tenaglia, M.; Rueda, L.E. Paleothermometry and distribution of calcite beef in the Vaca Muerta Formation, Neuquen Basin, Argentina. AAPG Bull. 2019, 103, 931–950. [Google Scholar] [CrossRef]
- Rodriguez Blanco, L.; Eberli, G.P.; Weger, R.J.; Swart, P.K.; Tenaglia, M.; Sanchez, L.E.R.; McNeill, D.F. Periplatform ooze in a mixed siliciclastic-carbonate system-Vaca Muerta Formation, Argentina. Sediment. Geol. 2020, 396, 105521. [Google Scholar] [CrossRef]
- Zeller, M. Facies, Geometries and Sequence Stratigraphy of the Mixed Carbonate–Siliciclastic Quintuco–Vaca Muerta System in the Neuquén Basin, Argentina: An Integrated Approach; University of Miami: Coral Gables, FL, USA, 2013. [Google Scholar]
- Weger, R.J.; Eberli, G.P.; Rodriguez Blanco, L.; Tenaglia, M.; Swart, P.K. Finding a VOICE in the Southern Hemisphere: A New Record of global organic carbon? GSA Bull. 2023, 135, 2107–2120. [Google Scholar] [CrossRef]
- Rodriguez Blanco, L. Distribution and Source of Carbonate-Rich Intervals within the Vaca Muerta-Quintuco Mixed System, Neuquén Basin, Argentina. University of Miami: Coral Gables, FL, USA, 2016. [Google Scholar]
- Eberli, G.P.; Weger, R.J.; Tenaglia, M.; Rueda, L.; Rodriguez, L.; Zeller, M.; McNeill, D.; Murray, S.; Swart, P.K. The Unconventional Play in the Neuquén Basin, Argentina–Insights from the Outcrop for the Subsurface. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; pp. 2208–2219. [Google Scholar]
- Birch, F. The velocity of compressional waves in rocks to 10 kilobars: 1. J. Geophys. Res. 1960, 65, 1083–1102. [Google Scholar] [CrossRef]
- Keng, E.Y. Air and belium pycnometer. Powder Technol. 1969, 3, 179–180. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Gurevich, B. A simple derivation of the effective stress coefficient for seismic velocities in porous rocks. Geophysics 2004, 69, 393–397. [Google Scholar] [CrossRef]
- Grana, D. Pressure–velocity relations in reservoir rocks: Modified MacBeth’s equation. J. Appl. Geophys. 2016, 132, 234–241. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Somerton, W.H.; King, M.S. Compressibility of porous rocks. J. Geophys. Res. Solid Earth 1986, 91, 12765–12777. [Google Scholar] [CrossRef]
- Gassmann, F. Elastic waves through a packing of spheres. Geophysics 1951, 16, 673–685. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook; Tools for Seismic Analysis in Porous Media; Cambridge University Press: Cambridge, UK, 1998; Volume 1, p. 329. [Google Scholar]
- Blackwood, D.; Hathaway, J.; Paskevich, V.; Poppe, L. A Laboratory Manual for X-Ray Powder Diffraction. Acetic Acid Treat. Remov. Carbonates 2001, 1, 1–88. Available online: https://pubs.usgs.gov/of/2001/of01-041/index.htm (accessed on 25 June 2025).
- Dang, S.T.; Sondergeld, C.H.; Rai, C.S. A New Approach to Measure Organic Density. In Proceedings of the Unconventional Resources Technology Conference (URTEC), Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Osipov, V. Density of clay minerals. Soil Mech. Found. Eng. 2011, 48, 231. [Google Scholar] [CrossRef]
- Baechle, G.T.; Weger, R.J.; Eberli, G.P.; Massaferro, J.L.; Sun, Y.-F. Changes of shear moduli in carbonate rocks: Implications for Gassmann applicability. Lead. Edge 2005, 24, 507–510. [Google Scholar] [CrossRef]
- Castagna, J.P. AVO Analysis-Tutorial and Review. In Offset Dependent Reflectivity-Theory and Practice of AVO; Castagna, J.P., Backus, M.M., Eds.; Investigations in Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 1993; pp. 3–36. [Google Scholar]
- Minear, J.W. Clay Models and Acoustic Velocities. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 26 September 1982. [Google Scholar]
- Han, D.-h.; Nur, A.; Morgan, D. Effects of Porosity and Clay Content on Wave Velocities in Sandstones. Geophysics 1986, 51, 2093–2107. [Google Scholar] [CrossRef]
- Tosaya, C.; Nur, A. Effects of diagenesis and clays on compressional velocities in rocks. Geophys. Res. Lett. 1982, 9, 5–8. [Google Scholar] [CrossRef]
- Castagna, J.P.; Batzle, M.L.; Eastwood, R.L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics 1985, 50, 571–581. [Google Scholar] [CrossRef]
- Vernik, L.; Nur, A. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics 1992, 57, 727–735. [Google Scholar] [CrossRef]
- Marion, D.; Nur, A.; Yin, H.; Han, D.-H. Compressional velocity and porosity in sand-clay mixtures. Geophysics 1992, 57, 554–563. [Google Scholar] [CrossRef]
- Kenter, J.; Anselmetti, F.; Kramer, P.; Westphal, H.; Vandamme, M. Acoustic properties of "young" carbonate rocks, ODP leg 166 and boreholes Clino and Unda, western Great Bahama Bank. J. Sediment. Res. 2002, 72, 129–137. [Google Scholar] [CrossRef]
- Christensen, N.I.; Szymanski, D.L. Seismic properties and the origin of reflectivity from a classic Paleozoic sedimentary sequence, Valley and Ridge province, southern Appalachians. Geol. Soc. Am. Bull. 1991, 103, 277–289. [Google Scholar] [CrossRef]
- Craddock, P.R.; Mossé, L.; Bernhardt, C.; Ortiz, A.C.; Tomassini, F.G.; Saldungaray, P.; Pomerantz, A.E. Characterization and range of kerogen properties in the Vaca Muerta Formation, Neuquén Basin, Argentina. Org. Geochem. 2019, 129, 42–44. [Google Scholar] [CrossRef]
- Capelli, I.A.; Scasso, R.A.; Spangenberg, J.E.; Kietzmann, D.A.; Cravero, F.; Duperron, M.; Adatte, T. Mineralogy and geochemistry of deeply-buried marine sediments of the Vaca Muerta-Quintuco system in the Neuquen Basin (Chacay Melehue section), Argentina: Paleoclimatic and paleoenvironmental implications for the global Tithonian-Valanginian reconstructions. J. South Am. Earth Sci. 2021, 107, 103103. [Google Scholar] [CrossRef]
- Capelli, I.A.; Scasso, R.A.; Cravero, F.; Kietzmann, D.A.; Vallejo, D.; Adatte, T. Late-diagenetic clay mineral assemblages in carbonatized ash beds of the Vaca Muerta Formation (Neuquén Basin, Argentina): Insights into the diagenetic formation of chlorite. Mar. Pet. Geol. 2021, 132, 105207. [Google Scholar] [CrossRef]
- Reijenstein, H.M.; Dominguez, R.F.; Bande, A.; Vallejo, M.D.; Notta, R.; Guerberoff, D.; Lanusse, I.; Kohler, G.; Borgnia, M.; Benoit, S.; et al. Transecta Sísmica Regional del Sistema Vaca Muerta–Quintuco: Interpretación de Facies Sísmicas Basada en Impedancia Acústica y Litofacies Dominantes. In Proceedings of the Geología de la Formación Vaca Muerta, XX Congreso Geológico Argentino, San Miguel de Tucumán, Argentina, 7–11 August 2017. [Google Scholar]
- Kietzmann, D.A.; Ambrosio, A.L.; Suriano, J.; Alonso, M.S.; Tomassini, F.G.; Depine, G.; Repol, D. The Vaca Muerta–Quintuco system (Tithonian–Valanginian) in the Neuquén Basin, Argentina: A view from the outcrops in the Chos Malal fold and thrust belt. AAPG Bull. 2016, 100, 743–771. [Google Scholar] [CrossRef]
- Dominguez, R.F.; Lanusse-Noguera, I.; Continanzia, M.J.; Mykietiuk, K.; Ponce, C.; Pérez, G.; Guerello, R.; Caneva, M.; Di Benedetto, M.; Catuneanu, O.; et al. Organic-Rich Stratigraphic Units in the Vaca Muerta Formation, and Their Distribution and Characterization in the Neuquen Basin (Argentina). In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; pp. 1439–1450. [Google Scholar]
- Buijs, H.; Ponce, J. An Engineered Approach to Hydraulically Fracture the Vaca Muerta shale. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018; p. D021S005R002. [Google Scholar]
- Khadeeva, Y.; Vernik, L. Rock-physics model for unconventional shales. Lead. Edge 2014, 33, 318–322. [Google Scholar] [CrossRef]
- Sayers, C.M.; Fisher, K.; Walsh, J.J. Sensitivity of P-and S-impedance to the presence of kerogen in the Eagle Ford Shale. Lead. Edge 2015, 34, 1482–1486. [Google Scholar] [CrossRef]
- Vernik, L.; Castagna, J.; Omovie, S.J. S-wave velocity prediction in unconventional shale reservoirs. Geophysics 2018, 83, MR35–MR45. [Google Scholar] [CrossRef]
- Vernik, L.; Milovac, J. Rock physics of organic shales. Lead. Edge 2011, 30, 318–323. [Google Scholar] [CrossRef]
- Avseth, P.; Carcione, J.M. Rock-physics analysis of clay-rich source rocks on the Norwegian Shelf. Lead. Edge 2015, 34, 1340–1348. [Google Scholar] [CrossRef]
- Wyllie, M.R.J. The Fundamentals of Well Log Interpretation, 3d ed., rev. and reset. ed.; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Castagna, J.P.; Batzle, M.L.; Kan, T.K. Rock Physics-The link Between Rock Properties and AVO Response. In Offset Dependent Reflectivity-Theory and Practice of AVO; Castagna, J.P., Backus, M.M., Eds.; Investigations in Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 1993; pp. 135–171. [Google Scholar]
- Tatham, R.H. Vp/Vs and lithology. Geophysics 1982, 47, 336–344. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T. Comparison of the Krief and critical porosity models for prediction of porosity and V-P/V-S. Geophysics 1998, 63, 925–927. [Google Scholar] [CrossRef]
- Ødegaard, E.; Avseth, P. Interpretation of Elastic Inversion Results using Rock Physics Templates. In Proceedings of the 65th EAGE Conference & Exhibition, Stavanger, Norway, 2–5 June 2003; p. cp–6-00337. [Google Scholar]
- Ødegaard, E.; Avseth, P. Well log and seismic data analysis using rock physics templates. First Break 2004, 22, 37–44. [Google Scholar]
- Goodway, B.; Chen, T.; Downton, J. Improved AVO Fluid Detection and Lithology Discrimination using Lamé Petrophysical Parameters; “λρ”, “μρ”, and “λ/μ Fluid Stack”, from P and S Inversions. In SEG Technical Program Expanded Abstracts 1997; Society of Exploration Geophysicists: Houston, TX, USA, 1997; pp. 183–186. [Google Scholar]
- Russell, B.; Goodway, B.; Avseth, P. Poroelasticity and rock-physics templates. Interpretation 2025, 13, T139–T152. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Altowairqi, Y.; Rezaee, R.; Evans, B.; Urosevic, M. Shale elastic property relationships as a function of total organic carbon content using synthetic samples. J. Pet. Sci. Eng. 2015, 133, 392–400. [Google Scholar] [CrossRef]
- Raj, R.; Jaiswal, P.; Wang, Y.; Grammer, G.M.; Weger, R.J. How Nanopores Influence Dry-Frame VP Pressure Sensitivity. Front. Earth Sci. 2021, 9, 641815. [Google Scholar] [CrossRef]





| (A) | # of | Vpwet (m/s) | Vswet (m/s) | Vpwet/Vswet (-) |
|---|---|---|---|---|
| Samples | Mean [Min–Max] | Mean [Min–Max] | Mean [Min–Max] | |
| Horizontal | 96 | 5022 [2933–6816] | 2729 [1854–3643] | 1.84 [1.46–2.06] |
| Diagonal | 28 | 5188 [3625–6572] | 2854 [1862–3524] | 1.84 [1.46–2.06] |
| Vertical | 86 | 4610 [2826–6638] | 2548 [1475–3527] | 1.82 [1.61–1.96] |
| Total | 210 | 4875 [2826–6816] | 2672 [1475–3643] | 1.81 [1.67–2] |
| (B) | # of | Vpdry (m/s) | Vsdry (m/s) | Vpdry/Vsdry (-) |
| Samples | Mean [Min–Max] | Mean [Min–Max] | Mean [Min–Max] | |
| Horizontal | 95 | 4873 [2757–6762] | 2792 [1770–3490] | 1.74 [1.46–1.97] |
| Diagonal | 25 | 5039 [3393–6370] | 2892 [2093–3450] | 1.74 [1.46–1.97] |
| Vertical | 84 | 4313 [2198–6400] | 2617 [1591–3719] | 1.74 [1.54–1.85] |
| Total | 204 | 4663 [2198–6762] | 2732 [1591–3719] | 1.64 [1.38–1.85] |
| (C) | # of | Porosity (%) | ρg (g/cm3) | ρb (g/cm3) |
| Samples | Mean [Min–Max] | Mean [Min–Max] | Mean [Min–Max] | |
| Horizontal | 96 | 5.9 [0.1–18.9] | 2.65 [2.49–2.87] | 2.56 [2.33–2.81] |
| Diagonal | 28 | 4.0 [0.3–16.4] | 2.66 [2.56–2.98] | 2.59 [2.38–2.84] |
| Vertical | 86 | 6.0 [0.0–19.4] | 2.66 [2.47–2.91] | 2.54 [2.32–2.82] |
| Total | 210 | 6.1 [0–19.4] | 2.66 [2.47–2.98] | 2.56 [2.32–2.84] |
| (D) | # of | Carbonate Content (%) | TOC (%) | Clay Content (%) |
| Samples | Mean [Min–Max] | Mean [Min–Max] | Mean [Min–Max] | |
| Horizontal | 96 | 66.3 [0.8–96] | 1.3 [0–5.3] | 9.3 [0–40.1] |
| Diagonal | 28 | 74.6 [50.9–92.1] | 1.4 [0.1–3.1] | 11 [0.1–25.1] |
| Vertical | 86 | 64.8 [0.8–98] | 1.3 [0–5.3] | 9.5 [0–38.4] |
| Total | 210 | 66.6 [0.8–98] | 1.3 [0–5.3] | 9.5 [0–40.1] |
| (A) | 5 MPa to 40 MPa | |||||||
| Saturated | Dry | |||||||
| n | Mean | Median | n | Mean | Median | |||
| Vp | Vertical | 84 | 4.79% | 3.92% | 69 | 7.29% | 5.21% | |
| Horizontal | 97 | 3.54% | 2.70% | 80 | 4.70% | 3.45% | ||
| Diagonal | 27 | 3.50% | 2.72% | 25 | 5.68% | 4.08% | ||
| All Samples | 208 | 4.04% | 3.15% | 172 | 5.86% | 4.32% | ||
| Vs | Vertical | 84 | 5.79% | 4.20% | 69 | 5.48% | 4.71% | |
| Horizontal | 97 | 4.59% | 3.45% | 80 | 4.56% | 3.63% | ||
| Diagonal | 27 | 4.70% | 3.37% | 25 | 5.25% | 4.18% | ||
| All Samples | 208 | 5.09% | 3.87% | 172 | 5.02% | 4.16% | ||
| (B) | 5 MPa to 20 MPa | |||||||
| Saturated | Dry | |||||||
| n | Mean | Median | n | Mean | Median | |||
| Vp | Vertical | 85 | 2.86% | 2.25% | 68 | 4.15% | 3.01% | |
| Horizontal | 97 | 2.08% | 1.59% | 80 | 2.71% | 2.02% | ||
| Diagonal | 28 | 2.10% | 1.61% | 25 | 3.70% | 2.82% | ||
| All Samples | 210 | 2.40% | 1.87% | 173 | 3.42% | 2.52% | ||
| Vs | Vertical | 85 | 3.32% | 2.64% | 68 | 3.27% | 2.80% | |
| Horizontal | 97 | 2.84% | 2.19% | 80 | 2.87% | 2.26% | ||
| Diagonal | 28 | 3.00% | 2.36% | 25 | 3.39% | 2.69% | ||
| All Samples | 210 | 3.06% | 2.37% | 173 | 3.10% | 2.40% | ||
| (C) | 20 MPa to 40 MPa | |||||||
| Saturated | Dry | |||||||
| n | Mean | Median | n | Mean | Median | |||
| Vp | Vertical | 84 | 1.92% | 1.61% | 84 | 3.25% | 2.38% | |
| Horizontal | 97 | 1.41% | 1.07% | 96 | 2.07% | 1.54% | ||
| Diagonal | 27 | 1.41% | 0.94% | 25 | 1.92% | 1.50% | ||
| All Samples | 208 | 1.62% | 1.29% | 203 | 2.53% | 1.75% | ||
| Vs | Vertical | 84 | 2.14% | 1.62% | 84 | 2.26% | 1.78% | |
| Horizontal | 97 | 1.68% | 1.29% | 96 | 1.76% | 1.31% | ||
| Diagonal | 27 | 1.68% | 1.34% | 25 | 1.82% | 1.23% | ||
| All Samples | 208 | 1.87% | 1.42% | 203 | 1.97% | 1.50% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuksek, M.K.; Eberli, G.P.; McNeill, D.F.; Weger, R.J. Controlling Parameters of Acoustic Velocity in Organic-Rich Mudstones (Vaca Muerta Formation, Argentina). Minerals 2025, 15, 694. https://doi.org/10.3390/min15070694
Yuksek MK, Eberli GP, McNeill DF, Weger RJ. Controlling Parameters of Acoustic Velocity in Organic-Rich Mudstones (Vaca Muerta Formation, Argentina). Minerals. 2025; 15(7):694. https://doi.org/10.3390/min15070694
Chicago/Turabian StyleYuksek, Mustafa Kamil, Gregor P. Eberli, Donald F. McNeill, and Ralf J. Weger. 2025. "Controlling Parameters of Acoustic Velocity in Organic-Rich Mudstones (Vaca Muerta Formation, Argentina)" Minerals 15, no. 7: 694. https://doi.org/10.3390/min15070694
APA StyleYuksek, M. K., Eberli, G. P., McNeill, D. F., & Weger, R. J. (2025). Controlling Parameters of Acoustic Velocity in Organic-Rich Mudstones (Vaca Muerta Formation, Argentina). Minerals, 15(7), 694. https://doi.org/10.3390/min15070694





