Abstract
This study employs density functional theory (DFT) simulations to systematically investigate the structural and optoelectronic modifications induced by the substitution of metal ions (Mg2+, Ca2+, Mn2+, Fe2+/3+, Co2+, and Ni2+) in kaolinite. First-principles calculations reveal distinct substitution behaviors: Na-Ni (II)-1 exhibits the lowest cell energy, indicating superior structural stability, while Na-Mn (II)-1 demonstrates the most favorable substitution energy (−5.44 eV). XRD simulations of divalent substitutions show a positive correlation between atomic number and diffraction intensity at 8.778° and 9.774°, suggesting a spectral marker for substitution detection. Electronic structure analysis identifies significant bandgap reduction, with Na-Fe (II)-4 achieving an ultranarrow gap of 1.014 eV, attributed to spin-polarized d-orbital contributions. X-ray absorption fine-structure (XAFS) simulations further reveal metal-specific bond elongation, with Fe3+ substitutions preserving near-pristine coordination distances. These findings establish a comprehensive framework linking metal substitution to structural distortion and optoelectronic response, providing theoretical insights for optimizing kaolinite-based material properties through computational feature extraction.
1. Introduction
Intelligent photoelectric separation, facilitated by artificial intelligence advancements, exhibits operational superiority over traditional coal gangue separation techniques such as manual sorting, gravity separation, and flotation. This approach enables non-destructive testing, remote-control functionality, and adaptability to subsurface conditions [1,2]. The technology identifies materials through optical signal acquisition via cameras and subsequent image recognition algorithms, though environmental factors, including unstable illumination and airborne particulates, limit its reliability [3,4]. To mitigate these constraints, X-ray detection technology has been integrated into sorting systems, exploiting the differential attenuation characteristics of X-rays in coal versus gangue [5,6,7]. While industrial deployment of X-ray transmission (XRT)-based sorting equipment has been achieved, the underlying interaction mechanisms between X-rays and gangue components require further elucidation. Of particular significance is kaolinite, a predominant clay mineral that serves dual roles as a major coal impurity and a critical industrial raw material, necessitating focused investigation in XRT-driven separation studies [8,9]. In natural kaolinite structures, Si4+ and Al3+ cations exhibit susceptibility to substitution by free metal ions. The ability to differentiate between substitutions of various metal ions, e.g., Mg2+, Ca2+, Fe2+/3+, Mn2+, Co2+, and Ni2+, could potentially enhance the efficiency of gangue photoelectric sorting processes [10,11]. This study investigated the theoretical feasibility of identifying these specific cation substitutions in kaolinite structures.
Kaolinite is a form of water-containing aluminosilicate. Its theoretical structure is Al2Si2O5(OH)4; octahedral aluminosilicate with a structure of 1:1 is formed by connecting the octahedral aluminosilicate with the tetrahedral aluminosilicate and stacking along the c axis [12,13,14]. Since kaolinite is a clay mineral commonly associated with coal in coal mines, it exhibits characteristics such as hydrolytic weakening and a negative surface charge. These properties significantly influence the sedimentation behavior of coal slurry during wet separation processes. Consequently, removing kaolinite from coal gangue through dry separation methods holds considerable significance. Naturally occurring kaolinite undergoes various forms of lattice substitution due to interactions with metal ions under high-temperature and -pressure conditions during its formation [15]. This includes the replacement of Al3+ in aluminum–oxygen octahedra and Si4+ in silicon–oxygen tetrahedra by ions including Mg2+, Ca2+, Fe3+, and Fe2+. Such lattice substitutions alter kaolinite’s properties, including its negative surface charge and crystal morphology, resulting in distinct macroscopic characteristics among different types of kaolinite. The separation and purification of kaolinite with varying lattice substitutions can be achieved by exploiting differences in these macroscopic characteristics.
X-ray absorption fine-structure spectroscopy (XAFS) is a widely used technique for material characterization [16]. It provides critical information about the atomic environment surrounding absorbing atoms, including oxidation states, average coordination numbers, interatomic distances, and structural disorder [17,18,19]. In kaolinite-related research, XAFS has been primarily applied to study surface adsorption phenomena and ion doping characteristics. However, no previous studies have explored XAFS for identifying kaolinite in coal gangue systems. This study investigates the X-ray absorption threshold shifts induced by structural distortion in kaolinite through XAFS simulations. These findings aim to establish theoretical foundations for kaolinite identification during photoelectric separation of coal gangue.
This study employed density functional theory (DFT) calculations implemented in Materials Studio 2017 software to systematically investigate the structural and electronic consequences of Mg2+, Ca2+, Fe2+/3+, Mn2+, Co2+, and Ni2+ substitutions within the kaolinite lattice. Through comprehensive analysis of optimized crystal structures, energy band configurations, and density-of-states profiles—complemented by XRD and XAFS spectral simulations—we elucidate fundamental differences between cation-substituted kaolinite derivatives and their pristine counterparts. These computational insights establish a theoretical framework for correlating macroscopic material properties with specific cationic substitution patterns, thereby enabling precise identification of isolated kaolinite variants through their characteristic macroscopic signatures.
2. Calculation
2.1. Model Construction
In the simulation, substitution was performed on the (001) surface of kaolinite. For each periodic 2 × 1 × 1 supercell model, metal cations, including Ca2+, Fe2+, Fe3+, Ni2+, Mg2+, Zn2+, and Mn2+, were systematically substituted for Al3+ in the aluminum–oxygen octahedron. The resulting negative charge imbalance was neutralized by Na+ [11,20,21].
As shown in Figure 1, we systematically substituted Al3+ ions at four distinct atomic sites (labeled ①–④) with metal cations. The resulting configurations are designated as Na-Xy+-1, Na-Xy+-2, Na-Xy+-3, and Na-Xy+-4, corresponding to substitution sites ① through ④, respectively. Notably, Fe3+ substitution requires no Na+ incorporation for charge compensation. These configurations are designated as Fe (III)-① through Fe (III)-④ based on their substitution sites.
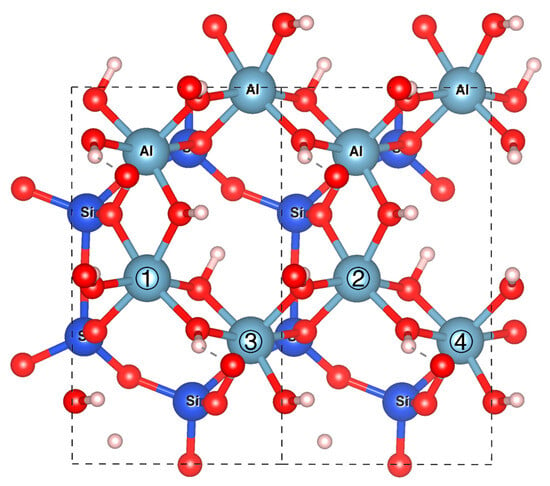
Figure 1.
Metal substitution at four Al3+ sites (labeled ①–④) on the kaolinite (001) plane. Atomic color codes: Al (gray), Si (blue), O (red), H (white).
Figure 2 illustrates the optimized substitution models: (a) Ca2+ at site ①, (b) Fe2+ at site ②, (c) Mg2+ at site ③, and (d) Zn2+ at site ④.
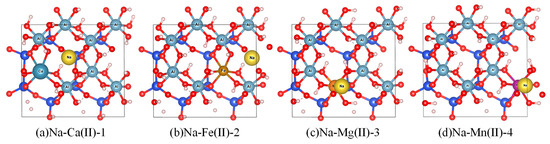
Figure 2.
Ca2+, Fe2+, Mg2+, and Mn2+ ions substituted for Al3+ at four distinct sites on the (001) plane. Atomic color codes: Na (pale yellow), Ca (dark gray), Fe (brown), Mg (orange), and Mn (purples).
2.2. Calculation Methods
This study employed density functional theory (DFT) through the Cambridge Serial Total Energy Package (CASTEP) to investigate the physical properties of kaolinite. The generalized gradient approximation with the Perdew–Burk–Ernzerhof (GGA-PBE) [22] functional was applied to optimize the primitive kaolinite unit cell structure.
DFT calculations performed using the CASTEP simulation code were used to study the substitutions. A Monkhorst-Pack 3 × 2× 3 k-point was employed, and the cutoff energy was set to 500 eV, the pseudopotentials were ultrasoft, and the SCF tolerance was determined to be 1.0 × 10−6 eV/atom with functional generalized gradient approximations (GGAs) with Perdew–Burke–Ernzerhof (PBE) techniques. Pseudoatomic investigations were completed for O-2s2 2p4, Na-2s2 2p6 3s1, Mg-2p63s2, Al-3s2 3p1, Si-3s2 3p2, Ca-3s2 3p6 4s2, Mn-3d5 4s2, Fe-3d6 4s2, Co-3d7 4s2, and Ni-3d8 4s2. Furthermore, the X-ray diffraction (XRD) patterns of the optimized structures were simulated using Materials Studio for comparative analysis.
The XAFS spectra were calculated based on molecular configurations derived from the ab initio simulations [17,19]. The amplitude reduction factor () was set to 1.0. Multiple scattering path lengths of up to 5.0 Å were taken into account. The radius of the cluster for self-consistent full multiple scattering calculations was set to 5.0 Å. Self-consistent field (SCF) and full multiple scattering (fms) were calculated for the unit cell. The Hedin–Lundqvist-type exchange–correlation potential was applied. The first coordination layer of aluminum and metal atoms at the k-edge was calculated and analyzed, and information on the coordination number, coordination distance, and species of ab-adsorbed atoms was obtained.
In the substitution model, substituted metal ions act as central atoms. Specifically, Mg2+ serves as the central atom in Na-Mg (II)-1, contrasting with Al3+ in pristine kaolinite. k-edge XAFS spectra of these central atoms were calculated via ab initio multiple scattering using the Demeter package. Data preprocessing involved the following: (1) linear background removal from pre-edge regions using Athena (Demeter 0.9.26), (2) normalization to atomic absorption, and (3) χ(k) extraction through quadratic polynomial subtraction of isolated-atom backgrounds. The resulting χ(k) data underwent k2-weighted and Hanning window filtering (k-rang 3-15 Å−1) prior to Fourier transformation into R-space, yielding radial structure functions (RSFs). These RSFs quantified interatomic distance distributions, enabling determination of coordination numbers, bond lengths, and local chemical environments through peak position and intensity analysis.
3. Results and Discussion
3.1. The Energy of the Substitutional Structure and Its Substitution Energy
Geometric and energy optimization of substituted kaolinite models revealed substantial system energy variations. Lower-energy configurations exhibit improved thermodynamic stability, indicating a higher probability of natural occurrence as dominant phases [23]. By comparing the total energies of the same substituent species across four distinct lattice sites, the configuration with the lowest energy, which corresponds to the highest thermodynamic stability, can be unambiguously identified [24]. This energy-based screening method enables systematic determination of optimal substitution patterns in aluminosilicate systems.
The lattice substitution energy refers to the energy required for impurity atoms to substitute into the mineral lattice. The formation energy (), which represents the energy required to create a substitutional defect in the bulk phase, is defined as follows:
In the formula, represents the total energy of the mineral containing impurity atoms, denotes the total energy of the bulk-phase mineral, and and correspond to the chemical potentials of the metal atoms and impurity atoms, respectively.
The chemical potentials (μ) of the metallic elements were obtained as follows: Na (−1302.63 eV), Mg (−972.29 eV), Al (−52.74 eV), Ca (−999.56 eV), Mn (−644.40 eV), Fe (−855.91 eV), Co (−1034.80 eV), and Ni (−1347.22 eV). These potentials were substituted into Equation (1) to calculate lattice substitution formation energies (). Lower values indicate reduced substitution energy barriers, thereby increasing substitution likelihood in crystalline systems.
Figure 3 demonstrates reduced total energies in all substitution models relative to pristine kaolinite. The total energies of all substituted models are reduced relative to pristine kaolinite, indicating the enhanced thermodynamic stability of the substitution configurations. Notably, the Fe3+-substituted model exhibits the highest total energy among all the systems, with its formation energy () approaching zero, signifying lower stability and reduced substitution feasibility compared to divalent ions. This instability arises from the strongly localized nature of Fe3+ in octahedral sites, which rigidifies bonding with neighboring O2−, whereas the larger ionic radius of Fe2+ allows adaptive bond length adjustments to minimize lattice strain. Furthermore, the 3d5 electronic configuration of Fe3+ promotes magnetic moment coupling, elevating the system energy [25]. Among all substitution models, Na-Ni (II)-1 and Na-Ni (II)-2 exhibit the lowest total system energies, indicating that Ni2+ substitution at specific Al3+ sites (① and ②) yields the most stable configurations. However, under natural conditions—characterized by warm, humid, and strongly oxidizing acidic environments where kaolinite forms—the redox sensitivity of Ni may drive mineralogical transformations of Ni2+-substituted kaolinite despite its computational stability [26].
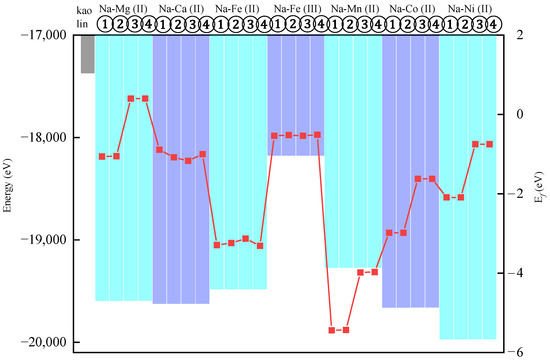
Figure 3.
Energy parameters of substituted kaolinite. The histograms represent the total energy of the system (lower values indicate higher stability), and the red squares denote the formation energy (), where reduced values correlate with enhanced substitution feasibility.
Crucially, Mg2+ substitutions at sites ③ and ④ show positive formation energies () exhibiting thermodynamic instability, contrasting with negative values in other configurations that reflect thermodynamic stability. The Na-Ni (II)-1 system exhibits the lowest total energy, suggesting enhanced structural stability. Formation energy analysis reveals Na-Mn (II)-2 as the most favorable substitution (), indicating superior energetic preference through its extreme negative value.
3.2. Substituted Structure Characterization Based on Simulated XRD
Based on the total energy calculations of the substitution model systems, the models with the lowest energy, and thus the most stable configurations, were selected from each substitution ion model: Na-Mg (II)-1, Na-Ca (II)-3, Na-Fe (II)-4, Fe (III)-3, Na-Mn (II)-1, Na-Co (II)-2, and Na-Ni (II)-1. The XRD patterns of the corresponding lattices for these selected models were then calculated.
As illustrated in Figure 4, metal-substituted kaolinite remains its core crystal structure, as evidenced by minimal XRD pattern deviations from the original sample. Notably, substituted models exhibit new diffraction peaks at 2θ = 8.778° and 9.774° (Figure 4b), which are absent in pristine kaolinite. This phenomenon can be attributed to the charge-balance-induced structural distortions [27,28], while substituted metal–Ox complexes maintain coordination numbers identical to original Al-Ox groups.
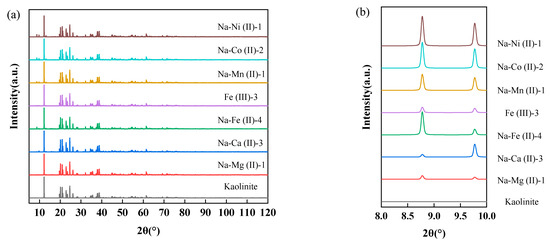
Figure 4.
(a) The XRD results of substitution structures; (b) partial schematic XRD patterns of substitution structures.
At 2θ = 8.778°, Na-Fe (II)-4, Na-Mn (II)-1, Na-Co (II)-2, and Na-Ni (II)-1 exhibit sharp diffraction peaks with enhanced peak height-to-full width at half maximum (HWHM) ratios, indicating superior structural integrity. In contrast, the broader diffraction peaks observed for Fe (III)-3, Na-Mg (II)-1, and Na-Ca (II)-3 confirm that substitutions of Fe3+, Mg2+, and Ca2+ induce relatively larger lattice distortions. However, as demonstrated in Figure 4a, the (001) planes of all the substituted crystals and pristine kaolinite consistently align at 2θ = 12.25°, reflecting structural coherence. This indicates that the substitution-induced modifications remain localized to the coordination environments of the substituted ions, while the overall crystalline framework retains its stability.
Therefore, after acquiring the XRD pattern data of natural kaolinite, it was possible to determine whether ion substitution occurred in the sample and identify the approximate type of metal ions by comparing the presence of any additional diffraction peaks not observed in ideal kaolinite phases and analyzing the intensity of existing diffraction peaks.
3.3. Band Structure and Density-of-States Analysis
The electronic band structure defines permissible electron energy levels in crystalline materials, governing their electrical and optical characteristics. Simultaneously, the density of states (DOS) quantifies available quantum states across energy ranges, determining charge transport properties through electronic state distributions. Metal ion substitution within the lattice induces modifications to both band structure configurations and DOS profiles, altering conduction mechanisms through impurity state generation and Fermi level shifts. These variations manifest as bandgap narrowing (ΔEg) and localized state formation, fundamentally impacting material performance in optoelectronics [29].
Figure 5 shows the high-symmetry Brillouin zone (BZ) points labeled G (0, 0, 0), F (0.5, 0, 0), Q (0, 0.5, 0), and Z (0, 0, 0.5). The Fermi energy level was set at zero. The conduction band minimum (VBM) is located at the G point of BZ [30]. Band structure calculations revealed that the metal ion substitutions significantly altered the bandgaps compared to pristine kaolinite. The measured bandgaps were as follows:
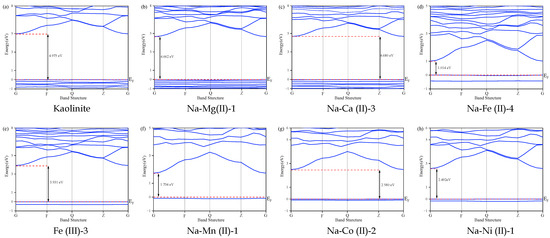
Figure 5.
Band structures of the kaolinite and substitution models.
As shown in Table 1, pristine kaolinite, Na-Mg (II)-1, Na-Ca (II)-3, and Fe (III)-3 exhibit bandgaps exceeding 3 eV, classifying them as insulators due to restricted electron excitation. However, substitutions involving Mg2+, Ca2+, and Fe3+ introduce new electronic orbitals that enhance electrical conductivity. Notably, Na-Fe (II)-4 showed a drastically reduced bandgap (1.014 eV) compared to Fe (III)-3 (3.931 eV). This difference arose due to the higher charge state of Fe3+, which promotes localized electronic states that hinder electron migration. In contrast, the lower charge state of Fe2+ facilitates electron mobility. Additionally, Fe2+ substitution generates a higher density of oxygen vacancies, creating additional conduction pathways that further improve conductivity.

Table 1.
The bandgaps of substituted kaolinite.
The introduction of intermediate energy levels through Mn2+, Co2+, and Ni2+ substitutions serves as an additional conduction pathway, further enhancing electrical conductivity. Spin polarization effects are evident in Na-Fe (II)-4, Fe (III)-3, Na-Mn (II)-1, Na-Co (II)-2, and Na-Ni (II)-1 systems, where unpaired electrons in magnetic elements induce energy band separation [31,32]. This phenomenon manifests as narrowed valence band maxima compared to the original condensed energy bands.
The density of states (DOS) and partial DOS of kaolinite and the substitution models are depicted in Figure 6. The Mg2+ and Ca2+ substitution atoms are positioned at the conduction band minimum due to the high energy levels of their unoccupied orbitals, 3s for Mg and 4s for C. In contrast, substitutions with Fe2+, Fe3+, Mn2+, Co2+, and Ni2+ primarily influence the valence band maximum by introducing acceptor energy levels that generate holes in the valence band, a phenomenon attributed to their partially filled d-orbitals.
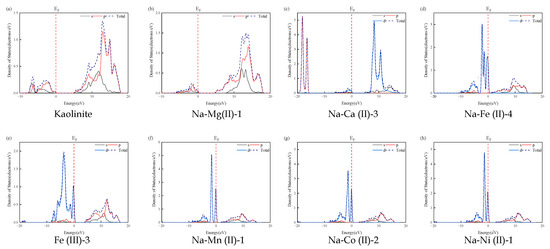
Figure 6.
The density of states of Al atoms in kaolinite and substituted atoms in the substitution models.
Analysis of band structures and density of states reveals that metal ion substitution significantly modifies the electronic states and chemical reactivity of kaolinite. The introduction of metal ions (Fe2+, Mn2+, Co2+, and Ni2+) reduces the bandgap from 4.975 eV (pristine insulator) to 0.1–3.0 eV, transforming kaolinite into a semiconductor. This bandgap narrowing serves as a critical indicator to distinguish substituted kaolinite from its pristine counterpart. Furthermore, the energy difference between the valence band maximum (VBM) and conduction band minimum (CBM) governs X-ray absorption behavior: a larger VBM-CBM gap increases the energy required for electron excitation, enhancing X-ray absorption and resulting in a higher contrast in X-ray imaging. These findings elucidate the structure–property relationships underlying metal-substituted kaolinite systems.
3.4. Localized Structure of Substituted Kalinite on XAFS
Figure 7 compares the radial structure function (RSF) diagrams of pristine kaolinite (Al3+ as the central atom) with metal-substituted models (ions as central atoms). The pristine kaolinite exhibits a shorter first-shell Al-O bond length (1.69 Å), as marked by the red dotted line in Figure 7, in contrast to the substituted metal–O distances. This difference can be attributed to the relatively small atomic radius of Al (approximately 1.18 Å) and its valence electron configuration of 3s2 3p1, which promotes the formation of covalent bonds with O. Notably, the Fe3+-O bond length (1.75 Å) closely matches that of Al-O, indicating that Fe (III) substitution induces minimal structural changes in the Fe-O octahedron compared to the Al-O octahedron, demonstrating minimal Fe-O octahedral distortion relative to Al-O coordination, thereby preserving the original crystal framework.
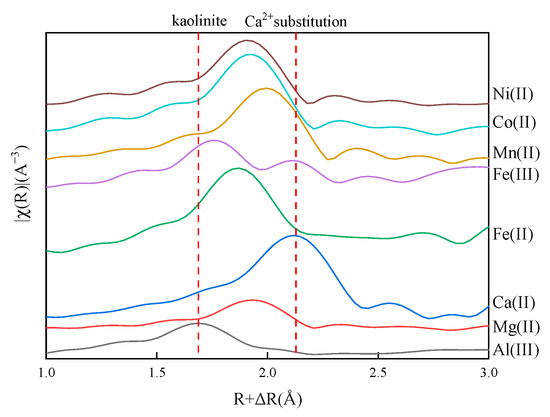
Figure 7.
The radial structure function of pristine kaolinite and substitution models.
Figure 8 presents the coordination structures of selected metal-substituted atoms. The RSF-derived bond lengths exhibit marginally smaller values compared to those measured by the model system. This discrepancy originates from the application of k-space functions, as opposed to window functions, for data amplification and truncation in EXAFS calculation [17]. Nevertheless, both methodologies demonstrate consistent trends in bond length variations across the investigated systems. Comparative analysis of average bond distances between metal substitution atoms and oxygen atoms within the first coordination shell reveals that the d-values for Mg2+, Fe2+, Mn2+, Co2+, and Ni2+ are relatively similar, ranging from 1.9 to 2.2 Å. In contrast, the d value for Ca2+ is 2.12 Å, identified by the red dotted line in the Figure 7, significantly larger than those for other metal ions. This discrepancy can be attributed to the atomic radius of Ca2+ being approximately 1.54 Å, which is larger than that of the other metal ions; besides, the weaker electrophilicity of Ca2+ results in a less pronounced interaction with the O atoms.
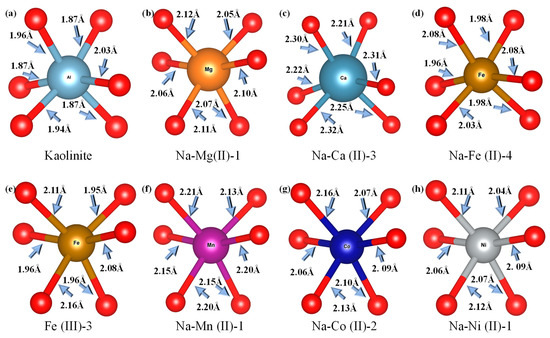
Figure 8.
Coordination structure of kaolinite and substitution models.
The radial structure function of the first shell layer substituted by Fe3+ is similar to that of pristine kaolinite, while substitution with other metal ions results in a notable increase in the d value. Theoretically, this phenomenon can serve as an indicator for preliminarily assessing whether metal ion substitution has occurred in kaolinite samples. With enhanced characterization accuracy, it may also be possible to identify the specific type of substituted metal ion.
4. Conclusions
This study establishes a structure–property correlation model for metal-substituted kaolinite through multiscale computational simulations, yielding the following key innovations: Systematic comparisons reveal that Ni2+ substitution achieves optimal structural stability, while Mn2+ substitution exhibits the lowest energy barrier ( = −5.44 eV). A positive correlation between the atomic number of divalent metals and XRD peak intensity at 2θ = 8.778 and 9.774° were identified, expanding the conventional application of XRD beyond phase identification to serve as a novel spectral marker for metal-type discrimination. By integrating XRD intensity, XAFS bond lengths, and bandgap data, a computational fingerprint system was constructed to identify metal substitutions, advancing material characterization from single-parameter analysis to multivariate feature correlation.
These discoveries not only deepen the mechanistic understanding of substitution effects in kaolinite but also establish a universal framework for computationally guided material design. Future studies should explore the generalizability of computational fingerprints across other layered silicates to validate their cross-material applicability.
Author Contributions
Conceptualization, Q.Z., J.X. and J.Z.; methodology, Q.Z. and J.X.; software, Q.Z. and J.X.; validation, Q.Z. and J.Z.; formal analysis, J.Y.; investigation, Q.Z.; resources, J.X. and J.Z.; data curation, W.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, Q.Z. and J.X.; visualization, Q.Z. and J.X.; supervision, J.X. and J.Z.; project administration, J.Z.; funding acquisition, Q.Z., J.X. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific Research Foundation of Education Department of Anhui Province of China [2023AH051195], the Guizhou Provincial Basic Research Program (Natural Science) (Qian Ke He Basic -ZK [2024] General 626).
Data Availability Statement
The data used to support the findings of the study are available from the first author upon request.
Acknowledgments
The authors would also like to express their sincere appreciation to the reviewers for their constructive comments on the revision and improvement of the manuscript. All the support is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, L.; Sun, Z.; Tao, H.; Wang, J.; Yi, W. Integration of Lightweight Network and Attention Mechanism for the Coal and Gangue Recognition Method. Min. Metall. Explor. 2025, 42, 191–204. [Google Scholar] [CrossRef]
- Ye, Z.; Hongwei, M.; Peng, W.; Wenjian, Z.; Xiangang, C.; Mingzhen, Z. Research on Efficient Matching Method of Coal Gangue Recognition Image and Sorting Image. Sci. Rep. 2024, 14, 25536. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, W.; Xu, Z.; Zhang, K.; Lv, H. Cascade Network for Detection of Coal and Gangue in the Production Context. Powder Technol. 2021, 377, 361–371. [Google Scholar] [CrossRef]
- Yin, J.; Zhu, J.; Zhu, H.; Pan, G.; Zhu, W.; Zeng, Q.; Shi, Q. Intelligent Photoelectric Identification of Coal and Gangue—A Review. Measurement 2024, 233, 114723. [Google Scholar] [CrossRef]
- Yang, Y.; Zeng, Q. Impact-Slip Experiments and Systematic Study of Coal Gangue “Category” Recognition Technology Part I: Impact-Slip Experiments between Coal Gangue Mixture and Top Coal Caving Hydraulic Support and the Study of Coal Gangue “Category” Recognition Technology. Powder Technol. 2021, 392, 224–240. [Google Scholar] [CrossRef]
- Li, Z.; Lu, J.; Zhou, S. A Novel Feature Extraction Method for Recognition of Coal and Gangue under Wetting Conditions. Powder Technol. 2023, 428, 118825. [Google Scholar] [CrossRef]
- Luan, H.; Xu, H.; Tang, W.; Tian, Y.; Zhang, Q. Coal and Gangue Classification in Actual Environment of Mines Based on Deep Learning. Measurement 2023, 211, 112651. [Google Scholar] [CrossRef]
- Gu, W.; Liu, Z.; Zhao, M.; He, Z.; Ding, Z. Preparation and Characterization of γ-Al2O3 from Coal-Bearing Kaolinite. JOM 2025, 77, 3964–3971. [Google Scholar] [CrossRef]
- Xie, Y.; Han, Z.; Khan, A.; Liang, Y.; Zhong, H.; He, Z. Highly Selective and Green Recovery of Lithium from Coal Gangue Using Recyclable Ammonium Fluoride Leaching System. JOM 2025, 77, 842–850. [Google Scholar] [CrossRef]
- Malden, P.J.; Meads, R.E. Substitution by Iron in Kaolinite. Nature 1967, 215, 844–846. [Google Scholar] [CrossRef]
- Shu, Q.; Min, F.; Chen, J. Influence of Ca2+ Substitution on the Surface Hydration Characteristics of Kaolinite: Combination of Simulations and Experiments. Appl. Surf. Sci. 2024, 678, 161097. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Gao, W.; Tian, Q. Influences of the Residual Water of Kaolin on the Structure and Properties of Phosphate Acid-Activated Metakaolin-Based Geopolymers. JOM 2023, 75, 4881–4886. [Google Scholar] [CrossRef]
- Cui, W.; Chen, J. Insight into Mineral Flotation Fundamentals through the DFT Method. Int. J. Min. Sci. Technol. 2021, 31, 983–994. [Google Scholar] [CrossRef]
- Liu, L.; Kong, C.; Zhao, H.; Lu, F. Elucidating the Enhancement of Kaolinite Flotation by Iron Content through Density Functional Theory: A Study on Sodium Oleate Adsorption Efficiency. Int. J. Min. Sci. Technol. 2024, 34, 855–866. [Google Scholar] [CrossRef]
- Chen, J.; Sun, Y.; Ling, Y.; Chu, X.; Cheng, Y.; Min, F. Effects of Mg(II) Doping Amount on the Hydration Characteristics of Kaolinite Surface: Molecular Dynamics Simulations and Experiments. Surf. Interfaces 2024, 45, 103869. [Google Scholar] [CrossRef]
- Pan, J.-X.; Zhao, L.-S.; Li, Z.; Feng, Z.-Y.; Liu, D.-P.; Chen, J.; Huang, X.-W. Adsorption of Rare Earth Elements and Aluminum on the Surface of Kaolinite: Insights from Sequential Chemical Extractions, XAFS, and DFT. Rare Met. 2025, 44, 4268–4278. [Google Scholar] [CrossRef]
- Ravel, B.; Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: Data Analysis for X-Ray Absorption Spectroscopy Using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537–541. [Google Scholar] [CrossRef]
- Rehr, J.J.; Kas, J.J.; Vila, F.D.; Prange, M.P.; Jorissen, K. Parameter-Free Calculations of X-Ray Spectra with FEFF9. Phys. Chem. Chem. Phys. 2010, 12, 5503–5513. [Google Scholar] [CrossRef]
- Jorissen, K.; Rehr, J.J. New Developments in FEFF: FEFF9 and JFEFF. J. Phys. Conf. Ser. 2013, 430, 012001. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.; Yang, H. Structural Modulation of Kaolinite Nanoclay via DFT and Molecular Dynamics Simulations: A Review. Appl. Clay Sci. 2024, 258, 107473. [Google Scholar] [CrossRef]
- Jige, M.; Takagi, T.; Takahashi, Y.; Kurisu, M.; Tsunazawa, Y.; Morimoto, K.; Hoshino, M.; Tsukimura, K. Fe-Kaolinite in Granite Saprolite beneath Sedimentary Kaolin Deposits: A Mode of Fe Substitution for Al in Kaolinite. Am. Mineral. 2018, 103, 1126–1135. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Für Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, Z.; Wu, G.; Jiang, D.; Lan, Y. Investigating the Influence of Impurity Defects on the Adsorption Behavior of Hydrated Sc3+ on the Kaolinite (001) Surface Using Density Functional Theory. Materials 2024, 17, 610. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Chen, J.; Min, F.; Ling, Y.; Shang, H.; Wang, T. Exploration of the Interaction between Fe-Doped Kaolinite Surface and H2O Based on DFT Simulation and Experiment. J. Mol. Liq. 2024, 395, 123901. [Google Scholar] [CrossRef]
- Liu, L.; Min, F.; Chen, J.; Zhang, M.; Lu, F. DFT Research on Lattice Substitution of Fe with Different Valence States in Coal Measures Kaolinite. J. China Univ. Min. Technol. 2019, 48, 903–910. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, H.; Tao, N.; Xu, F.; Ye, Q. Mineralogical and Geochemical Investigations of the Li-Rich Clay Strata from Central Yunnan, Southwest China. Ore Geol. Rev. 2025, 181, 106614. [Google Scholar] [CrossRef]
- Ható, Z.; Kristóf, T. On the Role of the Interlayer Interactions in Atomistic Simulations of Kaolinite Clay. Molecules 2024, 29, 4731. [Google Scholar] [CrossRef]
- Kwon, Y.-M.; Chang, I.; Cho, G.-C. Xanthan Biopolymer-Based Soil Treatment Effect on Kaolinite Clay Fabric and Structure Using XRD Analysis. Sci. Rep. 2023, 13, 11666. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, Y.; Chen, K.; Yi, C.; Nong, Y.; Chen, Z.; Chen, J. Adsorption of Polycarboxylate Ether Superplasticizer Incorporating Various Functional Groups on the Kaolin (001) Surface: Theoretical Study and Experimental Testing. MetaResource 2024, 1, 61–73. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Luan, Z.; He, M. First-Principles Analysis on Phase Transition, Atomic, Electronic, and Mechanical Properties of Kaolinite under Pressures. Phys. B Condens. Matter 2024, 674, 415554. [Google Scholar] [CrossRef]
- Yuan, L.-D.; Zhang, X.; Acosta, C.M.; Zunger, A. Uncovering Spin-Orbit Coupling-Independent Hidden Spin Polarization of Energy Bands in Antiferromagnets. Nat. Commun. 2023, 14, 5301. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Luo, W.; Ji, J.; Barone, P.; Picozzi, S.; Xiang, H. Band Splitting with Vanishing Spin Polarizations in Noncentrosymmetric Crystals. Nat. Commun. 2019, 10, 5144. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).