Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms
Abstract
1. Introduction
2. General Geological Setting of the Study Area
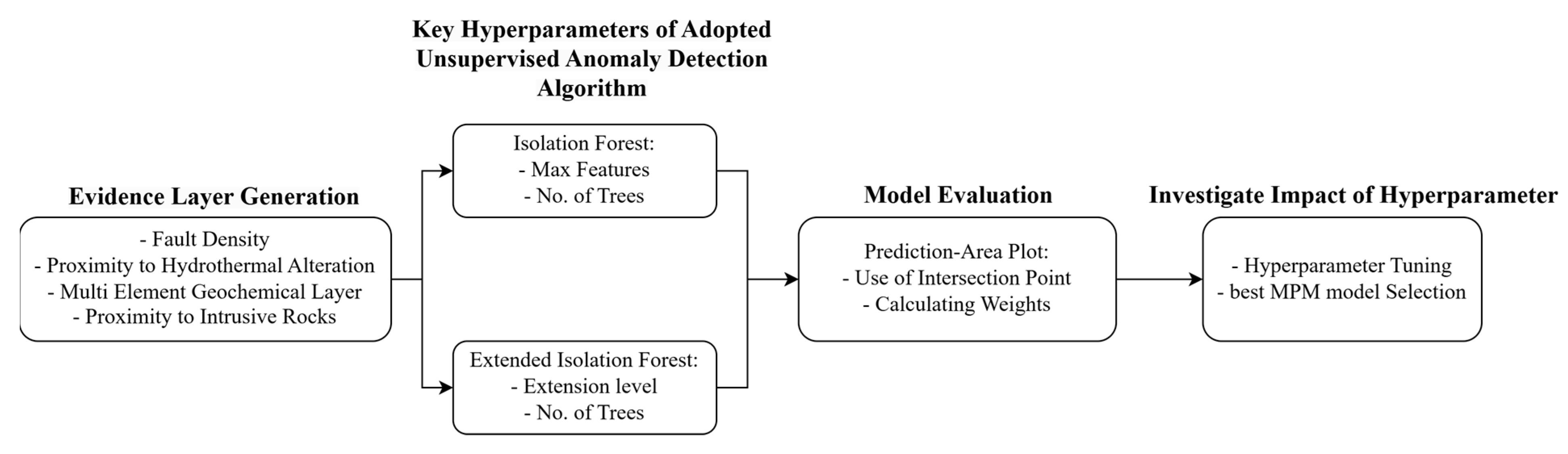
3. Raw Data and Creation of Evidence Layers
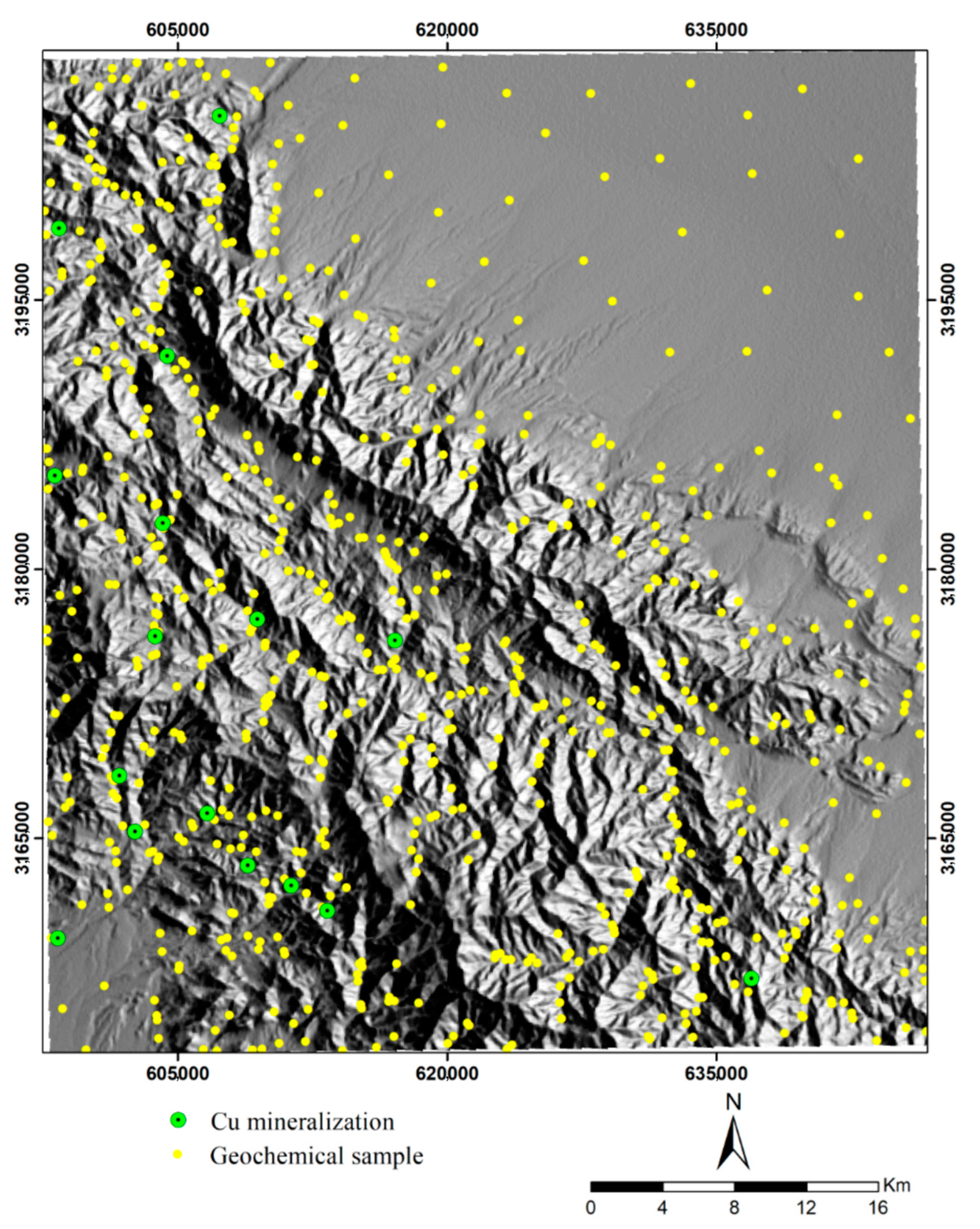
3.1. Remote Sensing and Geochemical Data
3.2. Geochemical Anomaly Evidence
3.3. Distance-Based Generation of Evidence Layers for Hydrothermal Alterations
3.4. Fault Density Evidence Layer
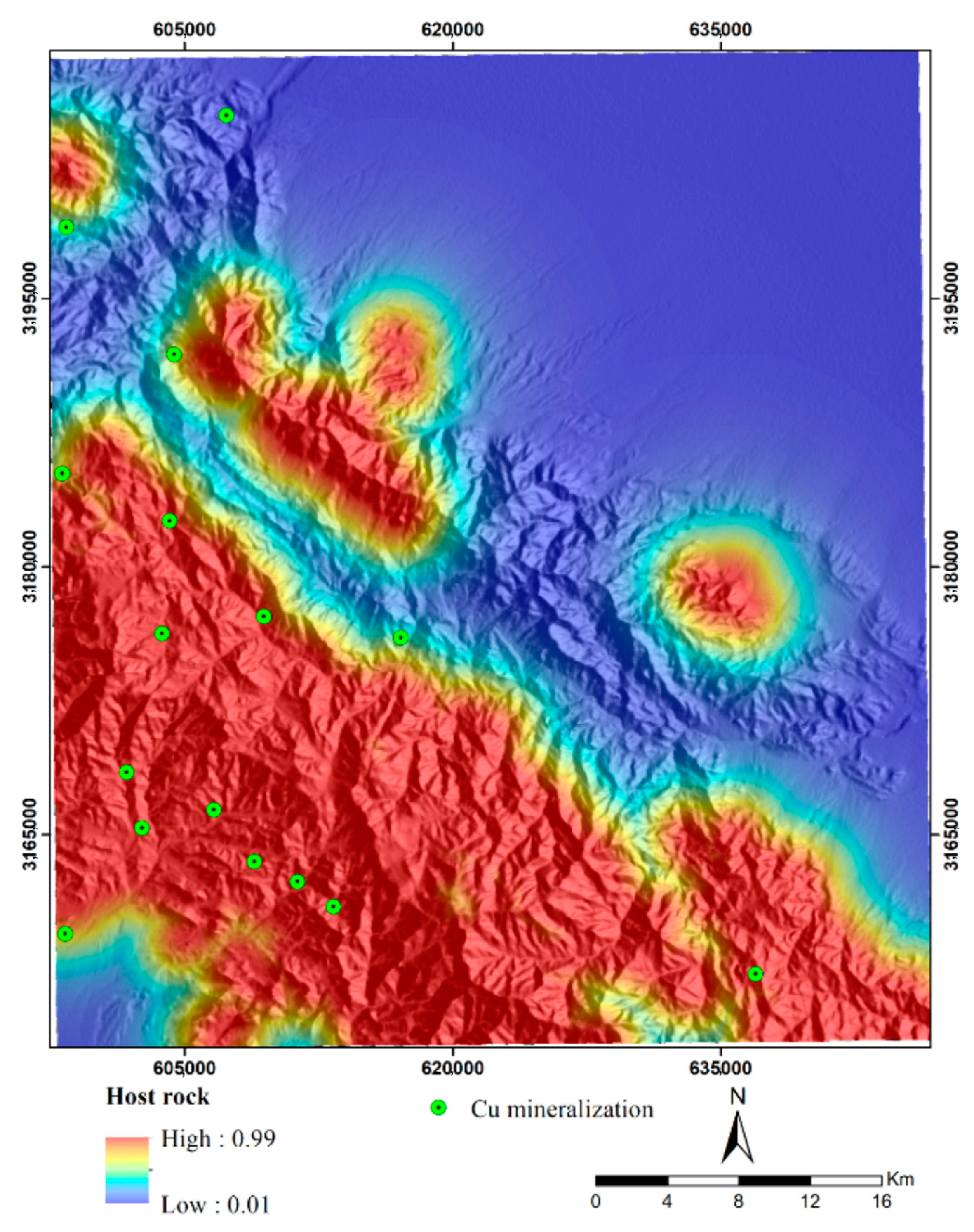
3.5. Host Rock Evidence Layer
4. Methodology
4.1. Predication-Area Plot
4.2. Isolation Forest
4.3. Extended Isolation Forest
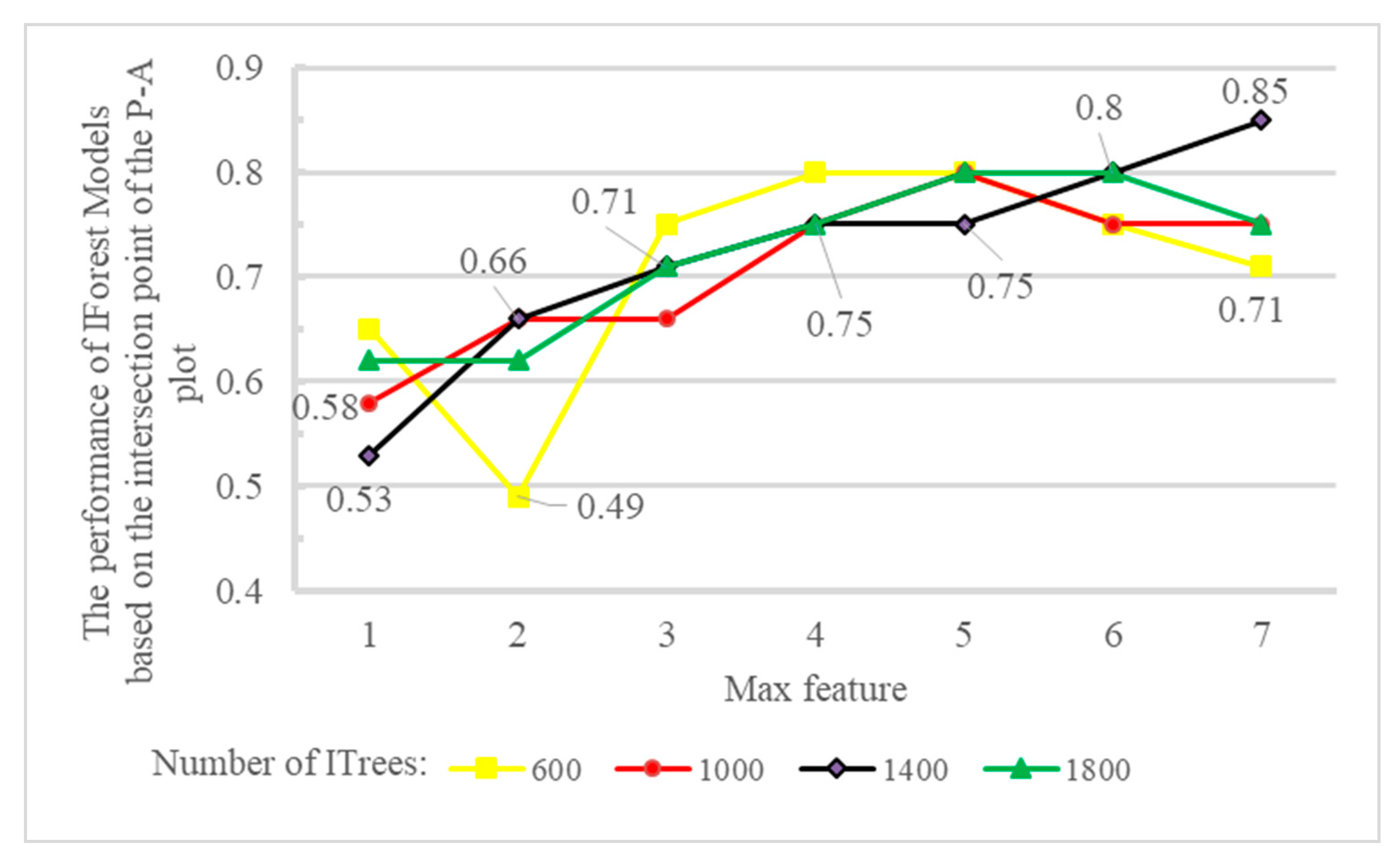
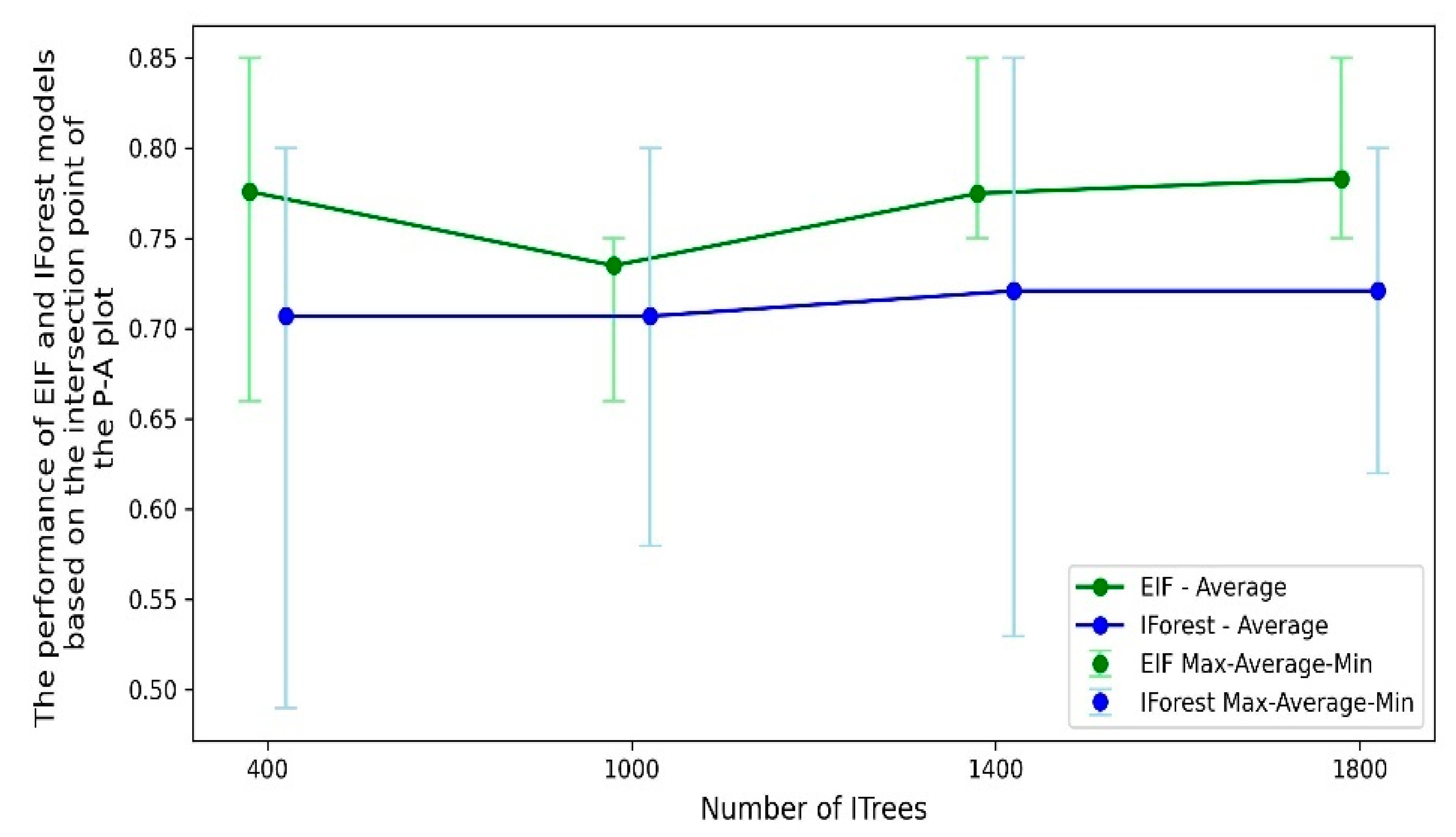
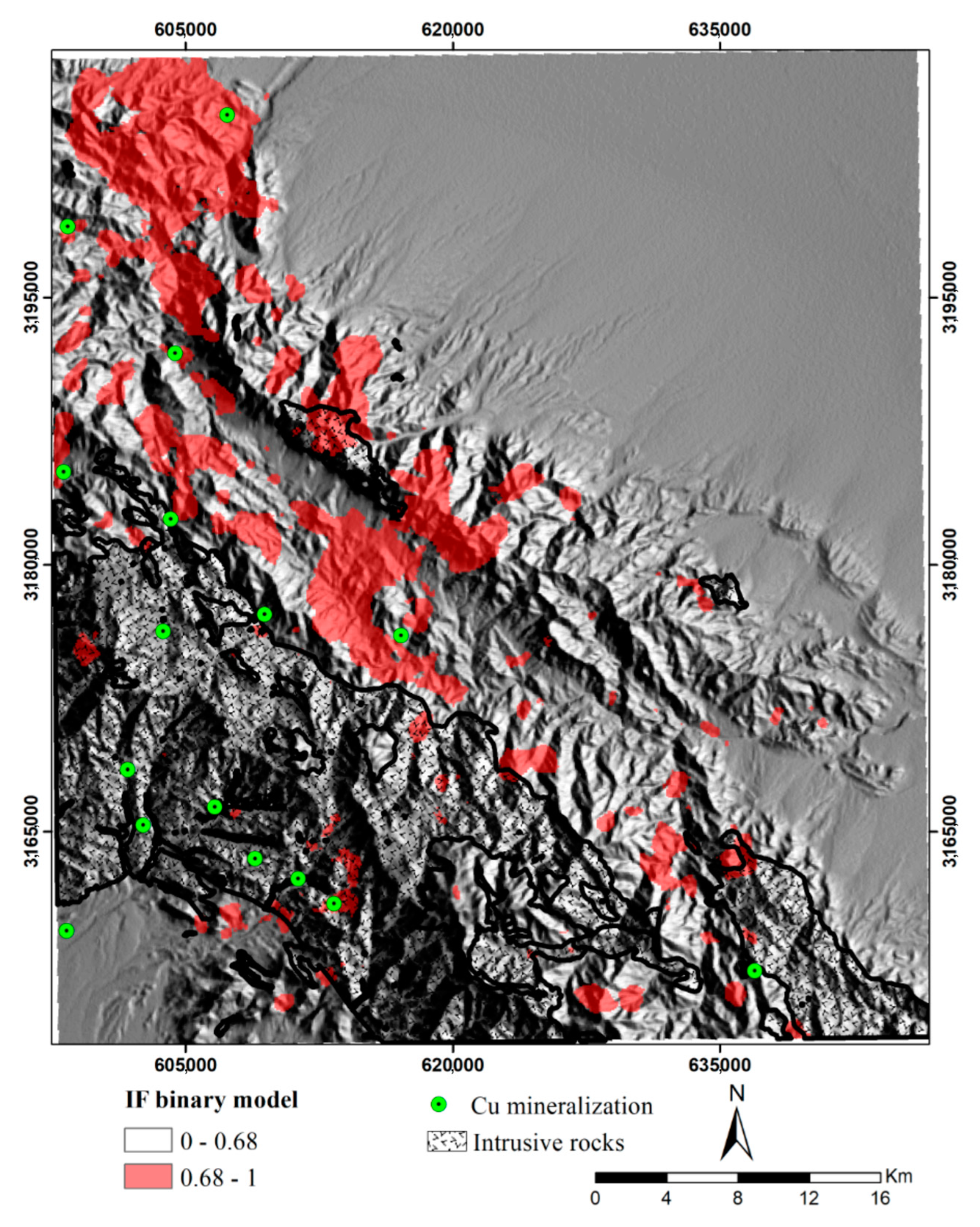
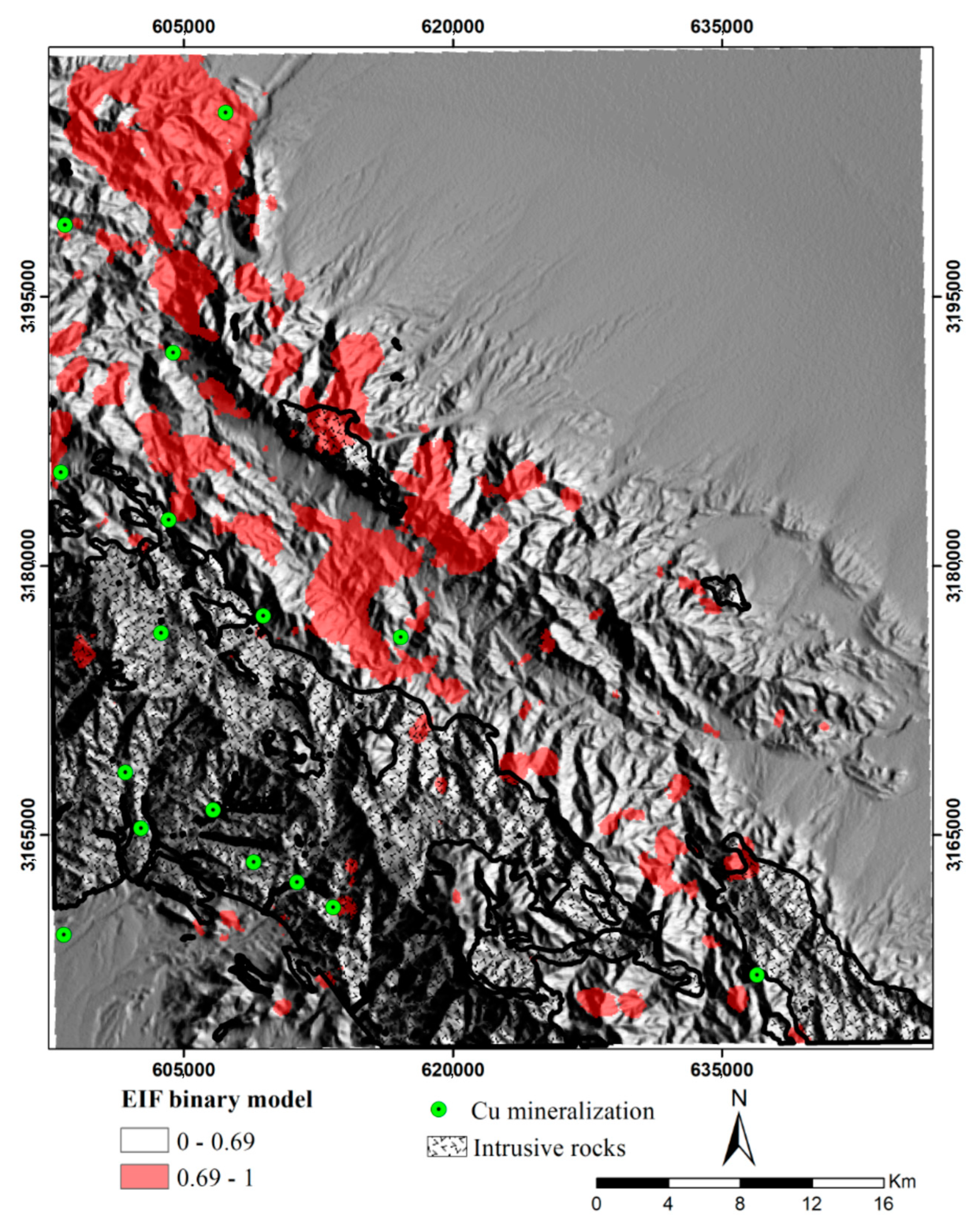
5. Algorithm Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yousefi, M.; Carranza, E.J.M. Geometric average of spatial evidence data layers: A GIS-based multi-criteria decision-making approach to mineral prospectivity mapping. Comput. Geosci. 2015, 83, 72–79. [Google Scholar] [CrossRef]
- Yin, B.; Zuo, R.; Sun, S. Mineral prospectivity mapping using deep self-attention model. Nat. Resour. Res. 2023, 32, 37–56. [Google Scholar] [CrossRef]
- Bahrami, Y.; Hasani, H.; Maghsoudi, A. Application of AHP-TOPSIS method to model copper mineral potencial in the Abhar 1:100000 geological map, NW Iran. Res. Earth Sci. 2021, 12, 41–57. [Google Scholar] [CrossRef]
- Aali, A.A.; Shirazy, A.; Shirazi, A.; Pour, A.B.; Hezarkhani, A.; Maghsoudi, A.; Hashim, M.; Khakmardan, S. Fusion of remote sensing, magnetometric, and geological data to identify polymetallic mineral potential zones in Chakchak Region, Yazd, Iran. Remote Sens. 2022, 14, 6018. [Google Scholar] [CrossRef]
- Shirazi, A.; Hezarkhani, A.; Beiranvand Pour, A.; Shirazy, A.; Hashim, M. Neuro-Fuzzy-AHP (NFAHP) technique for copper exploration using Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and geological datasets in the Sahlabad mining area, east Iran. Remote Sens. 2022, 14, 5562. [Google Scholar] [CrossRef]
- Bonham-Carter, G. Geographic Information Systems for Geoscientists: Modelling with GIS; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Hoseinzade, Z.; Shojaei, M.; Khademi, F.; Mokhtari, A.R.; Saremi, M. Integration of deep learning models for mineral prospectivity mapping: A novel Bayesian index approach to reducing uncertainty in exploration. Model. Earth Syst. Environ. 2025, 11, 161. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M.; Kreuzer, O.P.; Nykänen, V.; Hronsky, J.M.; Mihalasky, M.J. Data analysis methods for prospectivity modelling as applied to mineral exploration targeting: State-of-the-art and outlook. J. Geochem. Explor. 2021, 229, 106839. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Yousefi, M.; Nykänen, V.; Harris, J.; Hronsky, J.M.; Kreuzer, O.P.; Bertrand, G.; Lindsay, M. Overcoming survival bias in targeting mineral deposits of the future: Towards null and negative tests of the exploration search space, accounting for lack of visibility. Ore Geol. Rev. 2024, 172, 106214. [Google Scholar] [CrossRef]
- Abedi, M.; Kashani, S.B.M.; Norouzi, G.-H.; Yousefi, M. A deposit scale mineral prospectivity analysis: A comparison of various knowledge-driven approaches for porphyry copper targeting in Seridune, Iran. J. Afr. Earth Sci. 2017, 128, 127–146. [Google Scholar] [CrossRef]
- Yousefi, M.; Lindsay, M.D.; Kreuzer, O. Mitigating uncertainties in mineral exploration targeting: Majority voting and confidence index approaches in the context of an exploration information system (EIS). Ore Geol. Rev. 2024, 165, 105930. [Google Scholar] [CrossRef]
- Mirzabozorg, S.A.A.S.; Abedi, M. Recognition of mineralization-related anomaly patterns through an autoencoder neural network for mineral exploration targeting. Appl. Geochem. 2023, 158, 105807. [Google Scholar] [CrossRef]
- Saremi, M.; Bagheri Ghadikolaei, S.M.; Agha Seyyed Mirzabozorg, S.A.; Hassan, N.E.; Hoseinzade, Z.; Maghsoudi, A.; Rezania, S.; Ranjbar, H.; Zoheir, B.; Beiranvand Pour, A. Evaluation of Deep Isolation Forest (DIF) Algorithm for Mineral Prospectivity Mapping of Polymetallic Deposits. Minerals 2024, 14, 1015. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.-H. Integration of various geophysical data with geological and geochemical data to determine additional drilling for copper exploration. J. Appl. Geophys. 2012, 83, 35–45. [Google Scholar] [CrossRef]
- Qaderi, S.; Maghsoudi, A.; Pour, A.B.; Rajabi, A.; Yousefi, M. DCGAN-Based Feature Augmentation: A Novel Approach for Efficient Mineralization Prediction Through Data Generation. Minerals 2025, 15, 71. [Google Scholar] [CrossRef]
- Yousefi, M.; Kreuzer, O.P.; Nykänen, V.; Hronsky, J.M. Exploration information systems–A proposal for the future use of GIS in mineral exploration targeting. Ore Geol. Rev. 2019, 111, 103005. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Data-driven index overlay and Boolean logic mineral prospectivity modeling in greenfields exploration. Nat. Resour. Res. 2016, 25, 3–18. [Google Scholar] [CrossRef]
- Rezapour, M.J.; Abedi, M.; Bahroudi, A.; Rahimi, H. A clustering approach for mineral potential mapping: A deposit-scale porphyry copper exploration targeting. Geopersia 2020, 10, 149–163. [Google Scholar]
- Xiong, Y.; Zuo, R.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Chen, G.; Huang, N.; Wu, G.; Luo, L.; Wang, D.; Cheng, Q. Mineral prospectivity mapping based on wavelet neural network and Monte Carlo simulations in the Nanling W-Sn metallogenic province. Ore Geol. Rev. 2022, 143, 104765. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Liu, C. Overview on the development of intelligent methods for mineral resource prediction under the background of geological big data. Minerals 2022, 12, 616. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, Y. Mineral prospectivity mapping of tungsten polymetallic deposits using machine learning algorithms and comparison of their performance in the Gannan region, China. Earth Space Sci. 2023, 10, e2022EA002596. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.-H.; Bahroudi, A. Support vector machine for multi-classification of mineral prospectivity areas. Comput. Geosci. 2012, 46, 272–283. [Google Scholar] [CrossRef]
- Shirazi, A.; Shirazy, A.; Hezarkhani, A. An Artificial Intelligence (AI)-Based Model for Optimal Exploratory Surveys; GRIN Verlag: Munich, Germany, 2024. [Google Scholar]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Xiao, K.; Wei, H.; Yang, F.; Chen, Z.; Li, N.; Xiang, J. Mineral prospectivity mapping based on isolation forest and random forest: Implication for the existence of spatial signature of mineralization in outliers. Nat. Resour. Res. 2022, 31, 1981–1999. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Carranza, E.J.M.; Yang, F. Maximum entropy and random forest modeling of mineral potential: Analysis of gold prospectivity in the Hezuo–Meiwu district, west Qinling Orogen, China. Nat. Resour. Res. 2019, 28, 645–664. [Google Scholar] [CrossRef]
- Qaderi, S.; Maghsoudi, A.; Pour, A.B.; Yousefi, M. Geological Controlling Factors on Mississippi Valley-Type Pb-Zn Mineralization in Western Semnan, Iran. Minerals 2024, 14, 957. [Google Scholar] [CrossRef]
- Carranza, E.j.m.; Hale, M. Logistic regression for geologically constrained mapping of gold potential, Baguio district, Philippines. Explor. Min. Geol. 2001, 10, 165–175. [Google Scholar] [CrossRef]
- Rahimi, H.; Abedi, M.; Yousefi, M.; Bahroudi, A.; Elyasi, G.-R. Supervised mineral exploration targeting and the challenges with the selection of deposit and non-deposit sites thereof. Appl. Geochem. 2021, 128, 104940. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Liu, C.; Wang, Y. Mineral prospectivity prediction via convolutional neural networks based on geological big data. J. Earth Sci. 2021, 32, 327–347. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Xiang, J. Applications of deep convolutional neural networks in prospecting prediction based on two-dimensional geological big data. Neural Comput. Appl. 2020, 32, 2037–2053. [Google Scholar] [CrossRef]
- Mirzabozorg, S.A.A.S.; Abedi, M.; Yousefi, M. Enhancing training performance of convolutional neural network algorithm through an autoencoder-based unsupervised labeling framework for mineral exploration targeting. Geochemistry 2024, 84, 126197. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.; Xiao, K.; Yang, F.; Xiang, J.; Zhang, S.; Xu, Y. Data-driven mineral prospectivity mapping by joint application of unsupervised convolutional auto-encoder network and supervised convolutional neural network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, Z. Effects of random negative training samples on mineral prospectivity mapping. Nat. Resour. Res. 2020, 29, 3443–3455. [Google Scholar] [CrossRef]
- Cheng, Q. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Chen, Y. Mineral potential mapping with a restricted Boltzmann machine. Ore Geol. Rev. 2015, 71, 749–760. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Isolation forest as an alternative data-driven mineral prospectivity mapping method with a higher data-processing efficiency. Nat. Resour. Res. 2019, 28, 31–46. [Google Scholar] [CrossRef]
- Shahrestani, S.; Conoscenti, C.; Carranza, E.J.M. Assessment of LUNAR, iForest, LOF, and LSCP methodologies in delineating geochemical anomalies for mineral exploration. J. Geochem. Explor. 2025, 273, 107737. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Application of one-class support vector machine to quickly identify multivariate anomalies from geochemical exploration data. Geochem. Explor. Environ. Anal. 2017, 17, 231–238. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Fadul, A.M.A. Anomaly Detection Based on Isolation Forest and Local Outlier Factor. Master’s Thesis, Africa University, Mutare, Africa, 2023. [Google Scholar]
- Zheng, C.; Zhao, Q.; Fan, G.; Zhao, K.; Piao, T. Comparative study on isolation forest, extended isolation forest and generalized isolation forest in detection of multivariate geochemical anomalies. Glob. Geol. 2023, 26, 167–176. [Google Scholar]
- Chabchoub, Y.; Togbe, M.U.; Boly, A.; Chiky, R. An in-depth study and improvement of Isolation Forest. IEEE Access 2022, 10, 10219–10237. [Google Scholar] [CrossRef]
- Asadi, S.; Moore, F.; Zarasvandi, A. Discriminating productive and barren porphyry copper deposits in the southeastern part of the central Iranian volcano-plutonic belt, Kerman region, Iran: A review. Earth-Sci. Rev. 2014, 138, 25–46. [Google Scholar] [CrossRef]
- Sadigh, S.; Mirmohammadi, M.; Asghari, O.; Porwal, A. Spatial distribution of porphyry copper deposits in Kerman Belt, Iran. Ore Geol. Rev. 2023, 153, 105251. [Google Scholar] [CrossRef]
- Hezarkhani, A.; Williams-Jones, A.E. Controls of alteration and mineralization in the Sungun porphyry copper deposit, Iran; evidence from fluid inclusions and stable isotopes. Econ. Geol. 1998, 93, 651–670. [Google Scholar] [CrossRef]
- Honarmand, M.; Ranjbar, H.; Shahabpour, J. Application of principal component analysis and spectral angle mapper in the mapping of hydrothermal alteration in the Jebal–Barez Area, Southeastern Iran. Resour. Geol. 2012, 62, 119–139. [Google Scholar] [CrossRef]
- Fakhari, S.; Afzal, P.; Lotfi, M. Delineation of hydrothermal alteration zones for porphyry systems utilizing ASTER data in Jebal-Barez area, SE Iran. Iran. J. Earth Sci. 2019, 11, 80–92. [Google Scholar]
- Pour, A.B.; Hashim, M. The application of ASTER remote sensing data to porphyry copper and epithermal gold deposits. Ore Geol. Rev. 2012, 44, 1–9. [Google Scholar] [CrossRef]
- Hajaj, S.; El Harti, A.; Jellouli, A.; Pour, A.B.; Himyari, S.M.; Hamzaoui, A.; Hashim, M. ASTER data processing and fusion for alteration minerals and silicification detection: Implications for cupriferous mineralization exploration in the western Anti-Atlas, Morocco. Artif. Intell. Geosci. 2024, 5, 100077. [Google Scholar] [CrossRef]
- Shirazi, A.; Shirazy, A.; Karami, J. Remote sensing to identify copper alterations and promising regions, Sarbishe, South Khorasan, Iran. Int. J. Geol. Earth Sci. 2018, 4, 36–52. [Google Scholar]
- Shirazi, A.; Hezarkhani, A.; Shirazy, A.; Shahrood, I. Remote sensing studies for mapping of iron oxide regions, South of Kerman, Iran. Int. J. Sci. Eng. Appl. 2018, 7, 45–51. [Google Scholar] [CrossRef]
- Saremi, M.; Yousefi, S.; Yousefi, M. Combination of Geochemical and Structural Data to Determine Exploration Target of Copper Hydrothermal Deposits in Feizabad District. J. Min. Environ. 2024, 15, 1089–1101. [Google Scholar]
- Yousefi, M.; Kamkar-Rouhani, A.; Carranza, E.J.M. Geochemical mineralization probability index (GMPI): A new approach to generate enhanced stream sediment geochemical evidential map for increasing probability of success in mineral potential mapping. J. Geochem. Explor. 2012, 115, 24–35. [Google Scholar] [CrossRef]
- Parsa, M.; Maghsoudi, A.; Yousefi, M.; Sadeghi, M. Recognition of significant multi-element geochemical signatures of porphyry Cu deposits in Noghdouz area, NW Iran. J. Geochem. Explor. 2016, 165, 111–124. [Google Scholar] [CrossRef]
- Yousefi, M.; Kamkar-Rouhani, A.; Carranza, E.J.M. Application of staged factor analysis and logistic function to create a fuzzy stream sediment geochemical evidence layer for mineral prospectivity mapping. Geochem. Explor. Environ. Anal. 2014, 14, 45–58. [Google Scholar] [CrossRef]
- Ghasemzadeh, S.; Maghsoudi, A.; Yousefi, M.; Mihalasky, M.J. Information value-based geochemical anomaly modeling: A statistical index to generate enhanced geochemical signatures for mineral exploration targeting. Appl. Geochem. 2022, 136, 105177. [Google Scholar] [CrossRef]
- Chen, J.; Yousefi, M.; Zhao, Y.; Zhang, C.; Zhang, S.; Mao, Z.; Peng, M.; Han, R. Modelling ore-forming processes through a cosine similarity measure: Improved targeting of porphyry copper deposits in the Manzhouli belt, China. Ore Geol. Rev. 2019, 107, 108–118. [Google Scholar] [CrossRef]
- Yilmaz, H.; Yousefi, M.; Parsa, M.; Sonmez, F.N.; Maghsoodi, A. Singularity mapping of bulk leach extractable gold and− 80# stream sediment geochemical data in recognition of gold and base metal mineralization footprints in Biga Peninsula South, Turkey. J. Afr. Earth Sci. 2019, 153, 156–172. [Google Scholar]
- Shirazi, A.; Hezarkhani, A.; Shirazy, A.; Pour, A.B. Geochemical modeling of copper mineralization using geostatistical and machine learning algorithms in the Sahlabad area, Iran. Minerals 2023, 13, 1133. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Garrett, R.G. Factor analysis applied to regional geochemical data: Problems and possibilities. Appl. Geochem. 2002, 17, 185–206. [Google Scholar] [CrossRef]
- Hoseinzade, Z.; Bazobandi, M.H. Deep embedded clustering: Delineating multivariate geochemical anomalies in the Feizabad region. Geochemistry 2024, 84, 126208. [Google Scholar] [CrossRef]
- Yousefi, M.; Barak, S.; Salimi, A.; Yousefi, S. Should geochemical indicators be integrated to produce enhanced signatures of mineral deposits? A discussion with regard to exploration scale. J. Min. Environ. 2023, 14, 1011–1018. [Google Scholar]
- Bahri, E.; Alimoradi, A.; Yousefi, M. Mineral Potential Modeling of Porphyry Copper Deposits using Continuously-Weighted Spatial Evidence Layers and Union Score Integration Method. J. Min. Environ. 2021, 12, 743–751. [Google Scholar]
- Afzal, P.; Yusefi, M.; Mirzaie, M.; Ghadiri-Sufi, E.; Ghasemzadeh, S.; Daneshvar Saein, L. Delineation of podiform-type chromite mineralization using geochemical mineralization prospectivity index and staged factor analysis in Balvard area (SE Iran). J. Min. Environ. 2019, 10, 705–715. [Google Scholar]
- Yousefi, M.; Carranza, E.J.M. Fuzzification of continuous-value spatial evidence for mineral prospectivity mapping. Comput. Geosci. 2015, 74, 97–109. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. Identification of hydrothermal alteration minerals for exploring of porphyry copper deposit using ASTER data, SE Iran. J. Asian Earth Sci. 2011, 42, 1309–1323. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. Identifying areas of high economic-potential copper mineralization using ASTER data in the Urumieh–Dokhtar Volcanic Belt, Iran. Adv. Space Res. 2012, 49, 753–769. [Google Scholar] [CrossRef]
- Beygi, S.; Talovina, I.V.; Tadayon, M.; Pour, A.B. Alteration and structural features mapping in Kacho-Mesqal zone, Central Iran using ASTER remote sensing data for porphyry copper exploration. Int. J. Image Data Fusion 2021, 12, 155–175. [Google Scholar] [CrossRef]
- Hewson, R.; Cudahy, T.; Mizuhiko, S.; Ueda, K.; Mauger, A. Seamless geological map generation using ASTER in the Broken Hill-Curnamona province of Australia. Remote Sens. Environ. 2005, 99, 159–172. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Khalifani, F.M.; Bahroudi, A.; Aliyari, F.; Abedi, M.; Yousefi, M.; Mohammadpour, M. Generation of an efficient structural evidence layer for mineral exploration targeting. J. Afr. Earth Sci. 2019, 160, 103609. [Google Scholar] [CrossRef]
- Yousefi, M.; Hronsky, J.M. Translation of the function of hydrothermal mineralization-related focused fluid flux into a mappable exploration criterion for mineral exploration targeting. Appl. Geochem. 2023, 149, 105561. [Google Scholar] [CrossRef]
- Hezarkhani, A. Petrology of the intrusive rocks within the Sungun porphyry copper deposit, Azerbaijan, Iran. J. Asian Earth Sci. 2006, 27, 326–340. [Google Scholar] [CrossRef]
- Ghasemzadeh, S.; Maghsoudi, A.; Yousefi, M. Application of geometric average approach for Cu-porphyry prospectivity mapping in the Baft area, kerman. Sci. Q. J. Geosci. 2019, 29, 130–231. [Google Scholar]
- Saremi, M.; Maghsoudi, A.; Ghezelbash, R.; Yousefi, M.; Hezarkhani, A. Targeting of porphyry copper mineralization using a continuous-based logistic function approach in the Varzaghan district, north of Urumieh-Dokhtar magmatic arc. J. Min. Environ. 2024. [Google Scholar]
- Roshanravan, B.; Aghajani, H.; Yousefi, M.; Kreuzer, O. An improved prediction-area plot for prospectivity analysis of mineral deposits. Nat. Resour. Res. 2019, 28, 1089–1105. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Prediction–area (P–A) plot and C–A fractal analysis to classify and evaluate evidential maps for mineral prospectivity modeling. Comput. Geosci. 2015, 79, 69–81. [Google Scholar] [CrossRef]
- Hoseinzade, Z.; Zavarei, A.; Shirani, K. Application of prediction–area plot in the assessment of MCDM methods through VIKOR, PROMETHEE II, and permutation. Nat. Hazards 2021, 109, 2489–2507. [Google Scholar] [CrossRef]
- Maryam, M.; Zohre, H.; Kourosh, S. A comparison study on landslide prediction through FAHP and Dempster–Shafer methods and their evaluation by P–A plots. Environ. Earth Sci. 2020, 79, 76. [Google Scholar]
- Liao, L.; Luo, B. Entropy isolation forest based on dimension entropy for anomaly detection. In Proceedings of the Computational Intelligence and Intelligent Systems: 10th International Symposium, ISICA 2018, Jiujiang, China, 13–14 October 2018; Revised Selected Papers 10. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Hariri, S.; Kind, M.C.; Brunner, R.J. Extended isolation forest. IEEE Trans. Knowl. Data Eng. 2019, 33, 1479–1489. [Google Scholar] [CrossRef]
- Shahrestani, S.; Sanislav, I. How does dimensionality influence outlier detection effectiveness in multivariate geochemical data? insights from LOF and IF methods. Earth Sci. Inform. 2024, 18, 27. [Google Scholar] [CrossRef]





| Band | Spectral Region | Wavelength (µm) | Resolution (m) |
|---|---|---|---|
| B1 | VNIR | 0.520–0.60 | 15 |
| B2 | 0.630–0.690 | ||
| B3N | 0.760–0.860 | ||
| B3B | 0.760–0.860 | ||
| B4 | SWIR | 1.600–1.700 | 30 |
| B5 | 2.145–2.185 | ||
| B6 | 2.185–2.225 | ||
| B7 | 2.235–2.285 | ||
| B8 | 2.295–2.365 | ||
| B9 | 2.360–2.430 | ||
| B10 | TIR | 8.125–8.475 | 90 |
| B11 | 8.475–8.825 | ||
| B12 | 8.925–9.275 | ||
| B13 | 10.250–10.950 | ||
| B14 | 10.950–11.650 |
| Elements | Zn | Pb | Ag | Cu | As | Sb | Hg | Au |
|---|---|---|---|---|---|---|---|---|
| Zn | 1 | −0.126 | −0.409 | −0.020 | −0.381 | 0.032 | −0.181 | 0.430 |
| Pb | −0.126 | 1 | 0.596 | −0.595 | −0.007 | −0.412 | −0.595 | −0.144 |
| Ag | −0.409 | 0.596 | 1 | −0.500 | 0.229 | −0.354 | −0.375 | −0.181 |
| Cu | −0.020 | −0.595 | −0.500 | 1 | −0.043 | 0.482 | 0.677 | 0.012 |
| As | −0.381 | −0.007 | 0.229 | −0.043 | 1 | 0.533 | −0.025 | −0.292 |
| Sb | 0.032 | −0.412 | −0.354 | 0.482 | 0.533 | 1 | 0.351 | −0.087 |
| Hg | −0.181 | −0.595 | −0.375 | 0.677 | −0.025 | 0.351 | 1 | 0.001 |
| Au | 0.430 | −0.144 | −0.181 | 0.012 | −0.292 | −0.087 | 0.001 | 1 |
| Elements | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| Au | 0.031 | 0.685 | −0.186 |
| Hg | 0.872 | −0.209 | −0.036 |
| Sb | 0.437 | 0.081 | 0.829 |
| As | −0.131 | −0.363 | 0.861 |
| Cu | 0.872 | −0.019 | 0.097 |
| Ag | −0.654 | −0.525 | −0.076 |
| Pb | −0.803 | −0.207 | −0.162 |
| Zn | −0.034 | 0.906 | −0.033 |
| Algorithm | Hyperparameter | Values | Total |
|---|---|---|---|
| IF | Number of ITrees | [600, 1000, 1400, 1800] | 28 |
| Max features | [1, 2, 3, 4, 5, 6, 7] | ||
| EIF | Number of ITrees | [600, 1000, 1400, 1800] | 24 |
| Extension level | [1, 2, 3, 4, 5, 6] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saremi, M.; Hezarkhani, A.; Mirzabozorg, S.A.A.S.; DehghanNiri, R.; Shirazy, A.; Shirazi, A. Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms. Minerals 2025, 15, 411. https://doi.org/10.3390/min15040411
Saremi M, Hezarkhani A, Mirzabozorg SAAS, DehghanNiri R, Shirazy A, Shirazi A. Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms. Minerals. 2025; 15(4):411. https://doi.org/10.3390/min15040411
Chicago/Turabian StyleSaremi, Mobin, Ardeshir Hezarkhani, Seyyed Ataollah Agha Seyyed Mirzabozorg, Ramin DehghanNiri, Adel Shirazy, and Aref Shirazi. 2025. "Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms" Minerals 15, no. 4: 411. https://doi.org/10.3390/min15040411
APA StyleSaremi, M., Hezarkhani, A., Mirzabozorg, S. A. A. S., DehghanNiri, R., Shirazy, A., & Shirazi, A. (2025). Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms. Minerals, 15(4), 411. https://doi.org/10.3390/min15040411










