Mineral Prospectivity Mapping in Xiahe-Hezuo Area Based on Wasserstein Generative Adversarial Network with Gradient Penalty
Abstract
1. Introduction
2. Study Area and Dataset
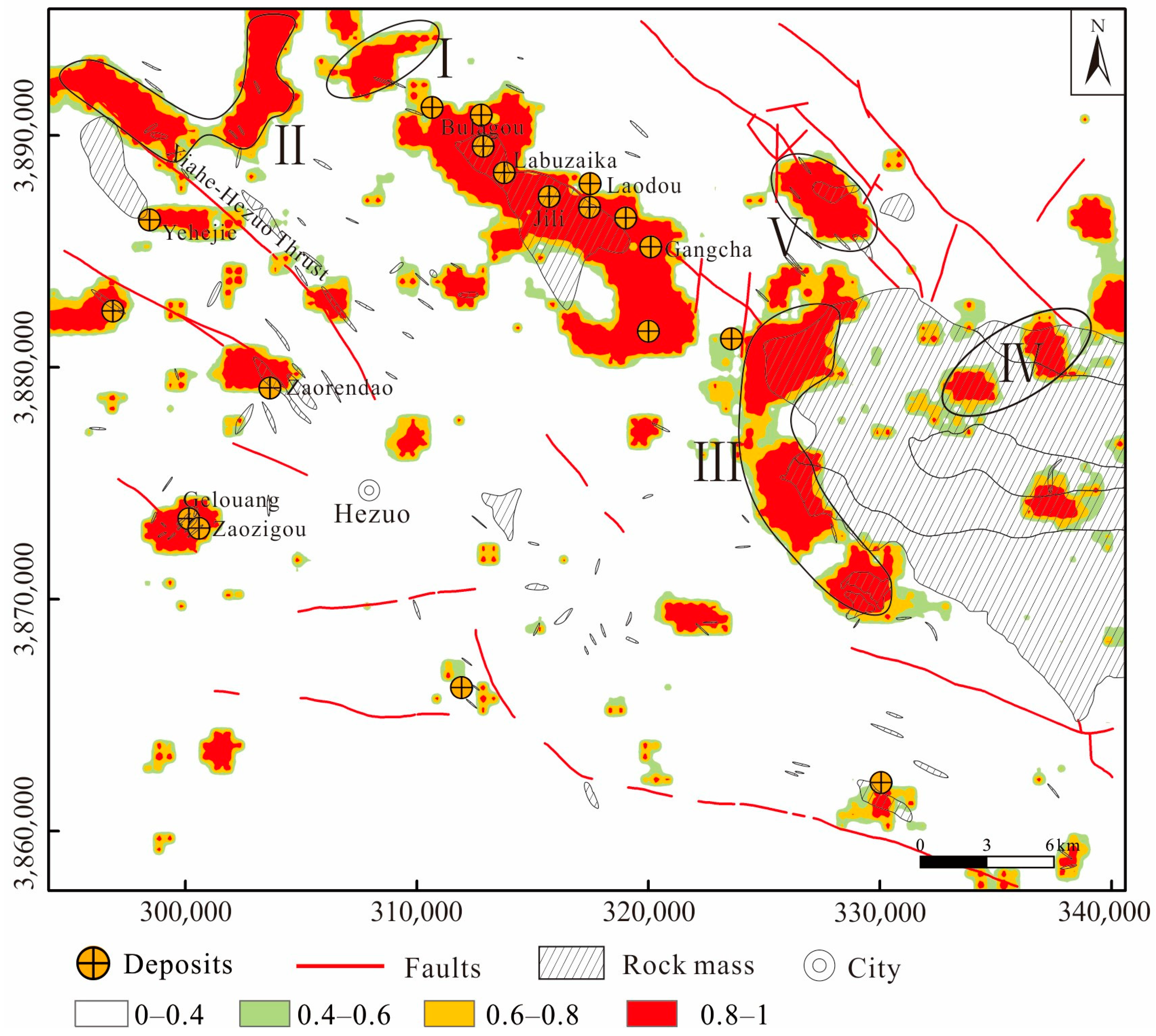
2.1. Geological Setting
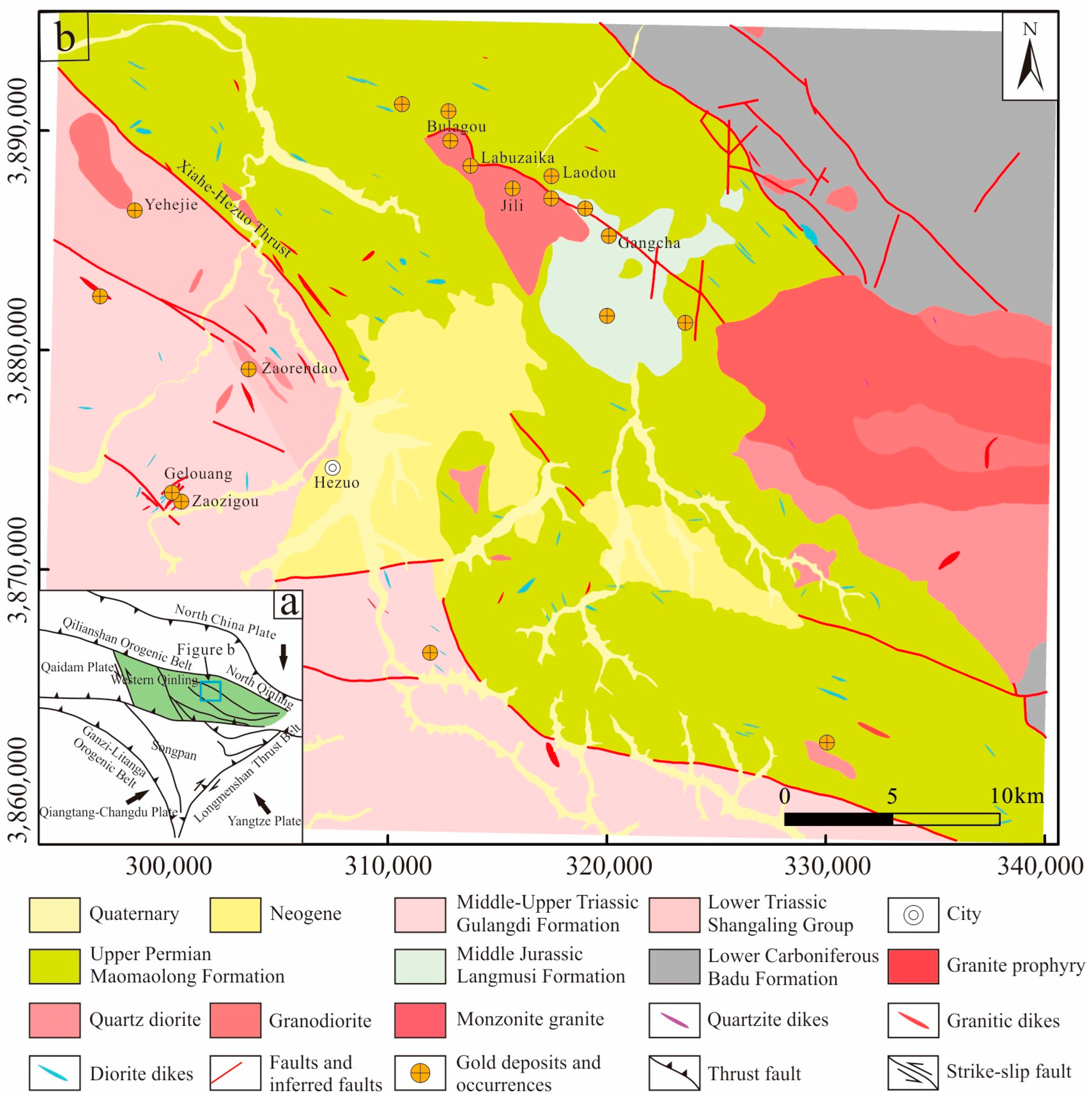
2.2. Geological Data
3. Method
3.1. Convolutional Neural Network
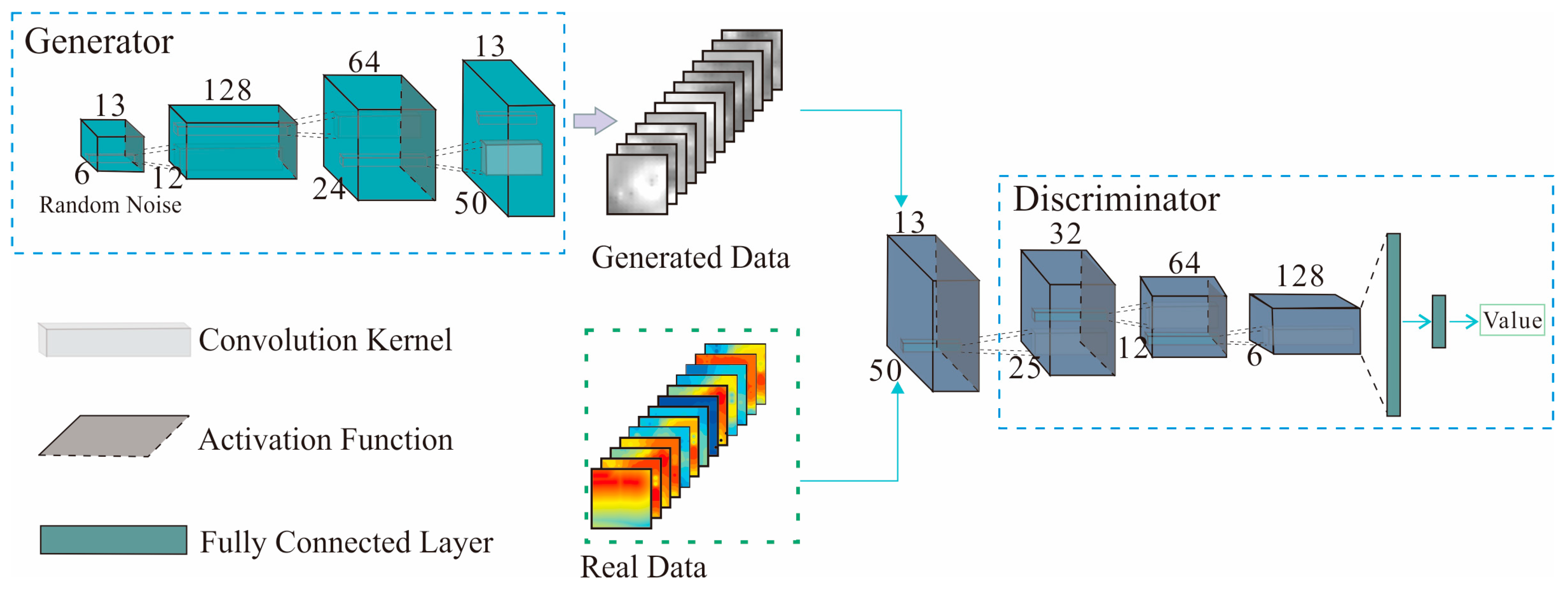
3.2. WGAN-GP-Based Data Augmentation
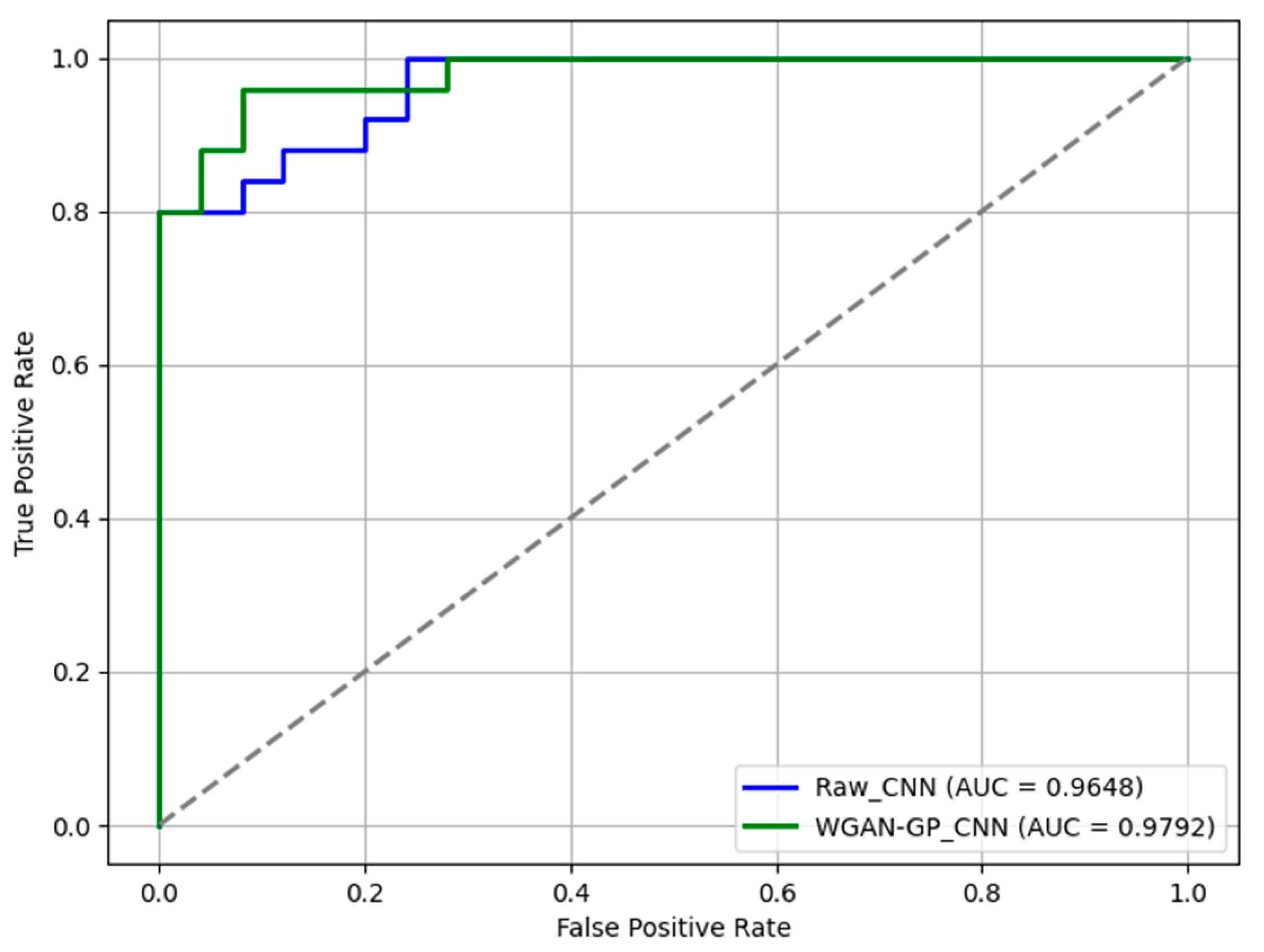
3.3. Assessment of the Quality of Data Augmentation
4. Results and Discussion
4.1. Data Preprocessing
4.2. WGAN-GP-Based Data Augmentation
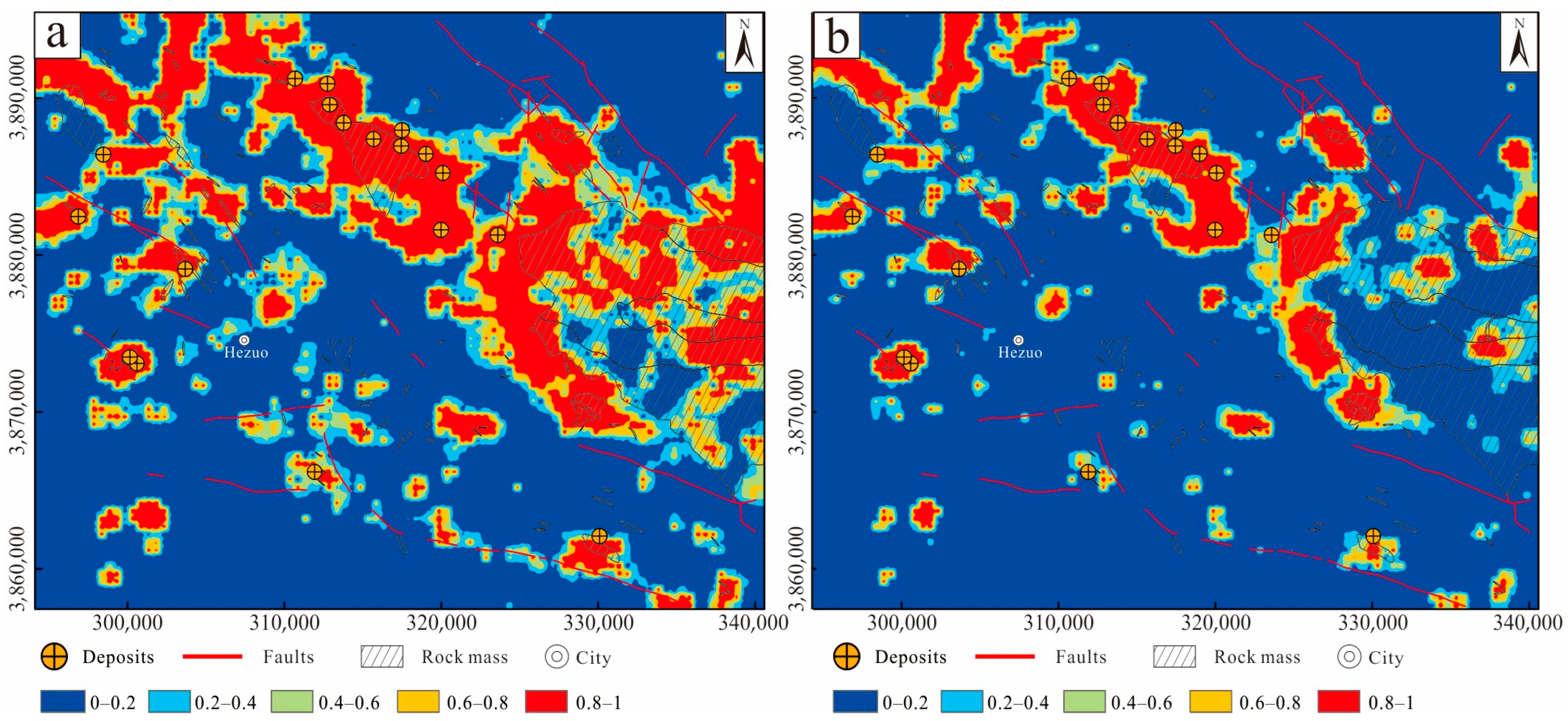
4.3. Mineral Prospectivity Mapping
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, H.B.; Yang, H.Q.; Zhao, G.B.; Tan, W.J.; Wen, Z.L.; Li, Z.H.; Gu, P.Y.; Li, J.Q.; Guo, P.H.; Wang, Y.H. Discussion on the Metallogenic Regularity in West Qinling Metallogenic Belt, China. Northwest. Geol. 2023, 56, 187–202, (In Chinese with English Abstract). [Google Scholar]
- Li, K.N.; Jia, R.Y.; Li, H.R.; Tang, L.; Liu, B.C.; Yan, K.; Wei, L.L. The Au-Cu polymetallic mineralization system related to intermediate to felsic intrusive rocks and the prospecting prediction in Xiahe-Hezuo area of Gansu, West Qinling orogenic belt. Geol. Bull. China 2020, 39, 1191–1203, (In Chinese with English Abstract). [Google Scholar]
- He, J.Z.; Ding, Z.J.; Zhu, Y.X.; Zhen, H.X.; Zhang, W.R.; Liu, J. The metallogenic series in West Qinling, Gansu Province, and their quantitative estimation. Earth Sci. Front. 2024, 31, 218–234, (In Chinese with English Abstract). [Google Scholar]
- Wang, L. Metallogenic Series, Regularity and Prospecting the Direction of the West Qinling Metallogenic Belt. Acta Geosci. Sin. 2023, 44, 649–659, (In Chinese with English Abstract). [Google Scholar]
- Liu, B.L.; Xie, M.; Kong, Y.H.; Tang, R.; Yu, Z.B.; Luo, D.J. Quantitative Gold Resources Prediction in Xiahe-Hezuo Area Based on Convolutional Auto-Encode Network. Acta Geosci. Sin. 2023, 44, 877–886, (In Chinese with English Abstract). [Google Scholar]
- Wu, Y.X.; Liu, B.L.; Gao, Y.X.; Li, C.; Tang, R.; Kong, Y.H.; Xie, M.; Li, K.N.; Dan, S.Y.; Qi, K.; et al. Mineral prospecting mapping with conditional generative adversarial network augmented data. Ore Geol. Rev. 2023, 105787. [Google Scholar] [CrossRef]
- Chen, Y.L.; Wu, W. Mapping mineral prospectivity using an extreme learning machine regression. Ore Geol. Rev. 2017, 80, 200–213. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Harris, D.; Zurcher, L.; Stanley, M.; Marlow, J.; Pan, G.C. A comparative analysis of favorability mappings by weights of evidence, probabilistic neural networks, discriminant analysis, and logistic regression. Nat. Resour. Res. 2003, 12, 241–255. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.; Fathianpour, N. Fuzzy outranking approach: A knowledge-driven method for mineral prospectivity mapping. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 556–567. [Google Scholar] [CrossRef]
- Zuo, R.G.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2010, 37, 1967–1975. [Google Scholar] [CrossRef]
- Geranian, H.; Tabatabaei, S.H.; Asadi, H.H.; Carranza, E.J.M. Application of discriminant analysis and support vector machine in mapping gold potential areas for further drilling in the Sari-Gunay gold deposit, NW Iran. Nat. Resour. Res. 2016, 25, 145–159. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Ran, X.J.; Xue, L.F.; Zhang, Y.Y.; Liu, Z.Y.; Sang, X.J.; He, J.X. Rock Classification from Field Image Patches Analyzed Using a Deep Convolutional Neural Network. Mathematics 2019, 7, 755. [Google Scholar] [CrossRef]
- Sang, X.J.; Xue, L.F.; Ran, X.J.; Li, X.S.; Liu, J.W.; Liu, Z.Y. Intelligent High-Resolution Geological Mapping Based on SLIC-CNN. ISPRS Int. J. Geo-Inf. 2020, 9, 99. [Google Scholar] [CrossRef]
- Guo, J.T.; Li, Y.Q.; Jessell, M.W.; Giraud, J.; Li, C.L.; Wu, L.X.; Li, F.D.; Liu, S.J. 3D geological structure inversion from Noddy-generated magnetic data using deep learning methods. Comput. Geosci. 2021, 149, 104701. [Google Scholar] [CrossRef]
- Liu, Y.P.; Zhu, L.X.; Zhou, Y.Z. Experimental Research on Big Data Mining and Intelligent Prediction of Prospecting Target Area—Application of Convolutional Neural Network Model. Geotecton. Metallog. 2020, 44, 192–202, (In Chinese with English Abstract). [Google Scholar]
- Cai, H.H.; Xu, Y.Y.; Li, Z.X.; Cao, H.H.; Feng, Y.X.; Chen, S.Q.; Li, Y.S. The division of metallogenic prospective areas based on convolutional neural network model: A case study of the Daqiao gold polymetallic deposit. Geol. Bull. 2019, 38, 1999–2009, (In Chinese with English Abstract). [Google Scholar]
- Li, T.; Zuo, R.G.; Xiong, Y.H.; Peng, Y. Random-Drop Data Augmentation of Deep Convolutional Neural Network for Mineral Prospectivity Mapping. Nat. Resour. Res. 2021, 30, 27–38. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.X.; Chen, F.; Zhu, Z.; Hu, Z.J. Data-Driven Predictive Modelling of Mineral Prospectivity Using Machine Learning and Deep Learning Methods: A Case Study from Southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.P.; Liu, C.; Wang, Y. Mineral Prospectivity Prediction via Convolutional Neural Networks Based on Geological Big Data. J. Earth Sci. 2021, 32, 327–347. [Google Scholar] [CrossRef]
- Zhang, C.J.; Zuo, R.G.; Xiong, Y.H. Detection of the multivariate geochemical anomalies associated with mineralization using a deep convolutional neural network and a pixel-pair feature method. Appl. Geochem. 2021, 130, 104994. [Google Scholar] [CrossRef]
- Xie, M.; Liu, B.L.; Wang, L.; Li, C.; Kong, Y.H.; Tang, R. Auto encoder generative adversarial networks-based mineral prospectivity mapping in Lhasa area, Tibet. J. Geochem. Explor. 2023, 255, 107326. [Google Scholar] [CrossRef]
- Xiong, Y.H.; Zuo, R.G.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Zuo, R.G.; Xiong, Y.H.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Cheng, Q.M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Hariharan, S.; Tirodkar, S.; Porwal, A.; Bhattacharya, A.; Joly, A. Random Forest-Based Prospectivity Modelling of Greenfield Terrains Using Sparse Deposit Data: An Example from the Tanami Region, Western Australia. Nat. Resour. Res. 2017, 26, 489–507. [Google Scholar] [CrossRef]
- Li, T.F.; Xia, Q.L.; Zhao, M.Y.; Gui, Z.; Leng, S. Prospectivity Mapping for Tungsten Polymetallic Mineral Resources, Nanling Metallogenic Belt, South China: Use of Random Forest Algorithm from a Perspective of Data Imbalance. Nat. Resour. Res. 2020, 29, 203–227. [Google Scholar] [CrossRef]
- Ma, D.; Tang, P.; Zhao, L.J. SiftingGAN: Generating and Sifting Labeled Samples to Improve the Remote Sensing Image Scene Classification Baseline In Vitro. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1046–1050. [Google Scholar] [CrossRef]
- Moreno-barea, F.J.; Strazzera, F.; Jerez, J.M.; Urda, D.; Franco, L. Forward Noise Adjustment Scheme for Data Augmentation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 728–734. [Google Scholar] [CrossRef]
- Devries, T.; Taylor, G.W. Improved regularization of convolutional neural networks with cutout. arXiv 2017, arXiv:170804552. [Google Scholar]
- Zuo, R.G.; Cheng, Q.M.; Xu, Y.; Yang, F.F.; Xiong, Y.H.; Wang, Z.Y.; Kreuzer, O.P. Explainable artificial intelligence models for mineral prospectivity mapping. Sci. China Earth Sci. 2024, 54, 2917–2928, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Li, W.; Wu, G.D.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Electron. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. lmproved training of Wasserstein GANs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Zhang, G.W.; Guo, A.L.; Yao, A.P. Western Qinling-Songpan continental tectonic nodein China’s continental tectonics. Earth Sci. Front. 2004, 11, 23–32, (In Chinese with English Abstract). [Google Scholar]
- Lu, Y.C. Skarn Copper (Gold) Metallogeny and Metallogenic Regularities in the West Section of the Western Qinling Orogen. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2017. (In Chinese with English Abstract). [Google Scholar]
- Wei, L.X.; Chen, Z.L.; Pang, Z.S.; Han, F.B.; Xiao, C.H. An Analysis of the Tectonic Stress Field in the Zaozigou Gold Deposit, Hezuo Area, Gansu Province. Acta Geosci. Sin. 2018, 39, 79–93, (In Chinese with English Abstract). [Google Scholar]
- Zhang, S. Multi-Geoinformation Integration for Mineral Prospectivity Mapping in the Hezuo-Meiwu District, Gansu Province. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2021. (In Chinese with English Abstract). [Google Scholar]
- Zhang, S. Comprehensive Information Mineral Exploration Prediction Research in the Hezuo-Mewu Area, Gansu Province. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2021. (In Chinese with English Abstract). [Google Scholar]
- Liang, Z.L.; Chen, G.Z.; Ma, H.S.; Zhang, Y.N. Evolution of Ore-controlling Faults in the Zaozigou Gold Deposit, Western Qinling. Geotecton. Metallog. 2016, 40, 354–366. [Google Scholar]
- Liu, C.X.; Cheng, Y.Y.; Luo, X.G.; Liang, Z.L.; Jing, D.G.; Ma, H.H. Study on characteristics and exploration significance of main ore belt and orebody of Zaozigou super large gold deposit in Hezuo, Gansu. Miner. Resour. Geol. 2018, 32, 969–977, (In Chinese with English Abstract). [Google Scholar]
- Gu, J.X.; Wang, Z.H.; Kuen, J.; Ma, L.Y.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.X.; Wang, G.; Cai, J.F.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Uang, C.M.; Yin, S.; Andres, P.; Reeser, W.; Yu, F.T. Shift-invariant interpattern association neural network. Appl. Opt. 1994, 33, 2147–2151. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Goodfellow, J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial Networks. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Radford, A. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Karras, T. A Style-Based Generator Architecture for Generative Adversarial Networks. arXiv 2019, arXiv:1812.04948. [Google Scholar]
- Ramesh, A.; Pavlov, M.; Goh, G.; Gray, S.; Voss, C.; Radford, A.; Chen, M.; Sutskever, L. Zero-shot text-to-image generation. Int. Conf. Mach. Learn. 2021, 139, 8821–8831. [Google Scholar] [CrossRef]
- Kong, J.; Kim, J.; Bae, J. Hifi-gan: Generative adversarial networks for efficient and high fidelity speech synthesis. Adv. Neural Inf. Process. Syst. 2020, 33, 17022–17033. [Google Scholar]
- Goodfellow, I.; Yoshua, B.; Aaron, C. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Mescheder, L.; Geiger, A.; Nowozin, S. Which training methods for GANs do actually converge? Int. Conf. Mach. Learn. 2018, 80, 3481–3490. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar] [CrossRef]
- Lopez-Paz, D.; Oquab, M. Revisiting classifier two-sample tests. arXiv 2016, arXiv:1610.06545. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8798–8807. [Google Scholar] [CrossRef]
- Nykänen, V.; Lahti, I.; Niiranen, T.; Korhonen, K. Receiver operating characteristics (ROC) as validation tool for prospectivity models—A magmatic Ni–Cu case study from the Central Lapland Greenstone Belt, Northern Finland. Ore Geol. Rev. 2015, 71, 853–860. [Google Scholar] [CrossRef]
- Zuo, R.G.; Kreuzer, O.P.; Wang, J.; Xiong, Y.H.; Zhang, Z.J.; Wang, Z.Y. Uncertainties in GIS-based mineral prospectivity mapping: Key types, potential impacts and possible solutions. Nat. Resour. Res. 2021, 30, 3059–3079. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.X.; Liu, W.X.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Data-driven evidential belief modeling of mineral potential using few prospects and evidence with missing values. Nat. Resour. Res. 2015, 24, 291–304. [Google Scholar] [CrossRef]


| Element | Minimum | Maximum | Median | Mean | Standard Deviation | Coefficient of Variation | National Average | Skewness |
|---|---|---|---|---|---|---|---|---|
| Ag | 0.04 | 3.87 | 0.12 | 0.13 | 0.08 | 0.62 | 0.08 | 18.59 |
| As | 2.47 | 6595.00 | 15.30 | 25.39 | 93.00 | 3.66 | 13.10 | 47.57 |
| Au | 0.30 | 773.00 | 1.10 | 2.21 | 14.95 | 6.77 | 1.96 | 36.02 |
| Ba | 235.00 | 1025.00 | 550.00 | 544.64 | 49.44 | 0.09 | 532.00 | −0.08 |
| Bi | 0.11 | 138.00 | 0.36 | 0.47 | 1.64 | 3.48 | 0.47 | 69.44 |
| Co | 5.10 | 82.80 | 14.30 | 14.40 | 2.64 | 0.18 | 12.40 | 5.44 |
| Cu | 6.80 | 974.00 | 26.60 | 27.86 | 14.82 | 0.53 | 23.60 | 37.05 |
| Hg | 6.43 | 927.00 | 31.30 | 37.72 | 32.46 | 0.86 | 52.00 | 10.92 |
| Mo | 0.00 | 12.15 | 0.84 | 0.88 | 0.27 | 0.31 | 1.08 | 15.73 |
| Pb | 8.40 | 341.00 | 25.30 | 26.41 | 10.23 | 0.39 | 27.60 | 14.02 |
| Sb | 0.29 | 1909.00 | 1.09 | 2.36 | 23.52 | 9.97 | 1.30 | 65.63 |
| W | 0.10 | 67.00 | 2.10 | 2.54 | 2.42 | 0.95 | 2.51 | 12.14 |
| Zn | 23.30 | 1380.00 | 88.50 | 88.56 | 21.58 | 0.24 | 72.00 | 25.52 |
| Hyperparameter | Positive Sample | Negative Sample |
|---|---|---|
| Initial Learning Rate | 0.0005 | 0.0005 |
| Penalty Coefficient | 7.5 | 6.5 |
| Generator Learning Rate Decay | 0.975 | 0.975 |
| Discriminator Learning Rate Decay | 0.97 | 0.97 |
| Batch Size | 32 | 32 |
| Number of Iterations | 3000 | 3000 |
| Optimizer | Adam | Adam |
| Layer Typer | Input Size | Output Size | Kernel Size |
|---|---|---|---|
| Conv2d_1 | [m,13,50,50] | [m,32,48,48] | 5 × 5 |
| BatchNorm2d | [m,32,48,48] | [m,32,48,48] | |
| ReLU | [m,32,48,48] | [m,32,48,48] | |
| MaxPooL_1 | [m,32,48,48] | [m,32,24,24] | 2 × 2 |
| Conv2d_2 | [m,32,24,24] | [m,64,24,24] | 3 × 3 |
| BatchNorm2d | [m,64,24,24] | [m,64,24,24] | |
| ReLU | [m,64,24,24] | [m,64,24,24] | |
| MaxPooL_2 | [m,64,24,24] | [m,64,12,12] | 2 × 2 |
| Conv2d_3 | [m,64,12,12] | [m,128,12,12] | 3 × 3 |
| BatchNorm2d | [m,128,12,12] | [m,128,12,12] | |
| ReLU | [m,128,12,12] | [m,128,12,12] | |
| MaxPooL_3 | [m,128,12,12] | [m,128,6,6] | 2 × 2 |
| Linear_1 | [m,4608] | [m,512] | |
| Linear_2 | [m,512] | [m,2] |
| Model | Train Acc | Test Acc |
|---|---|---|
| Raw_CNN | 92% | 90% |
| WGAN–GP_CNN | 97% | 92% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, J.; Li, Y.; Xie, M.; Kong, Y.; Tang, R.; Li, C.; Wu, Y.; Wu, Z. Mineral Prospectivity Mapping in Xiahe-Hezuo Area Based on Wasserstein Generative Adversarial Network with Gradient Penalty. Minerals 2025, 15, 184. https://doi.org/10.3390/min15020184
Gong J, Li Y, Xie M, Kong Y, Tang R, Li C, Wu Y, Wu Z. Mineral Prospectivity Mapping in Xiahe-Hezuo Area Based on Wasserstein Generative Adversarial Network with Gradient Penalty. Minerals. 2025; 15(2):184. https://doi.org/10.3390/min15020184
Chicago/Turabian StyleGong, Jiansheng, Yunhe Li, Miao Xie, Yunhui Kong, Rui Tang, Cheng Li, Yixiao Wu, and Zehua Wu. 2025. "Mineral Prospectivity Mapping in Xiahe-Hezuo Area Based on Wasserstein Generative Adversarial Network with Gradient Penalty" Minerals 15, no. 2: 184. https://doi.org/10.3390/min15020184
APA StyleGong, J., Li, Y., Xie, M., Kong, Y., Tang, R., Li, C., Wu, Y., & Wu, Z. (2025). Mineral Prospectivity Mapping in Xiahe-Hezuo Area Based on Wasserstein Generative Adversarial Network with Gradient Penalty. Minerals, 15(2), 184. https://doi.org/10.3390/min15020184





