Correlation Analysis Between Pore Structure and Mechanical Strength of Mine Filling Materials Based on Low-Field NMR and Fractal Theory
Abstract
1. Introduction
2. Methods and Theory
2.1. Raw Materials
2.2. Specimen Preparation
2.3. Experimental Test
2.4. Pore Structure Division, Fractal Dimension and Permeability Calculation
2.4.1. Pore Structure Division
2.4.2. Fractal Dimension Calculation
2.4.3. Permeability Coefficient Calculation
3. Analysis of Test Results
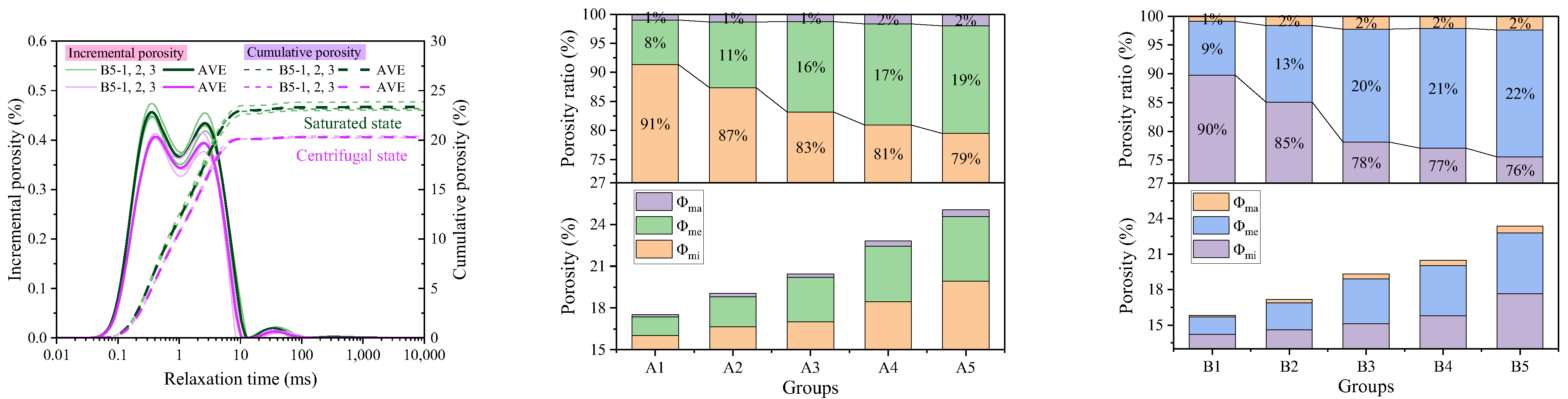
3.1. Evolution Characteristics of Pore Structure
3.1.1. T2 Spectral Characteristics and Pore Distribution
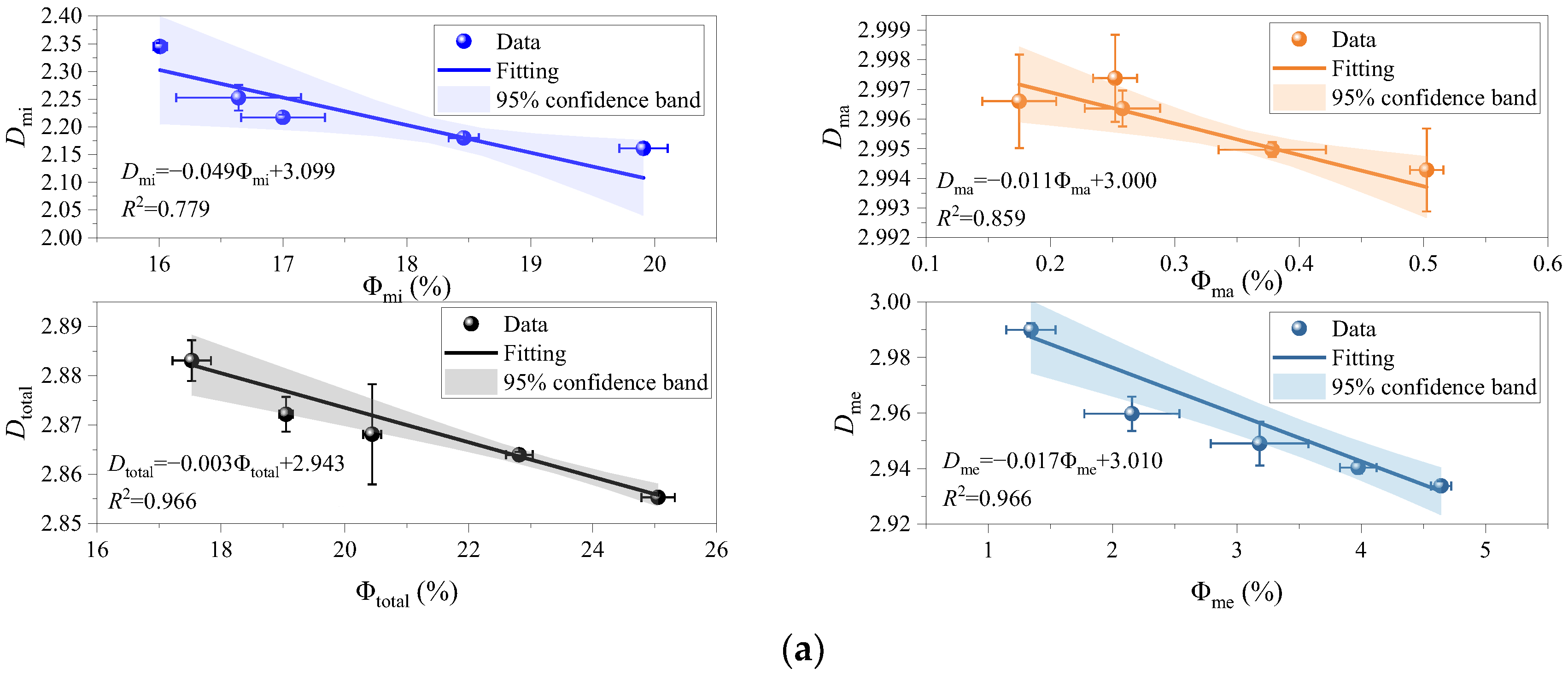
3.1.2. Fractal Dimension of Pore Structure
3.2. The Evolution Characteristics of the Mechanical Strength of Filling Materials
3.3. Multi-Scale Characteristic Analysis of Filling Materials
3.3.1. Porosity Fractal Dimension Correlation
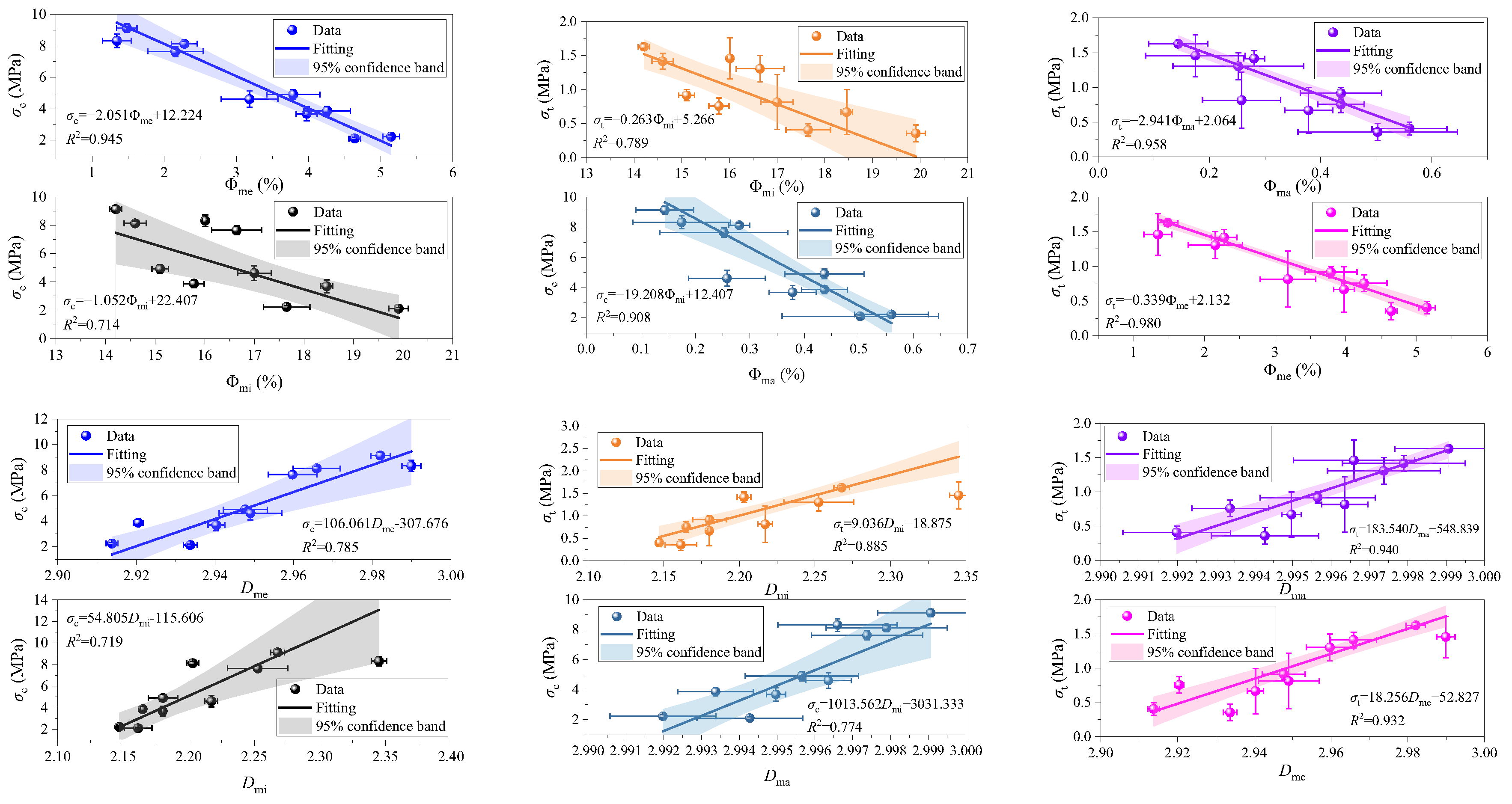
3.3.2. Analysis of the Correlation Between Pore Structure, Porosity and Mechanical Strength
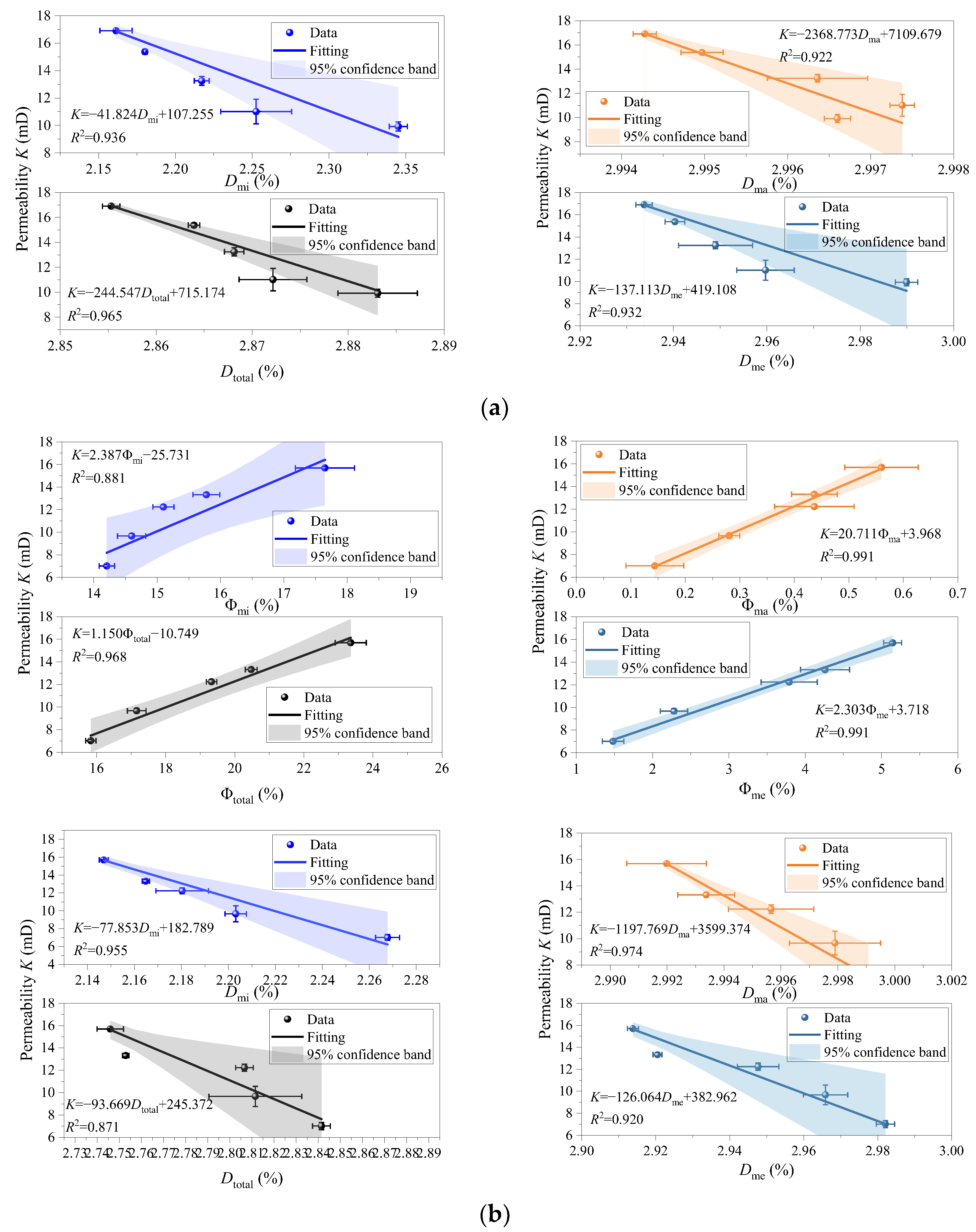
3.3.3. The Correlation Between Pore Structure Characteristics and Permeability Coefficient
4. Discussion
5. Conclusions
- (1)
- The Φtotal gradually increases as the cement-to-sand ratio decreases, with Φmi dominating over 79% of the total. The porosity component corresponding to the T2 spectrum of centrifugal specimens shows a significant reduction, indicating substantial free water separation from the filling material. As the cement-to-sand ratio decreases, hydration products gradually diminish, leaving voids between tailings particles unfilled. Consequently, Φtotal, Φmi, Φme, and Φma progressively increase. As mass concentration increases, the filling material becomes denser, resulting in more hydration products and reduced pore space, thereby decreasing Φtotal.
- (2)
- As the cement-to-sand ratio decreases or the mass concentration diminishes, the complexity of total pores, micropores, mesopores, and macropores progressively increases, revealing a strong correlation between porosity and fractal dimension. σc, Ec, σt and Et are positively correlated with the cement-to-sand ratio. The reduction in hydration products lowers the bonding strength between tailings particles, accelerating the expansion of pore tips under loading. As mass concentration increases, the internal structure of the filling material becomes denser, resulting in enhanced bonding strength. Under load conditions, the number of pore tip expansions decreases, leading to increased strength.
- (3)
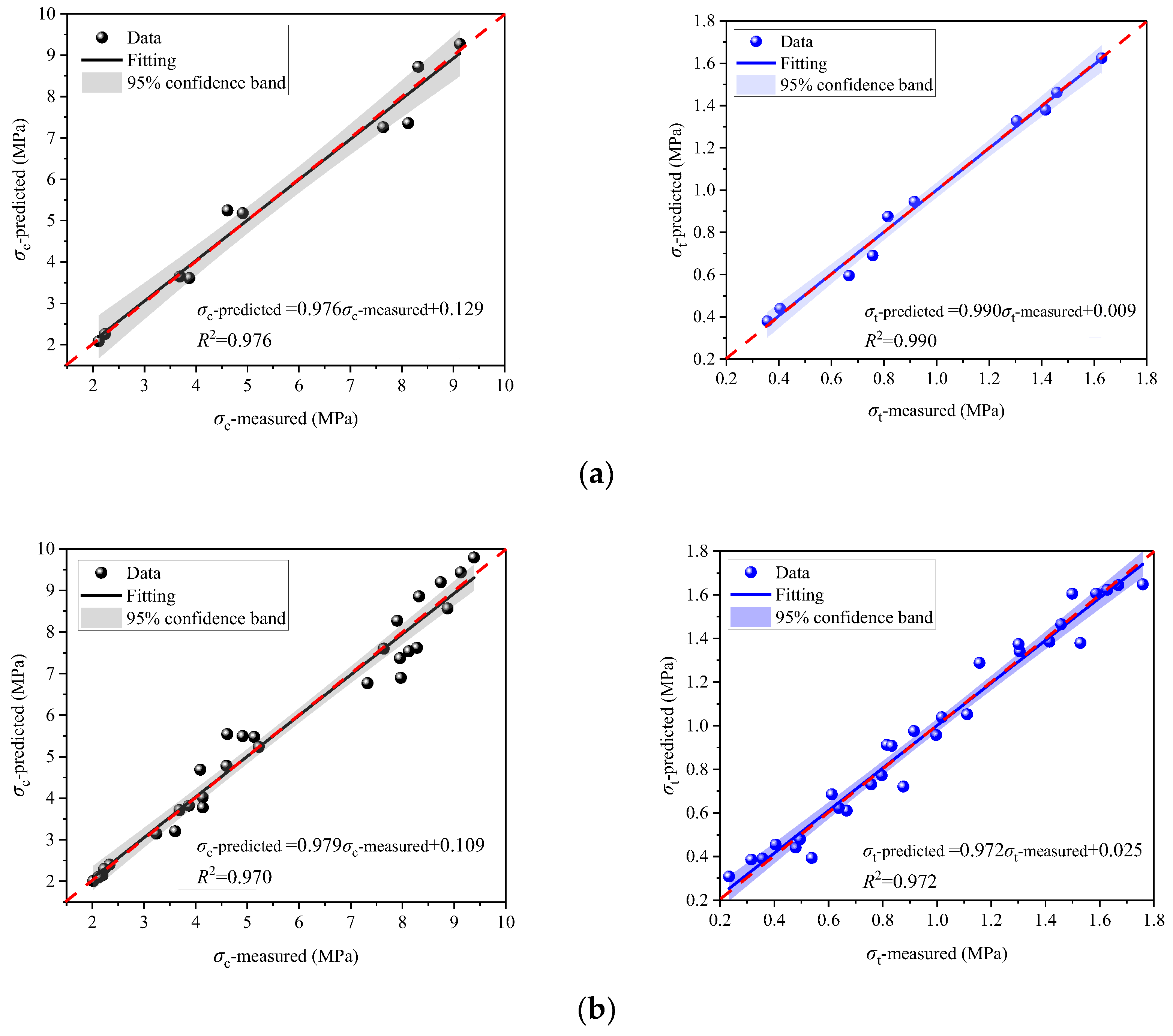
- Pore structure characteristics exhibit strong correlations with mechanical strength, confirmed by strength prediction models. As Φtotal increases, the solid skeleton area gradually decreases, the number of expanding pore tips increases, and the pressure resistance under loading gradually decreases. When Dtotal increases, the networked interlacing structure between pores also becomes more complex, which helps mitigate stress concentration phenomena.
- (4)
- The K of Group A filling material is located between 9.926 and 16.903 mD, while the K of Group B is located between 7.014 and 15.691 mD. It gradually increases as the cement-to-sand ratio decreases and gradually decreases as the mass concentration increases. A strong correlation also exists between pore structure characteristics and K. As pore quantity increases, pore connectivity gradually enhances, reducing fluid flow resistance. However, increased pore complexity lengthens seepage pathways, diminishing the number of effective permeable channels and thereby decreasing K values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, G.; Yilmaz, E.; Wang, Y. Progress and Prospects of Mining with Backfill in Metal Mines in China. Int. J. Min. Met. Mater. 2023, 30, 1455–1473. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Ren, Z.; Wang, F. Compaction and Seepage Characteristics of Broken Coal and Rock Masses in Coal Mining: A Review in Laboratory Tests. Rock Mech. Bull. 2024, 3, 100102. [Google Scholar] [CrossRef]
- Golik, V.I. Vibroactivation of Hardening Backfill Mixtures during Transportation over Extended Distances. Russ. Metall. Met. 2024, 2024, 1974–1979. [Google Scholar] [CrossRef]
- Huang, D.; Xing, D.; Chang, X.; Zhu, Y.; Gao, C. Analysis and Application of Filling Mining Technology in China’s Mining Area: A Case Study of YuXi Coal Mine. Arch. Min. Sci. 2021, 66, 611–624. [Google Scholar] [CrossRef]
- Sari, M.; Yilmaz, E.; Kasap, T.; Karasu, S. Exploring the Link Between Ultrasonic and Strength Behavior of Cementitious Mine Backfill by Considering Pore Structure. Constr. Build. Mater. 2023, 370, 130588. [Google Scholar] [CrossRef]
- Falah, M.; Ohenoja, K.; Obenaus-Emler, R.; Kinnunen, P.; Illikainen, M. Improvement of Mechanical Strength of Alkali-activated Materials Using Micro Low-alumina Mine Tailings. Constr. Build. Mater. 2020, 248, 118659. [Google Scholar] [CrossRef]
- Yaya, N.S.; Cao, S.; Yilmaz, E. Effect of 3D Printed Skeleton Shapes on Strength Behavior, Stress Evolution and Microstructural Response of Cement-based Tailings Backfills. Constr. Build. Mater. 2024, 432, 14. [Google Scholar] [CrossRef]
- Liu, S.; Shi, G.; Xu, Y.; Bao, X. Experimental Study of a Self-expanding Filling Material for Mine-sealing Walls. Adv. Cem. Res. 2023, 35, 70–80. [Google Scholar] [CrossRef]
- Hu, J.; Ren, Q.; Ma, S.; Jiang, Q.; Jiang, Y.; Shang, J.; Luo, Z. Macroscopic and Microscopic Trans-scale Characteristics of Pore Structure of Mine Grouting Materials. Trans. Nonferrous Met. Soc. China 2019, 29, 1067–1081. [Google Scholar] [CrossRef]
- Hefni, M.; Hassani, F. Experimental Development of a Novel Mine Backfill Material: Foam Mine Fill. Minerals 2020, 10, 564. [Google Scholar] [CrossRef]
- Cheng, K.; Tu, B.; Liu, L.; Zhang, B.; Qiu, H. Damage Strengthening Constitutive Model of Cemented Paste Backfill. Adv. Civ. Eng. 2021, 2021, 5593983. [Google Scholar] [CrossRef]
- Cetinta, S. Investigation of Pore and Filling Material Bond in Filled Travertine Used as a Building Material. Period. Polytech. Civ. Eng. 2023, 67, 80–92. [Google Scholar] [CrossRef]
- Majou, H.A.; Bruand, A.; Rozenbaum, O.; Le Trong, E. Evaluation of the Impact of Freezing Technique on Pore-structure Characteristics of Highly Decomposed Peat Using X-ray Micro-computed Tomography. Int. Agrophys. 2022, 36, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Ouellet, S.; Bussiere, B.; Aubertin, M.; Benzaazoua, M. Microstructural Evolution of Cemented Paste Backfill: Mercury Intrusion Porosimetry Test Results. Cem. Concr. Res. 2007, 37, 1654–1665. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, J.; Yang, Y.; Xiao, H.; Ma, F. Cross-Scale Study on Lime Modified Phosphogypsum Cemented Backfill by Fractal Theory. Minerals 2022, 12, 403. [Google Scholar] [CrossRef]
- Fridjonsson, E.O.; Hasan, A.; Fourie, A.B.; Johns, M.L. Pore Structure in a Gold Mine Cemented Paste Backfill. Miner. Eng. 2013, 53, 144–151. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, H.; Jiang, Z.; Lei, Y.; Wang, P.; Yu, S. Multi-scale Correlation Analysis of Filling Materials. Powder Technol. 2025, 465, 121364. [Google Scholar] [CrossRef]
- Qiu, J.; Xiong, X.; Zhou, K. Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill. Fractal Fract. 2025, 9, 367. [Google Scholar] [CrossRef]
- Yang, P.; Liu, L.; Suo, Y.; Zhu, M.; Xie, G.; Deng, S. Mechanical Properties, Pore Characteristics and Microstructure of Modified Magnesium Slag Cemented Coal-based Solid Waste Backfill Materials: Affected by Fly Ash Addition and Curing Temperature. Process Saf. Environ. 2023, 176, 1007–1020. [Google Scholar] [CrossRef]
- Zhao, K.; Ma, C.; Yang, J.; Wu, J.; Yan, Y.; Lai, Y.; Ao, W.; Tian, Y. Pore Fractal Characteristics of Fiber-reinforced Backfill Based on Nuclear Magnetic Resonance. Powder Technol. 2023, 426, 118678. [Google Scholar] [CrossRef]
- Deng, H.; Duan, T.; Tian, G.; Liu, Y.; Zhang, W. Research on Strength Prediction Model and Microscopic Analysis of Mechanical Characteristics of Cemented Tailings Backfill under Fractal Theory. Minerals 2021, 11, 886. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Wu, A.; Ruan, Z.; Wang, Z.; Liu, S. Study on Mechanical Strength, Volume Stability, and Hydration Mechanism of Cemented Tailings Backfill with Plastic Expansive Agent. Min. Metall. Explor. 2025, 19, 899–917. [Google Scholar] [CrossRef]
- Kasap, T.; Yilmaz, E.; Sari, M. Effects of Mineral Additives and Age on Microstructure Evolution and Durability Properties of Sand-reinforced Cementitious Mine Backfills. Constr. Build. Mater. 2022, 352, 129079. [Google Scholar] [CrossRef]
- Gao, R.; Wang, W.; Xiong, X.; Li, J.; Xu, C. Effect of Curing Temperature on the Mechanical Properties and Pore Structure of Cemented Backfill Materials with Waste Rock-tailings. Constr. Build. Mater. 2023, 409, 133850. [Google Scholar] [CrossRef]
- Yilmaz, E.; Benzaazoua, M.; Belem, T.; Bussiere, B. Effect of Curing under Pressure on Compressive Strength Development of Cemented Paste Backfill. Miner. Eng. 2009, 22, 772–785. [Google Scholar] [CrossRef]
- Liu, L.; Xin, J.; Qi, C.; Jia, H.; Song, K. Experimental Investigation of Mechanical, Hydration, Microstructure and Electrical Properties of Cemented Paste Backfill. Constr. Build. Mater. 2020, 263, 120137. [Google Scholar] [CrossRef]
- Tuylu, S. Effect of Different Particle Size Distribution of Zeolite on the Strength of Cemented Paste Backfill. Int. J. Environ. Sci. Technol. 2022, 19, 131–140. [Google Scholar] [CrossRef]
- Kesimal, A.; Yilmaz, E.; Ercikdi, B. Evaluation of Paste Backfill Mixtures Consisting of Sulphide-rich Mill Tailings and Varying Cement Contents. Cem. Concr. Res. 2004, 34, 1817–1822. [Google Scholar] [CrossRef]
- Gan, D.Q.; Li, H.B.; Chen, C.; Lu, H.J.; Zhang, Y.Z. An Experimental Study on Strength Characteristics and Hydration Mechanism of Cemented Ultra-Fine Tailings Backfill. Front. Mater. 2021, 8, 723878. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, X.; Elmo, D.; Xu, L.; Song, W. Experimental Study on Dynamic Mechanical Property of Cemented Tailings Backfill Under SHPB Impact Loading. Int. J. Min. Met. Mater. 2019, 26, 404–416. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.; Chen, W. The Investigation into the Mechanical Properties and Failure Mechanisms of Stratified Cemented Tailings Backfill with Enhancement Layer under Triaxial Compression. Eng. Fail. Anal. 2025, 182, 110128. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Zhou, J.; Yu, Z. Influence of Polypropylene Fiber Reinforcement on Tensile Behavior and Failure Mode of Tailings Cemented Paste Backfill. IEEE Access 2019, 7, 69015–69026. [Google Scholar] [CrossRef]
- Zheng, J.; Guo, L.; Sun, X.; Li, W.; Jia, Q. Study on the Strength Development of Cemented Backfill Body from Lead-Zinc Mine Tailings with Sulphide. Adv. Mater. Sci. Eng. 2018, 2018, 7278014. [Google Scholar] [CrossRef]
- Fall, M.; Celestin, J.C.; Pokharel, M.; Toure, M. A Contribution to Understanding the Effects of Curing Temperature on the Mechanical Properties of Mine Cemented Tailings Backfill. Eng. Geol. 2010, 114, 397–413. [Google Scholar] [CrossRef]
- Tu, B.; He, H.; Liu, L.; Ding, X.; Yang, Q. Comparative Analysis of Uniaxial and Triaxial Compression Characteristics of Cement Tailings Backfill. Min. Metall. Explor. 2025, 42, 335–345. [Google Scholar] [CrossRef]
- Shao, X.; Wang, Z.; Tang, R.; Zhao, B.; Ning, J.; Tian, C.; Wang, W.; Zhang, Y.; Du, X. Enhancing Mid-Term Strength and Microstructure of Fly Ash-Cement Paste Backfill with Silica Fume for Continuous Mining and Backfilling Operations. Materials 2024, 17, 6037. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M.; Ouellet, S. Experimental Characterization of the Influence of Tailings Fineness and Density on the Quality of Cemented Paste Backfill. Miner. Eng. 2005, 18, 41–44. [Google Scholar] [CrossRef]
- Kesimal, A.; Yilmaz, E.; Ercikdi, B.; Alp, I.; Deveci, H. Effect of Properties of Tailings and Binder on the Short-and Long-term Strength and Stability of Cemented Paste Backfill. Mater. Lett. 2005, 59, 3703–3709. [Google Scholar] [CrossRef]
- Eker, H.; Bascetin, A. Influence of Silica Fume on Mechanical Property of Cemented Paste Backfill. Constr. Build. Mater. 2022, 317, 126089. [Google Scholar] [CrossRef]
- Hefni, M.; Ali, M.A. The Potential to Replace Cement with Nano-Calcium Carbonate and Natural Pozzolans in Cemented Mine Backfill. Adv. Civ. Eng. 2021, 2021, 5574761. [Google Scholar] [CrossRef]
- Li, Y.; Fu, J.; Wang, K.; He, Z. Influence of Shell Ash on Pore Structure and Mechanical Characteristics of Cemented Tailings Backfill. Constr. Build. Mater. 2024, 411, 134473. [Google Scholar] [CrossRef]
- Qiu, J.; Li, J.; Xiong, X.; Zhou, K. Application of a Multi-Algorithm-Optimized CatBoost Model in Predicting the Strength of Multi-Source Solid Waste Backfilling Materials. Big Data Cogn. Comput. 2025, 9, 203. [Google Scholar] [CrossRef]
- Yin, S.; Yan, Z.; Chen, X.; Yan, R.; Chen, D.; Chen, J. Mechanical Properties of Cemented Tailings and Waste-rock Backfill (CTWB) Materials: Laboratory tests and deep learning modeling. Constr. Build. Mater. 2023, 369, 130610. [Google Scholar] [CrossRef]
- Niu, Y. Research on the Construction and Optimization of a Multi-Parameter Yield Stress Prediction Model for Filling Slurry Based on Machine Learning. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2020. [Google Scholar] [CrossRef]
- Cai, F.; Sun, W.; Zhang, S.; Zhu, A.; Ding, F.; Zhang, P.; Wen, Y.; Wang, S.; Xiao, Y. Strength and Crack Propagation Analysis of Layered Backfill Based on Energy Theory. Arch. Min. Sci. 2024, 69, 175–190. [Google Scholar] [CrossRef]
- Zhao, K.; Li, Q.; Yan, Y.; Zhou, K.; Gu, S.; Zhu, S. Numerical Calculation Analysis of the Structural Stability of Cemented Fill under Different Cement-Sand Ratios and Concentration Conditions. Adv. Civ. Eng. 2018, 2018, 1260787. [Google Scholar] [CrossRef]
- Jiang, Z.; Cai, G.; He, H.; Tian, G.; Liu, Y.; Wu, M. Pore Structure Evolution of Mortars with Manufactured Sand Aggregate under the Influence of Aggregate Size and Water Saturation Environment. Measurement 2025, 241, 115736. [Google Scholar] [CrossRef]
- GB/T 50080-2016; Standard Test Methods for Properties of Normal Concrete Mix. Ministry of Housing and Urban-Rural Development: Beijing, China, 2016. Available online: http://std.muren-it.com/web/detail?id=1106 (accessed on 14 November 2025).
- Jiang, Z.; Cai, G.; Liu, Y.; Wang, P.; Yu, S. Pore Structure and Mechanical Characteristics of CRS Mortar Based on NMR and Fractal Theory. Constr. Build. Mater. 2024, 457, 139459. [Google Scholar] [CrossRef]









| Groups | Mass Concentration | Cement Tailings Ratio | Fly Ash | Cement Paste | Tailings Slurry | Water | Number |
|---|---|---|---|---|---|---|---|
| A1 | 68% | 1/3 | 10% | 14.50% | 43.50% | 32% | 6 |
| A2 | 68% | 1/4 | 10% | 11.60% | 46.40% | 32% | 6 |
| A3 | 68% | 1/5 | 10% | 9.67% | 48.30% | 32% | 6 |
| A4 | 68% | 1/6 | 10% | 8.29% | 49.70% | 32% | 6 |
| A5 | 68% | 1/8 | 10% | 6.44% | 51.60% | 32% | 6 |
| B1 | 70% | 1/3 | 10% | 15.00% | 45.00% | 30% | 6 |
| B2 | 70% | 1/4 | 10% | 12.00% | 48.00% | 30% | 6 |
| B3 | 70% | 1/5 | 10% | 10.00% | 50.00% | 30% | 6 |
| B4 | 70% | 1/6 | 10% | 8.57% | 51.43% | 30% | 6 |
| B5 | 70% | 1/8 | 10% | 6.67% | 53.33% | 30% | 6 |
| Groups | Φtotal-AVE/% | ±SD | Φmi-AVE/% | ±SD | Φme-AVE/% | ±SD | Φma-AVE/% | ±SD |
|---|---|---|---|---|---|---|---|---|
| A1 | 17.528 | 0.310 | 16.009 | 0.054 | 1.344 | 0.199 | 0.175 | 0.030 |
| A2 | 19.049 | 0.106 | 16.642 | 0.503 | 2.156 | 0.383 | 0.252 | 0.018 |
| A3 | 20.440 | 0.143 | 17.000 | 0.339 | 3.183 | 0.392 | 0.258 | 0.030 |
| A4 | 22.813 | 0.216 | 18.459 | 0.122 | 3.976 | 0.147 | 0.378 | 0.043 |
| A5 | 25.054 | 0.271 | 19.910 | 0.196 | 4.642 | 0.082 | 0.503 | 0.013 |
| B1 | 15.832 | 0.149 | 14.206 | 0.122 | 1.482 | 0.141 | 0.144 | 0.053 |
| B2 | 17.159 | 0.270 | 14.598 | 0.224 | 2.280 | 0.179 | 0.281 | 0.019 |
| B3 | 19.326 | 0.151 | 15.100 | 0.166 | 3.790 | 0.368 | 0.437 | 0.073 |
| B4 | 20.475 | 0.171 | 15.779 | 0.212 | 4.259 | 0.322 | 0.437 | 0.042 |
| B5 | 23.356 | 0.449 | 17.650 | 0.467 | 5.146 | 0.118 | 0.560 | 0.067 |
| Groups | σc-AVE/MPa | ±SD | Ec-AVE/GPa | ±SD | σt-AVE/MPa | ±SD | Et-AVE/GPa | ±SD | K/mD | ±SD |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 8.322 | 0.421 | 1.715 | 0.121 | 1.458 | 0.301 | 0.257 | 0.041 | 9.926 | 0.325 |
| A2 | 7.639 | 0.314 | 1.581 | 0.114 | 1.305 | 0.194 | 0.234 | 0.054 | 11.013 | 0.901 |
| A3 | 4.613 | 0.523 | 1.308 | 0.152 | 0.815 | 0.203 | 0.165 | 0.032 | 13.248 | 0.326 |
| A4 | 3.686 | 0.449 | 0.991 | 0.149 | 0.667 | 0.129 | 0.134 | 0.029 | 15.375 | 0.178 |
| A5 | 2.108 | 0.090 | 0.535 | 0.030 | 0.356 | 0.123 | 0.115 | 0.010 | 16.903 | 0.040 |
| B1 | 9.131 | 0.256 | 1.855 | 0.141 | 1.628 | 0.041 | 0.293 | 0.004 | 7.014 | 0.120 |
| B2 | 8.126 | 0.156 | 1.631 | 0.104 | 1.415 | 0.114 | 0.245 | 0.001 | 9.670 | 0.210 |
| B3 | 4.909 | 0.312 | 1.428 | 0.122 | 0.915 | 0.082 | 0.185 | 0.006 | 12.237 | 0.190 |
| B4 | 3.871 | 0.267 | 1.029 | 0.129 | 0.757 | 0.119 | 0.153 | 0.009 | 13.320 | 0.156 |
| B5 | 2.231 | 0.102 | 0.655 | 0.080 | 0.405 | 0.090 | 0.132 | 0.007 | 15.691 | 0.132 |
| Fractal Dimension | Dtotal-AVE | ±SD | Dmi-AVE | ±SD | Dme-AVE | ±SD | Dma-AVE | ±SD |
|---|---|---|---|---|---|---|---|---|
| Group A1 | 2.883 | 0.004 | 2.345 | 0.006 | 2.990 | 0.002 | 2.997 | 0.002 |
| Group A2 | 2.872 | 0.004 | 2.253 | 0.023 | 2.960 | 0.006 | 2.997 | 0.001 |
| Group A3 | 2.868 | 0.010 | 2.217 | 0.005 | 2.949 | 0.008 | 2.996 | 0.001 |
| Group A4 | 2.864 | 0.001 | 2.180 | 0.001 | 2.940 | 0.002 | 2.995 | 0.000 |
| Group A5 | 2.855 | 0.001 | 2.161 | 0.011 | 2.934 | 0.002 | 2.994 | 0.001 |
| Group B1 | 2.841 | 0.004 | 2.268 | 0.005 | 2.982 | 0.003 | 2.999 | 0.001 |
| Group B2 | 2.812 | 0.021 | 2.203 | 0.005 | 2.966 | 0.006 | 2.997 | 0.002 |
| Group B3 | 2.807 | 0.004 | 2.180 | 0.011 | 2.948 | 0.006 | 2.996 | 0.002 |
| Group B4 | 2.753 | 0.002 | 2.165 | 0.002 | 2.920 | 0.001 | 2.993 | 0.001 |
| Group B5 | 2.746 | 0.006 | 2.147 | 0.002 | 2.914 | 0.002 | 2.992 | 0.001 |
| Strength | / | α0 | α1 | α2 | α3 |
|---|---|---|---|---|---|
| Compression | Value | −0.261 | 0.199 | 6.068 | −0.735 |
| Equation | σc = −0.261 + 0.199Φme + 6.068Ec − 0.735 (Φme·Ec) R2 = 0.964 p < 0.0001 | ||||
| Strength | / | β0 | β1 | β2 | β3 |
| Tensile | Value | 0.618 | −0.228 | 3.398 | 0.803 |
| Equation | σt = 0.618 − 0.228Φme + 3.398Ec + 0.803 (Φme·Et) R2 = 0.985 p < 0.0001 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, Y.; Lin, W.; Dou, L.; Liu, D.; Wang, Y.; Zhou, S.; Liu, Y. Correlation Analysis Between Pore Structure and Mechanical Strength of Mine Filling Materials Based on Low-Field NMR and Fractal Theory. Minerals 2025, 15, 1211. https://doi.org/10.3390/min15111211
Wang W, Wang Y, Lin W, Dou L, Liu D, Wang Y, Zhou S, Liu Y. Correlation Analysis Between Pore Structure and Mechanical Strength of Mine Filling Materials Based on Low-Field NMR and Fractal Theory. Minerals. 2025; 15(11):1211. https://doi.org/10.3390/min15111211
Chicago/Turabian StyleWang, Wei, Yajun Wang, Weixing Lin, Long Dou, Dongrui Liu, Yuding Wang, Shitong Zhou, and Yao Liu. 2025. "Correlation Analysis Between Pore Structure and Mechanical Strength of Mine Filling Materials Based on Low-Field NMR and Fractal Theory" Minerals 15, no. 11: 1211. https://doi.org/10.3390/min15111211
APA StyleWang, W., Wang, Y., Lin, W., Dou, L., Liu, D., Wang, Y., Zhou, S., & Liu, Y. (2025). Correlation Analysis Between Pore Structure and Mechanical Strength of Mine Filling Materials Based on Low-Field NMR and Fractal Theory. Minerals, 15(11), 1211. https://doi.org/10.3390/min15111211






