Benchmarking Hierarchical and Spectral Clustering for Geochemical Baseline and Anomaly Detection in Hyper-Arid Soils of Northern Chile
Abstract
1. Introduction
2. Materials and Methods
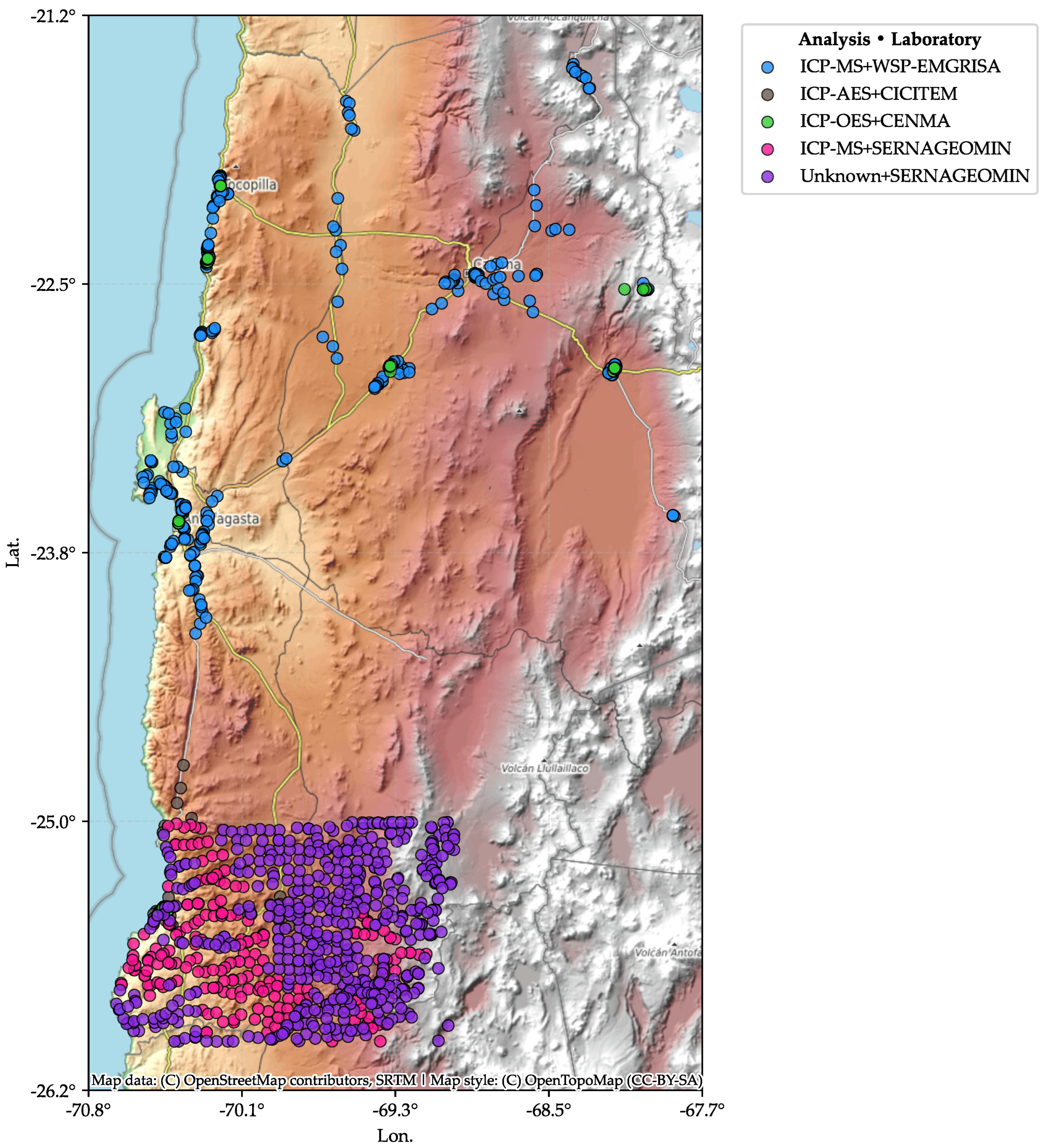
2.1. Geological and Sampling Context
2.2. Dataset and Subsets
2.3. Software and Libraries
2.4. Preprocessing
2.5. Dimensionality Reduction
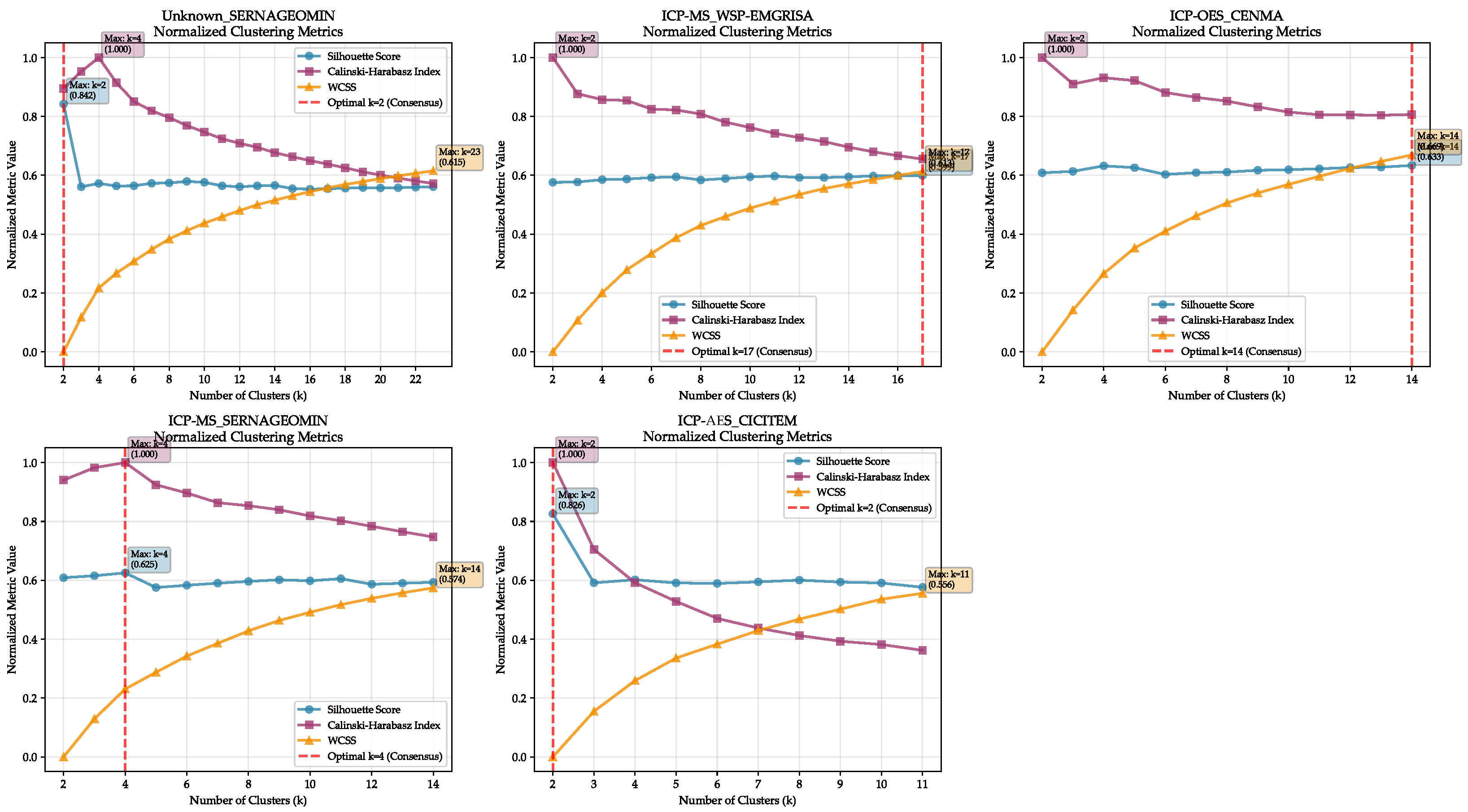
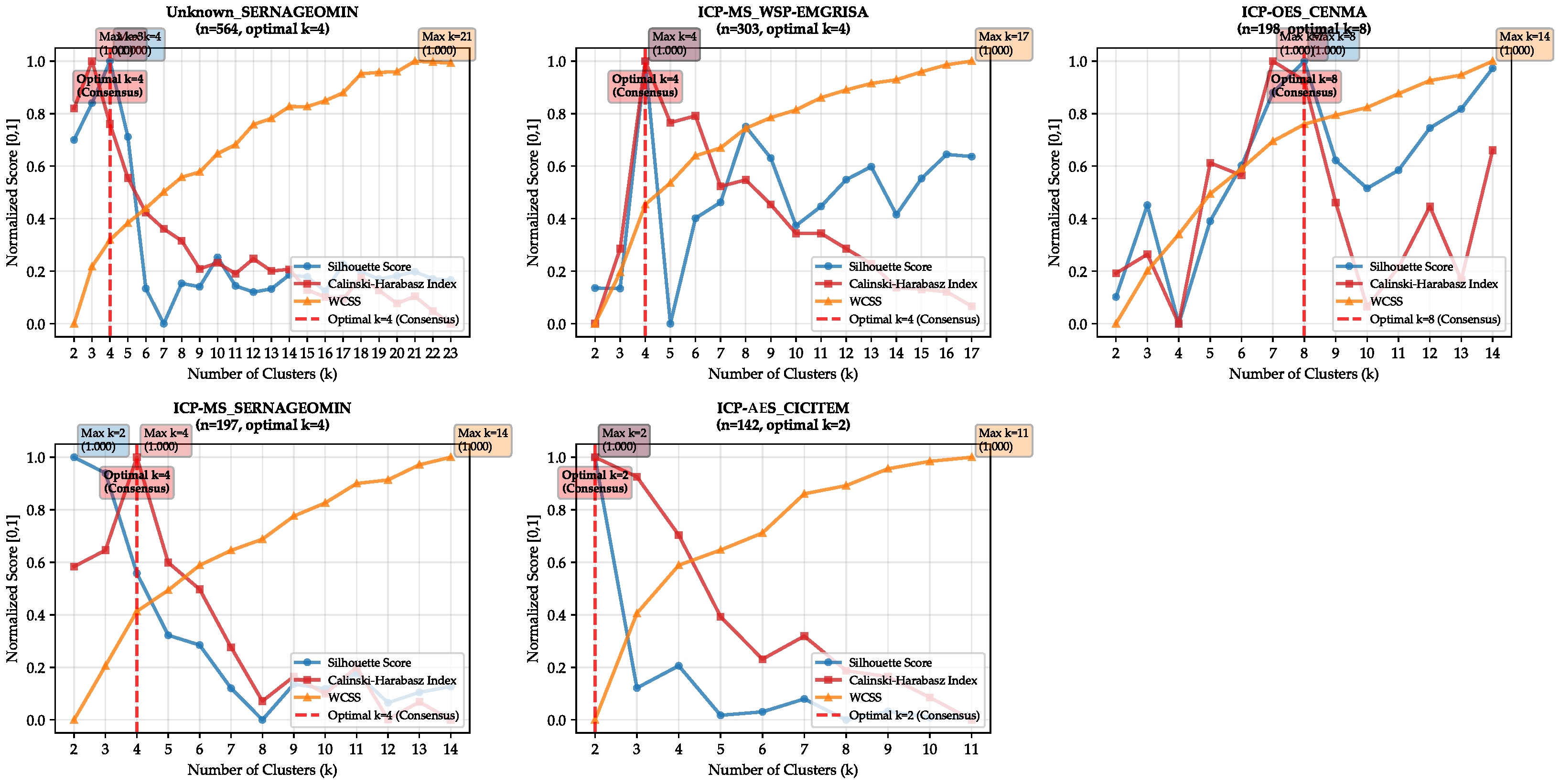
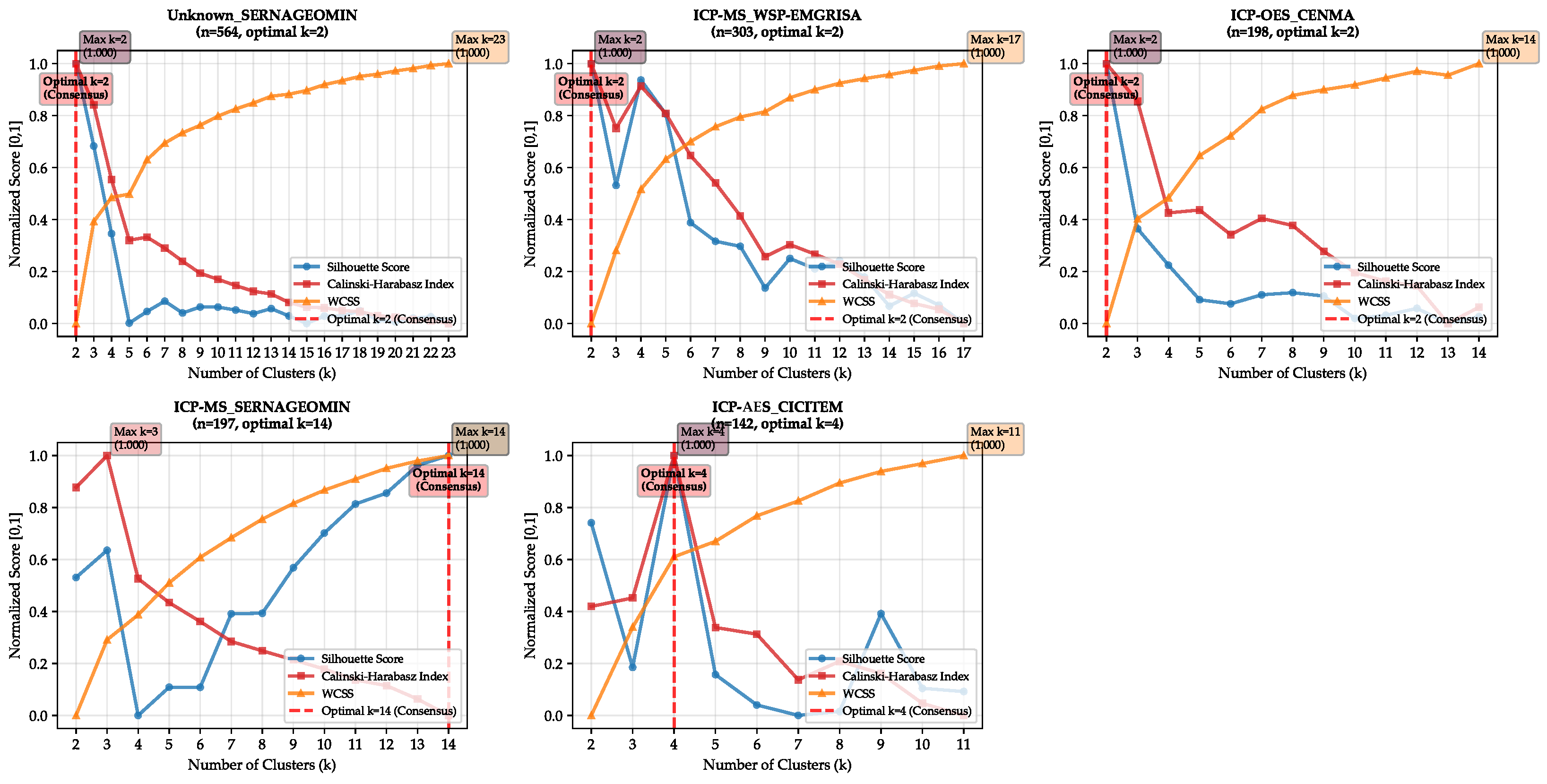
2.6. Clustering
2.7. Anomaly Detection Process
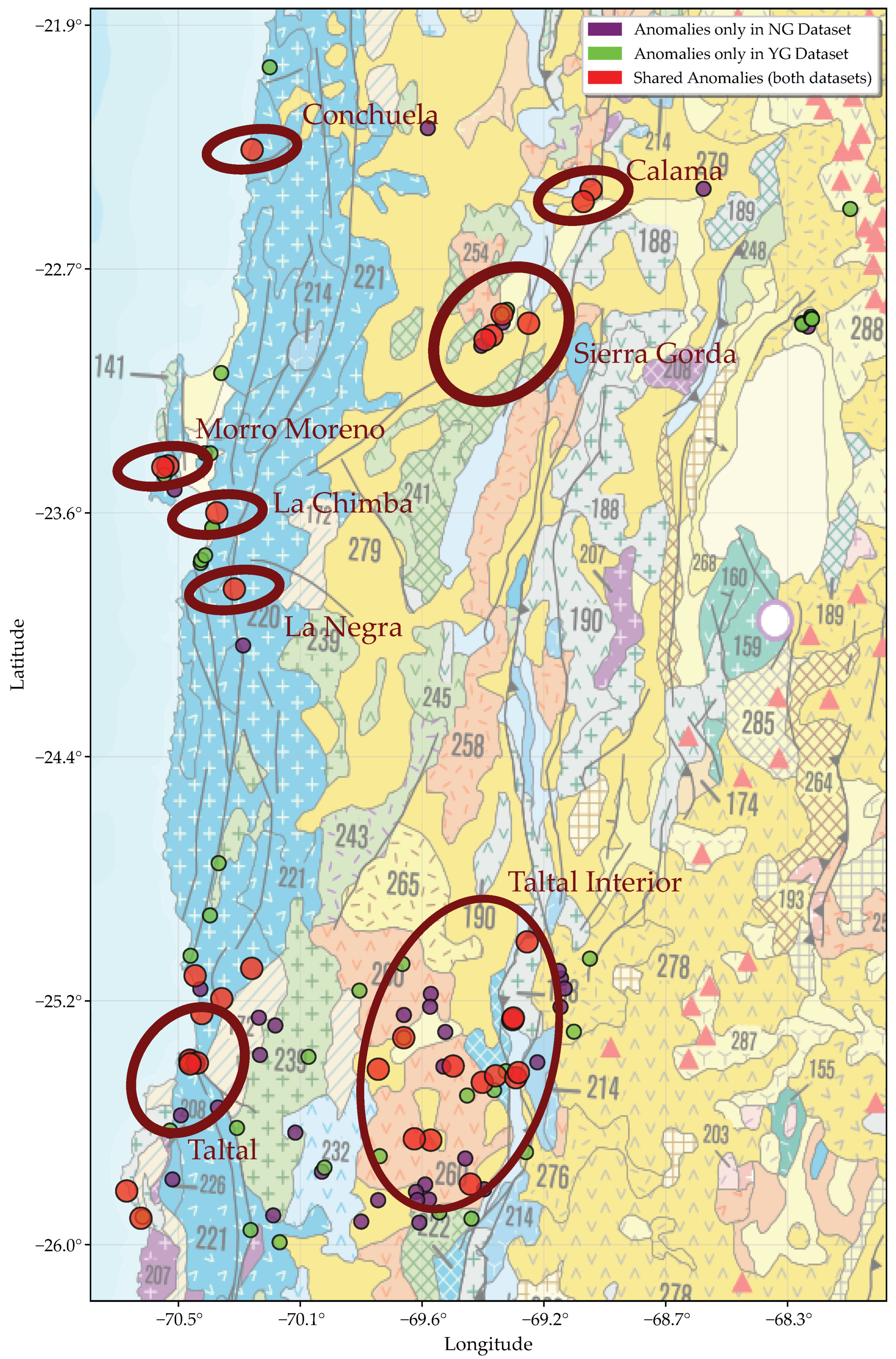
2.8. Geological Context of Identified Anomalies
2.9. Baseline Estimation Process
3. Results
3.1. Data Quality and Filtering
3.2. Dimensionality Reduction and Robust Filtering
3.3. Clustering Within the Geochemical-Only Workflow
3.3.1. Hierarchical Clustering in Principal Component Analysis
3.3.2. Hierarchical Clustering in Principal Component Analysis (Low-Rank)
3.3.3. Spectral Clustering in Principal Component Analysis
3.3.4. Spectral Clustering in Principal Component Analysis (Low-Rank)
3.4. Clustering in Spatial-Geochemical Analytical Workflow
3.4.1. Hierarchical Clustering in Principal Component Analysis (Spatial Data)
3.4.2. Hierarchical Clustering in Principal Component Analysis (Low-Rank Spatial Data)
3.4.3. Spectral Clustering in Principal Component Analysis (Spatial Data)
3.4.4. Spectral Clustering in Principal Component Analysis (Low Rank Spatial Data)
3.5. Anomaly Detection
3.6. Filtered Anomaly List
3.7. Baseline Estimation
3.7.1. Global Baseline
3.7.2. Subset Analysis by Technique and Laboratory
4. Discussion
4.1. Methodological Advances and Integration
4.2. Laboratory Heterogeneity and Analytical Challenges
4.3. Geochemical Patterns and Environmental Implications
4.4. Geochemical Anomalies
4.5. Baseline Interpretation Framework
4.6. Limitations and Uncertainties
4.7. Broader Applications and Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grantcharova, M.M.; Fernández-Caliani, J.C. Soil acidification, mineral neoformation and heavy metal contamination driven by weathering of sulphide wastes in a Ramsar wetland. Appl. Sci. 2021, 12, 249. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Garrett, R.G. Background and threshold: Critical comparison of methods of determination. Sci. Total Environ. 2005, 346, 1–16. [Google Scholar] [CrossRef]
- Reimann, C.; de Caritat, P. Establishing geochemical background variation and threshold values for 59 elements in Australian surface soil. Sci. Total Environ. 2017, 578, 633–648. [Google Scholar] [CrossRef]
- Tapia, J.; González, R.; Townley, B.; Oliveros, V.; Álvarez, F.; Aguilar, G.; Menzies, A.; Calderón, M. Geology and geochemistry of the Atacama Desert. Antonie Leeuwenhoek 2018, 111, 1273–1291. [Google Scholar] [CrossRef] [PubMed]
- Zanetta-Colombo, N.C.; Manzano, C.A.; Brombierstäudl, D.; Fleming, Z.L.; Gayo, E.M.; Rubinos, D.A.; Jerez, Ó.; Valdés, J.; Prieto, M.; Nüsser, M. Blowin’in the wind: Mapping the dispersion of metal (loid) s from Atacama mining. GeoHealth 2024, 8, e2024GH001078. [Google Scholar] [CrossRef] [PubMed]
- Reimann, C. Geochemical mapping: Technique or art? Geochem. Explor. Environ. Anal. 2005, 5, 359–370. [Google Scholar] [CrossRef]
- Filzmoser, P.; Hron, K.; Reimann, C. Principal component analysis for compositional data with outliers. Environmetrics 2009, 20, 621–632. [Google Scholar] [CrossRef]
- Grunsky, E.; Greenacre, M.; Kjarsgaard, B. GeoCoDA: Recognizing and validating structural processes in geochemical data. A workflow on compositional data analysis in lithogeochemistry. Appl. Comput. Geosci. 2024, 22, 100149. [Google Scholar] [CrossRef]
- Templ, M.; Filzmoser, P.; Reimann, C. Cluster analysis applied to regional geochemical data: Problems and possibilities. Appl. Geochem. 2008, 23, 2198–2213. [Google Scholar] [CrossRef]
- Ueki, K.; Hino, H.; Kuwatani, T. Geochemical discrimination and characteristics of magmatic tectonic settings: A machine-learning-based approach. Geochem. Geophys. Geosyst. 2018, 19, 1327–1347. [Google Scholar] [CrossRef]
- Filzmoser, P. Identification of multivariate outliers: A performance study. Austrian J. Stat. 2005, 34, 127–138. [Google Scholar] [CrossRef]
- Amirajlo, P.; Hassani, H.; Beiranvand Pour, A.; Habibkhah, N. Detection of multivariate geochemical anomalies using machine learning (ML) algorithms in Dehaq Pb-Zn mineralization, Sanandaj-Sirjan zone, Isfahan, Iran. Earth Sci. Inform. 2025, 18, 124. [Google Scholar] [CrossRef]
- Wen, W.; Yang, F.; Xie, S.; Wang, C.; Song, Y.; Zhang, Y.; Zhou, W. Determination of Geochemical Background and Baseline and Research on Geochemical Zoning in the Desert and Sandy Areas of China. Appl. Sci. 2024, 14, 10612. [Google Scholar] [CrossRef]
- Keith, B.F.; Lam, E.J.; Montofré, I.L.; Zetola, V.; Urrutia, J.; Herrera, C.; Bech, J. Evaluation of the geochemical background of soil in a hyper-arid zone using a multivariate statistical methodology: The case of the city of Antofagasta in the Atacama Desert. Chemosphere 2024, 366, 143472. [Google Scholar] [CrossRef]
- Salminen, R.; Gregorauskien, V. Considerations regarding the definition of a geochemical baseline of elements in the surficial materials in areas differing in basic geology. Appl. Geochem. 2000, 15, 647–653. [Google Scholar] [CrossRef]
- Hron, K.; Templ, M.; Filzmoser, P. Imputation of missing values for compositional data using classical and robust methods. Comput. Stat. Data Anal. 2010, 54, 3095–3107. [Google Scholar] [CrossRef]
- Prasianakis, N.; Laloy, E.; Jacques, D.; Meeussen, J.; Miron, G.; Kulik, D.; Idiart, A.; Demirer, E.; Coene, E.; Cochepin, B.; et al. Geochemistry and machine learning: Methods and benchmarking. Environ. Earth Sci. 2025, 84, 121. [Google Scholar] [CrossRef]
- Lam, E.J.; Keith, B.F.; Montofré, Í.L.; Gálvez, M.E. Copper uptake by Adesmia atacamensis in a mine tailing in an arid environment. Air Soil Water Res. 2018, 11, 1178622118812462. [Google Scholar] [CrossRef]
- Delouis, B.; Philip, H.; Dorbath, L.; Cisternas, A. Recent crustal deformation in the Antofagasta region (northern Chile) and the subduction process. Geophys. J. Int. 1998, 132, 302–338. [Google Scholar] [CrossRef]
- Blanco-Arrué, B.; Yogeshwar, P.; Tezkan, B.; Mörbe, W.; Díaz, D.; Farah, B.; Buske, S.; Ninneman, L.; Domagala, J.; Diederich-Leicher, J.; et al. Exploration of sedimentary deposits in the Atacama Desert, Chile, using integrated geophysical techniques. J. S. Am. Earth Sci. 2022, 115, 103746. [Google Scholar] [CrossRef]
- Gómez, J.; Schobbenhaus, C.; Montes, N. Geological Map of South America 2019. Scale 1:5000000; Commission for the Geological Map of the World (CGMW): Paris, France; Colombian Geological Survey, and Geological Survey of Brazil: Rio de Janeiro, Brazil, 2019. [Google Scholar] [CrossRef]
- Ramírez, L.E.; Palacios, C.; Townley, B.; Parada, M.; Sial, A.; Fernandez-Turiel, J.; Gimeno, D.; Garcia-Valles, M.; Lehmann, B. The Mantos Blancos copper deposit: An upper Jurassic breccia-style hydrothermal system in the Coastal Range of Northern Chile. Miner. Depos. 2006, 41, 246–258. [Google Scholar] [CrossRef][Green Version]
- Boric, R. Geología y Yacimientos Metalíferos de la Región de Antofagasta; Servicio Nacional de Geologia y Mineria: Santiago, Chile, 1990; Volume 40, p. 246. [Google Scholar][Green Version]
- Vivallo, W.; Henriquez, F. Génesis común de los yacimientos estratoligados y vetiformes de cobre del Jurásico Medio a Superior en la Cordillera de la Costa, Región de Antofagasta, Chile. Rev. Geol. Chile 1998, 25, 199–228. [Google Scholar] [CrossRef]
- Oliveros, V.; Féraud, G.; Aguirre, L.; Fornari, M.; Morata, D. The Early Andean Magmatic Province (EAMP): 40Ar/39Ar dating on Mesozoic volcanic and plutonic rocks from the Coastal Cordillera, northern Chile. J. Volcanol. Geotherm. Res. 2006, 157, 311–330. [Google Scholar] [CrossRef]
- Lam, E.J.; Montofré, I.L.; Álvarez, F.A.; Gaete, N.F.; Poblete, D.A.; Rojas, R.J. Methodology to prioritize chilean tailings selection, according to their potential risks. Int. J. Environ. Res. Public Health 2020, 17, 3948. [Google Scholar] [CrossRef]
- Servicio Nacional de Geología y Minería (SERNAGEOMIN). Geoquímica de Sedimentos, Hoja Taltal, Regiones de Antofagasta y Atacama; Technical Report Informe N° 11; SERNAGEOMIN: Santiago, Chile, 2022. [Google Scholar]
- WSP–EMGRISA. Geochemical Baseline Survey in Urban and Peri-Urban Soils of the Antofagasta Region: Sampling Design, ICP-MS Analytical Method and Quality-Control Procedures; Technical report; Internal technical report, Revision 2, November 2019; Williams Sale Partnership and Empresa para la Gestión de Residuos Industriales: Santiago, Chile, 2019. [Google Scholar]
- CENMA. QA/QC Manual for ICP-OES Determination of Trace Metals in Soils (USEPA 3052/6010C): Application to Environmental Monitoring Campaigns 2014–2019; Technical report; Laboratory procedure LE-174, updated July 2016; Centro Nacional del Medio Ambiente: Santiago, Chile, 2016. [Google Scholar]
- Tarvainen, T.; Reyes, A.; Sapon, S. Acceptable soil baseline levels in Taltal, Chile, and in Tampere, Finland. Appl. Geochem. 2020, 123, 104813. [Google Scholar] [CrossRef]
- Reimann, C. Experiences from 30 years of low-density geochemical mapping at the subcontinental to continental scale in Europe. Geochem. Explor. Environ. Anal. 2022, 22. [Google Scholar] [CrossRef]
- Helsel, D.R. Statistics for Censored Environmental Data Using Minitab® and R: Helsel/Statistics for Environmental Data 2E; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Noventa, S.; Pace, E.; Esposito, D.; Libralato, G.; Manfra, L. Handling concentration data below the analytical limit in environmental mixture risk assessment: A case-study on pesticide river monitoring. Sci. Total Environ. 2024, 907, 167670. [Google Scholar] [CrossRef]
- Eggen, O.A.; Reimann, C.; Flem, B. Reliability of geochemical analyses: Deja vu all over again. Sci. Total Environ. 2019, 670, 138–148. [Google Scholar] [CrossRef] [PubMed]
- Balaram, V.; Satyanarayanan, M. Data Quality in Geochemical Elemental and Isotopic Analysis. Minerals 2022, 12, 999. [Google Scholar] [CrossRef]
- Demetriades, A.; Smith, D.; Wang, X. General concepts of geochemical mapping at global, regional, and local scales for mineral exploration and environmental purposes. Geochim. Bras. 2018, 32, 136–179. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. Scipy 2010, 445, 51–56. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Jordahl, K.; Van den Bossche, J.; Wasserman, J.; McBride, J.; Fleischmann, M.; Gerard, J.; Tratner, J.; Perry, M.; Farmer, C.; Hjelle, G.A.; et al. Geopandas/Geopandas: V0. 7.0; Zenodo: Meyrin, Switzerland, 2021. [Google Scholar]
- Batjes, N.H.; Calisto, L.; de Sousa, L.M. Providing quality-assessed and standardised soil data to support global mapping and modelling (WoSIS snapshot 2023). Earth Syst. Sci. Data 2024, 16, 4735–4765. [Google Scholar] [CrossRef]
- Palarea-Albaladejo, J.; Martín-Fernández, J.A. zCompositions—R package for multivariate imputation of left-censored data under a compositional approach. Chemom. Intell. Lab. Syst. 2015, 143, 85–96. [Google Scholar] [CrossRef]
- Templ, M.; Hron, K.; Filzmoser, P. robCompositions: An R-package for robust statistical analysis of compositional data. In Compositional Data Analysis: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 341–355. [Google Scholar]
- Aitchison, J. The Statistical Analysis of Compositional Data. J. R. Stat. Soc. Ser. B Stat. Methodol. 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barcelo-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cartone, A.; Postiglione, P. Principal component analysis for geographical data: The role of spatial effects in the definition of composite indicators. Spat. Econ. Anal. 2021, 16, 126–147. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Sugar, C.A.; James, G.M. Finding the number of clusters in a dataset: An information-theoretic approach. J. Am. Stat. Assoc. 2003, 98, 750–763. [Google Scholar] [CrossRef]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. 2013, 1, 90–95. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Maier, M.; Luxburg, U.; Hein, M. Influence of graph construction on graph-based clustering measures. In Proceedings of the Advances in Neural Information Processing Systems 21 (NIPS 2008), Red Hook, NY, USA, 8–10 December 2008; Volume 21. [Google Scholar]
- Sreenivasulu, A. Evaluation of Cluster based Anomaly Detection. Master’s Thesis, University of Skövde, Skövde, Sweden, 2019. [Google Scholar]
- Hajihosseinlou, M.; Maghsoudi, A.; Ghezelbash, R. Intelligent mapping of geochemical anomalies: Adaptation of DBSCAN and mean-shift clustering approaches. J. Geochem. Explor. 2024, 258, 107393. [Google Scholar] [CrossRef]
- Varrica, D.; Medico, F.L.; Zuccolini, M.V.; Miola, M.; Alaimo, M.G. Geochemical baseline values determination and spatial distribution of trace elements in topsoils: An application in Sicily region (Italy). Sci. Total Environ. 2024, 955, 176951. [Google Scholar] [CrossRef] [PubMed]
- Demetriades, A.; Birke, M.; Albanese, S.; Schoeters, I.; De Vivo, B. Continental, regional and local scale geochemical mapping. J. Geochem. Explor. 2015, 154, 1–5. [Google Scholar] [CrossRef]
- Fernandez-Turiel, J.; Garcia-Valles, M.; Gimeno-Torrente, D.; Saavedra-Alonso, J.; Martinez-Manent, S. The hot spring and geyser sinters of El Tatio, Northern Chile. Sediment. Geol. 2005, 180, 125–147. [Google Scholar] [CrossRef]
- Kojima, S.; Trista-Aguilera, D.; Hayashi, K.i. Genetic Aspects of the Manto-type Copper Deposits Based on Geochemical Studies of North Chilean Deposits. Resour. Geol. 2009, 59, 87–98. [Google Scholar] [CrossRef]
- Sillitoe, R.H. Porphyry copper systems. Econ. Geol. 2010, 105, 3–41. [Google Scholar] [CrossRef]




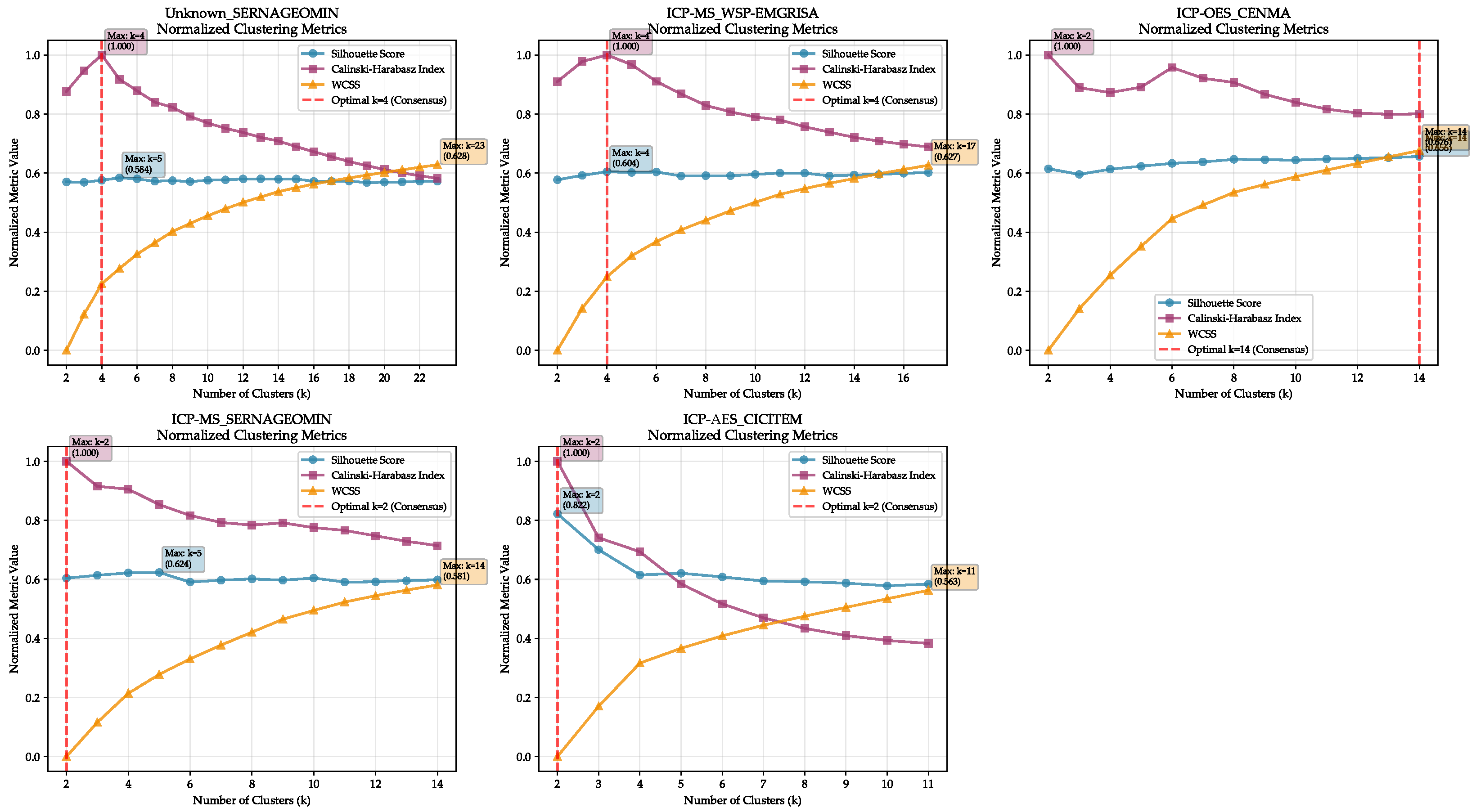
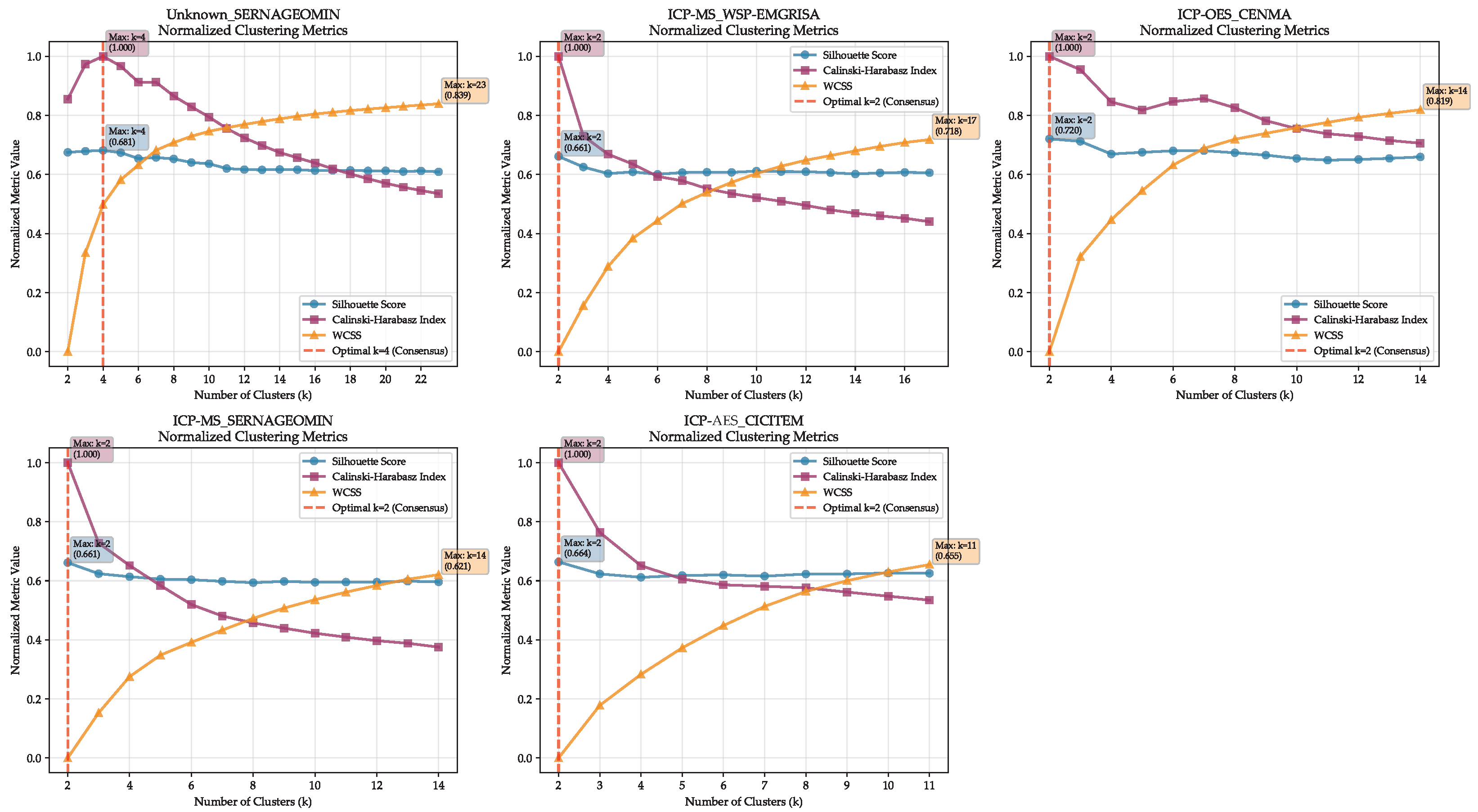
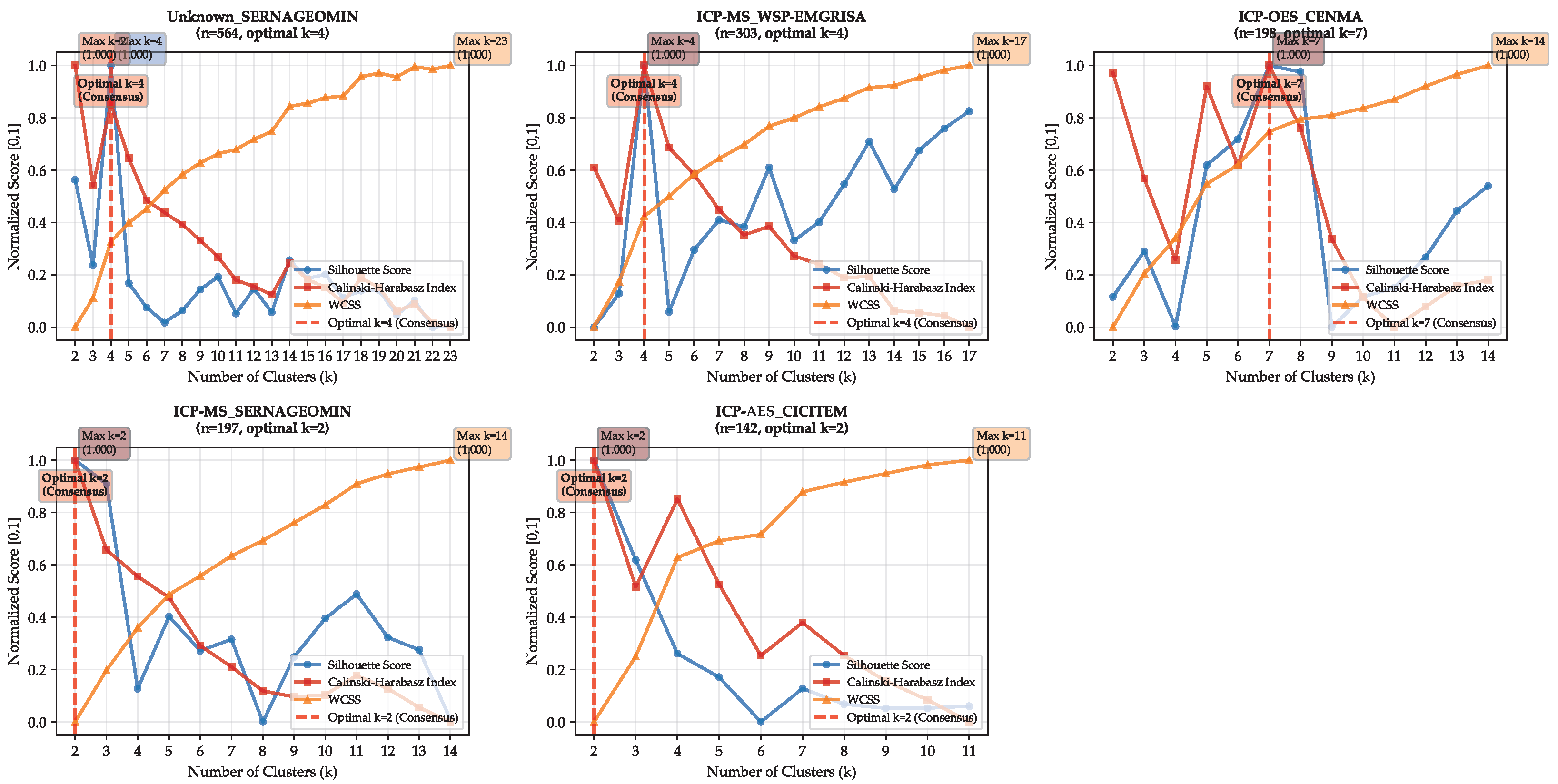
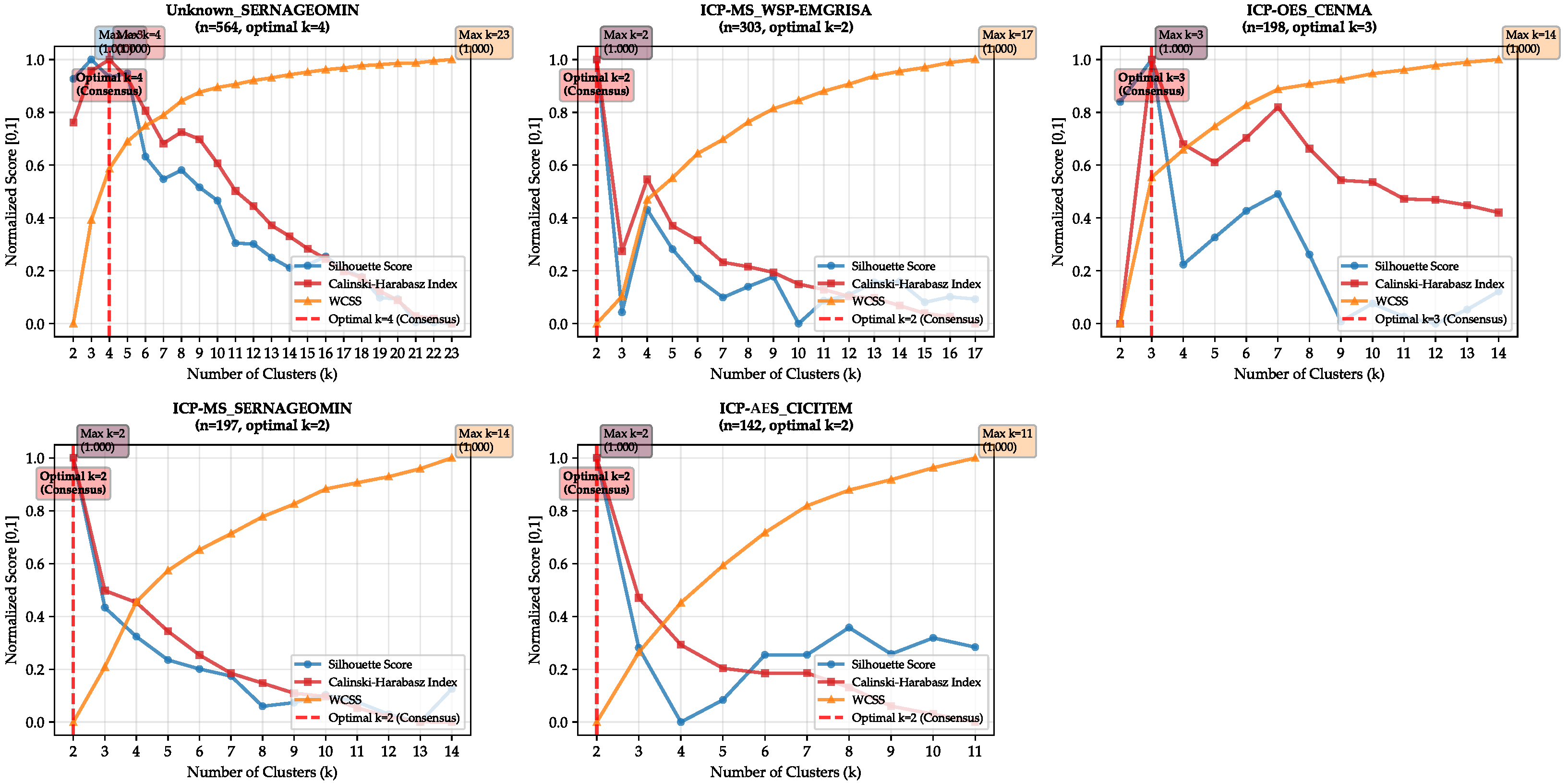


| Subset (Lab + Technique) | Samples (n) | Elements Before | Removed elements (>50% Missing) | Retained |
|---|---|---|---|---|
| Unknown – SERNAGEOMIN | 564 | 32 | 11: Al, Ca, Cr, Fe, Li, Mg, Mn, P, K, Na, Ti | 21 |
| ICP-MS – WSP-EMGRISA | 303 | 32 | – | 32 |
| ICP-OES – CENMA | 198 | 32 | 13: Sb, Bi, Ca, Li, Mg, P, K, Na, Sr, Tl, Sn, Ti, U | 19 |
| ICP-MS – SERNAGEOMIN | 197 | 32 | 11: Al, Ca, Cr, Fe, Li, Mg, Mn, P, K, Na, Ti | 21 |
| ICP-AES – CICITEM | 142 | 32 | 4: Cu, Li, Se, Sn | 28 |
| Pipeline | Initial Data | Analysis | Laboratory | # Original | # Retained | Reduction Rate (%) | Explained Variance (%) |
|---|---|---|---|---|---|---|---|
| NoGeo | Normalized | Unknown | SERNAGEOMIN | 21 | 15 | 28.6% | 95.5% |
| NoGeo | Normalized | ICP-MS | WSP-EMGRISA | 32 | 18 | 43.8% | 95.5% |
| NoGeo | Normalized | ICP-OES | CENMA | 19 | 12 | 36.8% | 95.4% |
| NoGeo | Normalized | ICP-MS | SERNAGEOMIN | 21 | 14 | 33.3% | 95.0% |
| NoGeo | Normalized | ICP-AES | CICITEM | 28 | 14 | 50.0% | 95.4% |
| NoGeo | Low-Rank | Unknown | SERNAGEOMIN | 15 | 4 | 73.3% | 96.7% |
| NoGeo | Low-Rank | ICP-MS | WSP-EMGRISA | 18 | 6 | 66.7% | 96.9% |
| NoGeo | Low-Rank | ICP-OES | CENMA | 12 | 4 | 66.7% | 96.2% |
| NoGeo | Low-Rank | ICP-MS | SERNAGEOMIN | 14 | 6 | 57.1% | 97.7% |
| NoGeo | Low-Rank | ICP-AES | CICITEM | 14 | 4 | 71.4% | 95.4% |
| Geo | Normalized | Unknown | SERNAGEOMIN | 23 | 16 | 30.4% | 95.5% |
| Geo | Normalized | ICP-MS | WSP-EMGRISA | 34 | 19 | 44.1% | 95.6% |
| Geo | Normalized | ICP-OES | CENMA | 21 | 13 | 38.1% | 95.5% |
| Geo | Normalized | ICP-MS | SERNAGEOMIN | 23 | 15 | 34.8% | 95.0% |
| Geo | Normalized | ICP-AES | CICITEM | 30 | 15 | 50.0% | 95.4% |
| Geo | Low-Rank | Unknown | SERNAGEOMIN | 16 | 4 | 75.0% | 96.5% |
| Geo | Low-Rank | ICP-MS | WSP-EMGRISA | 19 | 6 | 68.4% | 97.2% |
| Geo | Low-Rank | ICP-OES | CENMA | 13 | 3 | 76.9% | 95.3% |
| Geo | Low-Rank | ICP-MS | SERNAGEOMIN | 15 | 6 | 60.0% | 97.1% |
| Geo | Low-Rank | ICP-AES | CICITEM | 15 | 5 | 66.7% | 97.3% |
| Workflow | Analysis | Laboratory | Matrix Shape | Effective Rank | Sparsity (%) | Nuclear Norm | L1 Norm | Reconstruction Error (%) | Iterations | Converged |
|---|---|---|---|---|---|---|---|---|---|---|
| NoGeo | Unknown | SERNAGEOMIN | 564 × 15 | 9 | 11.0% | 46.40 | 5316.35 | Below Tol | 147 | Yes |
| NoGeo | ICP-MS | WSP-EMGRISA | 303 × 18 | 10 | 11.7% | 45.83 | 3970.33 | Below Tol | 164 | Yes |
| NoGeo | ICP-OES | CENMA | 198 × 12 | 7 | 13.0% | 26.46 | 1603.50 | Below Tol | 180 | Yes |
| NoGeo | ICP-MS | SERNAGEOMIN | 197 × 14 | 9 | 12.3% | 25.04 | 1931.66 | Below Tol | 163 | Yes |
| NoGeo | ICP-AES | CICITEM | 142 × 14 | 8 | 12.5% | 20.86 | 1329.74 | Below Tol | 169 | Yes |
| Geo | Unknown | SERNAGEOMIN | 564 × 16 | 11 | 10.4% | 57.98 | 5678.44 | Below Tol | 184 | Yes |
| Geo | ICP-MS | WSP-EMGRISA | 303 × 19 | 12 | 10.8% | 44.54 | 4225.01 | Below Tol | 193 | Yes |
| Geo | ICP-OES | CENMA | 198 × 13 | 8 | 13.2% | 28.15 | 1736.91 | Below Tol | 195 | Yes |
| Geo | ICP-MS | SERNAGEOMIN | 197 × 15 | 10 | 11.6% | 27.25 | 2102.32 | Below Tol | 139 | Yes |
| Geo | ICP-AES | CICITEM | 142 × 15 | 9 | 15.7% | 30.70 | 1321.85 | Below Tol | 183 | Yes |
| Subset | Method | Clusters (NG) | Anomalies (NG) | Clusters (YG) | Anomalies (YG) |
|---|---|---|---|---|---|
| ICP-AES CICITEM | HC-PCA | 13 | 10 | 3 | 11 |
| HC-PCA-LR | 11 | 6 | 2 | 4 | |
| SC-PCA | 3 | 12 | 3 | 11 | |
| SC-PCA-LR | 11 | 1 | 2 | 5 | |
| ICP-MS SERNAGEOMIN | HC-PCA | 13 | 14 | 13 | 13 |
| HC-PCA-LR | 2 | 10 | 2 | 11 | |
| SC-PCA | 8 | 10 | 7 | 10 | |
| SC-PCA-LR | 2 | 10 | 3 | 10 | |
| ICP-MS WSP-EMGRISA | HC-PCA | 3 | 18 | 2 | 13 |
| HC-PCA-LR | 13 | 19 | 2 | 17 | |
| SC-PCA | 4 | 14 | 2 | 13 | |
| SC-PCA-LR | 13 | 17 | 2 | 18 | |
| ICP-OES CENMA | HC-PCA | 14 | 13 | 5 | 12 |
| HC-PCA-LR | 4 | 12 | 2 | 13 | |
| SC-PCA | 5 | 8 | 4 | 10 | |
| SC-PCA-LR | 2 | 15 | 2 | 11 | |
| Unknown SERNAGEOMIN | HC-PCA | 2 | 29 | 4 | 30 |
| HC-PCA-LR | 2 | 29 | 4 | 30 | |
| SC-PCA | 4 | 29 | 4 | 29 | |
| SC-PCA-LR | 2 | 29 | 4 | 29 |
| Comune | Analysis | Laboratory | Code | Rock Type | Min. Period | Max. Period | Samples | NG Only | YG Only | Both |
|---|---|---|---|---|---|---|---|---|---|---|
| Antofagasta | ICP-MS | WSP-EMGRISA | J | Plutonic | Jurassic | Jurassic | 6 | 2 | 1 | 3 |
| Antofagasta | ICP-MS | WSP-EMGRISA | NQs1 | Sedimentary | Quaternary | Neogene | 2 | 0 | 1 | 1 |
| Calama | ICP-MS | WSP-EMGRISA | JKs1 | Sedimentary | Cretaceous | Jurassic | 1 | 0 | 0 | 1 |
| Calama | ICP-MS | WSP-EMGRISA | Ns1 | Sedimentary | Neogene | Neogene | 2 | 1 | 0 | 1 |
| Sierra Gorda | ICP-MS | WSP-EMGRISA | E | Plutonic | Paleogene | Paleogene | 2 | 0 | 1 | 1 |
| Sierra Gorda | ICP-MS | WSP-EMGRISA | Ns1 | Sedimentary | Neogene | Neogene | 3 | 1 | 0 | 2 |
| Sierra Gorda | ICP-OES | CENMA | E | Plutonic | Paleogene | Paleogene | 4 | 1 | 2 | 1 |
| Taltal | ICP-AES | CICITEM | J | Volcanic | Jurassic | Jurassic | 7 | 2 | 4 | 1 |
| Taltal | ICP-AES | CICITEM | Ns1 | Sedimentary | Neogene | Neogene | 1 | 0 | 0 | 1 |
| Taltal | ICP-MS | SERNAGEOMIN | J | Plutonic | Jurassic | Jurassic | 1 | 0 | 0 | 1 |
| Taltal | ICP-OES | CENMA | J | Volcanic | Jurassic | Jurassic | 10 | 5 | 3 | 2 |
| Taltal | Not specified | SERNAGEOMIN | CP | Plutonic | Permian | Carboniferous | 3 | 0 | 0 | 3 |
| Taltal | Not specified | SERNAGEOMIN | DCm1 | Metamorphic | Carboniferous | Devonian | 2 | 0 | 1 | 1 |
| Taltal | Not specified | SERNAGEOMIN | E | Volcanic | Paleogene | Paleogene | 21 | 10 | 5 | 6 |
| Taltal | Not specified | SERNAGEOMIN | JKs1 | Sedimentary | Cretaceous | Jurassic | 3 | 0 | 1 | 2 |
| Taltal | Not specified | SERNAGEOMIN | J | Plutonic | Jurassic | Jurassic | 4 | 1 | 0 | 3 |
| Taltal | Not specified | SERNAGEOMIN | J | Volcanic | Jurassic | Jurassic | 3 | 0 | 1 | 2 |
| Tocopilla | ICP-MS | WSP-EMGRISA | J | Volcanic | Jurassic | Jurassic | 1 | 0 | 0 | 1 |
| Elements | NG (with Outliers) | NG (Without Outliers) | YG (with Outliers) | YG (Without Outliers) |
|---|---|---|---|---|
| Ag | 1.06 | 1.06 | 1.06 | 1.06 |
| As | 75.479 | 66.946 | 75.479 | 69.45 |
| B | 168.185 | 165.375 | 168.185 | 164.327 |
| Ba | 988.2 | 985.762 | 988.2 | 983.565 |
| Be | 3.15 | 3.15 | 3.15 | 3.15 |
| Cd | 1.717 | 1.708 | 1.717 | 1.683 |
| Co | 26.961 | 26.756 | 26.961 | 26.79 |
| Hg | 1.711 | 1.548 | 1.711 | 1.265 |
| Mo | 7.071 | 6.698 | 7.071 | 6.517 |
| Ni | 32.846 | 32.597 | 32.846 | 31.873 |
| Pb | 56.555 | 53.596 | 56.555 | 55.6 |
| V | 307.716 | 307.046 | 307.716 | 306.267 |
| Zn | 167.875 | 167.625 | 167.875 | 166.83 |
| Samples | 1404 | 1328 | 1404 | 1321 |
| Element | ICP-MS + CICITEM (All) | ICP-MS + CICITEM (No Anomalies) | ICP-MS + SERNAGEOMIN (All) | ICP-MS + SERNAGEOMIN (No Anomalies) | ICP-MS + WSP-EMGRISA (All) | ICP-MS + WSP-EMGRISA (No Anomalies) | ICP-OES + CENMA (All) | ICP-OES + CENMA (No Anomalies) | N/A + SERNAGEOMIN (All) | N/A + SERNAGEOMIN (No Anomalies) |
|---|---|---|---|---|---|---|---|---|---|---|
| As | 34.33 | 34.18 | 40.75 | 40.86 | 69.89 | 69.53 | 611.5 | 589.69 | 53.45 | 50.93 |
| Ba | 184.83 | 191.25 | 647.83 | 645.88 | 121.95 | 120.54 | 558.7 | 506.63 | 815.13 | 801.33 |
| Be | 0.57 | 0.57 | 2.83 | 2.83 | 2 | 2 | 1.65 | 1.65 | 2.83 | 3.83 |
| B | 45 | 45 | 138.83 | 138.38 | 130.87 | 111.84 | 384.69 | 380.18 | 111.62 | 109.79 |
| Cd | 0.61 | 0.61 | 0.48 | 0.48 | 1.2 | 1.29 | 4.26 | 4.15 | 0.73 | 0.7 |
| Co | 27.83 | 27.83 | 25.7 | 25.64 | 18.57 | 18.9 | 34.37 | 33.45 | 23.88 | 23.59 |
| Pb | 109.79 | 110.36 | 30.59 | 31.59 | 20.04 | 19.87 | 370.99 | 334.41 | 43.16 | 38.22 |
| Hg | 0.53 | 0.53 | 0.05 | 0.06 | 3.03 | 3.03 | 5.49 | 4.84 | 0.08 | 0.08 |
| Mo | 6.33 | 6.38 | 3.56 | 3.59 | 3.02 | 3.01 | 57.03 | 44.58 | 5.07 | 4.77 |
| Ni | 23.32 | 23.63 | 31.29 | 31.9 | 20.73 | 20.95 | 92.42 | 94.89 | 25.07 | 24.15 |
| Ag | 1.17 | 1.09 | 0.1 | 0.1 | 0.6 | 0.6 | 2.68 | 2.66 | 0.17 | 0.13 |
| V | 145.37 | 145.35 | 344.33 | 341.8 | 153.73 | 159.5 | 194.8 | 192.26 | 307.63 | 307.13 |
| Zn | 358.87 | 375.8 | 153.03 | 153.28 | 125.39 | 128.63 | 258.79 | 247.3 | 125.95 | 121.5 |
| Samples | 142 | 138 | 197 | 188 | 303 | 287 | 198 | 189 | 564 | 526 |
| Element | ICP-MS + CICITEM (All) | ICP-MS + CICITEM (No Anomalies) | ICP-MS + SERNAGEOMIN (All) | ICP-MS + SERNAGEOMIN (No Anomalies) | ICP-MS + WSP-EMGRISA (All) | ICP-MS + WSP-EMGRISA (No Anomalies) | ICP-OES + CENMA (All) | ICP-OES + CENMA (No Anomalies) | N/A + SERNAGEOMIN (All) | N/A + SERNAGEOMIN (No Anomalies) |
|---|---|---|---|---|---|---|---|---|---|---|
| As | 34.333 | 34.333 | 40.753 | 40.843 | 69.892 | 70.258 | 611.496 | 645.572 | 53.451 | 51.643 |
| Ba | 184.833 | 193.333 | 647.833 | 647.367 | 121.95 | 121.858 | 558.697 | 543.326 | 815.133 | 813.233 |
| Be | 0.565 | 0.567 | 2.833 | 2.833 | 2 | 2 | 1.65 | 1.65 | 2.833 | 2.833 |
| B | 45 | 45 | 138.833 | 139.6 | 130.867 | 132.487 | 384.689 | 391.389 | 111.617 | 110 |
| Cd | 0.608 | 0.608 | 0.483 | 0.483 | 1.2 | 1.2 | 4.256 | 3.998 | 0.733 | 0.71 |
| Co | 27.833 | 27.833 | 25.703 | 25.777 | 18.57 | 18.947 | 34.368 | 36.154 | 23.883 | 23.692 |
| Pb | 109.792 | 114.575 | 30.587 | 31.427 | 20.038 | 19.99 | 370.994 | 362.449 | 43.156 | 39.923 |
| Hg | 0.533 | 0.533 | 0.048 | 0.048 | 3.033 | 3.033 | 5.486 | 5.191 | 0.078 | 0.078 |
| Mo | 6.333 | 6.483 | 3.557 | 3.54 | 3.017 | 3.015 | 57.034 | 47.327 | 5.073 | 4.767 |
| Ni | 23.317 | 23.633 | 31.29 | 31.72 | 20.733 | 21.077 | 92.423 | 90.827 | 25.073 | 24.185 |
| Ag | 1.167 | 1.093 | 0.1 | 0.1 | 0.6 | 0.6 | 2.681 | 2.701 | 0.167 | 0.167 |
| V | 145.367 | 143.533 | 344.333 | 342.7 | 153.733 | 160.438 | 194.803 | 193.831 | 307.625 | 307.267 |
| Zn | 358.867 | 375.8 | 153.033 | 154.933 | 125.392 | 130.212 | 258.79 | 196.582 | 125.95 | 121.783 |
| Samples | 142 | 132 | 197 | 189 | 303 | 282 | 198 | 183 | 564 | 535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ananganó-Alvarado, G.; Keith-Norambuena, B.; Lam, E.J.; Montofré, Í.L.; Flores, A.; Flores, C.; Bech, J. Benchmarking Hierarchical and Spectral Clustering for Geochemical Baseline and Anomaly Detection in Hyper-Arid Soils of Northern Chile. Minerals 2025, 15, 1185. https://doi.org/10.3390/min15111185
Ananganó-Alvarado G, Keith-Norambuena B, Lam EJ, Montofré ÍL, Flores A, Flores C, Bech J. Benchmarking Hierarchical and Spectral Clustering for Geochemical Baseline and Anomaly Detection in Hyper-Arid Soils of Northern Chile. Minerals. 2025; 15(11):1185. https://doi.org/10.3390/min15111185
Chicago/Turabian StyleAnanganó-Alvarado, Georginio, Brian Keith-Norambuena, Elizabeth J. Lam, Ítalo L. Montofré, Angélica Flores, Carolina Flores, and Jaume Bech. 2025. "Benchmarking Hierarchical and Spectral Clustering for Geochemical Baseline and Anomaly Detection in Hyper-Arid Soils of Northern Chile" Minerals 15, no. 11: 1185. https://doi.org/10.3390/min15111185
APA StyleAnanganó-Alvarado, G., Keith-Norambuena, B., Lam, E. J., Montofré, Í. L., Flores, A., Flores, C., & Bech, J. (2025). Benchmarking Hierarchical and Spectral Clustering for Geochemical Baseline and Anomaly Detection in Hyper-Arid Soils of Northern Chile. Minerals, 15(11), 1185. https://doi.org/10.3390/min15111185








