Investigating the Wear Evolution and Shape Optimize of SAG Mill Liners by DEM-FEM Coupled Simulation

Abstract

The shell liner is a core component of Semi-Autogenous Grinding (SAG) mills, suffering severe wear from ore impact and friction, and its shape directly affects grinding efficiency and maintenance costs. In this study, the Finnie wear model in EDEM2022 software was improved to predict the wear morphology evolution of shell liners. A Python-based coupled simulation of the Discrete Element Method (DEM, EDEM) and Finite Element Method (FEM, ABAQUS) was established to analyze liner wear mechanisms, stress states, and mill service performance (wear resistance, grinding efficiency, and stress distribution). The simulated wear profile showed high consistency with laser three-dimensional scanning (LTDS) results, confirming the improved Finnie-DEM model’s effectiveness in reproducing liner wear evolution. Shearing in crushing/grinding zones was the main wear cause, with additional contributions from relative sliding among ore, grinding balls, and liners in grinding/discharge zones. DEM-FEM coupling revealed two circumferential instantaneous wear extremes (Max^a > Max^b) and two lifter wear rate peaks (M^a > M^b). In the grinding zone, liner stress distribution matched wear distribution, with maximum instantaneous stress at characteristic points A and B—stress at A reflects liner impact degree, while stress at B indicates mill ore-crushing capacity. Optimizing flat liner shape adjusted wear rate peaks (M^a, M^b), improving overall liner wear. This optimization significantly affected stresses at A/B and ore normal collision but had little impact on mill energy efficiency.

1. Introduction

The semi-Autogenous Grinding (SAG) mill is widely used in metallurgy, mining, and other industries because of its advantages of short process, simple equipment, lower investment, and high degree of automation. The SAG mill utilizes shell liners which consist of flat liners and lifter bars to lift the ore and grinding balls to a certain height, then they are dropped and impact each other, so the ore becomes crushed. During the process, grinding is achieved by the shearing and edging action among the grinding balls, ore, and shell liner [1]. Here, the shell liner provides support, endures wear and tear, and resists shock, so the rational design of this system determined the grinding efficiency and economic efficiency of the SAG mill [2,3].

Numerical calculation methods proved effective means, in particular, the Discrete Element Method (DEM) has become an important tool for studying the service performance of mills and is used to find the optimal solution to balance the wear life of liners and grinding efficiency [4,5]. For the SAG mill, there are many factors that should be studied. For example, mill operating parameters [6], typically an appropriate mill filling rate [7] can not only ensure high grinding efficiency and low energy consumption, but also reduce liner wear [8]. The drum’s rotational speed affects the distribution of impact energy and increases the impact energy of the grinding balls. The higher the rotational speed is, the easier it is to crush the ore to be uniform-size particles, but if it is more severe, the liner will wear and tear [9]. Origin ore properties [10] such as size and shape are also key factors. If the particle size is larger, the liner wears more and more severely [11,12]. In addition, the service parameters [9,10] and structural dimensions [13,14] of shell liners are also main factors. As a key part of the SAG mill, the shape and dimensions of the cylinder liner play a vital role in improving the wear resistance, extending the service life and improving the service performance of the mill.

Previous studies have shown that liners in different structural forms can enhance the crushing effect of the grinding balls on the materials through adjusting the motion trajectory and loaded state of the grinding balls and mineral materials [15]. These studies focus on the lifter bars and less on the flat liner. Increasing the height of the lifter bars will gradually increase the wear and tear of shell liner [16], and in order to maintain a constant power consumption, a slower rotational speed is required [17]. A lower lifter bar will reduce the ejection height and collision frequency, thereby decreasing the grinding efficiency. Moreover, at low rotational speeds, the mill power exhibits a positive correlation with the height of the lifter bars and conversely an inverse relationship at high rotational speeds [18]. A suitable transition chamfer of the lifter bars’ cross-section can prevent premature liner wear failure and significantly improve the service performance of the mill [19]. In addition, the number of lifter bars also affects the efficiency and steady-state power input of the mill [20].

The Discrete Element Method (DEM) coupled with the Finite Element Method (FEM) can deliver a clear picture of bulk material behavior during different processes, and it can also be combined and used with FEM technology to further analyze the interaction between the structure and the bulk and illustrate the stress distribution and deformation characteristics of the liner. Here, how to realize the dynamic evolution of the wear profile of the lining plate is an important problem, which is to modify the model nodes’ coordination to simulate the wear process, thereby evaluating the strength and durability of the liner more accurately [2,21]. Another key problem is the selection of a suitable wear model. Based on different mechanisms of wear generation, there are four different wear models. Firstly, the Shear Impact Energy Model (SIEM) is an effective model for dealing with high-speed impact wear problems [8,16,22,23]. Secondly, the Filtering Impact Energy Erosion Model (FIEEM), eliminates the influence of low-collision energy particles by introducing a screening function [24,25] and focuses on the particle impact erosion on the loading behavior of the mill and the effect of liner wear. Thirdly, the Archard wear model [6,26] relates the wear rate to the contact pressure, sliding velocity, and material hardness, respectively, by means of a volumetric loss rate equation. This model mainly focuses on frictional losses at the contact surfaces. Finally, the Finnie wear model [21,27,28] relates the wear rate to the kinetic energy ratio of particle impact surfaces through a function, distinguishing between friction wear and impact wear, and is suitable for wear simulations involving particle impact surfaces. The latter two models are the most widely used. Based on the Archard wear model, researchers have simulated the dynamic grinding evolution process of a high-pressure experimental mill by the DEM-FEM coupling approach [29].

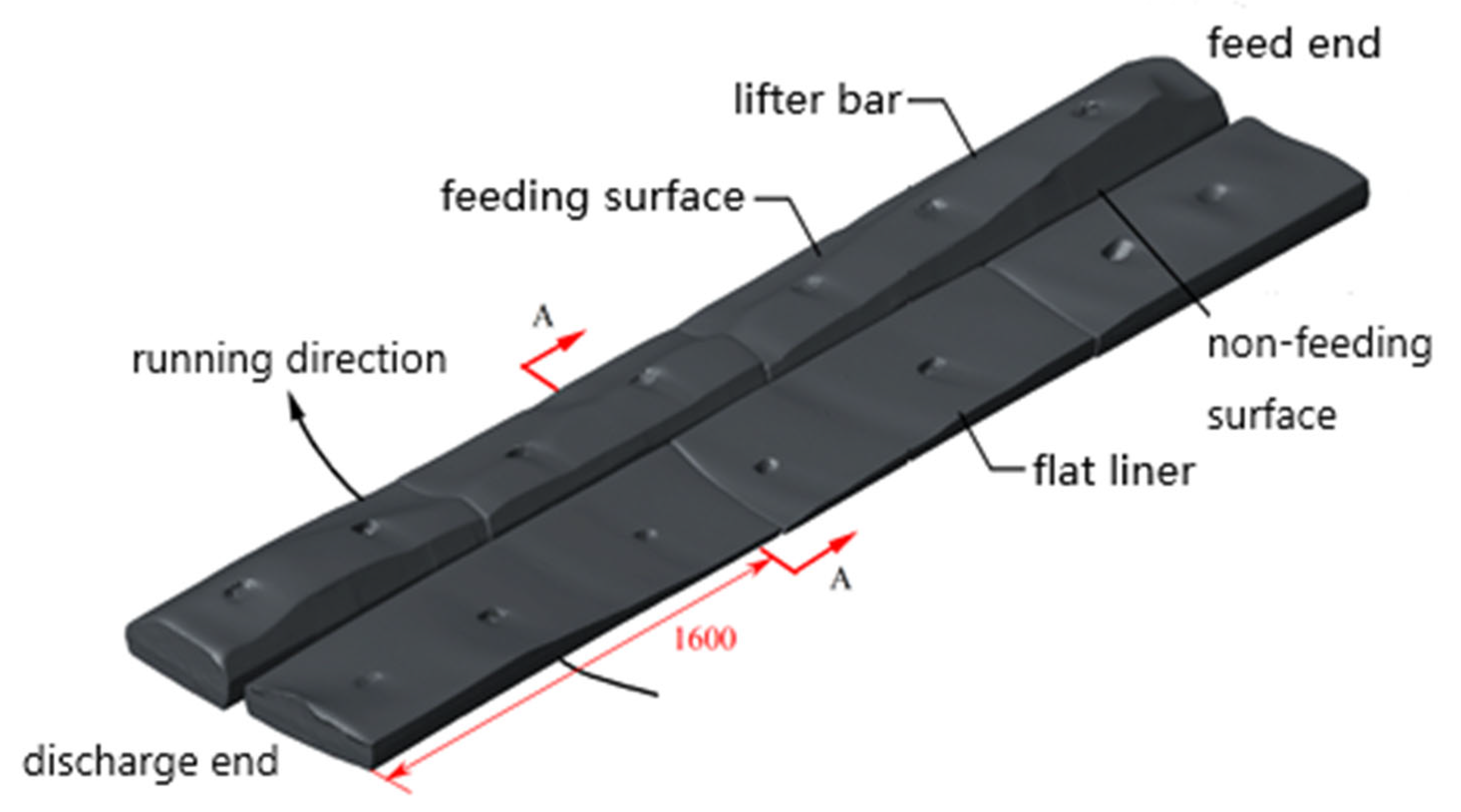
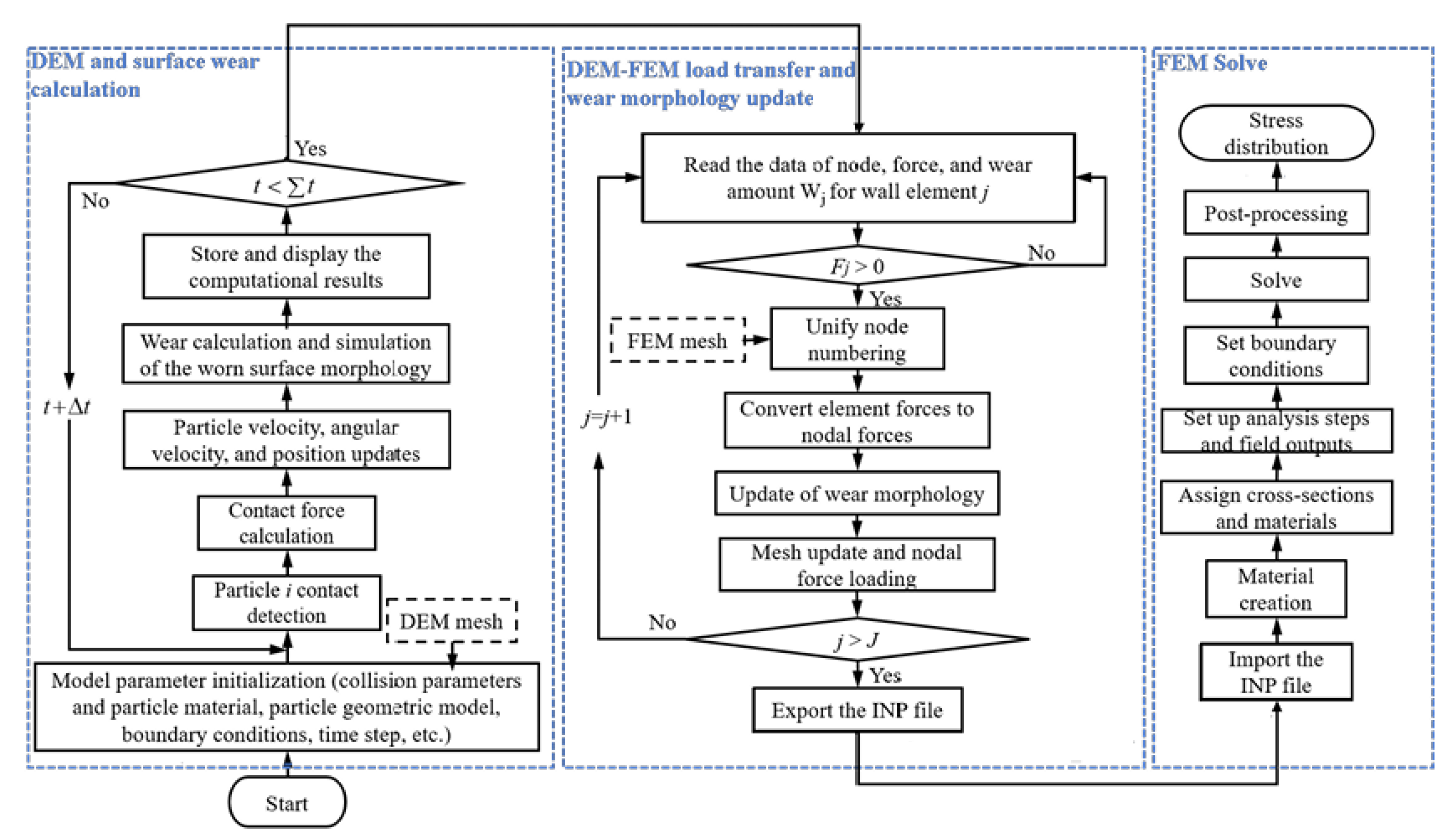
In this paper, the shell liner of a ϕ10.37 × 5.19 m SAG mill is investigated. A DEM-FEM coupling simulation program is constructed through Python code by use of the Finnie wear model, which considers the dynamic evolution of the liner wear process and realizes the grid model correction. Analysis on the service performance of the mill is conducted and the liner structural shapes are optimized, so as to support the technical design.

2. DEM-FEM Coupled Simulation Model

2.1. DEM Particle Model

When a particle i with mass m_i and moment of inertia I_i collides with a particle j (or boundary j), the contact force between the particle i and the particle j (or boundary j) has two components, the normal contact force $F_{ij}^n$ and the tangential contact force $F_{ij}^t$. The dynamic behavior of particle i can therefore be expressed by Newton’s law as the following:

$$m_i{\displaystyle \frac{d{v}_i}{dt}}=m_{i}g+{\displaystyle \sum _{j=1}^{n_j}(F_{ij}^n}+F_{ij}^t)$$

(1)

$$I_i{\displaystyle \frac{d{\omega }_i}{dt}}={\displaystyle \sum _{j=1}^{n_i}\mathrm{n}}{R}_i\times F_{ij}^t$$

(2)

where v_i is the velocity of particle i and i denotes the current colliding particle. ${\omega }_i$ is the angular velocity of particle i, n is the unit normal vector, and R_r is the distance from the contact point to the center of mass. The normal force $F_{ij}^n$ and the tangential force $F_{ij}^t$ are expressed as [30]

$$F_{ij}^n=k_n{\delta }_{ij}^n-{\eta }_n{v}_{ij}^n$$

(3)

$$F_{ij}^t=-k_t{\delta }_{ij}^t-{\eta }_t{v}_{ij}^t$$

(4)

where ${\mathit{\delta }}_{ij}^n$ and ${\mathit{\delta }}_{ij}^t$ are the normal and tangential overlap quantities, $v_{ij}^n$ and $v_{ij}^t$ are the normal and tangential velocities of particle i relative to particle j; $k_n$ and ${\eta }_n$, $k_t$, and ${\eta }_t$ are the normal or tangential elastic coefficient and normal damping coefficient of particle i, respectively. The calculation formulae are shown in

Table 1. Stiffness and damping coefficient [31,32].

	Stiffness (k)	Damping Coefficient (η)
Normal (n)	$k_n={\displaystyle \frac{4}{3}}{\left({\displaystyle \frac{1-v_i^2}{E_i}}+{\displaystyle \frac{1-v_j^2}{E_j}}\right)}^{-1}{\left(R^{*}{\delta }_{ij}^n\right)}^{1/2}$	${\eta }_n=-2\sqrt{{\displaystyle \frac{5}{4}}}\beta \sqrt{k_n{m}^{*}}$
Tangential (t)	$k_t=8{\left({\displaystyle \frac{1-v_i^2}{G_i}}+{\displaystyle \frac{1-v_j^2}{G_j}}\right)}^{-1}{\left(R^{*}{\delta }_{ij}^n\right)}^{1/2}$	${\eta }_t=-2\sqrt{{\displaystyle \frac{5}{6}}}\beta \sqrt{k_t{m}^{*}}$

$R^{*}={\displaystyle \frac{R_i{R}_j}{R_i+R_j}},m^{*}={\displaystyle \frac{m_i{m}_j}{m_i+m_j}},\beta ={\displaystyle \frac{\ln e}{\sqrt{{\ln }^{2}e+{\pi }^2}}},E-\mathrm{Young}’ \mathrm{smodulus};\mathrm{G}-\mathrm{Shear} \mathrm{modulus}.$.

.

2.2. Finnie-DEM Wear Model

According to Finnie’s wear theory, the volume, W of material worn is as follows [32]:

$$W={\displaystyle \frac{\mathrm{c}m{v}^2}{p\phi K}}f(\alpha )$$

(5)

$$f(\alpha )\left\{\begin{array}{c}\sin (2\alpha )-{\displaystyle \frac{6}{K}}{\sin }^2(\alpha ),\tan (\alpha )\le {\displaystyle \frac{K}{6}}\\ {\displaystyle \frac{K}{6}}{\cos }^2(\alpha ),\tan (\alpha )>{\displaystyle \frac{K}{6}}\end{array}\right.$$

(6)

where m is the particle mass; v is the particle velocity; α is the angle of incidence; p is the plastic flow pressure; K is the ratio of the normal force to the tangential force experienced by the particle during collision; and c is the volume fraction of particles in the particle flow that cause erosion and wear on the material surface.

The total wear loss on the material surface is determined by integrating the wear rate with the contact time. Since particles hardly wear away during the process of moving away from the contact surface, and according to Newton’s law of motion ∂v/∂t = dv/dt = F/m. Therefore, according to Formulas (5) and (6) the wear rate of the material surfaces is expressed as follows [21]:

$$w={\displaystyle \frac{dW}{dt}}\approx {\displaystyle \frac{\partial W}{\partial v}}{\displaystyle \frac{\partial v}{\partial t}}={\displaystyle \frac{2c}{p\phi K}}v\cdot rFf(\alpha ) v\cdot r\ge 0$$

(7)

So, the wear volume of particle is

$$W={\displaystyle {\int }_0^{t_p}w}dt={\displaystyle \frac{2c}{p\phi K}}{\displaystyle {\int }_0^{t_p}v}\cdot rFf(\alpha )dt v\cdot r\ge 0$$

(8)

where v is the velocity vector of the particle; r is the unit vector from the center of mass of the particle to the point of contact; F is the contact force; and t_p is the collision time. According to Finnie experiment, c is 0.5, φ is 2, and p is generally 1∼5 times the Vickers hardness, which is about 4.2 times for aluminum material and about 1.5 times for steel [33].

2.3. DEM-FEM Wear Morphology Evolution

The evolution of the surface wear morphology can be achieved by moving the grid nodes. Suppose that at time t particle i impacts the wall surface and acts on grid j (a triangular grid is used, with nodes p₀, p₁, and p₂ and the grid size is slightly smaller than the particle diameter), as shown in Figure 1. At this point, the depth of wear d_ij on the grid and the instantaneous displacement Δd_ij of the grid node are as follows:

$$d_{ij}={\displaystyle \frac{W_{ij}}{A_j}}={\displaystyle {\int }_t^{t+\Delta t}\Delta }{d}_{ij}dt={\displaystyle {\int }_t^{t+\Delta t}\frac{w_{ij}}{A_j}}dt$$

(9)

where A_j is the area of the corresponding grid cell; the coordinates of the grid node after wear are as follows:

$$p_n^{t+\Delta t}=p_n^t+\Delta d_{ij}^t\cdot {\lambda }_{ij} n=1,2,3$$

(10)

where ${\lambda }_{ij}$ is the unit vector in the direction of the contact force. It should be noted that when the node displacement of a single grid exceeds the limit of the grid size, the positions of its adjacent nodes remain unchanged, which will inevitably cause distortion of the elements. Therefore, to avoid this, the nodes in the vicinity of the nodes exceeding the limit need to be offset, as shown in Figure 2.

When the instantaneous displacement of the wear node is less than the minimum length of the wear grid:

$$\Delta d_{ij}<{\left|p_n-p_{n+1}\right|}_{\min }$$

(11)

The worn node moves directly, and the nearby nodes do not shift, as shown in Figure 2a. However, when the instantaneous displacement of the worn node is greater than or equal to the minimum length of the worn grid, as shown in Figure 2b:

$$\Delta d_{ij}\ge {\left|p_n-p_{n+1}\right|}_{\min }$$

(12)

Nodes near a worn node are moved according to the following rules:

$$\begin{array}{l}\epsilon =\left[{\displaystyle \frac{\Delta d_{ij}}{{\left|p_n-p_{n+1}\right|}_{\min }}}\right] \mathrm{truncate} \times c(\mathrm{where} c=2)\\ \Delta d_{P_{n-1-k}}={\displaystyle \sum _{k=0}^{ϵ}\frac{\epsilon -k}{\epsilon }}\Delta d_{ij}\\ \Delta d_{P_{n+1+k}}={\displaystyle \sum _{k=0}^{\epsilon }\frac{\epsilon -k}{\epsilon }}\Delta d_{ij}\end{array}$$

(13)

where c(ε−1) is the number of nodes that need to be offset and c is the number of nodes connected to the wear unit. The value of c depends on the meshing.

When the DEM is coupled with FEM simulation, in addition to updating the node coordinates of the surface to reflect the deformation of material wear, special attention needs to be paid to the aspect ratio of the grid elements [34]. The shape and size of the grid elements need to be dynamically adjusted to adapt to the deformation and movement of granular materials, so as to maintain the accuracy and stability of the simulation, as shown in Figure 3.

3. Liner Wear Experiment Verification and Construction of Coupling Simulation Model

3.1. Experimental Study on the Liner Wear of SAG Mill

A mine using a SAG mill marked ϕ10.37 × 5.19 m is shown in Figure 4, which has 33 pairs of lifter bars and flat liners alternately along the circumference of the shell. The parameters of the SAG mill are shown in

Table 2. On-site measured operating parameters of the semi-autogenous mill.

Rotational Speed (rpm)	Grinding Ball Diameter (mm)	Ball Fill Ratio (%)	Ore Fill Ratio (%)	Ore Particle Size (mm)
10.01	125	9 to 15	24 to 32	0 to 250

The “grinding ball diameter” refers to the median diameter of the mixed ball size distribution used in the simulation; the full distribution is provided in Table S1 Supplementary ball size distribution.

. The shell liner material is chromium-molybdenum alloy steel with a hardness of HRC35∼38.

The wear profile of the SAG mill liner is measured by using laser 3D scanning technology [35], as shown in Figure 5. The scan generates a complete set of 3D cloud point data for everything around the laser. Once received, the data are automatically processed, manipulated, and converted into a 3D model by the software. After 3192 h of on-site service, the shell liner was disassembled, and its 3D wear shape was measured via laser 3D scanning technology. Figure 6 presents the real-world measured 3D wear morphology of the liner. It is a shell liner, which consists of a lifer bar and a flat liner. It was found that the wear on the lifter bar was higher than that on the flat liner and the liner wear in the middle of the shell was greater than that at the ends. In the circumferential direction of the SAG mill, the amount of wear on the lifter bars showed a trend of first increasing and then decreasing, while the opposite tendency was shown on the flat liners.

The amount of wear on the lifter bars in the circumferential direction tends to increase first and then decrease, while that of the flat liner tends to be the opposite. This distribution characteristic is related to the impact and abrasive effect of the material on the liner. When lifting the bulk material including ores and grinding balls, they first contact the surface of the lifter bars. Then, relative sliding occurs between the materials and the flat liners, which causes wear on the flat liners. The wear patterns of the lifter bars and flat liner are the same in the axial direction of the drum, i.e., the wear loss first increases and then decreases from the feed to the discharge end and reaches a peak in the middle. This unevenness in axial wear is due to the uneven distribution of particles. The number of particles, total mass, and wear are minimized at the feed and discharge ends of the liner, as influenced by the conical surface of the end cap. The particles are squeezed towards the middle region due to the movement, so the wear in the middle of the liner increases [36].

3.2. EDM-FEM Coupling Method

3.2.1. Setup of the DEM Simulation on the Finnie Wear Model

The Finnie wear model is improved by using C++ language and the EDEM-API secondary development function, which can realize the wear evolution process. Firstly, the dynamic behavior illustration and the wear loss accumulation were in the EDEM2022 software, then a Python coupling program was written to transfer the load and wear data from the DEM to the FEM. The Finnie-DEM Simulation Process is shown in Figure 7. In order to ensure that the material movement reached a steady state, the data were extracted after the mill rotated four revolutions.

The analysis model is simplified by using periodic boundaries [37], a 0.6 m wide SAG shell was intercepted. The change in ore particle size caused by crushing and grinding was ignored. The details of DEM simulation parameters are shown in

Table 3. Basic DEM parameters.

Parameter		Ore	Grinding Ball	Liner
Density $\rho \left(\mathrm{kg}/{\mathrm{m}}^3\right)$		3140	7800	7800
Poisson’s ratio v		0.25	0.25	0.25
Young’s modulus E (Pa)		1 × 108	7 × 1010	7 × 1010
Restitution Coefficient e	Ore	0.5	-	-
	Grinding ball	0.5	0.5	-
	Liner	0.5	0.5	-
Static friction coefficient f	Ore	0.5	-	-
	Grinding ball	0.5	0.5	-
	Liner	0.5	0.5	-
Rolling wear coefficient fr	Ore	0.01	-	-
	Grinding ball	0.01	0.01	-
	Liner	0.01	0.01	-

. The grinding balls in the DEM simulation adopt a mixed-size distribution (Table S1) rather than a single diameter. This distribution is determined based on the on-site investigation of the target ϕ10.37 × 5.19 m SAG mill: 100 mm balls fill gaps between larger balls to avoid ore bypassing, 125 mm balls serve as the main medium for crushing medium-grain ore, 150 mm balls provide high impact energy for coarse ore crushing, and 175 mm balls handle large ore lumps. This mixed setup is consistent with full-scale SAG mill operation practices, where single ball sizes would lead to uneven grinding and excessive local liner wear. Ores and grinding balls were mixed and the ore size statistics on particle test are listed in

Table 4. Real-world measured particle size distribution of ore.

Sieve Size Range (mm)	Mass Fraction of Ore Retained (%)	Cumulative Mass Fraction (%)
<50.4	18	18
50.4–58.8	25	43
58.8–72.8	25	58
72.8–84.0	15	73
84.0–114.8	15	88
114.8–126.0	7	95
126.0–140.0	5	100

.

3.2.2. Setup of the DEM-FEM Simulation

The flowchart of DEM-FEM coupling is shown in Figure 8. Interactive communication between the DEM and FEM is a big challenge, especially because node coordinates of the FEM model need to be changed to realistically reflect the evolution of wear. This simulation method overcomes the problems of slow transmission speed caused by the large amount of data and complex structure, as well as the inaccuracy of results caused by the mismatch between the nodes of discrete elements and the meshes of structural vertices. The nodes in the DEM and FEM should be unified to ensure the accuracy of the load loading. The coupled Python code reads the force F_i and wear volume W_i of the DEM cell. The FEM grid topography is updated with the DEM wear data, and the load is applied on the FEM node in ABAQUS2022 Software.

4. Numerical Coupling Simulation

4.1. Material Movement Characteristics

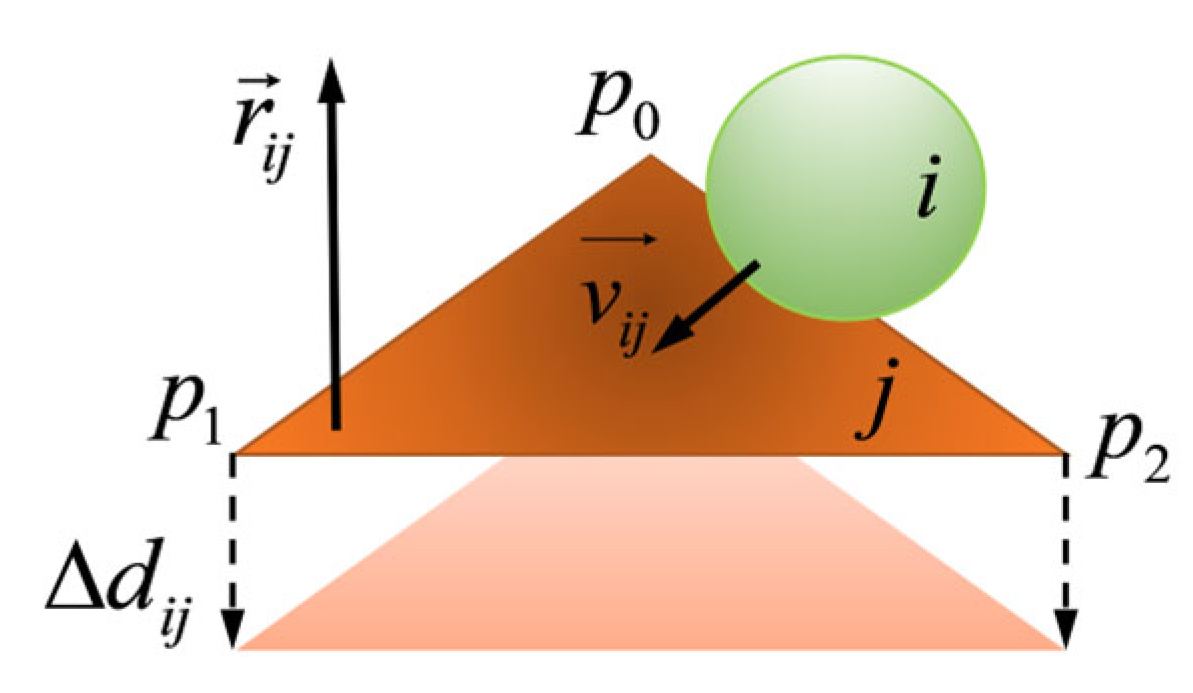
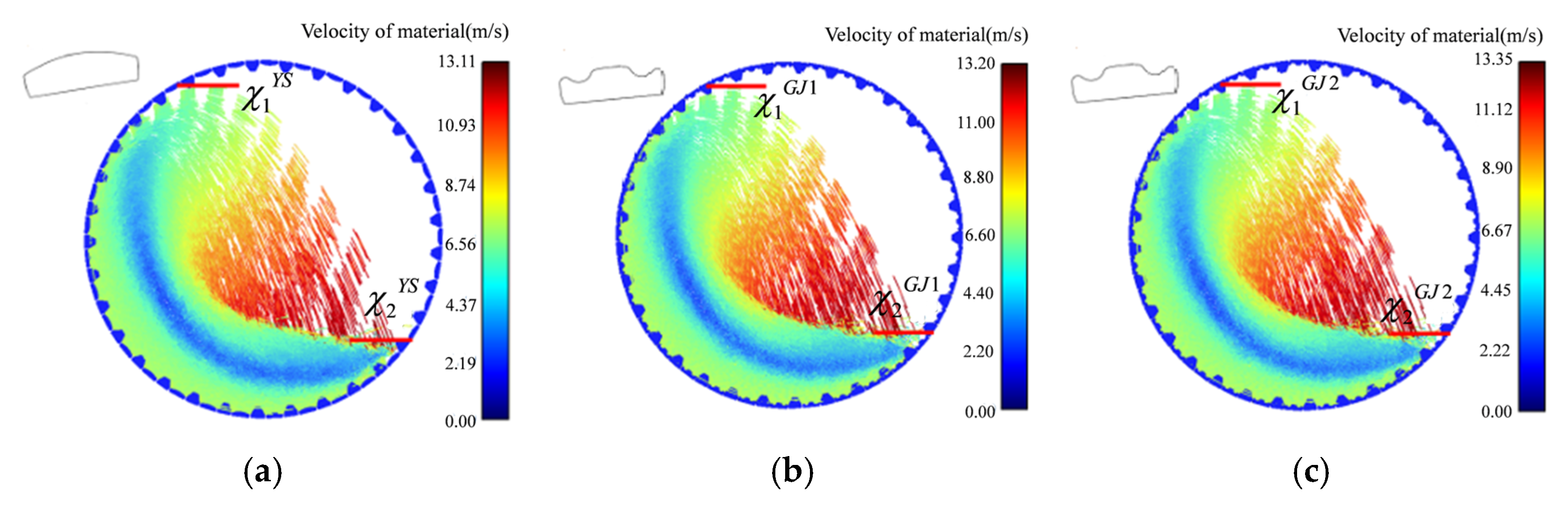
The grinding efficiency of the mill and the wear of the shell liners could be reflected by the movement of the material in the SAG cylinder [15,17], as shown in Figure 9. In the velocity trace diagram, points A, B, C, and D are, respectively, the detachment point, falling back point, transition point, and discharge point of the material as the cylinder rotates, and Ω1∼Ω6 indicate the blank area, throwing area, crushing area, grinding area, discharge area, and inertia area in turn. Although the inertia area has no obvious zone boundary, there is always an area where the material movement speed tends to zero. In addition, there is a shoulder and a toe in the velocity trajectories. The distance from the apex of the shoulder region to the center of the mill is symbolized as x₁, named shoulder height. The distances from the vertices of the toe areas to the center of the mill are called toe height, x₂. Their sum, x₁ + x₂, reflects the crushing performance of the mill. The larger the sum is, the better the crushing performance of the mill will be.

In the crushing zone, the material changes direction at the transition point C under the action of the shell liner and gradually accelerates to be the same speed as the liner. Then, in the grinding zone Ω₄, the materials are lifted by the liner. At the discharge point D some of them fall back to the crushing zone Ω₅ due to gravity and the remaining material is thrown back to the crushing zone again from the detachment point A, thus a cycle is completed. In this process, ores are ground and crushed, and at the same time the liner is worn and torn.

Ores are mainly ground in the dropping zone, Ω₂, because there are direct collisions among ores, grinding balls, and shell liners during the dropping process and also the shearing effect of the liners. In Figure 9b there are three typical grinding effects among the materials. Firstly, ores are ground at different speeds among the materials, which involves the materials in the discharge zone, the surface materials in the grinding zone, and the inner materials in the grinding zone. Secondly, the different movement directions of the inner materials cause ores to be ground. Thirdly, the various speeds between the bottom low-speed material and the inner higher-speed material cause grinding actions on the ores. In the grinding zone Ω₄ there are ring-shaped velocity traces, which means that the shearing effect is less in the elliptical orbit zone, so this zone is called the inertia zone Ω₆. In the inertia zone, minerals are hardly ground at all.

4.2. Wear Accumulated Simulation of the Cylinder Liner

Perazzo [38] et al. obtained the same wear amount through experimental verification and simulation methods by increasing the wear rate and shortening the calculating time in the simulation. Experimental studies by Yudong Zou [29] et al. and Nejad et al. [39] show that the wear volume and depth linearly increase with time. So in the paper, it is assumed that the wear rate is constant over the whole service life, so the test data are linearly extrapolated based on the actual service life of the liner.

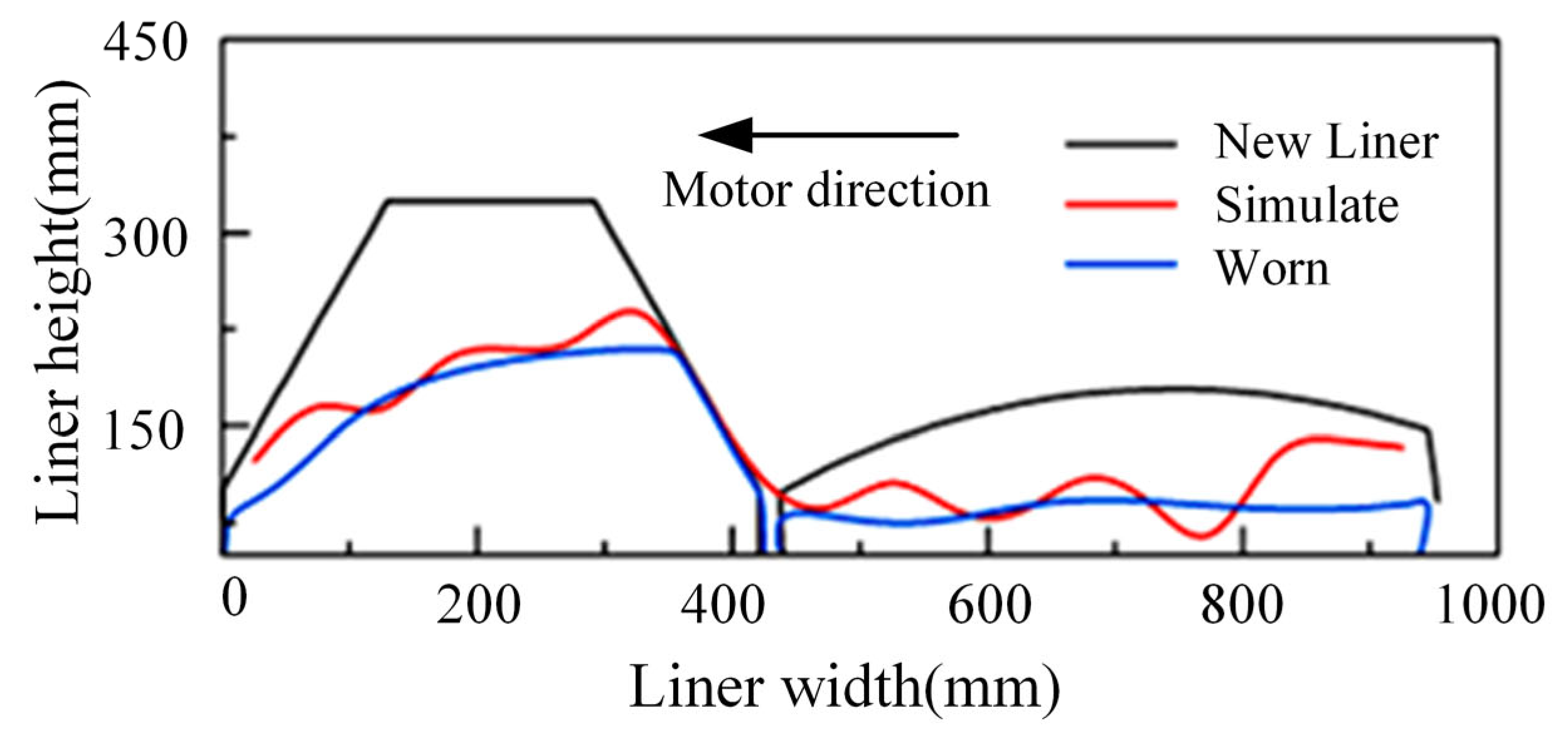
Figure 10 shows a comparison of the simulation data and the laser 3D scanning data for liner wear at section A-A in Figure 6. It can be seen that the simulated final wear data are in satisfactory agreement with the experimental data. Only at the extreme right end of the flat liner are there relatively significant differences between the simulation and the experimental data. This may be caused by ignoring the influence of liquid under actual working conditions and the fluidity of liquid enforces the wear.

It is important to note that this study did not directly simulate the full 3192 h service life of the liner using the DEM. The DEM model of the φ10.37 × 5.19 m SAG mill contains over 100,000 discrete particles, and the time step for a single contact calculation must be on the order of 10⁻⁶ seconds. Directly simulating 3192 h of operation would require more than 100,000 core hours of computing resources, which is not feasible in engineering practice. Therefore, this study adopted a scientific method of steady-state accelerated simulation combined with linear extrapolation to achieve equivalent simulation of the long-term service process, with the specific workflow as follows:

First, a DEM-FEM coupled simulation equivalent to four revolutions of the mill was conducted. Pre-verification results show that after four revolutions, the fluctuation range of key indicators of material movement is very small. The instantaneous wear rate of the liner extracted at this stage can accurately reflect the real wear intensity under stable working conditions, eliminating interference from initial transient motion.

Long-term wear tests confirmed that the wear volume and depth of the liners increase linearly with service time, with no significant acceleration or deceleration of wear during the normal service cycle. Based on this, the instantaneous wear rate obtained from the 24 min steady-state simulation was linearly extrapolated to the total wear amount over the 3192 h service cycle.

The simulated wear profile in Figure 10 is the result of the aforementioned extrapolation calculation. The average error between this profile and the on-site measured wear profile is almost the same. A slight deviation only exists at the right end of the flat liner, which arises from the omission of the liquid grinding-aid effect in actual working conditions during simulation. This further confirms that the steady-state accelerated simulation combined with linear extrapolation method can reliably reproduce the worn morphology of the liner after long-term service, while balancing computational efficiency and result authenticity.

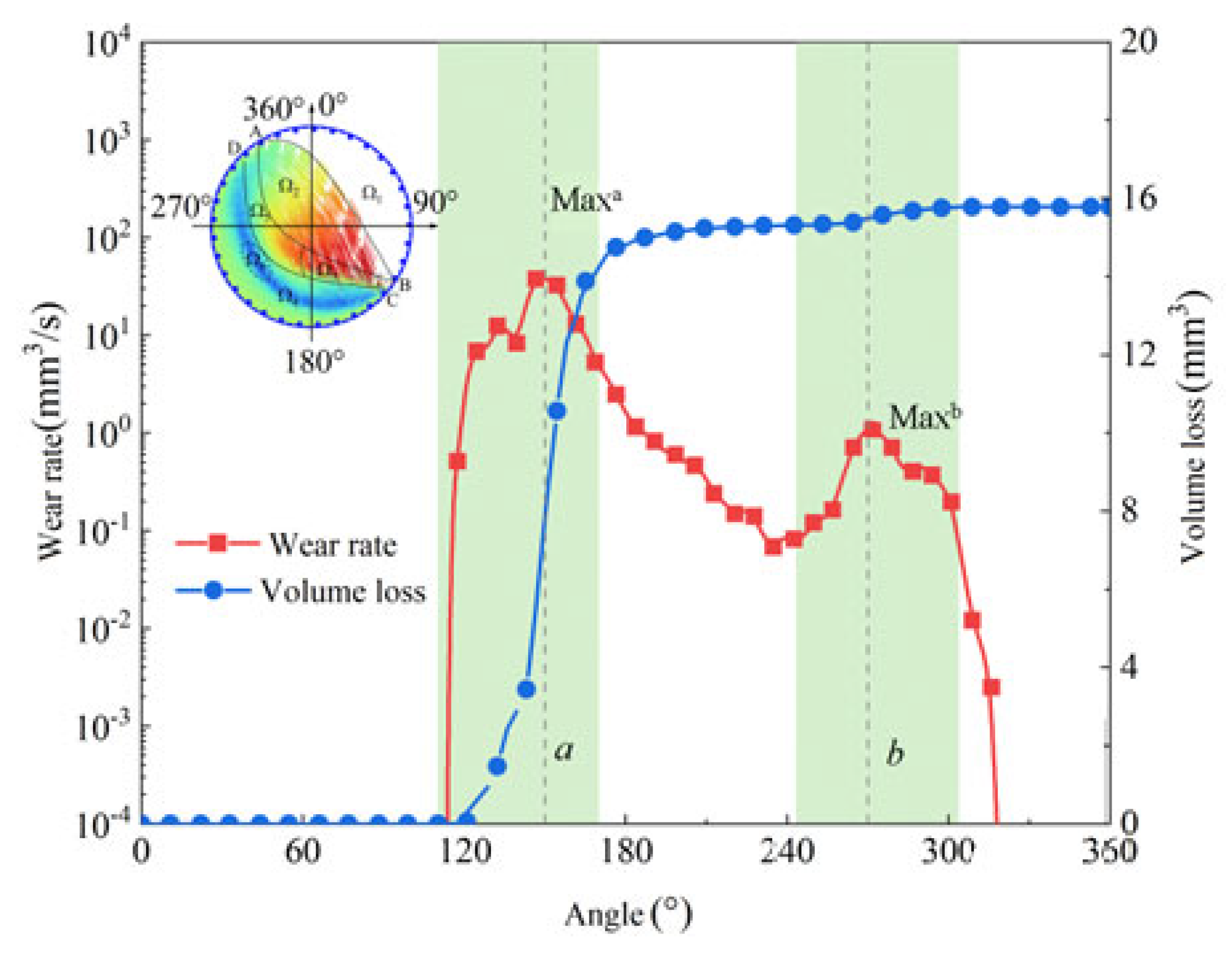
In order to reveal how the liner wears during the evolution process, the instantaneous wear rate curve and real-time mass loss of the mill shell liner during one revolution are reckoned and shown in Figure 11. In the figure, the wear rate and volume loss increase sharply when the liner reaches a position in the 113° direction where the liner enters the crushing zone from point B. Near point B, the high-speed impact of the materials in the crushing zone causes the wear rate of the liner to increase sharply. As the liner continues to rotate, the wear rate reaches a maximum value Max^a in the range of [113°, 170°] marked a and the materials are driven by the liner and drop to the bottom of the cylinder through the BC area. As before, the moving direction of the materials is changed and gradually accelerates to be the same as the liner. Then, speed variation in the materials causes a shearing movement between the materials and the liners. Therefore, the wear of the liners intensifies. After that, the relative movement is reduced between the materials and the liners, so the wear rate gradually decreases. When the liner is running the range of [243°, 302°] marked b, the wear rate gradually increases and reaches a sub-maximum value Max^b. Finally, the wear rate of the liner is reduced to zero. This process is shown as in Figure 9 corresponding to the CD and DA zones. In the latter half of the CD zone and the DA zone, the materials bore gravity greater than the friction forces provided by the liner. Therefore, the materials fall downward, the relative movement with the liner gradually increasing and the wear rate increases. In the DA zone, the material is thrown off, and the wear rate decreases to zero little by little as it separates from the liner.

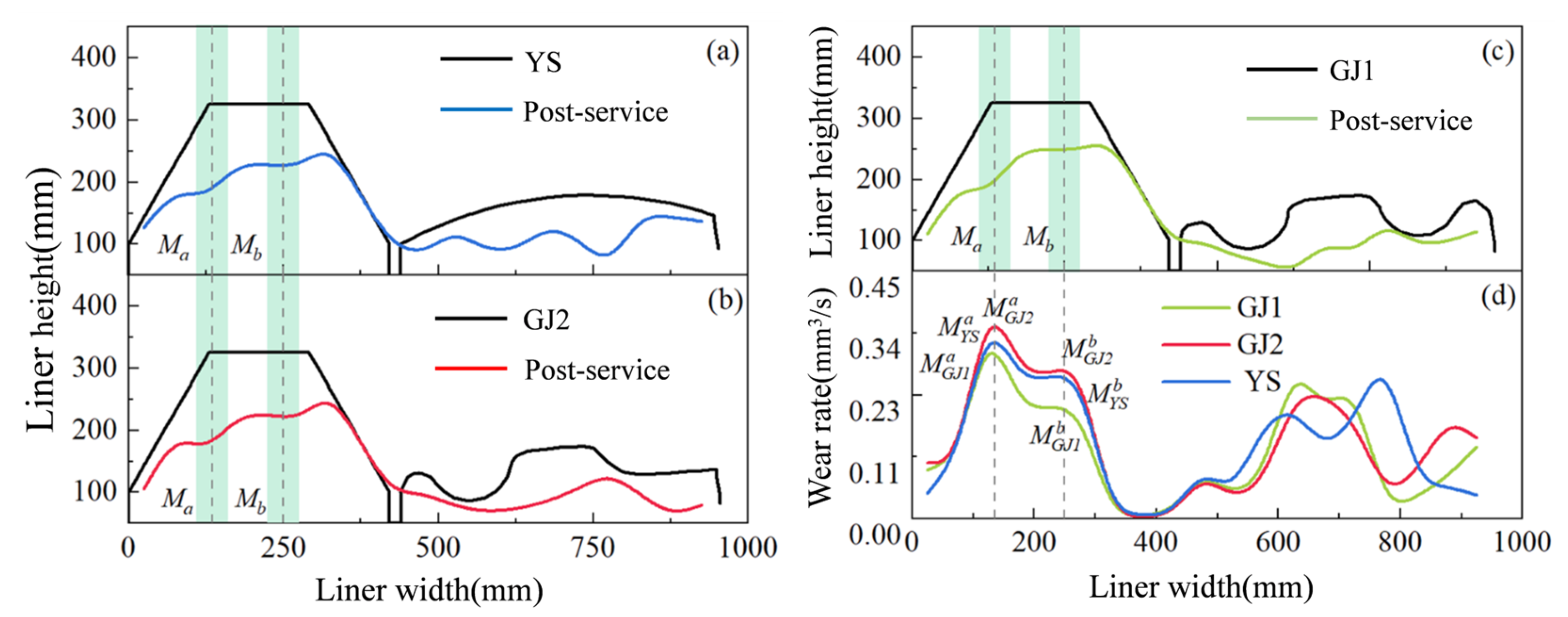
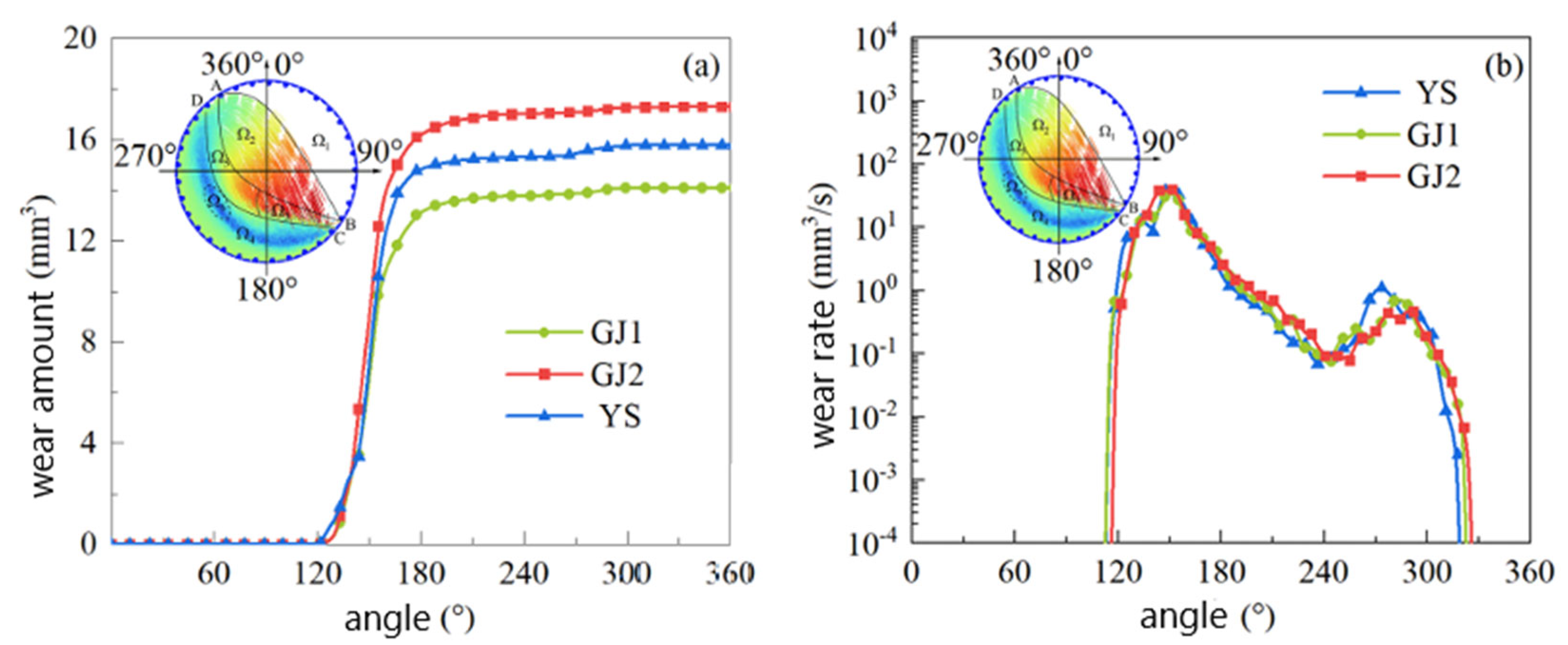
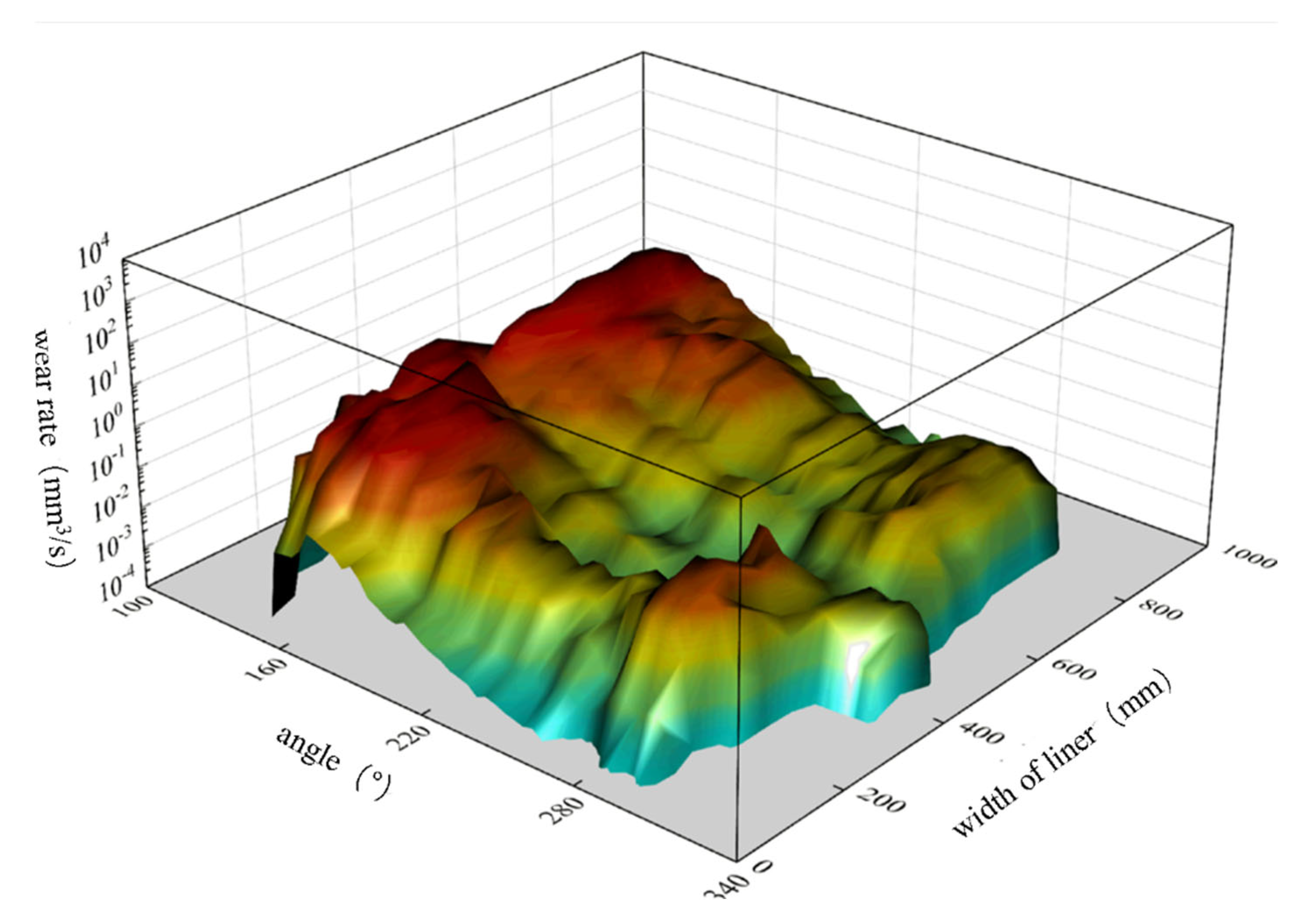
It is known that the wear loss is different in the width direction of the liner, and also different to that of the lifter bars and the flat liners in line with the simulation results and the experimental data. Figure 12 shows the wear rate in the width direction of the liner during one operating cycle of the SAG mill. It can be seen that the wear rates have two peaks, Max^a and Max^b, and the wear rate of the flat liner is lower than that of the lifter bars. In addition, due to the materials contacting with lifter bars and the flat liners in sequence, the phase difference between the peak wear rates of the lifter bars and the flat liner is about 6°, which is close to the installation angle. In Figure 12, the second peak of the wear rate on the flat liner is not obvious, because when the liner runs in the b area, the materials fall off under the force of gravity, and the material sliding against the flat liner is not severe. So, it can be inferred that the greater the lifting capacity of the flat liner, the greater its own wear. Inversely, if reducing the lifting capacity of the flat liner, the material will fall off more easily, which in turn will cause increased wear on the lifter bars.

4.3. Stress Distribution in the Shell Liner

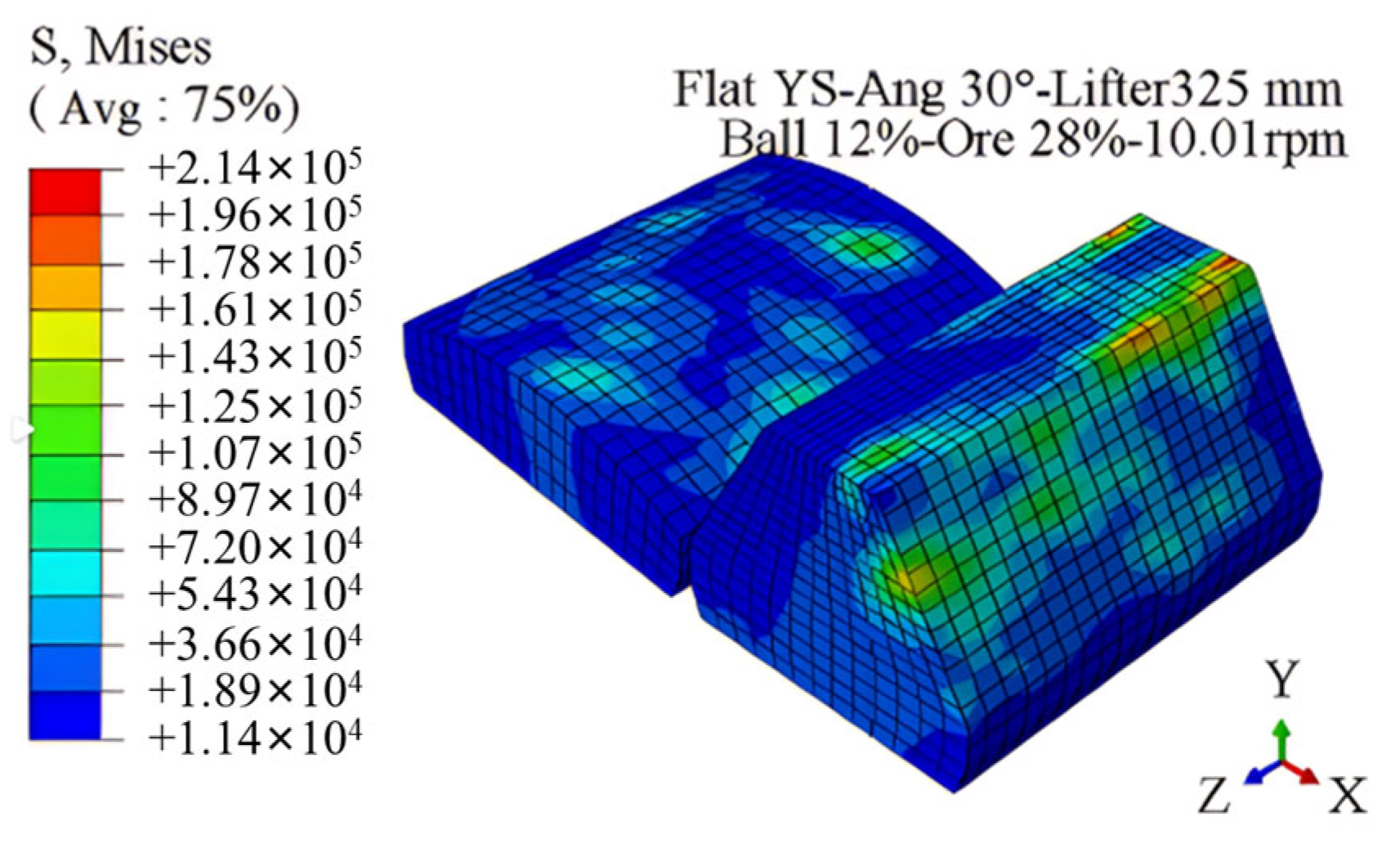
The stress nephogram of the shell liner when running to the lowest point is shown in Figure 13, which is not evenly distributed. The material-receiving surface of the lifter bars and the middle of the flat liner are under greater stress, while the non-material-receiving surface of the liner is under less stress. The stress distribution of the liner is consistent with the wear change rule of the liner, which further verifies the correctness of the liner wear evolution.

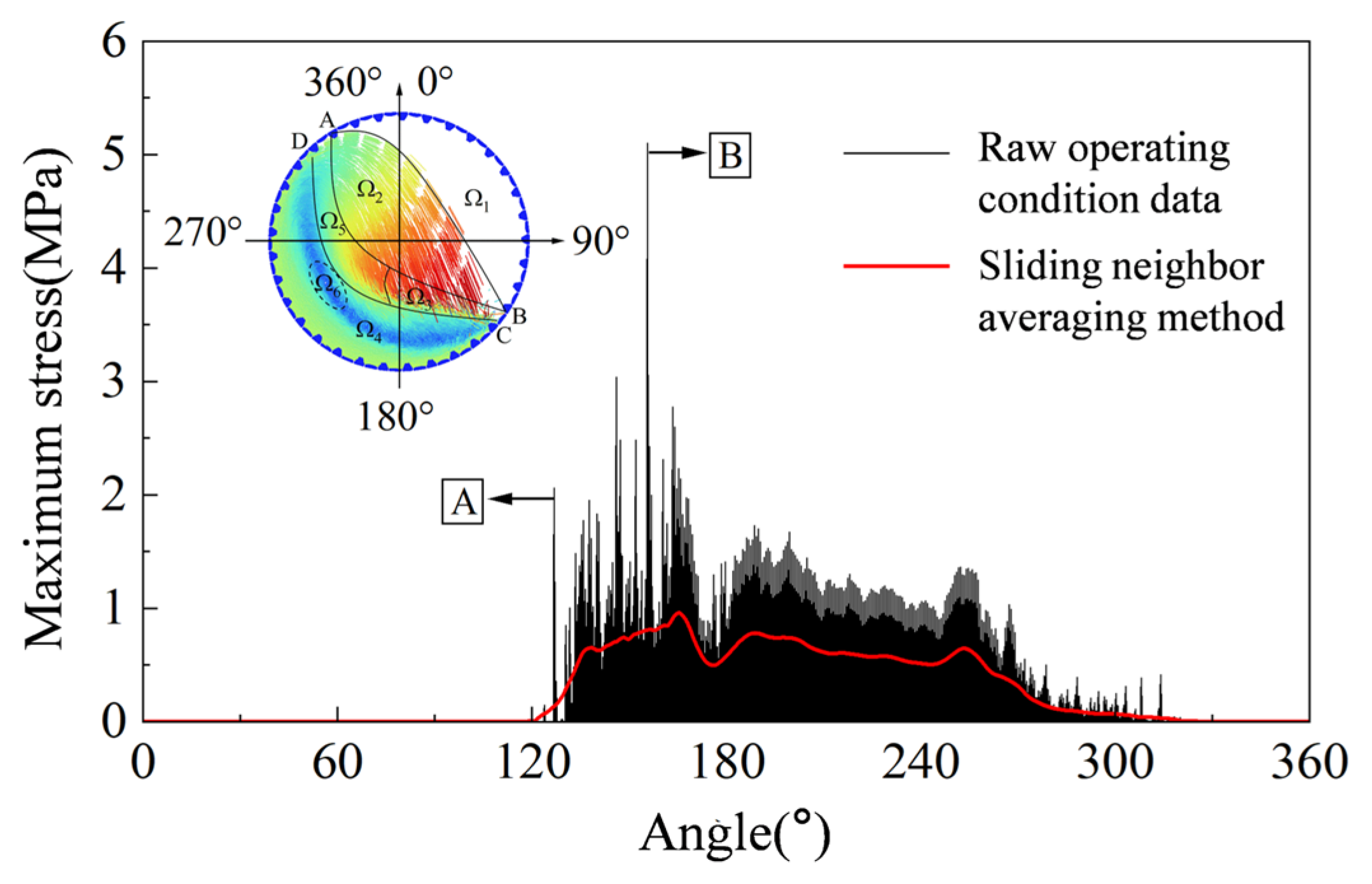
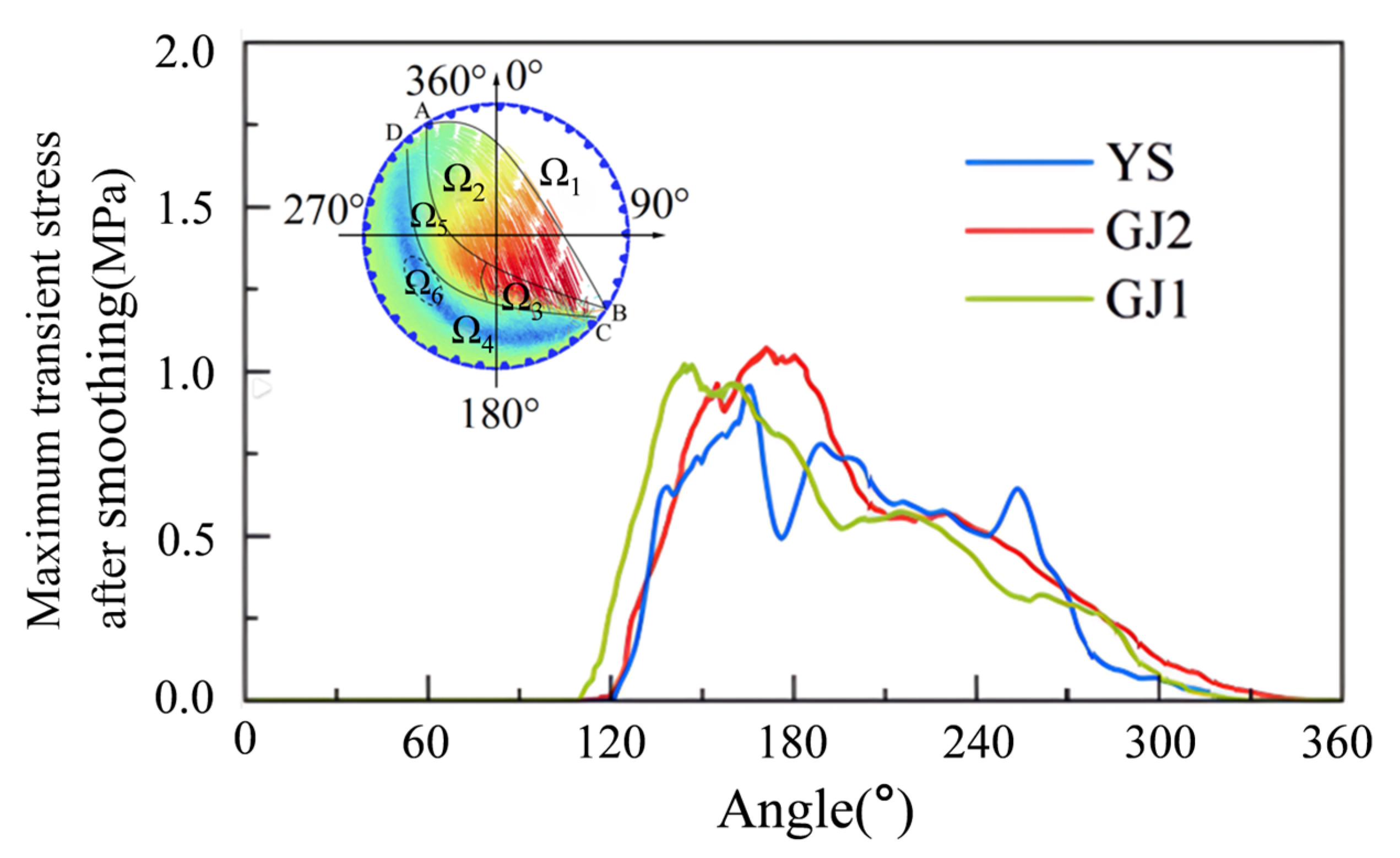
The instantaneous maximum stress–time history of the shell liner during one rotation was extracted as shown in Figure 14. The instantaneous maximum stress of the liner during operation shows a pulse distribution, which matches the instant impact of discrete particles. When the liner is near 120°, the stress increases sharply, which is most likely due to the direct impact of a few materials. As the liner rotates to around 150°, the stress reaches a maximum value. At this time, the liner is located in the grinding zone, where a large number of materials are squeezed on the upper layer of the grinding zone in the liner, so the stress reaches a maximum value. Just like the previous analysis, this is also the area of the liner where wear is greatest. Therefore, it can be reasonably inferred that the peak instantaneous stress, A, reflects the intensity of the impact on the liner. The greater the peak value, the more severe the impact on the liner, and the more likely the liner is to break and deform. Peak value B reflects the instantaneous maximum stress on the liner and the crushing effect on the material in the grinding zone. The higher the stress level near the peak, the better the crushing effect of the material in the grinding zone.

In addition, the instantaneous liner stress in Figure 14 is smoothed by the adjacent averaging method which can more clearly reflect that the instantaneous stress characteristics of the liner are consistent with the instantaneous wear rate characteristics. The stress is greatest in the grinding zone, which gradually decreases as the liner moves, and increases in the discharge zone.

5. Shape Optimize of the Flat Liner

5.1. Effect on Wear and Tear

The flat liner is primarily to provide a stable support to ensure that the lifter bars are able to operate efficiently, rather than being directly involved in the grinding process of the ore like the lifter bar. However, the change in the contact surface on the flat liner inevitably affects the stress state and further has an impact on the wear of the liner. Three typical flatliner shapes are studied in the paper, named as YS, GJ1, and GJ2, as shown in Figure 15. YS is the in-service structure and GJ1 and GJ2 are the updated designs based on the stress distribution with the total width and height unchanged.

The three velocity trace diagrams of the material in the cylinder are shown in Figure 16. The shoulder height and toe height of the material in the three cases are almost unchanged, and there is no obvious change in the distance of the material thrown down. However, the velocity of the materials are YS < GJ1 < GJ2, which means that the impact of the materials is becoming more and more serious.

After 3192 h of operation, the wear of the three structures and the instantaneous wear rates at different locations of the liner are shown in Figure 17. There is not a very significant difference in the wear distribution of the liners, and the extremes of the wear rate of the lifter bars are as follows: $M_{\mathrm{GJ}2}^a>M_{\mathrm{YS}}^a>M_{\mathrm{GJ}1}^a, M_{\mathrm{GJ}2}^b>M_{\mathrm{YS}}^b>M_{\mathrm{GJ}1}^b$.

Figure 18 represents the volume loss and instantaneous wear rate of the liner during one round of operation and the data are listed in

Table 5. Wear condition of liners with different flat liners.

Flat Liner	Loss (mm3)	Main Sources of Liner Wear			Extreme Values (mm3/s)		Average (mm3/s)
		Area a (°)	Area b (°)	Total (°)	Maxa	Maxb
GJ1	14.10	[111°, 175°]	[241°, 298°]	187°	35.46	0.74	2.30
YS	15.78	[113°, 170°]	[243°, 302°]	189°	38.40	1.09	2.57
GJ2	17.28	[115°, 172°]	[253°, 302°]	187°	38.95	0.50	2.83

. The liner wear is GJ2 > YS > GJ1 and the wear rate in region extremes Max^a are also GJ2 > YS > GJ1.

The data suggests that shape changes in the flat liner will inevitably affect the wear on the lifter bar. Therefore, in order to reveal how the flat liner’s affects, the extreme value positions for the wear rate of lifter bars are taken as the characteristic regions for further analysis. These are regions M^a and M^b in Figure 17. The wear rate values of these two regions are shown in Figure 19a,b.

It can be seen that the shape change in the flat liner has a greater effect on the region M^a, as shown in Figure 19a. The flat liner GJ2 exacerbates the impact of the lifter bar into the grinding zone, but at the same time reduces the wear in the relief zone. Conversely, the flat liner GJ1 reduces both, the details are as follows: $Ma{x}_{a,GJ2}^a>Ma{x}_{a,YS}^a>Ma{x}_{a,GJ1}^a$, $Ma{x}_{a,YS}^b>Ma{x}_{a,GJ1}^b>Ma{x}_{a,GJ2}^b$. In addition, with the flat liner YS, the wear rate fluctuates the most near the extremes, implying a more violent relative motion between the material and the liner and a poor lifting capacity of the liner. Comprehensively analyzing the structure of the three kinds of flat liners, the wave structure on the surface of the flat liner enhances the lifting capacity of the liner and reduces the wear of the liner. For region M^b, as shown in Figure 19b, the extreme values of wear rate with different flat liners are as follows: $Ma{x}_{b,GJ2}^a>Ma{x}_{b,YS}^a>Ma{x}_{b,GJ1}^a$, $Ma{x}_{b,YS}^b>Ma{x}_{b,GJ1}^b>Ma{x}_{b,GJ2}^b$.

The extreme values of wear rate in specific regions M^a and M^b are shown in

Table 6. Extreme values of wear rate on areas M_a and M_b.

Flat Liner		Ma				Mb
		Extreme Values (mm3/s)		Angles (°)		Extreme Values (mm3/s)		Angles (°)
		$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{a}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{b}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{a}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{b}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{a}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{b}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{a}}$$	$$\mathit{M}\mathit{a}{\mathit{x}}_{\mathit{a}}^{\mathit{b}}$$
YS		6.34	0.32	163°	279°	3.99	0.53	163°	281°
GJ1		4.59	0.044	140°	289°	3.91	0.38	158°	287°
GJ2		12.33	0.021	146°	284°	7.50	0.20	155°	292°
Compared to YS	GJ1	−27.6%	−86.3%	−23°	+10°	−2.0%	−28.3%	−5°	+6°
	GJ2	+94.5%	−93.4%	−17°	+5°	+88.0%	−62.3%	−8°	+11°

. A comprehensive analysis shows that the surface shape of the flat liner is an important factor in the wear of the lifter bar. The fewer and smoother the peaks are on the surface, the more violent the sliding movement between the materials and the liners are, which results in more severe wear of the lifter bar. In addition, for asymmetric flat liner GJ2, although the front surface is made with a smooth transition to the lifter bars, it exacerbates the relative motion between the materials and the liners while the liners run into the grinding zone.

The smooth transition of the flat liners may make the material stability in the grinding zone worse, causing the material to undergo secondary movement and resulting in increased wear of the lifters. Complex flat liner surface profiles allow material movement to equalize more quickly, which obviously improves wear and tear. As a result, the appropriate increase in the flat liner camber improves lifter bar wear.

5.2. Effects on Stress Distribution

Instantaneous maximum stress at different rotation angles of the mill cylinder is shown in Figure 20. For three shapes of flat liners, the stress distribution was significantly affected within the following two intervals, one is 0° up to about 120° and two is between 150° and 210°, they are the crushing zone and the grinding zone, respectively. The stresses distribution is consistent with the wear condition, in other words, the stress can also indirectly reflect wear. The liner stress in the crushing zone reflects the direct impact of the materials, while the stress in the grinding zone reflects the crushing effect. Therefore, as shown in Figure 20, both the direct impact and the crushing effect are increased by use of the flat liners GJ2 and GJ1.

5.3. Impact on Mill Grinding Performance

5.3.1. Energy Spectrum Analysis of Ores

The strength of the grinding action on the ore depends on the tangential collision energy, while the strength of the crushing action depends on the normal collision energy [40]. By summing up the collision energy of ores and categorizing it to the energy level, the collision energy spectrum of the ore can be obtained. Then, it can then be used to evaluate the grinding performance of the mill. Figure 21 shows the normal and tangential collision energy of ores; the greater the energy level, the higher the mill’s grinding efficiency. In the figure, the normal collision energy is generally lower than the tangential energy. When changing the shape of the flat liner, the normal energy sorts as GJ1 > GJ2 > YS and the tangential energy sorts as GJ2 > YS > GJ1 in descending order. For all of the ores, more than 95% of the collisions are at low energy levels, and the total normal collision energy is generally lower than the total tangential collision energy. It is implied that at low energy levels, the grinding capacity is greater than its crushing capacity. At high energy levels, the normal energy is usually higher than the tangential energy, i.e., the crushing energy is usually greater than the grinding energy.

The collision energy calculation in this section is based on the actual physical properties of the iron ore sampled from the target ϕ10.37 × 5.19 m SAG mill, detailed in Section 3.1 and Table 3. Tangential collision energy is derived from the ore’s shear modulus G which is calculated using the ore’s Young’s modulus E and Poisson’s ratio v in Table 3. This ensures that the tangential energy reflects the ore’s actual shear resistance during grinding. Normal collision energy is determined by the ore’s compressive strength, measured via on-site rock mechanics tests of the sampled ore, avoiding overestimation/underestimation of crushing energy caused by ignoring material strength. Additionally, the conclusion of low-energy-level grinding dominance is supported by the ore particle size evolution in simulation; after 3192 h of operation, the mass fraction of fine ore under the GJ1 flat liner structure increases by 18.7%, from the initial 18% to 36.7%, which aligns with the tangential energy distribution as Figure 21b shows, confirming that moderate tangential energy balances fine ore grinding and liner wear, rather than it being a hypothetical inference.

5.3.2. Energy Utilization Analysis of Collisions

For SAG mills, the collisions occur between ores and ores, grinding balls and grinding balls, ores and grinding balls, ores and liners, and grinding balls and liners, but not all collisions are effective. Among them, the collisions of ore with ore and grinding ball with ore are undoubtedly useful, the collision of ore with liner is unavoidable and positive, while the collisions of grinding ball with grinding ball and grinding ball with liner are completely negative. The type of collision that produces a positive effect is referred to as an effective collision, and its opposite is an ineffective collision. Obviously, the larger the effective collision percentage and the larger the effective collision energy, the more efficient the grinding is. Therefore, the normal force, tangential force, normal velocity, tangential velocity, and collision duration of each collision were extracted and the collision energy at each collision was calculated with the following equation:

$$E_{\mathrm{sum}}={\displaystyle \sum _i^n{\displaystyle {\int }_{t_0}^{t_1}{F}_i}}\cdot v_i\cdot tdt$$

(14)

where E is the total energy; n is the total number of collisions; and t₀ and t₁ are the collision start time and end time. The distribution of collision energy for different collision types is calculated for one week of mill operation and the results are shown in Figure 22. It can be seen that the change in flat liner structure has basically no effect on the collision energy distribution, but the GJ1 structure has a larger percentage of energy from the grinding ball-to-ore collision compared to the rest of the structures.

To quantify the link between collision energy distribution and grinding performance, we further analyzed the effective collision ratio and its correlation with liner wear and ore fineness. Compared with the original flat liner, the GJ1 structure increases the effective collision ratio by 3.2%, from 50.84% to 53.04%, while the GJ2 structure decreases it by 0.17%, from 50.84% to 50.67%. This trend is consistent with the wear loss results, confirming that the GJ1 structure not only reduces liner wear but also enhances the proportion of energy used for effective grinding. The GJ1 structure, with the highest effective collision ratio, also achieves an 18.7% increase in fine ore mass fraction, while GJ2 structure shows only a 12.3% increase in fine ore fraction. This indicates that the flat liner shape affects grinding performance by adjusting effective collision energy, rather than having no practical impact. The GJ1 structure optimizes the allocation of energy to effective grinding (reducing energy waste from ineffective collisions like ball–ball), which is a key practical value of the liner shape’s optimization.

6. Discussion

6.1. Interpretation of Core Research Findings

The core objective of this study was to address the limitations of traditional numerical simulation methods in reproducing the dynamic wear evolution of Semi-Autogenous Grinding (SAG) mill liners and clarify the mechanism by which flat liner shape affects the overall service performance of the mill. Through developing an improved Finnie-DEM wear model and a Python-based DEM-FEM bidirectional coupling framework, key findings were obtained, and their engineering and theoretical significance are interpreted as follows:

First, the validation results of the improved Finnie-DEM model showed that the simulated wear profile of the liner was highly consistent with the laser three-dimensional scanning (LTDS) data of the industrial φ10.37 × 5.19 m SAG mill after 3192 h of service. The only minor discrepancy at the right end of the flat liner was attributed to omitting the liquid grinding-aid effect in the simulation—an unavoidable simplification in numerical modeling, but one that did not affect the overall reliability of the model. This consistency confirms that the model effectively overcomes the defect of traditional wear models that only quantify wear volume without reproducing a morphological evolution. By dynamically updating the displacement of FEM mesh nodes based on wear volume, the model realizes synchronous simulation of “wear amount–surface morphology–stress distribution”, making it closer to the actual progressive wear process of industrial liners.

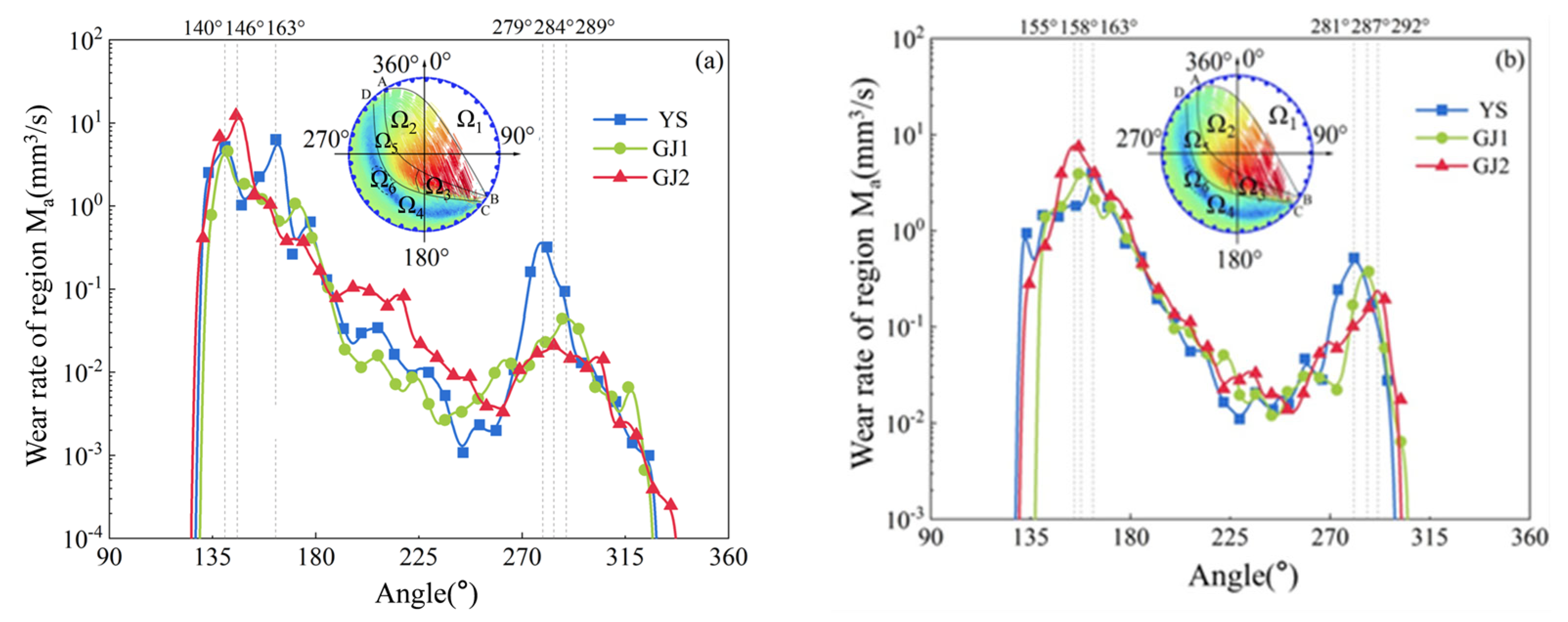
Second, DEM-FEM coupling analysis revealed two circumferential instantaneous wear extremes (Max^a > Max^b) and two lifter bar wear rate peaks (M^a > M^b). The liner’s stress distribution was consistent with its wear distribution, with the maximum instantaneous stress occurring at characteristic points A and B: stress at A reflects the impact intensity of materials on the liner, and stress at B indicates the mill’s ore-crushing capacity. This stress–wear correlation is a key insight that traditional single DEM or FEM simulations cannot capture. It provides a quantitative basis for evaluating liner service life.

Finally, flat liner shape optimization showed that the GJ1-type flat liner reduced the total wear loss of the liner by 10.6% compared to the in-service YS-type, while increasing the mill’s effective collision ratio by 3.2% and the mass fraction of fine ore by 18.7%. In contrast, the GJ2-type flat liner, despite its smooth surface transition, increased wear loss by 9.5% due to enhanced relative sliding between the materials and liners. This finding challenges the traditional perception that “smooth flat liners reduce wear” and clarifies that the flat liner’s surface profile affects wear and grinding efficiency by regulating the movement trajectory of ore and grinding balls. Specifically, the moderate camber of the GJ1-type flat liner balances the lifting capacity of materials and the stability of the grinding zone, avoiding both excessive wear caused by over-lifting and reducing the grinding efficiency caused by insufficient lifting.

6.2. Comparison with Existing Wear Models

To highlight the innovations and advantages of the proposed model, a comparative analysis was conducted with four typical wear models widely used in SAG/ball mill liner research. The comparison focuses on model principles, simulation capabilities, applicability, and limitations, as shown in

Table 7. Comparison of the improved Finnie-DEM model with existing wear models.

Model Type	Core Principle	Key Simulation Capabilities	Applicable Scenarios	Limitations
Archard Model	Relates wear rate to contact pressure, sliding velocity, and material hardness via a volumetric loss equation	Calculates frictional wear volume; suitable for steady-state frictional wear scenarios	Low-impact wear	Cannot capture impact wear
Original Finnie Model	Relates wear rate to the kinetic energy ratio of particle impact; distinguishes between friction and impact wear	Calculates both friction and impact wear volume; considers particle impact angle	Medium-impact wear	Fixed liner morphology
Shear Impact Energy Model (SIEM)	Uses shear impact energy to quantify wear; focuses on high-speed impact wear	Accurately simulates high-impact wear	High-impact wear scenarios	Overestimates wear in low-impact grinding zones; no morphological evolution
One-way DEM-FEM Coupling Model	Transfers contact force from the DEM to FEM for stress analysis; no feedback of FEM morphology to the DEM	Simulates wear volume (via DEM) and liner stress (via FEM) separately	Qualitative analysis of wear-stress trends	No bidirectional data interaction; stress and wear distribution mismatch
Improved Finnie-DEM Model (This Study)	Improved Finnie model + DEM-FEM bidirectional coupling; dynamic update of mesh nodes via Python	1. Synchronous simulation of wear volume, morphology evolution, and stress distribution 2. Bidirectional feedback between material movement and liner deformation 3. Quantification of flat liner shape impact on wear/efficiency	Industrial-scale SAG mills	Omits liquid grinding-aid effect

.

As shown in Table 7, the improved Finnie-DEM model in this study addresses the critical limitations of existing models:

(1) By integrating the dynamic mesh update mechanism, it realizes the simulation of liner wear morphology evolution, which is absent in the Archard model, original Finnie model, and SIEM;

(2) Through bidirectional DEM-FEM coupling, it solves the problem of stress–wear mismatch in one-way coupling models, ensuring that the stress distribution reflects the actual wear state;

(3) It is applicable to the comprehensive wear scenario of industrial SAG mills, whereas existing models are limited to single wear types. These advantages make the model a more practical tool for industrial liner design and optimization.

6.3. Theoretical and Engineering Implications

6.3.1. Theoretical Implications

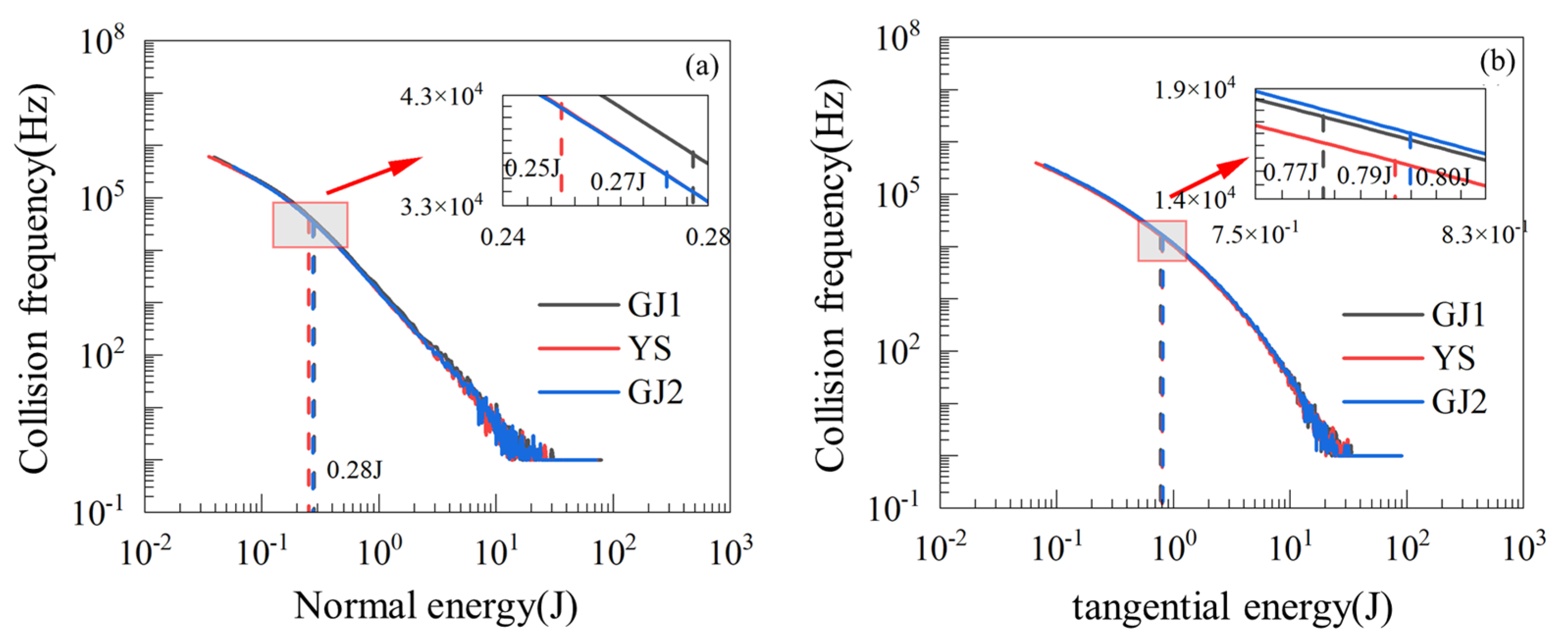
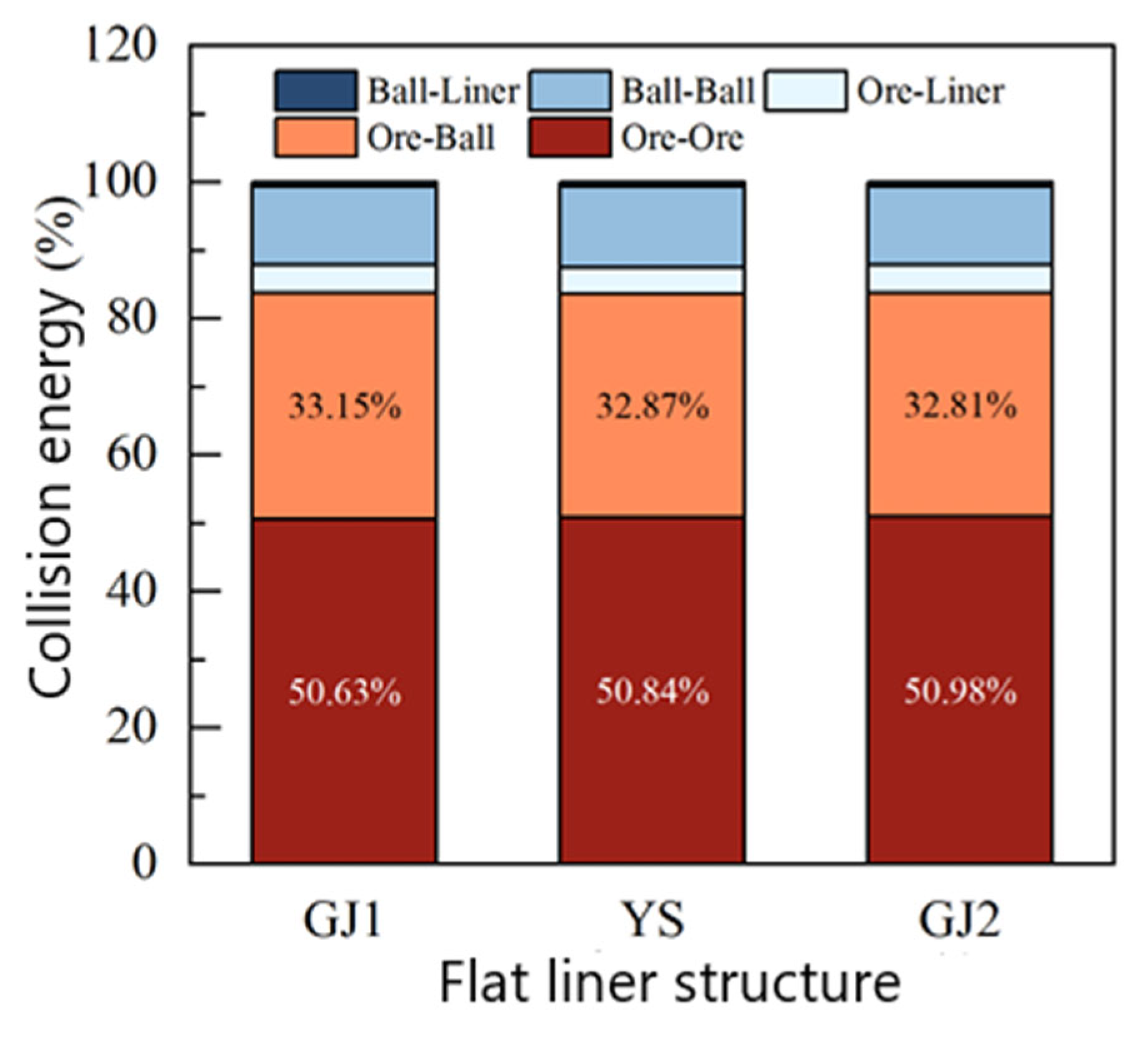
This study enriches the theoretical system of numerical simulation for SAG mill liner wear in two aspects: First, it proposes a “wear morphology–stress feedback” framework, which clarifies that the dynamic change in liner morphology affects the movement trajectory of ore/grinding balls, thereby altering the contact force distribution and further regulating the wear rate. This framework fills the theoretical gap in traditional models where “wear and stress are independent of each other”. Second, it quantifies the correlation between flat liner shape and mill energy utilization—by analyzing the ore collision energy spectrum, it was found that the normal collision energy and tangential collision energy are regulated by the flat liner’s surface profile, and the GJ1-type flat liner optimizes the energy allocation between crushing and grinding, providing a theoretical basis for the “shape–efficiency” design of liners.

6.3.2. Engineering Implications

The research findings have direct guiding significance for industrial SAG mill operations and liner design: (1) the improved Finnie-DEM model can be used to predict the service life of liners, helping mines formulate maintenance plans; (2) the GJ1-type flat liner optimized in this study can be directly applied to the φ10.37 × 5.19 m SAG mill, reducing maintenance costs by 10.6% (based on wear loss data) and improving grinding efficiency by 3.2% (based on effective collision ratio); (3) the model can be extended to other sizes of SAG/ball mills by adjusting key parameters, providing a universal numerical tool for the mining industry.

6.4. Limitations and Future Research Directions

Despite the contributions of this study, it has certain limitations: (1) The simulation omitted the liquid grinding-aid effect in actual mill operations, which led to minor discrepancies in the wear profile of the flat liner’s right end. Future research can integrate Computational Fluid Dynamics (CFD) into the DEM-FEM framework to simulate the coupled effect of solid and liquid phases; (2) The study assumed a constant wear rate over the liner’s service life, which may deviate from the actual wear acceleration in the late service stage. Future work can incorporate material fatigue damage models to improve the accuracy of long-term wear prediction; (3) The research focused on chromium–molybdenum alloy steel liners, and the applicability of the model to other materials needs further verification.

In future research, we will address the above limitations and explore the application of the model in intelligent mill control—for example, establishing a real-time feedback loop between the simulated wear rate and actual mill operating parameters to achieve adaptive optimization of mill performance.

7. Conclusions

The wear and wear process of SAG mill shell liners are studied in this paper. A Finnie-DEM wear model is established to consider the evolution of the surface morphology of the liners. The coupled DEM-FEM simulation code was written in Python to realize data transfer between software EDEM and software ABAQUS. In detail, the collision effect of discrete materials acted on the finite element in the form of forces to analyze whether the liner stress and node coordinate was corrected by the wear loss in the EDEM to simulate the evolution of the surface morphology of liner wear. The main results are as follows:

(1) The improved Finnie-DEM wear model can predict and simulate the wear evolution of the surface morphology of the liners with effects. The DEM-FEM coupling simulation by the Python program avoids a large number of data interactions and non-correspondence of nodes between DEM and FEM software, and also realizes the FEM model corrected to simulate the stress–time history during the wear evolution process.

(2) The liner wear analysis of an extra-large SAG mill was carried out by using the DEM-FEM coupling simulation method, and the profile of the simulated surface is more in line with the experimental wear results.

(3) The influence of the flat liner shape on wearing and tearing was analyzed by a stress nephogram. There are two extreme values of Max^a and Max^b for the instantaneous wear rate of the liner in the circumferential upward direction of the cylinder, and Max^a dominates. The stress distribution in the liner is consistent with the wear distribution and the instantaneous maximum stress when the liner runs into the grinding zone. For two characteristic value points A and B, the stress at point A reflects the magnitude of the direct impact on the liners and the stress at point B reflects the crushing capacity of the mill.

(4) The influence of the flat liner’s shape on the wear of lifter bars was analyzed. The results show that the flat liner shape could affect the magnitude of wear rate extremes M^a and M^b on the lifter bar, and smoothly curved surfaces or curved surfaces without peaks should be avoided, so it is desirable to adopt the structural type of GJ1. Different shapes of the flat liner have a significant effect on the stresses at points A and B, that is, it changes the direct impact force on the lining plate and the crushing capacity of the mill. Variations had a significant effect on the normal collision of material against ore but hardly affected the energy utilization of the mill.