A Novel Method of Magnetic Sources Edge Detection Based on Gradient Tensor
Abstract
1. Introduction
2. Method
2.1. Magnetic Gradient Tensor
2.2. Edge Detection Method
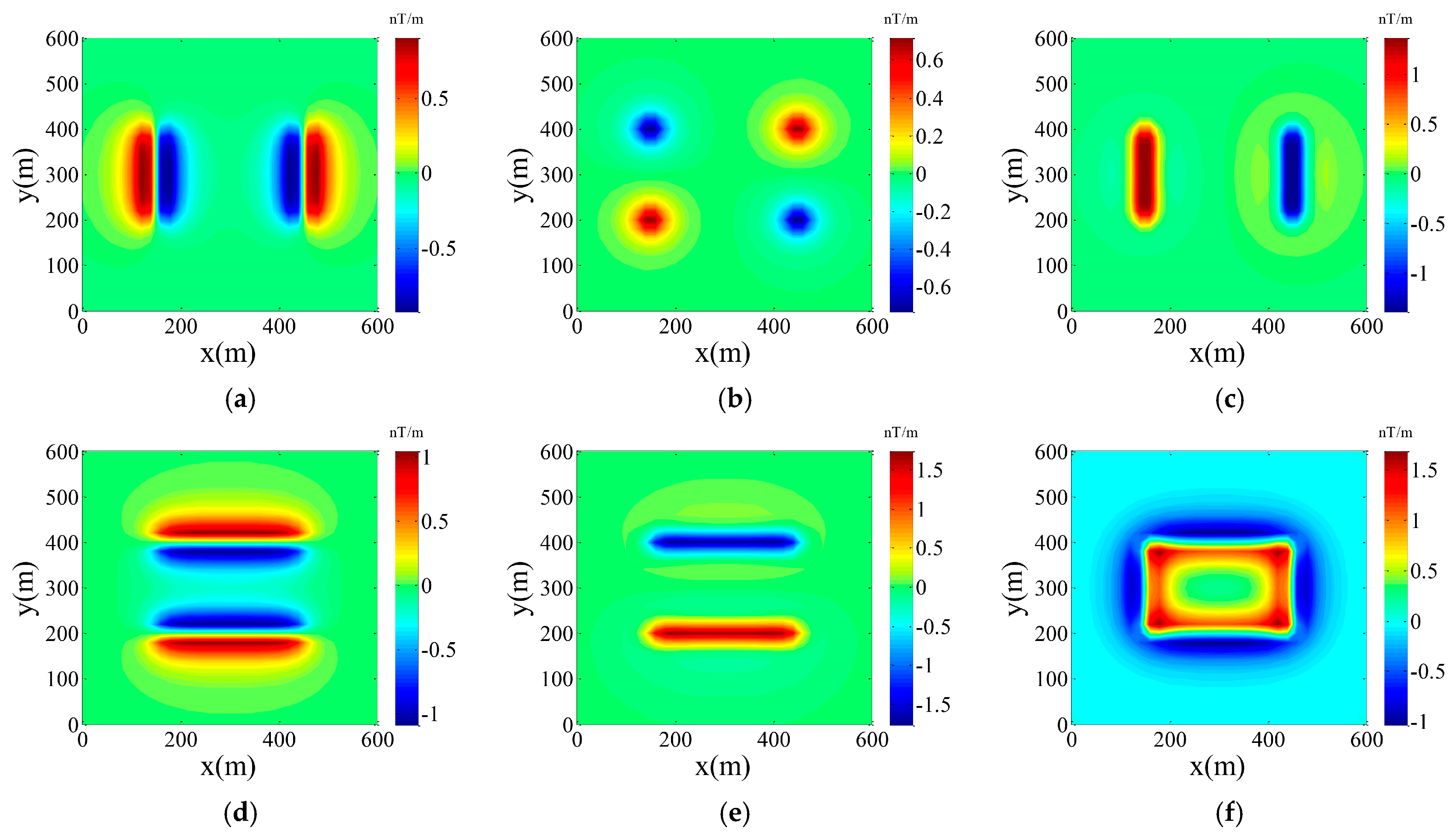
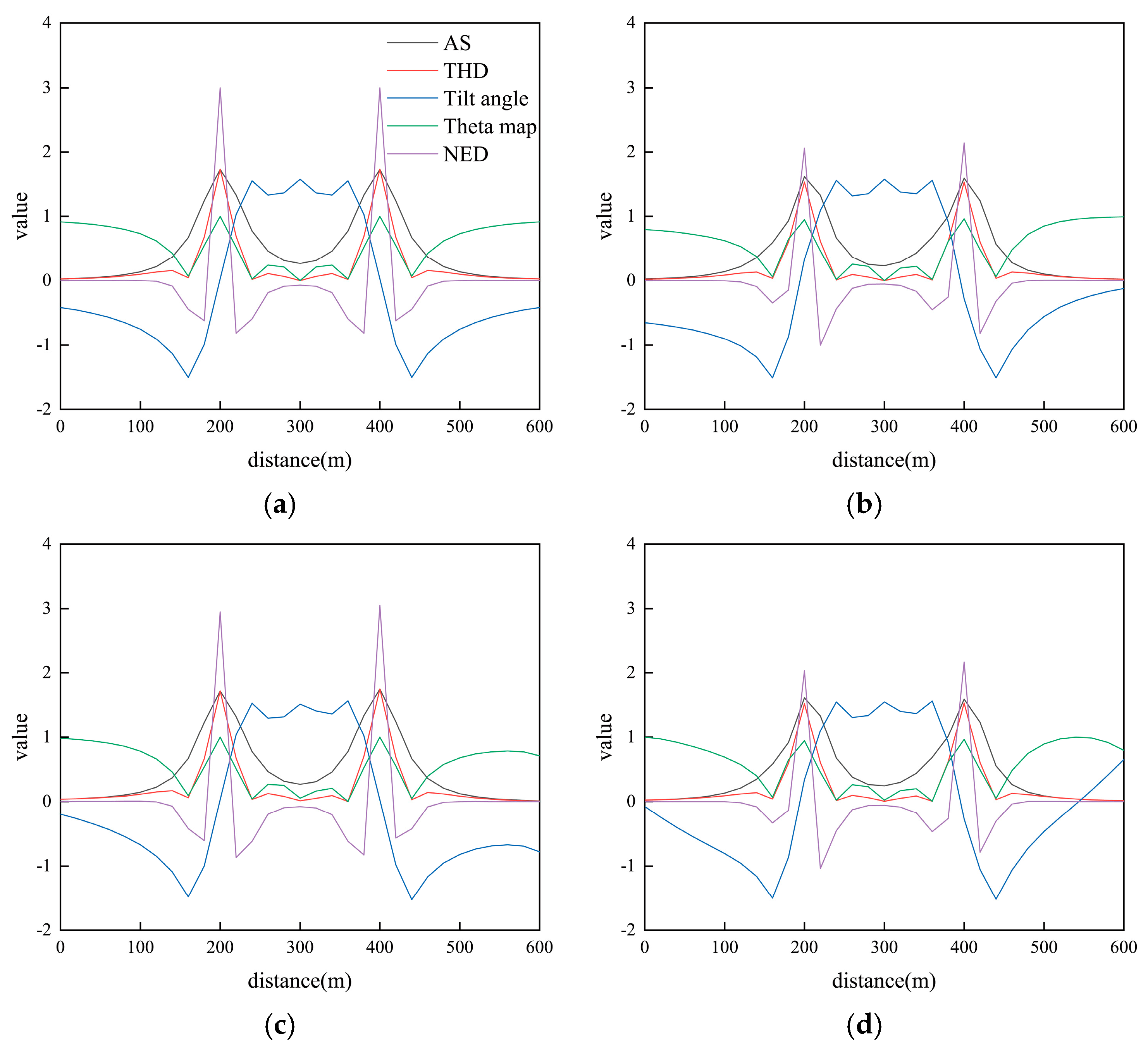
3. Edge Detection Simulation
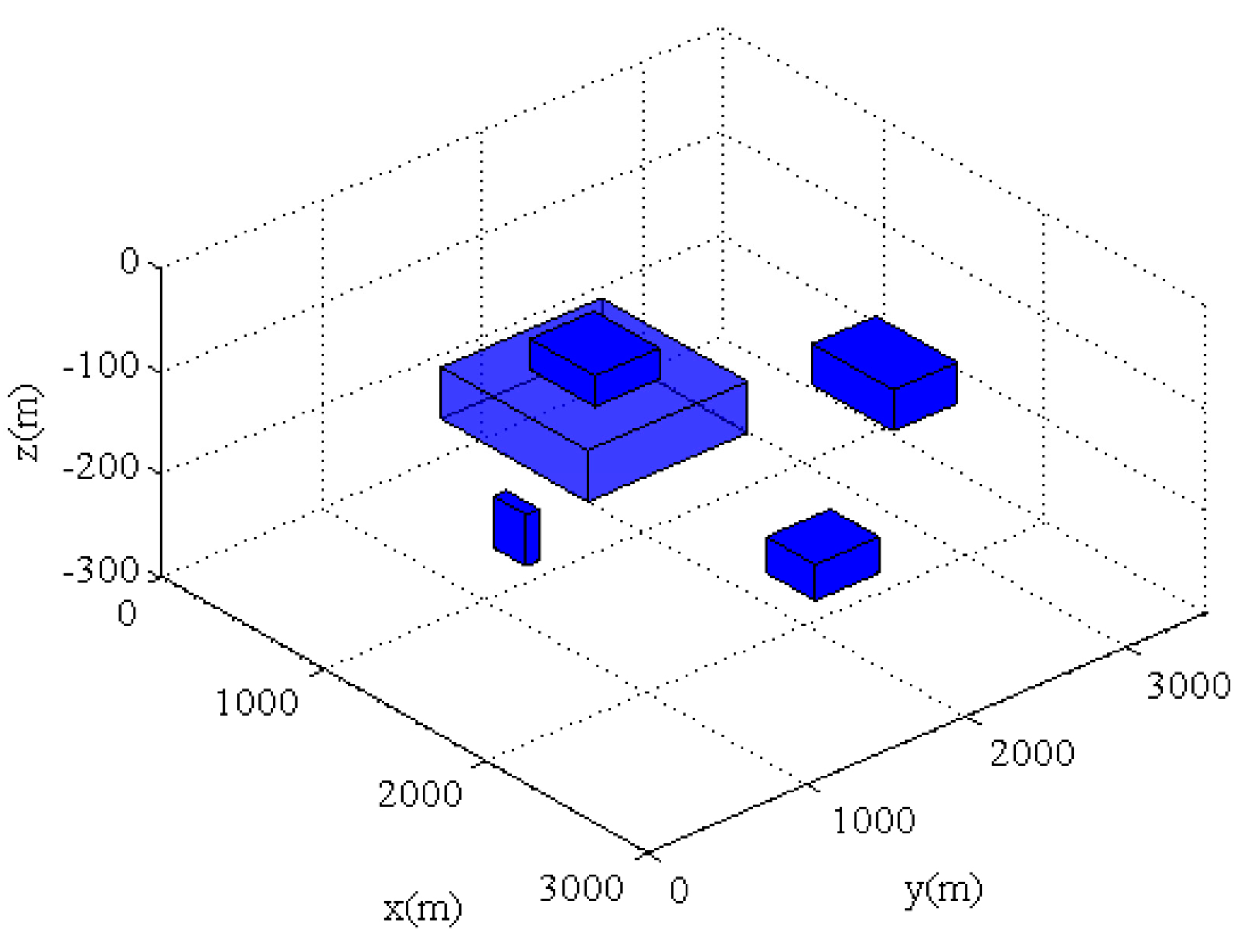
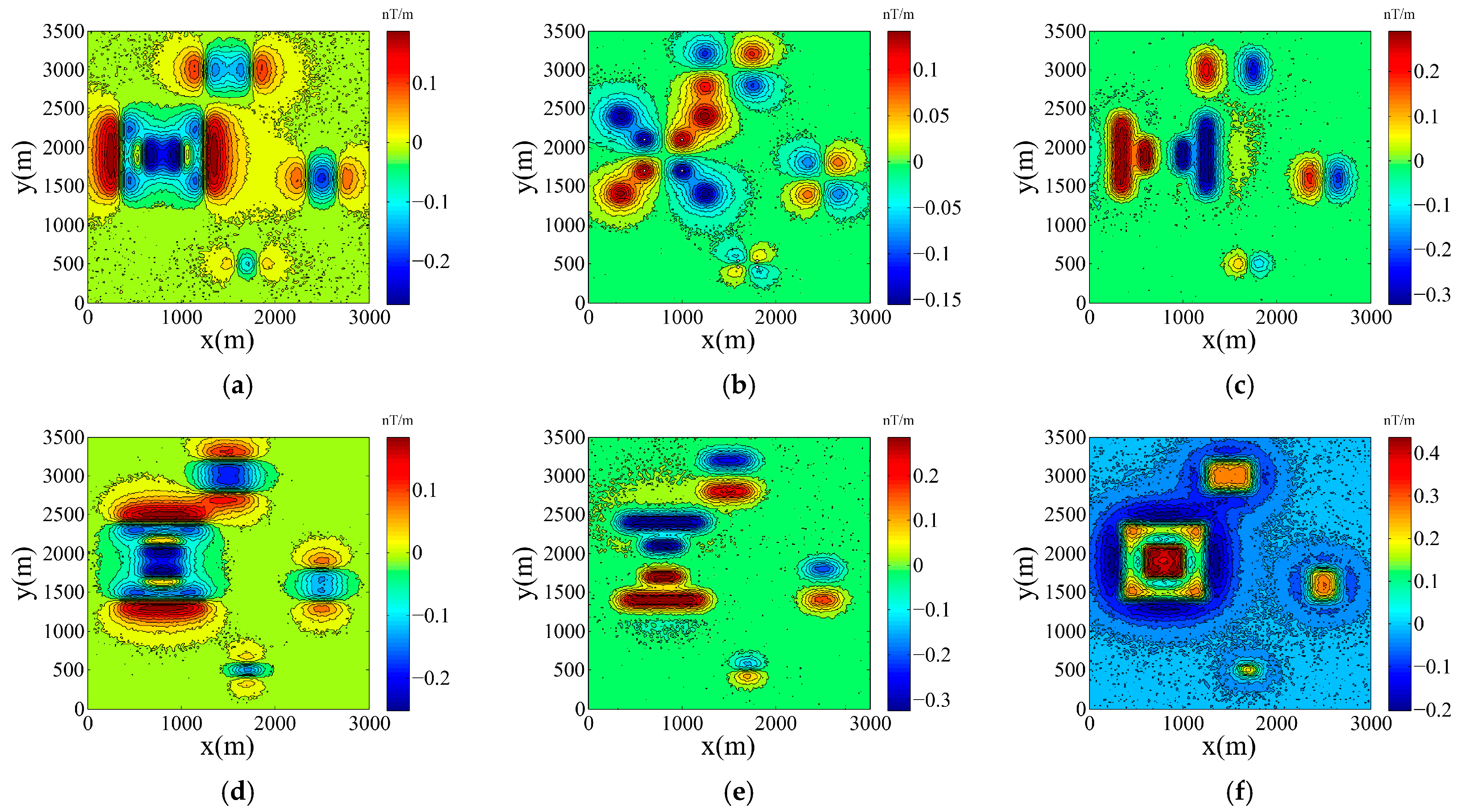
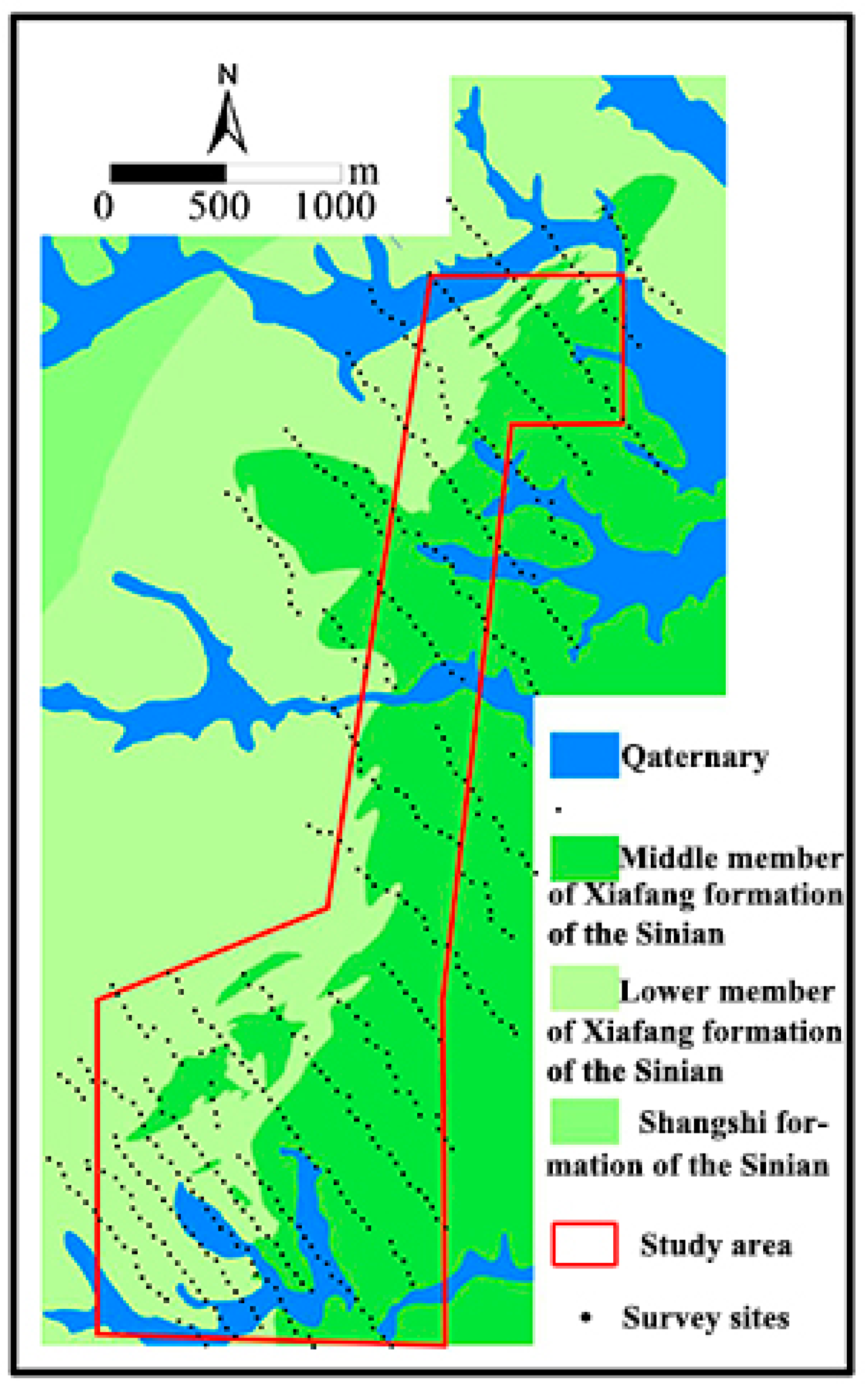
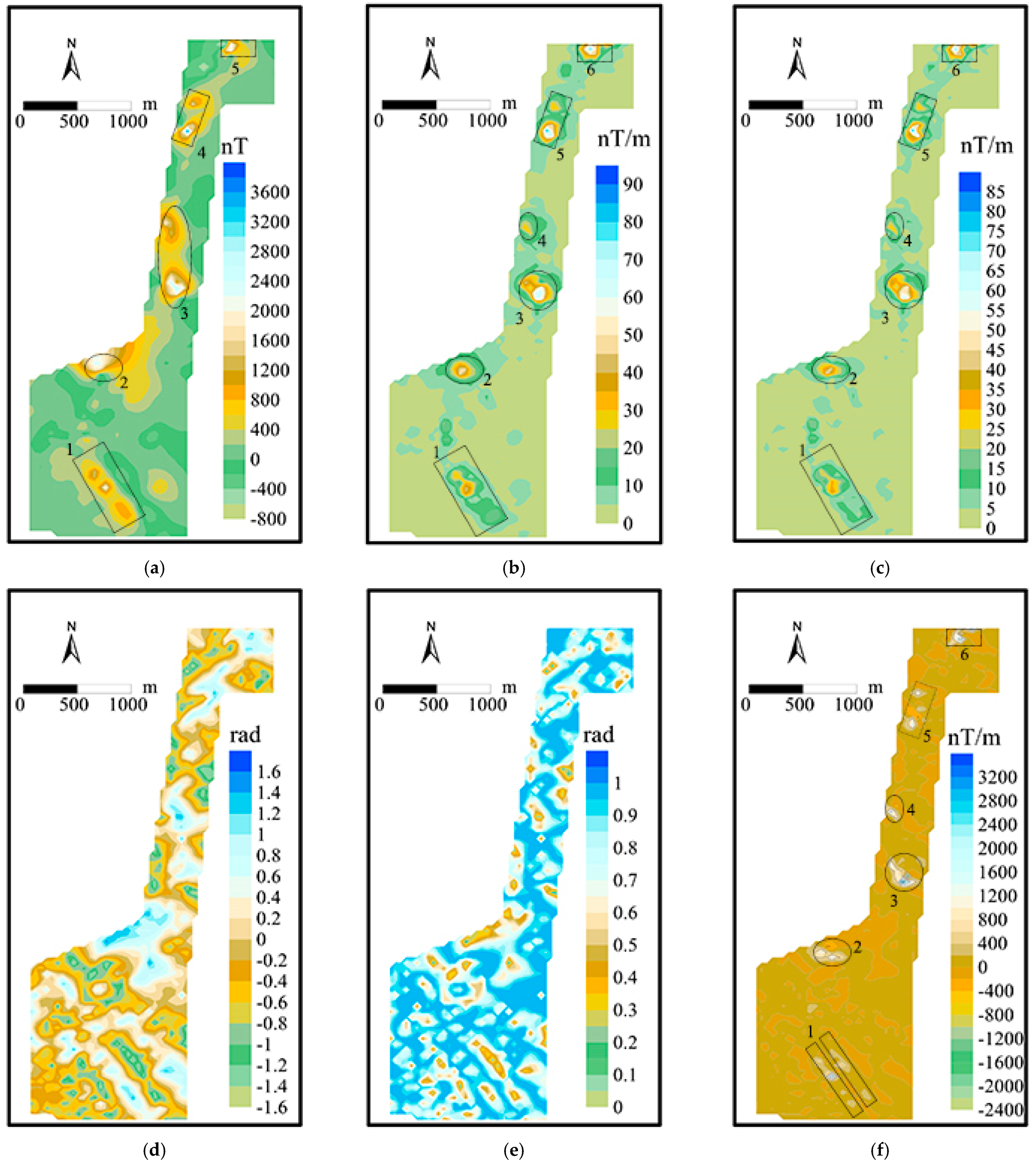
4. Field Example
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, X.; Yan, S.; Li, B. A Novel Method of Localization for Moving Objects with an Alternating Magnetic Field. Sensors 2017, 17, 923. [Google Scholar] [CrossRef] [PubMed]
- Rong, S.; Wu, J.; Liu, J.; Li, Q.; Ren, C.; Cao, X. Environmental Magnetic Characteristics and Heavy Metal Pollution Assessment of Sediments in the Le’an River, China. Minerals 2023, 13, 145. [Google Scholar] [CrossRef]
- Ding, X.; Li, Y.; Luo, M.; Chen, J.; Li, Z.; Liu, H. Estimating Locations and Moments of Multiple Dipole-Like Magnetic Sources From Magnetic Gradient Tensor Data Using Differential Evolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5904913. [Google Scholar] [CrossRef]
- Xu, L.; Gu, H.; Chang, M.; Fang, L.; Lin, P.; Lin, C. Magnetic Target Linear Location Method Using Two-Point Gradient Full Tensor. IEEE Trans. Instrum. Meas. 2021, 70, 6007808. [Google Scholar] [CrossRef]
- Xu, L.; Huang, X.; Dai, Z.; Yuan, F.; Wang, X.; Fan, J. Blind Spots Analysis of Magnetic Tensor Localization Method. Remote Sens. 2023, 15, 2199. [Google Scholar] [CrossRef]
- Wynn, W.; Frahm, C.; Carroll, P.; Clark, R.; Wellhoner, J.; Wynn, M. Advanced Superconducting Gradiometer/Magnetometer Arrays and a Novel Signal Processing Technique. IEEE Trans. Magn. 1975, 11, 701–707. [Google Scholar] [CrossRef]
- Chwala, A.; Stolz, R.; Zakosarenko, V.; Fritzsch, L.; Schulz, M.; Rompel, A.; Polome, L.; Meyer, M.; Meyer, H.G. Full Tensor SQUID Gradiometer for Airborne Exploration. ASEG Ext. Abstr. 2012, 2012, 1–4. [Google Scholar] [CrossRef]
- Schmidt, P.; Clark, D.; Leslie, K.; Bick, M.; Tilbrook, D.; Foley, C. GETMAG—A SQUID Magnetic Tensor Gradiometer for Mineral and Oil Exploration. Explor. Geophys. 2004, 35, 297–305. [Google Scholar] [CrossRef]
- Stolz, R.; Fritzsch, L.; Meyer, H.-G. LTS SQUID Sensor with a New Configuration. Supercond. Sci. Technol. 1999, 12, 806–808. [Google Scholar] [CrossRef]
- Schiffler, M.; Queitsch, M.; Stolz, R.; Chwala, A.; Krech, W.; Meyer, H.-G.; Kukowski, N. Calibration of SQUID Vector Magnetometers in Full Tensor Gradiometry Systems. Geophys. J. Int. 2014, 198, 954–964. [Google Scholar] [CrossRef]
- Schmidt, P.; Clark, D. Advantages of Measuring the Magnetic Gradient Tensor. Preview 2000, 85, 26–30. [Google Scholar]
- Schmidt, P.W.; Clark, D.A. The Magnetic Gradient Tensor: Its Properties and Uses in Source Characterization. Lead. Edge 2006, 25, 75–78. [Google Scholar] [CrossRef]
- Clark, D.A. Corrigendum to: New Methods for Interpretation of Magnetic Vector and Gradient Tensor Data I: Eigenvector Analysis and the Normalised Source Strength. Explor. Geophys. 2014, 45, 267–282. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, L.; Jiang, H.; Wei, Z.; Xie, Y. A Closed-Form Formula for Magnetic Dipole Localization by Measurement of Its Magnetic Field Vector and Magnetic Gradient Tensor. J. Magn. Magn. Mater. 2020, 499, 166274. [Google Scholar] [CrossRef]
- Lin, S.; Pan, D.; Wang, B.; Liu, Z.; Liu, G.; Wang, L.; Li, L. Improvement and Omnidirectional Analysis of Magnetic Gradient Tensor Invariants Method. IEEE Trans. Ind. Electron. 2021, 68, 7603–7612. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, N.; Fang, L.; Lin, P.; Chen, H.; Chang, M. Error Analysis of Cross-Shaped Magnetic Gradient Full Tensor Measurement System. AIP Adv. 2020, 10, 125201. [Google Scholar] [CrossRef]
- Nabighian, M.N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: Its properties and use for automated anomaly interpretation. Geophysics 1972, 37, 507–517. [Google Scholar] [CrossRef]
- Roest, W.R.; Verhoef, J.; Pilkington, M. Magnetic Interpretation Using the 3-D Analytic Signal. Geophysics 1992, 57, 116–125. [Google Scholar] [CrossRef]
- Qin, S. An Analytic Signal Approach to the Interpretation of Total Field Magnetic Anomalies. Geophys. Prospect. 1994, 42, 665–675. [Google Scholar] [CrossRef]
- Nabighian, M.N. Toward a Three-dimensional Automatic Interpretation of Potential Field Data via Generalized Hilbert Transforms: Fundamental Relations. Geophysics 1984, 49, 780–786. [Google Scholar] [CrossRef]
- Beiki, M. Analytic Signals of Gravity Gradient Tensor and Their Application to Estimate Source Location. Geophysics 2010, 75, I59–I74. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, Q. Edge Detection in Potential-Field Gradient Tensor Data by Use of Improved Horizontal Analytical Signal Methods. Pure Appl. Geophys. 2015, 172, 461–472. [Google Scholar] [CrossRef]
- Yuan, Y.; Geng, M. Directional Total Horizontal Derivatives of Gravity Gradient Tensor and Their Application to Delineat the Edges. In Proceedings of the 76th EAGE Conference & Exhibition, Amsterdam, The Netherlands, 16–19 June 2014. [Google Scholar] [CrossRef]
- Miller, H.G.; Singh, V. Potential Field Tilt—A New Concept for Location of Potential Field Sources. J. Appl. Geophys. 1994, 32, 213–217. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shi, Z.; Fan, H. Application of Helbig Integrals to Magnetic Gradient Tensor Multi-Target Detection. Measurement 2022, 200, 111612. [Google Scholar] [CrossRef]
- Gang, Y.; Yingtang, Z.; Hongbo, F.; Zhining, L.; Guoquan, R. Detection, Localization and Classification of Multiple Dipole-like Magnetic Sources Using Magnetic Gradient Tensor Data. J. Appl. Geophys. 2016, 128, 131–139. [Google Scholar] [CrossRef]
- Ferreira, F.J.F.; de Souza, J.; de B. e S. Bongiolo, A.; de Castro, L.G. Enhancement of the Total Horizontal Gradient of Magnetic Anomalies Using the Tilt Angle. Geophysics 2013, 78, J33–J41. [Google Scholar] [CrossRef]
- Verduzco, B.; Fairhead, J.D.; Green, C.M.; MacKenzie, C. New Insights into Magnetic Derivatives for Structural Mapping. Lead. Edge 2004, 23, 116–119. [Google Scholar] [CrossRef]
- Wijns, C.; Perez, C.; Kowalczyk, P. Theta Map: Edge Detection in Magnetic Data. Geophysics 2005, 70, L39–L43. [Google Scholar] [CrossRef]
- Eldosouky, A.M.; Mohamed, H. Edge Detection of Aeromagnetic Data as Effective Tools for Structural Imaging at Shilman Area, South Eastern Desert, Egypt. Arab. J. Geosci. 2021, 14, 13. [Google Scholar] [CrossRef]
- Ma, G.; Li, L. Edge Detection in Potential Fields with the Normalized Total Horizontal Derivative. Comput. Geosci. 2012, 41, 83–87. [Google Scholar] [CrossRef]
- Oruç, B. Location and Depth Estimation of Point-Dipole and Line of Dipoles Using Analytic Signals of the Magnetic Gradient Tensor and Magnitude of Vector Components. J. Appl. Geophys. 2010, 70, 27–37. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Fan, H.; Li, Z. Preprocessed Method and Application of Magnetic Gradient Tensor Data. IEEE Access 2019, 7, 173738–173752. [Google Scholar] [CrossRef]
- Li, G.; Liu, S.; Shi, K.; Hu, X. Normalized Edge Detectors Using Full Gradient Tensors of Potential Field. Pure Appl. Geophys. 2023, 180, 2327–2349. [Google Scholar] [CrossRef]
- Beiki, M.; Clark, D.A.; Austin, J.R.; Foss, C.A. Estimating Source Location Using Normalized Magnetic Source Strength Calculated from Magnetic Gradient Tensor Data. Geophysics 2012, 77, J23–J37. [Google Scholar] [CrossRef]
- Phillips, J.D.; Nabighian, M.N.; Smith, D.V.; Li, Y. Estimating Locations and Total Magnetization Vectors of Com-pact Magnetic Sources from Scalar, Vector, or Tensor Magnetic Measurements through Combined Helbig and Euler Analysis. In SEG Technical Program Expanded Abstracts 2007; Society of Exploration Geophysicists: Houston, TX, USA, 2007; pp. 770–774. [Google Scholar] [CrossRef]
- Salem, A.; Ravat, D. A Combined Analytic Signal and Euler Method (AN-EUL) for Automatic Interpretation of Magnetic Data. Geophysics 2003, 68, 1952–1961. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, H.; Wang, Y.; Rong, L.; Shi, Y.; Chen, Y. Three-dimensional Inversion of Full Magnetic Gradient Tensor Data Based on Hybrid Regularization Method. Geophys. Prospect. 2019, 67, 226–261. [Google Scholar] [CrossRef]
- Prasad, K.N.D.; Pham, L.T.; Singh, A.P.; Eldosouky, A.M.; Abdelrahman, K.; Fnais, M.S.; Gómez-Ortiz, D. A Novel Enhanced Total Gradient (ETG) for Interpretation of Magnetic Data. Minerals 2022, 12, 1468. [Google Scholar] [CrossRef]
- Pham, L.T.; Oksum, E.; Vu, M.D.; Vo, Q.T.; Du Le-Viet, K.; Eldosouky, A.M. An Improved Approach for Detecting Ridge Locations to Interpret the Potential Field Data for More Accurate Structural Mapping: A Case Study from Vredefort Dome Area (South Africa). J. Afr. Earth Sci. 2021, 175, 104099. [Google Scholar] [CrossRef]
- Eldosouky, A.M.; Pham, L.T.; Henaish, A. High Precision Structural Mapping Using Edge Filters of Potential Field and Remote Sensing Data: A Case Study from Wadi Umm Ghalqa Area, South Eastern Desert, Egypt. Egypt. J. Remote Sens. Space Sci. 2022, 25, 501–513. [Google Scholar] [CrossRef]
- Eldosouky, A.M.; Pham, L.T.; Duong, V.-H.; Kemgang Ghomsi, F.E.; Henaish, A. Structural Interpretation of Potential Field Data Using the Enhancement Techniques: A Case Study. Geocarto Int. 2022, 37, 16900–16925. [Google Scholar] [CrossRef]
- Ekwok, S.E.; Eldosouky, A.M.; Ben, U.C.; Achadu, O.-I.M.; Akpan, A.E.; Othman, A.; Pham, L.T. An Integrated Approach of Advanced Methods for Mapping Geologic Structures and Sedimentary Thickness in Ukelle and Adjoining Region (Southeast Nigeria). Earth Sci. Res. J. 2023, 27, 251–258. [Google Scholar] [CrossRef]
- Thanh Pham, L.; Anh Nguyen, D.; Eldosouky, A.M.; Abdelrahman, K.; Van Vu, T.; Al-Otaibi, N.; Ibrahim, E.; Kharbish, S. Subsurface Structural Mapping from High-Resolution Gravity Data Using Advanced Processing Methods. J. King Saud Univ.-Sci. 2021, 33, 101488. [Google Scholar] [CrossRef]
- Thanh Pham, L.; Eldosouky, A.M.; Melouah, O.; Abdelrahman, K.; Alzahrani, H.; Oliveira, S.P.; Andráš, P. Mapping Subsurface Structural Lineaments Using the Edge Filters of Gravity Data. J. King Saud Univ.-Sci. 2021, 33, 101594. [Google Scholar] [CrossRef]
- Eldosouky, A.M.; Elkhateeb, S.O.; Mahdy, A.M.; Saad, A.A.; Fnais, M.S.; Abdelrahman, K.; Andráš, P. Structural Analysis and Basement Topography of Gabal Shilman Area, South Eastern Desert of Egypt, Using Aeromagnetic Data. J. King Saud Univ.-Sci. 2022, 34, 101764. [Google Scholar] [CrossRef]
- Eldosouky, A.M.; Pham, L.T.; Abdelrahman, K.; Fnais, M.S.; Gomez-Ortiz, D. Mapping Structural Features of the Wadi Umm Dulfah Area Using Aeromagnetic Data. J. King Saud Univ.-Sci. 2022, 34, 101803. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shi, Z.; Fan, H. Multi-Target Magnetic Positioning Using SAFCM Clustering and Invariants-Improved Tilt Angle. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5924015. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shi, Z.; Fan, H. Magnetic Object Recognition with Magnetic Gradient Tensor System Heading-Line Surveys Based on Kernel Extreme Learning Machine and Sparrow Search Algorithm. Measurement 2022, 203, 111967. [Google Scholar] [CrossRef]
- Deng, H.; Hu, X.; Cai, H.; Liu, S.; Peng, R.; Liu, Y.; Han, B. 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals 2022, 12, 566. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, M.-P.; Wang, P.; Duan, S.-L.; Liu, H.-J.; Wang, J.-L.; An, Z.-F. Full Magnetic Gradient Tensor from Triaxial Aeromagnetic Gradient Measurements: Calculation and Application. Appl. Geophys. 2015, 12, 283–291. [Google Scholar] [CrossRef]
- Prasad, K.N.D.; Pham, L.T.; Singh, A.P. Structural Mapping of Potential Field Sources Using BHG Filter. Geocarto Int. 2022, 37, 11253–11280. [Google Scholar] [CrossRef]
- Prasad, K.N.D.; Pham, L.T.; Singh, A.P. A Novel Filter “ImpTAHG” for Edge Detection and a Case Study from Cambay Rift Basin, India. Pure Appl. Geophys. 2022, 179, 2351–2364. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G. NHF as an Edge Detector of Potential Field Data and Its Application in the Yili Basin. Minerals 2022, 12, 149. [Google Scholar] [CrossRef]



| Parameter | Rectangle |
|---|---|
| Center (m) | (300, 300, 35) |
| Width (m) | 300 |
| Height (m) | 200 |
| Thickness (m) | 10 |
| Susceptibility (SI) | 100 |
| Parameter | Rectangle1 | Rectangle2 | Rectangle3 | Rectangle4 | Rectangle5 |
|---|---|---|---|---|---|
| Center (m) | (800, 1900, 185) | (1500, 3000, 170) | (1700, 500, 135) | (2500, 1600, 157.5) | (800, 1900, 145) |
| Width (m) | 900 | 500 | 200 | 300 | 400 |
| Height (m) | 1000 | 400 | 80 | 400 | 400 |
| Thickness (m) | 50 | 40 | 50 | 35 | 30 |
| Susceptibility (SI) | 100 | 100 | 100 | 100 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Huang, P.; Yang, Y.; Luo, Q.; Xie, S.; Fu, C. A Novel Method of Magnetic Sources Edge Detection Based on Gradient Tensor. Minerals 2024, 14, 657. https://doi.org/10.3390/min14070657
Lv W, Huang P, Yang Y, Luo Q, Xie S, Fu C. A Novel Method of Magnetic Sources Edge Detection Based on Gradient Tensor. Minerals. 2024; 14(7):657. https://doi.org/10.3390/min14070657
Chicago/Turabian StyleLv, Wenjie, Pei Huang, Yaxin Yang, Qibin Luo, Shangping Xie, and Chen Fu. 2024. "A Novel Method of Magnetic Sources Edge Detection Based on Gradient Tensor" Minerals 14, no. 7: 657. https://doi.org/10.3390/min14070657
APA StyleLv, W., Huang, P., Yang, Y., Luo, Q., Xie, S., & Fu, C. (2024). A Novel Method of Magnetic Sources Edge Detection Based on Gradient Tensor. Minerals, 14(7), 657. https://doi.org/10.3390/min14070657






