Study on the Dynamic Evolution of Mining-Induced Stress and Displacement in the Floor Coal-Rock Induced by Protective Layer Mining
Abstract
1. Introduction
2. Similar Experiments of Upper Protective Layer Mining
2.1. Similarity Theory
2.1.1. Laws of Similarity
2.1.2. Similarity Criterion
2.2. Geological Background
2.3. Similarity Experiment
2.4. Experiment Method
3. Numerical Simulation Description
3.1. Overview for Numerical Simulation
3.2. Numerical Model
4. Experiment Results
4.1. Movement Characteristic
4.2. Deformation Characteristics of Protected Layer
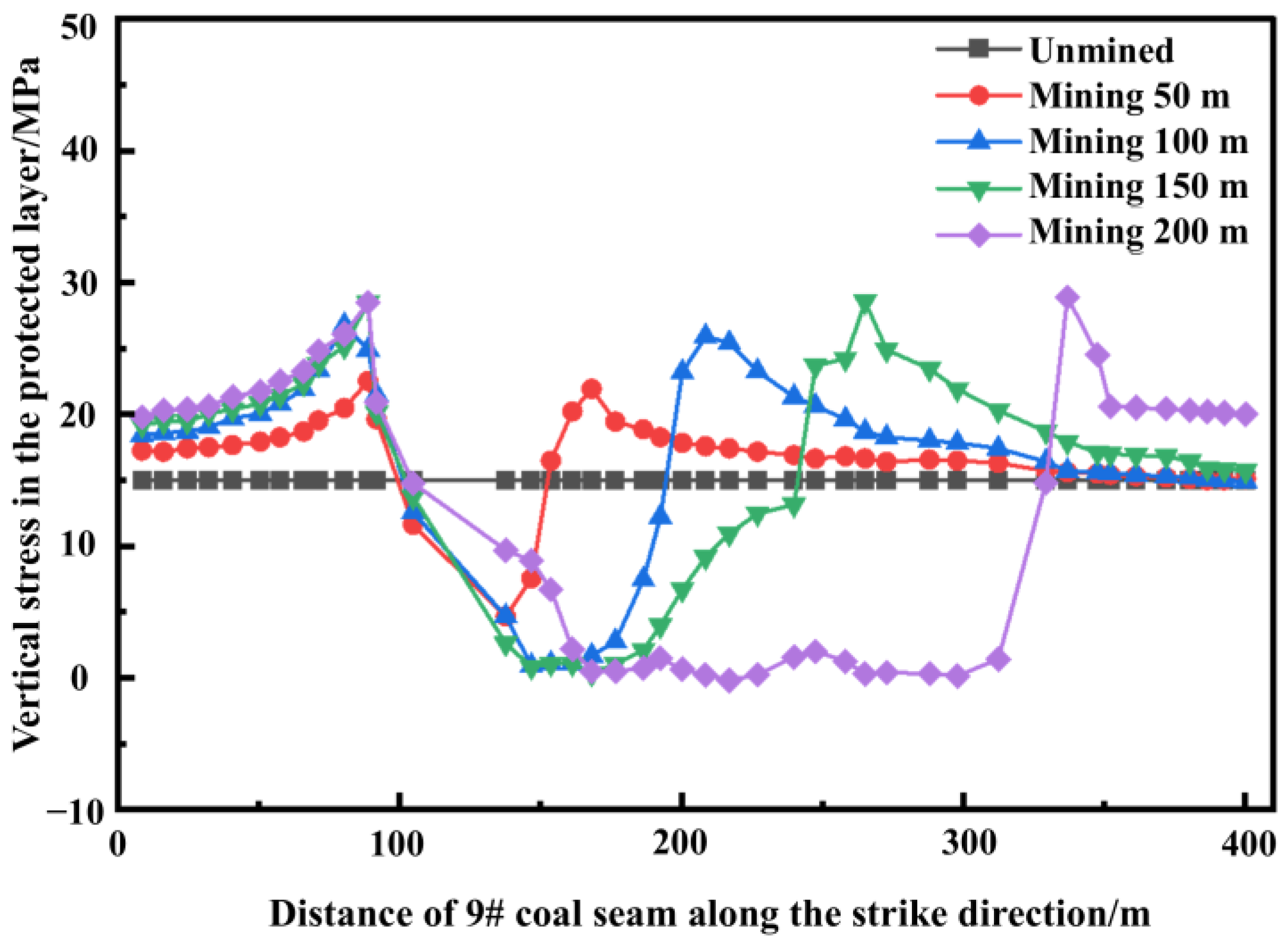
4.3. Stress Characteristics of Protected Layer
5. Numerical Simulation Results
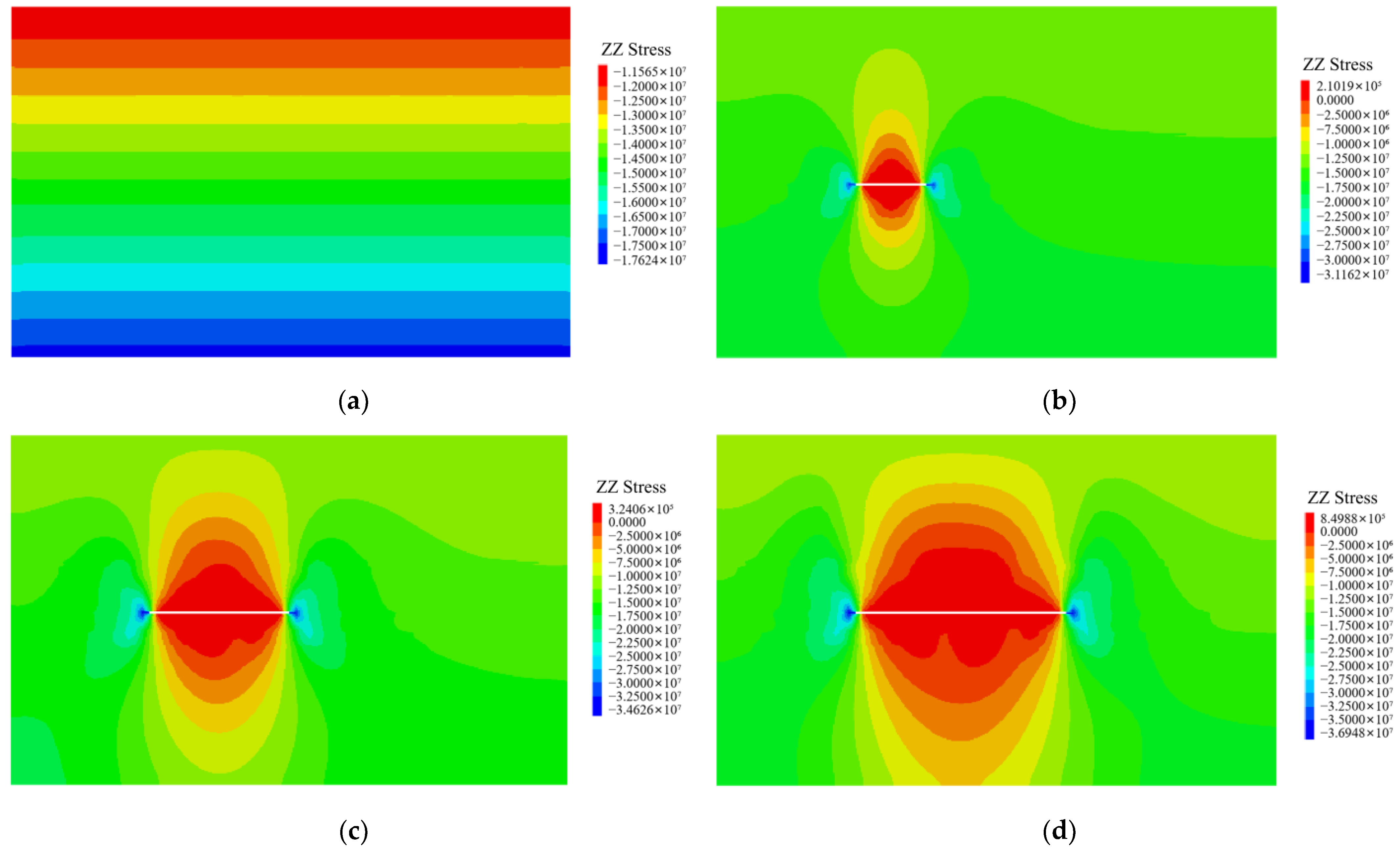
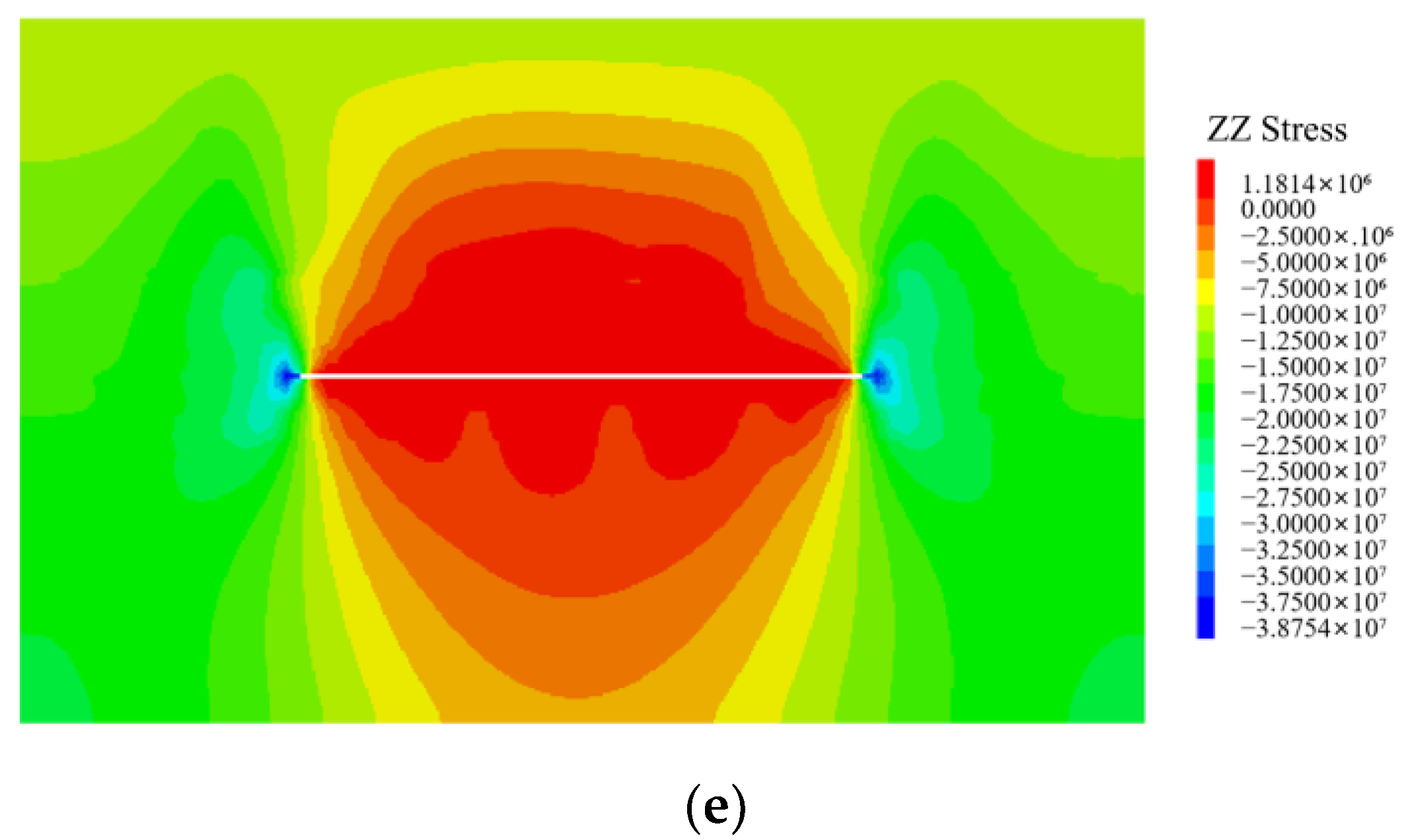
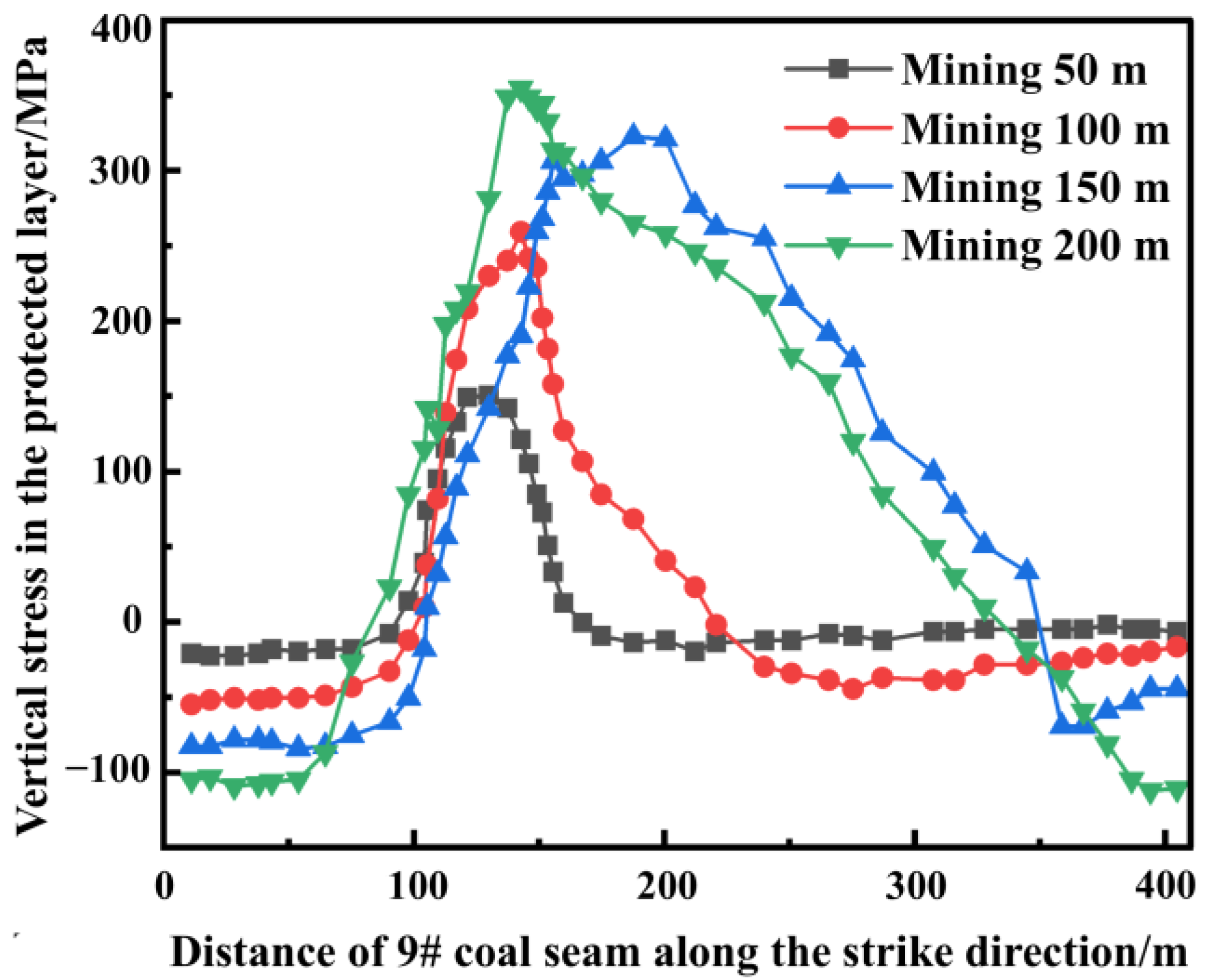
5.1. Analysis of Stress Characteristics During the Protective Layer Mining
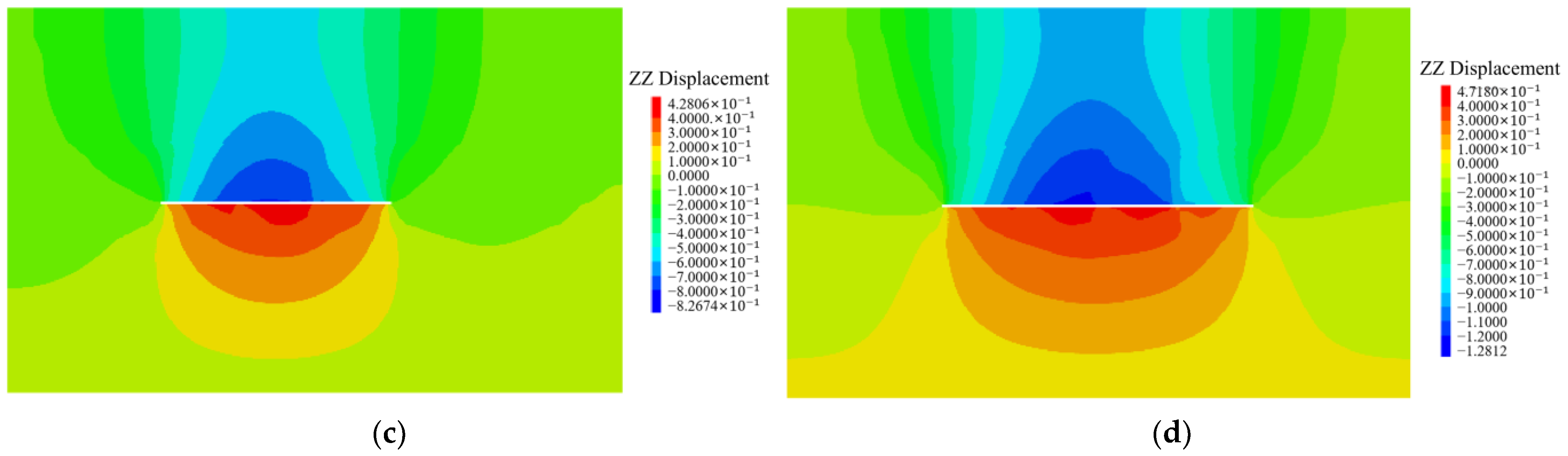
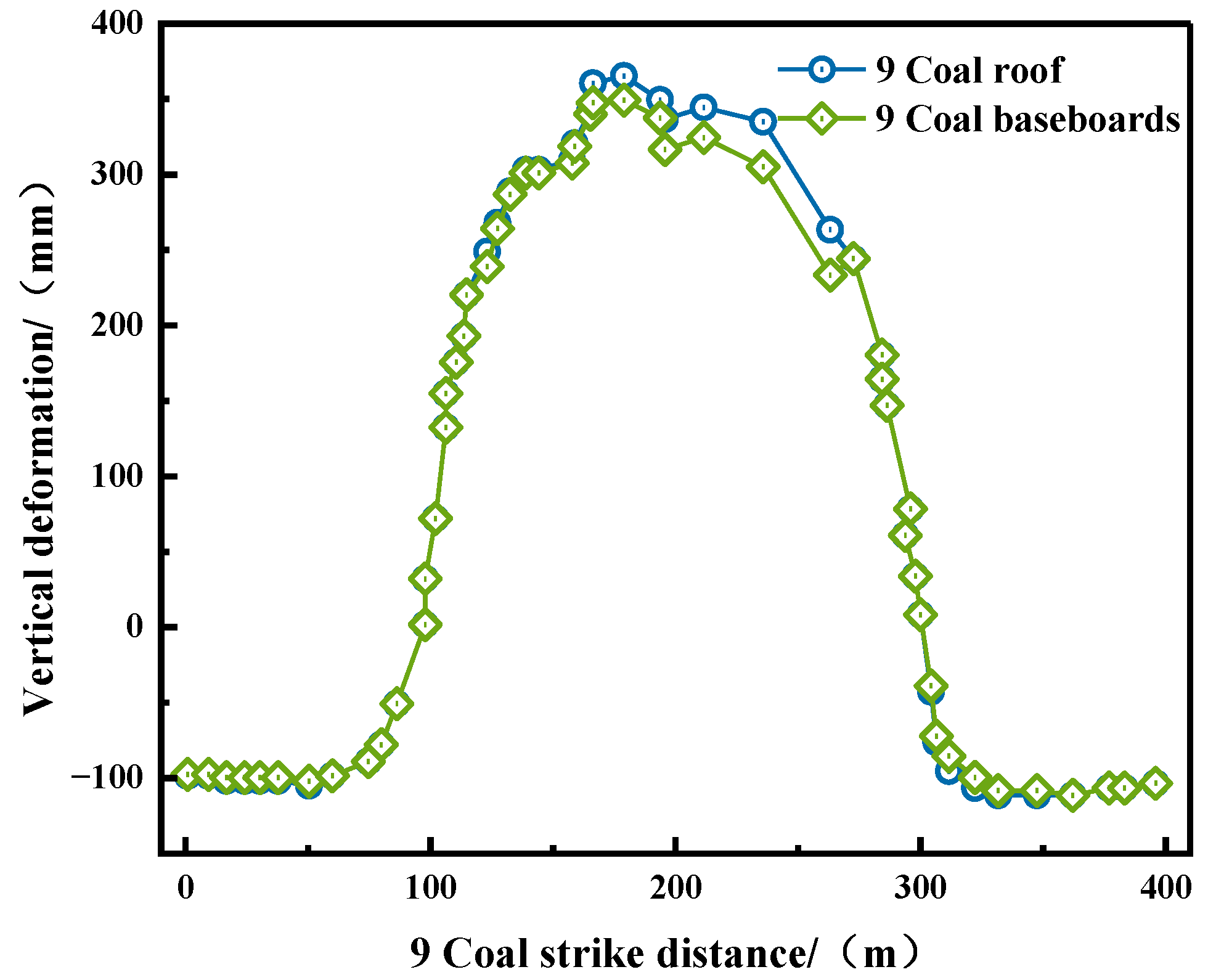
5.2. Analysis of the Deformation
6. Discussion
7. Conclusions
- Through similarity simulation experiments, the maximum strike expansion deformation rate is 11.3‰ in the 9# coal seam after the mining of the 82# coal seam. Stress monitoring during the protective layer mining reveals that the stress concentration zone is within 32 m ahead of the working face, the original stress zone is beyond 32 m ahead of the working face, the stress relief zone is within 51 m behind the working face, and the stress recovery zone is beyond 51 m behind the working face.
- Through FLAC3D numerical simulation, it can be concluded that the vertical stress of the underlying mass is reduced due to the mining of the protective layer. The reduction rate of vertical stress gradually increases as the working face advances, reaching up to 99.6%. The stress concentration zone gradually forms and enlarges in front of the goaf and behind the open-off cut. The displacement and deformation of the underlying mass is affected by the protective layer mining, forming a funnel-shaped displacement above the goaf and a semicircular displacement below. The displacement increases gradually as the working face advances; eventually the displacement of the roof and floor is symmetrically distributed, and the maximum expansion deformation in the upper goaf reaches 15.6 mm. The pressure relief effect is exerted on the underlying 9# coal seam after the mining of the 82# coal seam, with an average pressure relief rate of 86.2%, demonstrating a good pressure relief effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, S.-h.; Jiao, X.-m.; Zheng, D.-Z.; Zhang, Y.-n.; Xie, H.-p.; Guo, Z.-q. Demand and fluctuation range of China’s coal production under the dual carbon target. Energy Rep. 2024, 11, 3267–3282. [Google Scholar]
- Li, K.-z.; Xiao, L.; Qi, K.; Song, Y.-m. Clean energy transition and energy security in metropolises: A case study of Beijing under the “coal-to-gas” movement. Elem. Sci. Anthr. 2024, 12, 00074. [Google Scholar] [CrossRef]
- Zhang, X.-y; Cui, J.; Dong, F.; Xu, L.-y.; Zhu, X.-z.; Li, Y.-f. Carbon inequality under domestic value chain fragmentation. J. Clean. Prod. 2024, 471, 143309. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, L.; Liu, H.; Kong, S.; Yang, Q.; Zhu, J.; Tu, Q. Definition, theory, methods, and applications of the safe and efficient simultaneous extraction of coal and gas. Int. J. Coal Sci. Technol. 2015, 2, 52–65. [Google Scholar] [CrossRef]
- Yin, G.; Li, M.; Wang, J.G.; Xu, J.; Li, W. Mechanical behavior and permeability evolution of gas infiltrated coals during protective layer mining. Int. J. Rock Mech. Min. Sci. 2015, 80, 292–301. [Google Scholar] [CrossRef]
- Wang, K.; Du, F. Coal-gas compound dynamic disasters in China: A review. Process Saf. Environ. Prot. 2020, 133, 1–17. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, Y. The elimination of coal and gas outburst disasters by long distance lower protective seam mining combined with stress-relief gas extraction in the Huaibei coal mine area. J. Nat. Gas Sci. Eng. 2015, 27, 346–353. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, Z.; Yao, B.; Chen, X. Numerical simulation on stress evolution and deformation of overlying coal seam in lower protective layer mining. Alex. Eng. J. 2020, 59, 3623–3633. [Google Scholar] [CrossRef]
- Cheng, Z.; Pan, H.; Zou, Q.; Li, Z.; Chen, L.; Cao, J.; Zhang, K.; Cui, Y. Gas Flow Characteristics and Optimization of Gas Drainage Borehole Layout in Protective Coal Seam Mining: A Case Study from the Shaqu Coal Mine, Shanxi Province, China. Nat. Resour. Res. 2020, 30, 1481–1493. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, N.; Xie, Z.-z; Han, C.-l.; Zhang, C.-h.; Yuan, Y.-x.; He, Z.; Liu, J.-h. A three-dimensional supporting technology, optimization and inspiration from a deep coal mine in China. Rock Mech. Rock Eng. 2024, 57, 655–677. [Google Scholar] [CrossRef]
- Dang, J.-x; Tu, M.; Zhang, X.-y; Bu, Q.-w. Research on the bearing characteristics of brackets in thick hard roof mining sites and the effect of blasting on roof control. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 18. [Google Scholar] [CrossRef]
- Gai, Q.-k; He, M.-c; Gao, Y.-b; Lu, C.-s. A two-dimensional model test system for floor failure during automatic roadway formation mining without pillars above confined water. Eng. Fail. Anal. 2024, 162, 108369. [Google Scholar] [CrossRef]
- Majid, K.; He, X.; Guo, J.; Song, D.-z. Accurate prediction of indicators for engineering failures in complex mining environments. Eng. Fail. Anal. 2024, 155, 107736. [Google Scholar]
- Zhou, J.; Zhang, Y.-l; Li, C.-q; He, H.-b.; Li, X.-b. Rockburst prediction and prevention in underground space excavation. Undergr. Space 2024, 14, 70–98. [Google Scholar] [CrossRef]
- Cai, M. Rockburst risk control and mitigation in deep mining. Deep Resour. Eng. 2024, 1, 100019. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, H.; Chen, C.-m; Guo, J.; Jin, Y.-f.; Zheng, X.-z.; Cheng, X.-j.; Li, D.-l. Research status and development trend of coal spontaneous combustion fire and prevention technology in China: A review. ACS Omega 2024, 9, 21727–21750. [Google Scholar] [CrossRef]
- Gu, Y.-f.; Li, H.-d.; Dou, L.-h.; Wu, M.; Guo, H.-n.; Huang, W.-s.; Gu, J.-p.; Babaee, S.; Jiang, L.-l.; Feng, L.-l. Advance in Detection and Management for Underground Coal Fires: A Global Technological Overview. Combust. Sci. Technol. 2024, 1–38. [Google Scholar] [CrossRef]
- Acharya, B.S.; Kharel, G. Acid mine drainage from coal mining in the United States—An overview. J. Hydrol. 2020, 588, 125061. [Google Scholar] [CrossRef]
- Agboola, O.; Babatunde, D.E.; Fayomi, O.S.I.; Sadiku, E.R.; Popoola, P.; Moropeng, L.; Yahaya, A.; Mamudu, O.A. A review on the impact of mining operation: Monitoring, assessment and management. Results Eng. 2020, 8, 100181. [Google Scholar] [CrossRef]
- Song, S.-l.; Liu, X.-s.; Tan, Y.-l.; Fan, D.-y.; Ma, Q.; Wang, H.-l. Study on Failure Modes and Energy Evolution of Coal-Rock Combination under Cyclic Loading. Shock. Vib. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Cheng, Z.-b.; Li, L.-h.; Zhang, Y.-n. Laboratory investigation of the mechanical properties of coal-rock combined body. Bull. Eng. Geol. Environ. 2019, 79, 1947–1958. [Google Scholar] [CrossRef]
- Du, X.-h.; Xue, J.-h.; Ma, Q.; Chen, Z.-h.; Zhan, K.-l. Energy Evolution Characteristics of Coal–Rock Composite Bodies Based on Unidirectional Load. Nat. Resour. Res. 2022, 31, 1647–1663. [Google Scholar] [CrossRef]
- Li, Z.-l.; He, X.-q.; Dou, L.-m.; Song, D.-z.; Wang, G.-f. Numerical investigation of load shedding and rockburst reduction effects of top-coal caving mining in thick coal seams. Int. J. Rock Mech. Min. Sci. 2018, 110, 266–278. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Luo, L. Structural Evolution and Motion Characteristics of a Hard Roof During Thickening Coal Seam Mining. Front. Earth Sci. 2022, 9, 527–546. [Google Scholar] [CrossRef]
- He, W.; He, F.; Zhao, Y. Field and simulation study of the rational coal pillar width in extra -thick coal seams. Energy Sci. Eng. 2020, 8, 627–646. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, R.; Gao, M.-Z.; Li, G.; Zhang, Z.-T.; Liu, Q.-Y. Numerical approach to the top coal caving process under different coal seam thicknesses. Therm. Sci. 2015, 19, 1423–1428. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, Y.; Ji, C.; Kang, T.; Guo, X. Effect of Mining Thickness on Overburden Movement and Underground Pressure Characteristics for Extrathick Coal Seam by Sublevel Caving with High Bottom Cutting Height. Adv. Civ. Eng. 2018, 18, 143–158. [Google Scholar] [CrossRef]
- Xiong, X.-y.; Dai, J.; Chen, X.-n.; Ouyang, Y.-b. Complex function solution for deformation and failure mechanism of inclined coal seam roadway. Sci. Rep. 2022, 12, 439–452. [Google Scholar] [CrossRef]
- Xiong, X.-y.; Dai, J.; Ouyang, Y.-b.; Shen, P. Experimental analysis of control technology and deformation failure mechanism of inclined coal seam roadway using non-contact DIC technique. Sci. Rep. 2021, 11, 539–563. [Google Scholar] [CrossRef]
- Tao, Z.; Zhu, C.; Zheng, X.; Wang, D.; Liu, Y.; He, M.; Wang, Y. Failure mechanisms of soft rock roadways in steeply inclined layered rock formations. Geomat. Nat. Hazards Risk 2018, 9, 1186–1206. [Google Scholar] [CrossRef]
- Cheng, G.Q.; Yan, M.J.; Zhu, H.L.; Yu, H.-f. Study of Asymmetric Failure Law and Support for Large Embedded Depth Roadway Driving along the Roof in Inclined Coal Seam. In Proceedings of the Mining 2014: Taishan Academic Forum—Project on Mine Disaster Prevention and Control, Qingdao, China, 17–20 October 2014; Volume 27, pp. 195–202. [Google Scholar]
- Fu, Y.; Wang, H.; Wang, X. Similarity theory and scaling laws for low-temperature plasma discharges: A comprehensive review. Rev. Mod. Plasma Phys. 2023, 7, 10. [Google Scholar] [CrossRef]
- Irzik, G.; Nola, R. Revisiting the foundations of the family resemblance approach to nature of science: Some new ideas. Sci. Educ. 2023, 32, 1227–1245. [Google Scholar] [CrossRef]
- Martynenko, S.I.; Varaksin, A.Y. A Physical Insight into Computational Fluid Dynamics and Heat Transfer. Mathematics 2024, 12, 2122. [Google Scholar] [CrossRef]
- Zhu, H.; Qu, Z.; Wang, Q.; Zhang, J. Dimension unification and dominance evaluation of multi-physical parameters for nanochannel-based ionic thermoelectric energy conversion using similarity principle. Energy Convers. Manag. 2023, 276, 116589. [Google Scholar] [CrossRef]
- Ni, M.; Zhao, X.; Wang, W.; Zhang, Q.; Wang, H.; Wang, J. Research on Resistance Characteristics of Fire Zone of Mine Tunnel Fire and Construction of Calculation Model. Fire 2024, 7, 197. [Google Scholar] [CrossRef]
- Fan, C.; Xu, L.; Elsworth, D.; Luo, M.; Liu, T.; Li, S.; Zhou, L.; Su, W. Spatial–temporal evolution and countermeasures for coal and gas outbursts represented as a dynamic system. Rock Mech. Rock Eng. 2023, 56, 6855–6877. [Google Scholar] [CrossRef]
- Zhao, P.; Zhuo, R.; Li, S.; Lin, H.; Shu, C.-M.; Shuang, H.; Wei, Z. Greenhouse gas protection and control based upon the evolution of overburden fractures under coal mining: A review of methods, influencing factors, and techniques. Energy 2023, 284, 129158. [Google Scholar] [CrossRef]
- Shan, C.; Sun, J.; Jia, X.; Wu, R.; Lu, X. The mechanical behavior of cylindrical shell with composite corrugations under uniform and concentrated pressure. Ocean. Eng. 2024, 298, 117148. [Google Scholar] [CrossRef]
- Cappellesso, V.; Van Mullem, T.; Gruyaert, E.; Van Tittelboom, K.; De Belie, N. Enhancing concrete durability in chloride-rich environments through manual application of healing agents. J. Build. Eng. 2024, 90, 109380. [Google Scholar] [CrossRef]
- Condé-Wolter, J.; Ruf, M.G.; Liebsch, A.; Lebelt, T.; Koch, I.; Drechsler, K.; Gude, M. Hydrogen permeability of thermoplastic composites and liner systems for future mobility applications. Compos. Part A Appl. Sci. Manuf. 2023, 167, 107446. [Google Scholar] [CrossRef]
- Kang, H.; Gao, F.; Xu, G.; Ren, H. Mechanical behaviors of coal measures and ground control technologies for China’s deep coal mines—A review. J. Rock Mech. Geotech. Eng. 2023, 15, 37–65. [Google Scholar] [CrossRef]
- Fan, J.; Yuan, Q.; Chen, J.; Ren, Y.; Zhang, D.; Yao, H.; Hu, B.; Qu, Y. Investigation of surrounding rock stability during proximal coal seams mining process and feasibility of ground control technology. Process Saf. Environ. Prot. 2024, 186, 1447–1459. [Google Scholar] [CrossRef]
- Liu, J.; Shen, W.; Bai, J.; Shan, C.; Liu, X. Experiment on separated layer rock failure technology for stress reduction of entry under coal pillar in mining conditions. Front. Ecol. Evol. 2023, 11, 1265883. [Google Scholar] [CrossRef]
- Zhang, R.; Gomaa, S.M.M.H.; Hussein, M.; Zayed, T.; Meguid, M. Review of numerical approaches used in soil-pipe interaction analysis of water mains. Transp. Geotech. 2023, 42, 101008. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Hou, S. Evaluation of rockburst risk in deep tunnels considering structural planes based on energy dissipation rate criterion and numerical simulation. Tunn. Undergr. Space Technol. 2023, 137, 105128. [Google Scholar] [CrossRef]
- Zhang, W.; Han, D.; Wang, B.; Chen, Y.; Jiao, K.; Gong, L.; Yu, B. Thermal-hydraulic-mechanical-chemical modeling and simulation of an enhanced geothermal system based on the framework of extended finite element methods-Embedded discrete fracture model. J. Clean. Prod. 2023, 415, 137630. [Google Scholar] [CrossRef]
- Shi, H.; Chen, W.; Zhang, H.; Song, L. A novel obtaining method and mesoscopic mechanism of pseudo-shear strength parameter evolution of sandstone. Environ. Earth Sci. 2023, 82, 60. [Google Scholar] [CrossRef]
- Yao, N.; Deng, X.; Luo, B.; Oppong, F.; Li, P. Strength and failure mode of expansive slurry-inclined layered rock mass composite based on Mohr–Coulomb criterion. Rock Mech. Rock Eng. 2023, 56, 3679–3692. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Zhang, S.; Feng, L.; Qiu, L. Experimental study on compression characteristics of fractured soft rock and its Mohr-Coulomb criterion. Theor. Appl. Fract. Mech. 2023, 125, 103820. [Google Scholar] [CrossRef]
- Zhao, Y.; Mishra, B.; Shi, Q.; Zhao, G. Size-dependent Mohr–Coulomb failure criterion. Bull. Eng. Geol. Environ. 2023, 82, 218. [Google Scholar] [CrossRef]
- Zahtila, T.; Lu, W.; Chan, L.; Ooi, A. A systematic study of the grid requirements for a spectral element method solver. Comput. Fluids 2023, 251, 105745. [Google Scholar] [CrossRef]
- Weiss, M.; Kalscheuer, T.; Ren, Z. Spectral element method for 3-D controlled-source electromagnetic forward modelling using unstructured hexahedral meshes. Geophys. J. Int. 2023, 232, 1427–1454. [Google Scholar] [CrossRef]



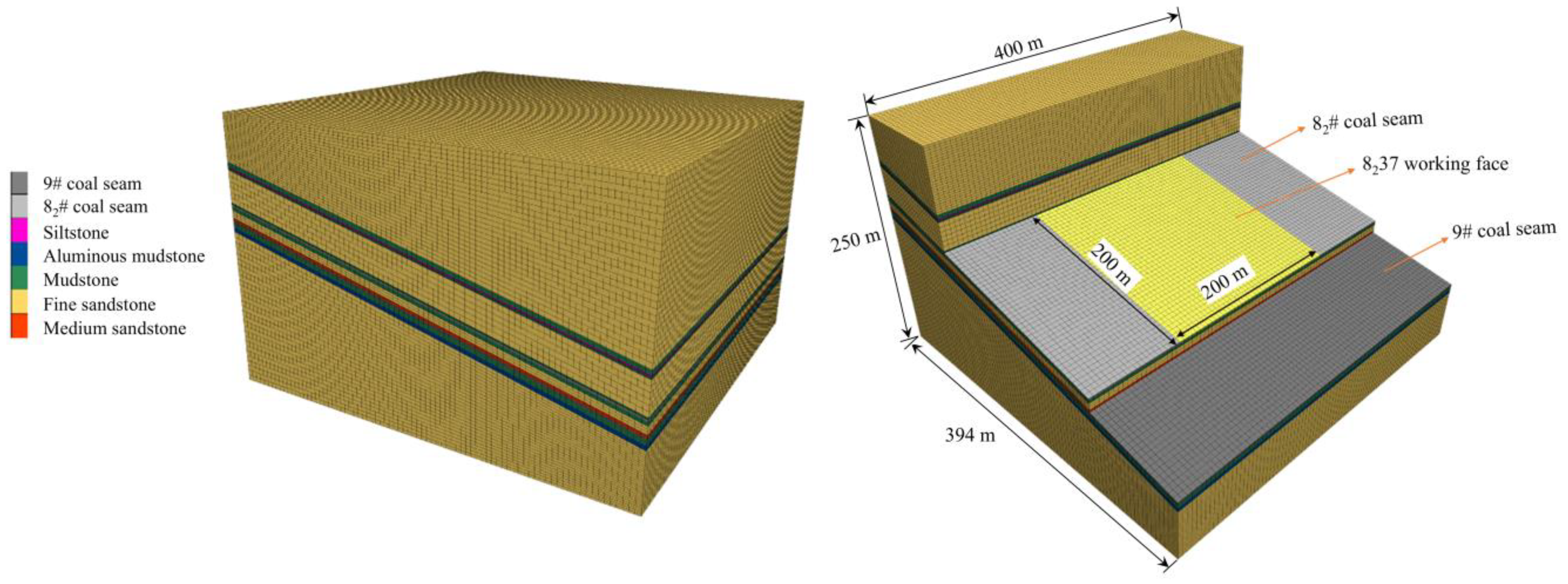


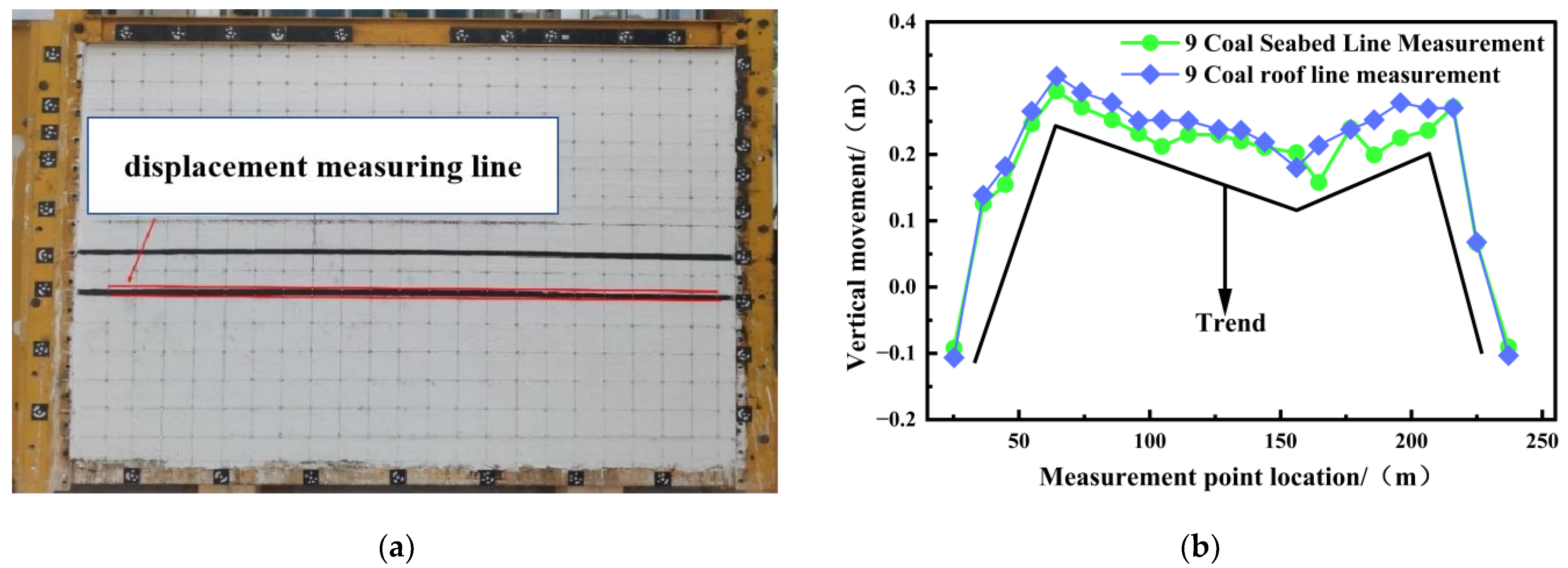
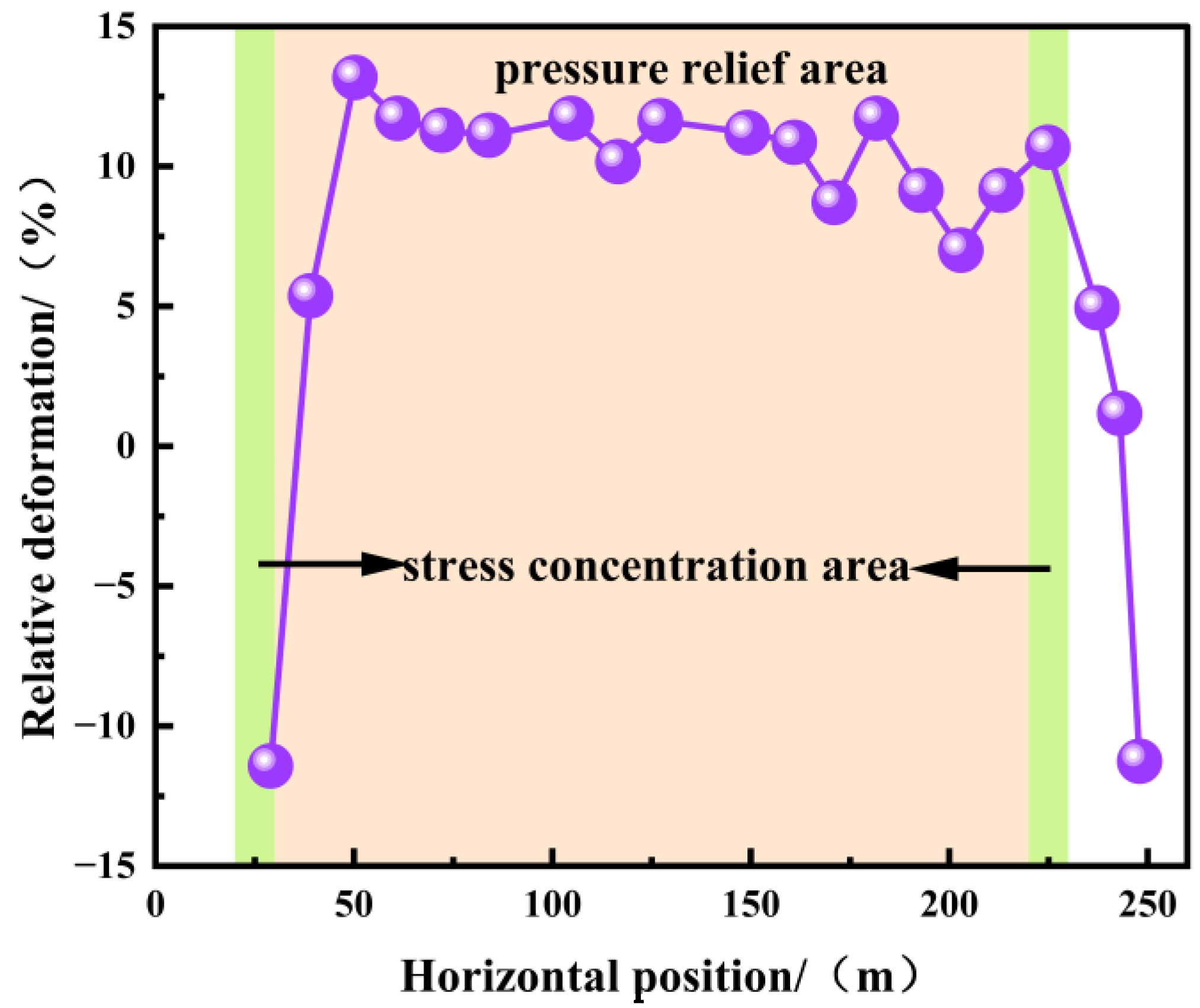
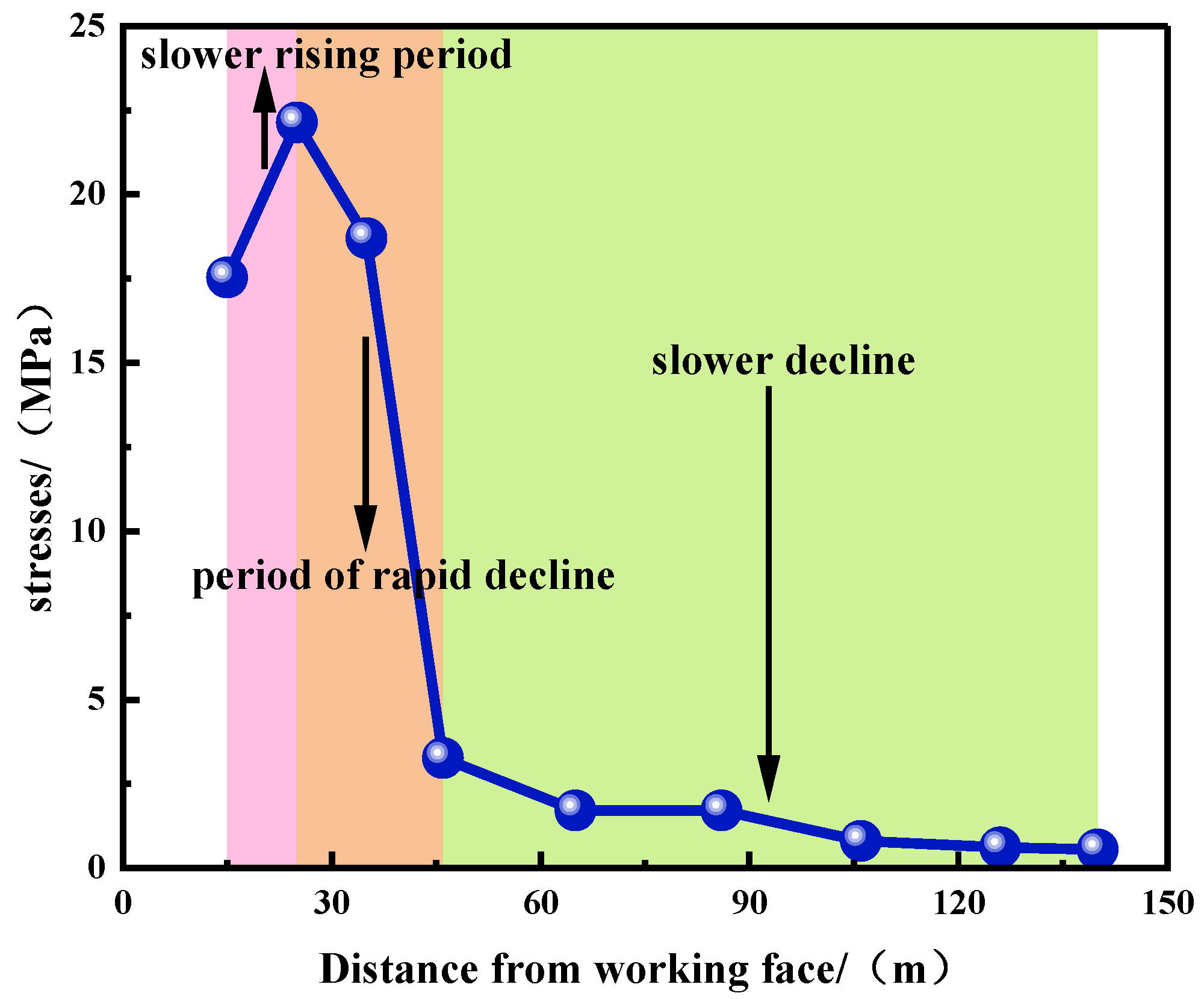


| Lithology | Thickness/cm | Total Weight/kg | Accumulated Thickness/cm | Ration Number | Sand/kg | Calcium Carbonate/kg | Gypsum/kg | Water/kg |
|---|---|---|---|---|---|---|---|---|
| Mudstone | 10.0 | 150 | 149.0 | 473 | 90.00 | 15.75 | 6.75 | 16.7 |
| Fine sandstone | 23.0 | 345 | 139.0 | 437 | 207.00 | 15.53 | 36.23 | 38.3 |
| Mudstone | 4.0 | 60 | 116.0 | 473 | 36.00 | 6.30 | 2.70 | 6.7 |
| 7# coal seam | 3.7 | 55.5 | 112.0 | 773 | 36.38 | 3.60 | 1.58 | 6.2 |
| Mudstone | 2.0 | 30 | 108.3 | 473 | 18.00 | 3.15 | 1.35 | 3.3 |
| Fine sandstone | 29.0 | 435 | 106.3 | 437 | 261.00 | 19.58 | 45.68 | 48.3 |
| Mudstone | 2.0 | 30 | 77.3 | 473 | 18.00 | 3.15 | 1.35 | 3.3 |
| 82# coal seam | 1.8 | 27 | 75.3 | 773 | 17.70 | 1.80 | 0.75 | 3.0 |
| Mudstone | 3.0 | 45 | 73.5 | 473 | 27.00 | 4.73 | 2.03 | 5.0 |
| Fine sandstone | 7.5 | 112.5 | 70.5 | 437 | 67.50 | 5.06 | 11.81 | 12.5 |
| Medium sandstone | 2.0 | 30 | 63.0 | 437 | 18.00 | 1.35 | 3.15 | 3.3 |
| 9# coal seam | 2.0 | 30 | 61.0 | 773 | 19.73 | 1.95 | 0.83 | 3.3 |
| Mudstone | 4.0 | 60 | 59.0 | 473 | 36.00 | 6.30 | 2.70 | 6.7 |
| Fine sandstone | 18.0 | 270 | 55.0 | 437 | 162.00 | 12.15 | 28.35 | 30.0 |
| Medium sandstone | 3.0 | 45 | 37.0 | 437 | 27.00 | 2.03 | 4.73 | 5.0 |
| Mudstone | 8.0 | 120 | 34.0 | 473 | 72.00 | 12.60 | 5.40 | 13.3 |
| Fine sandstone | 26.0 | 390 | 26.0 | 437 | 234.00 | 17.55 | 40.95 | 43.3 |
| Lithology | Density (kg/m3) | Volume Modulus (GPa) | Shear Modulus (GPa) | Cohesion (MPa) | Internal Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| Fine sandstone | 2500 | 16.7 | 17 | 6.8 | 40 | 3.8 |
| Medium sandstone | 2560 | 17 | 14 | 5.1 | 39 | 3.6 |
| Siltstone | 2500 | 8.3 | 6.25 | 3.5 | 37 | 1.5 |
| 82# coal seam | 1400 | 4.91 | 2.01 | 1.25 | 32 | 0.15 |
| 9# coal seam | 1400 | 4.91 | 2.01 | 1.25 | 32 | 0.15 |
| Mudstone | 2430 | 9.5 | 6.6 | 0.85 | 36 | 1.6 |
| Aluminum mudstone | 2483 | 9.97 | 7.35 | 1.2 | 32 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Man, Z.; Li, M. Study on the Dynamic Evolution of Mining-Induced Stress and Displacement in the Floor Coal-Rock Induced by Protective Layer Mining. Minerals 2024, 14, 1084. https://doi.org/10.3390/min14111084
Liu C, Man Z, Li M. Study on the Dynamic Evolution of Mining-Induced Stress and Displacement in the Floor Coal-Rock Induced by Protective Layer Mining. Minerals. 2024; 14(11):1084. https://doi.org/10.3390/min14111084
Chicago/Turabian StyleLiu, Chun, Zhongyi Man, and Maolin Li. 2024. "Study on the Dynamic Evolution of Mining-Induced Stress and Displacement in the Floor Coal-Rock Induced by Protective Layer Mining" Minerals 14, no. 11: 1084. https://doi.org/10.3390/min14111084
APA StyleLiu, C., Man, Z., & Li, M. (2024). Study on the Dynamic Evolution of Mining-Induced Stress and Displacement in the Floor Coal-Rock Induced by Protective Layer Mining. Minerals, 14(11), 1084. https://doi.org/10.3390/min14111084






