Parameterization of Multi-Angle Shaker Based on PSO-BP Neural Network
Abstract
1. Introduction
2. Establishment of Vibrating Screen Model and Evaluation of Screen Performance
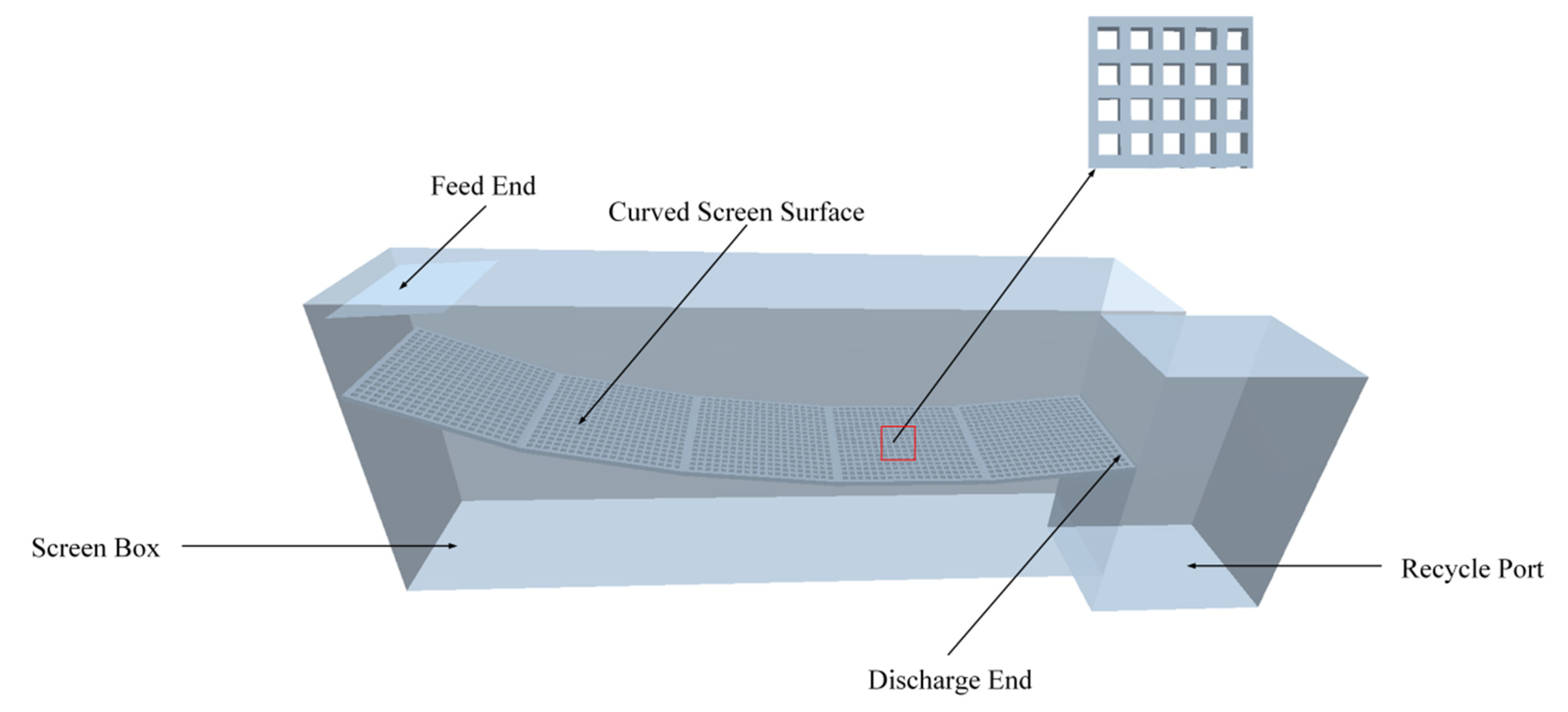
2.1. EDEM Model Machine and Simulation Parameters
2.2. Screening Evaluation Criteria
3. Experimental Design and Simulation Analysis
3.1. Experimental Design
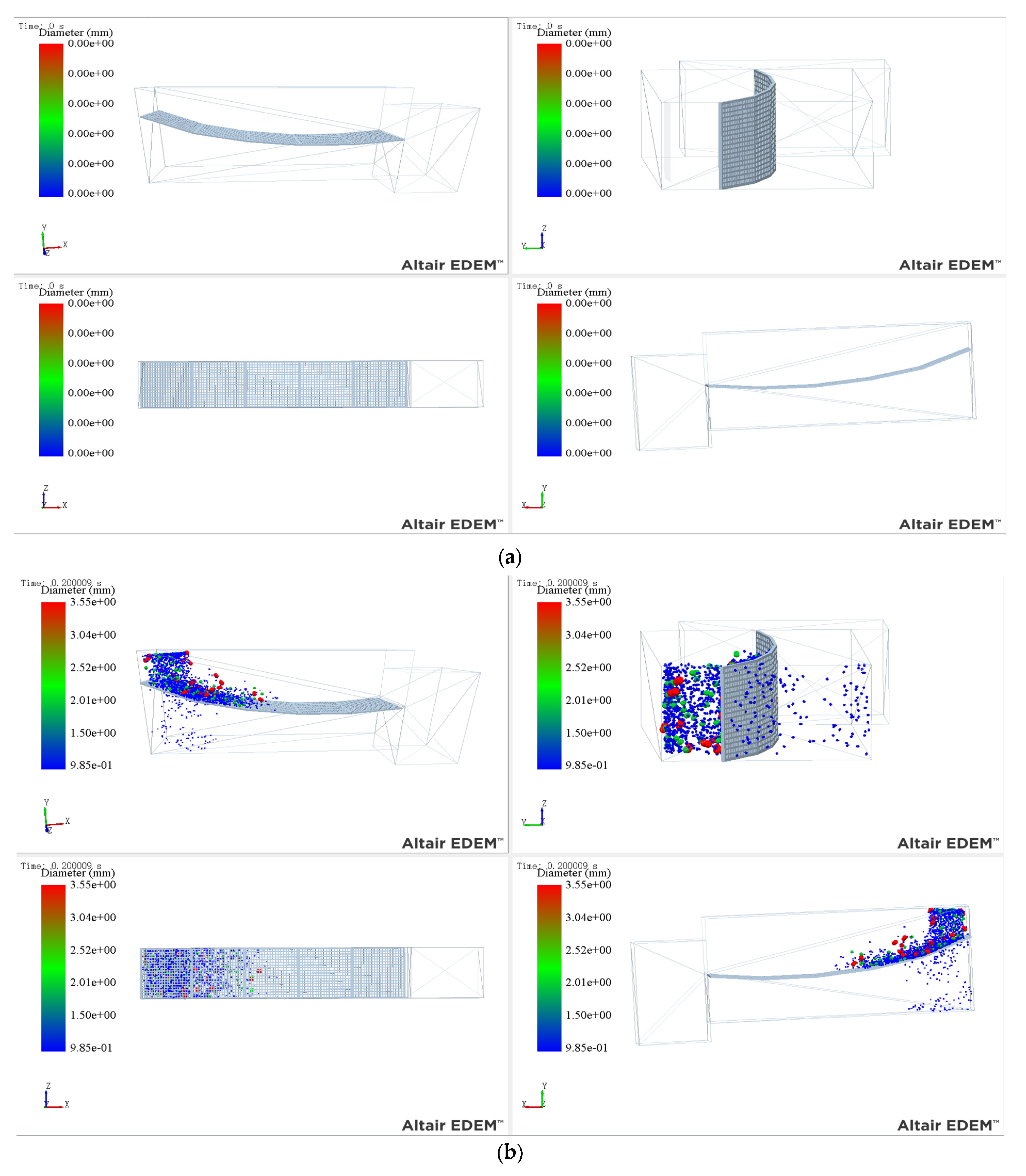
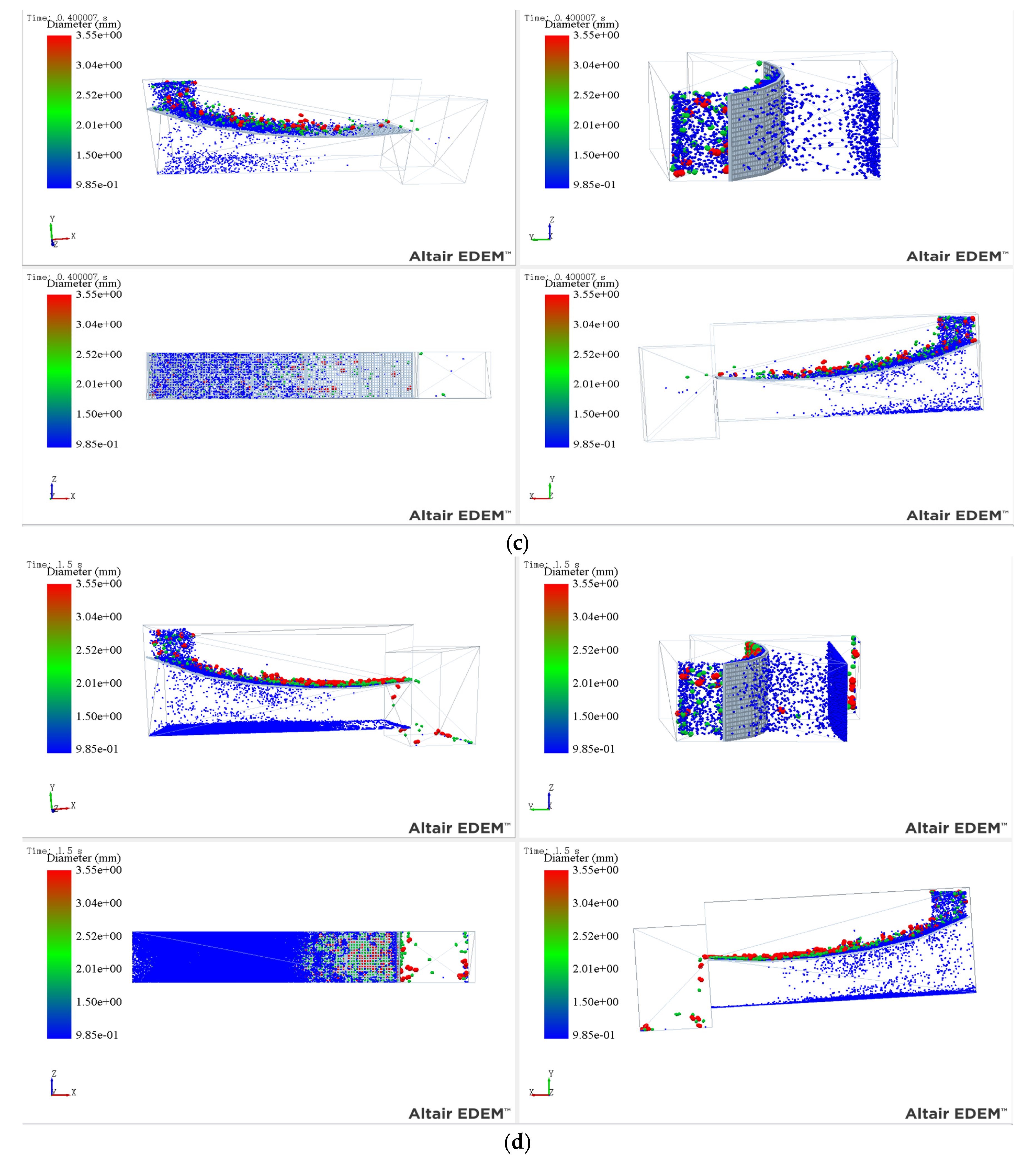
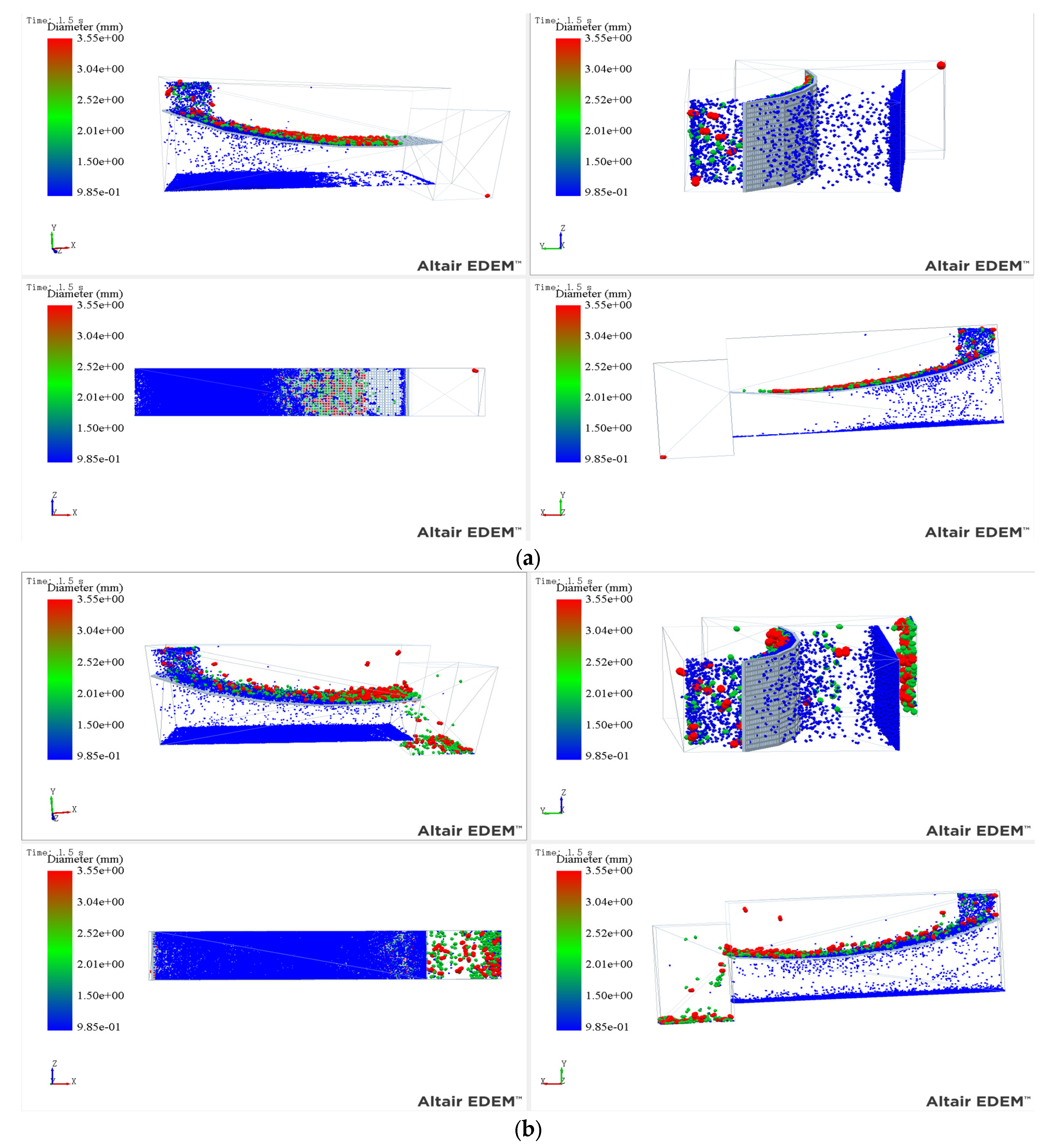
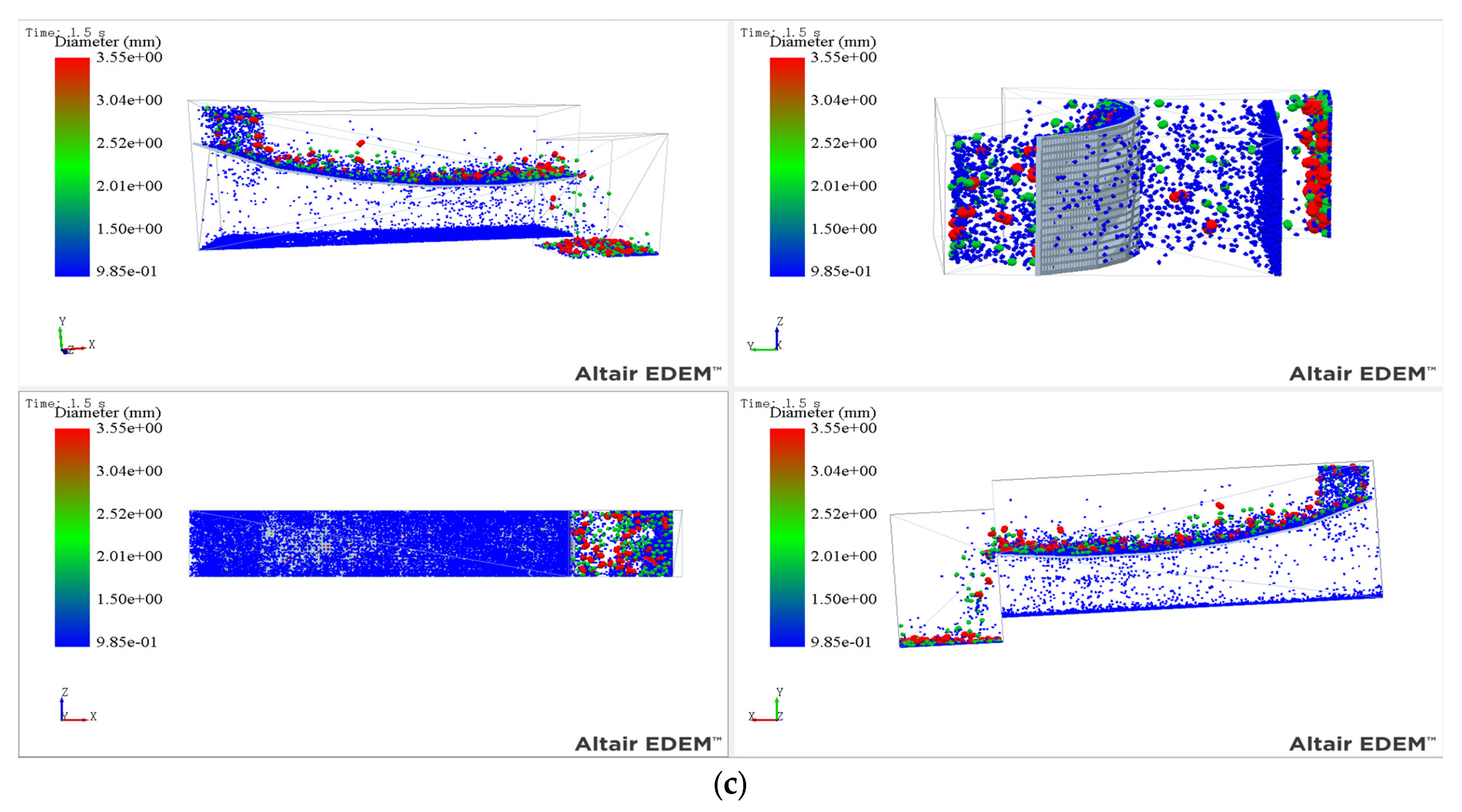
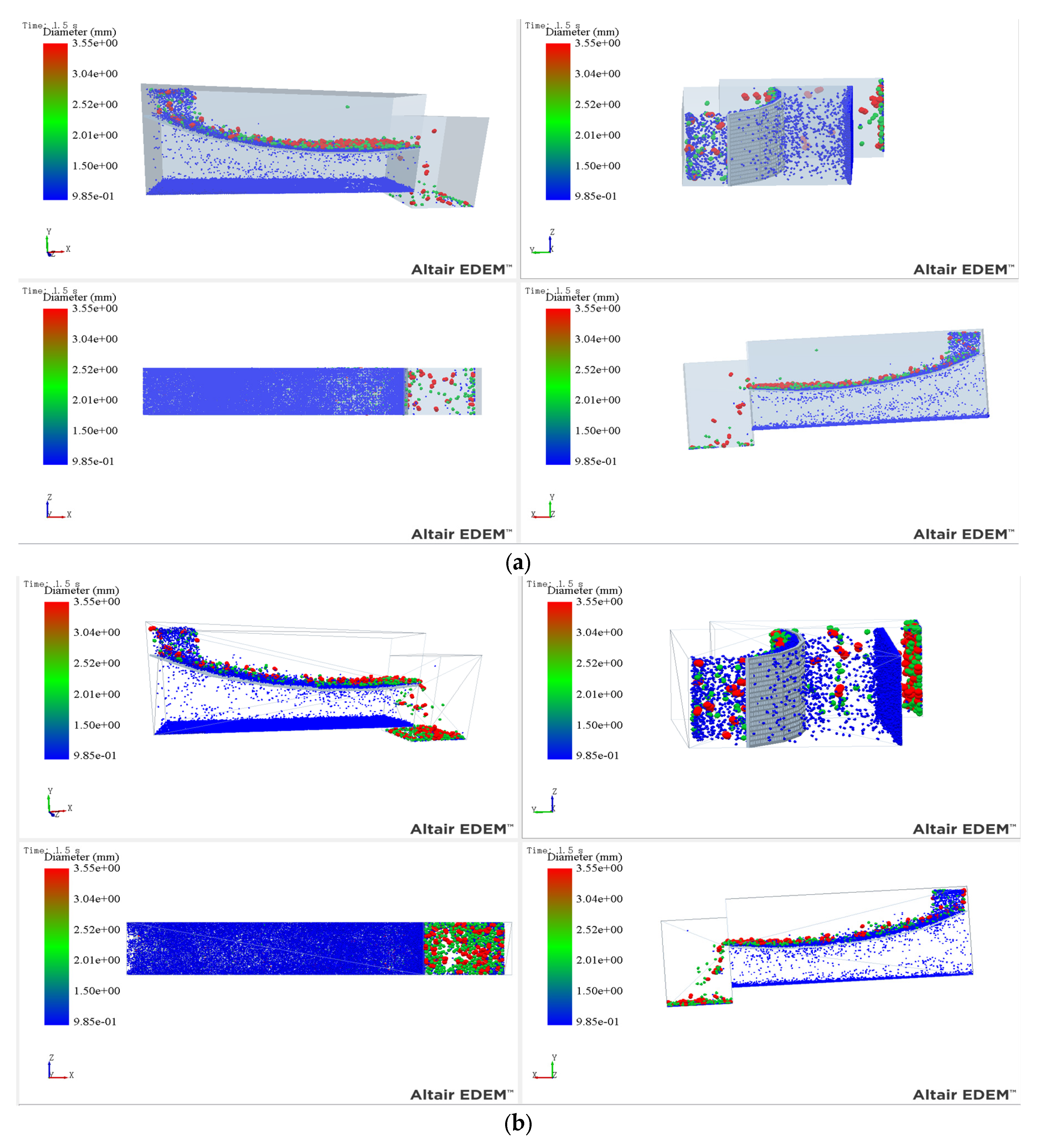
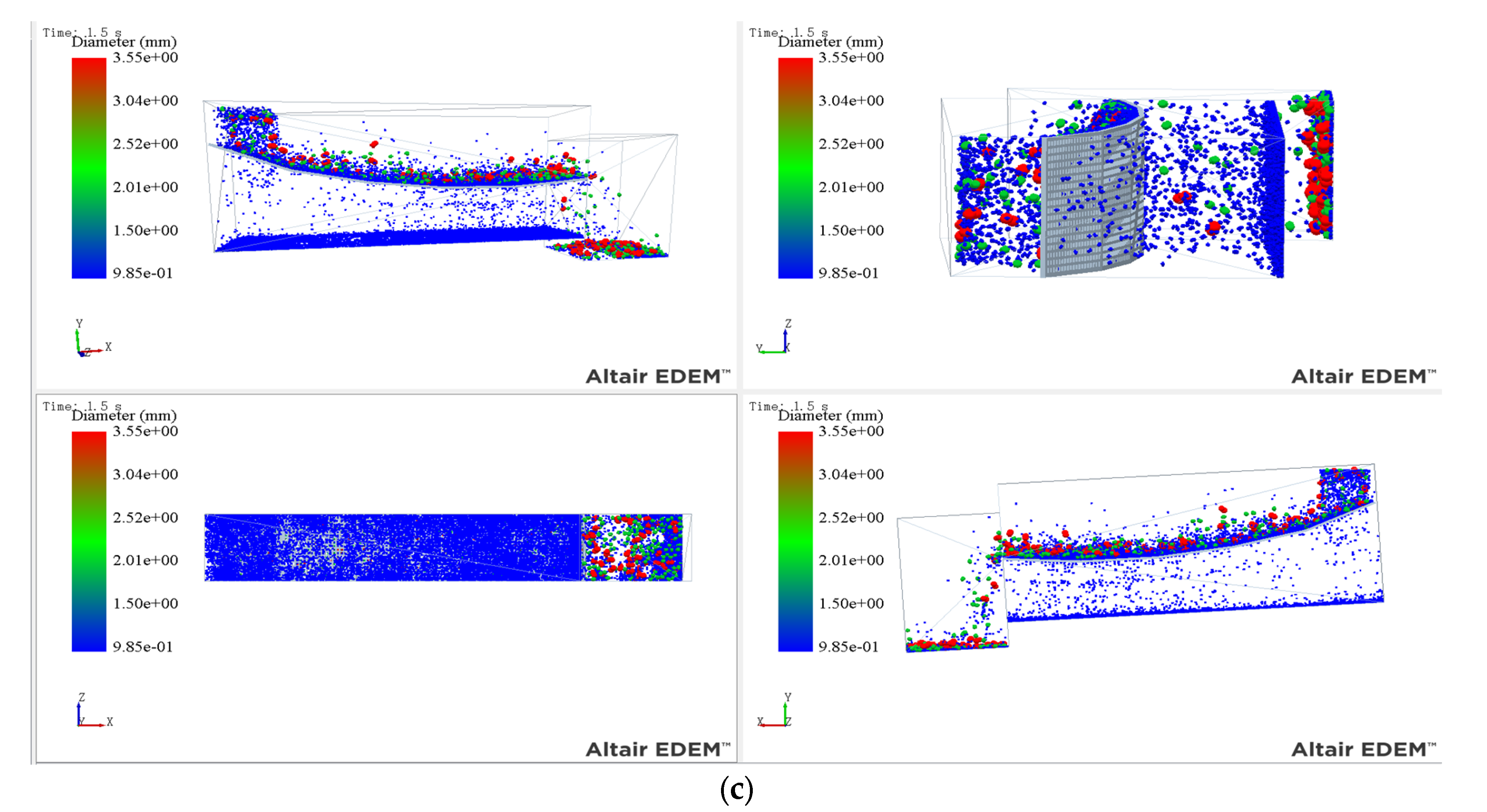
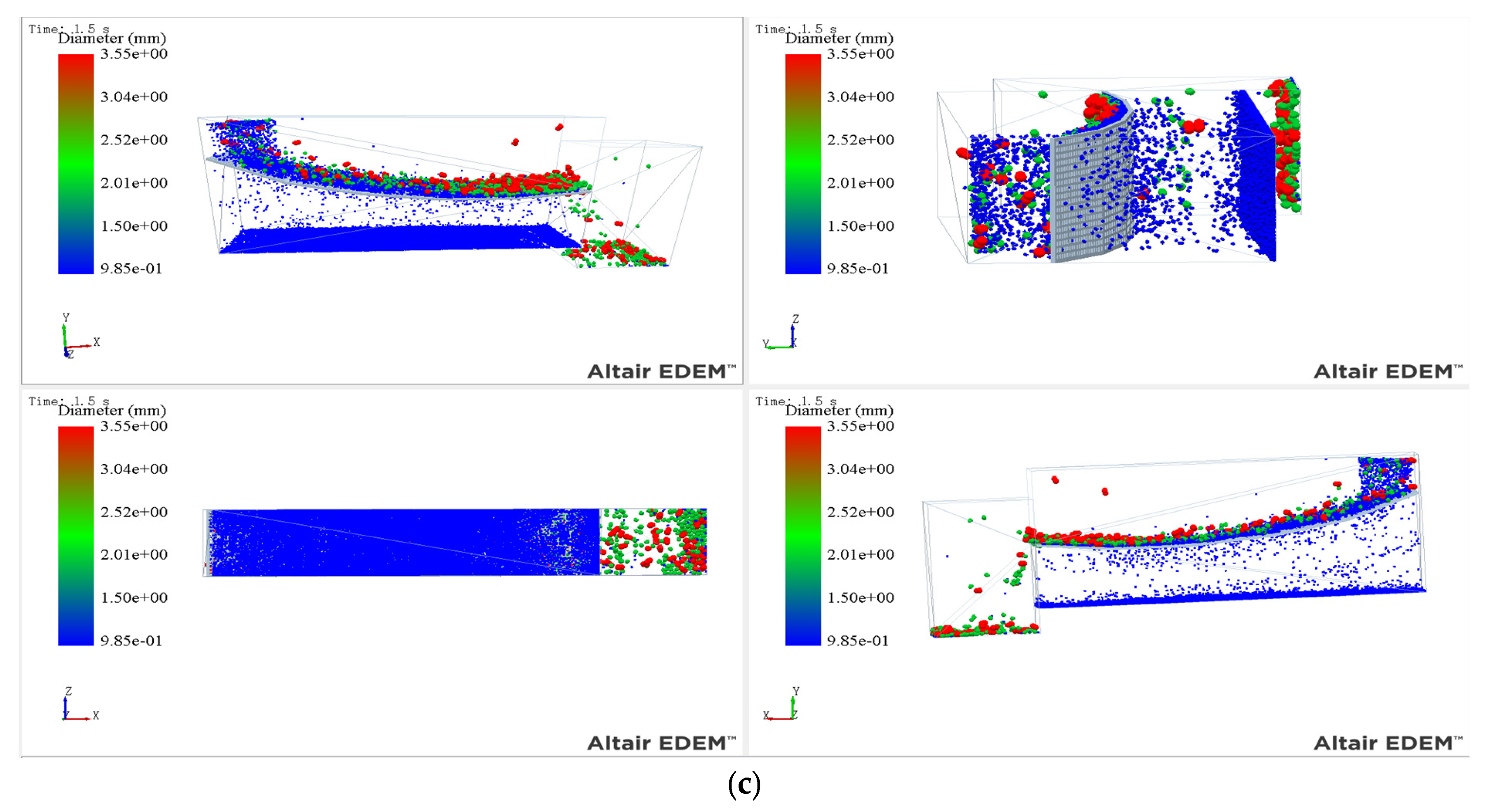
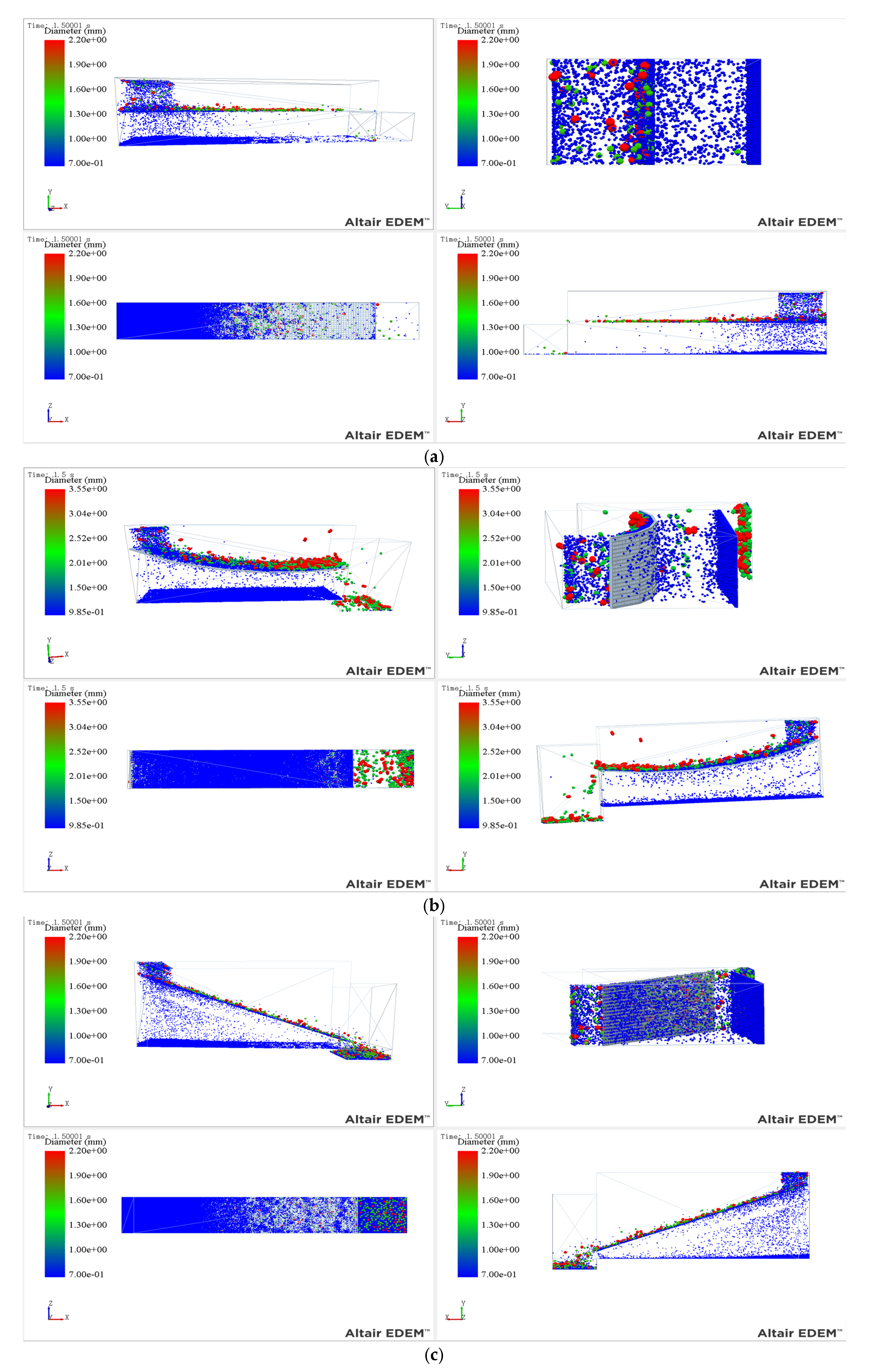
3.2. Analysis of Simulation Phenomena in Different Parameter Scenarios
4. BP Neural Network Model Establishment
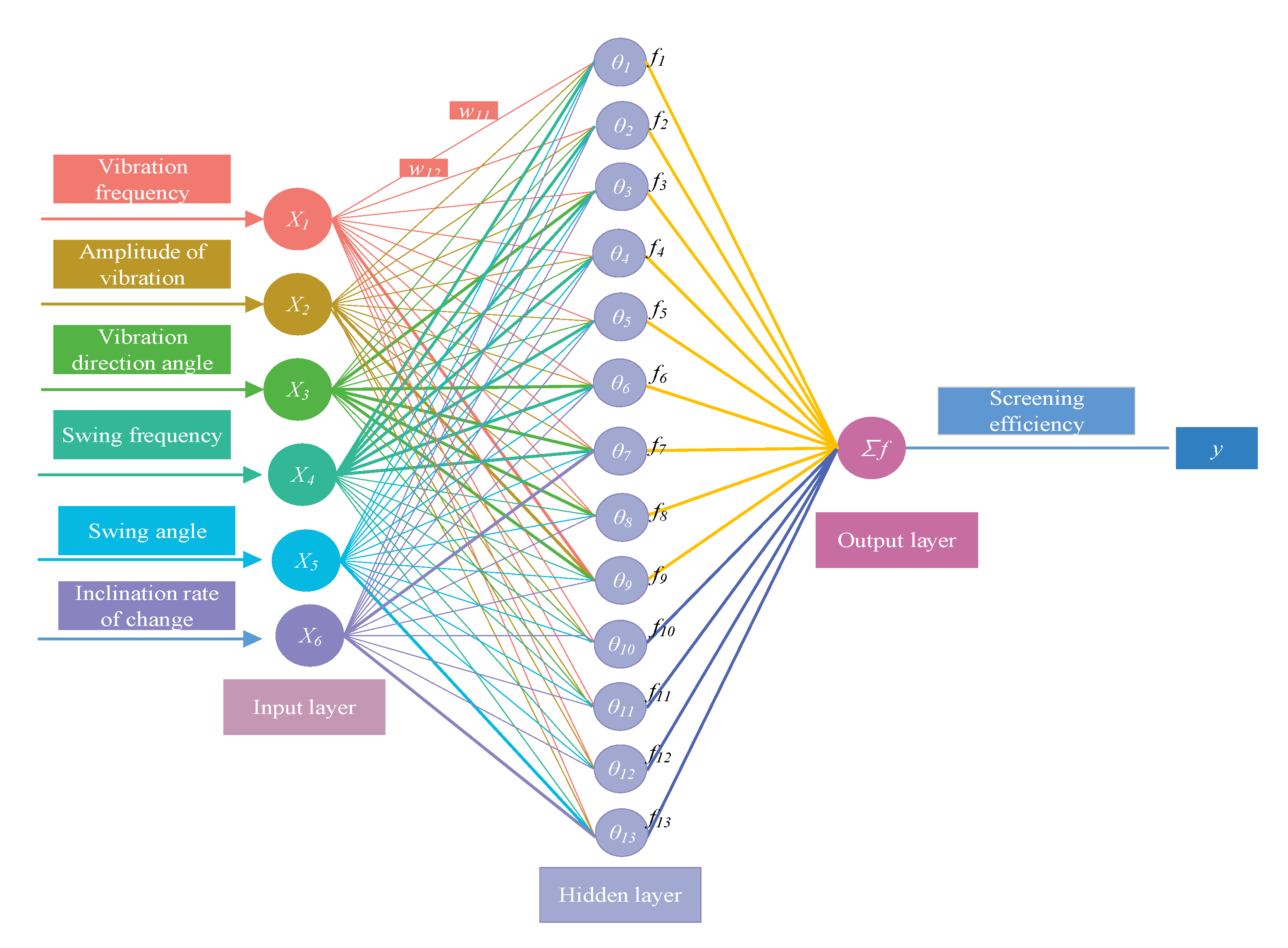
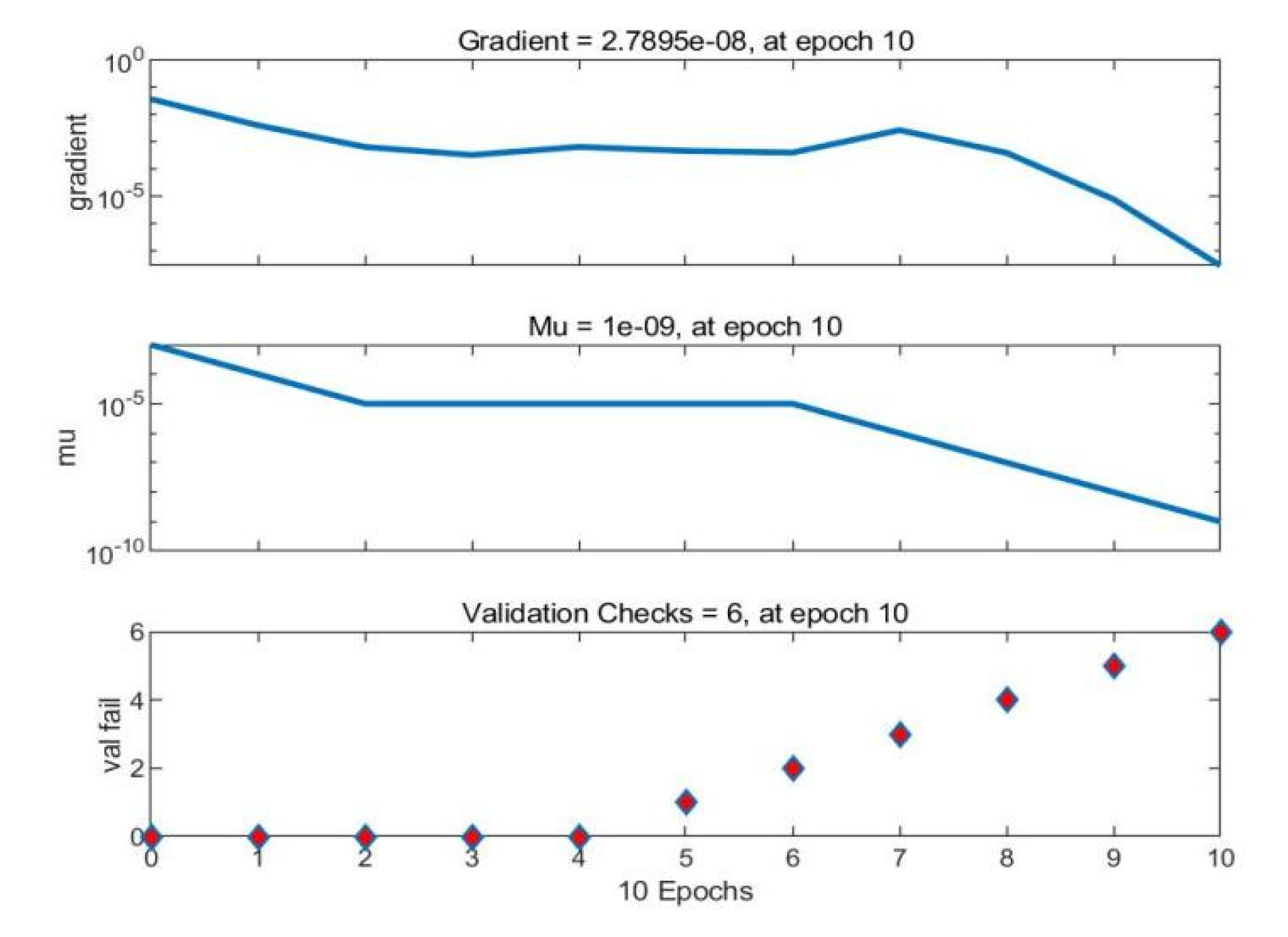
4.1. Backpropagation Neural Network (BPNN)
4.2. Integrated Learning and Prediction of Models
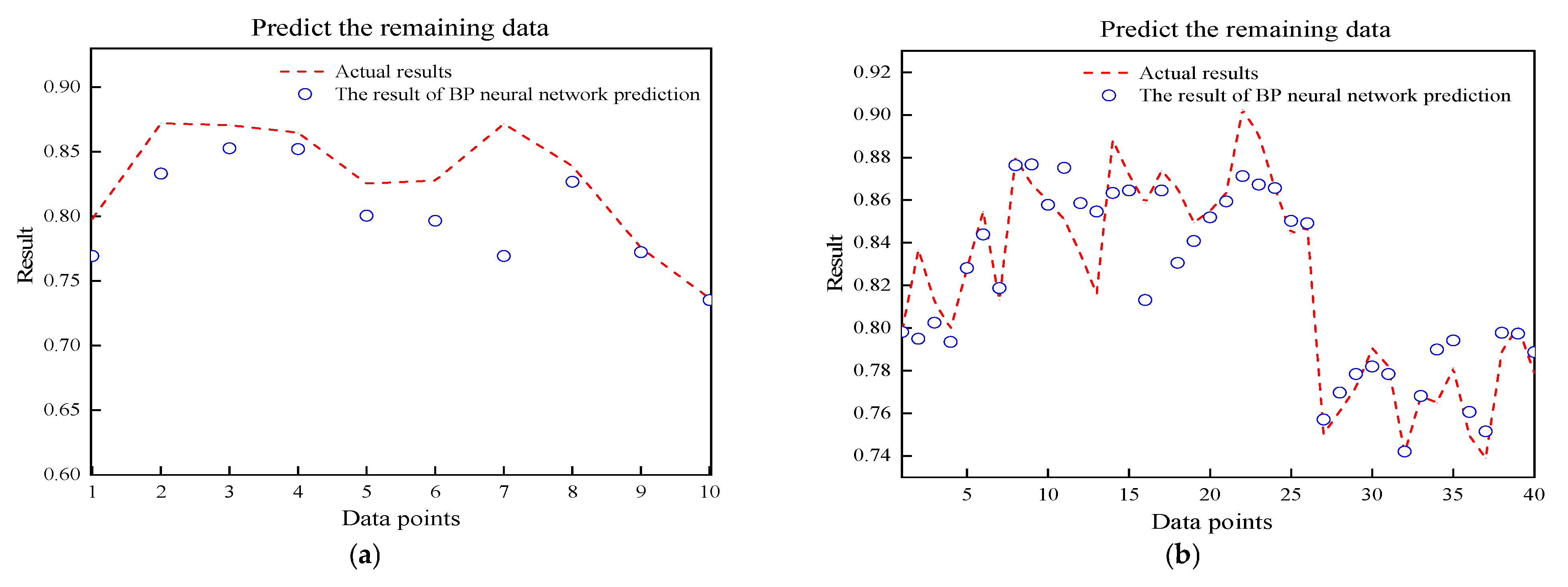
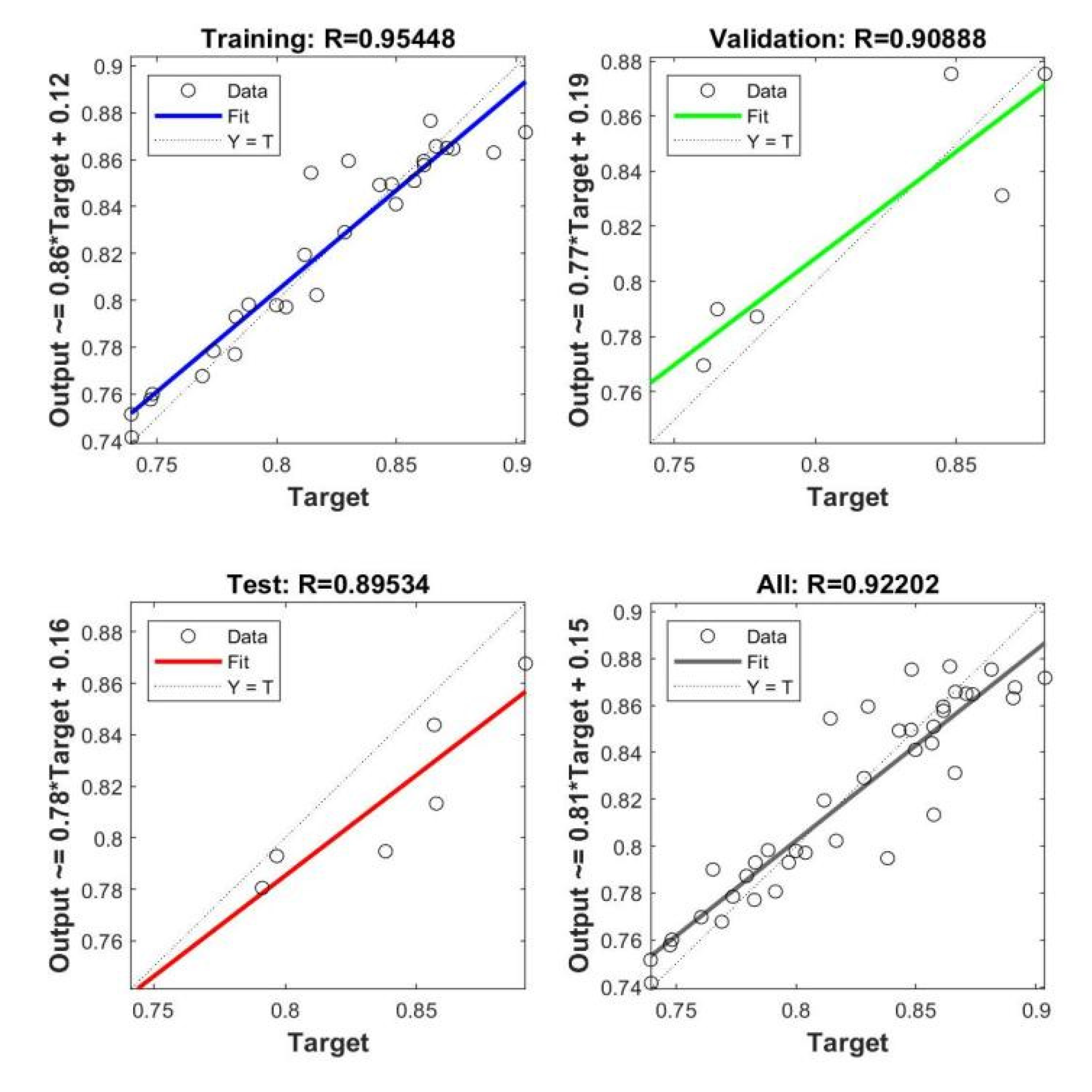
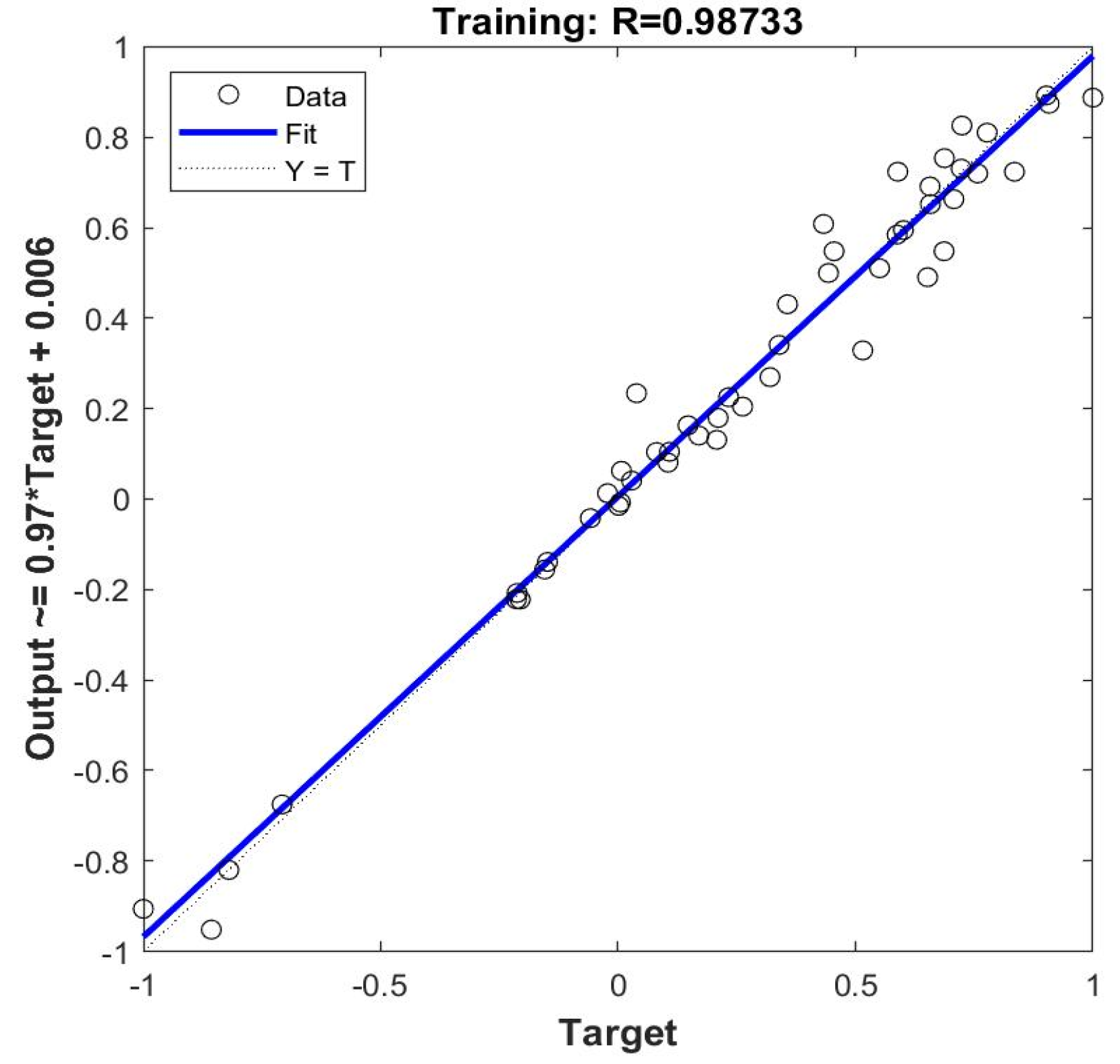
4.3. Analysis of Model Prediction Results
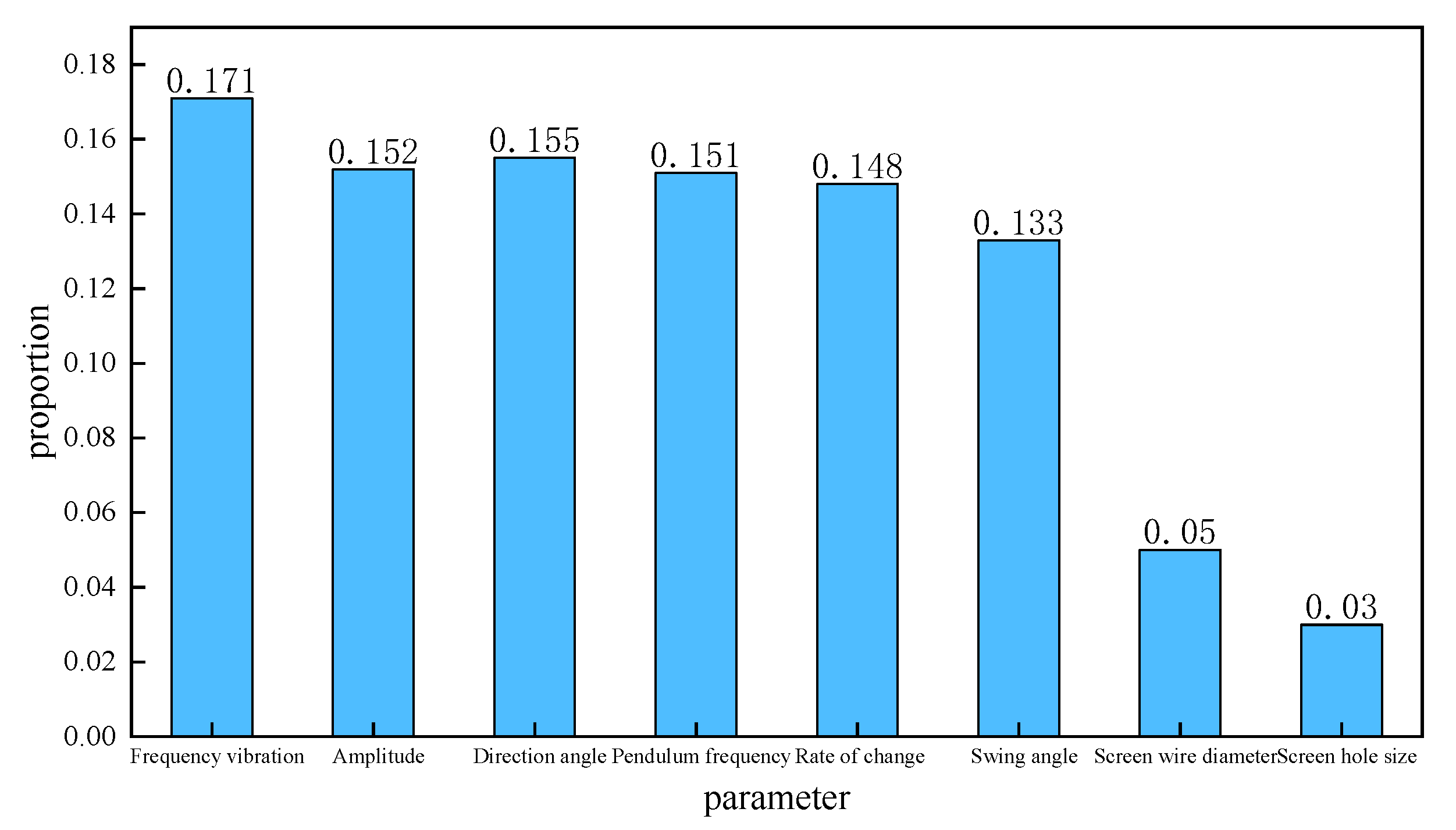
4.4. Analysis of Impact Weights
5. Optimization of BP Neural Network by PSO Algorithm
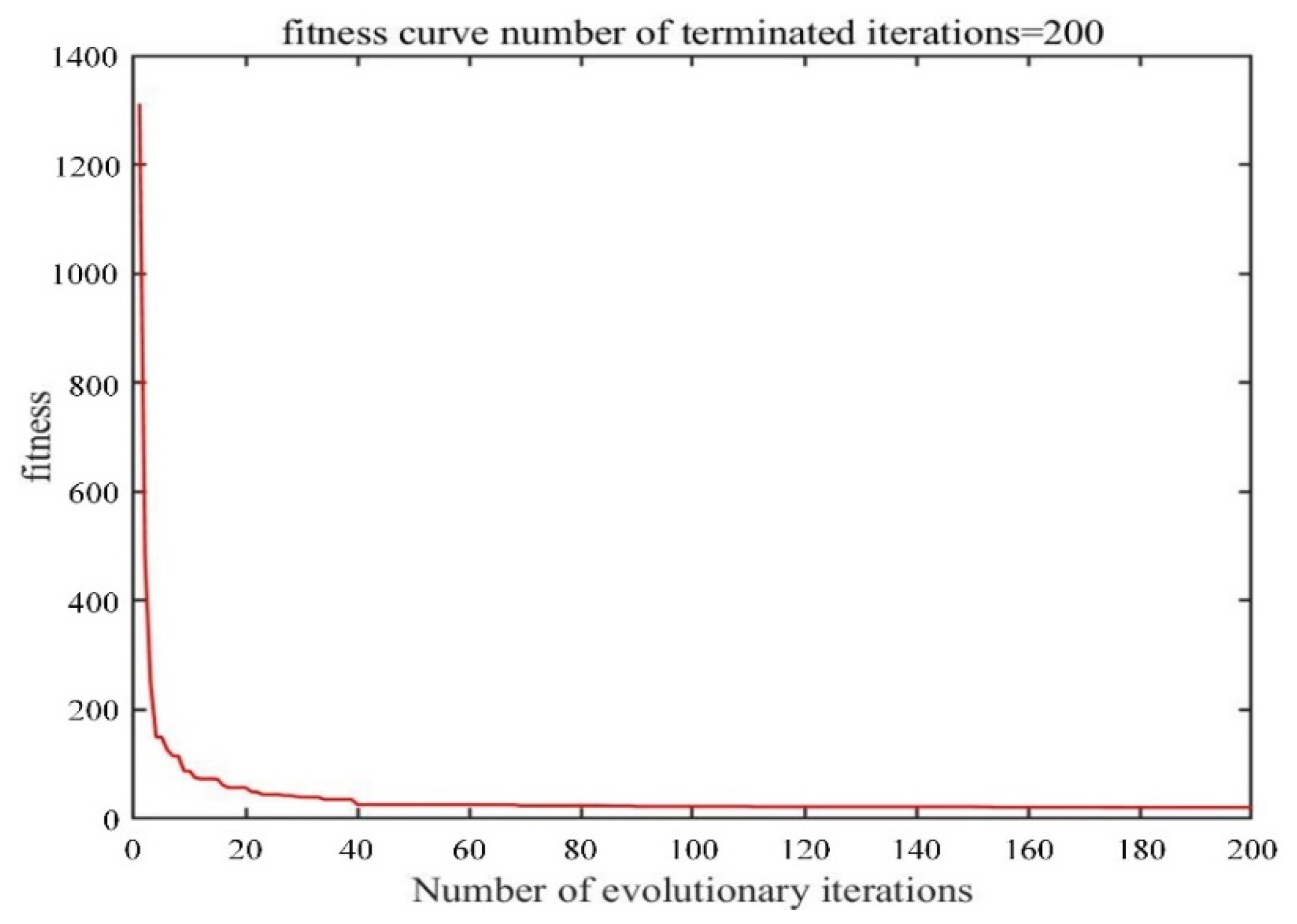
5.1. Particle Swarm Optimization
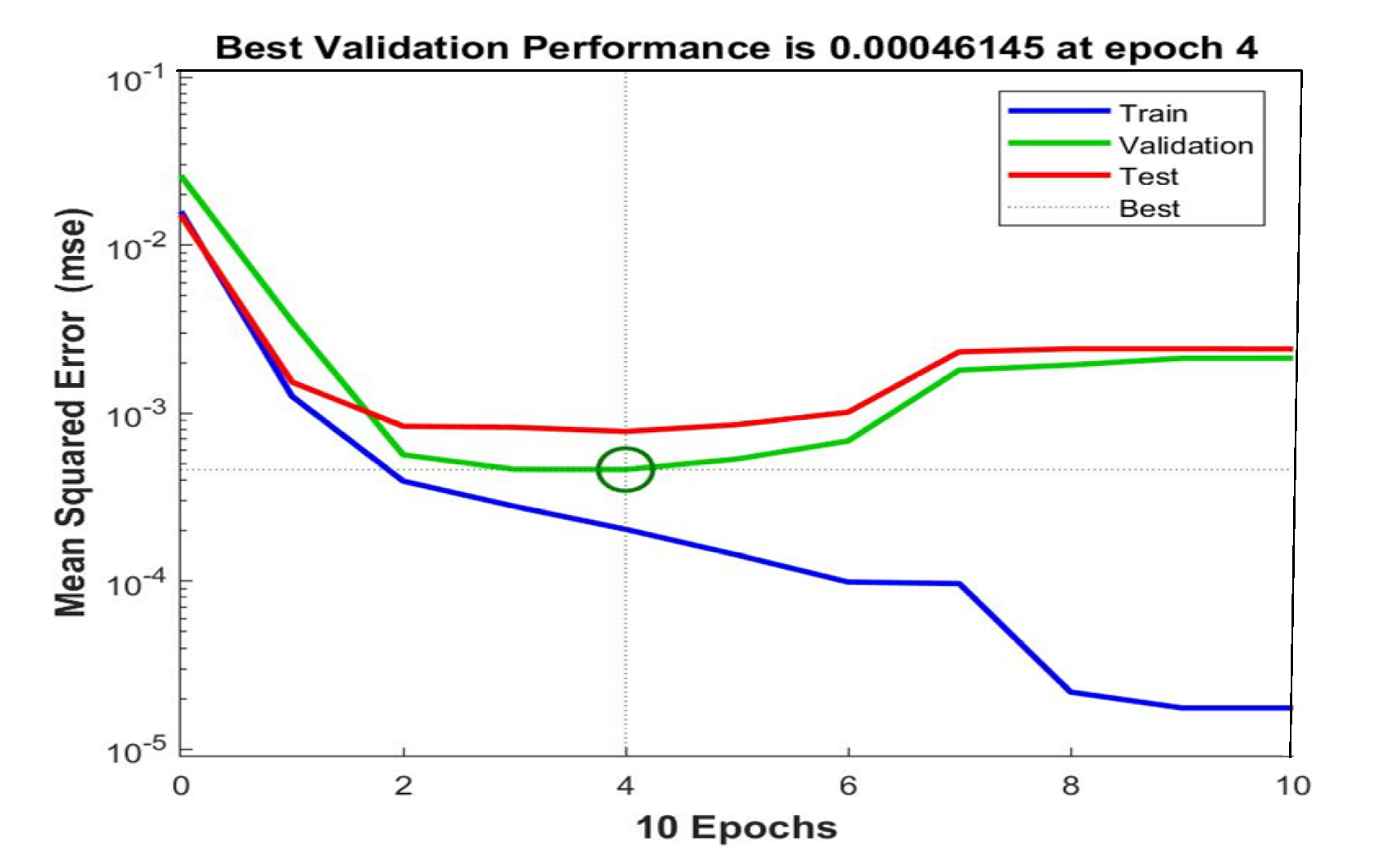
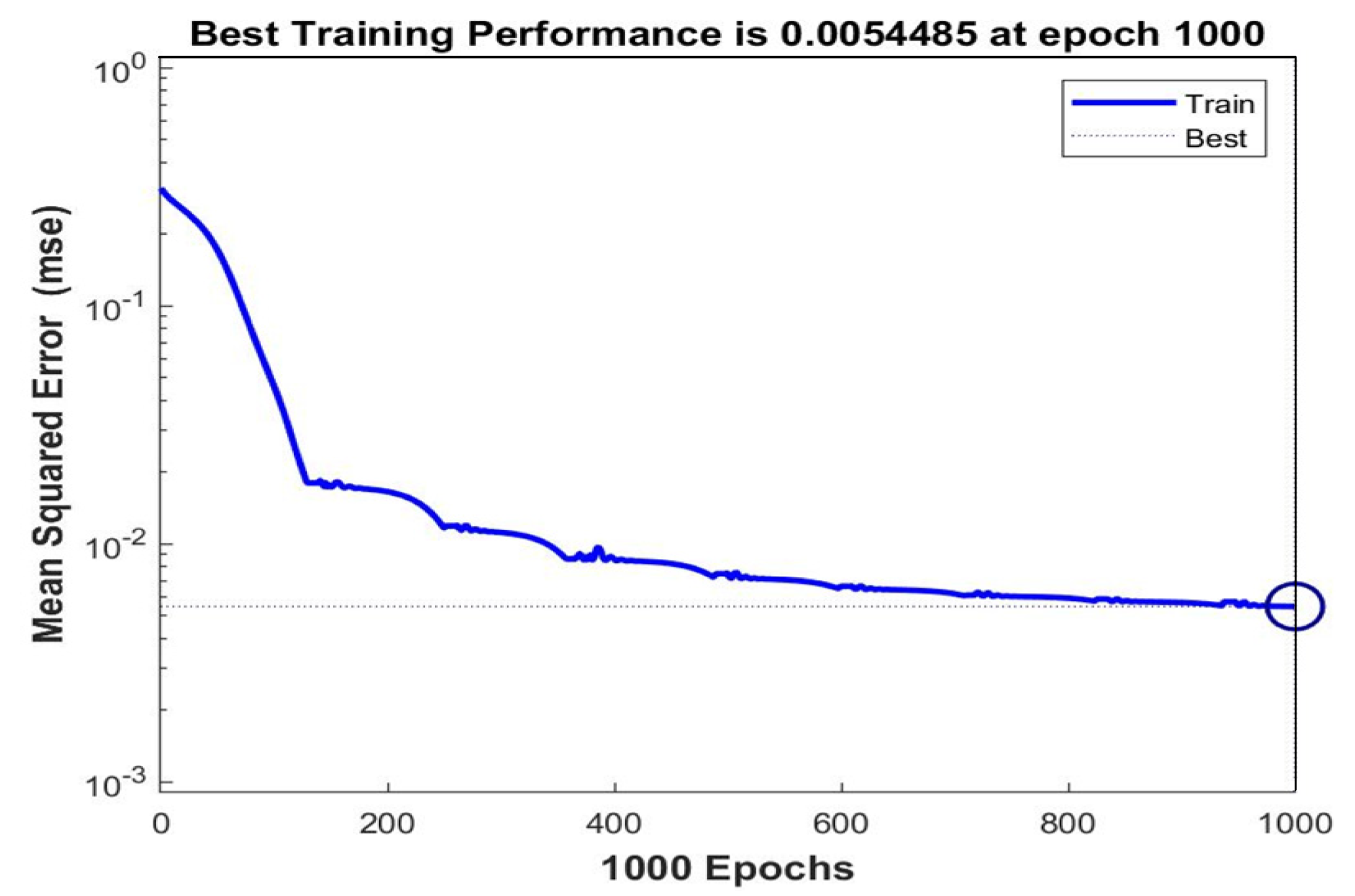
5.2. Model Performance Evaluation
5.3. Analysis of Prediction Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BP | Backpropagation |
| MAE | Mean Absolute Error |
| MARE | Mean Absolute Relative Error |
| MSRE | Mean Square Relative Error |
| PSO | Particle Swarm Optimization |
| PSO-BP | Particle Swarm Optimization-Backpropagation |
| RMSE | Root Mean Square Error |
References
- Shen, G.; Chen, Z.; Wu, X.; Li, Z.; Tong, X. Stepwise shape optimization of the surface of a vibrating screen. Particuology 2021, 58, 26–34. [Google Scholar] [CrossRef]
- Yu, C.; Lin, D.; Wang, X.; Pu, K.; Wang, Z.; Zhao, G.; Geng, R.; Gong, S. DEM simulation of particle flow and separation in a vibrating flip-flow screen. Particuology 2023, 73, 113–127. [Google Scholar] [CrossRef]
- Li, Y.; Fan, H.; Xu, Y.; Cui, T.; Su, Y.; Qiao, M.; Han, S.; Qian, J.; Zheng, Z. CFD-DEM investigation of particle dispersion degree on a novel vibrating screen. Powder Technol. 2022, 404, 117497. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Xia, H.; Tong, X. Performance optimization of the elliptically vibrating screen with a hybrid MACO-GBDT algorithm. Particuology 2021, 56, 193–206. [Google Scholar] [CrossRef]
- Wang, G.; Chen, S.; Hu, G.; Pang, D.; Wang, Z. Detection algorithm of abnormal flow state fluid on closed vibrating screen based on improved YOLOv5. Eng. Appl. Artif. Intell. 2023, 123, 106272. [Google Scholar] [CrossRef]
- Ahad, A.H.; Caner, O.E.; Levent, E.S. Discrete element modelling of vibrating screens. Miner. Eng. 2018, 121, 107–121. [Google Scholar]
- Lin, D.; Ji, J.C.; Wang, X.; Wang, X.; Wang, Y.; Xu, N.; Ni, Q.; Zhao, G.; Feng, K. A rigid-flexible coupled dynamic model of a flip-flow vibrating screen considering the effects of processed materials. Powder Technol. 2023, 427, 118753. [Google Scholar] [CrossRef]
- Zhao, G.; Pu, K.; Xu, N.; Gong, S.; Wang, X. Simulation of particles motion on a double vibrating flip-flow screen surface based on FEM and DEM coupling. Powder Technol. 2023, 421, 118422. [Google Scholar] [CrossRef]
- Jiang, H.; Duan, C.; Wu, J.; Zhao, Y.; Liu, C.; Luo, Z.; Dong, L.; Zhang, B.; Wang, Z.; Zhang, C.; et al. Kinematics characteristics of the vibrating screen with rigid-flexible screen rod and the behavior of moist coal particles during the dry deep screening process. Powder Technol. 2017, 319, 92–101. [Google Scholar] [CrossRef]
- Xiao, J.; Tong, X. Particle stratification and penetration of a linear vibrating screen by the discrete element method. Int. J. Min. Sci. Technol. 2012, 22, 357–362. [Google Scholar] [CrossRef]
- Xia, X.; Gou, L.; Zhang, Z.; Wang, L.; Guo, Y.; Jing, W. Collaborative optimization of linear vibrating screen screening efficiency and dynamic response stability based on coupled DEM-MBK simulation. Particuology 2023, 78, 49–61. [Google Scholar] [CrossRef]
- Zhao, Z.; Jin, M.; Qin, F.; Simon, X. Yang. A novel neural network approach to modeling particles distribution on vibrating screen. Powder Technol. 2021, 382, 254–261. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Wan, L.; Ma, X.; Song, J.; Huang, J. Optimising the design of ball racks to improve the sorting efficiency of vibrating screen seed cleaners using discrete element method modelling and experiment. Biosyst. Eng. 2023, 225, 99–117. [Google Scholar] [CrossRef]
- Liu, H.; Jia, J.; Liu, N.; Hu, X.; Zhou, X. Effect of material feed rate on sieving performance of vibrating screen for batch mixing equipment. Powder Technol. 2018, 338, 898–904. [Google Scholar] [CrossRef]
- Li, Z.; Si, Q.; Jia, P.; Xiao, G.; Tong, X. Research on particle swarm screening mechanism and performance optimization based on simulated lunar microgravity. Adv. Space Res. 2023, 063, 0273–1177. [Google Scholar] [CrossRef]
- Barbosa, V.P.; Menezes, A.L.; Gedraite, R.; Ataíde, C.H. Vibration screening: A detailed study using image analysis techniques to characterize the bed behavior in solid–liquid separation. Miner. Eng. 2020, 154, 106383. [Google Scholar] [CrossRef]
- Chen, J.; Hsieh, H.; Do, Q. Forecasting Hoabinh Reservoir’s Incoming Flow: An Application of Neural Networks with the Cuckoo Search Algorithm. Information 2014, 5, 570–586. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, D.; Zhou, W.; Ding, W.; Gong, J. Research on Network Traffic Identification Based on Improved BP Neural Network. Appl. Math. Inf. Sci. 2013, 7, 389–398. [Google Scholar] [CrossRef]
- Ning, Y.; Fuh, J.Y.H.; Wong, Y.; Loh, H.T. An intelligent parameter selection system for the direct metal laser sintering process. Int. J. Prod. Res. 2004, 42, 183–199. [Google Scholar] [CrossRef]
- Feng, Z.; Min, X.; Jiang, W.; Song, F.; Li, X. Study on Thermal Error Modeling for CNC Machine Tools Based on the Improved Radial Basis Function Neural Network. Appl. Sci. 2023, 13, 5299. [Google Scholar] [CrossRef]
- Silva, T.M.P.; Hameury, C.; Ferrari, G.; Balasubramanian, P.; Franchini, G.; Amabili, M. Particle swarm optimization of a non-collocated MIMO PPF active vibration control of a composite sandwich plate. J. Sound Vib. 2023, 555, 117723. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, S.; Ouyang, H.; Li, S.; Wang, G. Hybrid multi-group stochastic cooperative particle swarm optimization algorithm and its application to the photovoltaic parameter identification problem. Energy Rep. 2023, 9, 4654–4681. [Google Scholar] [CrossRef]
- Huang, H.; Qin, H.; Hao, Z.; Lim, A. Example-based learning particle swarm optimization for continuous optimization. Inf. Sci. 2011, 182, 125–138. [Google Scholar] [CrossRef]
- Fu, X.; Zheng, Q.; Jiang, G.; Roy, K.; Huang, L.; Liu, C.; Li, K.; Chen, H.; Song, X.; Chen, J.; et al. Water quality prediction of copper-molybdenum mining-beneficiation wastewater based on the PSO-SVR model. Front. Environ. Sci. Eng. 2023, 17, 98. [Google Scholar] [CrossRef]


| Poisson’s Ratio | Shear Modulus/MPa | Density/(kg/m3) | |
|---|---|---|---|
| Particles | 0.30 | 23.00 | 2678 |
| Screen mesh | 0.29 | 80.92 | 7850 |
| Elastic Coefficient of Restitution | Static Friction Coefficient | Coefficient of Rolling Friction | |
|---|---|---|---|
| Particles to Particles | 0.1 | 0.545 | 0.01 |
| Particles to Screen mesh | 0.2 | 0.500 | 0.01 |
| Number | Vibration Frequency (Hz) | Swing Frequency (Hz) | Vibration Amplitude (mm) | Direction Angle (°) | Swing Angle (°) | Angle Change Rate | Screening Efficiency (%) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 7 | 1.9 | 40 | 0.9 | 0.6 | 80.38 |
| 2 | 16 | 7 | 1.9 | 40 | 0.9 | 0.6 | 83.81 |
| 3 | 19 | 7 | 1.9 | 40 | 0.9 | 0.6 | 81.66 |
| 4 | 22 | 7 | 1.9 | 40 | 0.9 | 0.6 | 79.68 |
| 5 | 13 | 10 | 1.9 | 40 | 0.9 | 0.6 | 82.83 |
| 6 | 16 | 10 | 1.9 | 40 | 0.9 | 0.6 | 85.66 |
| 7 | 22 | 10 | 1.9 | 40 | 0.9 | 0.6 | 81.16 |
| 8 | 16 | 13 | 1.9 | 40 | 0.9 | 0.6 | 88.14 |
| 9 | 16 | 16 | 1.9 | 40 | 0.9 | 0.6 | 86.41 |
| 10 | 16 | 13 | 1.9 | 40 | 1.3 | 0.3 | 86.14 |
| 11 | 16 | 13 | 1.9 | 40 | 0.9 | 0.6 | 84.81 |
| 12 | 16 | 13 | 2.2 | 40 | 0.9 | 0.6 | 82.99 |
| 13 | 16 | 13 | 2.5 | 40 | 0.9 | 0.6 | 81.42 |
| 14 | 16 | 13 | 2.8 | 40 | 0.9 | 0.6 | 89.05 |
| 15 | 16 | 13 | 1.9 | 30 | 0.9 | 0.6 | 87.09 |
| 16 | 16 | 13 | 1.9 | 40 | 0.9 | 1.2 | 85.74 |
| 17 | 16 | 13 | 1.9 | 50 | 0.9 | 0.6 | 87.36 |
| 18 | 16 | 13 | 1.9 | 60 | 0.9 | 0.6 | 86.62 |
| 19 | 16 | 13 | 2.2 | 40 | 0.5 | 0.6 | 84.97 |
| 20 | 16 | 13 | 2.2 | 40 | 0.7 | 0.6 | 85.73 |
| 21 | 16 | 13 | 2.2 | 40 | 0.9 | 0.6 | 86.13 |
| 22 | 16 | 13 | 1.9 | 40 | 1.1 | 0.6 | 90.38 |
| 23 | 16 | 13 | 1.9 | 40 | 1.3 | 0.6 | 89.13 |
| 24 | 16 | 13 | 1.9 | 40 | 1.3 | 0.9 | 86.64 |
| 25 | 16 | 13 | 1.9 | 40 | 1.3 | 0.1 | 84.29 |
| 26 | 16 | 13 | 1.9 | 40 | 1.3 | 1.2 | 84.79 |
| 27 | 13 | 7 | 1.9 | 40 | 0.5 | 0.6 | 74.73 |
| 28 | 13 | 7 | 1.9 | 40 | 0.7 | 0.6 | 76.03 |
| 29 | 13 | 7 | 1.9 | 40 | 0.9 | 0.6 | 77.35 |
| 30 | 13 | 7 | 1.9 | 40 | 1.1 | 0.6 | 79.13 |
| 31 | 13 | 7 | 1.9 | 40 | 1.3 | 0.6 | 78.25 |
| 32 | 13 | 7 | 2.8 | 40 | 0.5 | 0.6 | 73.94 |
| 33 | 13 | 7 | 1.6 | 40 | 0.5 | 0.6 | 76.89 |
| 34 | 13 | 7 | 1.9 | 30 | 1.3 | 0.6 | 76.52 |
| 35 | 13 | 7 | 1.9 | 20 | 1.3 | 0.6 | 78.29 |
| 36 | 13 | 7 | 1.9 | 50 | 1.3 | 0.6 | 74.81 |
| 37 | 13 | 7 | 1.9 | 60 | 1.3 | 0.6 | 73.92 |
| 38 | 19 | 10 | 1.6 | 40 | 1.1 | 0.9 | 78.82 |
| 39 | 19 | 10 | 1.9 | 40 | 1.1 | 0.9 | 79.98 |
| 40 | 19 | 10 | 2.5 | 40 | 1.1 | 0.9 | 77.92 |
| 41 | 19 | 10 | 2.8 | 40 | 1.1 | 0.9 | 76.84 |
| 42 | 22 | 16 | 1.9 | 30 | 0.5 | 0.1 | 63.27 |
| 43 | 22 | 16 | 1.9 | 30 | 0.5 | 0.3 | 65.21 |
| 44 | 22 | 16 | 1.9 | 30 | 0.5 | 0.6 | 67.23 |
| 45 | 22 | 16 | 1.9 | 30 | 0.5 | 1.2 | 65.71 |
| 46 | 19 | 13 | 1.6 | 60 | 1.1 | 0.6 | 79.64 |
| 47 | 19 | 13 | 1.6 | 60 | 1.1 | 0.3 | 76.92 |
| 48 | 19 | 10 | 1.9 | 40 | 0.9 | 0.6 | 82.69 |
| 49 | 19 | 13 | 1.6 | 60 | 1.1 | 0.9 | 77.21 |
| 50 | 19 | 13 | 1.6 | 60 | 1.1 | 1.2 | 74.03 |
| Statistical Indices | BP | PSO-BP |
|---|---|---|
| RMSE | 0.0795 | 0.0184 |
| MSRE | 0.0416 | 0.0132 |
| MAE | 0.0482 | 0.0102 |
| MARE | 0.0230 | 0.0050 |
| R2 | 0.9110 | 0.9748 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Y.; Niu, F.; Zhang, H.; Li, S.; Wang, Y. Parameterization of Multi-Angle Shaker Based on PSO-BP Neural Network. Minerals 2023, 13, 929. https://doi.org/10.3390/min13070929
Zhang J, Wang Y, Niu F, Zhang H, Li S, Wang Y. Parameterization of Multi-Angle Shaker Based on PSO-BP Neural Network. Minerals. 2023; 13(7):929. https://doi.org/10.3390/min13070929
Chicago/Turabian StyleZhang, Jinxia, Yan Wang, Fusheng Niu, Hongmei Zhang, Songyi Li, and Yanpeng Wang. 2023. "Parameterization of Multi-Angle Shaker Based on PSO-BP Neural Network" Minerals 13, no. 7: 929. https://doi.org/10.3390/min13070929
APA StyleZhang, J., Wang, Y., Niu, F., Zhang, H., Li, S., & Wang, Y. (2023). Parameterization of Multi-Angle Shaker Based on PSO-BP Neural Network. Minerals, 13(7), 929. https://doi.org/10.3390/min13070929





