A Model Linking Compressive Strength and Porosity in Ternary System: Metakaolin, Limestone, Cement
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Test Methods
2.3. Mix Designs
2.4. Calculated Surface Area
2.5. Reactivity Factor
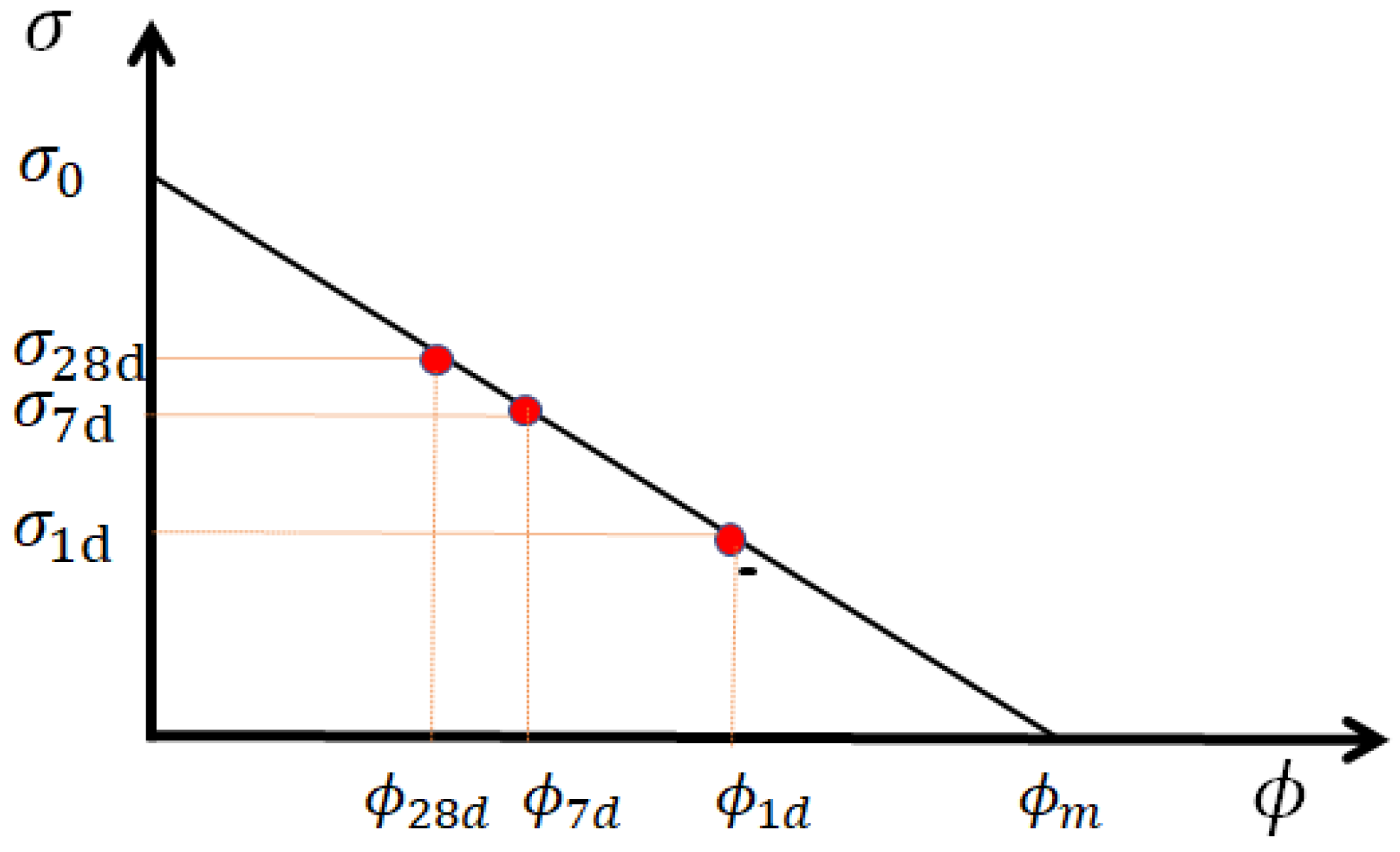
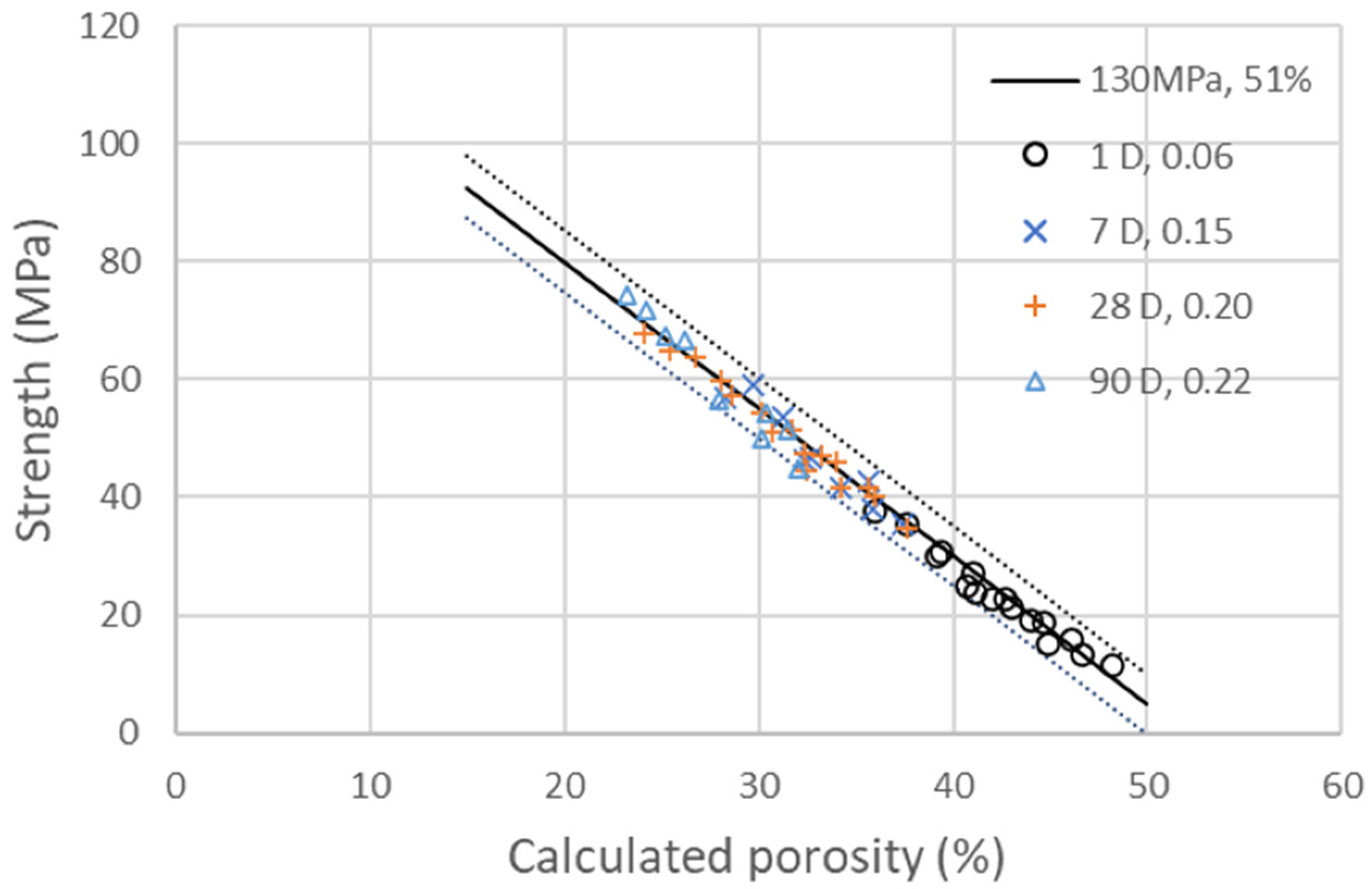
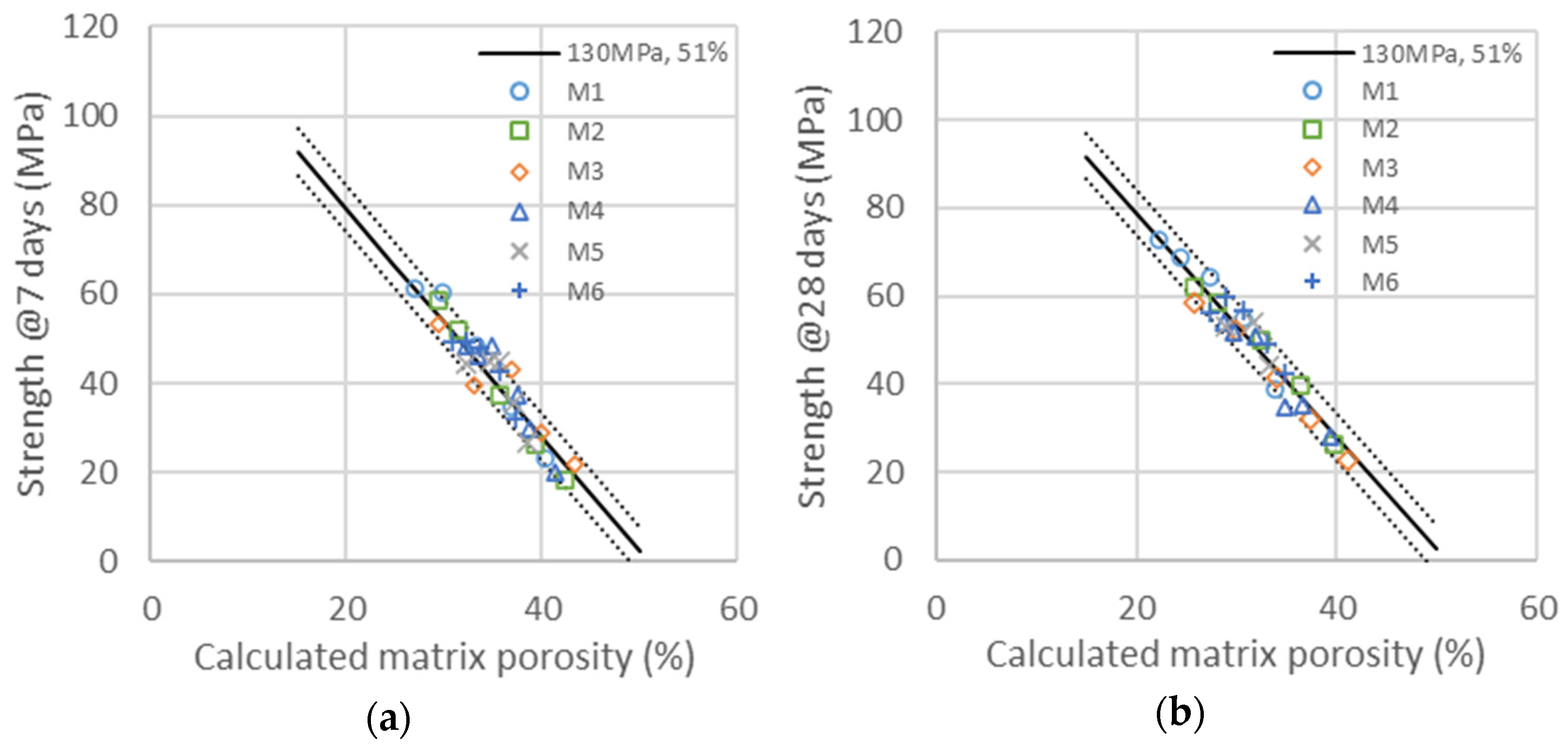
2.6. Link between Porosity and Strength
3. Results
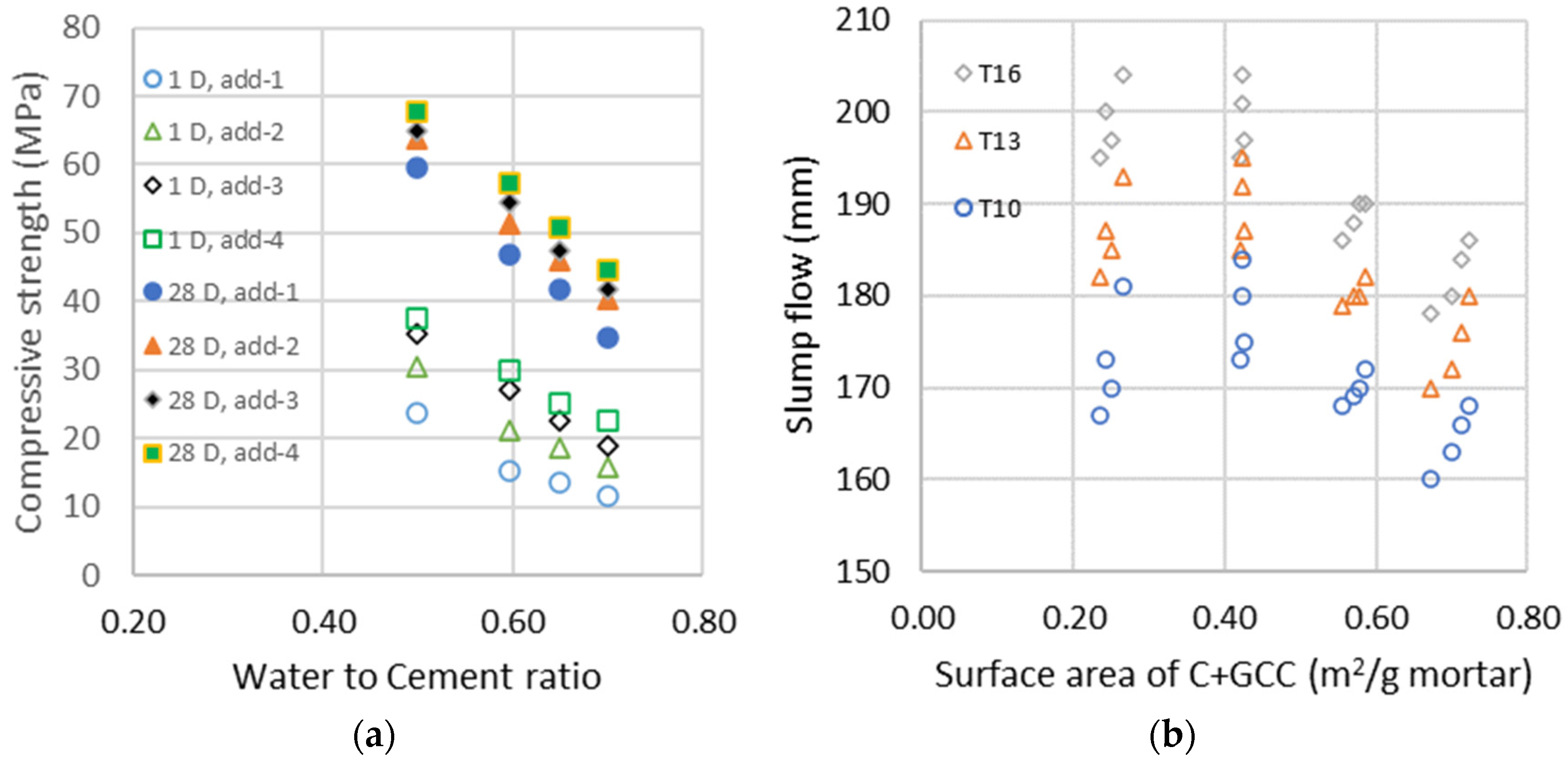
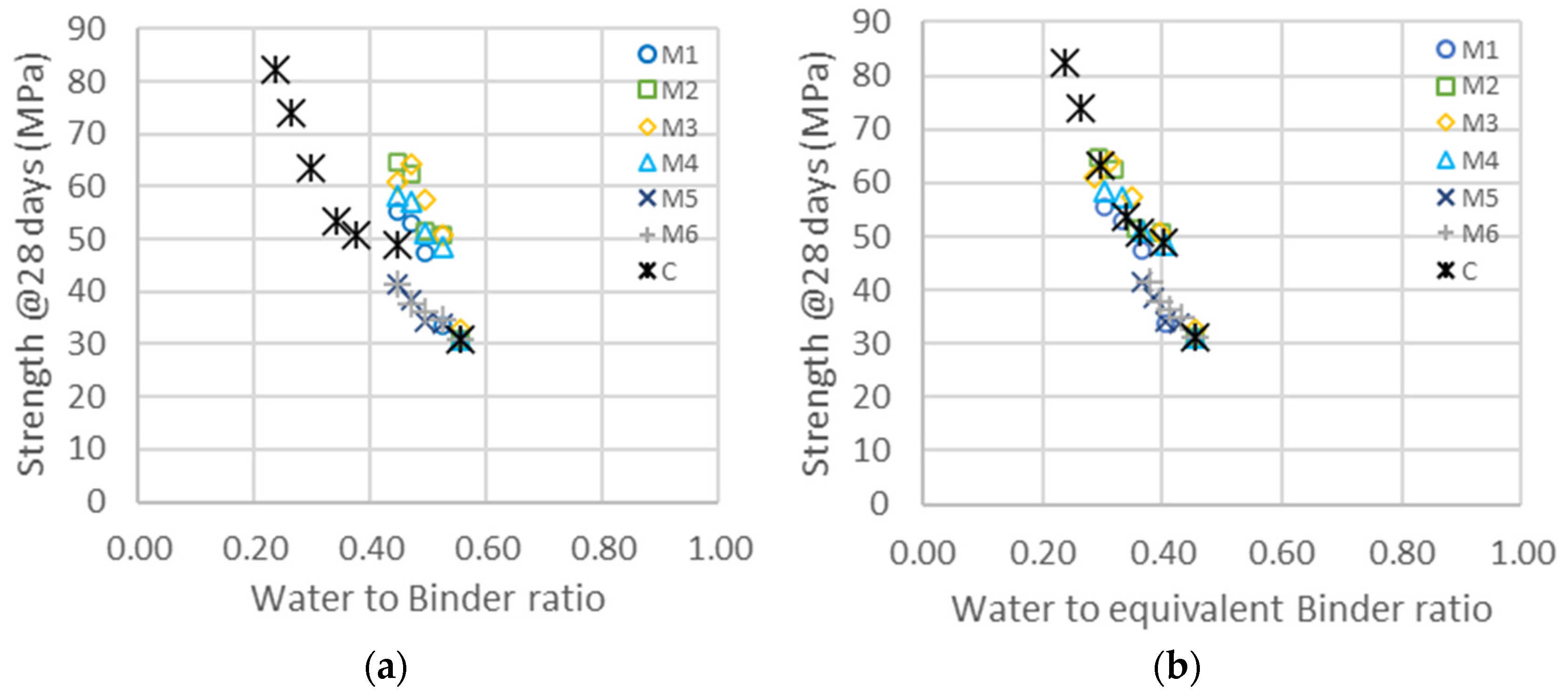
3.1. Binary Clinker/GCC System
3.2. Binary Clinker/Metakaolin System
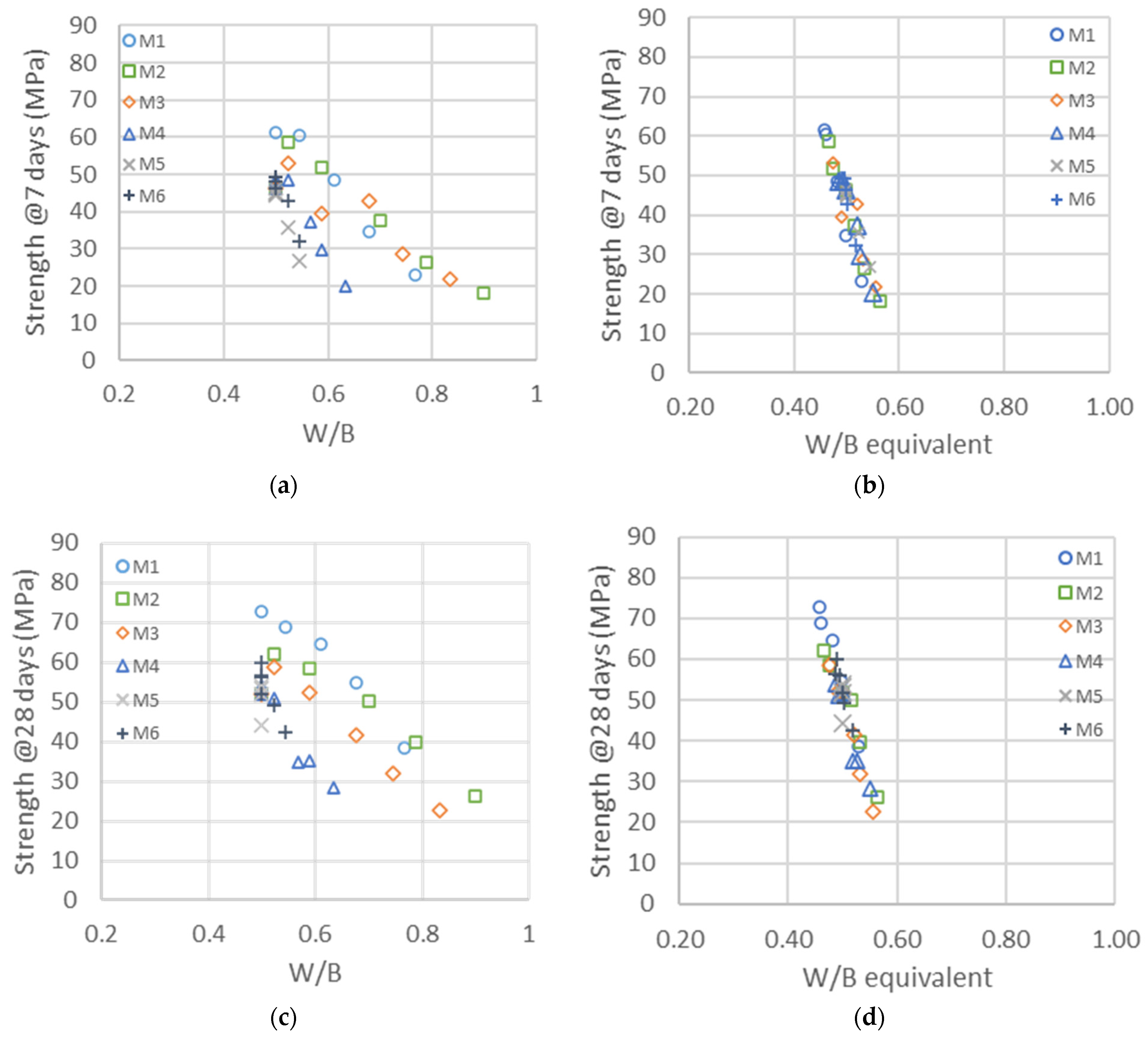
3.3. Cement/GCC/Metakaolin Ternary System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEA International Energy Agency. Buildings—A Source of Enormous Untapped Efficiency Potential. 2021. Available online: https://www.iea.org/topics/buildings (accessed on 1 January 2023).
- Shi, C.; Jiménez, A.F.; Palomo, A. New cements for the 21st century: The pursuit of an alternative to Portland cement. Cem. Concr. Res. 2011, 41, 750–763. [Google Scholar] [CrossRef]
- Ijaz, N.; Ye, W.; ur Rehman, Z.; Ijaz, Z. Novel application of low carbon limestone calcined clay cement (LC3) in expansive soil stabilization: An eco-efficient approach. J. Clean. Prod. 2022, 371, 133492. [Google Scholar] [CrossRef]
- Hajer, M.; Swilling, M.; Suh, S.; Ramaswami, A.; Baynes, T.; Bergesen, J.; Labbé, F.; Musango, J.; Robinson, B.; Salat, S. The Weight of Cities: Resource Requirements of Future Urbanization. 2018. Available online: https://www.resourcepanel.org/reports/weight-cities (accessed on 1 May 2017).
- Miller, S.A.; Van Roijen, E.; Cunningham, P.; Kim, A. Opportunities and challenges for engineering construction materials as carbon sinks. RILEM Tech. Lett. 2021, 6, 105–118. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials and the Environment: Eco-Informed Material Choice, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Xi, F.; Davis, S.J.; Ciais, P.; Crawford-Brown, D.; Guan, D.; Pade, C.; Shi, F.X.T.; Syddall, D.C.-B.M.; Lv, J.; Liu, Z. Substantial global carbon uptake by cement carbonation. Nat. Geosci. 2016, 9, 880–883. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U. Optimization of COVID-19 face mask waste fibers and silica fume as a balanced mechanical ameliorator of fat clay using response surface methodology. Environ. Sci. Pollut. Res. 2022, 29, 17001–17016. [Google Scholar] [CrossRef]
- Tisserant, A.; Pauliuk, S.; Merciai, S.; Schmidt, J.; Fry, J.; Wood, R.; Tukker, A. Solid waste and the circular economy: A global analysis of waste treatment and waste footprints. J. Ind. Ecol. 2017, 21, 628–640. [Google Scholar] [CrossRef]
- Kaza, S.; Yao, L.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank Publications: Washington, DC, USA, 2018. [Google Scholar]
- Antunes, M.; Santos, R.L.; Pereira, J.; Rocha, P.; Horta, R.B.; Colaço, R. Alternative clinker technologies for reducing carbon emissions in cement industry: A critical review. Materials 2022, 15, 209. [Google Scholar] [CrossRef]
- Muzenda, T.R.; Hou, P.; Kawashima, S.; Sui, T.; Cheng, X. The role of limestone and calcined clay on the rheological properties of LC3. Cem. Concr. Compos. 2020, 107, 103516. [Google Scholar] [CrossRef]
- Hosseinzadeh Zaribaf, B. Metakaolin-Portland Limestone Cements: Evaluating the Effects of Chemical Admixtures on Early and Late Age Behavior. Doctoral Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2017. Available online: http://hdl.handle.net/1853/60123 (accessed on 9 August 2017).
- Juenger, M.C.; Snellings, R.; Bernal, S.A. Supplementary cementitious materials: New sources, characterization, and performance insights. Cem. Concr. Res. 2019, 122, 257–273. [Google Scholar] [CrossRef]
- Buttiens, K.; Leroy, J.; Negro, P.; Thomas, J.S.; Edwards, K.; De Lassat, Y. The carbon cost of slag production in the blast furnace: A scientific approach. J. Sustain. Metall. 2016, 2, 62–72. [Google Scholar] [CrossRef]
- Obrist, M.D.; Kannan, R.; Schmidt, T.J.; Kober, T. Decarbonization pathways of the Swiss cement industry towards net zero emissions. J. Clean. Prod. 2021, 288, 125413. [Google Scholar] [CrossRef]
- Junaid, M.F.; ur Rehman, Z.; Kuruc, M.; Medved’, I.; Bačinskas, D.; Čurpek, J.; Čekon, M.; Ijaz, N.; Ansari, W.S. Lightweight concrete from a perspective of sustainable reuse of waste byproducts. Constr. Build. Mater. 2022, 319, 126061. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ferraris, C.F.; Jones, S.Z.; Lootens, D.; Zunino, F. Limestone and silica powder replacements for cement: Early-age performance. Cem. Concr. Compos. 2017, 78, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Scrivener, K.; Favier, A. Calcined clays for sustainable concrete. In Calcined Clays for Sustainable Concrete: Proceedings of the 1st International Conference on Calcined Clays for Sustainable Concrete (RILEM 2015), Ecublens, Switzerland, 23–25 June 2015; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Dekeukelaere, A. Evaluation of a New Low CO2 Cement Introduction within the European Emission Trading System. Doctoral Dissertation, Harvard University, Cambridge, MA, USA, 2020. Available online: https://nrs.harvard.edu/URN-3:HUL.INSTREPOS:37365064 (accessed on 12 December 2022).
- Benghida, D. CO2 reduction from cement industry. In Advanced Materials, Mechanical and Structural Engineering, Proceedings of the 2nd International Conference of Advanced Materials, Mechanical and Structural Engineering (AMMSE), Jeju Island, Republic of Korea, 18–20 September 2015; Routledge: London, UK, 2015; pp. 127–130. Available online: https://www.taylorfrancis.com/chapters/edit/10.1201/b19934-29/co2-reduction-cement-industry-benghida (accessed on 10 November 2022).
- Proske, T.; Hainer, S.; Rezvani, M.; Graubner, C.A. Eco-friendly concretes with reduced water and cement contents—Mix design principles and laboratory tests. Cem. Concr. Res. 2013, 51, 38–46. [Google Scholar] [CrossRef]
- Nie, Y.; Shi, J.; He, Z.; Zhang, B.; Peng, Y.; Lu, J. Evaluation of high-volume fly ash (HVFA) concrete modified by metakaolin: Technical, economic and environmental analysis. Powder Technol. 2022, 397, 117121. [Google Scholar] [CrossRef]
- Juhart, J.; Autischer, M.; Sakoparnig, M.; Krüger, M. The Realization of Clinker-Reduced, Performance-Based Sustainable Concrete by the Micro-Filler, Eco-Filler Concept. Materials 2021, 14, 4958. [Google Scholar] [CrossRef]
- Aïtcin, P.C. Portland cement. In Science and Technology of Concrete Admixtures; Woodhead Publishing: Sawston, UK, 2016; pp. 27–51. [Google Scholar] [CrossRef]
- Hassannezhad, K.; Akyol, Y.; Dursun, M.C.; Ow-Yang, C.W.; Gulgun, M.A. Effect of Metakaolin and Lime on Strength Development of Blended Cement Paste. Constr. Mater. 2022, 2, 297–313. [Google Scholar] [CrossRef]
- Badogiannis, E.; Papadakis, V.G.; Chaniotakis, E.; Tsivilis, S. Exploitation of poor Greek kaolins: Strength development of metakaolin concrete and evaluation by means of k-value. Cem. Concr. Res. 2004, 34, 1035–1041. [Google Scholar] [CrossRef]
- Busari, A.; Akinmusuru, J.; Dahunsi, B. Strength and durability properties of concrete using metakaolin as a sustainable material: Review of literature. Int. J. Civil Eng. Technol. 2019, 10, 1893–1902. [Google Scholar]
- Siddique, R.; Klaus, J. Influence of metakaolin on the properties of mortar and concrete: A review. Appl. Clay Sci. 2009, 43, 392–400. [Google Scholar] [CrossRef]
- Juenger, M.C.; Won, M.C.; Fowler, D.W.; Suh, C.; Edson, A. Effects of Supplementary Cementing Materials on the Setting Time and Early Strength of Concrete; No. FHWA/TC-08/0-5550-1. 2008. Available online: https://ctr.utexas.edu/wp-content/uploads/pubs/0_5550_1.pdf (accessed on 10 September 2015).
- Badogiannis, E.; Tsivilis, S.; Papadakis, V.; Chaniotakis, E. The effect of metakaolin on concrete properties. International Congress: Challenges of Concrete Construction. 2002, pp. 81–89. Available online: https://www.icevirtuallibrary.com/doi/abs/10.1680/iadicmac.31791.0008 (accessed on 7 July 2015).
- Güneyisi, E.; Gesoğlu, M.; Mermerdaş, K. Improving strength, drying shrinkage, and pore structure of concrete using metakaolin. Mater. Struct. 2008, 41, 937–949. [Google Scholar] [CrossRef]
- Wild, S.; Khatib, J.M.; Jones, A. Relative strength, pozzolanic activity and cement hydration in superplasticised metakaolin concrete. Cem. Concr. Res. 1996, 26, 1537–1544. [Google Scholar] [CrossRef]
- Changling, H.; Osbaeck, B.; Makovicky, E. Pozzolanic reaction of six principal clay minerals: Activation reactivity assessments and technological effects. Cem. Concr. Res. 1995, 25, 1691–1702. [Google Scholar] [CrossRef]
- Kuzielová, E.; Žemlička, M.; Bartoničková, E.; Palou, M.T. The correlation between porosity and mechanical properties of multicomponent systems consisting of Portland cement–slag–silica fume–metakaolin. Constr. Build. Mater. 2017, 135, 306–314. [Google Scholar] [CrossRef]
- Tang, J.; Wei, S.; Li, W.; Ma, S.; Ji, P.; Shen, X. Synergistic effect of metakaolin and limestone on the hydration properties of Portland cement. Constr. Build. Mater. 2019, 223, 177–184. [Google Scholar] [CrossRef]
- Dinakar, P.; Sahoo, P.K.; Sriram, G. Effect of metakaolin content on the properties of high strength concrete. Int. J. Concr. Struct. Mater. 2013, 7, 215–223. [Google Scholar] [CrossRef]
- EN 197-1:2011; Cement–Part 1: Composition, Specifications and Conformity Criteria for Common Cements. European Committee for Standardisation, British Standard: London, UK, 2011. Available online: http://168.101.26.37/notific_otros_miembros/mwi40_t.pdf (accessed on 6 January 2021).
- Ferraz, E.; Andrejkovicova, S.; Hajjaji, W.; Velosa, A.L.; Silva, A.S.; Rocha, F. Pozzolanic activity of metakaolins by the French standard of the modified Chapelle test: A direct methology. Acta Geodyn. Geomater. 2015, 12, 289–298. Available online: http://hdl.handle.net/10400.26/38418 (accessed on 20 January 2016). [CrossRef]
- Hernández, J.F.M.; Almenares-Reyes, R.; Zunino, F.; Alujas-Diaz, A.; Scrivener, K.L. Color control in industrial clay calcination. RILEM Tech. Lett. 2020, 5, 1–7. [Google Scholar] [CrossRef]
- EN 196-1:2016; CEN European Committee for Standardization, Methods of Testing of Cement: Part 1. Determination of Strength, The European Standard. CEN: Brussels, Belgium, 2016.
- EN 1015-3:1999; Methods of Test for Mortar for Masonry—Part 3: Determination of Consistence of Fresh Mortar (by Flow Table). CEN: Brussels, Belgium, 1999.
- Puerta-Falla, G.; Balonis, M.; Le Saout, G.; Neithalath, N.; Sant, G. The influence of metakaolin on limestone reactivity in cementitious materials. In Calcined Clays for Sustainable Concrete: Proceedings of the 1st International Conference on Calcined Clays for Sustainable Concrete (RILEM 2015), Ecublens, Switzerland, 23–25 June 2015; Springer: Dordrecht, The Netherlands, 2015; pp. 11–19. [Google Scholar] [CrossRef]
- Chen, J.J.; Li, Q.H.; Ng, P.L.; Li, L.G.; Kwan, A.K.H. Cement equivalence of metakaolin for workability, cohesiveness, strength and sorptivity of concrete. Materials 2020, 13, 1646. [Google Scholar] [CrossRef]
- Smith, I.A. The design of fly-ash concretes. Proc. Inst. Civ. Eng. 1967, 36, 769–790. [Google Scholar] [CrossRef]
- Yu, J.; Wu, H.L.; Mishra, D.K.; Li, G.; Leung, C.K. Compressive strength and environmental impact of sustainable blended cement with high-dosage Limestone and Calcined Clay (LC2). J. Clean. Prod. 2021, 278, 123616. [Google Scholar] [CrossRef]
- Rössler, M.; Odler, I. Investigations on the relationship between porosity, structure, and strength of hydrated portland cement pastes I. Effect of porosity. Cem. Concr. Res. 1985, 15, 320–330. [Google Scholar] [CrossRef]
- Kearsley, E.P.; Wainwright, P.J. The effect of porosity on the strength of foamed concrete. Cem. Concr. Res. 2002, 32, 233–239. [Google Scholar] [CrossRef]
- Lootens, D.; Bentz, D.P. On the relation of setting and early-age strength development to porosity and hydration in cement-based materials. Cem. Concr. Compos. 2016, 68, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Bentz, D.P.; Zunino, F.; Lootens, D. Chemical vs. physical acceleration of cement hydration. Concr. Int. Des. Constr. 2016, 38, 37. [Google Scholar]
- Briendl, L.G.; Mittermayr, F.; Baldermann, A.; Steindl, F.R.; Sakoparnig, M.; Letofsky-Papst, I.; Galan, I. Early hydration of cementitious systems accelerated by aluminium sulphate: Effect of fine limestone. Cem. Concr. Res. 2020, 134, 106069. [Google Scholar] [CrossRef]
- Wyrzykowski, M.; Assmann, A.; Hesse, C.; Lura, P. Microstructure development and autogenous shrinkage of mortars with CSH seeding and internal curing. Cem. Concr. Res. 2020, 129, 105967. [Google Scholar] [CrossRef]
- Neto, C.S.; Campiteli, V.C. The influence of limestone additions on the rheological properties and water retention value of Portland cement slurries. Carbonate Addit. Cem. 1990, 100, 24–29. [Google Scholar]
- Jiang, D.; Li, X.; Lv, Y.; Zhou, M.; He, C.; Jiang, W.; Liu, Z.; Li, C. Utilization of limestone powder and fly ash in blended cement: Rheology, strength and hydration characteristics. Constr. Build. Mater. 2020, 232, 117228. [Google Scholar] [CrossRef]
- Gotaszewska, M.; Giergiczny, Z. Influence of limestone addition to cement on rheological properties of mortars. In Proceedings of the 12th Fib International Ph.D. Symposium in Civil Engineering, Prague, Czech Republic, 29–31 August 2018; pp. 59–64. [Google Scholar]
- Yahia, A.; Tanimura, M.; Shimoyama, Y. Rheological properties of highly flowable mortar containing limestone filler-effect of powder content and W/C ratio. Cem. Concr. Res. 2005, 35, 532–539. [Google Scholar] [CrossRef]
- Khatib, J.M.; Negim, E.M.; Gjonbalaj, E. High volume metakaolin as cement replacement in mortar. World J. Chem. 2012, 7, 7–10. Available online: https://www.idosi.org/wjc/7(1)12/2.pdf (accessed on 27 August 2015).
- Cassagnabère, F.; Diederich, P.; Mouret, M.; Escadeillas, G.; Lachemi, M. Impact of metakaolin characteristics on the rheological properties of mortar in the fresh state. Cem. Concr. Compos. 2013, 37, 95–107. [Google Scholar] [CrossRef]
- Badogiannis, E.; Kakali, G.; Dimopoulou, G.; Chaniotakis, E.; Tsivilis, S. Metakaolin as a main cement constituent. Exploitation of poor Greek kaolins. Cem. Concr. Compos. 2005, 27, 197–203. [Google Scholar] [CrossRef]
- Kropyvnytska, T.; Rucinska, T.; Ivashchyshyn, H.; Kotiv, R. Development of eco-efficient composite cements with high early strength. In Proceedings of the CEE 2019: Advances in Resource-Saving Technologies and Materials in Civil and Environmental Engineering, Kyiv, Ukraine, 22–23 April 2020; Volume 18, pp. 211–218. [Google Scholar] [CrossRef]
- Zhao, D.; Khoshnazar, R. Hydration and microstructural development of calcined clay cement paste in the presence of calcium-silicate-hydrate (C–S–H) seed. Cem. Concr. Compos. 2021, 122, 104162. [Google Scholar] [CrossRef]
- Redondo-Soto, C.; Morales-Cantero, A.; Cuesta, A.; Santacruz, I.; Gastaldi, D.; Canonico, F.; Aranda, M.A. Limestone calcined clay binders based on a Belite-rich cement. Cem. Concr. Res. 2023, 163, 107018. [Google Scholar] [CrossRef]


| Materials | Concrete | Mortar | Brick | Steel | Wood | Plastic | Al | Total |
|---|---|---|---|---|---|---|---|---|
| Quantity (GT) | 25 | 5 | 5 | 1.9 | 1 | 0.065 | 0.03 | 38 |
| Weight ratio (%) | 65.8 | 13.1 | 13.1 | 5 | 2.6 | >0.2 | >0.1 | 100 |
| CO2 factor (kg/t) | 120 | 400 | 250 | 1850 | 300 | 3000 | 10,000 | |
| Quantity CO2 (GT) | 3.00 | 2.00 | 1.50 | 3.52 | 0.30 | 0.20 | 0.30 | 10.8 |
| CO2 ratio (%) | 27.75 | 18.50 | 13.88 | 32.52 | 2.78 | 1.80 | 2.78 | 100 |
| Types | Clinker | MK | Slag | Fly Ash | Silica Fume | Limestone | Sand Aggregate |
|---|---|---|---|---|---|---|---|
| Carbon footprint (kg/t) | 800 | 300 | 500 | 50 | 50 | >50 | 30 |
| Quantity GT | 4 | Large | 0.4 | 0.4 | 0.4 | Large | Large |
| Cement Type | Clinker % | Limestone % | Pozzolan % | CO2 kg/t | C_Red % |
|---|---|---|---|---|---|
| Pure clinker | 100 | 0 | 0 | 800 | 0 |
| Average cement | 70 | 20 | 10 | 650 | 22 |
| LC3 | 50 | 30 | 20 | 525 | 40 |
| Cement/limestone 50% | 50 | 50 | 0 | 475 | 47 |
| Clinker | Cement * | LC3 | C-50% | C-75% | |
|---|---|---|---|---|---|
| Concrete CO2 (kg/t) | 160 | 130 | 104 | 97 | 65 |
| Mortar CO2 (kg/t) | 378 | 300 | 228 | 208 | 123 |
| Concrete reduction (%) | 19 | 0 | −21 | −25 | −50 |
| Mortar reduction (%) | 21 | 0 | −25 | −30 | −59 |
| M1 | M2 | M3 | M4 | M5 | M6 | ||
|---|---|---|---|---|---|---|---|
| Whiteness | Yellowness | 10.6 | 8.64 | 14.9 | 17.3 | 49.9 | 44.7 |
| L | 96.6 | 95.59 | 91.7 | 90.4 | 72.3 | 66.3 | |
| Size | µm | 1.3 | 1.4 | 1.5 | 6 | 3.5 | 8 |
| Surface area | m2/g | 14.2 | 17.9 | 25 | 20 | 15.65 | - |
| Chapelle test | mg/g | 1146 | 1560 | 1400 | 1100 | 773.9 | - |
| SiO2 + Al2O3 | % | >97 | >93 | 94 | 95 | >92 | >92 |
| Density | kg/m3 | 2600 | 2200 | 2400 | 2400 | 2550 | 2550 |
| Test | CEM | L | W | W/C | T10 | T13 | T16 | D | Rc1d | Rc7d | Rc28d | Rc90d | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit | % | % | % | % | mm | mm | mm | kg/L | MPa | MPa | MPa | MPa | |
| A-1a | 67 | 0 | 33 | 0.50 | 46.8 | 181 | 193 | 204 | 2.27 | 24 | 47 | 60 | 67 |
| A-3a | 58 | 13 | 29 | 0.50 | 45.3 | 168 | 179 | 186 | 2.27 | 35 | 59 | 65 | 72 |
| A-4a | 55 | 18 | 27 | 0.50 | 43.9 | 160 | 170 | 178 | 2.28 | 38 | 57 | 68 | 74 |
| A-1b | 63 | 0 | 37 | 0.60 | 42.5 | 170 | 185 | 197 | 2.25 | 15 | 36 | 47 | 51 |
| A-2b | 58 | 8 | 35 | 0.60 | 49.9 | 180 | 192 | 201 | 2.25 | 21 | 43 | 52 | 54 |
| A-3b | 54 | 14 | 32 | 0.60 | 48.4 | 169 | 180 | 188 | 2.24 | 27 | - | 54 | - |
| A-3d | 50 | 20 | 30 | 0.60 | 46.8 | 163 | 172 | 180 | 2.26 | 30 | 46 | 57 | 56 |
| A-1c | 61 | 0 | 39 | 0.65 | 45.3 | 173 | 187 | 200 | 2.25 | 14 | - | 42 | - |
| A-2c | 56 | 8 | 36 | 0.65 | 51.4 | 184 | 195 | 204 | 2.24 | 19 | - | 46 | - |
| A-3c | 52 | 15 | 34 | 0.65 | 49.9 | 170 | 180 | 190 | 2.24 | 23 | - | 48 | - |
| A-4c | 48 | 21 | 31 | 0.65 | 48.2 | 166 | 176 | 184 | 2.25 | 25 | 42 | 51 | 50 |
| A-1d | 59 | 0 | 41 | 0.70 | 46.6 | 167 | 182 | 195 | 2.25 | 12 | - | 35 | - |
| A-2d | 54 | 8 | 38 | 0.70 | 52.7 | 175 | 187 | 197 | 2.22 | 16 | - | 40 | - |
| A-3d | 50 | 15 | 35 | 0.70 | 51.1 | 172 | 182 | 190 | 2.21 | 19 | - | 42 | - |
| A-4d | 46 | 22 | 32 | 0.70 | 49.4 | 168 | 180 | 186 | 2.24 | 23 | 38 | 45 | 45 |
| Test | Sand | CEM | MK | W | W/B | T16 | Density | Rc7D | Rc28D | |
|---|---|---|---|---|---|---|---|---|---|---|
| % | % | % | % | - | % | mm | kg/L | MPa | MPa | |
| Ref-b | 67 | 22 | 0 | 11 | 0.50 | 48.4 | 218 | 2.28 | 46 | 52 |
| M1-1 | 67 | 20 | 2 | 11 | 0.50 | 50.0 | 192 | 2.25 | 61 | 73 |
| M1-2 | 66 | 18 | 4 | 12 | 0.54 | 50.3 | 192 | 2.22 | 61 | 69 |
| M1-3 | 65 | 15 | 7 | 13 | 0.61 | 51.1 | 188 | 2.18 | 49 | 65 |
| M1-4 | 64 | 13 | 9 | 14 | 0.68 | 52.5 | 185 | 2.14 | 35 | 55 |
| M1-5 | 63 | 10 | 10 | 16 | 0.77 | 53.8 | 185 | 2.09 | 23 | 39 |
| M2-1 | 66 | 20 | 2 | 12 | 0.52 | 50.5 | 203 | 2.23 | 59 | 62 |
| M2-2 | 65 | 17 | 4 | 13 | 0.59 | 51.4 | 188 | 2.18 | 52 | 59 |
| M2-3 | 64 | 15 | 6 | 15 | 0.70 | 52.6 | 197 | 2.12 | 38 | 50 |
| M2-4 | 63 | 13 | 8 | 16 | 0.79 | 54.4 | 187 | 2.06 | 26 | 40 |
| M2-5 | 61 | 10 | 10 | 18 | 0.90 | 55.5 | 185 | 2.01 | 18 | 26 |
| M3-1 | 66 | 20 | 2 | 12 | 0.52 | 50.2 | 200 | 2.24 | 53 | 59 |
| M3-2 | 65 | 17 | 4 | 13 | 0.59 | 51.5 | 195 | 2.19 | 40 | 52 |
| M3-3 | 64 | 15 | 6 | 14 | 0.68 | 52.8 | 196 | 2.14 | 43 | 42 |
| M3-4 | 63 | 13 | 8 | 16 | 0.74 | 54.1 | 182 | 2.09 | 29 | 32 |
| M3-5 | 62 | 10 | 10 | 17 | 0.83 | 55.9 | 180 | 2.03 | 22 | 23 |
| M4-1 | 67 | 20 | 2 | 11 | 0.50 | 48.2 | 195 | 2.27 | 52 | 54 |
| M4-2 | 66 | 18 | 4 | 12 | 0.52 | 48.9 | 189 | 2.24 | 52 | 51 |
| M4-3 | 66 | 15 | 7 | 12 | 0.57 | 49.2 | 193 | 2.21 | 40 | 35 |
| M4-4 | 65 | 13 | 9 | 13 | 0.59 | 48.7 | 184 | 2.19 | 32 | 35 |
| M4-5 | 65 | 11 | 11 | 14 | 0.63 | 49.4 | 192 | 2.16 | 22 | 28 |
| M5-1 | 67 | 20 | 2 | 11 | 0.50 | 48.4 | 210 | 2.27 | 45 | 53 |
| M5-2 | 67 | 18 | 4 | 11 | 0.50 | 49.5 | 196 | 2.24 | 45 | 54 |
| M5-3 | 67 | 16 | 7 | 11 | 0.50 | 49.2 | 182 | 2.23 | 45 | 44 |
| M5-4 | 66 | 13 | 9 | 12 | 0.52 | 48.8 | 184 | 2.21 | 36 | 47 |
| M5-5 | 66 | 11 | 11 | 12 | 0.54 | 48.5 | 195 | 2.20 | 27 | 53 |
| M6-1 | 67 | 20 | 2 | 11 | 0.50 | 49.2 | 209 | 2.26 | 49 | 56 |
| M6-2 | 67 | 18 | 4 | 11 | 0.50 | 49.2 | 197 | 2.24 | 49 | 60 |
| M6-3 | 67 | 16 | 7 | 11 | 0.50 | 49.5 | 185 | 2.22 | 48 | 57 |
| M6-4 | 66 | 13 | 9 | 12 | 0.52 | 49.9 | 188 | 2.20 | 43 | 49 |
| Test | Sand | CEM | L | MK | W | w/b | SP | A | Flow | Density | Rc28d |
|---|---|---|---|---|---|---|---|---|---|---|---|
| % | % | % | % | % | % | m2/g | mm | kg/L | MPa | ||
| Ref-c | 60 | 18 | 12 | 0 | 10 | 0.55 | 0.08 | 0.08 | 382 | 2.25 | 31 |
| M1-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.08 | 0.10 | 380 | 2.27 | 34 |
| M1-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.13 | 0.12 | 390 | 2.28 | 47 |
| M1-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.19 | 0.14 | 398 | 2.27 | 53 |
| M1-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.22 | 0.16 | 376 | 2.25 | 55 |
| M2-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.13 | 0.10 | 402 | 2.30 | 51 |
| M2-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.17 | 0.13 | 365 | 2.26 | 52 |
| M2-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.24 | 0.15 | 390 | 2.26 | 63 |
| M2-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.32 | 0.17 | 395 | 2.27 | 65 |
| M3-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.12 | 0.10 | 380 | 2.28 | 48 |
| M3-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.17 | 0.12 | 400 | 2.26 | 55 |
| M3-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.23 | 0.14 | 398 | 2.26 | 61 |
| M3-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.30 | 0.16 | 380 | 2.26 | 58 |
| M4-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.12 | 0.10 | 380 | 2.28 | 49 |
| M4-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.18 | 0.12 | 390 | 2.28 | 51 |
| M4-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.24 | 0.14 | 398 | 2.27 | 57 |
| M4-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.31 | 0.15 | 382 | 2.26 | 58 |
| M5-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.10 | 0.09 | 396 | 2.28 | 34 |
| M5-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.12 | 0.10 | 380 | 2.27 | 34 |
| M5-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.16 | 0.10 | 400 | 2.26 | 39 |
| M5-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.19 | 0.11 | 368 | 2.27 | 42 |
| M6-6 | 59 | 18 | 12 | 1 | 10 | 0.52 | 0.10 | 0.09 | 392 | 2.28 | 35 |
| M6-7 | 58 | 18 | 12 | 2 | 10 | 0.49 | 0.12 | 0.10 | 372 | 2.27 | 36 |
| M6-8 | 57 | 18 | 12 | 3 | 10 | 0.47 | 0.15 | 0.10 | 394 | 2.28 | 38 |
| M6-9 | 55 | 18 | 12 | 4 | 10 | 0.45 | 0.18 | 0.11 | 390 | 2.28 | 42 |
| C1-1 | 60 | 23 | 7 | 0 | 10 | 0.45 | 0.12 | 0.10 | 394 | 2.31 | 49 |
| C1-2 | 60 | 27 | 3 | 0 | 10 | 0.37 | 0.18 | 0.12 | 368 | 2.32 | 51 |
| C1-3 | 60 | 30 | 0 | 0 | 10 | 0.34 | 0.25 | 0.13 | 355 | 2.33 | 54 |
| C1-4 | 55 | 34 | 0 | 0 | 10 | 0.30 | 0.32 | 0.15 | 378 | 2.35 | 63 |
| C1-5 | 51 | 39 | 0 | 0 | 10 | 0.26 | 0.35 | 0.17 | 353 | 2.36 | 74 |
| C1-6 | 47 | 43 | 0 | 0 | 10 | 0.24 | 0.45 | 0.19 | 364 | 2.39 | 82 |
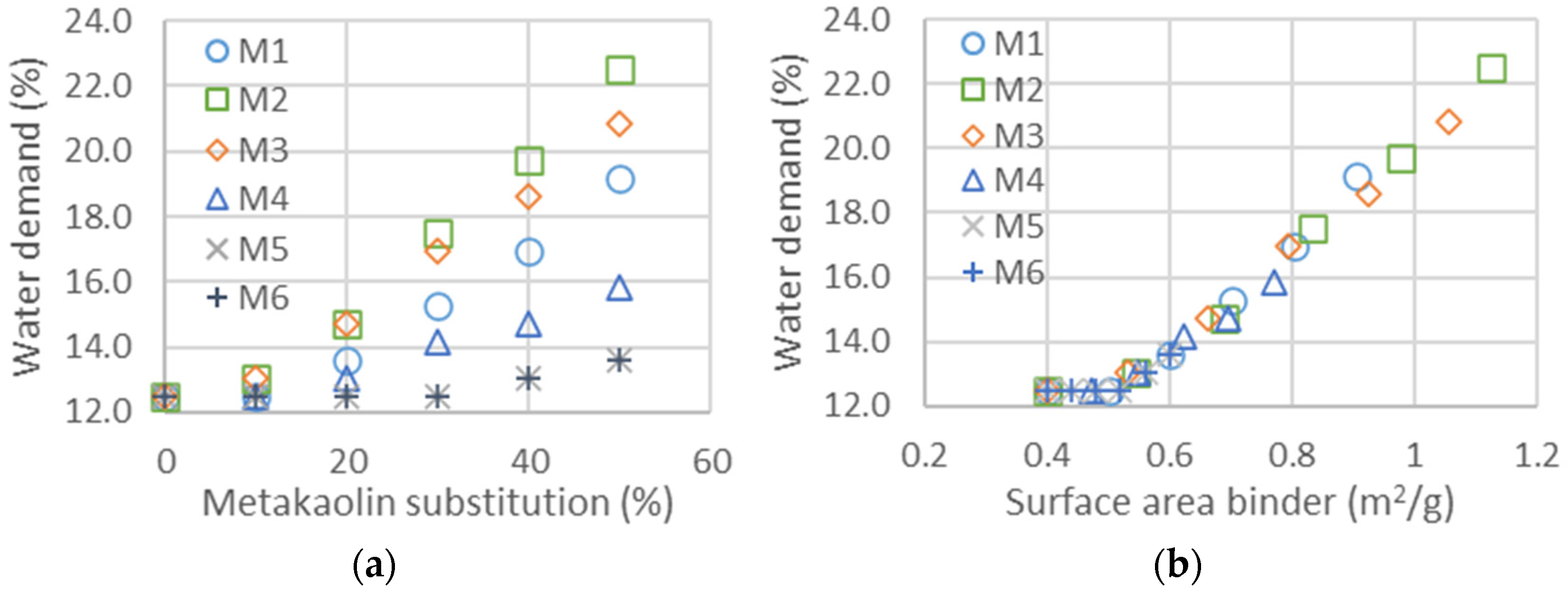
| Metakaolin | M1 | M2 | M3 | M4 | M5 | M6 | |
|---|---|---|---|---|---|---|---|
| (data sheet) | µm | 1.3 | 1.4 | 1.5 | 6 | 3.5 | 8 |
| (water demand) | µm | 1.7 | 1.3 | 1.4 | 1.9 | 3 | 3 |
| (superplasticizer dosage) | µm | 1.9 | 1.3 | 1.4 | 1.5 | 3 | 3 |
| Surface area (data sheet) | m2/g | 14.2 | 17.9 | 25 | 20 | 15.7 | - |
| Surface area (calculated) | m2/g | 1.41 | 1.84 | 1.71 | 1.14 | 0.8 | 0.8 |
| Metakaolin | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| binary system (7 and 28 d) | 1.9 | 2.2 | 2 | 1.3 | 1 | 1.15 |
| 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | |
| 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | |
| 0.15 | 0.15 | 0.15 | 0.02 | 0.06 | 0.10 | |
| 0.30 | 0.20 | 0.18 | 0.04 | 0.06 | 0.13 | |
| and B | 0.35 | 0.40 | 0.35 | 0.12 | 0.05 | 0.10 |
| Metakaolin | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| ternary system (28 d) | 2.5 | 2.8 | 3 | 2.5 | 1.2 | 1 |
| 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | |
| 0.25 | 0.35 | 0.35 | 0.35 | 0.10 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonnon, P.; Lootens, D. A Model Linking Compressive Strength and Porosity in Ternary System: Metakaolin, Limestone, Cement. Minerals 2023, 13, 454. https://doi.org/10.3390/min13040454
Gonnon P, Lootens D. A Model Linking Compressive Strength and Porosity in Ternary System: Metakaolin, Limestone, Cement. Minerals. 2023; 13(4):454. https://doi.org/10.3390/min13040454
Chicago/Turabian StyleGonnon, Pascal, and Didier Lootens. 2023. "A Model Linking Compressive Strength and Porosity in Ternary System: Metakaolin, Limestone, Cement" Minerals 13, no. 4: 454. https://doi.org/10.3390/min13040454
APA StyleGonnon, P., & Lootens, D. (2023). A Model Linking Compressive Strength and Porosity in Ternary System: Metakaolin, Limestone, Cement. Minerals, 13(4), 454. https://doi.org/10.3390/min13040454





