Study on the Improved Method for Calculating Traveltime and Raypath of Multistage Fast Marching Method
Abstract
1. Introduction
2. Calculation Method of Traveltime
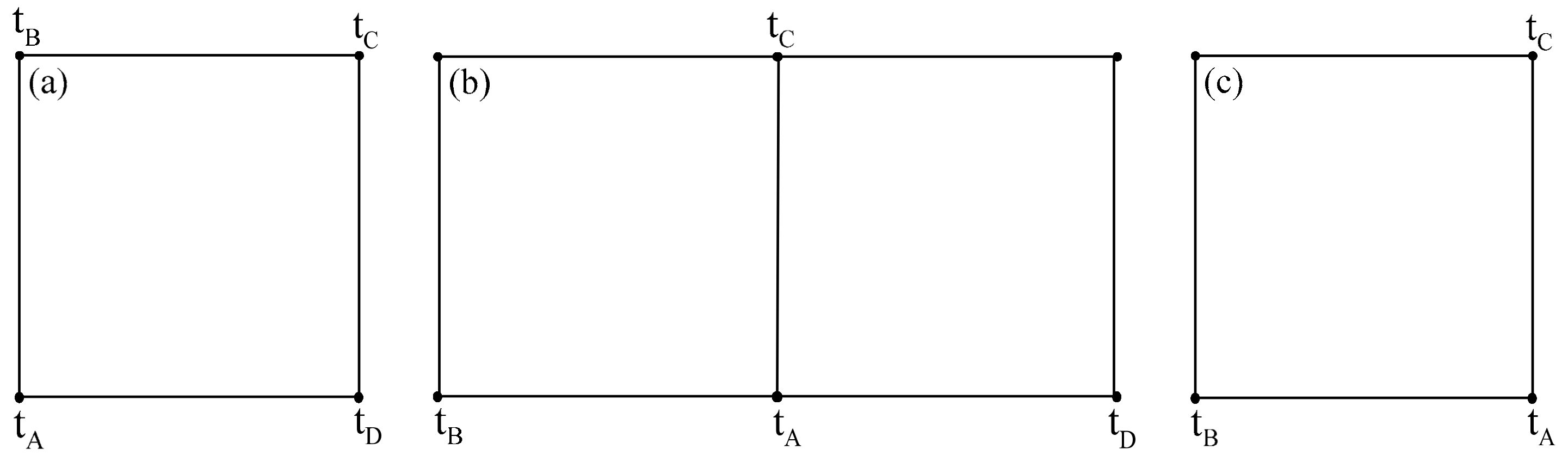
2.1. Finite-Difference Scheme
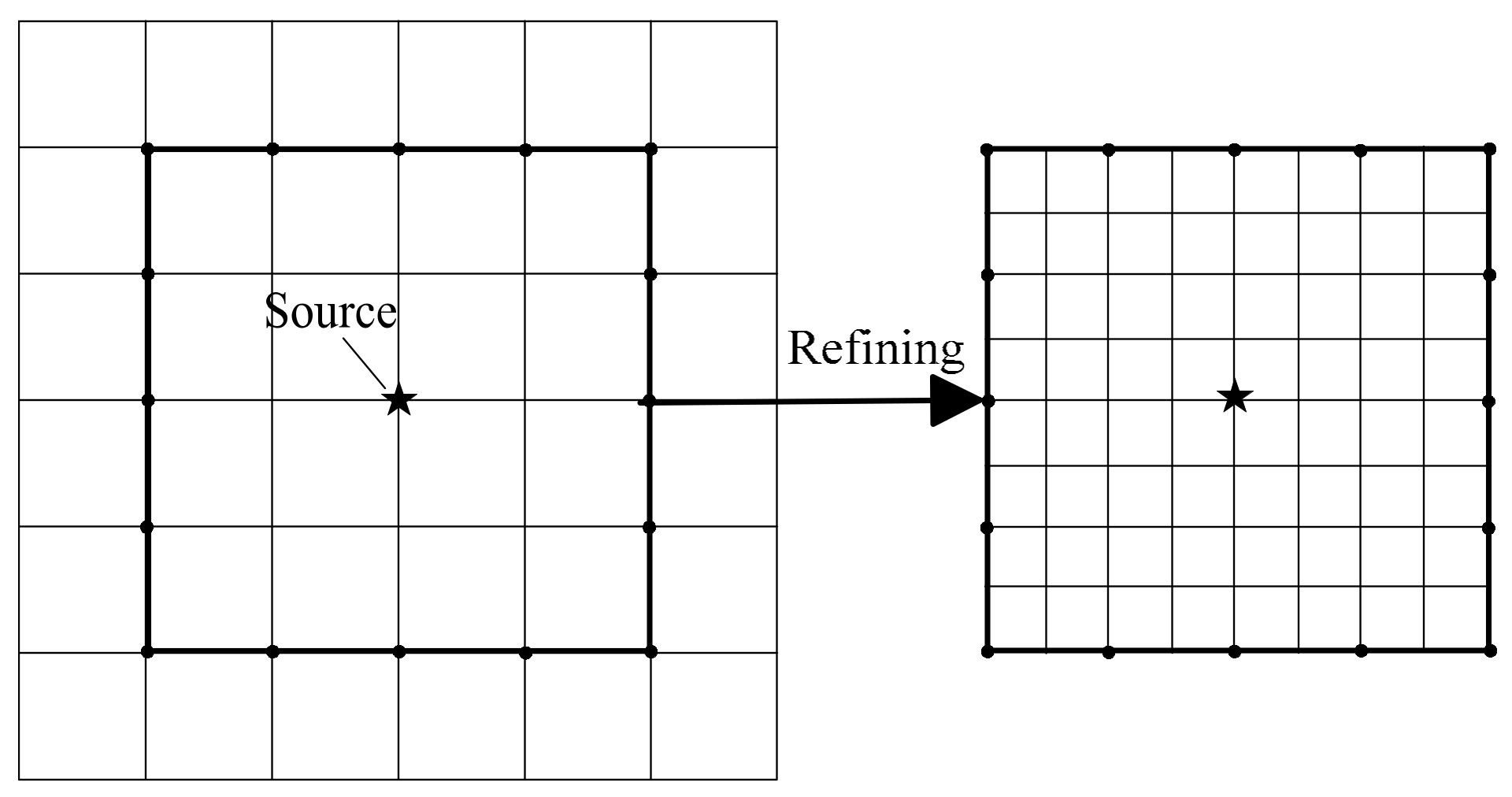
2.2. Double-Grid Technology
3. Calculation Method of Raypath
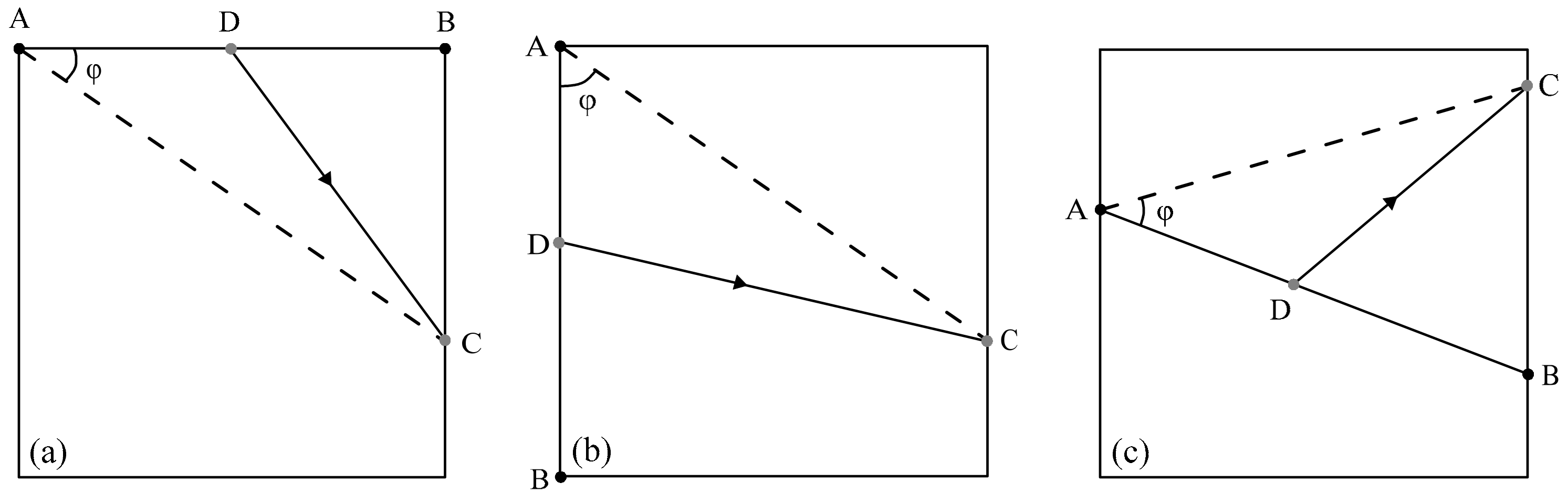
3.1. The Linear Interpolation Method
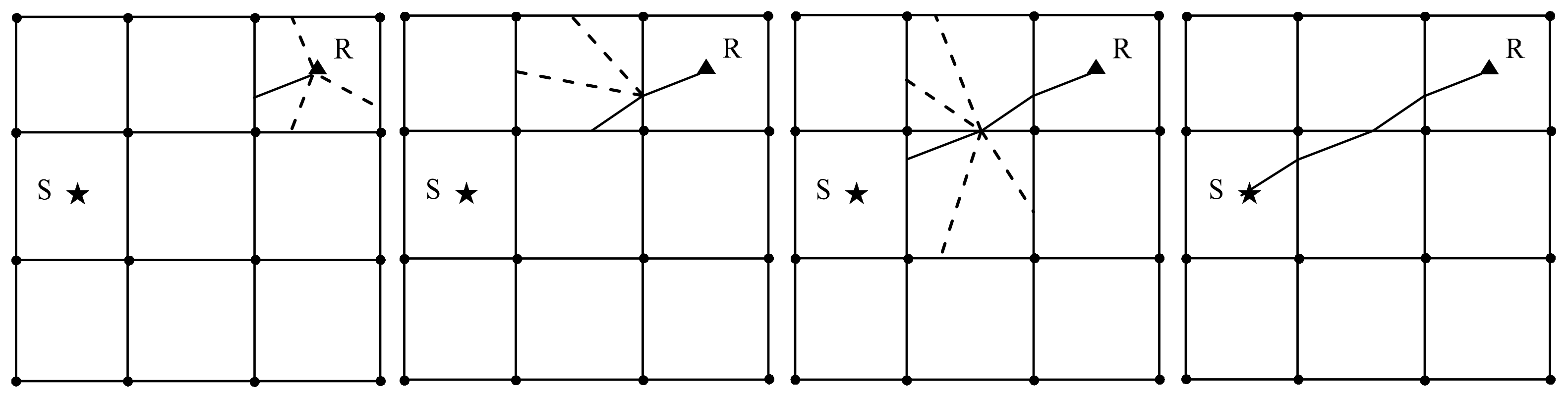
3.2. Raypath Tracing Process
4. Model Test
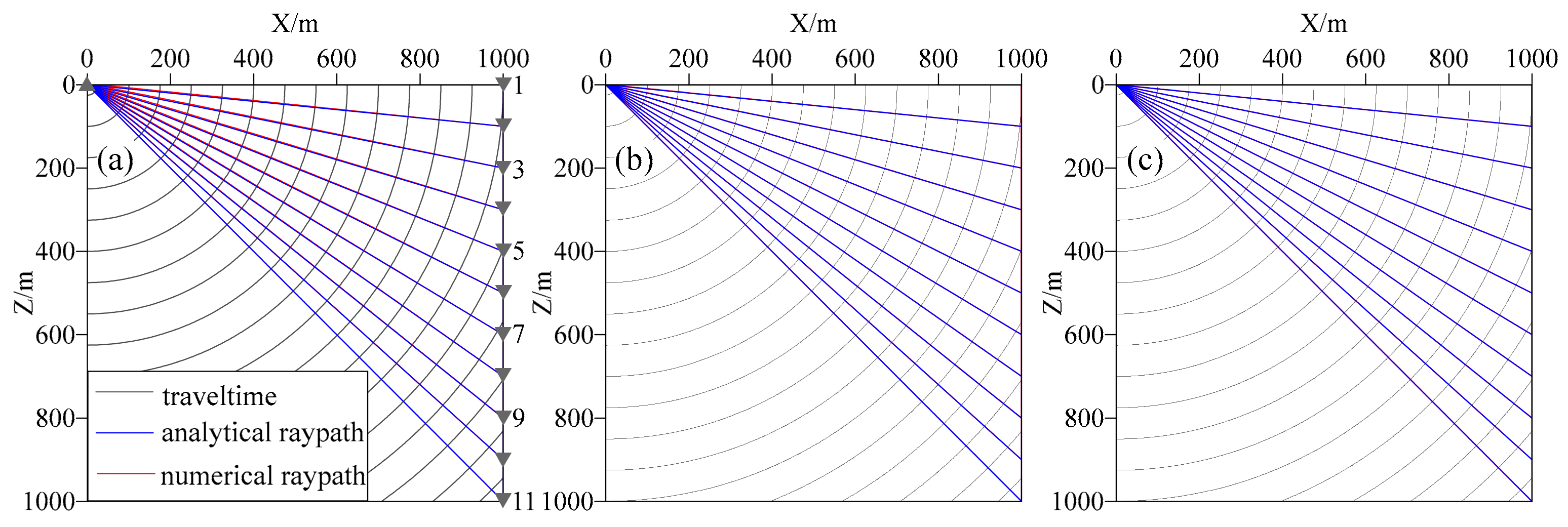
4.1. Homogeneous Model
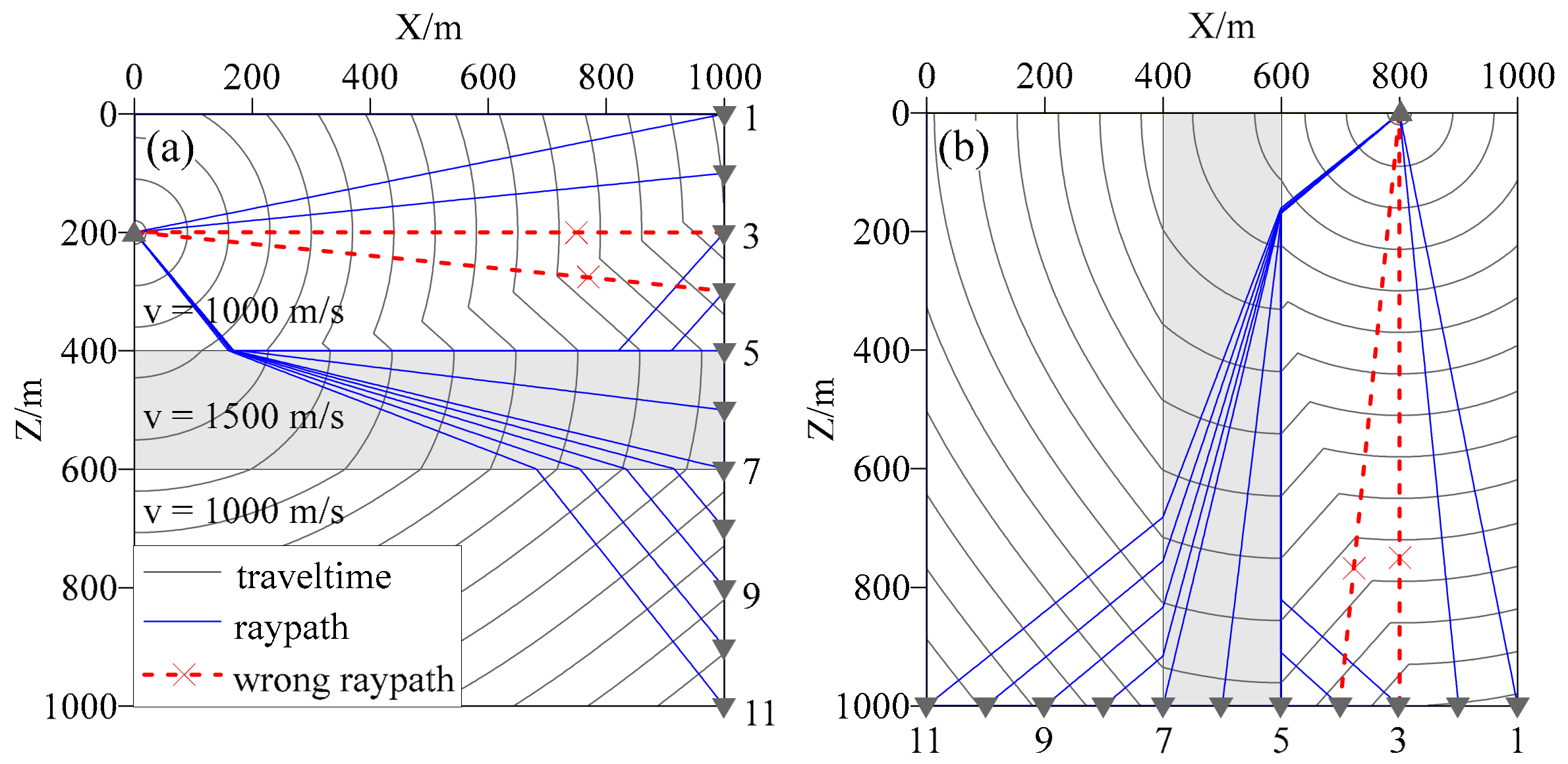
4.2. High-Speed Sandwich Model
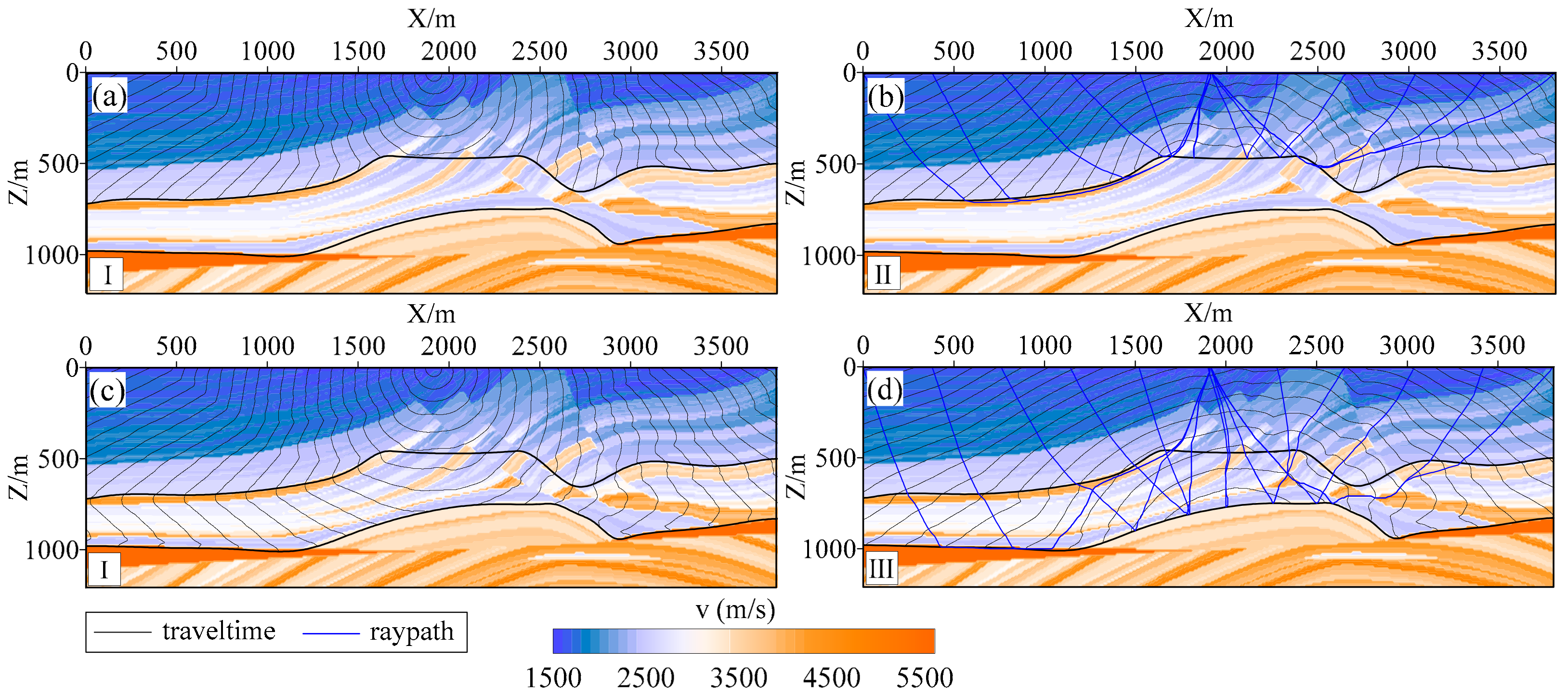
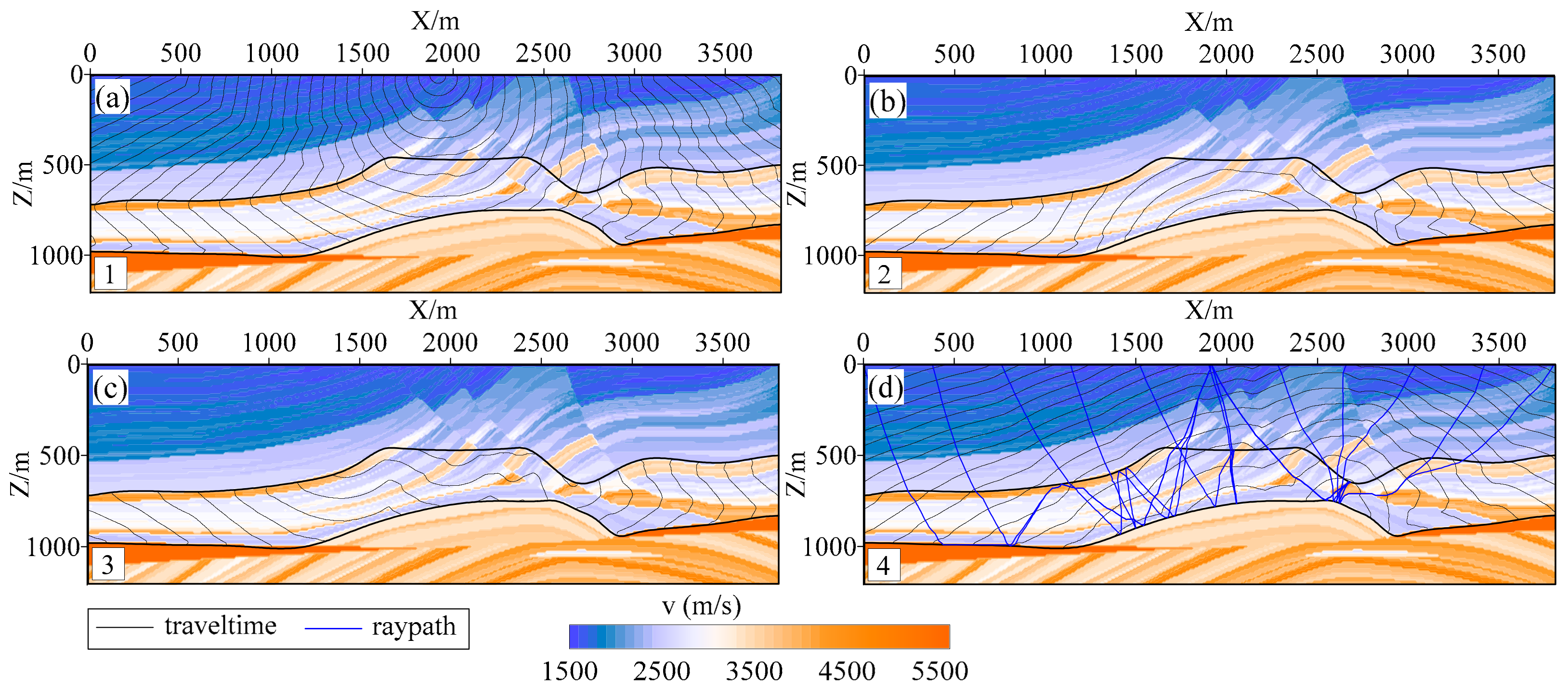
4.3. Marmousi Model
5. MFMM Ray Tracing
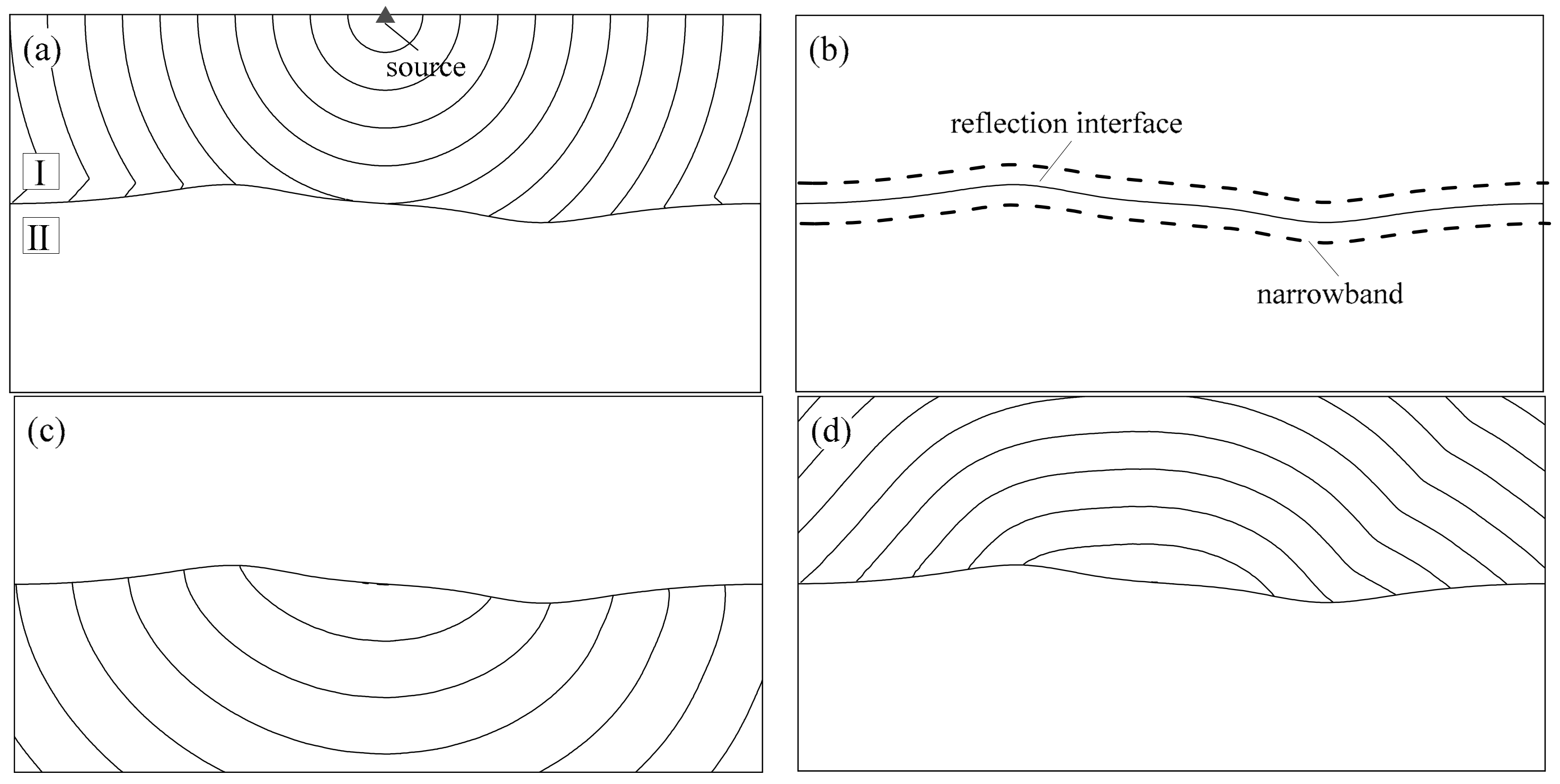
5.1. Multistage Approach
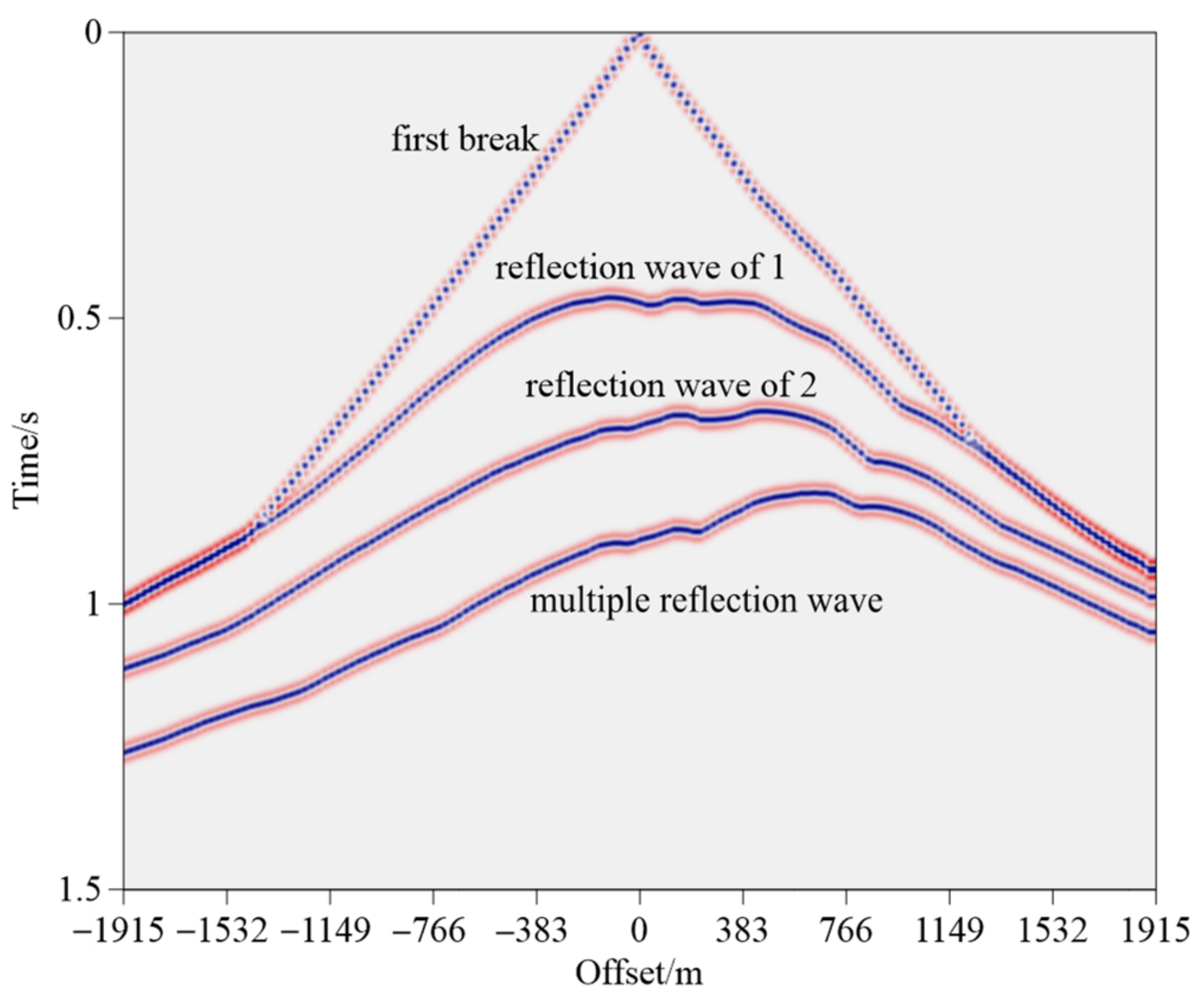
5.2. Marmousi Model Test
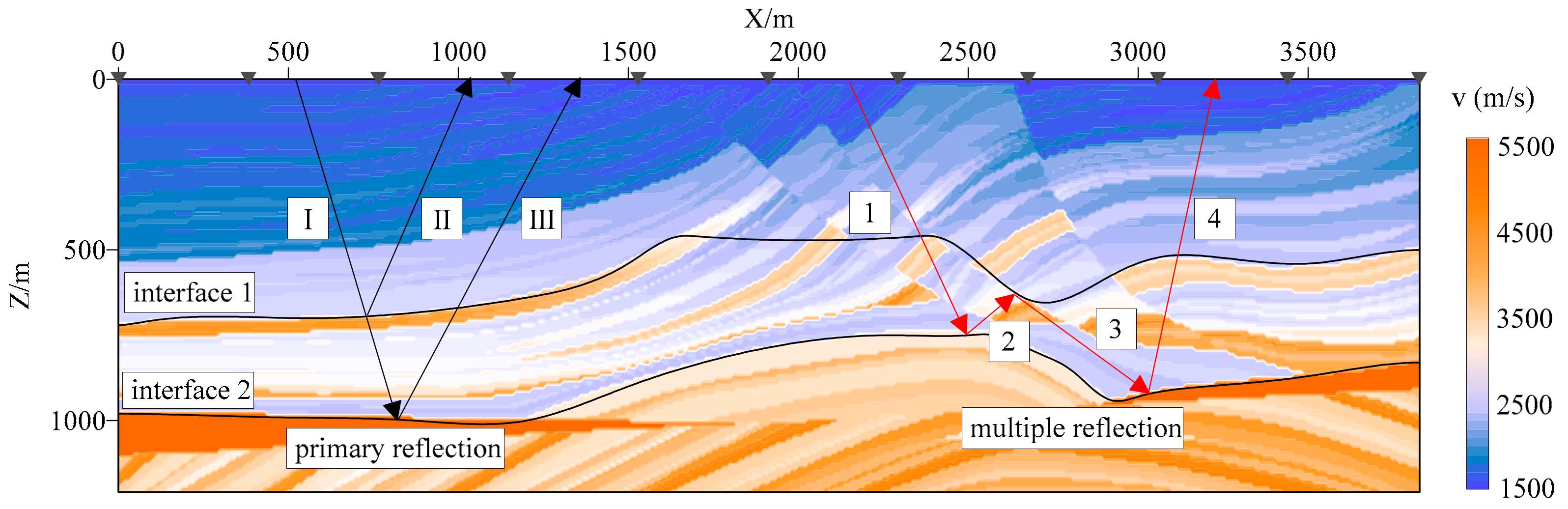
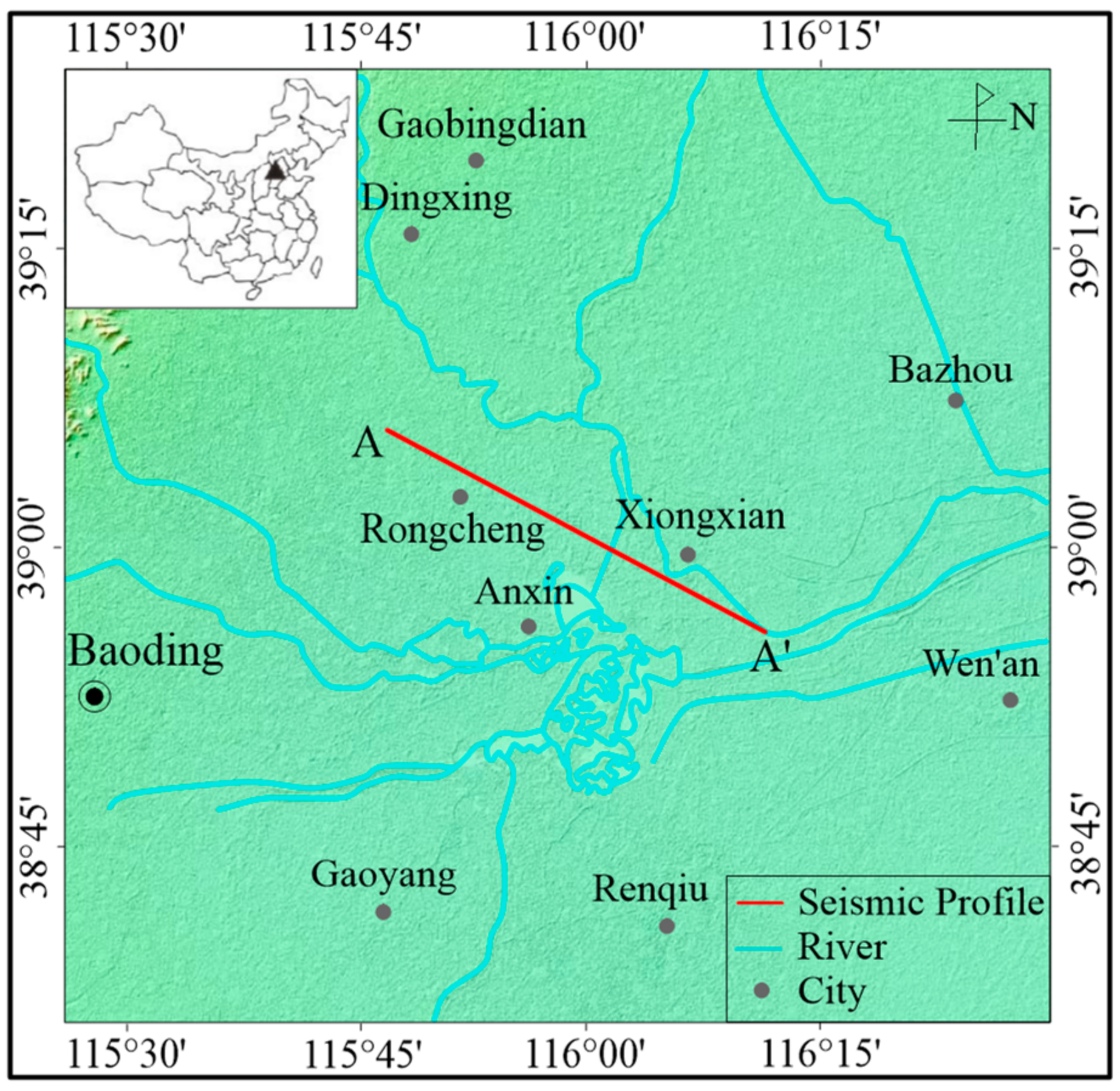
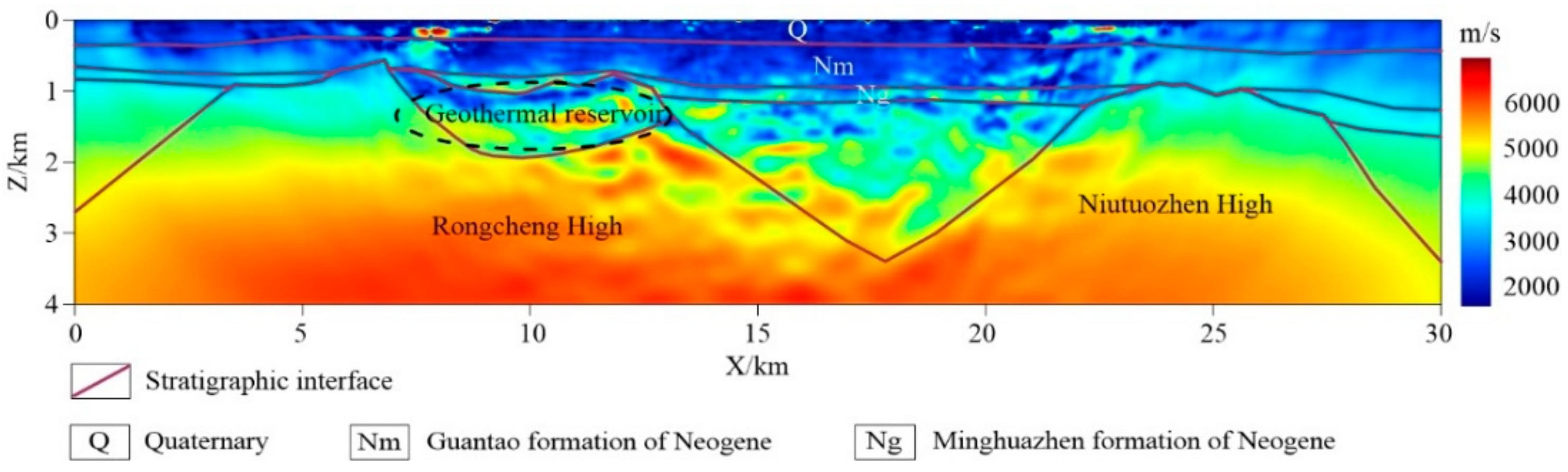
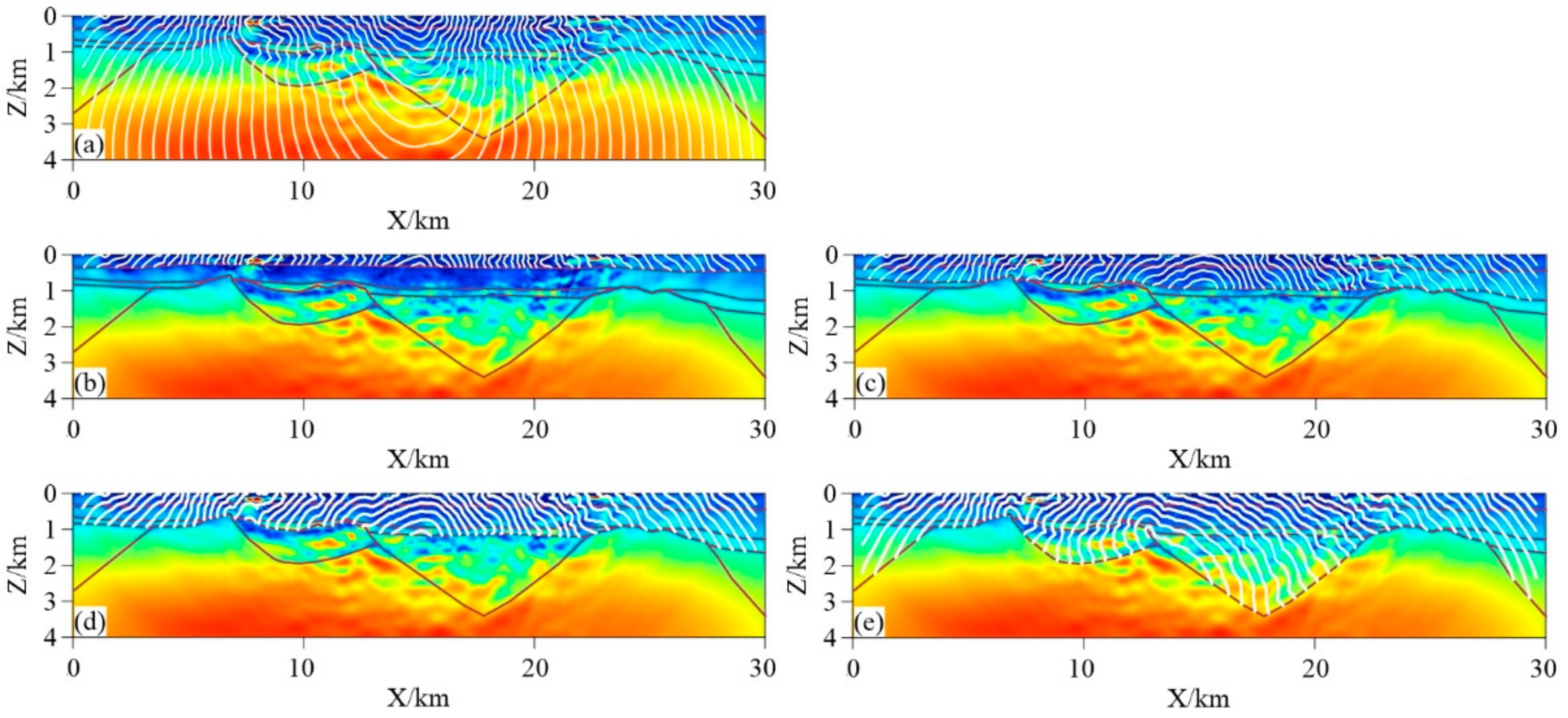
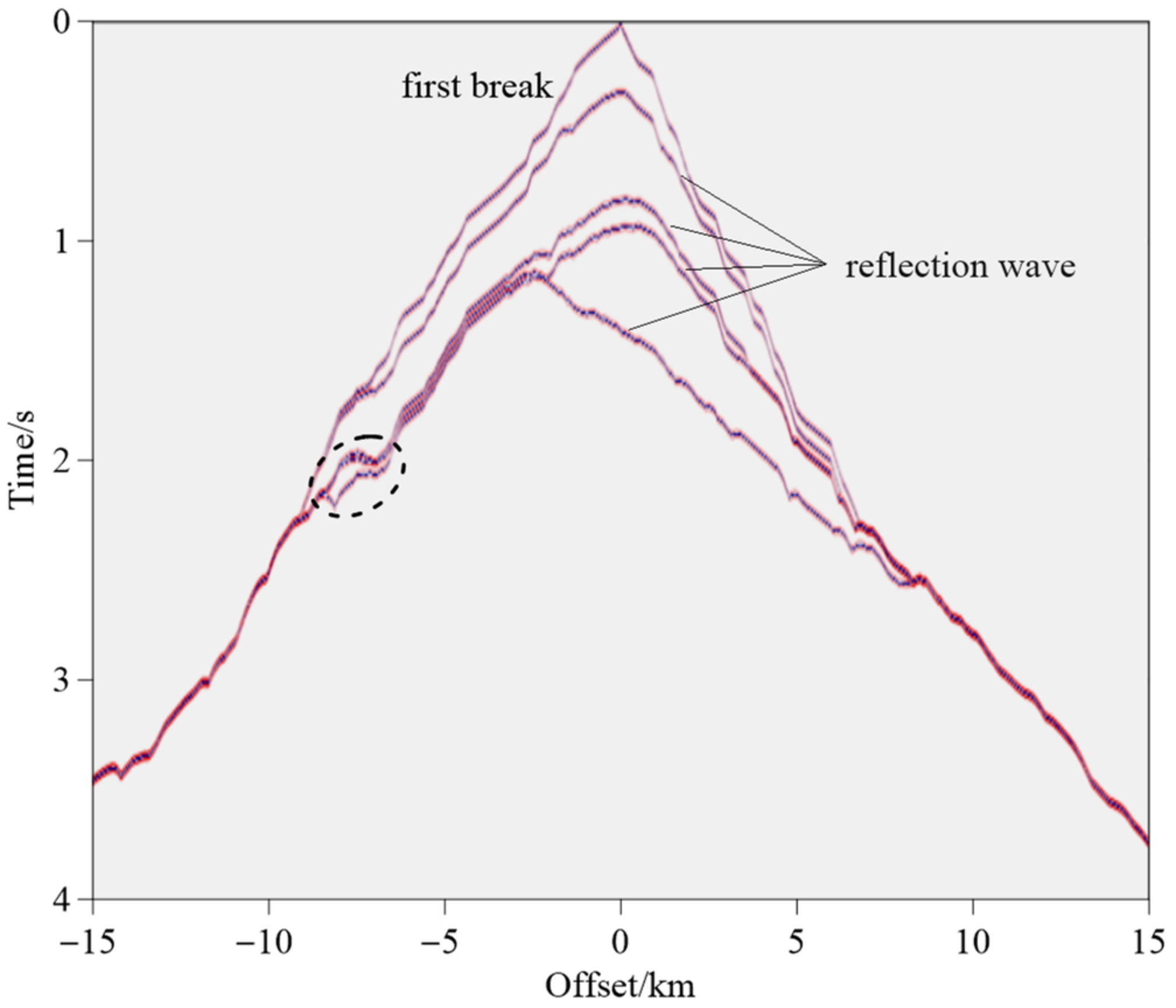
5.3. A Field Example: Xiong’an New Area
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vidale, J.E. Finite-difference calculation of traveltimes. Bull. Seismol. Soc. Am. 1988, 78, 2062–2076. [Google Scholar]
- Vidale, J.E. Finite-difference calculations of traveltimes in three dimensions. Geophysics 1990, 55, 521–526. [Google Scholar] [CrossRef]
- Trier, J.V.; Symes, W.W. Upwind finite-difference calculation of traveltimes. Geophysics 1991, 56, 812–821. [Google Scholar] [CrossRef]
- Podvin, P.; Lecomte, I. Finite difference computation of traveltimes in very contrasted velocity model: A massively parallel approach and its associated tools. Geophys. J. R. Astron. Soc. 1991, 105, 271–284. [Google Scholar] [CrossRef]
- Qin, F.H.; Luo, Y.; Olsen, K.B.; Cai, W.Y.; Schuster, G.T. Finite-difference solution of the eikonal equation along expanding wavefronts. Geophysics 1992, 57, 478–487. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef]
- Sethian, J.A.; Popovicit, A.M. 3-D traveltime computation using the fast marching method. Geophysics 1999, 64, 516–523. [Google Scholar] [CrossRef]
- Popovicit, A.M.; Sethian, J.A. 3-D imaging using higher order fast marching traveltimes. Geophysics 2002, 67, 604–609. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics 2004, 69, 1338–1350. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophys. J. Int. 2004, 156, 631–647. [Google Scholar] [CrossRef]
- Hassouna, M.S.; Farag, A.A. Multistencils fast marching methods: A highly accurate solution to the eikonal equation on cartesian domains. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1563–1574. [Google Scholar] [CrossRef]
- Kim, S. An o(n) level set method for eikonal equations. SIAM J. Sci. Comput. 2001, 22, 2178–2193. [Google Scholar] [CrossRef]
- Danielsson, P.E.; Lin, Q.F. A modified fast marching method. Lect. Notes Comput. Sci. 2003, 2749, 1154–1161. [Google Scholar]
- Yatziv, L.; Alberto, B.; Guillermo, S. O(N) implementation of the fast marching algorithm. J. Comput. Phys. 2005, 212, 393–399. [Google Scholar] [CrossRef]
- Merino-Caviedes, S.; Cordero-Grande, L.; Pérez, M.T.; Casaseca-de-la-Higuera, P.; Martín-Fernández, M.; Deriche, R.; Alberola-López, C. A Second Order Multi-Stencil Fast Marching Method with a Non-Constant Local Cost Model. IEEE Trans. Image Process. 2019, 28, 1967–1979. [Google Scholar] [CrossRef]
- Liu, H.; Meng, F.L.; Li, Y.M. The interface grid method for seeking global minimum travel-time and the correspondent raypath. Chin. J. Geophys. 1995, 38, 823–832. [Google Scholar]
- Zhang, F.X.; Wu, Q.J.; Li, Y.H.; Zhang, R.Q.; Pan, J.T. Application of FMM ray tracing to forward and inverse problems of seismology. Prog. Geophys. 2010, 25, 1197–1205. [Google Scholar]
- Zhang, D.; Zhang, T.T.; Zhang, X.L.; Yang, Y.; Hu, Y.; Qin, Q.Q. A new 3-D ray tracing method based on LTI using successive partitioning of cell interfaces and traveltime gradients. J. Appl. Geophys. 2013, 92, 20–29. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, T.T.; Qiao, Y.F.; Zhang, Y.; Hu, Y.; Qin, Q.Q. A 3-D ray tracing method based on B-spline traveltime interpolation. Oil Geophys. Prospect. 2013, 48, 559–566. [Google Scholar]
- Serretti, P.; Morelli, A. Seismic rays and traveltime tomography of strongly heterogeneous mantle structure: Application to the Central Mediterranean. Geophys. J. Int. 2011, 187, 1708–1724. [Google Scholar] [CrossRef]
- Li, X.Z.; Zhang, W. Application of Snell’s law in reflection raytracing using the multistage fast marching method. Earthq. Res. Adv. 2021, 1, 41–48. [Google Scholar] [CrossRef]
- Rawlinson, N.; Sambridge, M.; Hauser, J. Multipathing, reciprocal traveltime fields and raylets. Geophys. J. Int. 2010, 181, 1077–1092. [Google Scholar] [CrossRef]
- Wei, P.L.; Sun, J.G.; Meng, X.Y. A ray path calculation method based on grid traveltime. Oil Geophys. Prospect. 2018, 53, 722–729. [Google Scholar]
- Wang, F.; Qu, X.X.; Liu, S.X.; Li, Y.P.; Wu, J.J. A new 3-D ray tracing approach based on both multi-stencils fast marching and the steepest descent. Oil Geophys. Prospect. 2014, 49, 1106–1114. [Google Scholar]
- Asakawa, E.; Kawanaka, T. Seismic ray tracing using linear traveltime interpolation. Geophys. Prospect. 1993, 41, 99–111. [Google Scholar] [CrossRef]
- Zhang, T.T.; Qiu, D.; Zhang, D. A modified 3D traveltime gradient ray tracing method. Oil Geophys. Prospect. 2016, 51, 916–923. [Google Scholar]
- Miao, H.; Sun, J.G.; Wang, R.; Yan, H.Q.; Yi, C.; Wei, L.P. 3D traveltime ray tracing based on Chebyshev polynomials. Oil Geophys. Prospect. 2018, 53, 462–468. [Google Scholar]
- Sun, J.G.; Li, Y.L.; Sun, Z.Q.; Miao, H. Computation of Seismic Traveltimes and Raypath Based on Model Parameterization. J. Jilin Univ. 2018, 48, 343–349. [Google Scholar]
- Zhang, Y.; Yan, X.; Bai, C.Y. Multi-phase seismic ray tracing in 3D undulated layered media based on multistage FMM algorithm. Prog. Geophys. 2018, 33, 1013–1021. [Google Scholar]
- Li, W.J.; Wei, X.C.; Ning, J.R.; Zhang, J.W. A method using improved eikonal equation to compute travel time. Oil Geophys. Prospect. 2008, 43, 589–594. [Google Scholar]
- Wang, K.; Feng, X.; Malcolm, A.; Williams, C.; Wang, X.J.; Zhang, K.; Zhang, B.W.; Yue, H.Y. Multiscale full-waveform inversion with land seismic field data: A case study from the jizhong depression, middle eastern China. Energies 2022, 15, 3223. [Google Scholar] [CrossRef]
- Yue, H.Y.; Wang, K.; Zhang, J.; Liu, J.X.; Wang, X.J.; Zhang, B.W. High-precision imaging technology of deep reflection seismic in Xiong’an New Area and its surroundings. Oil Geophys. Prospect. 2022, 57, 855–869. [Google Scholar]
- Radad, M.; Gholami, A.; Siahkoohi, H.R. A fast method for generating high resolution single-frequency seismic attributes. J. Seism. Explor. 2016, 25, 11–25. [Google Scholar]
- Mafakheri, J.; Kahoo, A.R.; Anvari, R.; Mohammadi, M.; Radad, M.; Monfared, M.S. Expand Dimensional of Seismic Data and Random Noise Attenuation Using Low-Rank Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2773–2781. [Google Scholar] [CrossRef]
- Mousavi, J.; Radad, M.; Soleimani Monfared, M.; Roshandel Kahoo, A. Fault Enhancement in Seismic Images by Introducing a Novel Strategy Integrating Attributes and Image Analysis Techniques. Pure Appl. Geophys. 2022, 179, 1645–1660. [Google Scholar] [CrossRef]
- Ye, P.; Li, Q.C. Improvements of linear traveltime interpolation ray tracing for the accuracy and efficiency. J. Jilin Univ. 2013, 43, 291–298. [Google Scholar]
- Li, S.Z.; Suo, Y.H.; Dai, L.M.; Liu, L.P.; Jiao, Q. Development of the Bohai Bay Basin and destruction of the North China Craton. Earth Sci. Front. 2010, 17, 64–89. [Google Scholar]
- He, D.; Shan, S.; Zhang, Y.; Lu, R.; Zhang, R.; Cui, Y. 3-D geologic architecture of Xiong’an New Area: Constraints from seismic reflection data. Sci. China Earth Sci. 2018, 61, 1007–1022. [Google Scholar] [CrossRef]



| Finite-Difference Scheme | Grid Spacing | ||
|---|---|---|---|
| 20 m | 20 m (Double-Grid) | 1 m | |
| First order | 0.1094 s | 0.4531 s | 2.1250 s |
| Second order | 0.2137 s | 1.3437 s | 5.8437 s |
| Vidale | 0.1250 s | 0.6719 s | 3.0156 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Mi, H.-Z.; Li, Y.-B.; Li, Y.-G. Study on the Improved Method for Calculating Traveltime and Raypath of Multistage Fast Marching Method. Minerals 2022, 12, 1624. https://doi.org/10.3390/min12121624
Wu Q, Mi H-Z, Li Y-B, Li Y-G. Study on the Improved Method for Calculating Traveltime and Raypath of Multistage Fast Marching Method. Minerals. 2022; 12(12):1624. https://doi.org/10.3390/min12121624
Chicago/Turabian StyleWu, Qiong, Hong-Ze Mi, Yong-Bo Li, and Yan-Gui Li. 2022. "Study on the Improved Method for Calculating Traveltime and Raypath of Multistage Fast Marching Method" Minerals 12, no. 12: 1624. https://doi.org/10.3390/min12121624
APA StyleWu, Q., Mi, H.-Z., Li, Y.-B., & Li, Y.-G. (2022). Study on the Improved Method for Calculating Traveltime and Raypath of Multistage Fast Marching Method. Minerals, 12(12), 1624. https://doi.org/10.3390/min12121624








