Simulation Study on the Disaster-Causing Mechanism of Geothermal Water in Deep High-Temperature Heat-Damaged Mines

Abstract

This paper takes the bottom pumping roadway of 33190 machine roadway in the No.10 mine of China PingMeiShenMa Group as the engineering background. This mine is a hydrothermal mine, with strong heat conduction and thermal convection activities between the surrounding rock and geothermal water. This forms a geothermal anomaly area, making the overall temperature of the surrounding rock temperature field increase and affecting the mine thermal environment. According to the measured field data and the engineering geological conditions of the roadway, a roadway seepage-heat transfer model is constructed using the comsol numerical simulation software, emulating the effect of geothermal water upwelling to the roadway through random cracks in the surrounding rock at different temperatures and pressures, which has an impact on the airflow temperature field of the roadway. The study shows that the evolution law of the airflow temperature field in the roadway under different water upwelling temperatures and pressures is roughly the same, and the temperature at the entrance of the roadway is almost unchanged: the heating rate is 0, and then increases linearly. The variation in the airflow outlet temperature is analyzed, both under the conditions of same temperature but different pressure, and under the same pressure but different temperature. The water upwelling temperature and the cooling efficiency are positively correlated, and the overall growth rate of the airflow temperature is positively correlated with the water upwelling temperature and pressure; however, the effect of temperature is far greater than that of pressure. The upwelling temperature of geothermal water is the main influencing factor on the temperature field of the airflow in the roadway. Therefore, it is possible to reduce the temperature of upwelling water by laying heat insulation materials on the bottom plate, evacuating geothermal water and circulating cold-water by injection, so as to improve the thermal environment of water-heated mines and increase their production efficiency.

1. Introduction

For many years, the development of our society has been powered by coal resources as the main source of energy [1,2]. The high dependence on coal resources over the years has led to the near depletion of shallow resources and deep well mining has become the norm [3,4]. However, as the mining depth continues to extend downward, the surrounding rock temperature will also gradually increase, resulting in an abnormal thermal environment at the working face, which not only affects the safe and efficient production of the mine, but also seriously threatens the lives and health of underground workers [5,6]. Therefore, the prevention and control of thermal hazards in mines is one of the topics requiring close attention for the future.

In China, the high-temperature mines are mainly concentrated in the north [7,8], such as Hebei, Henan, Jiangsu and Anhui, where high temperature geothermal water is present in most mines in the region, thus forming hydrothermal mines [9,10]. Defining the geothermal water upwelling channel and analyzing the influence of geothermal water upwelling on the roadway surrounding the rock and its thermal environment are important bases for developing a scientific and reasonable control plan of the thermal environment in the mine.

At present, the influence of groundwater seepage-heat transfer on the temperature field of the roadway surrounding rock in underground mines has been explored by domestic and foreign scholars from different perspectives. Zhang Yanjun et al. [11] studied the influence of different thermal physical parameters on the distribution of the temperature field in surrounding rock by establishing a numerical model of heat-flow coupling in parallel double fissures, and carried out a sensitivity analysis which concluded that the sensitivity of temperature to model parameters tends to decrease in the direction of fluid flow. Chen, L. et al. [12,13] studied the distribution law of temperature field of surrounding rock and fracture water by establishing a three-dimensional non-constant coupled model of large sparsely fractureed surrounding rock in deep subsurface space. The influence of seepage velocity and fracture aperture on the temperature field of fracture water was discussed. It was concluded that the fracture characteristics have an important influence on the temperature field of large sparsely fractured surrounding rock. Stepanov et al. [14,15] designed a multi-scale simulation method using the generalized multiscale finite element method, which was used to simulate the seepage-heat transfer model, and verified the efficiency and accuracy of the proposed method. Yulong Shao [16] constructed a complex fractured rock seepage-heat transfer model, and found that the fracture network is the main water conduction channel through the model study. Ghafoori [17] monitored the seepage-heat transfer model using distributed temperature sensors; their study found that the faster the seepage rate, the faster the temperature conduction and cooling rate. Chen Liu et al. [18,19] determined the temperature field of fractured perimeter rocks by establishing a coupled heat transfer model of fractured perimeter rocks, analyzing the effects of ventilation time, perimeter porosity, fracture pore size, permeability of perimeter rocks, solid thermal conductivity, initial temperature and ventilation temperature of perimeter rocks on the temperature field distribution. Ma Y et al. [20] discussed the effects of percolation path curvature, pore size and initial temperature on heat transfer characteristics, and concluded that the overall convective heat transfer coefficient of specimens with seepage paths was lower than that of specimens with smooth fractures. Xin-xin L et al. [21] simulated the heat recovery process of a fractured rock body containing a large fracture network by modeling a geothermal bimodal system, andfound that the fracture pore size was an important factor affecting heat transfer. Zhaoying Y et al. [22] investigated the seepage and convective heat transfer behavior of fractured granite during geothermal extraction based on numerical simulation of fracture flow in geothermal reservoirs, revealing the effects of five different fracture patterns, i.e., single fracture, trapezoidal fracture, parallel fracture, Y-shaped fracture and cross fracture, on heat transfer capacity. Luo J et al. [23] studied the hydraulic and heat transfer properties of two sets of artificially fractured granite samples. The results showed that the hydraulic properties were mainly influenced by the area ratio: the larger the area ratio, the larger the fracture pore size and the higher the hydraulic conductivity. Maghoul et al. [24] derived mass conservation by heat conduction and heat convection, and established a seepage heat transfer model to discuss the influence of groundwater on the temperature field of the surrounding rock during seasonal changes. It is believed that the insulation affects the temperature and ice water content distribution in the soil.

The above-mentioned scholars analyzed the coupled model by establishing different percolation heat transfer mechanisms. The research results showed that the pressurized geothermal water takes the fracture as the main upwell channel, and the geothermal water changes the temperature field distribution of the roadway surrounding the rock through the seepage-heat transfer in the upwell process, which affects the temperature field of airflow in the roadway. The effects of seepage velocity and fracture pore size or ventilation time, as well as the basic parameters of the surrounding rock, on the temperature field of the surrounding rock were partially verified. Therefore, in this paper, we take the No.10 mine of China PingMeiShenMa Group as the research background and in order to propose solutions for the main influencing factors, and provide ideas for the cooling of the mine, we establish a seepage-heat transfer numerical model, in which geothermal water is subjected to pressure and upwelling through fractures to the interior of the roadway; deeply study the influence of temperature and pressure of geothermal water on the temperature field of roadway airflow; analyze the heat conduction and heat exchange in the process of geothermal water upwelling; study the variation laws of airflow temperature; and determine the disaster-causing mechanism of geothermal water.

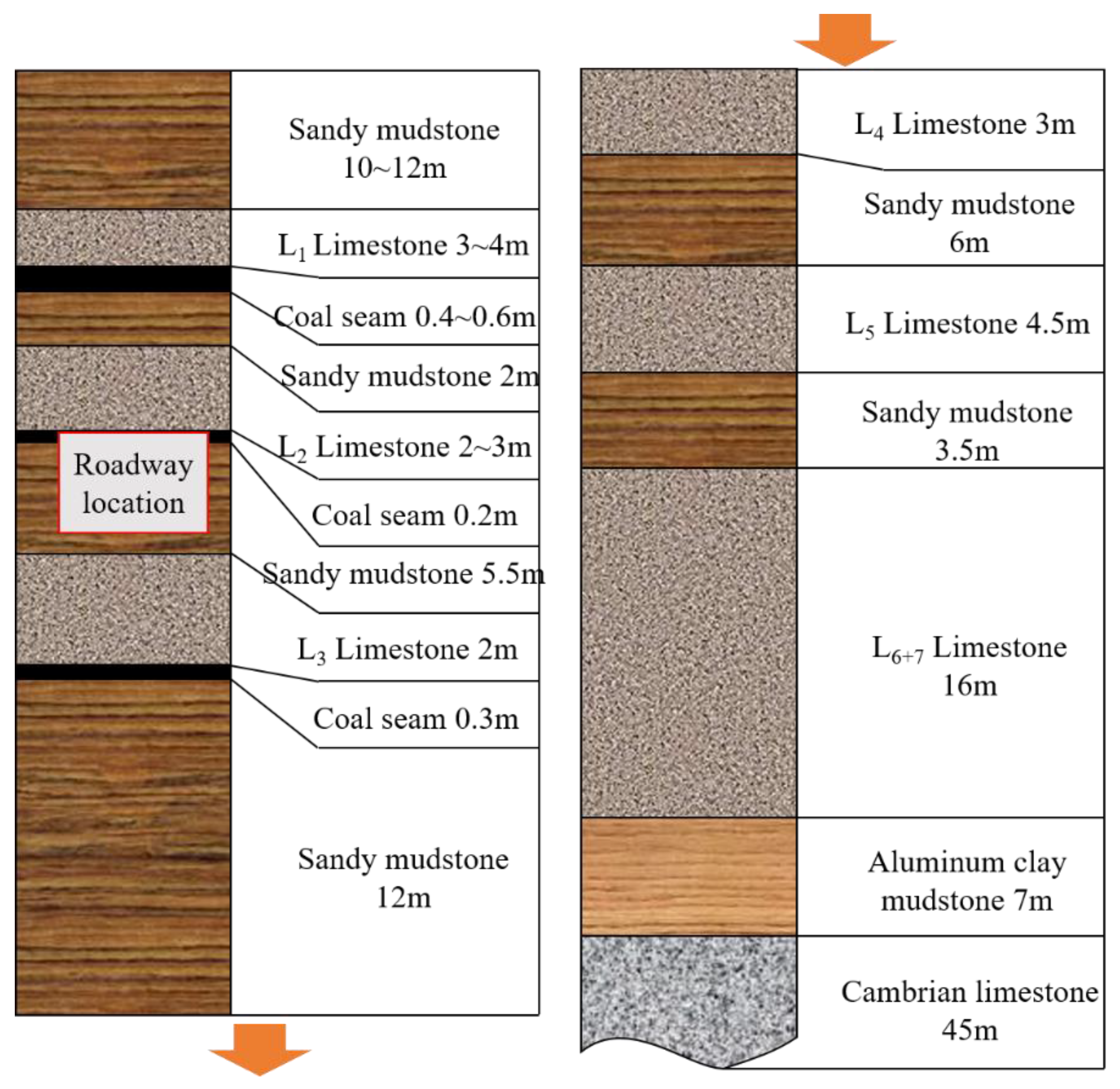
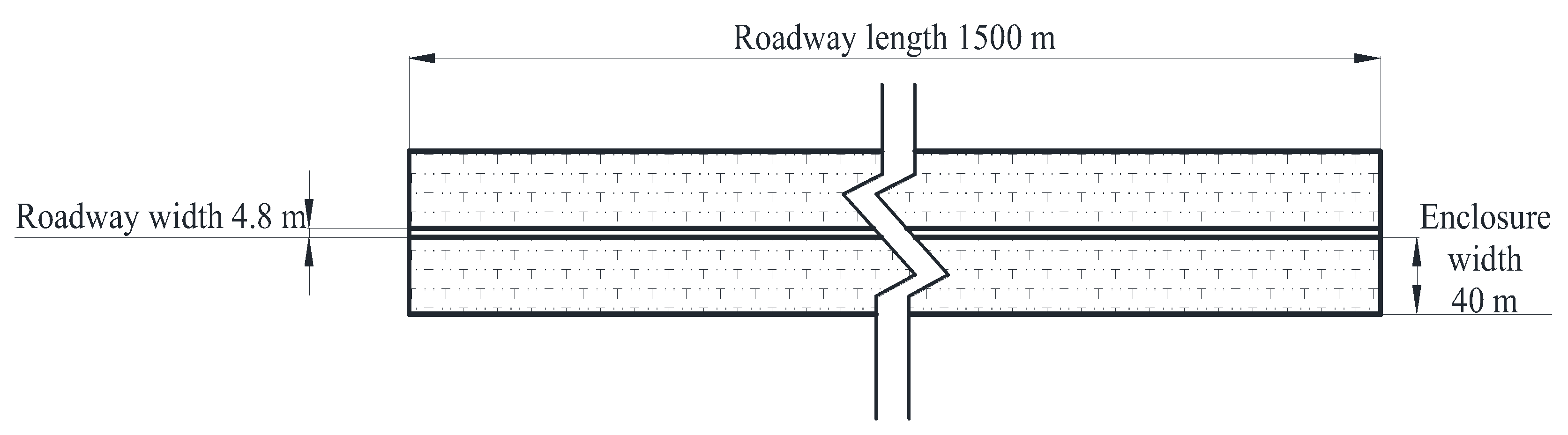
2. Overview of the Mine

The No.10 mine of China PingMeiShenMa Group is located in the northeastern part of Pingdingshan City, with a north-south tendency of about 6.0 km long and an east-west width of about 2.0~4.7 km. The machine floor roadway of hex 15-17-33190 roadway in the No.10 mine was selected for in-depth analysis. The bottom plate roadway is located in the most eastern part of the flank of the hexagonal mining area at the level of −870 m. The roadway is 1500 m long, with a rectangular section of width × height = 4800 mm × 3800 mm, and the top of the roadway is dug along the limestone floor, 16~22 m away from the bottom of the upper coal seam. The stratigraphic column diagram of the roadway is shown in Figure 1.

In order to explore the water upwelling condition of the bottom slab roadway of 33190 machine roadway, the hydrogeological conditions of the roadway were investigated on site. In addition to the top plate sandstone fissure water, we also found 33190 roadway showed bottom plate tuff pressurized water, bottom plate water gushing directly or indirectly from the Carboniferous Taiyuan Group aquifer and Cambrian tuff water, due to the tuff karst fracture groundwater with extremely uneven characteristics. As the mining depth increases, water-conducting small faults and mining fractures increase, as does the formation of local water-rich sections, which leads to an increase in the risk of sudden water. Combined with the No.10 mine information of the water drainage hole, we established the bottom slab roadway of 33190 machine roadway water drainage hole upwelling water flowrate to be 7.81~8.41 m³/min; upwelling water pressure to be 7.2~8.1 MPa; and upwelling water temperature to be 49.69~51.24 °C.

3. Determination of Thermal Environment Parameters in the Mine

3.1. Determination of the Thermal Parameters of the Roadway Airflow

The thermodynamic parameters of the airflow in the bottom slab roadway of 33190 machine roadway were measured on site, mainly including the dry and wet bulb temperature, and relative humidity and airflow speed of the airflow, as shown in Figure 2. Measurements were taken every ten days from the time the production workings were penetrated to the end of mining. The field measurement was carried out at the base point of the roadway entrance, and every measurement point was arranged 50 m along the roadway digging direction. The CFJD25 type coal mine mechanical electronic anemometer was used to determine the field airflow speed, and the YWSD50/100(A) mine intrinsically safe temperature and humidity detector was used to determine the dry and wet bulb temperature and relative humidity of the airflow.

The field measurement results show that the average airflow humidity in the roadway is 73%, the average dry bulb temperature is 29.2 °C and the average wet bulb temperature is 27.1 °C. The temperature along the airflow rises gradually, and when the surface temperature is 15 °C, the ambient temperature of the underground roadway can reach between 28 °C and 30 °C. Operating in such a high temperature and high humidity environment inevitably increases accidents and reduces the mine production efficiency. Therefore, it is of great practical significance to clarify the influence of geothermal water upwelling in mines on the airflow temperature, and to develop a corresponding management plan.

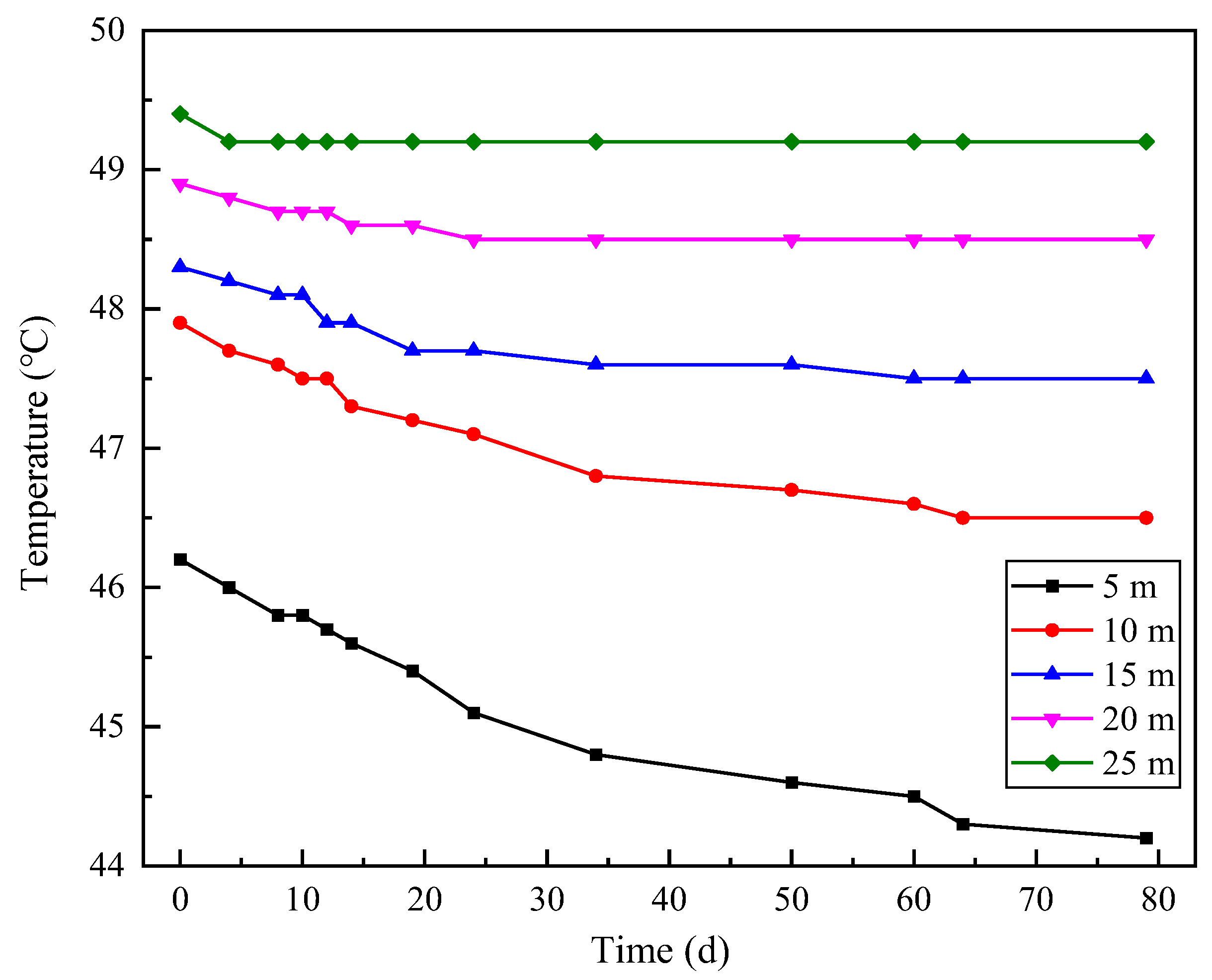
3.2. Determination of the Original Rock Temperature of the Roadway

The temperature of the raw rock of the roadway was measured by drilling into the roadway gang at 600 m from the roadway entrance in the bottom slab roadway of 33190 machine roadway. The holes were drilled to a depth of 25 m, and temperature sensors were arranged in sections at 5, 10, 15, 20, and 25 m. After drilling the temperature measurement holes, the grouting pipes, temperature measurement wires and rigid rubber tubes were bundled, and a high-strength non-woven bag was set up in sections to form a sealed grouting system. After the bundle was completed, the grouting pipe was sent into the temperature measurement borehole, the temperature sensor was sent to the pre-buried position, and then the borehole was sealed by grouting, section by section. The process flow is shown in Figure 3.

The following describes the measurement process. After everything is installed, wait for the temperature sensor to have enough sensing time, and then use the instrument to measure the temperature of the original rock. At the initial stage, the temperature sensor and the surrounding rock had not yet reached thermal equilibrium, and the observation was frequent. The frequency was gradually reduced at a later stage after the ground temperature stabilized, and the test results are shown in Figure 4. It can be seen that the initial ground temperature measurement value is large because the temperature field of the surrounding rock is disturbed and its temperature increases due to the frictional heat generated by the high speed rotation of the drill bit in the surrounding rock in the early stage. The deeper the depth of the measurement point, the higher the ground temperature obtained, and there is a certain gradient relationship. As the airflow through the roadway continues to exchange heat with the surrounding rock, it will lead to changing and decreasing ground temperature data at shallow locations. However, as test depth increases, the less the temperature field of the surrounding rock is disturbed by the airflow, and the ground temperature data is more stable. Within the heat-regulating circle of the roadway, there is a temperature gradient due to airflow disturbance, but beyond it, the temperature of the surrounding rock remains stable and is the original rock temperature. After analysis, the ground temperature data measured at 25 m remained basically unchanged after 5 days, while the other four ground temperature curves continued to change and gradually showed a temperature gradient. The ground temperature data at the 25 m measurement point was therefore taken as the original rock temperature, at 49.2 °C.

3.3. Test of the Thermal Physics Parameters of the Surrounding Rock

Two samples of sandy mudstone and limestone were taken from the 33190 roadway, which were sealed and packed and sent to the plant to be processed into standard specimens, after which they were sealed and packed again and sent to the laboratory, then numbered and subjected to a series of physical property tests, including density, porosity, and thermal conductivity. The density and water content of the specimens were tested as in Figure 5, the porosity was tested as in Figure 6, and the thermal conductivity was determined as in Figure 7. The results obtained are shown in

Table 1. Thermal physics parameters of the surrounding rock.

Specimen Number	Rock Characteristics	Natural Density (g/cm3)	Dry Density (g/cm3)	Water Content (%)	Porosity	Thermal Conductivity W/(m·K)
1	sandy mudstone	2.59	2.56	1.14%	12.26%	2.13
2	sandy mudstone	2.57	2.54	1.13%	11.53%	2.11
3	sandy mudstone	2.58	2.55	1.13%	11.86%	2.19
	average value	2.58	2.55	1.13%	11.88%	2.15
4	limestone	2.71	2.71	0.09%	8.97%	2.72
5	limestone	2.71	2.71	0.09%	9.16%	2.68
6	limestone	2.70	2.69	0.11%	9.07%	2.67
	average value	2.71	2.70	0.096%	9.07%	2.69

.

4. Numerical Model for Seepage-Heat Transfer of Pressurized Geothermal Water Upwelling

4.1. Model Assumptions

For numerical simulation of the temperature field of the surrounding rock, rationalization assumptions need to be made for the surrounding rock in order to facilitate analysis and calculations, as follows.

• Free flow of airflow from the mouth of the roadway with no return flow.
• Disregard the effect of roadway excavation on the extension of fractures, which are much longer than their width.
• Ignore the effect of fractures in the overburden of the roadway, and ignore smaller fractures.
• The fractured rock is isotropic and thermal physics parameters stable.
• The fracture flow is a steady laminar flow of incompressible fluid with no phase change during flow.

Using comsol version 6.0 for numerical simulation. Comsol numerical simulation software defaults the airflow to flow freely from the entrance of the roadway, and the setting of return flow is not possible. The return flow will cause the cold air from the external connected roadway to flow back into the roadway, so that the temperature of the airflow at the exit of the roadway will be affected. Random fissures in the roadway are randomly generated using the Monte Carlo method, but they are fixed, so it is impossible to simulate the deformation and expansion of fissures in the roadway, and the path of geothermal water upwelling is also to be fixed. The nature of the fractured rock in real life is not clear, therefore for easier calculation and modeling, the surrounding rock properties of the fractures are set to be the same in all directions. The compression of geothermal water under pressure generates energy; however, the pressure changes continuously, thus this process cannot be emulated in the model. All of these steps have an effect on the roadway temperature field, yet the effect is relatively small and difficult to implement in the model, so assumptions are made and their effects are ignored when the model is established.

4.2. Model Building

Based on the measured data in the field and the hydrogeological conditions of the bottom slab roadway of 33190 machine roadway, the comsol numerical simulation software was used to establish a geothermal water seepage-heat transfer model along the fracture when the roadway was not excavated Figure 8. A horizontal model coupling seepage-heat transfer and convective heat transfer was also established after excavation of the roadway Figure 9. Thereafter, a mesh was generated in the model; the overall mesh was divided by physical field and refined with triangular meshes, ensuring compliance with the mesh standard. The complete mesh in the model has a total of 40,174 vertices and 72,422 elements. In the quality measurement of mesh skewness, the minimum element quality was 0.2574, the average element quality was 0.6304, and the element area ratio was 0.00248, which met the standards for 2D mesh construction.

4.3. Model Mesh-Independence Verification

Using comsol numerical simulation software to generate the grid, a grid division of a total of nine was obtained, as shown in

Table 2. Error analysis of each measurement point after gradual encryption of the model grid.

Grid Division	Location of Measurement Points/m
	0	300	600	900	1200	1500
Extremely Coarsening	20	20.48	21.61	22.91	24.18	25.37
Super Coarsening	20	20.48	21.60	22.88	24.14	25.33
More Coarsening	20	20.63	21.82	23.12	24.79	25.67
Coarsening	20	20.96	22.37	23.67	25.01	26.14
General	20	21.01	22.41	23.75	25.04	26.23
Refining	20	21.10	22.56	23.89	25.15	26.38
More Refining	20	21.02	22.41	23.78	25.08	26.29
Super Refining	20	20.76	22.07	23.36	24.65	25.94
Extremely Refining	20	20.82	22.17	23.51	24.82	26.02
Average Temperature	20	20.81	22.11	23.43	24.76	25.93
Maximum Error	0	1.43%	2.02%	1.95%	1.57%	1.73%
Average Error	1.74%

. When increasing the number of grids does not lead to much change in the calculation results, doing so becomes irrelevant. The upwelling water temperature and pressure is set to 50 °C, 8 MPa, the airflow temperature is set to 20 °C, observation of the airflow temperature distribution in the roadway is at steady state, and a measurement point is set every 300 m in the roadway. The number of grids was continuously increased to observe the change of airflow temperature, as shown in Table 2, greatly increasing the calculation steps. Despite fluctuations in the data of each measurement point, the distribution of airflow temperature in the roadway remained approximately the same. It can be concluded that although the grid encryption has an effect on the data, after further analysis, since the error was found to be only 1.74%, which is within the standard range, this proves the irrelevance of the grid, and verifies the stability and feasibility of the model.

4.4. Model Parameters and Boundary Condition Settings

In the comsol numerical simulation software, based on the actual measured data in the field, the initial temperature of the airflow in the model was set to 20 °C and the initial airflow speed was set to 1.5 m/s. The temperature and pressure boundaries were set based on the data of water upwelling from the spar holes in the bottom slab roadway of 33190 machine roadway, and gradients were set for the study in order to analyze the effects of water temperature and pressure on the temperature field of airflow in the roadway, respectively. Through experimental measurements, the range of gradients was set on the model for the parameters of the thermal physics of the surrounding rock as shown in

Table 3. Gradient range of parameter settings in the surrounding rock section of the model.

Thermal Conductivity	Convection Heat Transfer Coefficient	Density	Constant Pressure Specific Heat Capacity	Porosity	Permeability
2.1~2.7 W/(m·K)	25 W/(m2·K)	2600~2700 kg/m3	680~870 J/(kg·K)	0.06~0.09	1 × 10−16 to 1 × 10−14 m2

.

After field research, the lower boundary upwelling water pressure of the surrounding rock was set to 6, 7, 8, 9 and 10 MPa and the upwelling water temperature was set to 40, 45, 50, 55 and 60 °C, by controlling a single variable and analyzing the effect of pressure and temperature variations on the temperature field of the airflow.

The fluid in the model as a whole conforms to the Navier–Stokes equation, which contains two equations for conservation of mass and conservation of momentum, as follows.

Conservation of mass.

$$\frac{\partial \rho }{\partial t}+\nabla (\rho \times u)=0$$

The conservation of momentum equation is shown in Figure 10.

The heat transfer control equation in the model is shown in Figure 11.

In the above equations: ρ is the fluid density; $u$ is the fluid flow velocity; $t$ is the flow time; and T is the temperature.

The fractures in the surrounding rock are set as the boundary heat source, and are set as the thermal thin approximation condition; the non-conducting fracture mouth is set as no flow and thermal insulation; and the fractures entrance pressure is set as the same as the lower upwelling pressure. The intersection of the fractures flow to the roadway and the roadway wall is set as the point heat flux.

The airflow in the roadway is set to a weakly compressible and fully developed flow; the inlet air temperature is set to 20 °C; the airflow speed is 1.5 m/s; and the two walls of the roadway are free of slippage and set to two conditions of thermal convection and heat flux.

The heat flux boundary is given by

$$Q=h(T_{ext}-T)$$

In the above equation: $Q$ represents the convective heat flux, W/m²; $h$ represents the convective heat transfer coefficient, W/(m² × K); $T_{ext}$ represents the temperature of the external domain of the heat flux boundary, °C; and $T$ represents the temperature of the internal domain of the heat flux boundary, °C.

4.5. Model Characteristics

The numerical model of pressurized geothermal water upwelling seepage-heat transfer established in this paper has the following characteristics.

• A geothermal gradient was set for the model as a whole, and the sandy mudstone and limestone rock layers were assigned values between them by a segmentation function, consistent with field measurements.
• Generation of random fractures in tuffs by the Monte Carlo method.
• Groundwater upwelling process is local rapid upwelling along the fracture, the fracture set as a heat source, and the rock around the fracture for heat exchange causes perturbation to the surrounding rock temperature field.
• The rock stratum is a porous medium; the solid medium is the lower surrounding rock; and the fluid medium is groundwater, containing heat conduction and heat convection, setting up its internal fluid flow to satisfy Darcy’s law, so that the overall flow of geothermal water within it is a seepage upwelling process.
• Coupling of fracture flow and Darcy flow fields, coupling of fracture heat transfer and porous media heat transfer, setting heat fluxes and boundary heat sources to fractures.
• Coupling of airflow laminar flow field and Darcy flow field, coupling of fluid heat transfer and porous media heat transfer, and setting up convective heat transfer and heat conduction on both sides of the rock wall.

5. Simulation Results and Analyses

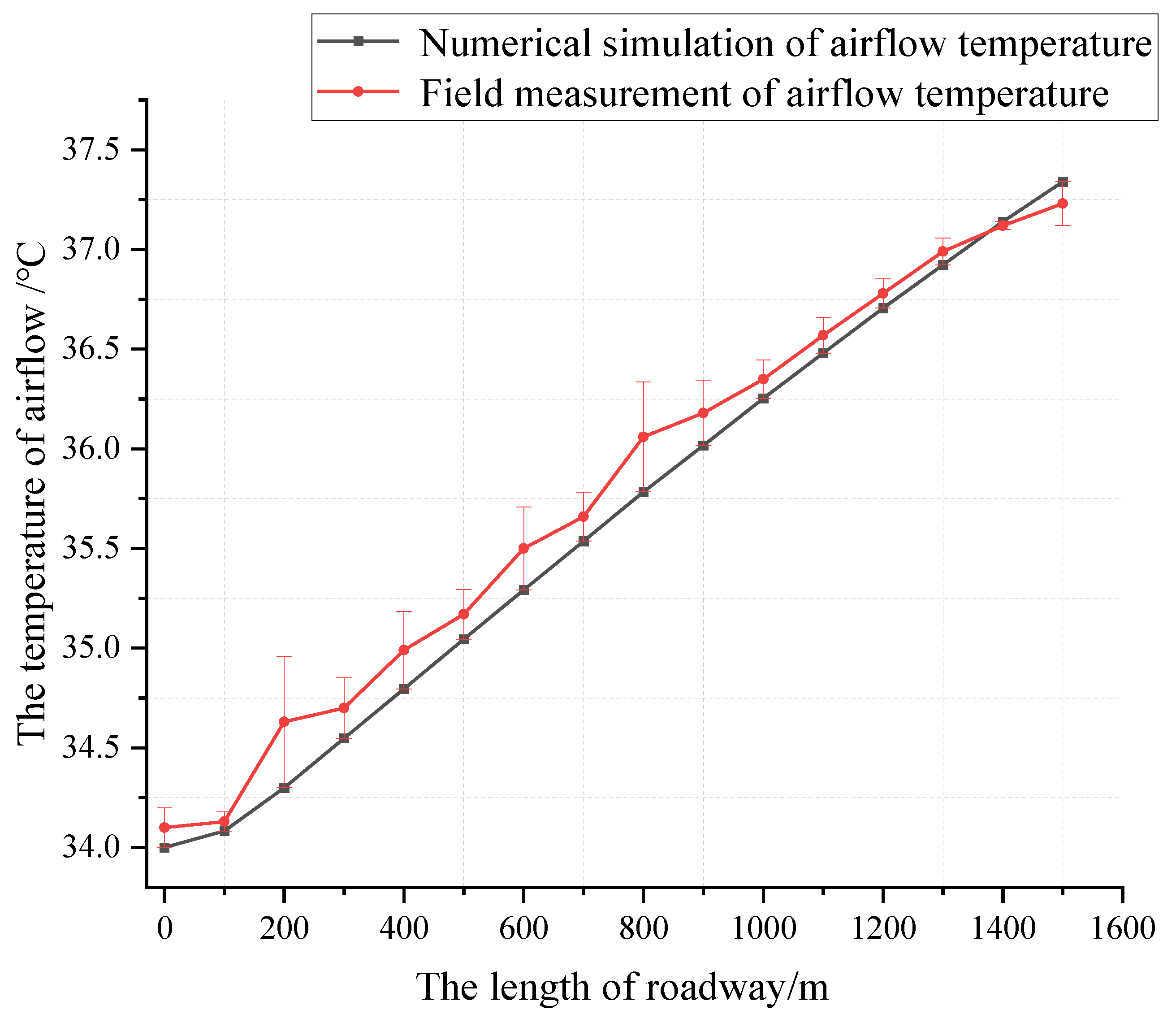
5.1. Model Validation and Error Analysis

According to the site records, in the bottom pumping roadway of 33190 machine roadway, geothermal water gushing water pressure measured in drill holes was about 8 MPa; and gushing water temperature was about 50 °C. Therefore, the water upwelling temperature and pressure in the model were set as the actual measured data in the field, and finally the airflow temperature in the roadway was obtained as shown in

Table 4. Numerical simulation and field measurement of roadway airflow temperature and the error between them.

Location of Measurement Points/m	Roadway Airflow Temperature from Numerical Simulation/°C	On-Site Measurement of Roadway Airflow Temperature/°C	Error(%)
0	34	34.1	0.29%
100	34.08	34.13	0.14%
200	34.3	34.63	0.96%
300	34.55	34.7	0.44%
400	34.8	34.99	0.56%
500	35.05	35.17	0.36%
600	35.29	35.5	0.59%
700	35.54	35.66	0.35%
800	35.78	36.06	0.77%
900	36.02	36.18	0.45%
1000	36.25	36.35	0.27%
1100	36.48	36.57	0.24%
1200	36.71	36.78	0.20%
1300	36.92	36.99	0.18%
1400	37.14	37.12	0.05%
1500	37.34	37.23	0.29%
Average error		0.38%

, and the temperature distribution curve along the roadway as shown in Figure 12. The measurement points were arranged every 100 m in this roadway, and the airflow temperature and humidity statistics were carried out several times, with the average temperature finally obtained shown in Table 4, and the error of the results obtained from numerical simulation also shown in Table 4.

As shown in Table 3, the average error produced by the model is 0.38%, which is in accordance with the standard. The model-derived airflow temperature grows slowly within 100 m of the roadway entrance and then grows linearly and steadily, while the overall trend of the field measured data is the same as the model data, but fluctuates up and down. After comparing the two graph lines, it is found that the measured wind flow temperature in the field is generally higher than that obtained from the model. The possible reason is that there will be some oxidation reactions in the coal and rock in the tunnel and heat will be released, while the model mainly considers the influence of geothermal water and ignores the heat generated chemically. There is also heat dissipation from personnel and some from mechanical equipment in the field roadway, for example. Thus, the error temperature at 200 m and 800 m is 0.33 °C and 0.28 °C, respectively, because this is the place where workers gather to rest and work, and the measured temperature at these two points will be high and the error will be large. At the exit of the roadway, the measured temperature is lower than that obtained from the model, probably because the model assumes that there is no backflow of wind flow and the fissure rock is isotropic and thermophysical properties are stable, so it will deviate from the real data. The return flow of the airflow will bring back the cold air in the connected alley and thus reduce the temperature. The thermal and physical properties of the surrounding rock may change due to the well-developed fissures at the exit of the roadway, which may affect the temperature of the air flow in the roadway.

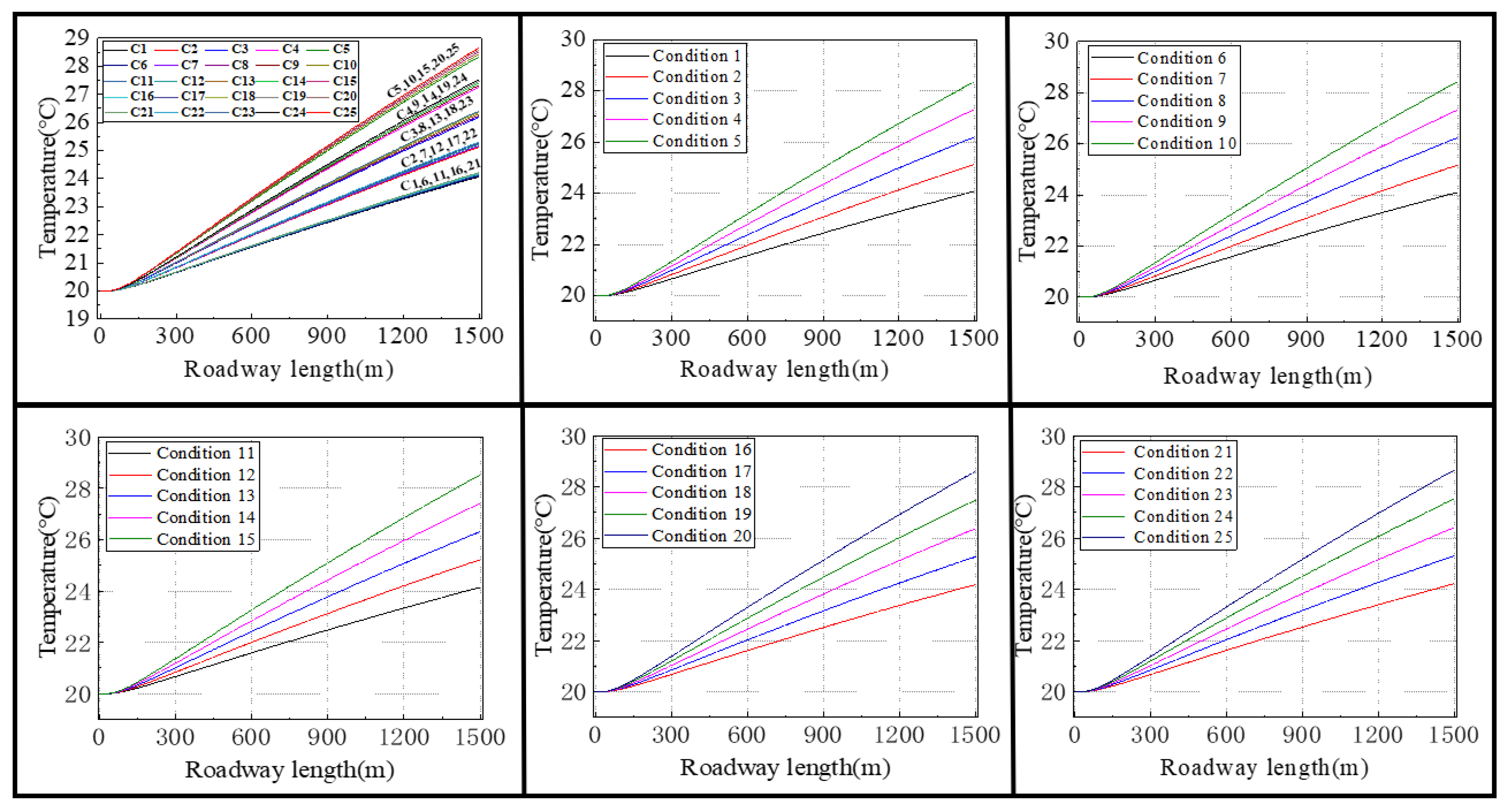
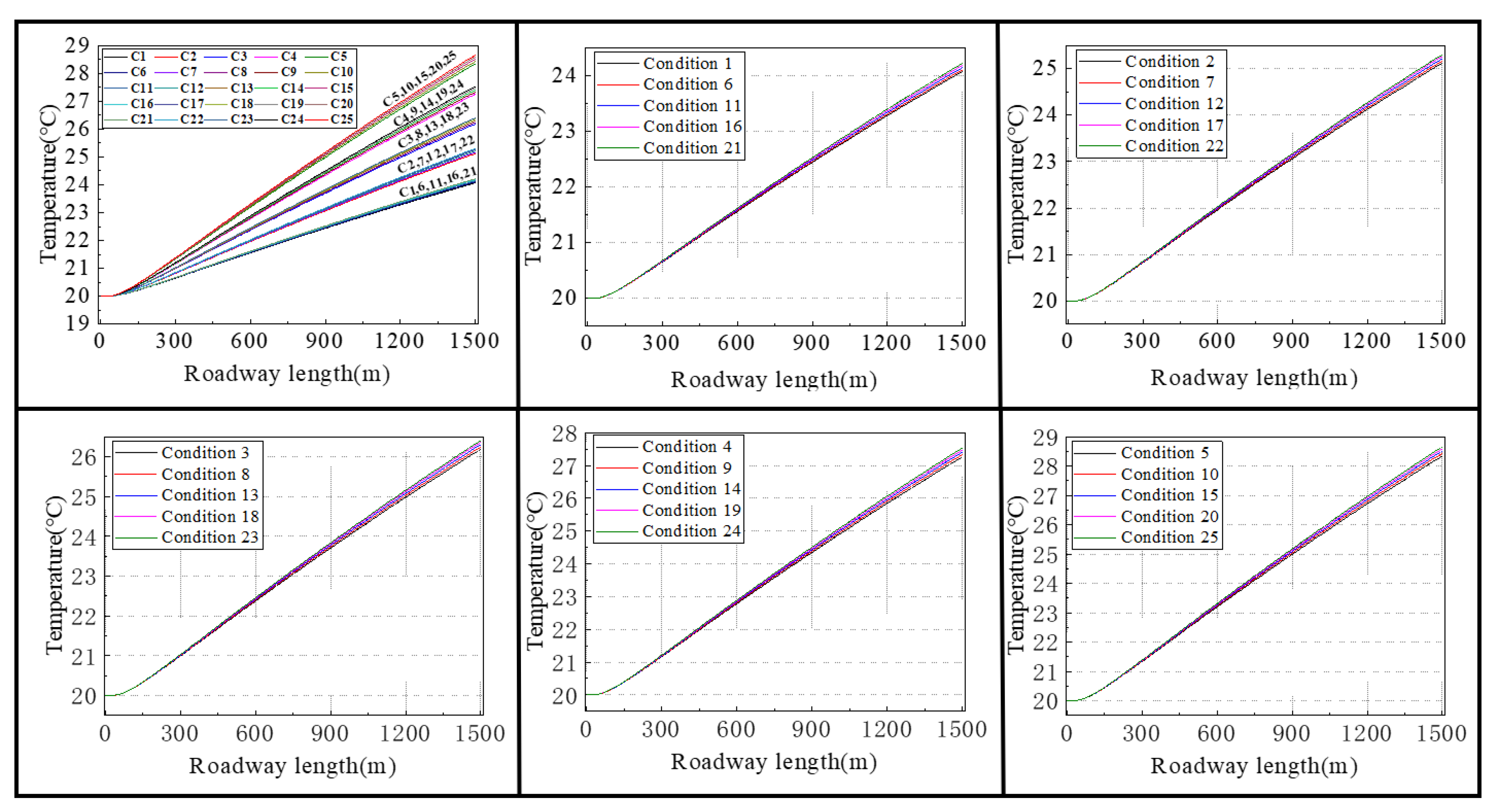
5.2. Distribution of Airflow Temperature Field in Roadway

In order to study the change law of the airflow temperature field of the roadway disturbed by geothermal water, the following process was followed. When the roadway was not excavated, the process of geothermal water seepage-heat transfer along the fractures was simulated in the geothermal water seepage-heat transfer model (as shown in Figure 8), and the temperature and pressure of the rock layer where the roadway was located at steady state were obtained. The obtained data were applied to the horizontal model of the coupling of seepage-heat transfer and convective heat transfer after excavation of the roadway as shown in Figure 9, with the conditions set as shown in

Table 5. Different water upwelling temperature and pressure conditions.

Water Upwelling Temperature/°C	Water Upwelling Pressure/MPa
	6	7	8	9	10
40	C 1	C 2	C 3	C 4	C 5
45	C 6	C 7	C 8	C 9	C 10
50	C 11	C 12	C 13	C 14	C 15
55	C 16	C 17	C 18	C 19	C 20
60	C 21	C 22	C 23	C 24	C 25

. In the model, airflow is considered for convective heat transfer with the surrounding rock, while the surrounding rock is considered for seepage-heat transfer with the geothermal water. The airflow temperature field is considered stable, through the analysis of air temperature along the whole roadway, by examining the airflow temperature at each position of the roadway in steady state with different upwelling water temperatures and the same upwelling water pressure as shown in Figure 11; and the same upwelling water temperature and different upwelling water pressures of the roadway in steady state with each position of the airflow temperature as shown in Figure 12. The first small figure for the overall 25 groups of data, and the remaining five small figures are grouped analysis of the total figure.

As shown in Figure 13 and Figure 14 for different conditions of the temperature field of airflow in the roadway, the overall change law is roughly the same, each phase of the law being as follows.

• In the 0~50 m stage, the airflow temperature is basically unchanged and the same as the airflow temperature at the entrance of the roadway, and the warming rate is basically 0. Because the temperature of the airflow into the roadway is 20 °C, before the thermal equilibrium, the difference between the airflow temperature and the roadway surrounding rock temperature is very big. There will therefore be energy continuously flowing from the high temperature surrounding rock into the low temperature airflow, and the heat exchange efficiency of the two becomes larger. The temperature of the surrounding rock decreases at it loses energy, and the temperature of the airflow gaining energy increases; the temperature difference between the two gradually decreases, but the outside world will also continuously reduce the temperature of the airflow, so that the temperature of the airflow will always stay the same. The energy gained by the surrounding rock from the geothermal water is much smaller than the energy lost, so the temperature of the surrounding rock will keep decreasing until it is the same as that of the wind flow, and fanally reaches thermal equilibrium. After that, the temperature of the surrounding rock has basically been reduced to 20 °C, at which time the heat exchange efficiency is almost 0, and the airflow temperature will not be warmed up.
• In the 50~130 m stage, the airflow temperature begins to change, and the slope of the curve represents the airflow heat rate beginning to increase. The reason for this is that with the continuous extension of the roadway, the heat contributed by the geothermal water to the surrounding rock at each stage will also accumulate. Thus, the temperature of the surrounding rock will gradually increase, and the energy absorbed by the airflow to the surrounding rock will gradually be smaller than the energy contributed by the geothermal water to the surrounding rock, at which time the temperature difference between the two will continuously increase, and the heat exchange efficiency will increase. The cooling efficiency of airflow will gradually slow down, but it will still absorb heat from the surrounding rock to raise its own temperature and reduce the heating rate of the surrounding rock.
• In the final stage of over 130 m, the warming rate of the airflow remains basically the same, and the temperature of the airflow increases linearly along the course until it exits the roadway as this goes ever deeper. This is because after 130 m, the heat contributed by the geothermal water to the surrounding rock and the heat absorbed by the airflow is already in equilibrium, and the heat exchange between the airflow and the surrounding rock is already saturated and unchanged, so the heating rate will remains basically unchanged until the exit of the roadway.

Overall, when the geothermal water upwelling water temperature is stable, the greater the pressure, the greater the airflow and surrounding rock heat transfer efficiency, and eventually steady state will be reached in the roadway along the airflow temperature field, decreasingly influenced by the pressure, and showing fluctuations generally of only 0.2~0.5 °C. When geothermal water upwelling pressure is unchanged, the influence of upwelling water temperature obviously changes the roadway airflow temperature field, and leads to a temperature rise in roadway surrounding rock and airflow; moreover, the difference between the temperature of the two increases, heat transfer efficiency increases, and the airflow temperature in the outlet of the roadway increases. In the 50 °C high temperature upwelling water roadway, the export airflow temperature rises to more than 6 °C, resulting in mine heat damage.

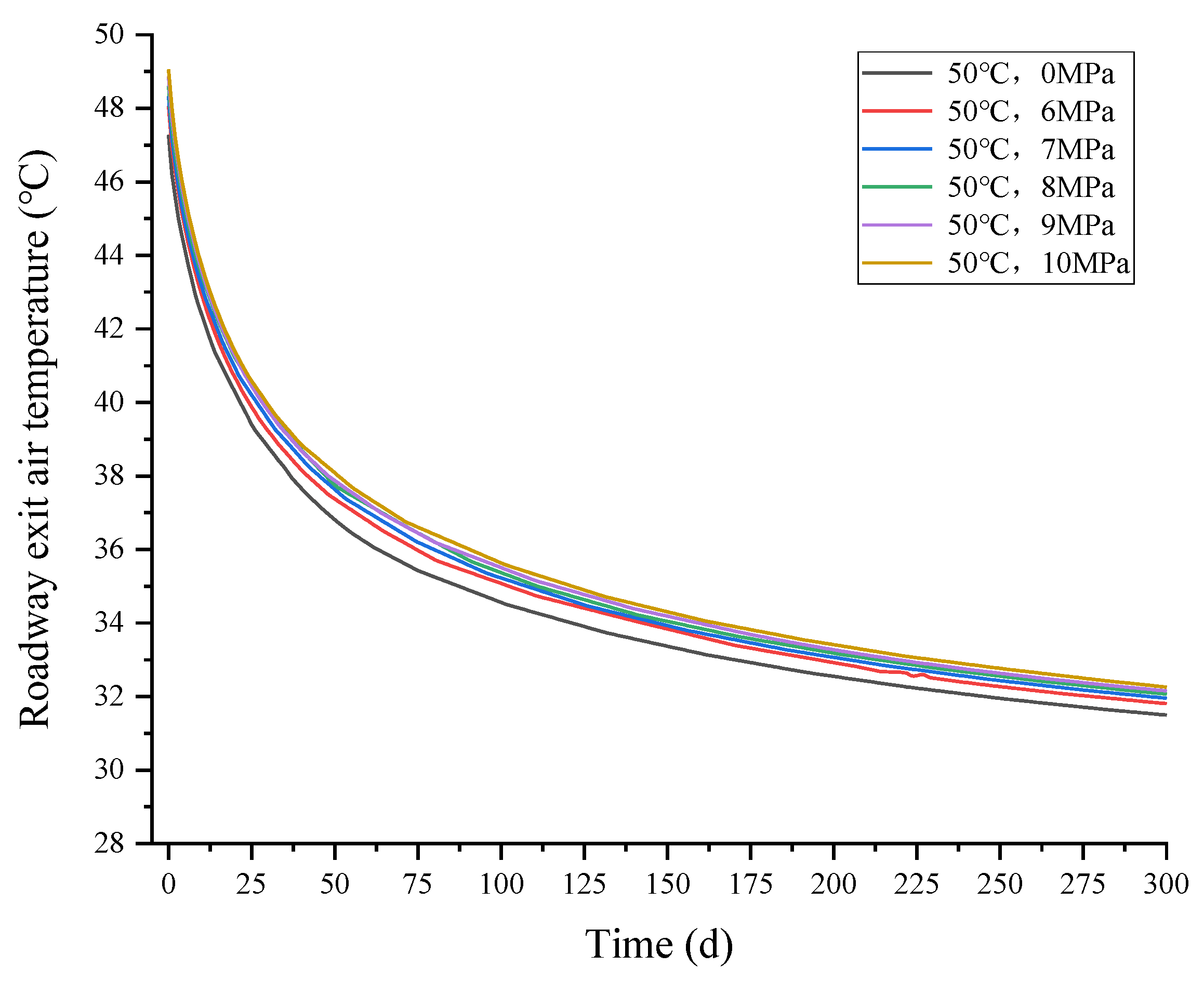
5.3. Effect of Hot Storage Geothermal Water Pressure on Airflow Temperature in the Roadway

Figure 15 shows the airflow temperature of roadway exit change law with time, under the conditions of same temperature and different pressure. The starting value of the airflow temperature in the outlet of the roadway is lower than the temperature of the upwelling water, and the temperature decreases sharply in the first 25 days, after which the rate of change of airflow temperature gradually slows down and finally tends to be constant. The main reason is that in the process of geothermal water upwelling, the geothermal water with higher temperature will continuously contribute energy to the surrounding rock with lower temperature, so that the temperature of the surrounding rock will continuously increase; at the same time, the energy of geothermal water will decrease and the temperature will also decrease. The temperature will already be lower than 50 °C when it finally reaches both sides of the roadway, and the energy contributed to the wind flow will not lead to it exceeding this temperature. The wind flow out of the exit of the roadway is heated by the surrounding rock. Initially, the temperature of the surrounding rock is the highest and the heat exchange efficiency is the largest, but the airflow will continuously absorb the heat from the surrounding rock and raise its own temperature, while lowering the temperature of the surrounding rock, so that the temperature of the airflow out of the exit is continuously reduced. As the surrounding rock and the airflow reach thermal equilibrium, the heat exchange between the two gradually stabilizes and the curve becomes flat. As the geothermal upwelling water pressure decreases, the temperature field of the roadway surrounding rock at the same time is disturbed less, the overall temperature of the surrounding rock is also reduced, and the warming effect on the airflow is also reduced. Under conditions of different upwelling water pressure, the export airflow temperature transformation law is roughly the same, upwelling water pressure on the roadway airflow temperature does not have significant influence, and the temperature difference is less than 1 °C. When the passing airflow temperature is 20 °C and the upwelling water temperature is 50 °C, the roadway exit airflow temperature will eventually be reduced from 50 °C by about 18 °C, to approximately 32~33 °C.

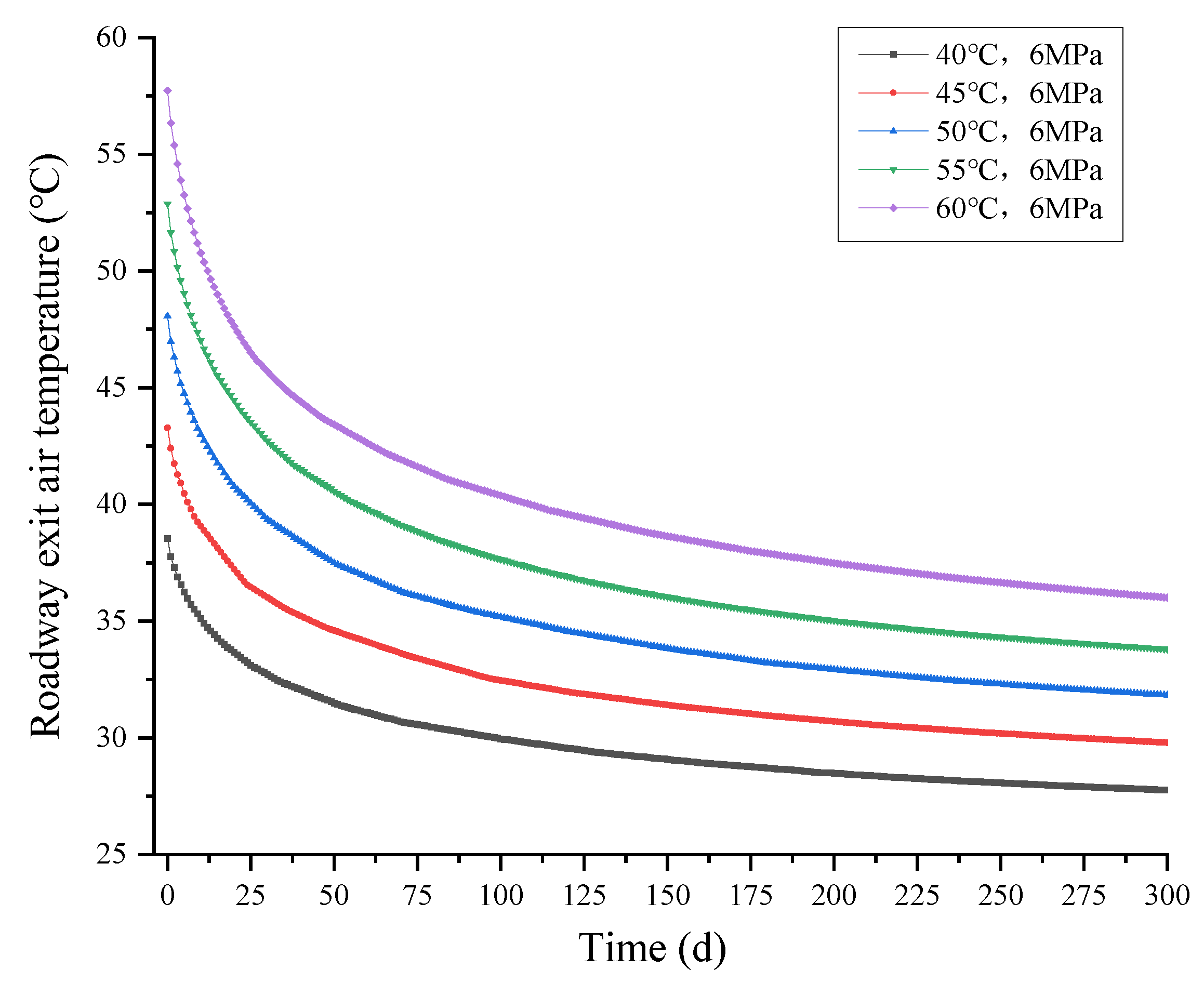
5.4. Effect of Hot Storage Geothermal Water Temperature on Airflow Temperature in the Roadway

Figure 16 shows the airflow temperature of roadway exit change law with time, under the same pressure but different temperatures. Whatever the upwelling water temperature, the shape of roadway exit airflow temperature change curve is roughly the same: in the first 25 days there is a sharp reduction, it then gradually flattens, and finally balances. The main reason is that in the initial stage, after the rise in water temperature, the temperature difference between the roadway surrounding rock and the airflow increases, as the heat contributed by the geothermal water to the surrounding rock is much larger than the heat absorbed by the airflow. On the first day, the airflow is heated to the highest temperature, but over time, the heat of the surrounding rock keeps being absorbed, thus the temperature keeps decreasing, and the heating effect on the airflow becomes smaller, and the temperature of the airflow gradually decreases. Eventually, about 125 days later, the amount of heat exchange is at convergence, cooling rates are also roughly the same, and hot water temperature not longer affects the time taken for the roadway and airflow to reach thermal equilibrium.

It has thus been found that the difference in hot water temperature does not affect the time for the roadway and airflow to reach thermal equilibrium, and this is the law of change under the same temperature and different pressure, in turn giving an export wind temperature change law. After a comparative analysis, airflow temperature is mainly influenced by the upwelling water temperature: when this increases, geothermal water contribution of heat to the surrounding rock increases, so that the surrounding rock and airflow temperature difference increases, the airflow absorbs more heat, and airflow temperature also increases. As shown in

Table 6. Temperature difference of airflow cooling.

Upwelling Water Temperature/°C	Airflow Temperature in the Outlet after 300 days/°C	Temperature Difference/°C
40	27.7	12.3
45	29.8	15.2
50	31.8	18.2
55	33.8	21.2
60	36	24

, when the airflow temperature is stable, the water temperature is directly proportional to airflow cooling efficiency. The greater the difference between the temperature of the upwelling water and the temperature of the airflow, the better the heat exchange efficiency, and the better the cooling effect of the airflow on the surrounding rock. When the roadway upwelling water temperature is 50 °C, after 300 days, the temperature will be reduced by 291.35 K.

6. Conclusions

In this paper, the modeling is carried out by using actual field measurement data, and the multi-physical features such as airflow, surrounding rock and fracture are coupled and simulated: the following useful conclusions are finally obtained.

• Analysis has been carried out of the influence of geothermal water upwelling on the distribution law of airflow temperature field inside the roadway and the change law of air temperature at the exit of the roadway by establishing the model and controlling the variables of upwelling water temperature and upwelling water pressure.
• A roadway seepage-heat transfer model has been established with actual data as the standard, and the error of the model verified, generating random fissures by the Monte Carlo method, and studying the influence of temperature and pressure of geothermal water upwelling through fissures on the temperature field of roadway airflow.
• At steady state, the temperature of airflow in the roadway rises at a slow rate 50 m from the roadway entrance. With increasing depth of the roadway, the warming effect of the surrounding rock temperature on the airflow becomes gradually more obvious, the heat exchange efficiency between the two increases, and the airflow temperature starts to rise steadily in a linear relationship after thermal equilibrium.
• With different upwelling water temperature and upwelling water pressure, the law of change in airflow temperature with time remains basically the same. At the beginning, after 1500 m of the roadway, the airflow is heated to its highest temperature; with the continuous injection of fresh cold airflow, cooling rate and efficiency take 0–25 days to reach their maximum. With increasing time, the surrounding rock heat is absorbed by the airflow thus reducing the temperature, and the cooling effect gradually slows down. When the roadway upwelling water temperature is 50 °C, after 300 days, the temperature will be reduced by 18 °C.
• The temperature of upwelling geothermal water has a huge impact on the heat exchange efficiency and temperature field of the surrounding rock, and the highest difference of 4.3 °C in the temperature of the roadway when the temperature of the upwelling water differs by 20 °C. The temperature in the roadway is basically the same when the difference in upwelling water pressure is 4 MPa, with the highest difference of 0.3 °C.
• Research shows that the main factor affecting the airflow in the roadway is the temperature of the upwelling geothermal water. Therefore, measures such as laying heat insulation materials at the bottom of the roadway, evacuating and releasing geothermal water, and circulating and injecting cold water could be applied to effectively reduce the influence of geothermal water temperature on the temperature field of roadway airflow and improve the mine thermal environment.