Compositional Closure—Its Origin Lies Not in Mathematics but Rather in Nature Itself

Abstract

Compositional closure, spurious negative correlations in data sets of a fixed sum (e.g., fractions and percent), is often encountered in geostatistical analyses, particularly in mineralogy, petrology, and geochemistry. Techniques to minimize the effects of closure (e.g., log-ratio transformations) can provide consistent geostatistical results. However, such approaches do not remove these effects because closure does not result from mathematical operations but is an inherent property of the physical systems under study. The natural world causes physical closure; mathematics simply describes that closure and cannot alter it by manipulations. Here, we examine the distinct types of geologic systems and samples to determine in which situations closure (physical and mathematical) does or does not ensue and the reasons therefor. We parse compositional systems based on (1) types of components under study, immutable (e.g., elements) or reactive (minerals), and (2) whether the system is open or closed to component transfer. Further, open systems can be (1) displacive in which addition of a component physically crowds out others, or (2) accommodative in which addition or subtraction of components does not affect the others. Only displacive systems are subject to compositional closure. Accommodative systems, even with components expressed as percent or fractions, are not closed physically or, therefore, mathematically.

1. Introduction

More than a century ago, Karl Pearson warned of the generation of spurious correlation inherent in the use of ratios with the same denominator in the study of animal organs (e.g., bones) by biologists [1]. Of particular relevance, we now understand that the correlation between variables of concentration or abundance fall under this same shibboleth. Half a century later, Felix Chayes issued a similar warning to the geological community on correlations between variables with a common sum [2,3]. He demonstrated that the null value for correlation between constant-sum variables is not generally zero, calling into question even rudimentary interpretation of bivariate relationships. By 1971, he expanded this theme in his textbook on ratio correlation but with no definitive solution [4].

With the increasing use of multivariate techniques in the geosciences, particularly principal component analysis and related methods based in correlation or covariance, the problem of compositional closure received considerable attention. Workers of the 1900s understood that the problems related to closure and compositional data required revision in the framework by which the data were analyzed, rather than the need for new analysis techniques. Aitchinson’s textbook defined compositional data as those comprised by relative parts (though not necessarily adding to a constant sum), and presented one putative solution, the application of log-ratio transforms, to permit a multivariate analysis of closed data sets [5]. His approach was to address the problems of working with compositional data by: (1) recognizing that they are confined to a hyperplane in positive real space (i.e., the simplex), and (2) to develop methods utilizing a proper algebraic–geometric system to analyze them based on a family of log-ratio transformations. The log-ratio approach, the basis of compositional data analysis (CoDA), has been popular across many fields of discipline and provided evidence that major changes in data analysis approaches (beyond application of methods to handle noisy or problematic data) were required. Unfortunately, the log-ratio transformations render results into a form that cannot be interpreted in terms of original abundance. Closure remains a significant problem to this day as evidenced by the existence of even more extensive interest in the subject [6]. Mathematical geology conferences still contain substantial and tense discussion and argument about the most appropriate methods to overcome the impacts of closure on datasets. Thus, despite more than 100 years to consider and investigate the issue of compositional closure, the problem has yet to be completely overcome.

In this analysis, we focus on the distinct types of natural systems and samples that mineralogists, petrologists, and geochemists, among others, study, in order to better understand the situations in which closure does or does not ensue. We do not present a mathematical approach to the problem but rather an analysis of the relationship between mineralogical, petrological, and geochemical systems and closure.

Further, we demonstrate how statistical closure does not result from mathematical structure but is an inherent property of the physical systems being sampled and studied. In this view, the natural world causes statistical closure; mathematics accurately reflects nature. This new understanding of closure is relevant not only to mineralogy, but to any field that supports the analysis of compositional data, including other natural sciences, medicine, economics, and social sciences.

2. Components—The Physical Variables Being Measured in a Sample

A very large number of different physical variables have been measured in the many different types of geoscience studies. Nonetheless, each of those variables fits into one of the following two categories.

2.1. Immutable Variables

These are variables that do not change within the appropriate time frame and setting of the systems under study. These include: elements (under all circumstances except relatively short-lived radio-decay, nuclear reactions, etc.), sand grains in a river, and ore minerals in a mine.

2.2. Reactive Variables

Variables in this class can separate or combine with other components within the appropriate time frame and setting of the systems. Examples include: minerals in magma, gas molecules in the atmosphere, and organic compounds in an oil-generating system.

3. Systems—Whether Components Can Enter or Leave

Mineralogical, petrological, and geochemical systems have been characterized as open or closed relative to the flux of components into and out of the locus under study. However, there are differences in open systems that have relevance to statistical closure of compositional data.

3.1. Closed Systems

In closed systems, there is no component flux with surroundings. Examples include an isolated cooling/crystallizing magma chamber (ignoring contact effects at boundaries) or sealed beaker or Parr™ reactor laboratory experiments.

3.2. Open Systems

In open systems, component exchange with surroundings occurs. The nature of such exchanges can have profound consequences for statistical closure of compositional data in these systems. We introduce, first, the concept of component crowding and then that of component independence.

3.2.1. Displacive Open Systems—Crowding

In displacive open systems, the addition of any component, in effect, forces one or more others out of the sample system, which is limited to a fixed volume. Likewise, removal of a component forces one or more other components into the sample system. This represents the classic traditional case of closure in compositional data. Examples are well known in igneous petrology in the examination of elements and of minerals.

3.2.2. Accommodative Open Systems

Less well-recognized are accommodative open systems in which we contend that the addition or subtraction of a component does not exclude or introduce other components. In such systems, compositional data are not always subject to statistical closure. Thus, the range of problems identified in the analysis of compositional data by Chayes and others is not universal. There is a controlling phenomenon that determines when a system will exhibit statistical closure, i.e., whether or not the gain or loss of a portion of a component affects the relative values of other components. In particular, when measured components are expressed as a ratio or percent (or ppm, etc.) of a large measured component of a different or unrelated type, closure does not necessarily ensue. Examples of this situation include: trace elements in sea water as ppm, mg L⁻¹, mol L⁻¹, etc. (relative to seawater—mass or volume); or heavy metals in airborne particulate matter as ng m³⁻, etc. (relative to air volume).

We can distinguish two categories of accommodative open systems—those of constant volume (the previous two examples) and those of changing volume. An example of the latter is the injection of new magma into a laccolith, where the volume of the entire laccolith increases. As will be seen later, the laccolith as a whole is accommodative, but a sampled sub-volume is not.

3.2.3. Partly Accommodative Systems

Not surprisingly, there are systems that are somewhere between the accommodative and displacive end-members in which the requirements for accommodative open systems (large component as a denominator, unrelated to numerator components, and/or changing volume) are not fully realized. The presence and extent of closure in such systems remains an open question. Examples include subsurface concentrated brines, e.g., 100,000 ppm Na⁺ (numerator approaching denominator).

4. Results

4.1. The Six Combinations of Systems and Components

Combining these categories yields six possible situations, wherein the interpretation of the data is surprisingly different. In the figures that follow, the different combined systems are plotted opposite one another at the poles of an axis to indicate that there may be intermediate situations between immutable and reactive components. This depends on the degree of reactivity of components within the time scale under investigation.

4.1.1. The Two Closed System Types

There are two combinations—closed systems with immutable components and closed systems hosting reactive components. Figure 1 presents the two poles of the combined closed systems.

In immutable closed systems, there are no correlations; these systems can be considered dead relative to any change. As compositional materials are not able to enter or leave and transformations between immutable components cannot occur (by their definition), there is little to investigate beyond basic characterization. For our present analysis, there is no reason to consider them further.

In reactive closed systems, there is no compositional closure. Although the growth of, for example, one mineral must come from the consumption of one or more other minerals in the system, the negative correlation or covariance between minerals accurately describes the conversion of minerals into others. A correlation coefficient of r = 0 validly indicates no statistical relationship between the relevant variables. For example, if in the system A + B → C and D + E → F, and if these two reactions are unrelated to each other, the measured correlation between, for example, A and E = 0. For the purposes of this investigation, we will not deal further with these closed systems.

4.1.2. The Four Open System Types

There are four combinations of congestion and component type: open accommodative systems with immutable components, open accommodative systems with reactive components, open displacive systems with immutable components, and open displacive systems with reactive components. Figure 2 presents these as four poles of the accommodative and displacive combined open systems. Black text describes the components and systems, cyan text labels the degree of compositional closure, and purple text indicates examples.

5. Discussion

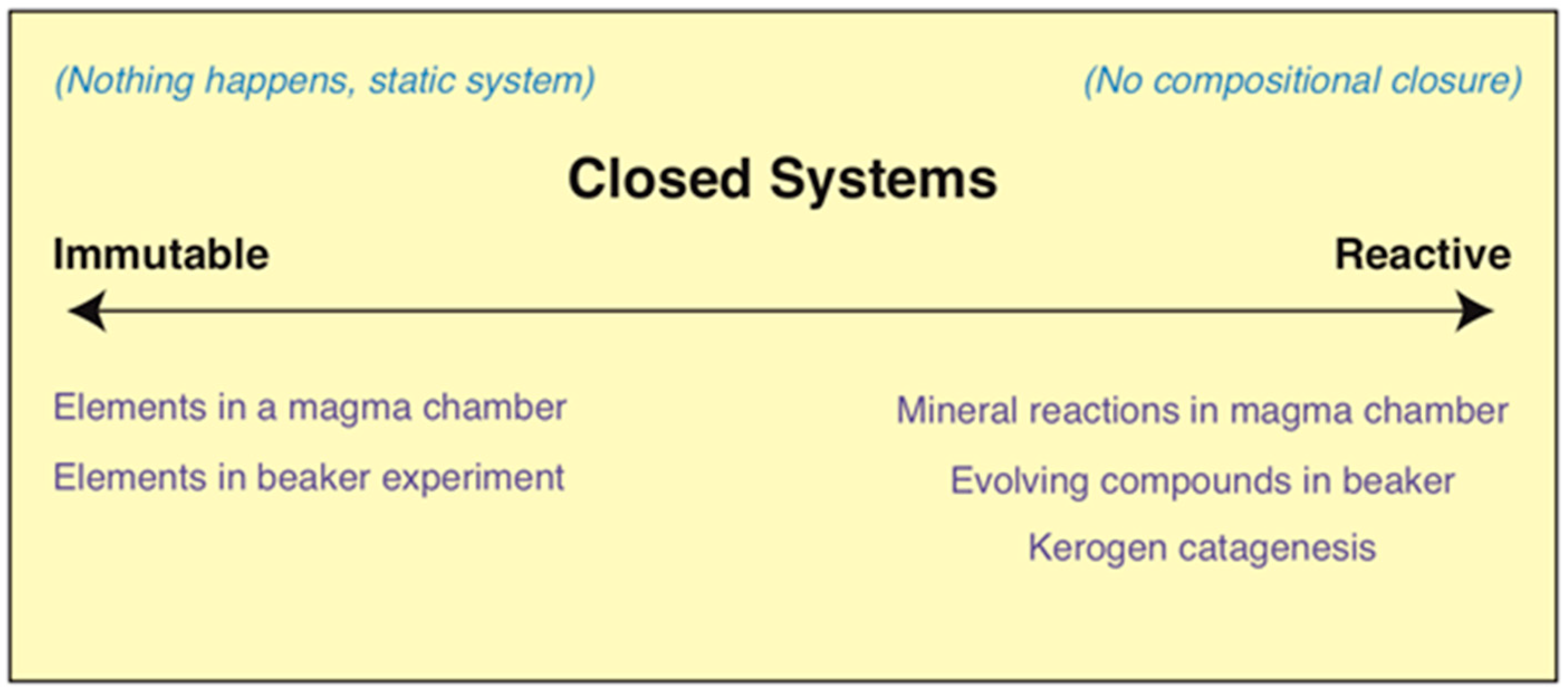
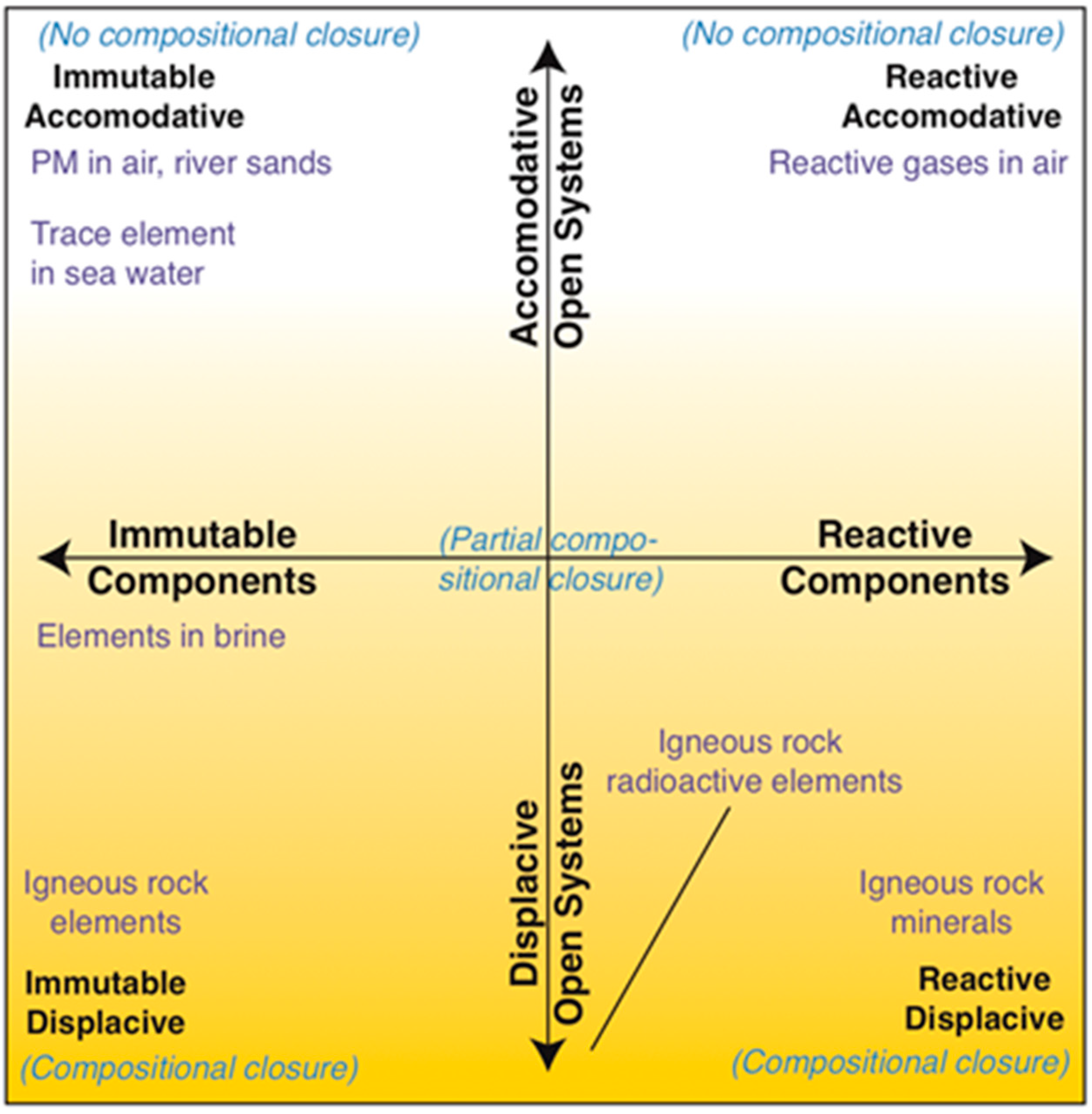
5.1. Statistical Closure Implications

It should be clear from our parsing of the various mineralogical, petrological, and geochemical systems that not all compositional data are subject to statistical closure. Specifically, in accommodative open systems, correlations are valid, with r = 0 indicating no correlation between the two tested variables (i.e., the null hypothesis for correlation is a slope of 0). Likewise, such multivariate techniques as principal component analysis can be performed directly from the correlation or covariance matrix, without such manipulations as log-ratios or CoDA. These approaches can still be applied, but results focus on the relative nature of the components and information, and antithetical relationships (e.g., negative correlations) are lost. These findings apply equally to accommodative open systems with either immutable or displacive components.

5.2. Intermediate Open Systems

We have not yet formally parsed the details of these intermediate open systems with regard to closure. For the moment, we posit that the value of the correlation coefficient corresponding to no correlation gradually deviates increasingly from zero as the amount of “crowding” between components or between components and the denominator variable increases. In this view, in open systems with less than complete accommodation, closure can be a matter of degree rather than an absolute. An advantage of log-ratios and CoDA, from this perspective, is that they provide consistent results regardless of the degree of compositional closure.

5.3. Immutable vs. Reactive Displacive Systems

Changes in immutable displacive systems, by their definition, occur only as the result of transfer of components. Thus, slopes in the correlation constituents of an immutable displacive system simply indicate the relative flux of the two items into or out of the basis, which we define as the denominator in the unit of measurement. In contrast, changes in reactive displacive systems can occur by transfer of components, by reactions between components, or by both processes. Thus, interpretation of data from a reactive displacive system is more challenging when trying to determine how much of the change is the result of ingress/egress of components in the basis and how much is the result of reactions between the components. This is an important aspect of the closure problem in mineralogy, petrology, and geochemistry.

One might consider a continuum of situations between the end-member extremes of all displacement due to a reaction between components and all displacement due to ingress–egress of reactive components. Note that the latter is the situation in immutable displacive systems. Thus, we can consider, in effect, a horizontal continuum between the lower left and lower right corners of Figure 2. Rather than intermediate positions representing the degree of reactivity of the components, such positions would represent the relative proportion of change due to ingress–egress vs. reactions.

Determining the relative roles of reaction and exchange can be a significant problem in such areas as igneous petrology. Petrographic evidence in the mineral suite, e.g., corrosion rims, replacement textures, etc., can provide important clues in this regard.

5.4. The Accommodative–Displacive System Paradox

Many commonly studied mineralogical, petrological, and geochemical systems are not physically displacive in the sense that the “room was full” and someone had to leave for someone new to enter. Further, most such systems (e.g., those in igneous petrology) are sampled in space as a proxy for time. Nonetheless, the geochemical process under study becomes displacive when and because the variables are presented relative to a fixed mass. This is not, of course, mathematics altering nature, but rather the researcher studying a different system.

As an illustration, consider a comparison of the 10 major elemental compositions of, say, a dozen separate plutons. The geochemical approach is to examine the correlation between these elements via an n × N (10 × 12) table. What kind of system is this?

If we consider each pluton as a whole, we are dealing with open accommodative systems. Each pluton reached its current crystallized state after, probably, a number of discrete injections of magma. Thus, these systems were open; addition of new magma and minor loss of material by such processes as gas venting in no way crowded out certain elements at the expense of entering ones. The plutons simply grew larger, accommodating the additions of mass. Inter-elemental correlation coefficients are valid (i.e., r = 0 represents no correlation) if the 10 × 12 data set consists of the total mass of each element in each pluton rather than a concentration. Although an unusual approach, the masses of each element are, in fact, the absolute composition of each pluton. Yes, these are compositional data even though they are not ratios, and thus, even in the traditional view they would not be subject to closure. (These masses might have been estimated or calculated by averaging many conventional samples for each pluton even if those samples initially were measured as mass percent.)

In contrast, if the average composition of each pluton is characterized in mass percent, something striking occurs. The system becomes a displacive one, and compositional closure ensues. A rather “Schrödingerian” turn of events results: our choice of measurement alters the statistical result!

Why? Apparently, sampling a specific mass and reporting results per mass changes the system under study from the whole pluton (an open accommodative system) to a fixed-mass sub-portion of the pluton (an open displacive system). The salient point is that during the evolution of the pluton, magma flux through such a sub-portion acted in a displacive fashion, with added material crowding out occupying components. This system exhibits statistical closure. Such closure is not simply an artifact of the mathematics of ratios, but actually reflects a physical reality—the sampling of a displacive open system.

Expressed slightly differently, the entire pluton is an accommodative open system. Any individual sample of the pluton can be considered a small fixed box, the history of which was a displacive open system. The whole, being of unlimited volume, is accommodative, but the part, being of fixed volume or mass, is displacive. (A minor issue, possible loss of fluids or gasses to the enclosing rock, is not being considered here.)

Viewed another way, the entire pluton encompasses the summation of its evolution. In contrast, any sub-system (a given volume within the pluton) does not retain the information of ingress and egress of material to and from the other volumes in the pluton. Thus, it is not possible to reconstruct this history from mathematical manipulation of its final composition. Following, there is no mathematical function to reverse the effect of closure—it is simply intrinsic.

5.5. Another Example of the Accommodative–Displacive System Paradox

Consider, next, a data set of trace elements in seawater from various locations, expressed as ppm relative to sample mass—water plus dissolved solids (one could also take the data as grams per liter or moles per liter). We have shown that such a system is open accommodative because, physically, the addition of small masses of different elements does not crowd out other elements. The data do not exhibit closure so long as the salinity of the samples remains relatively constant, such that they do not induce displacement. In this case, there can be a difference between results from conventional and compositional data analysis approaches, but that is largely a product of the log scaling in the latter, which moves from an emphasis on linear variance to that of log variance [7].

If instead we present these data as ppm or percent of each element relative to total dissolved solids, once again closure ensues, as the system under study converts to open displacive. What is the physical meaning? Figuratively and perhaps literally, the water has evaporated. Seawater is no longer being studied; in effect, an evaporite deposit is. The sample now comprises a fixed mass of a part of an evaporite deposit. As such, it is an open displacive system, similar to the pluton sample and characterized, therefore, by compositional closure. However, if there were samples with a different degree of evaporation, the total amount of salt varies as does its relative composition, making for a system of mixed absolute (i.e., total salt content) and relative/compositional data. Point count data are similar in this manner—they can be interpreted either directly as abundance data (which are devoid of closure) or as proportions (controlled by closure). Work by Pawlowsky-Glahn et al. [8] developed a compositional approach that considers a scenario where both relative and absolute variations are important (i.e., consider the same system from both absolute and relative differences), but it is unclear how the results would vary from systems ranging along the accommodative–displacive continuum. Regardless, the paradox is clear—a single system can be viewed or considered in different aspects, which can change both the nature and interpretation of the results.

6. Conclusions

Although the basis of this work is conceptual rather than quantitative, the outcomes are surprising, and they suggest pathways forward to further explore compositional closure. As closure is inherent in specific systems being studied, methods to completely remove the effects of closure through mathematical means cannot be fully successful. Most critically, then, we need to understand what such manipulations as log-ratios and CoDA actually achieve. At a first pass, they provide consistent results regardless of the system under study, be it compositionally open, compositionally closed, or somewhere in between. However, some information loss appears to occur when these methods are applied. Thus, we are actively working on new approaches that recognize the intrinsic nature of closure in sample space.

From a practical standpoint, it is evident that the tools applied in the analysis of compositional data and the approach taken depend upon the samples one starts with. Moreover, one needs to have a firm understanding of the history or processes that have impacted the systems and/or the data under investigation. While this appears as common sense to a data analyst, a lack of understanding of these conceptual basics up to this point suggests that more attention to this is necessary. Analysis of compositional data will only allow valid interpretations if we have investigated the likely behavior, events, and processes that have impacted our samples.

This discussion reveals two salient points. First, not all compositional data exhibit closure. Therefore, the researcher must be aware of the types of systems and components under study. Second, statistical compositional closure of a set of samples, when it does occur, is a consequence of, and inherent in, the natural system under investigation. As such, it is not possible to mathematically reverse the effects of that closure.