Coupling NCA Dimensionality Reduction with Machine Learning in Multispectral Rock Classification Problems
Abstract
:1. Introduction
2. Methodology for Coupling NCA Dimensionality Reduction with Machine Learning
2.1. Hyperspectral Imaging
2.2. Dimensionality Reduction
2.2.1. Supervised vs. Unsupervised Methods
2.2.2. Why Use NCA
2.3. Why Machine Learning?
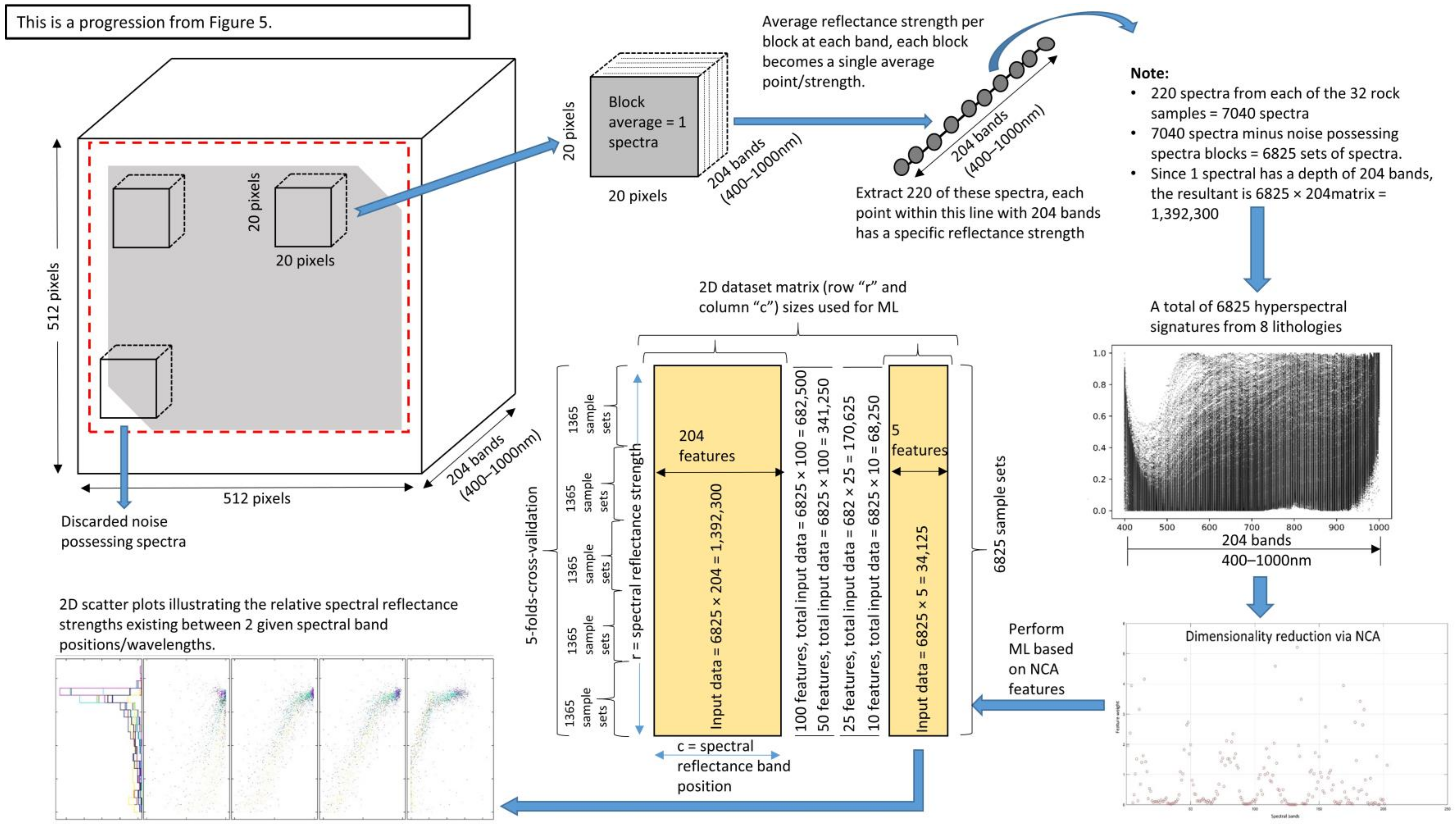
3. Practical Experiments
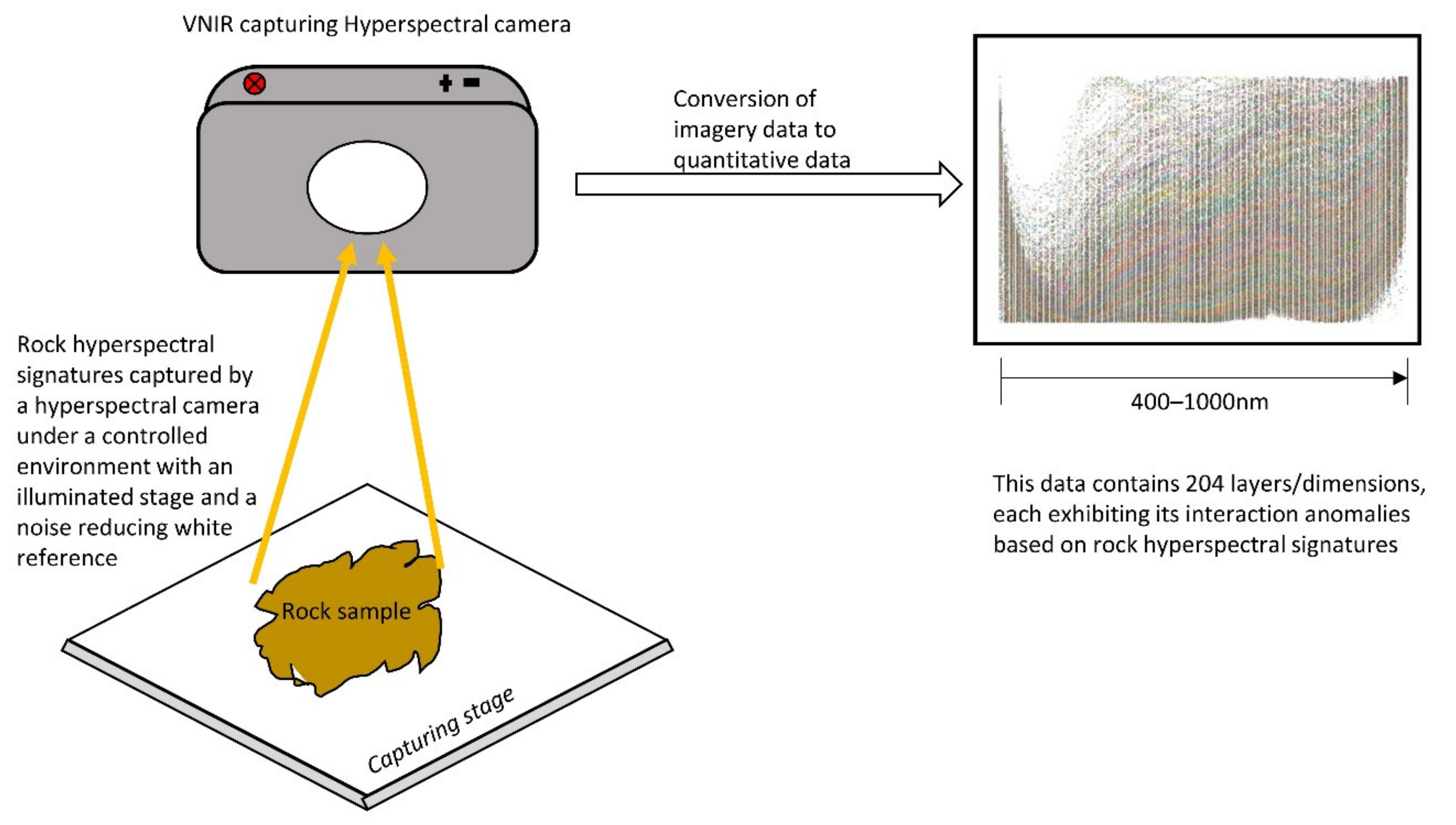
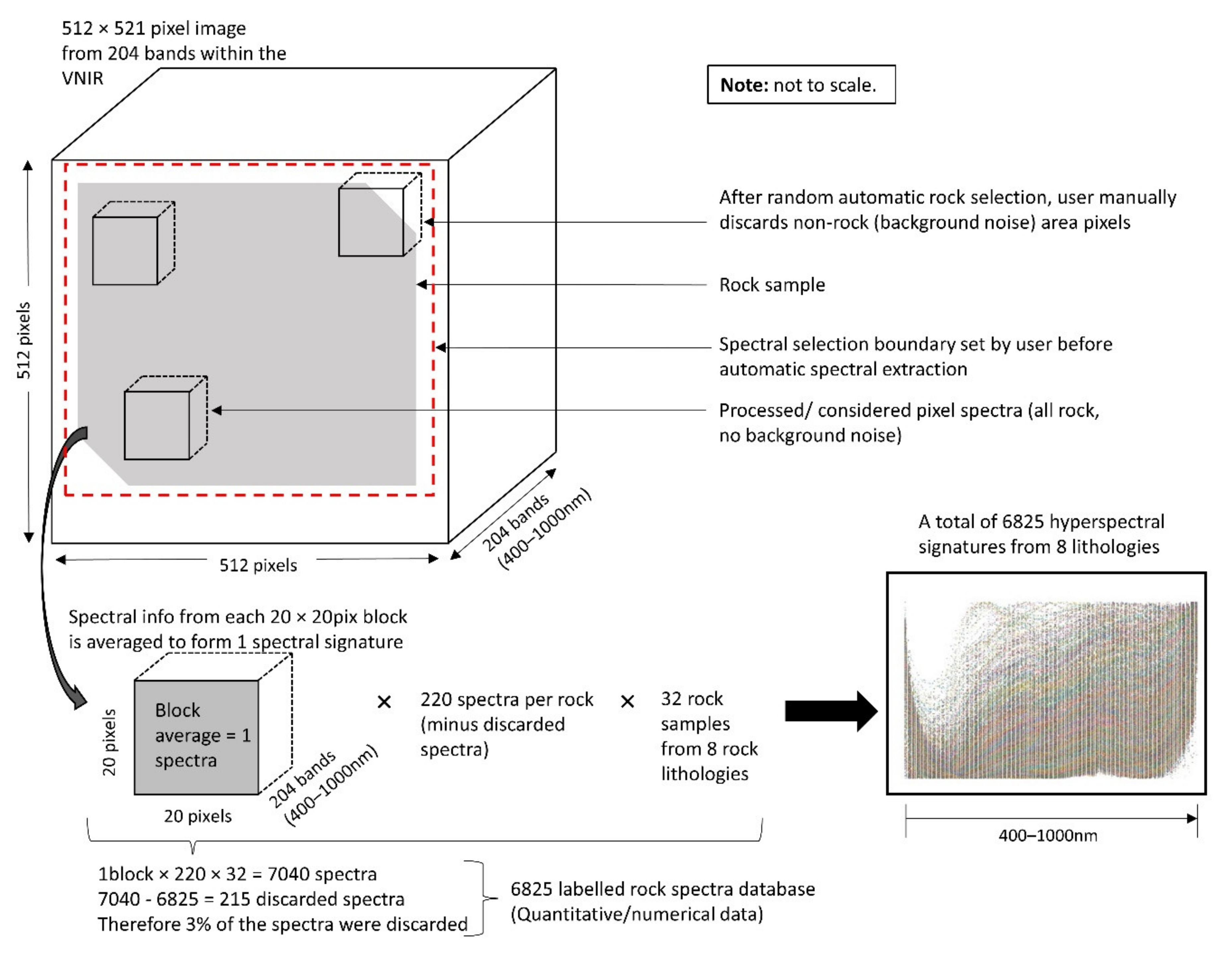
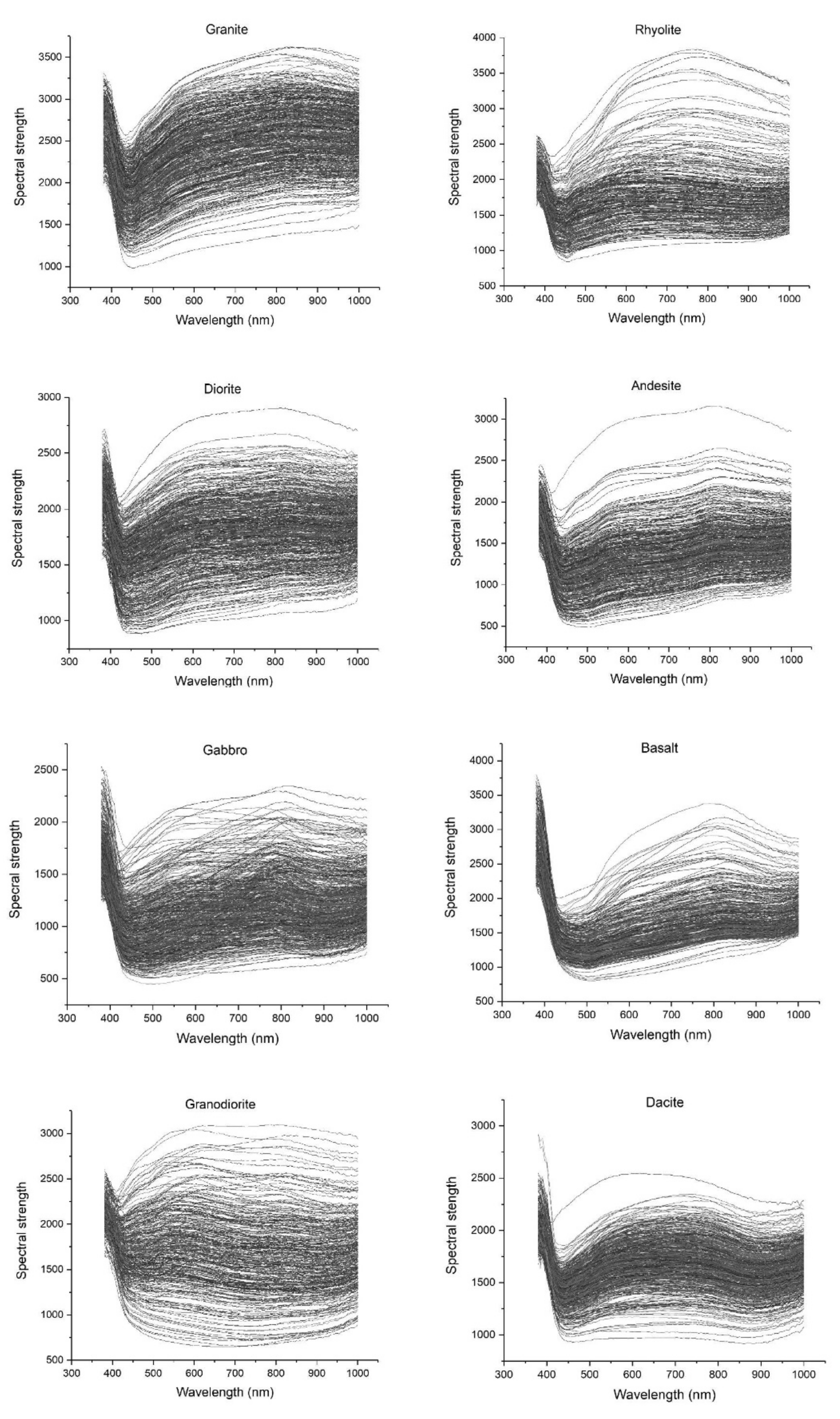
3.1. Capturing Rock Hyperspectral Signatures
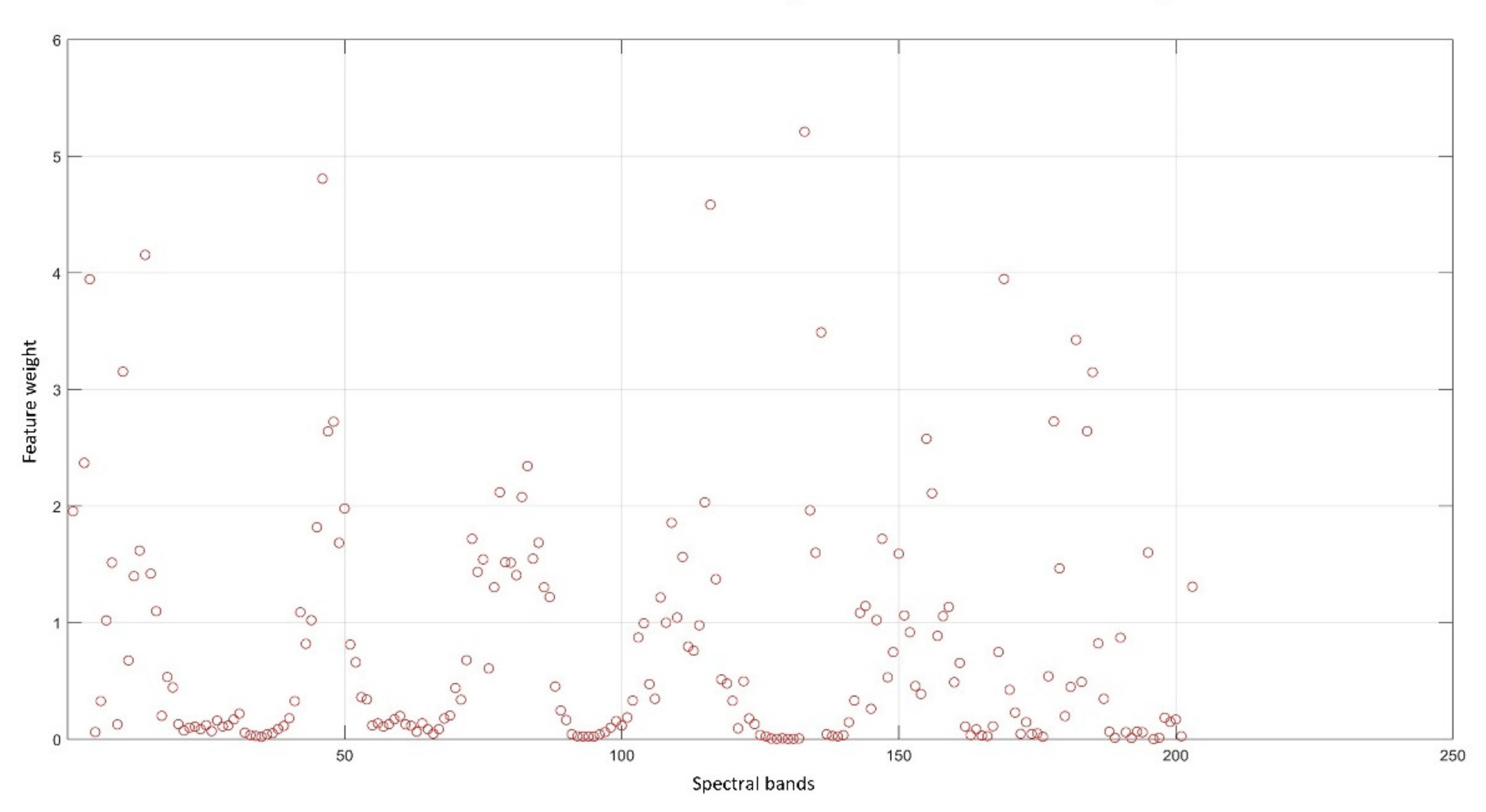
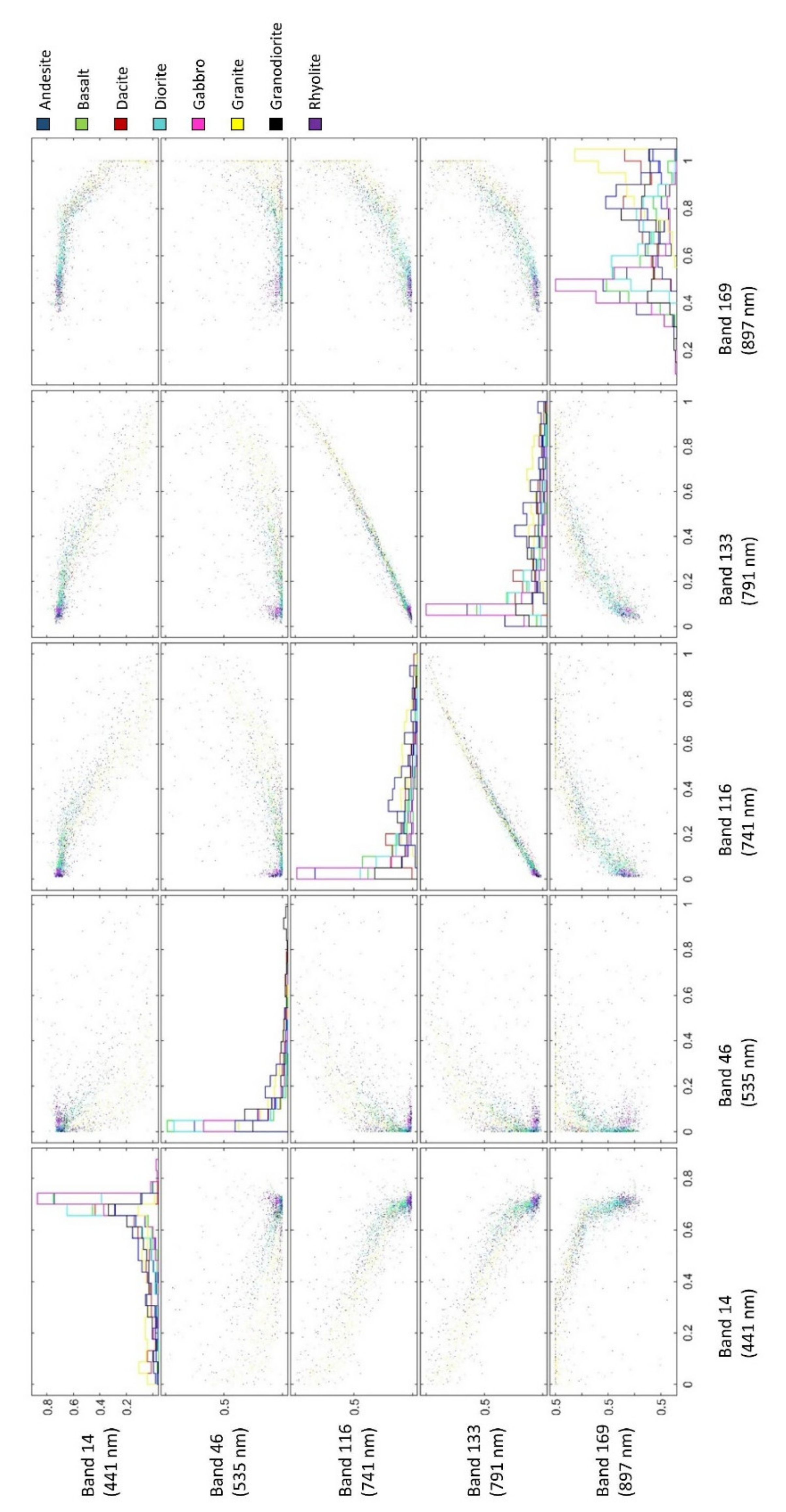
3.2. Selecting the Appropriate Feature Bands
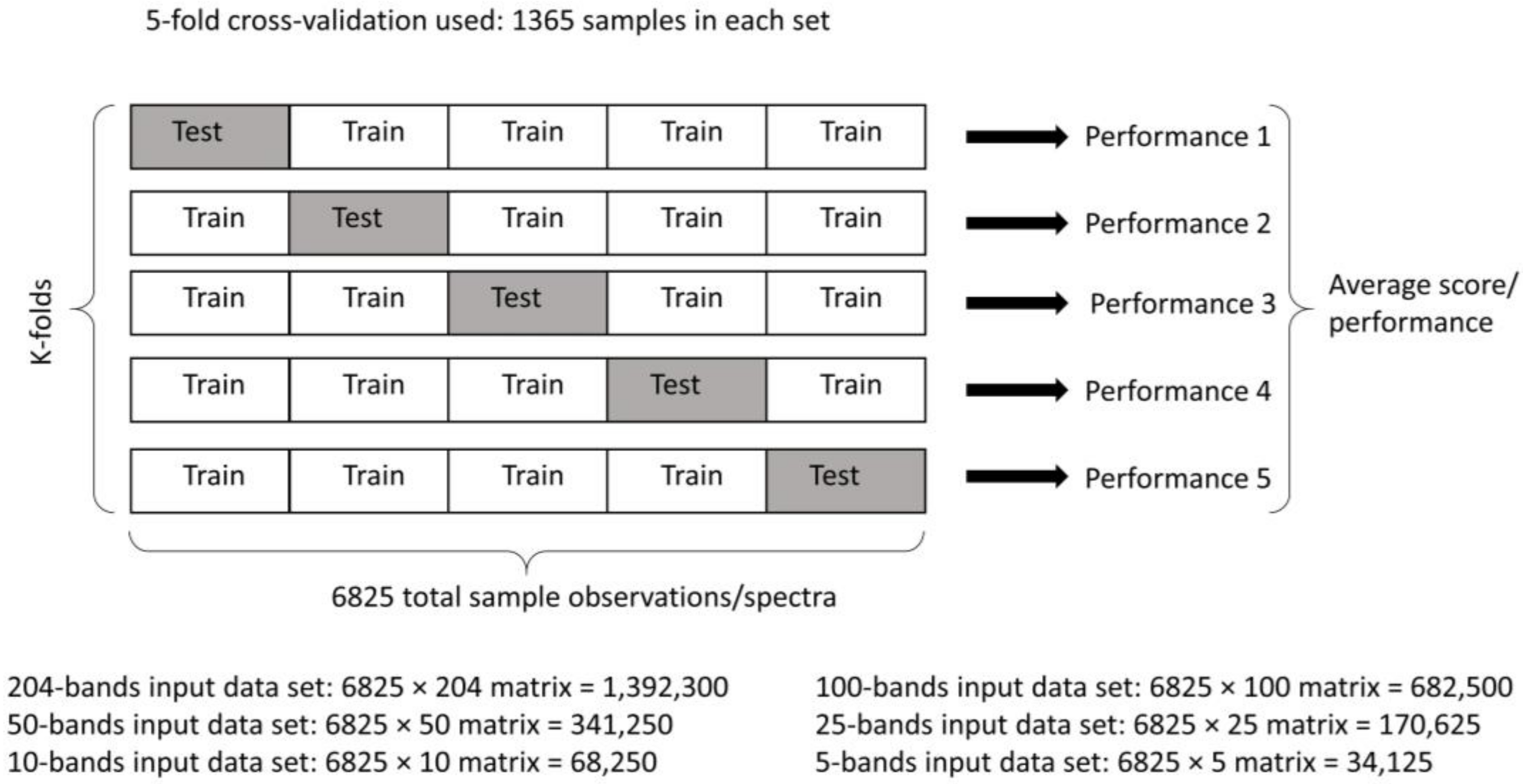
3.3. Post-NCA Classification via ML
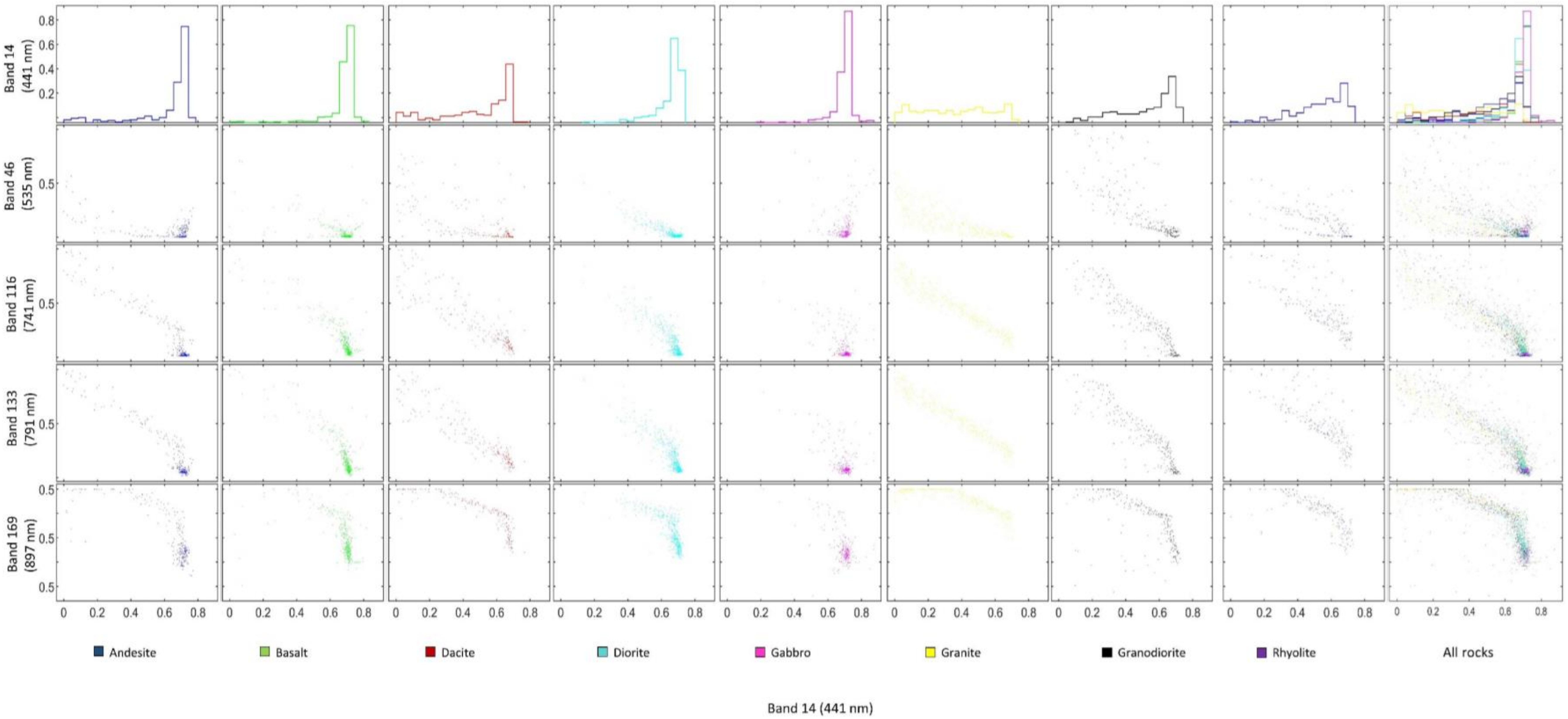
4. Experimental and Analytical Results
4.1. Findings Based on Hyperspectral Imaging
4.2. Findings Based on NCA
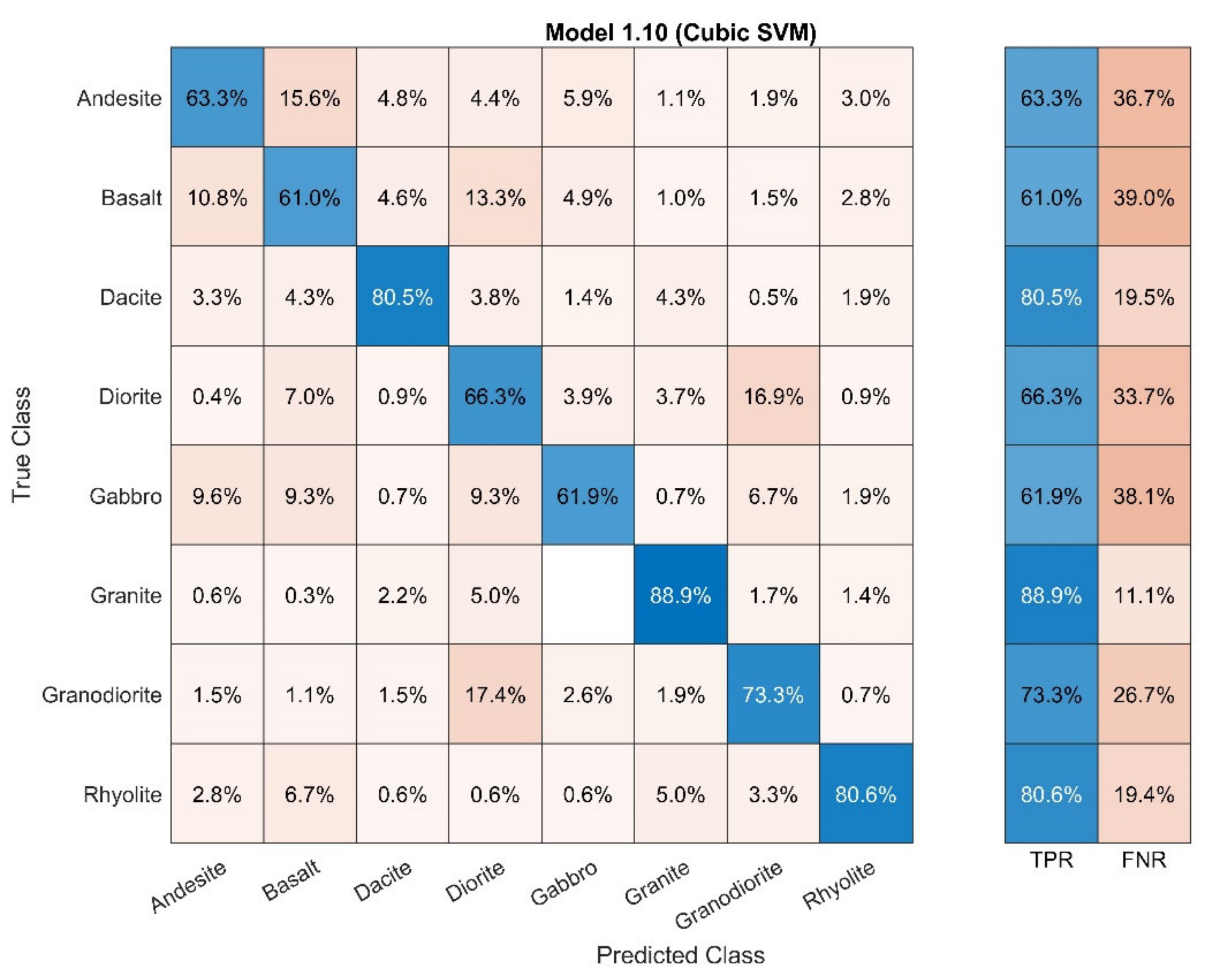
4.3. Classification with ML, Post-NCA
5. Significance of Proposed System
- Through DR, we can reduce the storage capacity required to store and handle a database, thereby reducing storage costs as we have proven there is no need to collect, store and process redundant data;
- With DR, we were able to break down hyperspectral signature data into different dimensionalities, hence the ability to plot such data in 2D planes, which as a result allows for easy visual assessment;
- As proven with post-NCA specialised multispectral imaging, we can attain respectable classification accuracies. This proves that multispectral imaging is a good enough option as it can be programmed to be highly specialised, costs less, has lower operation costs, has the flexibility of being applied in specialised multispectral imaging, such as on a UAV drone. Having said this, it is important to note that samples used in this study were clean and manually prepared before analysis, which is not the state in which rocks are found in the field, due to dirt and other matter. Therefore, classification accuracy variations in our envisioned identification of these rocks in the field, compared to the study’s attained results, are likely to exist;
- Through ML, we can analyse and classify multispectral signatures produced by rocks and minerals with high accuracies. By finding the right model for a particular dataset, subsequent related data is relatively easier to classify as the training data always assists the model in future predictions as proven;
- With our proposed combined system, we have proved that any industry looking to cut spectral data (or equivalent) analysis costs whilst still retaining high classification accuracies, DR via a feature selection supervised NCA algorithm to specify the most discriminative bands, and verifying the viability of selected bands via ML, thereafter employing these 5-bands (or more, depending on application) in future specialised classifications, could potentially be the key to achieving several system design optimisations;
- Via a post-NCA 5-band rock and mineral classification specialised multispectral camera mounted on a UVA drone, such as the ‘DJI P4 Multispectral drone used in agricultural applications’, there is a plethora of applications in which this specialised technology could find potential use. This, as a result, minimises purchase, operation and data interpretation costs as compared to a hyperspectral imaging system. This could aid in remote sensing from long distances without the need for physical presence, as well as rapid in situ assessments of the state of the environment via the UAV drone, possibilities are endless.
- Lastly, there is potential to employ such a post-NCA specialised multispectral camera in the frequent monitoring of mine dams. This would allow quicker assessment of contaminants based on spectral signatures produced by unexpected and/or anticipated metal contaminants. Hence, we deem this proposed system viable in all mining-related stages, from exploration, operation and closure.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep Neural Networks: A Promising Tool for Fault Characteristic Mining and Intelli-gent Diagnosis of Rotating Machinery with Massive Data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P. Lithological Mapping from Hyperspectral Data by Improved Use of Spectral Angle Mapper. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 95–109. [Google Scholar] [CrossRef]
- Van der Meer, F. The Effectiveness of Spectral Similarity Measures for the Analysis of Hyperspectral Imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Galdames, F.J.; Perez, C.A.; Estévez, P.A.; Adams, M. Rock Lithological Classification by Hyperspectral, Range 3D and Color Images. Chemom. Intell. Lab. Syst. 2019, 189, 138–148. [Google Scholar] [CrossRef]
- Ruiz Hidalgo, D.; Bacca Cortés, B.; Caicedo Bravo, E. Dimensionality Reduction of Hyperspectral Images of Vegetation and Crops Based on Self-Organized Maps. Inf. Process. Agric. 2020. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Zhang, H. Recognition, Location, Measurement, and 3D Reconstruction of Concealed Cracks Using Con-volutional Neural Networks. Constr. Build. Mater. 2017, 146, 775–787. [Google Scholar] [CrossRef]
- Sinaice, B.B.; Kawamura, Y.; Kim, J.; Okada, N.; Kitahara, I.; Jang, H. Application of Deep Learning Approaches in Igneous Rock Hyperspectral Imaging. In Proceedings of the 28th International Symposium on Mine Planning and Equipment Selec-tion—MPES 2019; Springer Series in Geomechanics and Geoengineering; Topal, E., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 228–235. [Google Scholar] [CrossRef]
- Sharma, N.; Sharma, R.; Jindal, N. Machine Learning and Deep Learning Applications—A Vision. Glob. Transit. Proc. 2021, 2, 24–28. [Google Scholar] [CrossRef]
- Asscher, Y.; Angelini, I.; Secco, M.; Parisatto, M.; Chaban, A.; Deiana, R.; Artioli, G. Mineralogical Interpretation of Multispectral Images: The Case Study of the Pigments in the Frigidarium of the Sarno Baths, Pompeii. J. Archaeol. Sci. Rep. 2021, 35, 102774. [Google Scholar] [CrossRef]
- Rahimi, B.; Sharifzadeh, M.; Feng, X.-T. A Comprehensive Underground Excavation Design (CUED) Methodology for Geotechnical Engineering Design of Deep Underground Mining and Tunneling. Int. J. Rock Mech. Min. Sci. 2021, 143, 104684. [Google Scholar] [CrossRef]
- Goldberger, J.; Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighbourhood Components Analysis. 8. Available online: https://www.cs.toronto.edu/~hinton/absps/nca.pdf (accessed on 5 February 2021).
- Venna, J. Dimensionality Reduction for Visual Exploration of Similarity Structures. 82. Available online: https://www.researchgate.net/publication/27516587 (accessed on 23 March 2021).
- Saha, D.; Annamalai, M. Machine Learning Techniques for Analysis of Hyperspectral Images to Determine Quality of Food Products: A Review. Curr. Res. Food Sci. 2021, 4, 28–44. [Google Scholar] [CrossRef] [PubMed]
- Salles, R.D.R.; de Souza Filho, C.R.; Cudahy, T.; Vicente, L.E.; Monteiro, L.V.S. Hyperspectral Remote Sensing Applied to Uranium Exploration: A Case Study at the Mary Kathleen Metamorphic-Hydrothermal U-REE Deposit, NW, Queensland, Australia. J. Geochem. Explor. 2017, 179, 36–50. [Google Scholar] [CrossRef]
- Kruse, F.A. Mapping Surface Mineralogy Using Imaging Spectrometry. Geomorphology 2012, 137, 41–56. [Google Scholar] [CrossRef]
- Ganesh, U.K.; Kannan, S.T. Creation of Hyper Spectral Library and Lithological Discrimination of Granite Rocks Using SVCHR -1024: Lab Based Approach. J. Hyperspectral Remote. Sens. 2017, 7, 168–177. [Google Scholar]
- Li, Y.; Chai, Y.; Zhou, H.; Yin, H. A Novel Dimension Reduction and Dictionary Learning Framework for High-Dimensional Data Classification. Pattern Recognit. 2021, 112, 107793. [Google Scholar] [CrossRef]
- Li, J.; Wang, T. Dimension Reduction in Binary Response Regression: A Joint Modeling Approach. Comput. Stat. Data Anal. 2021, 156, 107131. [Google Scholar] [CrossRef]
- Zuniga, M.M.; Murangira, A.; Perdrizet, T. Structural Reliability Assessment through Surrogate Based Importance Sampling with Dimension Reduction. Reliab. Eng. Syst. Saf. 2021, 207, 107289. [Google Scholar] [CrossRef]
- Koren, Y.; Carmel, L. Robust Linear Dimensionality Reduction. IEEE Trans. Vis. Comput. Graph. 2004, 10, 459–470. [Google Scholar] [CrossRef]
- Bar-Hillel, A.; Hertz, T.; Shental, N.; Weinshall, D. Learning a Mahalanobis Metric from Equivalence Constraints. J. Mach. Learn. Res. 2005, 6, 937–965. [Google Scholar]
- Zhang, C.; Lei, Y.-K.; Zhang, S.; Yang, J.; Hu, Y. Orthogonal Discriminant Neighborhood Analysis for Tumor Classification. Soft Comput. 2016, 20, 263–271. [Google Scholar] [CrossRef]
- Hu, H.; Feng, D.-Z.; Chen, Q.-Y. A Novel Dimensionality Reduction Method: Similarity Order Preserving Discriminant Analysis. Signal Process. 2021, 182, 107933. [Google Scholar] [CrossRef]
- Kalia, V.; Walker, D.I.; Krasnodemski, K.M.; Jones, D.P.; Miller, G.W.; Kioumourtzoglou, M.-A. Unsupervised Dimen-sionality Reduction for Exposome Research. Curr. Opin. Environ. Sci. Health 2020, 15, 32–38. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, J. High Dimensional Structural Reliability with Dimension Reduction. Struct. Saf. 2017, 69, 35–46. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S. Discriminant Common Vecotors Versus Neighbourhood Components Analysis. 32. Image Vis. Comput. 2006, 24, 249–262. [Google Scholar] [CrossRef]
- Kartun-Giles, A.P.; Bianconi, G. Beyond the Clustering Coefficient: A Topological Analysis of Node Neighbourhoods in Complex Networks. Chaos Solitons Fractals X 2019, 1, 100004. [Google Scholar] [CrossRef]
- Gunduz, H. An Efficient Dimensionality Reduction Method Using Filter-Based Feature Selection and Variational Auto encoders on Parkinson’s Disease Classification. Biomed. Signal Process. Control 2021, 66, 102452. [Google Scholar] [CrossRef]
- Jain, U.; Nathani, K.; Ruban, N.; Joseph Raj, A.N.; Zhuang, Z.; Mahesh, V.G.V. Cubic SVM Classifier Based Feature Extraction and Emotion Detection from Speech Signals. In Proceedings of the 2018 International Conference on Sensor Networks and Signal (SNSP), Xi’an, China, 28–31 October 2018. [Google Scholar] [CrossRef]
- Taylor, G.R. Mineral and Lithology Mapping of Drill Core Pulps Using Visible and Infrared Spectrometry. Nat. Resour. Res. 2000, 9, 257–268. [Google Scholar] [CrossRef]
- Bar-Hillel, A.; Hertz, T.; Shental, N.; Weinshall, D. Learning Distance Functions Using Equivalence Relations. In Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington, DC, USA, 21–24 August 2003; Available online: https://www.researchgate.net/publication/221344999_Learning_Distance_Functions_using_Equivalence_Relations (accessed on 23 March 2021).
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and Comparative Study of Dimensionality Reduction Techniques for High Dimensional Data. Inf. Technol. Control 2020, 59, 44–58. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Geng, Y.; Zhang, Z.; Li, X.; Du, Q. Unsupervised Spatial–Spectral Feature Learning by 3D Convolutional Auto-encoder for Hyperspectral Classification. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 6808–6820. [Google Scholar] [CrossRef]


| Number of Classification Bands Post-NCA | Machine Learning Algorithm | Global Accuracy (%) | Average per-Class Precision (%) | Training Time (s) |
|---|---|---|---|---|
| 204-bands 1 | SVM (Cubic SVM) | 90.7 | 90.0 | 28.7 |
| SVM (Quadratic SVM) | 87.0 | 86.0 | 27.3 | |
| SVM (Linear SVM) | 79.1 | 76.5 | 13.8 | |
| Linear discriminant | 80.4 | 78.4 | 4.6 | |
| Ensemble (Subspace discriminant) | 81.2 | 79.3 | 41.5 | |
| 100-bands | SVM (Cubic SVM) | 89.4 | 88.7 | 37.7 |
| SVM (Quadratic SVM) | 84.7 | 83.8 | 21.8 | |
| Quadratic Discriminant | 77.9 | 77.5 | 1.0 | |
| SVM (Linear SVM) | 76.9 | 76.0 | 5.9 | |
| Linear Discriminant | 76.7 | 75.6 | 1.1 | |
| 50-bands | SVM (Cubic SVM) | 86.9 | 85.7 | 39.1 |
| SVM (Quadratic SVM) | 84.3 | 82.1 | 23.2 | |
| Quadratic Discriminant | 79.1 | 78.9 | 1.1 | |
| SVM (Linear SVM) | 76.1 | 75.4 | 5.3 | |
| Ensemble (Subspace KNN) | 75.2 | 75.0 | 34.9 | |
| 25-bands | SVM (Cubic SVM) | 86.3 | 86.2 | 45.1 |
| SVM (Quadratic SVM) | 83.9 | 82.6 | 28.2 | |
| SVM (Fine Gaussian SVM) | 75.9 | 70.6 | 6.7 | |
| Quadratic Discriminant | 75.7 | 75.3 | 1.2 | |
| Ensemble (Subspace KNN) | 75.4 | 70.0 | 29.2 | |
| 10-bands | SVM (Cubic SVM) | 81.0 | 80.3 | 78.2 |
| SVM (Quadratic SVM) | 78.2 | 76.0 | 40.7 | |
| SVM (Fine Gaussian SVM) | 72.7 | 70.1 | 8.2 | |
| Ensemble (Bagged tress) | 71.0 | 69.8 | 19.1 | |
| Ensemble (Subspace KNN) | 70.6 | 70.3 | 17.9 | |
| 5-bands | SVM (Cubic SVM) | 70.9 | 72.0 | 182.1 |
| Ensemble (Bagged trees) | 68.6 | 67.0 | 12.3 | |
| SVM (Quadratic SVM) | 68.4 | 65.8 | 76.7 | |
| SVM (Fine Gaussian SVM) | 68.4 | 66.6 | 7.5 | |
| KNN (Fine KNN) | 67.3 | 66.0 | 5.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinaice, B.B.; Owada, N.; Saadat, M.; Toriya, H.; Inagaki, F.; Bagai, Z.; Kawamura, Y. Coupling NCA Dimensionality Reduction with Machine Learning in Multispectral Rock Classification Problems. Minerals 2021, 11, 846. https://doi.org/10.3390/min11080846
Sinaice BB, Owada N, Saadat M, Toriya H, Inagaki F, Bagai Z, Kawamura Y. Coupling NCA Dimensionality Reduction with Machine Learning in Multispectral Rock Classification Problems. Minerals. 2021; 11(8):846. https://doi.org/10.3390/min11080846
Chicago/Turabian StyleSinaice, Brian Bino, Narihiro Owada, Mahdi Saadat, Hisatoshi Toriya, Fumiaki Inagaki, Zibisani Bagai, and Youhei Kawamura. 2021. "Coupling NCA Dimensionality Reduction with Machine Learning in Multispectral Rock Classification Problems" Minerals 11, no. 8: 846. https://doi.org/10.3390/min11080846
APA StyleSinaice, B. B., Owada, N., Saadat, M., Toriya, H., Inagaki, F., Bagai, Z., & Kawamura, Y. (2021). Coupling NCA Dimensionality Reduction with Machine Learning in Multispectral Rock Classification Problems. Minerals, 11(8), 846. https://doi.org/10.3390/min11080846






