The Effect of Stoichiometry, Mg-Ca Distribution, and Iron, Manganese, and Zinc Impurities on the Dolomite Order Degree: A Theoretical Study
Abstract
:1. Introduction
2. Calculation Procedure
3. Results and Discussion
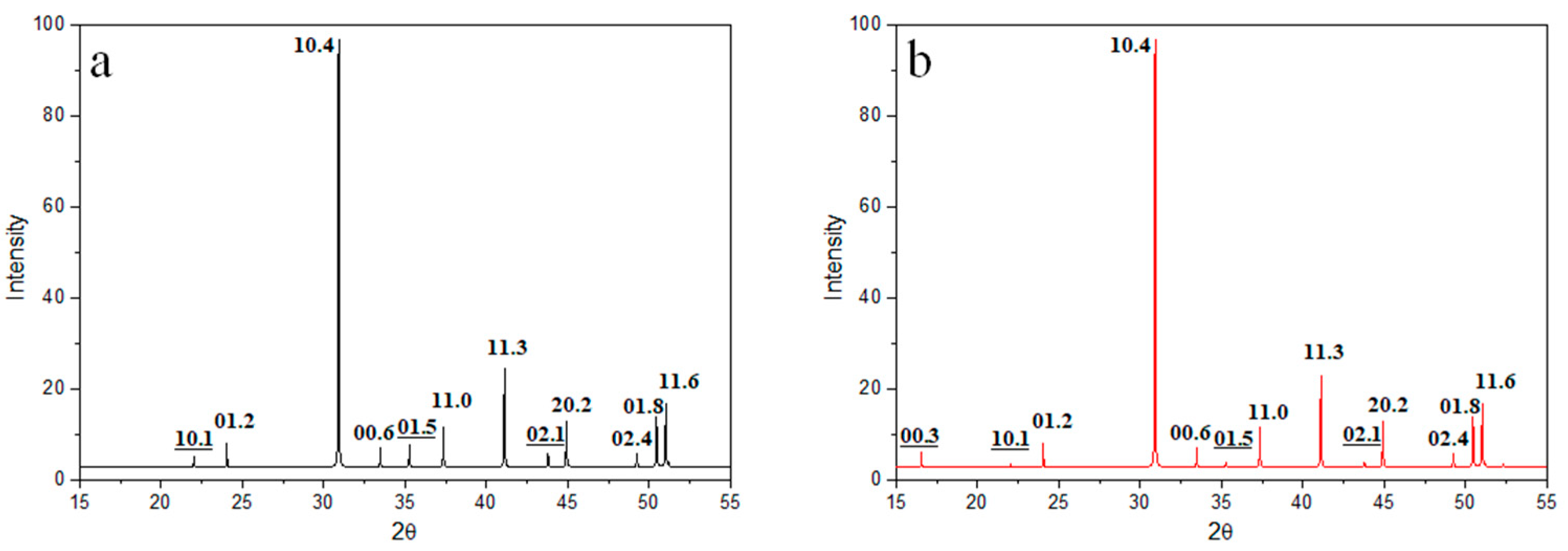
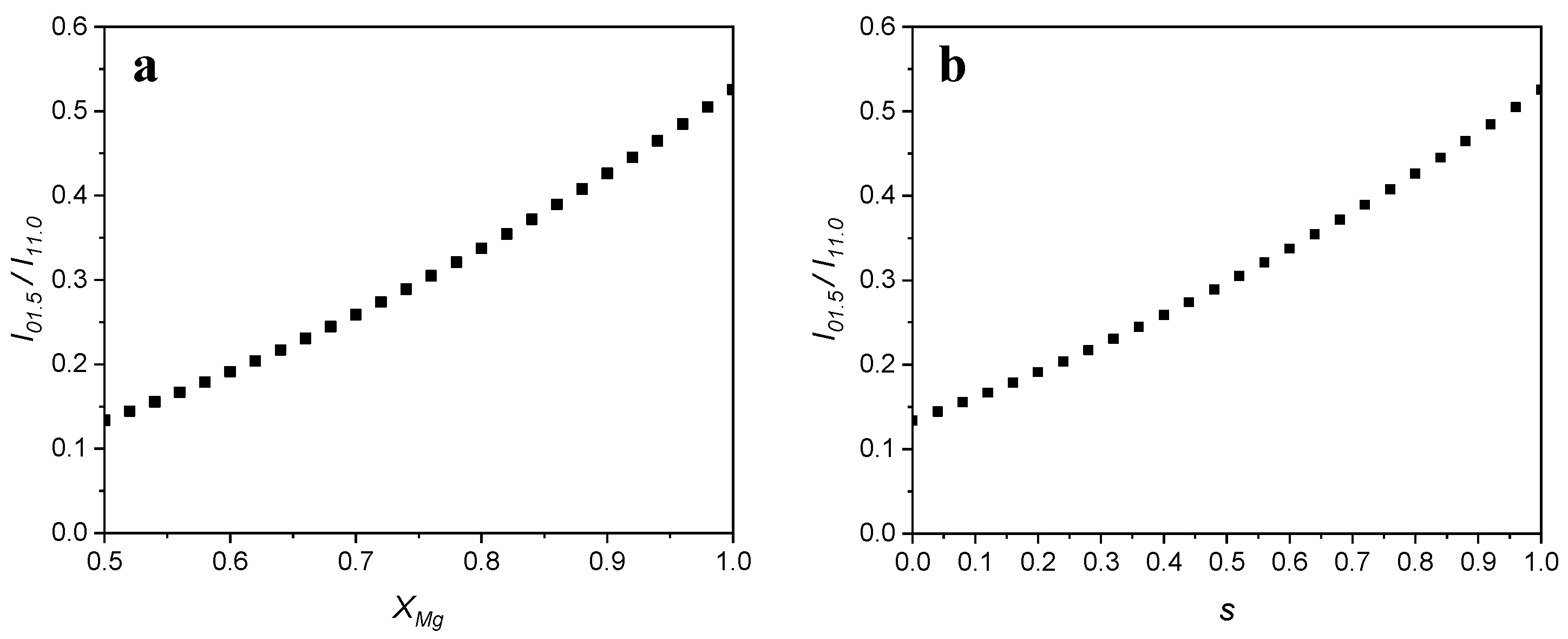
3.1. Stoichiometric Dolomites
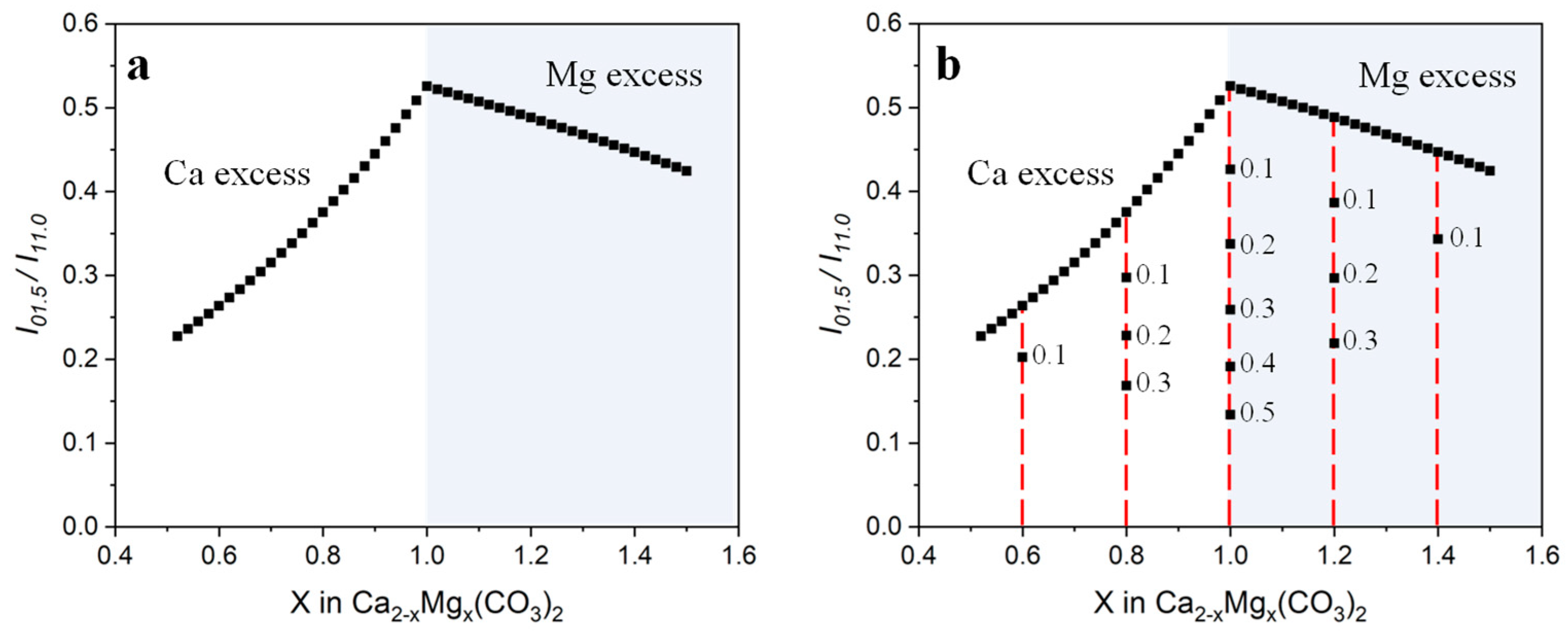
3.2. Non-Stoichiometric Dolomites
3.3. Dolomites with Iron, Manganese, and Zinc Impurities
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaczmarek, S.E.; Sibley, D.F. On the evolution of dolomite stoichiometry and cation order during high-temperature synthesis experiments: An alternative model for the geochemical evolution of natural dolomites. Sediment. Geol. 2011, 240, 30–40. [Google Scholar] [CrossRef]
- Kell-Duivestein, I.J.; Baldermann, A.; Mavromatis, V.; Dietzel, M. Controls of temperature, alkalinity and calcium carbonate reactant on the evolution of dolomite and magnesite stoichiometry and dolomite cation ordering degree—An experimental approach. Chem. Geol. 2019, 529, 119292. [Google Scholar] [CrossRef]
- Montes-Hernandez, G.; Findling, N.; Renard, F. Dissolution-precipitation reactions controlling fast formation of dolomite under hydrothermal conditions. Appl. Geochem. 2016, 73, 169–177. [Google Scholar] [CrossRef]
- Hammouda, T.; Andrault, D.; Koga, K.T.; Katsura, T.; Martin, A.M. Ordering in double carbonates and implications for processes at subduction zones. Contrib. Miner. Pet. 2010, 161, 439–450. [Google Scholar] [CrossRef]
- Luth, R.W. Experimental determination of the reaction aragonite + magnesite = dolomite at 5 to 9 GPa. Contrib. Miner. Pet. 2001, 141, 222–232. [Google Scholar] [CrossRef]
- Putnis, A. Introduction to Mineral Sciences; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Zucchini, A.; Prencipe, M.; Comodi, P.; Frondini, F. Ab initio study of cation disorder in dolomite. Calphad 2012, 38, 177–184. [Google Scholar] [CrossRef]
- Graf, D.L.; Goldsmith, J.R. Some Hydrothermal Syntheses of Dolomite and Protodolomite. J. Geol. 1956, 64, 173–186. [Google Scholar] [CrossRef]
- Hird, K. Petrography and Geochemistry of Some Carboniferous and Precambrian Dolomites. Ph.D. Thesis, Durham University, Durham, UK, 1985. [Google Scholar]
- McKenzie, J.A. Holocene Dolomitization of Calcium Carbonate Sediments from the Coastal Sabkhas of Abu Dhabi, U.A.E.: A Stable Isotope Study. J. Geol. 1981, 89, 185–198. [Google Scholar] [CrossRef]
- Schultz-Güttler, R. The influence of disordered, non-equilibrium dolomites on the Mg-solubility in calcite in the system CaCO3-MgCO3. Contrib. Miner. Pet. 1986, 93, 395–398. [Google Scholar] [CrossRef]
- Lippmann, F. Sedimentary Carbonate Minerals; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Alonso-Zarza, A.M.; Martín-Pérez, A. Dolomite in caves: Recent dolomite formation in oxic, non-sulfate environments. Castañar Cave, Spain. Sediment. Geol. 2008, 205, 160–164. [Google Scholar] [CrossRef] [Green Version]
- Pina, C.M.; Pimentel, C.; Crespo, Á. Dolomite cation order in the geological record. Chem. Geol. 2020, 547, 119667. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Benning, L.G. A route for the direct crystallization of dolomite. Am. Miner. 2015, 100, 1172–1181. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Miser, D.E.; Swinnea, J.S.; Steinfink, H. TEM Observations and X-Ray Crystal-Structure Refinement of a Twinned Dolomite with a Modulated Microstructure. Am. Mineral. 1987, 72, 188–193. [Google Scholar]
- Maslen, E.N.; Streltsov, V.A.; Streltsova, N.R.; Ishizawa, N. Electron density and optical anisotropy in rhombohedral carbonates. III. Synchrotron X-ray studies of CaCO3, MgCO3 and MnCO3. Acta Crystallogr. Sect. B Struct. Sci. 1995, 51, 929–939. [Google Scholar] [CrossRef] [Green Version]
- Izumi, F.; Momma, K. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 2007, 130, 15–20. [Google Scholar] [CrossRef]
- Manche, C.J.; Kaczmarek, S.E. A global study of dolomite stoichiometry and cation ordering through the Phanerozoic. J. Sediment. Res. 2021, 91, 520–546. [Google Scholar] [CrossRef]
- Mayayo, M.; Bauluz, B.; Galindo, A.L.; González-López, J. Mineralogy and geochemistry of the carbonates in the Calatayud Basin (Zaragoza, Spain). Chem. Geol. 1996, 130, 123–136. [Google Scholar] [CrossRef]
- Drits, V.A.; Mccarty, D.K.; Sakharov, B.; Milliken, K.L. New Insight into Structural and Compositional Variability in Some Ancient Excess-Ca Dolomite. Can. Miner. 2005, 43, 1255–1290. [Google Scholar] [CrossRef]
- Reeder, R.J. Constraints on Cation Order in Calcium-rich Sedimentary Dolomite. Aquat. Geochem. 2000, 6, 213–226. [Google Scholar] [CrossRef]
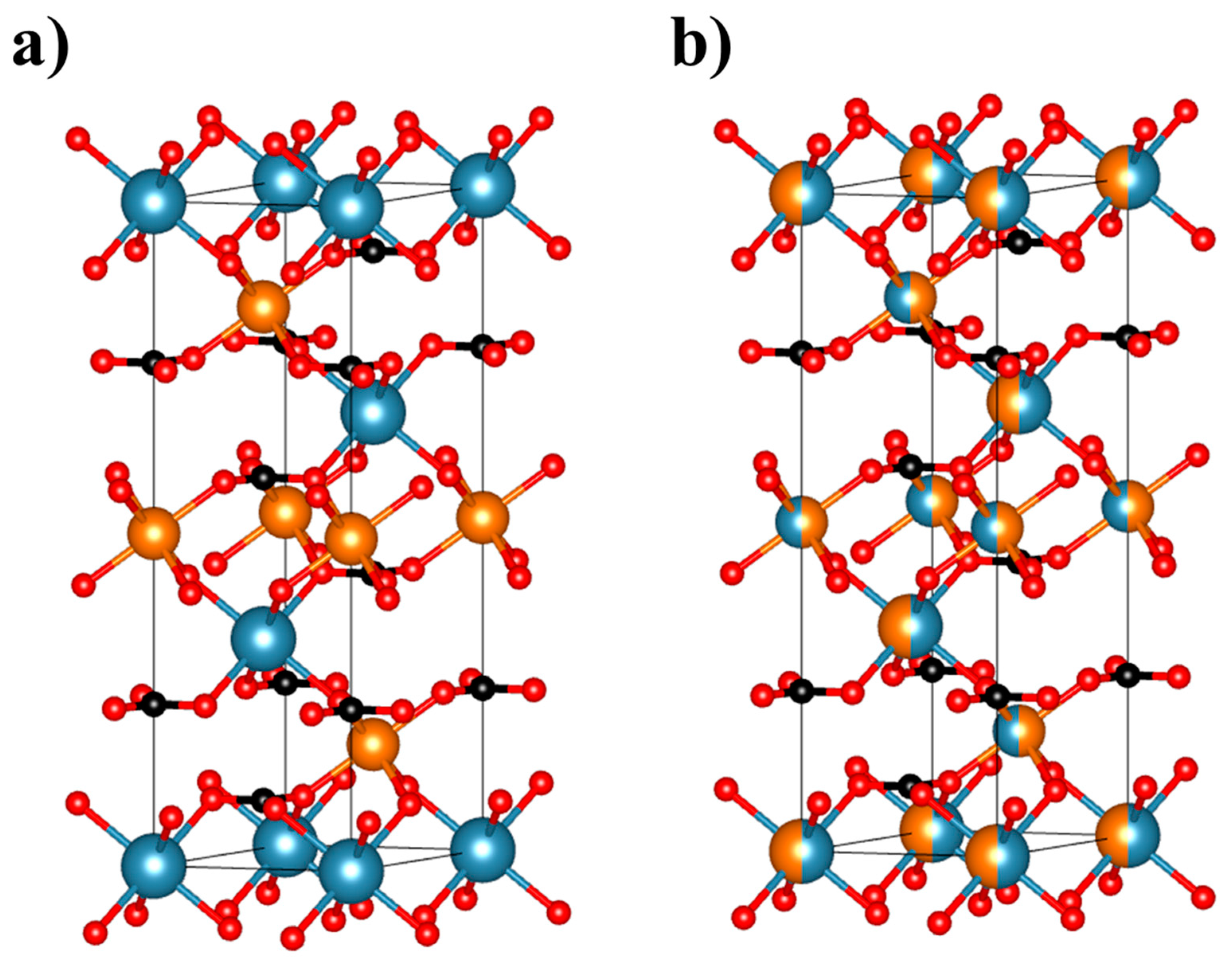
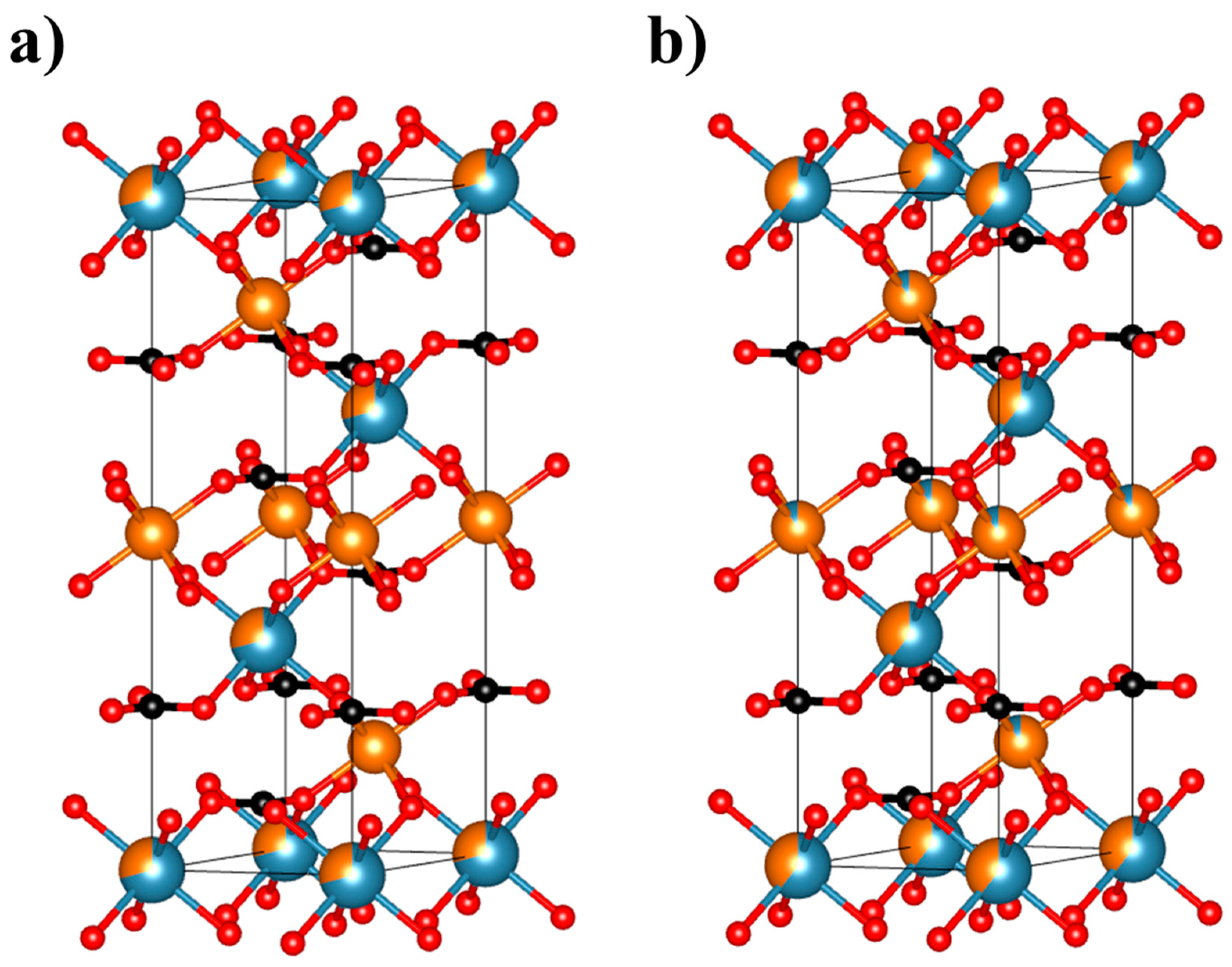
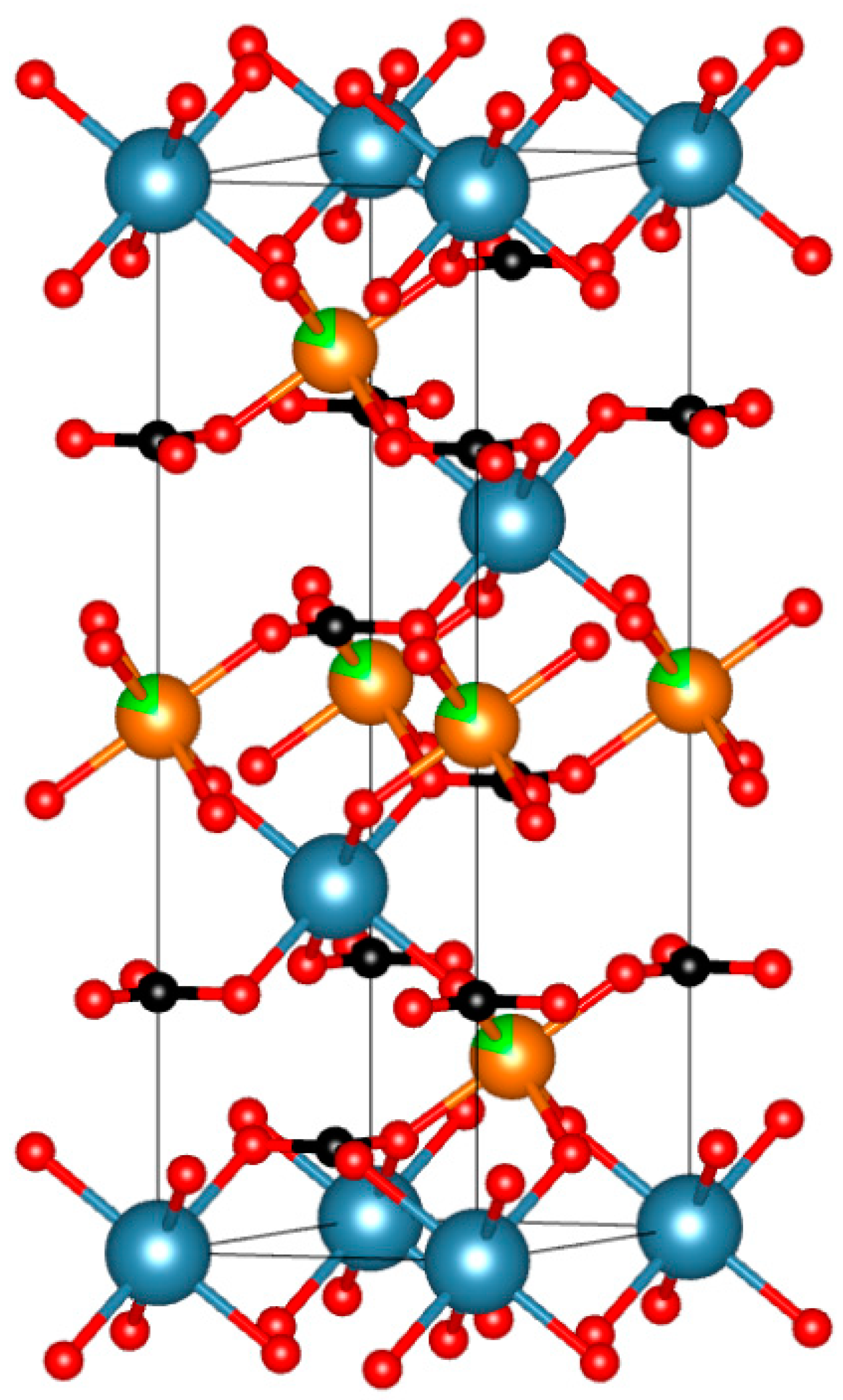

| Dolomite | Calcite | |
|---|---|---|
| a = b (NM) | 0.4811 | 0.4988 |
| c (NM) | 1.6047 | 1.7068 |
| α = β (º) | 90 | 90 |
| γ (º) | 120 | 120 |
| S.G. | R | Rc |
| Ca (X, Y, Z) | 0, 0, 0 | 0, 0, 0 |
| Mg (X, Y, Z) | 0, 0, 0.5 | - |
| C (X, Y, Z) | 0, 0, 0.2430 | 0, 0, 0.25 |
| O (X, Y, Z) | 0.2476, 0.9650, 0.2441 | 0.257, 0, 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zvir, Y.; Pimentel, C.; Pina, C.M. The Effect of Stoichiometry, Mg-Ca Distribution, and Iron, Manganese, and Zinc Impurities on the Dolomite Order Degree: A Theoretical Study. Minerals 2021, 11, 702. https://doi.org/10.3390/min11070702
Zvir Y, Pimentel C, Pina CM. The Effect of Stoichiometry, Mg-Ca Distribution, and Iron, Manganese, and Zinc Impurities on the Dolomite Order Degree: A Theoretical Study. Minerals. 2021; 11(7):702. https://doi.org/10.3390/min11070702
Chicago/Turabian StyleZvir, Yuliya, Carlos Pimentel, and Carlos M. Pina. 2021. "The Effect of Stoichiometry, Mg-Ca Distribution, and Iron, Manganese, and Zinc Impurities on the Dolomite Order Degree: A Theoretical Study" Minerals 11, no. 7: 702. https://doi.org/10.3390/min11070702
APA StyleZvir, Y., Pimentel, C., & Pina, C. M. (2021). The Effect of Stoichiometry, Mg-Ca Distribution, and Iron, Manganese, and Zinc Impurities on the Dolomite Order Degree: A Theoretical Study. Minerals, 11(7), 702. https://doi.org/10.3390/min11070702








