Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations
Abstract
1. Introduction
2. Methods
3. Results and Discussion
3.1. Atomic Structure and Mechanical Property of Na-MMT and Mg-MMT at Ideal Condition
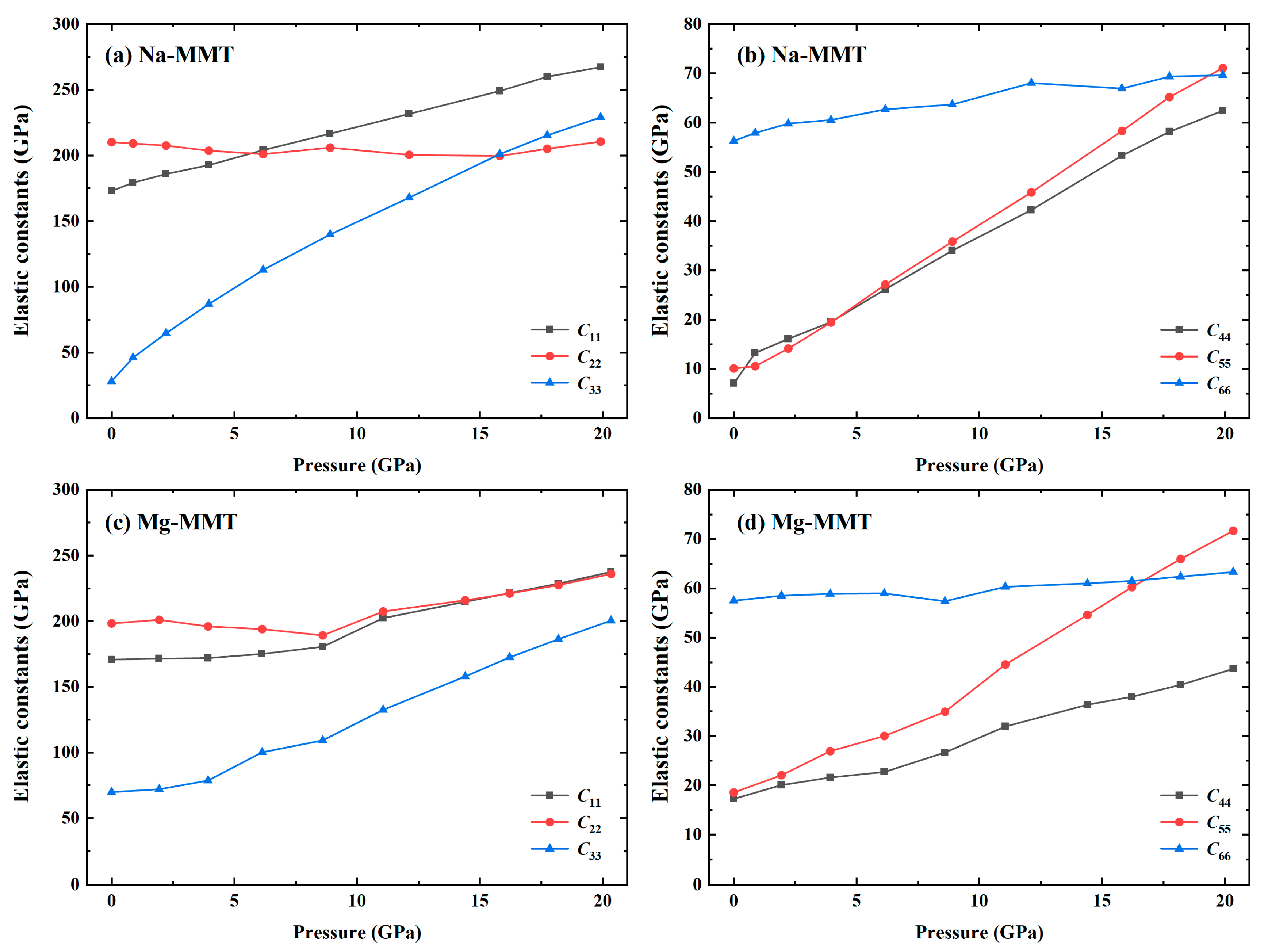
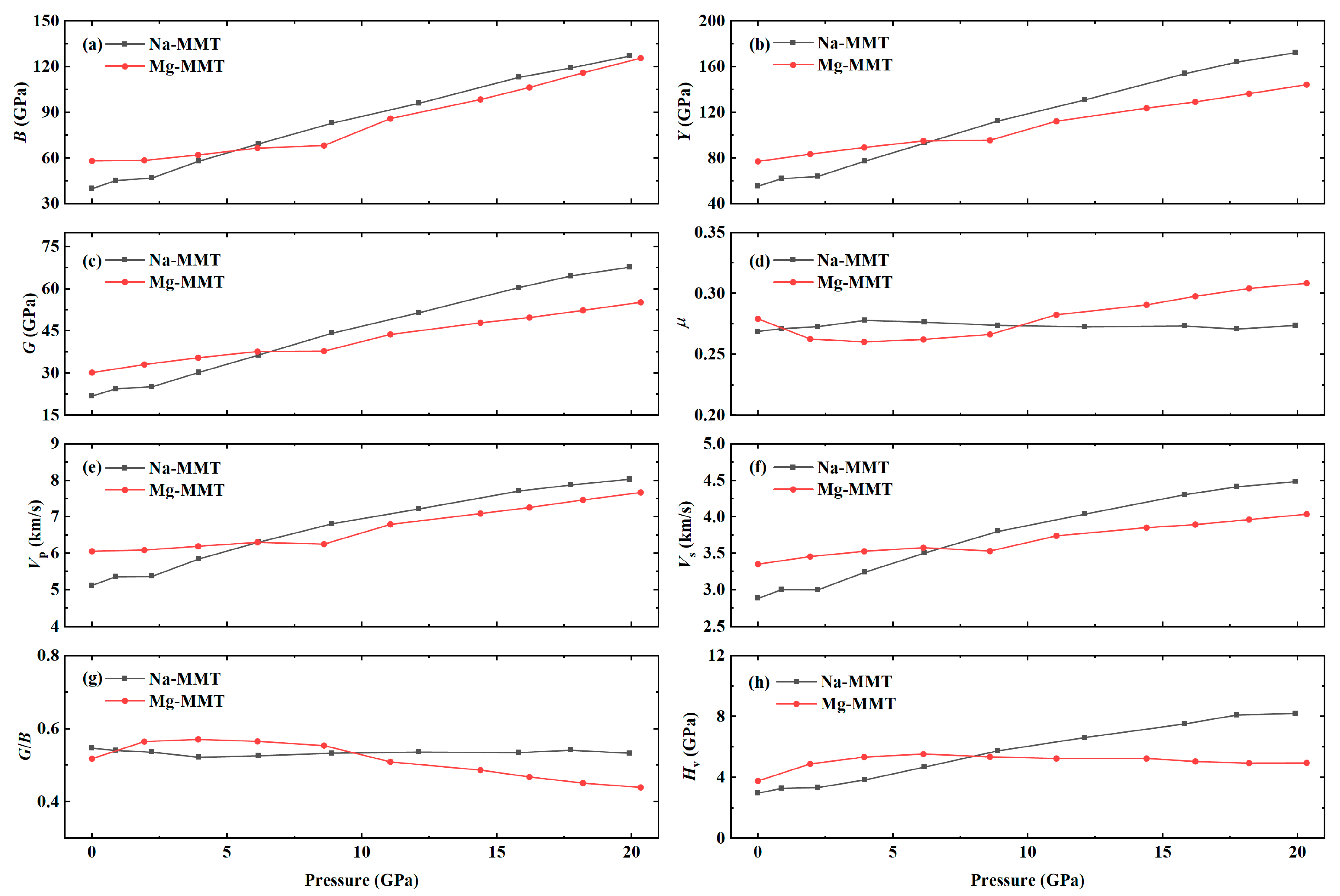
3.2. Effects of Pressure on Atomic Structure and Mechanical Properties of Na-MMT and Mg-MMT
4. Conclusions
- The calculated structural parameters of Na-MMT and Mg-MMT have been compared favorably with available experimental measurements and other theoretical works at ideal condition. With increasing the pressure, the volume, lattice parameters, and major bond lengths of Na-MMT and Mg-MMT decreased gradually, indicating that the effects of pressure on atomic structure is obvious.
- The charge density distribution, density of states, and band structure of Na-MMT and Mg-MMT were calculated from 0 GPa to 20 GPa. With increasing the pressure, the charge density distribution and density of states changed slightly, while the width of the band gap was broadened of Na-MMT and Mg-MMT. The results implied that the electronic property of montmorillonite changed slightly under high pressure.
- The calculated results of mechanical properties at zero pressure are in good agreement with the experimental values, which proves the reliability of the calculation. The major elastic constants of Na-MMT and Mg-MMT were increasing with increasing the pressure. As a result, the mechanical parameters of Bulk modulus, Shear modulus, and Young’s modulus increased with increasing the pressure, indicating the elastic mechanics of montmorillonite was significantly improved. Especially, the elastic modulus of Na-MMT increased more rapidly than that of Mg-MMT.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aldersley, M.F.; Joshi, P.C.; Price, J.D.; Ferris, J.P. The role of montmorillonite in its catalysis of RNA synthesis. Appl. Clay Sci. 2011, 54, 1–14. [Google Scholar] [CrossRef]
- Neubauer, V.; Humer, E.; Mann, E.; Kröger, I.; Reisinger, N.; Wagner, M.; Zebeli, Q.; Petri, R.M. Effects of clay mineral supplementation on particle-associated and epimural microbiota, and gene expression in the rumen of cows fed high-concentrate diet. Anaerobe 2019, 59, 38–48. [Google Scholar] [CrossRef]
- Özdemir, G.; Yapar, S. Preparation and characterization of copper and zinc adsorbed cetylpyridinium and N-lauroylsarcosinate intercalated montmorillonites and their antibacterial activity. Colloids Surf. B Biointerfaces 2020, 188, 110791. [Google Scholar] [CrossRef]
- Arabkhani, P.; Asfaram, A.; Ateia, M. Easy-to-prepare graphene oxide/sodium montmorillonite polymer nanocomposite with enhanced adsorption performance. J. Water Process Eng. 2020, 38, 101651. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, R.; Wang, L.; Xue, K.; Chen, J. Strong adsorption of phosphate from aqueous solution by zirconium-loaded Ca-montmorillonite. Appl. Clay Sci. 2020, 192, 105638. [Google Scholar] [CrossRef]
- Uddin, F. Current Topics in the Utilization of Clay in Industrial and Medical Applications; IntechOpen: London, UK, 2018; Chapter 1. [Google Scholar]
- Bergaya, F.; Lagaly, G. Developments in Clay Science; Bergaya, F., Lagaly, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 5, pp. 1–19. [Google Scholar]
- Zhu, R.; Chen, Q.; Zhou, Q.; Xi, Y.; Zhu, J.; He, H. Adsorbents based on montmorillonite for contaminant removal from water: A review. Appl. Clay Sci. 2016, 123, 239–258. [Google Scholar] [CrossRef]
- Maryan, A.S.; Montazer, M. Natural and organo-montmorillonite as antibacterial nanoclays for cotton garment. J. Ind. Eng. Chem. 2015, 22, 164–170. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, Z.; Tang, J.; Wang, F.; Liao, L. Applied properties of oil-based drilling fluids with montmorillonites modified by cationic and anionic surfactants. Appl. Clay Sci. 2016, 121–122, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, F.; Li, Y.; Wu, T.; Sun, D.; Zhang, G.; Huang, X.; Wang, G. Effects of Na–montmorillonite particles on the emulsification stability of polymer flooding produced water. Colloids Surf. A Physicochem. Eng. Asp. 2012, 410, 125–129. [Google Scholar] [CrossRef]
- Weng, Z.; Wang, J.; Senthil, T.; Wu, L. Mechanical and thermal properties of ABS/montmorillonite nanocomposites for fused deposition modeling 3D printing. Mater. Des. 2016, 102, 276–283. [Google Scholar] [CrossRef]
- Asgari, M.; Abouelmagd, A.; Sundararaj, U. Silane functionalization of sodium montmorillonite nanoclay and its effect on rheological and mechanical properties of HDPE/clay nanocomposites. Appl. Clay Sci. 2017, 146, 439–448. [Google Scholar] [CrossRef]
- Yang, F.; Mubarak, C.; Keiegel, R.; Kannan, R.M. Supercritical carbon dioxide (scCO2) dispersion of poly (ethylene terephthalate)/clay nanocomposites: Structural, mechanical, thermal, and barrier properties. J. Appl. Polym. Sci. 2017, 134, 1–11. [Google Scholar] [CrossRef]
- Ammar, A.; Elzatahry, A.; Al-Maadeed, M.; Alenizi, A.M.; Huq, A.F.; Karim, A. Nanoclay compatibilization of phase separated polysulfone/polyimide films for oxygen barrier. Appl. Clay Sci. 2017, 137, 123–134. [Google Scholar] [CrossRef]
- Ma, Y.; Lv, L.; Guo, Y.; Fu, Y.; Shao, Q.; Wu, T.; Guo, S.; Sun, K.; Guo, X.; Wujcik, E.K.; et al. Porous lignin based poly (acrylic acid)/organo-montmorillonite nanocomposites: Swelling behaviors and rapid removal of Pb (II) ions. Polymer 2017, 128, 12–23. [Google Scholar] [CrossRef]
- Hofmann, U.; Endell, K.; Wilm, D. Kristallstruktur und Quellung von Montmorillonit. Z. Krist. Cryst. Mater. 1933, 86, 340–348. [Google Scholar] [CrossRef]
- Mooney, R.W.; Keenan, A.G.; Wood, L.A. Adsorption of Water Vapor by Montmorillonite. II. Effect of Exchangeable Ions and Lattice Swelling as Measured by X-Ray Diffraction. J. Am. Chem. Soc. 1952, 74, 1371–1374. [Google Scholar] [CrossRef]
- Cowley, J.M.; Goswami, A. Electron Diffraction Patterns from Montmorillonite. Acta Crystallogr. 1961, 14, 1071–1079. [Google Scholar] [CrossRef]
- Nadeau, P.H.; Wilson, M.J.; Mchardy, W.J.; Tait, J.M. Interstratified Clays as Fundamental Particles. Science 1984, 225, 923–925. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, H.; Cates, M.E. Effective elastic properties of solid clays. Geophysics 2001, 66, 428–440. [Google Scholar] [CrossRef]
- Vanorio, T.; Prasad, M.; Nur, A. Elastic properties of dry clay mineral aggregates, suspensions and sandstones. Geophys. J. Int. 2003, 155, 319–326. [Google Scholar] [CrossRef]
- Mondol, N.H.; Jahren, J.; Bjørlykke, K.; Brevik, I. Elastic properties of clay minerals. Lead. Edge 2008, 27, 758–770. [Google Scholar] [CrossRef]
- Bridgeman, C.H. Ab-initio total energy study of uncharged 2:1 clays and their interaction with water. Mol. Phys. 1996, 89, 879–888. [Google Scholar] [CrossRef]
- Refson, K.; Park, S.H.; Sposito, G. Ab Initio Computational Crystallography of 2:1 Clay Minerals: 1. Pyrophyllite-1Tc. J. Phys. Chem. B 2003, 107, 3376–13383. [Google Scholar] [CrossRef]
- Zartman, G.D.; Liu, H.; Akdim, B.; Pachter, R.; Heinz, H. Nanoscale Tensile, Shear, and Failure Properties of Layered Silicates as a Function of Cation Density and Stress. J. Phys. Chem. C 2010, 114, 1763–1772. [Google Scholar] [CrossRef]
- Chatterjee, A.; Iwasaki, T.; Hayashi, H.; Ebina, T.; Torii, K. Electronic and structural properties of montmorillonite—A quantum chemical study. J. Mol. Catal. A Chem. 1998, 136, 195–202. [Google Scholar] [CrossRef]
- Sainz-Díaz, C.I.; Timón, V.; Botella, V.; Artacho, E.; Hernández-Laguna, A. Quantum mechanical calculations of dioctahedral 2:1 phyllosilicates: Effect of octahedral cation distributions in pyrophyllite, illite, and smectite. Am. Mineral. 2002, 87, 958–965. [Google Scholar] [CrossRef]
- Chatterjee, A.; Ebina, T.; Onodera, Y.; Mizukami, F. Effect of exchangeable cation on the swelling property of 2:1 dioctahedral smectite—A periodic first principle study. J. Chem. Phys. 2004, 120, 3414–3424. [Google Scholar] [CrossRef] [PubMed]
- Berghout, A.; Tunega, D.; Zaoui, A. Density Functional Theory (DFT) Study of the Hydration Steps of Na+/Mg2+/Ca2+/Sr2+/Ba2+-Exchanged Montmorillonites. Clays Clay Miner. 2010, 58, 174–187. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B Condens. Matter 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Benazzouz, B.K.; Zaoui, A. Phase diagram of kaolinite from Molecular Dynamics calculations. Phys. B Condens. Matter 2012, 407, 2462–2470. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Zhou, C.; Tong, D.; Yu, W. Nanomaterials from Clay Minerals; Wang, A., Wang, W., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 335–364. [Google Scholar]
- Tsipursky, S.I.; Drits, V. The Distribution of Octahedral Cations in the 2:1 Layers of Dioctahedral Smectites Studied by Oblique-Texture Electron Diffraction. Clay Miner. 1984, 19, 177–193. [Google Scholar] [CrossRef]
- Voora, V.K.; Al-Saidi, W.A.; Jordan, K.D. Density Functional Theory Study of Pyrophyllite and M-Montmorillonites (M = Li, Na, K, Mg, and Ca): Role of Dispersion Interactions. J. Phys. Chem. A 2011, 115, 9695–9703. [Google Scholar] [CrossRef] [PubMed]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. Ser. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Wang, Z. Fundamentals of seismic rock physics. Geophysics 2001, 66, 398–412. [Google Scholar] [CrossRef]
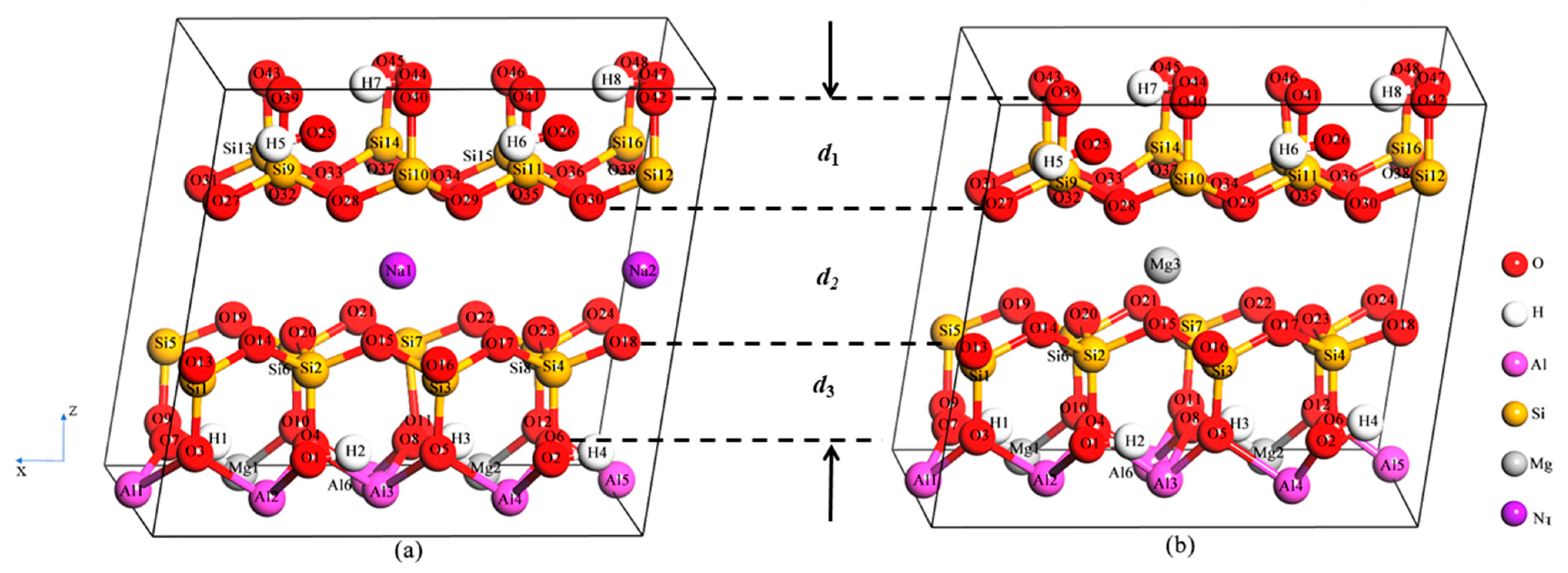

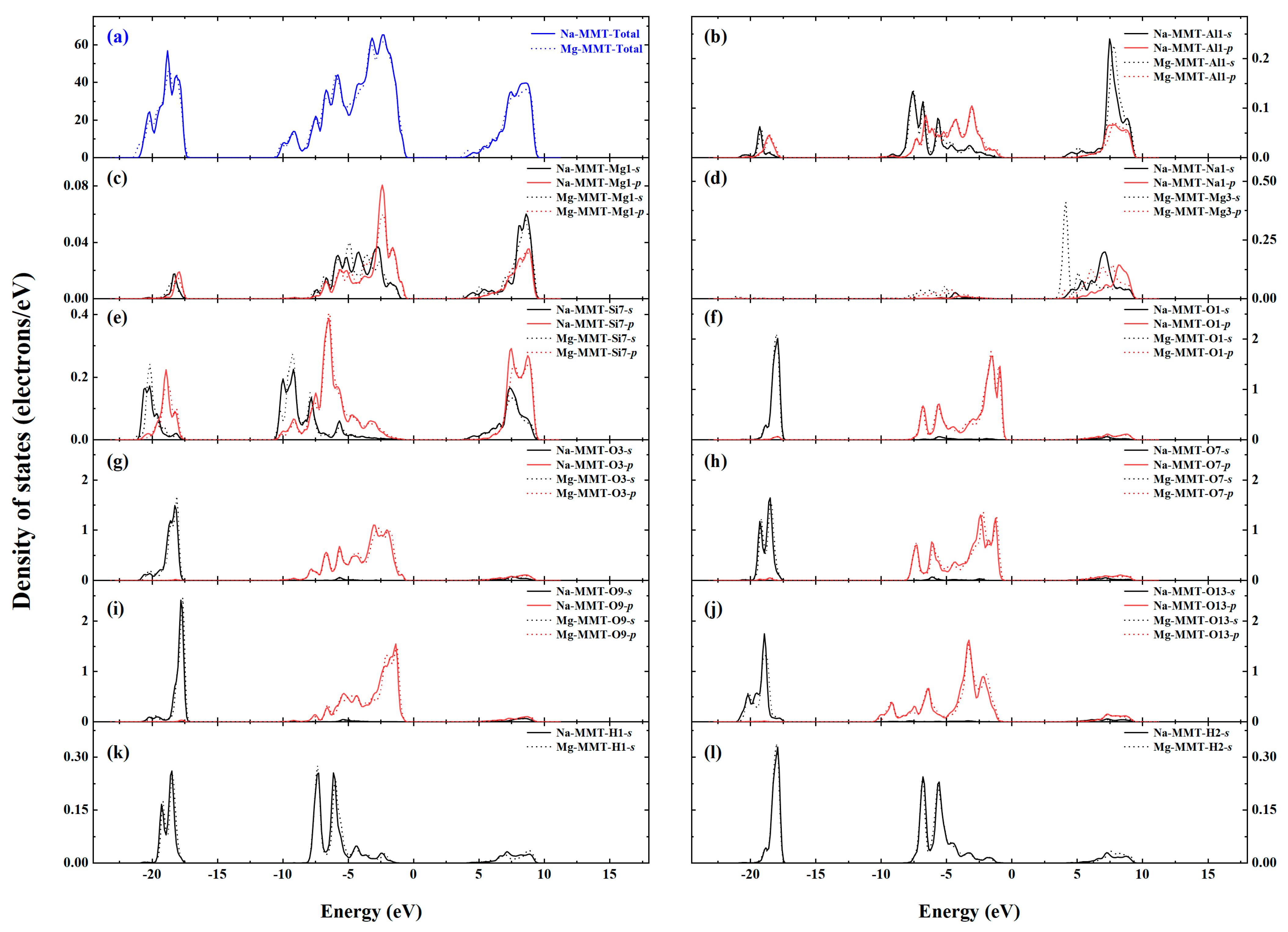
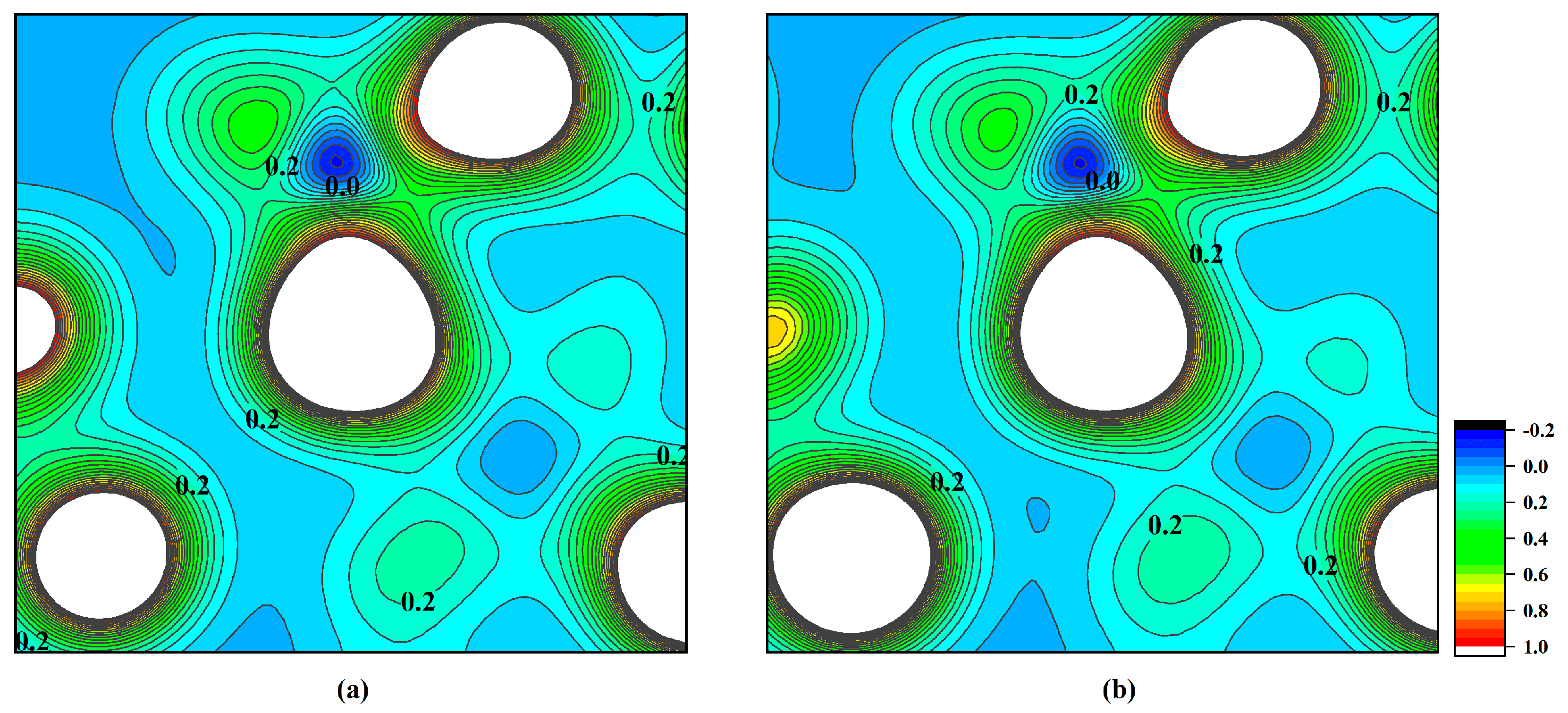
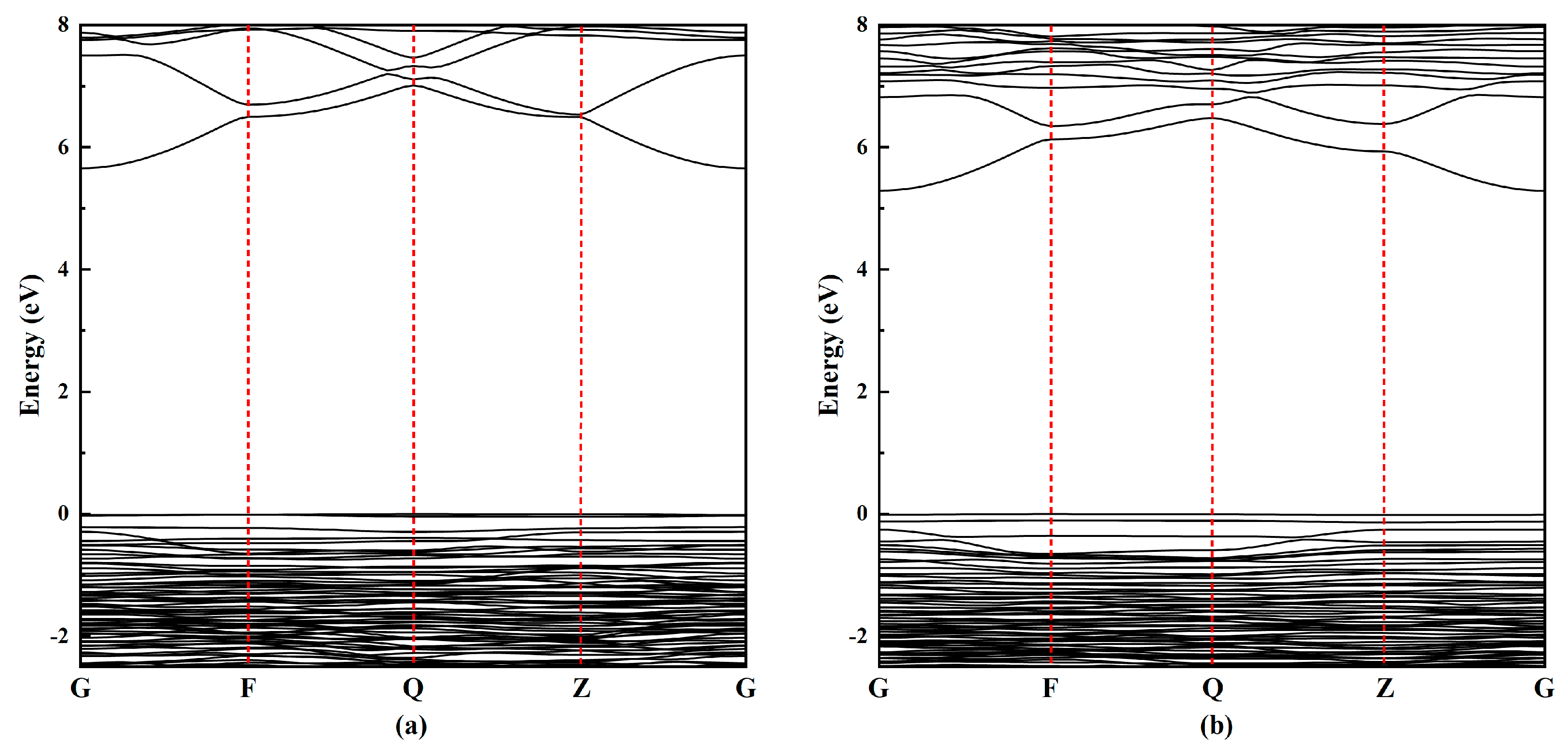

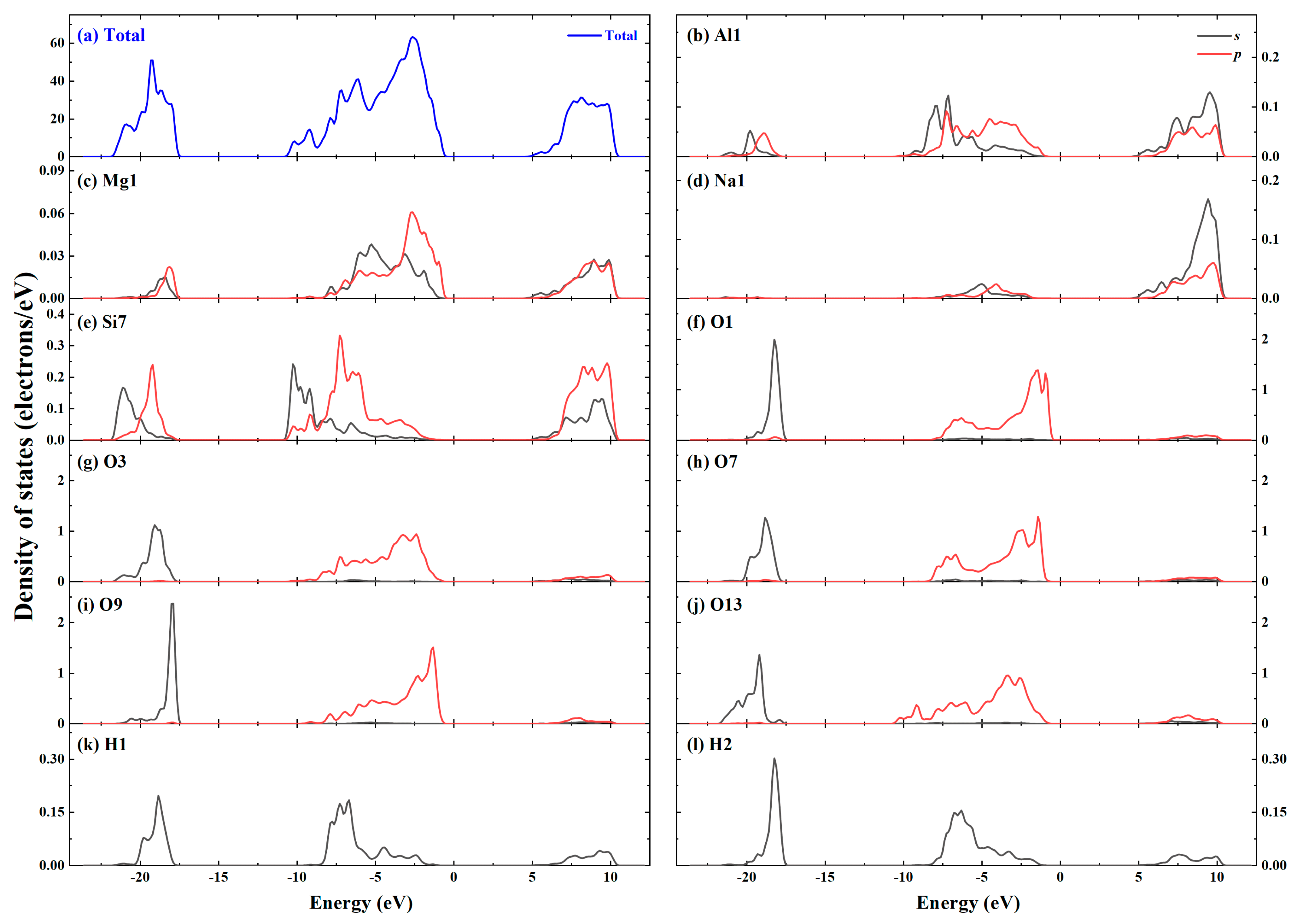
| Type | Phase | 2a(Å) | b(Å) | c(Å) | α(deg) | β(deg) | γ(deg) |
|---|---|---|---|---|---|---|---|
| Na-MMT | This work | 10.50 | 9.07 | 9.98 | 83.48 | 97.16 | 89.88 |
| Experiment [40] | 10.36 | 8.98 | 10.10 | 90.00 | 99.50 | 90.00 | |
| Calculated [41] | 10.45 | 9.07 | 9.57 | 99.37 | 99.18 | 90.14 | |
| Mg-MMT | This work | 10.49 | 9.06 | 9.69 | 81.12 | 96.95 | 89.95 |
| Calculated [41] | 10.39 | 9.02 | 9.30 | 80.60 | 96.47 | 89.75 |
| Bond | O-H | Oa-Al | Oa-Mg | Ob-Al | Oc-Si | Od-Si | Od-Al | Od-Mg | Oe-Si | Oe-Al |
|---|---|---|---|---|---|---|---|---|---|---|
| Na-MMT | 0.972 | 1.858 | 2.057 | 1.925 | 1.639 | 1.613 | 1.936 | 2.082 | 1.645 | 1.966 |
| Mg-MMT | 0.971 | 1.857 | 2.049 | 1.919 | 1.643 | 1.611 | 1.912 | 2.081 | 1.645 | 1.963 |
| HS Point | Site | s | p | HS Point | Site | s | p | HS Point | Site | s | p | HS Point | Site | s | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G(v) | Al1 | 0 | 0.003 | G(c) | Al1 | 0 | 0 | F(v) | Al1 | 0.001 | 0.003 | F(c) | Al1 | 0.005 | 0 |
| Mg1 | 0 | 0 | Mg1 | 0 | 0.001 | Na1 | 0 | 0 | Na1 | 0.021 | 0 | ||||
| O1 | 0 | 0.002 | O1 | 0 | 0.136 | Si1 | 0 | 0.003 | Si1 | 0.003 | 0 | ||||
| O3 | 0 | 0.016 | O3 | 0 | 0.008 | O1 | 0 | 0.001 | O1 | 0 | 0.004 | ||||
| O7 | 0 | 0.032 | O7 | 0 | 0 | O3 | 0 | 0.009 | O3 | 0.003 | 0.001 | ||||
| O9 | 0.001 | 0.008 | O9 | 0 | 0.009 | O7 | 0 | 0.010 | O7 | 0.006 | 0.001 | ||||
| O13 | 0 | 0.010 | O13 | 0 | 0.003 | O9 | 0 | 0.007 | O9 | 0.001 | 0.002 | ||||
| H1 | 0 | 0.001 | H1 | 0 | 0 | O13 | 0 | 0.009 | O13 | 0 | 0.003 | ||||
| H2 | 0 | 0 | H2 | 0 | 0.002 | H1 | 0.002 | 0 | H1 | 0.001 | 0.002 | ||||
| Q(v) | Al1 | 0 | 0.001 | Q(c) | Al1 | 0.005 | 0 | Z(v) | Al1 | 0 | 0.001 | Z(c) | Al1 | 0 | 0 |
| Mg1 | 0 | 0 | Mg1 | 0.002 | 0 | Mg1 | 0.001 | 0 | Mg1 | 0 | 0.001 | ||||
| Na1 | 0 | 0 | Na1 | 0.009 | 0.001 | Na1 | 0 | 0 | Na1 | 0 | 0 | ||||
| Si1 | 0 | 0.001 | Si1 | 0.007 | 0 | Si1 | 0 | 0.001 | Si1 | 0 | 0 | ||||
| O1 | 0 | 0.001 | O1 | 0.005 | 0.003 | O1 | 0 | 0.002 | O1 | 0 | 0.136 | ||||
| O3 | 0.001 | 0.009 | O3 | 0.006 | 0.001 | O3 | 0 | 0.002 | O3 | 0 | 0.009 | ||||
| O7 | 0 | 0.006 | O7 | 0.007 | 0.003 | O7 | 0 | 0.012 | O7 | 0 | 0 | ||||
| O9 | 0 | 0.013 | O9 | 0.004 | 0.002 | O9 | 0 | 0.007 | O9 | 0 | 0.009 | ||||
| O13 | 0.001 | 0.063 | O13 | 0.006 | 0.003 | O13 | 0 | 0.010 | O13 | 0 | 0.003 | ||||
| H1 | 0 | 0 | H1 | 0.001 | 0.002 | H1 | 0 | 0 | H2 | 0 | 0 | ||||
| H2 | 0 | 0 | H2 | 0.001 | 0.002 | H2 | 0 | 0 | H2 | 0 | 0.002 |
| HS Point | Site | s | p | HS Point | Site | s | p | HS Point | Site | s | p | HS Point | Site | s | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G(v) | Al1 | 0 | 0.001 | G(c) | Al1 | 0 | 0 | F(v) | Al1 | 0 | 0.001 | F(c) | Al1 | 0 | 0.001 |
| Mg3 | 0 | 0 | Mg3 | 0 | 0 | Si1 | 0 | 0.002 | Si1 | 0 | 0 | ||||
| O1 | 0.001 | 0.002 | O1 | 0 | 0.013 | O1 | 0 | 0.002 | O1 | 0 | 0.010 | ||||
| O3 | 0 | 0.002 | O3 | 0 | 0.001 | O3 | 0 | 0.021 | O3 | 0 | 0.002 | ||||
| O7 | 0 | 0.001 | O7 | 0 | 0 | O7 | 0.001 | 0.007 | O7 | 0 | 0.001 | ||||
| O9 | 0 | 0.001 | O9 | 0 | 0.003 | O9 | 0 | 0.021 | O9 | 0 | 0.002 | ||||
| O13 | 0 | 0.014 | O13 | 0 | 0.002 | O13 | 0.001 | 0.048 | O13 | 0 | 0.001 | ||||
| Q(v) | Al1 | 0 | 0.001 | Q(c) | Al1 | 0 | 0.001 | Z(v) | Al1 | 0 | 0.002 | Z(c) | Al1 | 0 | 0 |
| Mg3 | 0 | 0 | Mg3 | 0 | 0 | Mg3 | 0 | 0.001 | Mg3 | 0 | 0 | ||||
| O1 | 0 | 0.001 | O1 | 0 | 0.016 | O1 | 0 | 0.005 | O1 | 0 | 0.026 | ||||
| O3 | 0 | 0.003 | O3 | 0 | 0.003 | O3 | 0 | 0.006 | O3 | 0 | 0.002 | ||||
| O7 | 0 | 0.001 | O7 | 0 | 0.002 | O7 | 0 | 0.002 | O7 | 0 | 0 | ||||
| O9 | 0 | 0.006 | O9 | 0 | 0.003 | O9 | 0 | 0.001 | O9 | 0 | 0.003 | ||||
| O13 | 0 | 0.007 | O13 | 0 | 0.002 | O13 | 0 | 0.009 | O13 | 0 | 0.002 | ||||
| H1 | 0 | 0 | H1 | 0 | 0 | H1 | 0.001 | 0 | H1 | 0 | 0 |
| Type | Oa | Ob | Oc | Od | Oe | H | Al | Si | Na | MgI | MgO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Na-MMT | −1.43 | −1.44 | −1.59 | −1.59 | −1.60 | 0.61 | 2.48 | 3.15 | 0.87 | / | 1.67 |
| Mg-MMT | −1.42 | −1.43 | −1.59 | −1.59 | −1.61 | 0.60 | 2.49 | 3.15 | / | 0.72 | 1.67 |
| Phase | Elastic Constants (GPa) | ||||||
|---|---|---|---|---|---|---|---|
| Na-MMT | C11 | C22 | C33 | C44 | C55 | C66 | C12 |
| 173.02 | 210.11 | 27.99 | 7.02 | 10.07 | 56.26 | 50.22 | |
| C13 | C14 | C15 | C16 | C23 | C24 | C25 | |
| 12.54 | 2.07 | −27.60 | 2.08 | 9.22 | 4.34 | −8.90 | |
| C26 | C34 | C35 | C36 | C45 | C46 | C56 | |
| 0.43 | 5.91 | 6.47 | 3.69 | 2.05 | −8.92 | 1.42 | |
| Mg-MMT | C11 | C22 | C33 | C44 | C55 | C66 | C12 |
| 170.69 | 198.32 | 69.89 | 17.25 | 18.57 | 57.51 | 60.94 | |
| C13 | C14 | C15 | C16 | C23 | C24 | C25 | |
| 12.94 | 7.43 | −20.84 | 3.18 | 21.63 | 13.84 | −1.59 | |
| C26 | C34 | C35 | C36 | C45 | C46 | C56 | |
| 5.36 | 9.01 | 13.55 | −1.04 | 6.64 | −8.25 | 3.37 | |
| Mechanical Quantity | Na-MMT | Mg-MMT | Experiment [21] | |
|---|---|---|---|---|
| Na-MMT | Mg-MMT | |||
| Bulk modulus B (GPa) | 39.85 | 58.14 | 34.7 | 63.4 |
| Young’s modulus Y (GPa) | 55.27 | 77.09 | / | / |
| Shear modulus G (GPa) | 21.78 | 30.13 | 20.3 | 26.2 |
| Poisson’s ratio μ | 0.269 | 0.279 | 0.255 | 0.318 |
| Compression wave velocity Vp (km/s) | 5.12 | 6.06 | 4.88 | 6.07 |
| Shear wave velocity Vs (km/s) | 2.88 | 3.35 | 2.80 | 3.13 |
| Pugh’s modulus G/B ratio | 0.547 | 0.518 | / | / |
| Vickers hardness Hv (GPa) | 2.96 | 3.76 | / | / |
| Volume | Pressure (GPa) | O-H | Oa-Al | Oa-Mg | Ob-Al | Oc-Si | Od-Si | Od-Al | Od-Mg | Oe-Si | Oe-Al |
|---|---|---|---|---|---|---|---|---|---|---|---|
| V0 | 0 | 0.972 | 1.858 | 2.057 | 1.925 | 1.639 | 1.613 | 1.936 | 2.082 | 1.645 | 1.966 |
| 0.99V0 | 0.87 | 0.972 | 1.857 | 2.054 | 1.927 | 1.637 | 1.612 | 1.907 | 2.075 | 1.644 | 1.961 |
| 0.98V0 | 2.22 | 0.973 | 1.854 | 2.050 | 1.927 | 1.635 | 1.610 | 1.902 | 2.068 | 1.642 | 1.955 |
| 0.97V0 | 3.96 | 0.973 | 1.850 | 2.042 | 1.926 | 1.632 | 1.608 | 1.894 | 2.059 | 1.639 | 1.949 |
| 0.96V0 | 6.17 | 0.973 | 1.846 | 2.032 | 1.924 | 1.629 | 1.605 | 1.887 | 2.048 | 1.635 | 1.940 |
| 0.95V0 | 8.90 | 0.974 | 1.841 | 2.023 | 1.919 | 1.625 | 1.602 | 1.879 | 2.035 | 1.631 | 1.931 |
| 0.94V0 | 12.12 | 0.975 | 1.836 | 2.013 | 1.911 | 1.621 | 1.598 | 1.872 | 2.022 | 1.627 | 1.922 |
| 0.93V0 | 15.81 | 0.979 | 1.837 | 2.006 | 1.894 | 1.614 | 1.600 | 1.875 | 2.015 | 1.662 | 1.916 |
| 0.925V0 | 17.74 | 0.979 | 1.832 | 2.001 | 1.891 | 1.613 | 1.598 | 1.867 | 2.007 | 1.622 | 1.912 |
| 0.92V0 | 19.92 | 0.980 | 1.829 | 1.994 | 1.886 | 1.611 | 1.597 | 1.879 | 1.985 | 1.620 | 1.906 |
| Volume | Pressure (GPa) | O-H | Oa-Al | Oa-Mg | Ob-Al | Oc-Si | Od-Si | Od-Al | Od-Mg | Oe-Si | Oe-Al |
|---|---|---|---|---|---|---|---|---|---|---|---|
| V0 | 0 | 0.971 | 1.857 | 2.049 | 1.919 | 1.643 | 1.611 | 1.912 | 2.081 | 1.645 | 1.963 |
| 0.99V0 | 1.94 | 0.972 | 1.853 | 2.036 | 1.911 | 1.639 | 1.609 | 1.906 | 2.067 | 1.643 | 1.954 |
| 0.98V0 | 3.93 | 0.972 | 1.848 | 2.024 | 1.904 | 1.635 | 1.608 | 1.900 | 2.054 | 1.642 | 1.946 |
| 0.97V0 | 6.13 | 0.972 | 1.843 | 2.011 | 1.896 | 1.632 | 1.606 | 1.913 | 2.023 | 1.640 | 1.938 |
| 0.96V0 | 8.60 | 0.973 | 1.846 | 2.033 | 1.924 | 1.629 | 1.605 | 1.910 | 2.020 | 1.635 | 1.940 |
| 0.95V0 | 11.06 | 0.973 | 1.829 | 1.988 | 1.892 | 1.626 | 1.605 | 1.878 | 2.019 | 1.636 | 1.920 |
| 0.94V0 | 14.4 | 0.973 | 1.823 | 1.976 | 1.885 | 1.623 | 1.603 | 1.871 | 2.006 | 1.633 | 1.910 |
| 0.935V0 | 16.21 | 0.973 | 1.821 | 1.973 | 1.882 | 1.620 | 1.603 | 1.871 | 1.997 | 1.633 | 1.906 |
| 0.93V0 | 18.2 | 0.973 | 1.818 | 1.967 | 1.878 | 1.619 | 1.602 | 1.866 | 1.993 | 1.631 | 1.901 |
| 0.925V0 | 20.34 | 0.974 | 1.815 | 1.962 | 1.874 | 1.617 | 1.600 | 1.862 | 1.987 | 1.629 | 1.896 |
| Na-MMT | Pressure (GPa) | 0 | 0.87 | 2.22 | 3.96 | 6.17 | 8.90 | 12.12 | 15.81 | 17.74 | 19.92 |
| d1 | 2.254 | 2.271 | 2.270 | 2.245 | 2.226 | 2.209 | 2.192 | 2.229 | 2.206 | 2.200 | |
| d2 | 3.265 | 3.080 | 2.881 | 2.709 | 2.568 | 2.455 | 2.361 | 2.298 | 2.270 | 2.242 | |
| d3 | 2.271 | 2.294 | 2.257 | 2.242 | 2.234 | 2.227 | 2.222 | 2.200 | 2.203 | 2.195 | |
| d4 | 2.191 | 2.208 | 2.200 | 2.178 | 2.160 | 2.143 | 2.124 | 2.098 | 2.090 | 2.081 | |
| Mg-MMT | Pressure (GPa) | 0 | 1.94 | 3.93 | 6.13 | 8.60 | 11.06 | 14.4 | 16.21 | 18.2 | 20.34 |
| d1 | 2.275 | 2.274 | 2.272 | 2.268 | 2.267 | 2.256 | 2.247 | 2.249 | 2.243 | 2.237 | |
| d2 | 2.951 | 2.852 | 2.758 | 2.670 | 2.586 | 2.508 | 2.432 | 2.394 | 2.359 | 2.328 | |
| d3 | 2.270 | 2.275 | 2.274 | 2.272 | 2.269 | 2.255 | 2.249 | 2.242 | 2.238 | 2.233 | |
| d4 | 2.199 | 2.197 | 2.196 | 2.195 | 2.185 | 2.191 | 2.185 | 2.180 | 2.176 | 2.172 |
| Pressure (GPa) | 0 | 0.87 | 2.22 | 3.96 | 6.17 | 8.90 | 12.12 | 15.81 | 17.74 | 19.92 |
|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 173.02 | 179.18 | 185.87 | 192.64 | 204.10 | 216.54 | 231.56 | 248.99 | 259.90 | 267.22 |
| C22 | 210.11 | 209.16 | 207.51 | 203.62 | 201.00 | 205.95 | 200.47 | 199.60 | 204.98 | 210.60 |
| C33 | 27.99 | 45.97 | 64.64 | 86.92 | 112.84 | 139.88 | 167.80 | 200.98 | 215.27 | 228.96 |
| C44 | 7.02 | 13.24 | 16.10 | 19.52 | 26.15 | 34.02 | 42.25 | 53.28 | 58.15 | 62.42 |
| C55 | 10.07 | 10.54 | 14.14 | 19.43 | 27.12 | 35.84 | 45.82 | 58.30 | 65.19 | 71.09 |
| C66 | 56.26 | 57.93 | 59.81 | 60.53 | 62.67 | 63.70 | 68.02 | 66.93 | 69.35 | 69.61 |
| C12 | 50.22 | 54.31 | 55.76 | 55.93 | 56.12 | 56.16 | 61.18 | 70.45 | 72.72 | 80.48 |
| C13 | 12.54 | 16.59 | 23.28 | 28.52 | 34.20 | 42.64 | 52.51 | 71.59 | 73.74 | 81.18 |
| C14 | 2.07 | −0.63 | −2.23 | −1.28 | −1.78 | −2.60 | −4.92 | −12.39 | −15.08 | −15.56 |
| C15 | −27.60 | −24.54 | −21.88 | −18.72 | −15.93 | −12.65 | −11.21 | −12.37 | −9.74 | −8.64 |
| C16 | 2.08 | 1.76 | 2.18 | 4.36 | 5.76 | 5.98 | 2.48 | −1.99 | −2.41 | −2.87 |
| C23 | 9.22 | 15.49 | 18.54 | 29.14 | 38.91 | 43.29 | 51.53 | 55.62 | 62.87 | 67.07 |
| C24 | 4.34 | 4.64 | 2.19 | 3.24 | 2.64 | −0.05 | 0.04 | −1.80 | −2.59 | −3.11 |
| C25 | −8.90 | −2.81 | −1.40 | −1.63 | −2.12 | −4.33 | −4.53 | −1.53 | 1.56 | −2.73 |
| C26 | 0.43 | 1.44 | 0.43 | 0.49 | −1.01 | −3.55 | 0.59 | −7.63 | −7.32 | −8.04 |
| C34 | 5.91 | 14.60 | 19.27 | 27.92 | 36.20 | 40.54 | 43.62 | 40.43 | 39.91 | 39.22 |
| C35 | 6.47 | 8.41 | 17.37 | 21.82 | 25.12 | 28.80 | 33.15 | 28.12 | 35.21 | 35.52 |
| C36 | 3.69 | 1.18 | 3.03 | 3.59 | 3.45 | 3.95 | 3.46 | 4.14 | 4.27 | 5.03 |
| C45 | 2.05 | 1.81 | 3.07 | 7.10 | 8.40 | 8.64 | 7.86 | 7.19 | 8.25 | 7.26 |
| C46 | −8.92 | −8.79 | −7.17 | −5.71 | −5.24 | −4.37 | −3.81 | −3.54 | −5.55 | −4.37 |
| C56 | 1.42 | 2.58 | 2.75 | 4.35 | 4.44 | 4.74 | 2.93 | 2.80 | 1.70 | 2.14 |
| Pressure (GPa) | 0 | 1.94 | 3.93 | 6.13 | 8.60 | 11.06 | 14.40 | 16.21 | 18.20 | 20.34 |
|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 170.69 | 171.48 | 171.79 | 175.07 | 180.54 | 202.33 | 214.74 | 221.30 | 228.61 | 237.52 |
| C22 | 198.32 | 200.98 | 195.97 | 193.88 | 189.16 | 207.32 | 215.82 | 221.09 | 227.49 | 235.91 |
| C33 | 69.89 | 72.03 | 78.69 | 100.14 | 109.24 | 132.49 | 157.94 | 172.42 | 186.33 | 200.47 |
| C44 | 17.25 | 20.06 | 21.58 | 22.71 | 26.67 | 31.95 | 36.38 | 38.00 | 40.42 | 43.66 |
| C55 | 18.57 | 22.06 | 26.94 | 30.02 | 34.95 | 44.54 | 54.59 | 60.23 | 65.97 | 71.67 |
| C66 | 57.51 | 58.48 | 58.88 | 58.95 | 57.37 | 60.31 | 60.99 | 61.47 | 62.38 | 63.30 |
| C12 | 60.94 | 55.23 | 52.50 | 43.36 | 50.77 | 54.63 | 66.62 | 75.19 | 83.79 | 91.51 |
| C13 | 12.94 | 16.28 | 18.61 | 16.17 | 16.60 | 49.85 | 54.26 | 59.81 | 66.12 | 71.85 |
| C14 | 7.43 | 3.25 | −4.18 | −3.21 | −3.04 | −4.71 | −6.50 | −7.88 | −9.88 | −12.88 |
| C15 | −20.84 | −19.07 | −18.30 | −12.31 | −8.20 | −6.71 | −5.47 | −3.02 | −3.45 | −4.39 |
| C16 | 3.18 | 2.19 | 1.90 | 1.6 | 2.84 | 1.16 | 0.80 | 1.25 | 1.19 | 1.38 |
| C23 | 21.63 | 27.38 | 34.68 | 40.54 | 51.84 | 55.71 | 66.71 | 73.00 | 80.66 | 88.05 |
| C24 | 13.84 | 7.27 | 4.39 | −2.15 | −2.25 | 0.22 | −3.89 | −5.39 | −8.05 | −11.51 |
| C25 | −1.59 | −1.43 | −0.70 | −0.20 | 5.16 | 2.07 | 2.26 | 2.76 | 2.53 | 3.48 |
| C26 | 5.36 | 1.23 | −0.07 | −1.64 | −4.46 | −0.02 | 0.22 | −0.07 | −0.17 | −0.44 |
| C34 | 9.01 | 13.07 | 17.19 | 21.87 | 30.25 | 27.14 | 31.08 | 33.21 | 35.92 | 37.41 |
| C35 | 13.55 | 19.56 | 17.36 | 18.68 | 22.56 | 35.36 | 40.21 | 41.38 | 42.78 | 44.11 |
| C36 | −1.04 | 2.81 | 4.39 | 4.43 | 8.14 | −1.13 | −1.87 | −2.45 | −2.99 | −3.34 |
| C45 | 6.64 | 5.73 | 6.59 | 9.19 | 8.81 | 1.82 | −0.54 | −2.20 | 0.78 | 2.64 |
| C46 | −8.25 | −8.19 | −8.26 | −8.13 | −7.39 | −5.95 | −5.93 | −5.73 | −5.97 | −6.61 |
| C56 | 3.37 | 3.70 | 3.93 | 5.73 | 7.45 | 4.61 | 3.73 | 3.14 | 3.47 | 3.04 |
| Pressure (GPa) | 0 | 0.87 | 2.22 | 3.96 | 6.17 | 8.90 | 12.12 | 15.81 | 17.74 | 19.92 |
|---|---|---|---|---|---|---|---|---|---|---|
| B (GPa) | 39.85 | 45.13 | 46.88 | 57.97 | 69.29 | 82.93 | 95.98 | 113.09 | 119.29 | 127.02 |
| Y (GPa) | 55.27 | 61.97 | 63.91 | 77.28 | 92.93 | 112.56 | 130.95 | 153.81 | 164.03 | 172.39 |
| G (GPa) | 21.78 | 24.38 | 25.11 | 30.24 | 36.40 | 44.18 | 51.45 | 60.40 | 64.54 | 67.67 |
| μ | 0.269 | 0.271 | 0.273 | 0.278 | 0.277 | 0.274 | 0.273 | 0.273 | 0.271 | 0.274 |
| Vp (km/s) | 5.12 | 5.36 | 5.40 | 5.85 | 6.30 | 6.81 | 7.22 | 7.71 | 7.87 | 8.03 |
| Vs (km/s) | 2.88 | 3.00 | 3.00 | 3.24 | 3.50 | 3.80 | 4.04 | 4.30 | 4.41 | 4.48 |
| G/B | 0.547 | 0.540 | 0.536 | 0.522 | 0.525 | 0.533 | 0.536 | 0.534 | 0.541 | 0.533 |
| Hv (GPa) | 2.96 | 3.28 | 3.32 | 3.83 | 4.68 | 5.74 | 6.62 | 7.51 | 8.09 | 8.20 |
| Pressure (GPa) | 0 | 1.94 | 3.93 | 6.13 | 8.60 | 11.06 | 14.40 | 16.21 | 18.20 | 20.34 |
|---|---|---|---|---|---|---|---|---|---|---|
| B (GPa) | 58.14 | 58.53 | 62.11 | 66.58 | 68.24 | 86.04 | 98.46 | 106.45 | 116.09 | 125.67 |
| Y (GPa) | 77.09 | 83.40 | 89.37 | 95.02 | 95.68 | 112.29 | 123.70 | 129.20 | 136.49 | 144.46 |
| G (GPa) | 30.13 | 33.03 | 35.46 | 37.64 | 37.78 | 43.78 | 47.92 | 49.78 | 52.33 | 55.21 |
| μ | 0.279 | 0.263 | 0.260 | 0.262 | 0.266 | 0.282 | 0.291 | 0.298 | 0.304 | 0.308 |
| Vp (km/s) | 6.06 | 6.09 | 6.20 | 6.30 | 6.26 | 6.79 | 7.09 | 7.26 | 7.47 | 7.67 |
| Vs (km/s) | 3.35 | 3.46 | 3.53 | 3.58 | 3.53 | 3.74 | 3.85 | 3.90 | 3.96 | 4.04 |
| G/B | 0.518 | 0.564 | 0.571 | 0.565 | 0.554 | 0.509 | 0.487 | 0.468 | 0.451 | 0.439 |
| Hv (GPa) | 3.76 | 4.89 | 5.33 | 5.53 | 5.34 | 5.24 | 5.24 | 5.05 | 4.94 | 4.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Cao, Y.; Wang, L.; Zhang, H.-J.; He, M.-C. Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations. Minerals 2021, 11, 613. https://doi.org/10.3390/min11060613
Zhao J, Cao Y, Wang L, Zhang H-J, He M-C. Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations. Minerals. 2021; 11(6):613. https://doi.org/10.3390/min11060613
Chicago/Turabian StyleZhao, Jian, Yu Cao, Lei Wang, Hai-Jiang Zhang, and Man-Chao He. 2021. "Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations" Minerals 11, no. 6: 613. https://doi.org/10.3390/min11060613
APA StyleZhao, J., Cao, Y., Wang, L., Zhang, H.-J., & He, M.-C. (2021). Investigation on Atomic Structure and Mechanical Property of Na- and Mg-Montmorillonite under High Pressure by First-Principles Calculations. Minerals, 11(6), 613. https://doi.org/10.3390/min11060613






