Composition and Pressure Effects on Partitioning of Ferrous Iron in Iron-Rich Lower Mantle Heterogeneities
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Phase Identification
3.2. Compositions of Coexisting Phases and Partitioning
3.3. Thermodynamic Modeling
4. Discussion
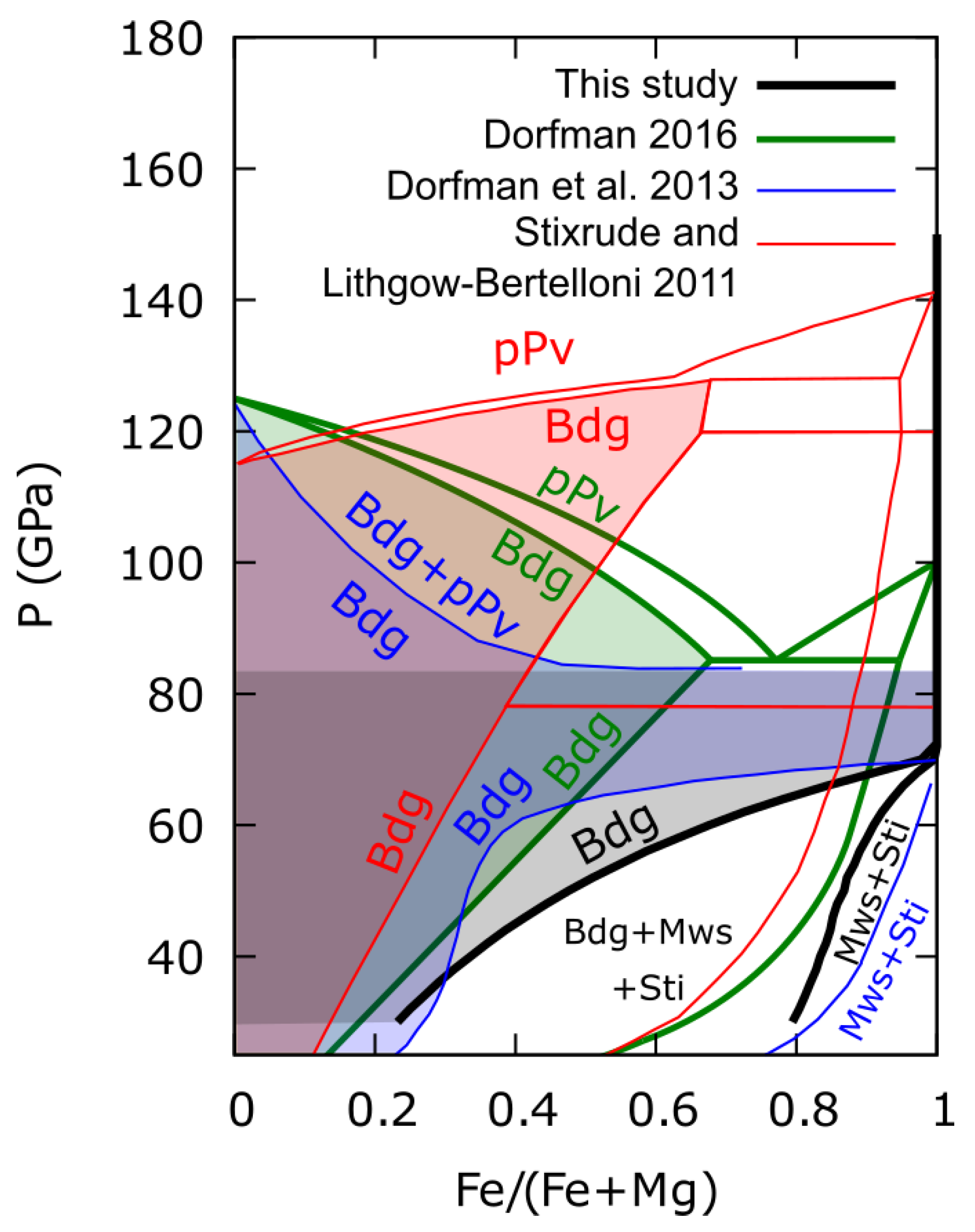
4.1. Multivariable Effects on Partitioning
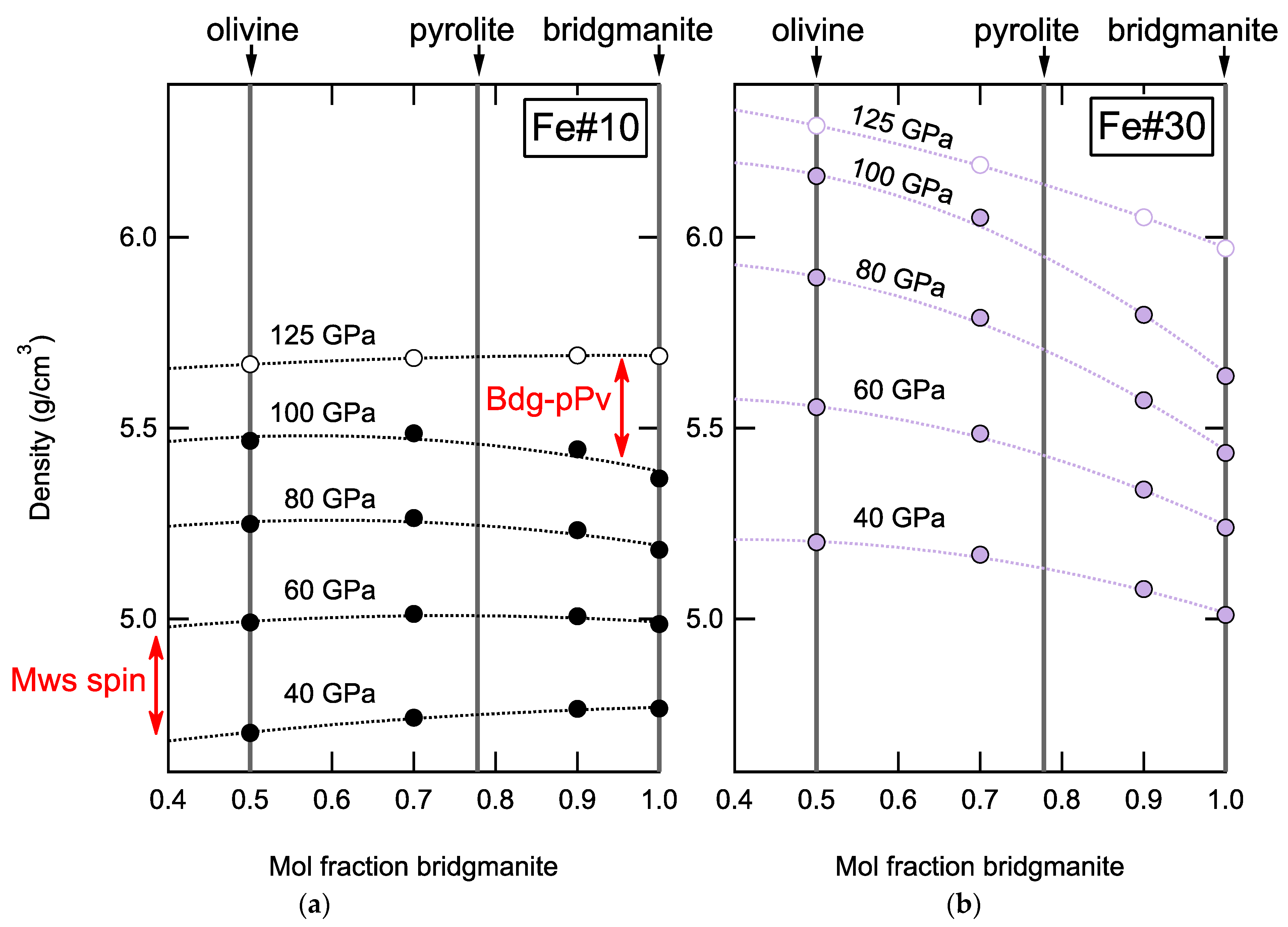
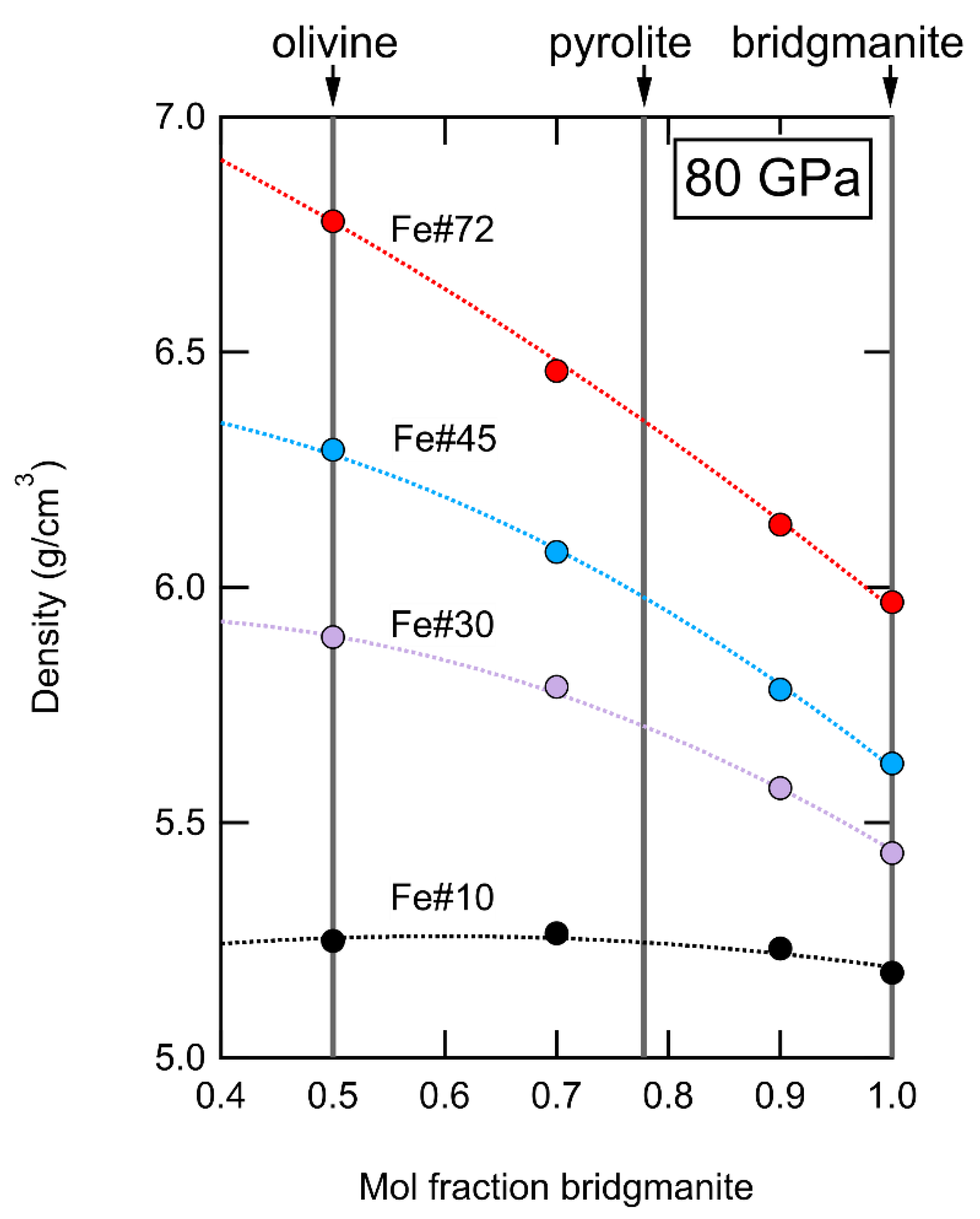
4.2. Physical Properties of Mantle Heterogeneities
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Physical Properties of Iron-Rich Mantle Phases
References
- Deschamps, F.; Konishi, K.; Fuji, N.; Cobden, L. Radial thermo-chemical structure beneath Western and Northern Pacific from seismic waveform inversion. Earth Planet. Sci. Lett. 2019, 520, 153–163. [Google Scholar] [CrossRef]
- Mao, W.L.; Shen, G.; Prakapenka, V.B.; Meng, Y.; Campbell, A.J.; Heinz, D.L.; Shu, J.; Hemley, R.J.; Mao, H.-K. Ferromagnesian postperovskite silicates in the D’’ layer of the Earth. Proc. Natl. Acad. Sci. USA 2004, 101, 15867–15869. [Google Scholar] [CrossRef]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W. Very low sound velocities in iron-rich (Mg,Fe)O: Implications for the core-mantle boundary region. Geophys. Res. Lett. 2010, 37, L15304. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Duffy, T.S. Effect of Fe-enrichment on seismic properties of perovskite and post-perovskite in the deep lower mantle. Geophys. J. Int. 2014, 197, 910–919. [Google Scholar] [CrossRef]
- Labrosse, S.; Hernlund, J.W.; Coltice, N. A crystallizing dense magma ocean at the base of the Earth’s mantle. Nature 2007, 450, 866–869. [Google Scholar] [CrossRef] [PubMed]
- Dobson, D.P.; Brodholt, J.P. Subducted banded iron formations as a source of ultralow-velocity zones at the core–mantle boundary. Nature 2005, 434, 371–374. [Google Scholar] [CrossRef]
- Williams, Q.; Garnero, E.J. Seismic Evidence for Partial Melt at the Base of Earth’s Mantle. Science 1996, 273, 1528–1530. [Google Scholar] [CrossRef]
- Auzende, A.-L.; Badro, J.; Ryerson, F.J.; Weber, P.K.; Fallon, S.J.; Addad, A.; Siebert, J.; Fiquet, G. Element partitioning between magnesium silicate perovskite and ferropericlase: New insights into bulk lower-mantle geochemistry. Earth Planet. Sci. Lett. 2008, 269, 164–174. [Google Scholar] [CrossRef]
- Irifune, T.; Shinmei, T.; McCammon, C.A.; Miyajima, N.; Rubie, D.C.; Frost, D.J. Iron Partitioning and Density Changes of Pyrolite in Earth’s Lower Mantle. Science 2009, 327, 193–195. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, Y.; Frost, D.J.; Rubie, D.C. Ferrous iron partitioning between magnesium silicate perovskite and ferropericlase and the composition of perovskite in the Earth’s lower mantle. J. Geophys. Res. Solid Earth 2012, 117, B08201. [Google Scholar] [CrossRef]
- Sakai, T.; Ohtani, E.; Terasaki, H.; Miyahara, M.; Nishijima, M.; Hirao, N.; Ohishi, Y.; Sata, N. Fe–Mg partitioning between post-perovskite and ferropericlase in the lowermost mantle. Phys. Chem. Miner. 2010, 37, 487–496. [Google Scholar] [CrossRef]
- Sakai, T.; Ohtani, E.; Terasaki, H.; Sawada, N.; Kobayashi, Y.; Miyahara, M.; Nishijima, M.; Hirao, N.; Ohishi, Y.; Kikegawa, T. Fe-Mg partitioning between perovskite and ferropericlase in the lower mantle. Am. Miner. 2009, 94, 921–925. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K.; Seto, Y.; Fujino, K.; Sata, N.; Ohishi, Y.; Nishio-Hamane, D. Partitioning of iron between perovskite/postperovskite and ferropericlase in the lower mantle. J. Geophys. Res. Solid Earth 2008, 113, 11. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K.; Muto, S.; Ohishi, Y.; Yasuhara, A. The valence state and partitioning of iron in the Earth’s lowermost mantle. J. Geophys. Res. Solid Earth 2011, 116, B07205. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K. Iron partitioning in pyrolitic lower mantle. Phys. Chem. Miner. 2013, 40, 107–113. [Google Scholar] [CrossRef]
- Muir, J.M.; Brodholt, J.P. Ferrous iron partitioning in the lower mantle. Phys. Earth Planet. Inter. 2016, 257, 12–17. [Google Scholar] [CrossRef]
- Xu, S.; Lin, J.-F.; Morgan, D. Iron partitioning between ferropericlase and bridgmanite in the Earth’s lower mantle. J. Geophys. Res. Solid Earth 2017, 122, 1074–1087. [Google Scholar] [CrossRef]
- Piet, H.; Badro, J.; Nabiei, F.; Dennenwaldt, T.; Shim, S.-H.; Cantoni, M.; Hébert, C.; Gillet, P. Spin and valence dependence of iron partitioning in Earth’s deep mantle. Proc. Natl. Acad. Sci. USA 2016, 113, 11127–11130. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Meng, Y.; Prakapenka, V.B.; Duffy, T.S. Effects of Fe-enrichment on the equation of state and stability of (Mg,Fe)SiO3 perovskite. Earth Planet. Sci. Lett. 2013, 361, 249–257. [Google Scholar] [CrossRef]
- Hsu, H.; Umemoto, K.; Blaha, P.; Wentzcovitch, R.M. Spin states and hyperfine interactions of iron in (Mg,Fe)SiO3 perovskite under pressure. Earth Planet. Sci. Lett. 2010, 294, 19–26. [Google Scholar] [CrossRef]
- Mao, Z.; Lin, J.-F.; Fu, S.; Okuchi, T.; Prakapenka, V.B.; Chow, P.; Wang, F.; Yang, J.; Wu, X.; Tomioka, N.; et al. Equation of state and hyperfine parameters of high-spin bridgmanite in the Earth’s lower mantle by synchrotron X-ray diffraction and Mössbauer spectroscopy. Am. Miner. 2017, 102, 357–368. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Badro, J.; Rueff, J.-P.; Chow, P.; Xiao, Y.; Gillet, P. Composition dependence of spin transition in (Mg,Fe)SiO3 bridgmanite. Am. Miner. 2015, 100, 2246–2253. [Google Scholar] [CrossRef]
- Badro, J.; Fiquet, G.; Guyot, F.; Rueff, J.-P.; Struzhkin, V.V.; Vankó, G.; Monaco, G. Iron Partitioning in Earth’s Mantle: Toward a Deep Lower Mantle Discontinuity. Science 2003, 300, 789–791. [Google Scholar] [CrossRef] [PubMed]
- Badro, J.; Rueff, J.-P.; Vankó, G.; Monaco, G.; Fiquet, G.; Guyot, F. Electronic Transitions in Perovskite: Possible Nonconvecting Layers in the Lower Mantle. Science 2004, 305, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.-F.; Speziale, S.; Mao, Z.; Marquardt, H. Effects of the Electronic Spin Transitions of Iron in Lower Mantle Minerals: Implications for Deep Mantle Geophysics and Geochemistry. Rev. Geophys. 2013, 51, 244–275. [Google Scholar] [CrossRef]
- Badro, J. Spin Transitions in Mantle Minerals. Annu. Rev. Earth Planet. Sci. 2014, 42, 231–248. [Google Scholar] [CrossRef]
- Caracas, R.; Ozawa, H.; Hirose, K.; Ishii, H.; Hiraoka, N.; Ohishi, Y.; Hirao, N. Identifying the spin transition in Fe2+-rich MgSiO3 perovskite from X-ray diffraction and vibrational spectroscopy. Am. Miner. 2014, 99, 1270–1276. [Google Scholar] [CrossRef]
- Mao, W.L.; Meng, Y.; Shen, G.; Prakapenka, V.B.; Campbell, A.J.; Heinz, D.L.; Shu, J.; Caracas, R.; Cohen, R.E.; Fei, Y.; et al. Iron-rich silicates in the Earth’s D’’ layer. Proc. Natl. Acad. Sci. USA 2005, 102, 9751–9753. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Sata, N.; Ohishi, Y. Solubility of FeO in (Mg,Fe)SiO3 perovskite and the post-perovskite phase transition. Phys. Earth Planet. Inter. 2007, 160, 319–325. [Google Scholar] [CrossRef]
- Hirose, K.; Takafuji, N.; Fujino, K.; Shieh, S.R.; Duffy, T.S. Iron partitioning between perovskite and post-perovskite: A transmission electron microscope study. Am. Miner. 2008, 93, 1678–1681. [Google Scholar] [CrossRef]
- Akahama, Y.; Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 310GPa. J. Appl. Phys. 2006, 100, 043516. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Prakapenka, V.B.; Meng, Y.; Duffy, T.S. Intercomparison of pressure standards (Au, Pt, Mo, MgO, NaCl and Ne) to 2.5 Mbar. J. Geophys. Res. Solid Earth 2012, 117, B08210. [Google Scholar] [CrossRef]
- Prakapenka, V.B.; Kubo, A.; Kuznetsov, A.; Laskin, A.; Shkurikhin, O.; Dera, P.; Rivers, M.L.; Sutton, S.R. Advanced flat top laser heating system for high pressure research at GSECARS: Application to the melting behavior of germanium. High Press. Res. 2008, 28, 225–235. [Google Scholar] [CrossRef]
- Carrez, P.; Leroux, H.; Cordier, P.; Guyot, F. Electron-irradiation-induced phase transformation and fractional volatilization in (Mg, Fe)2SiO4 olivine thin films. Philos. Mag. A 2001, 81, 2823–2840. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K. The Soret diffusion in laser-heated diamond-anvil cell. Phys. Earth Planet. Inter. 2010, 180, 172–178. [Google Scholar] [CrossRef]
- Tange, Y.; Takahashi, E.; Nishihara, Y.; Funakoshi, K.-I.; Sata, N. Phase relations in the system MgO-FeO-SiO2 to 50 GPa and 2000 °C: An application of experimental techniques using multianvil apparatus with sintered diamond anvils. J. Geophys. Res. Solid Earth 2009, 114, B02214. [Google Scholar] [CrossRef]
- Frost, D.J.; Liebske, C.; Langenhorst, F.; McCammon, C.A.; Trønnes, R.G.; Rubie, D.C. Experimental evidence for the existence of iron-rich metal in the Earth’s lower mantle. Nature 2004, 428, 409–412. [Google Scholar] [CrossRef] [PubMed]
- Andrault, D. Evaluation of (Mg,Fe) partitioning between silicate perovskite and magnesiowustite up to 120 GPa and 2300 K. J. Geophys. Res. Solid Earth 2001, 106, 2079–2087. [Google Scholar] [CrossRef]
- Mao, H.K.; Hemley, R.J.; Fei, Y.; Shu, J.F.; Chen, L.C.; Jephcoat, A.P.; Wu, Y.; Bassett, W.A. Effect of pressure, temperature, and composition on lattice parameters and density of (Fe,Mg)SiO3-perovskites to 30 GPa. J. Geophys. Res. Solid Earth 1991, 96, 8069–8079. [Google Scholar] [CrossRef]
- Speziale, S.; Milner, A.; Lee, V.E.; Clark, S.M.; Pasternak, M.P.; Jeanloz, R. Iron spin transition in Earth’s mantle. Proc. Natl. Acad. Sci. USA 2005, 102, 17918–17922. [Google Scholar] [CrossRef]
- Fei, Y.; Zhang, L.; Corgne, A.; Watson, H.; Ricolleau, A.; Meng, Y.; Prakapenka, V. Spin transition and equations of state of (Mg, Fe)O solid solutions. Geophys. Res. Lett. 2007, 34, 17307. [Google Scholar] [CrossRef]
- Fischer, R.A.; Campbell, A.J.; Shofner, G.A.; Lord, O.T.; Dera, P.; Prakapenka, V.B. Equation of state and phase diagram of FeO. Earth Planet. Sci. Lett. 2011, 304, 496–502. [Google Scholar] [CrossRef]
- Ozawa, H.; Hirose, K.; Ohta, K.; Ishii, H.; Hiraoka, N.; Ohishi, Y.; Seto, Y. Spin crossover, structural change, and metallization in NiAs-type FeO at high pressure. Phys. Rev. B 2011, 84, 134417. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Y.; Mao, W.L. Effect of pressure and composition on lattice parameters and unit-cell volume of (Fe,Mg)SiO3 post-perovskite. Earth Planet. Sci. Lett. 2012, 317–318, 120–125. [Google Scholar] [CrossRef]
- Frost, D.J. Fe2+-Mg partitioning between garnet, magnesiowüstite, and (Mg,Fe)2SiO4phases of the transition zone. Am. Miner. 2003, 88, 387–397. [Google Scholar] [CrossRef]
- Stixrude, L.; Lithgow-Bertelloni, C. Thermodynamics of mantle minerals—II. Phase equilibria. Geophys. J. Int. 2011, 184, 1180–1213. [Google Scholar] [CrossRef]
- Dorfman, S.M. Phase Diagrams and Thermodynamics of Lower Mantle Materials. In Deep Earth: Physics and Chemistry of the Lower Mantle and Core; Terasaki, H., Fischer, R.A., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 241–252. [Google Scholar]
- Prescher, C.; Langenhorst, F.; Dubrovinsky, L.S.; Prakapenka, V.B.; Miyajima, N. The effect of Fe spin crossovers on its partitioning behavior and oxidation state in a pyrolitic Earth’s lower mantle system. Earth Planet. Sci. Lett. 2014, 399, 86–91. [Google Scholar] [CrossRef]
- Mao, H.-K.; Shen, G.; Hemley, R.J. Multivariable Dependence of Fe-Mg Partitioning in the Lower Mantle. Science 1997, 278, 2098–2100. [Google Scholar] [CrossRef]
- Lin, J.-F.; Struzhkin, V.V.; Jacobsen, S.D.; Hu, M.Y.; Chow, P.; Kung, J.; Liu, H.; Mao, H.-K.; Hemley, R.J. Spin transition of iron in magnesiowüstite in the Earth’s lower mantle. Nature 2005, 436, 377–380. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Potapkin, V.; Lv, M.; Greenberg, E.; Kupenko, I.; Chumakov, A.I.; Bi, W.; Alp, E.E.; Liu, J.; Magrez, A.; et al. Effects of composition and pressure on electronic states of iron in bridgmanite. Am. Miner. 2020, 105, 1030–1039. [Google Scholar] [CrossRef]
- Bengtson, A.; Persson, K.; Morgan, D. Ab initio study of the composition dependence of the pressure-induced spin crossover in perovskite (Mg1−x,Fex)SiO3. Earth Planet. Sci. Lett. 2008, 265, 535–545. [Google Scholar] [CrossRef]
- Umemoto, K.; Wentzcovitch, R.M.; Yu, Y.G.; Requist, R. Spin Transition in (Mg,Fe)SiO3 Perovskite under Pressure. Earth Planet. Sci. Lett. 2008, 276, 198–206. [Google Scholar] [CrossRef]
- Catalli, K.; Shim, S.-H.; Prakapenka, V. Thickness and Clapeyron slope of the post-perovskite boundary. Nature 2009, 462, 782–785. [Google Scholar] [CrossRef]
- Andrault, D.; Muñoz, M.; Bolfan-Casanova, N.; Guignot, N.; Perrillat, J.-P.; Aquilanti, G.; Pascarelli, S. Experimental evidence for perovskite and post-perovskite coexistence throughout the whole D” region. Earth Planet. Sci. Lett. 2010, 293, 90–96. [Google Scholar] [CrossRef]
- Deschamps, F.; Cobden, L.; Tackley, P.J. The primitive nature of large low shear-wave velocity provinces. Earth Planet. Sci. Lett. 2012, 349–350, 198–208. [Google Scholar] [CrossRef]
- Catalli, K.; Shim, S.-H.; Prakapenka, V.B.; Zhao, J.; Sturhahn, W.; Chow, P.; Xiao, Y.; Liu, H.; Cynn, H.; Evans, W.J. Spin state of ferric iron in MgSiO3 perovskite and its effect on elastic properties. Earth Planet. Sci. Lett. 2010, 289, 68–75. [Google Scholar] [CrossRef]
- Dyar, M.D.; Sklute, E.C.; Menzies, O.N.; Bland, P.A.; Lindsley, D.; Glotch, T.; Lane, M.D.; Schaefer, M.W.; Wopenka, B.; Klima, R.; et al. Spectroscopic Characteristics of synthetic olivine: An integrated multi-wavelength and multi-technique approach. Am. Mineral. 2009, 94, 883–898. [Google Scholar] [CrossRef]
- Dyar, M.D.; Agresti, D.G.; Schaefer, M.W.; Grant, C.A.; Sklute, E.C. Mössbauer spectroscopy of earth and planetary materials. Annu. Rev. Earth Planet. Sci. 2006, 34, 83–125. [Google Scholar] [CrossRef]
- Lundin, S.; Catalli, K.; Santillán, J.; Shim, S.-H.; Prakapenka, V.; Kunz, M.; Meng, Y. Effect of Fe on the equation of state of mantle silicate perovskite over 1 Mbar. Phys. Earth Planet. Inter. 2008, 168, 97–102. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Speziale, S.; Zha, C.-S.; Duffy, T.S.; Hemley, R.J.; Mao, H.-K. Quasi-hydrostatic compression of magnesium oxide to 52 GPa: Implications for the pressure-volume-temperature equation of state. J. Geophys. Res. Solid Earth 2001, 106, 515–528. [Google Scholar] [CrossRef]
- Wicks, J.; Jackson, J.M.; Sturhahn, W.; Zhang, D. Sound velocity and density of magnesiowüstites: Implications for ultralow-velocity zone topography. Geophys. Res. Lett. 2017, 2016GL071225. [Google Scholar] [CrossRef]
- Guignot, N.; Andrault, D.; Morard, G.; Bolfancasanova, N.; Mezouar, M. Thermoelastic properties of post-perovskite phase MgSiO3 determined experimentally at core–mantle boundary P–T conditions. Earth Planet. Sci. Lett. 2007, 256, 162–168. [Google Scholar] [CrossRef]
- Nishio-Hamane, D.; Yagi, T. Equations of state for postperovskite phases in the MgSiO3–FeSiO3–FeAlO3 system. Phys. Earth Planet. Inter. 2009, 175, 145–150. [Google Scholar] [CrossRef]
- Chen, B.; Jackson, J.M.; Sturhahn, W.; Zhang, D.; Zhao, J.; Wicks, J.K.; Murphy, C.A. Spin crossover equation of state and sound velocities of (Mg0.65Fe0.35)O ferropericlase to 140 GPa. J. Geophys. Res. Solid Earth 2012, 117, B08208. [Google Scholar] [CrossRef]
- Mao, Z.; Lin, J.-F.; Liu, J.; Prakapenka, V.B. Thermal equation of state of lower-mantle ferropericlase across the spin crossover. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Marquardt, H.; Speziale, S.; Reichmann, H.J.; Frost, D.J.; Schilling, F.R.; Garnero, E.J. Elastic Shear Anisotropy of Ferropericlase in Earth’s Lower Mantle. Science 2009, 324, 224–226. [Google Scholar] [CrossRef]
- Richet, P.; Mao, H.-K.; Bell, P.M. Bulk moduli of magnesiowüstites from static compression measurements. J. Geophys. Res. 1989, 94, 3037–3045. [Google Scholar] [CrossRef]
- Solomatova, N.V.; Sturhahn, W.; Toellner, T.S.; Kalkan, B.; Steinhardt, W.M.; Jackson, J.M.; Wicks, J.K.; Zhao, J. Equation of state and spin crossover of (Mg,Fe)O at high pressure, with implications for explaining topographic relief at the core-mantle boundary. Am. Miner. 2016, 101, 1084–1093. [Google Scholar] [CrossRef]
- Tange, Y.; Nishihara, Y.; Tsuchiya, T. Unified analyses for P-V-T equation of state of MgO: A solution for pressure-scale problems in high P-Texperiments. J. Geophys. Res. Solid Earth 2009, 114, B03208. [Google Scholar] [CrossRef]
- ZhuravlevJ, K.K.; Jackson, J.M.; Wolf, A.S.; Wicks, J.K.; Yan, J.; Clark, S.M. Isothermal compression behavior of (Mg,Fe)O using neon as a pressure medium. Phys. Chem. Miner. 2010, 37, 465–474. [Google Scholar] [CrossRef]
- Speziale, S.; Lee, V.E.; Clark, S.M.; Lin, J.F.; Pasternak, M.P.; Jeanloz, R. Effects of Fe spin transition on the elasticity of (Mg,Fe)O magnesiowüstites and implications for the seismological properties of the Earth’s lower mantle. J. Geophys. Res. Solid Earth 2007, 112, B10212. [Google Scholar] [CrossRef]
- Kondo, T.; Ohtani, E.; Hirao, N.; Yagi, T.; Kikegawa, T. Phase transitions of (Mg,Fe)O at megabar pressures. Phys. Earth Planet. Inter. 2004, 143–144, 201–213. [Google Scholar] [CrossRef]
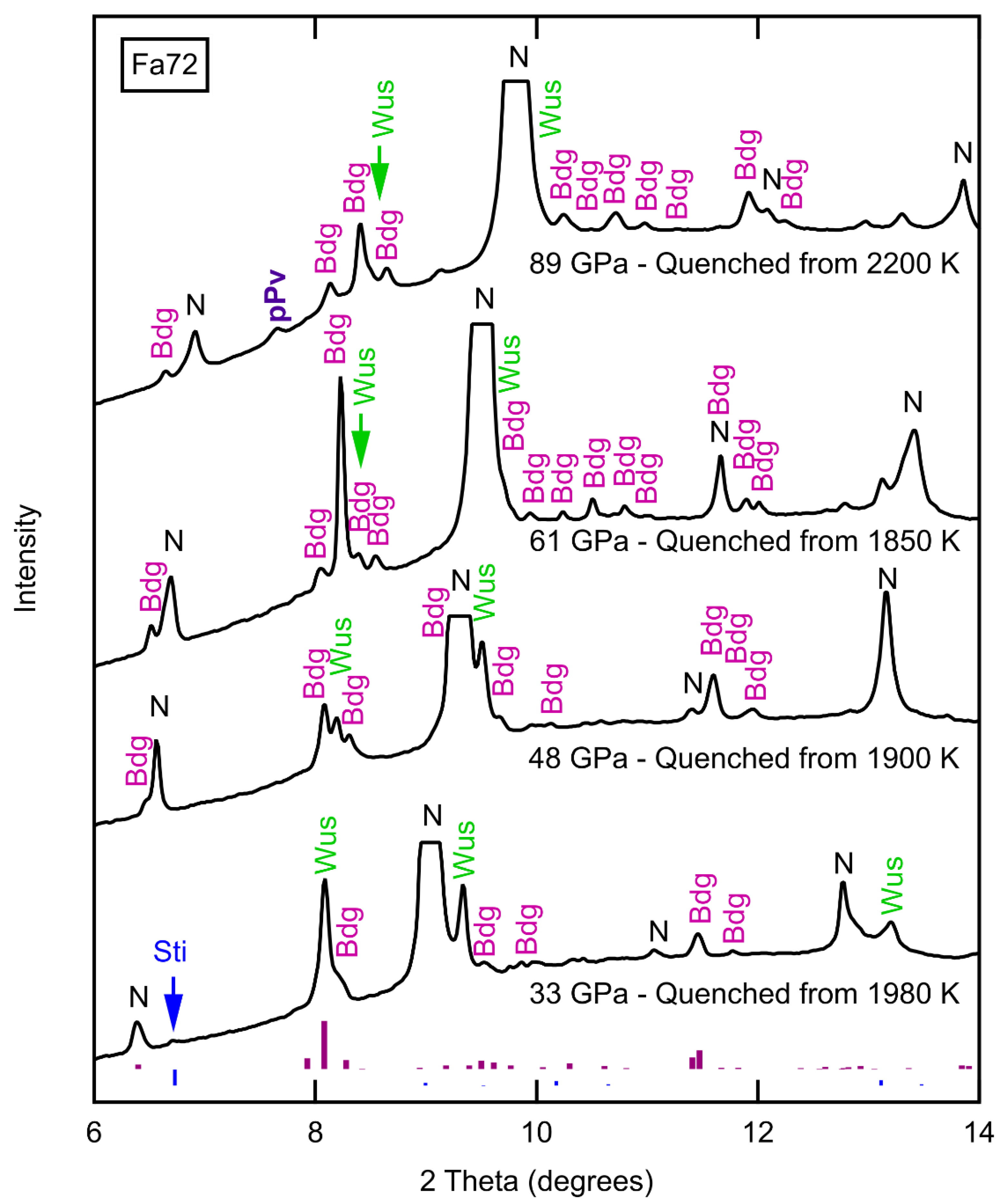
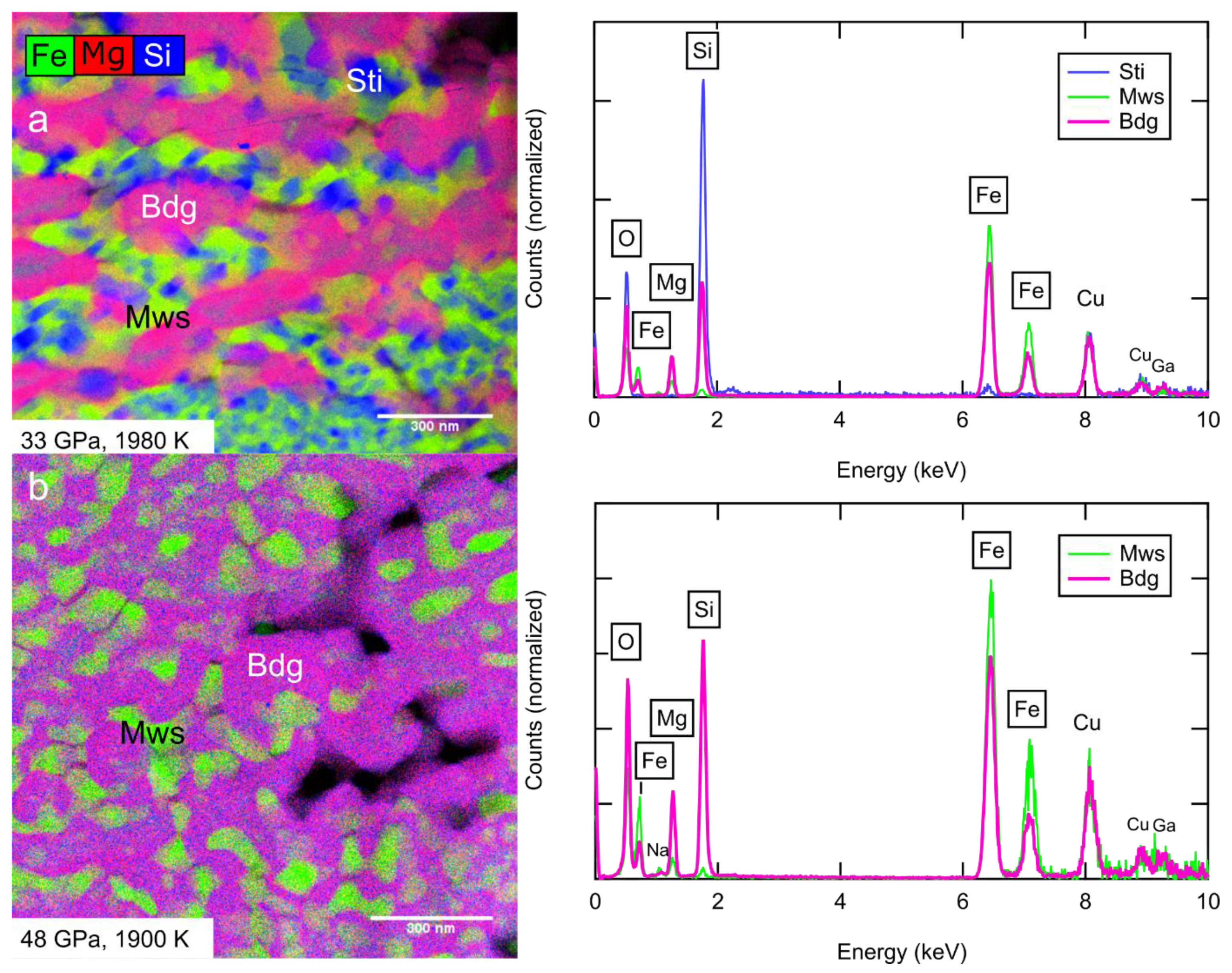
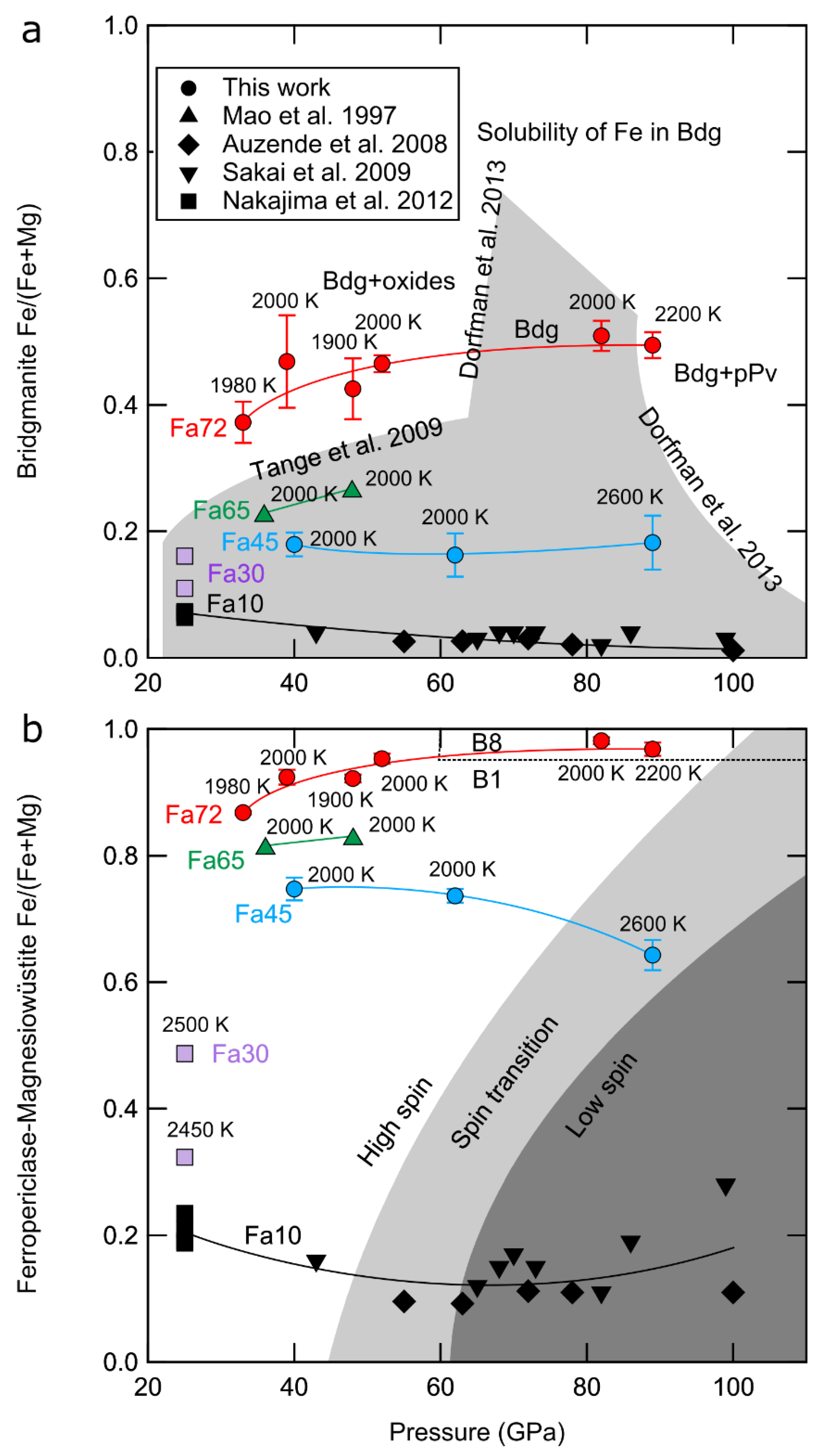
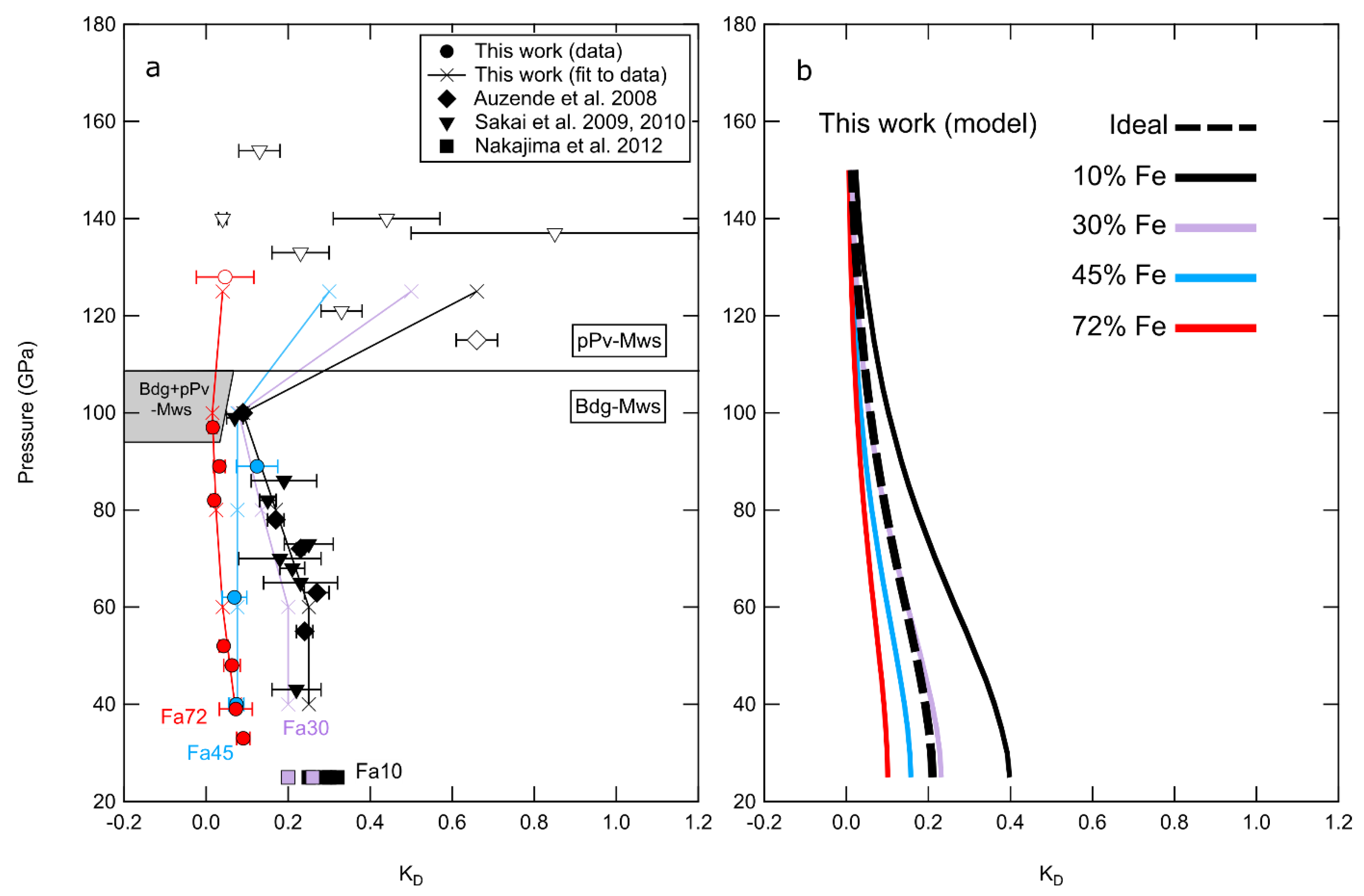
| Sample | P (GPa) | T (K) | t (min) | Phases | (XRD) | KD | ||
|---|---|---|---|---|---|---|---|---|
| Fa45 * | 40 | 2000 | 10 | Mws, Bdg, Sti (1 grain) | 25 ± 5 | 17.9 ± 1.9 | 74.7 ± 1.8 | 0.074 ± 0.018 |
| Fa45 * | 46 | 2050 | 20 | Mws, Bdg | 14 ± 5 | Recovery failed | ||
| Fa45 * | 62 | 2000 | 15 | Mws, Bdg | 27 ± 5 | 16 ± 3 | 73.6 ± 1.1 | 0.07 ± 0.03 |
| Fa45 * | 66 | 2250 | 15 | Mws, Bdg | 21 ± 5 | Recovery failed | ||
| Fa45 * | 71 | 2440 | 20 | Mws, Bdg | 18 ± 5 | TS | - | |
| Fa45 * | 89 | 2600 | 15 | Mws, Bdg | 4 ± 5 | 18 ± 4 | 64 ± 2 | 0.12 ± 0.05 |
| Fa72 * | 33 | 1980 | 15 | Mws, Bdg, Sti | 56 ± 5 | 37 ± 3 | 86.8 ± 0.3 | 0.089 ± 0.016 |
| Fa72 | 39 | 2000 | 30 | Mws, Bdg, Sti | 69 ±5 | 47 ± 7 | 92.4 ± 1.2 | 0.07 ± 0.04 |
| Fa72 * | 48 | 1900 | 15 | Mws, Bdg | NR | 43 ± 5 | 92.2 ± 0.6 | 0.06 ± 0.02 |
| Fa72 | 52 | 2000 | 30 | Mws, Bdg | NA | 46.5 ± 1.3 | 95.3 ± 0.8 | 0.043 ± 0.011 |
| Fa72 * | 61 | 1850 | 20 | Mws, Bdg | 55 ± 5 | TS | - | |
| Fa72 | 82 | 2000 | 20 | Mws, Bdg, Fe | NA | 51 ± 2 | 98.2 ± 0.5 | 0.019 ± 0.009 |
| Fa72 * | 89 | 2200 | 35 | Mws, Bdg, pPv | 31 ± 5 | 49 ± 2 | 96.8 ± 1.1 | 0.032 ± 0.014 |
| Fa72 | 128 | 2700 | 60 | Mw, pPv | NA | pPv: 59.1 ± 0.8 | 97 ± 3 | 0.05 ± 0.07 |
| Fa72 in MgO | 83 | 2200 | 45 | Fp, Mws, Bdg | NA | 4.2 ± 0.7 | 21.9 ± 0.9, 96.4 ± 0.5 | - |
| Previous Parameters | Revised Parameters | |
|---|---|---|
| V0 (cm3/mol) | 12.26 a | 12.26 |
| K0 (GPa) | 179 a | 149 b |
| K0′ | 4.9 a | 3.6 b |
| γ0 | 1.53 a | 1.53 |
| q | 1.7 a | 1.7 |
| θ0 (K) | 454 a | 454 |
| F0 (×103 J/mol) | −242 a | −235 c |
| W (×103 J/mol) | 13 a | 14.746 c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorfman, S.M.; Nabiei, F.; Boukaré, C.-E.; Prakapenka, V.B.; Cantoni, M.; Badro, J.; Gillet, P. Composition and Pressure Effects on Partitioning of Ferrous Iron in Iron-Rich Lower Mantle Heterogeneities. Minerals 2021, 11, 512. https://doi.org/10.3390/min11050512
Dorfman SM, Nabiei F, Boukaré C-E, Prakapenka VB, Cantoni M, Badro J, Gillet P. Composition and Pressure Effects on Partitioning of Ferrous Iron in Iron-Rich Lower Mantle Heterogeneities. Minerals. 2021; 11(5):512. https://doi.org/10.3390/min11050512
Chicago/Turabian StyleDorfman, Susannah M., Farhang Nabiei, Charles-Edouard Boukaré, Vitali B. Prakapenka, Marco Cantoni, James Badro, and Philippe Gillet. 2021. "Composition and Pressure Effects on Partitioning of Ferrous Iron in Iron-Rich Lower Mantle Heterogeneities" Minerals 11, no. 5: 512. https://doi.org/10.3390/min11050512
APA StyleDorfman, S. M., Nabiei, F., Boukaré, C.-E., Prakapenka, V. B., Cantoni, M., Badro, J., & Gillet, P. (2021). Composition and Pressure Effects on Partitioning of Ferrous Iron in Iron-Rich Lower Mantle Heterogeneities. Minerals, 11(5), 512. https://doi.org/10.3390/min11050512






