Biogenic Orthorhombic α-Calcium Formate from Sediments of Alkali Lake, Oregon, USA
Abstract
1. Introduction
2. Materials and Methods
3. Results
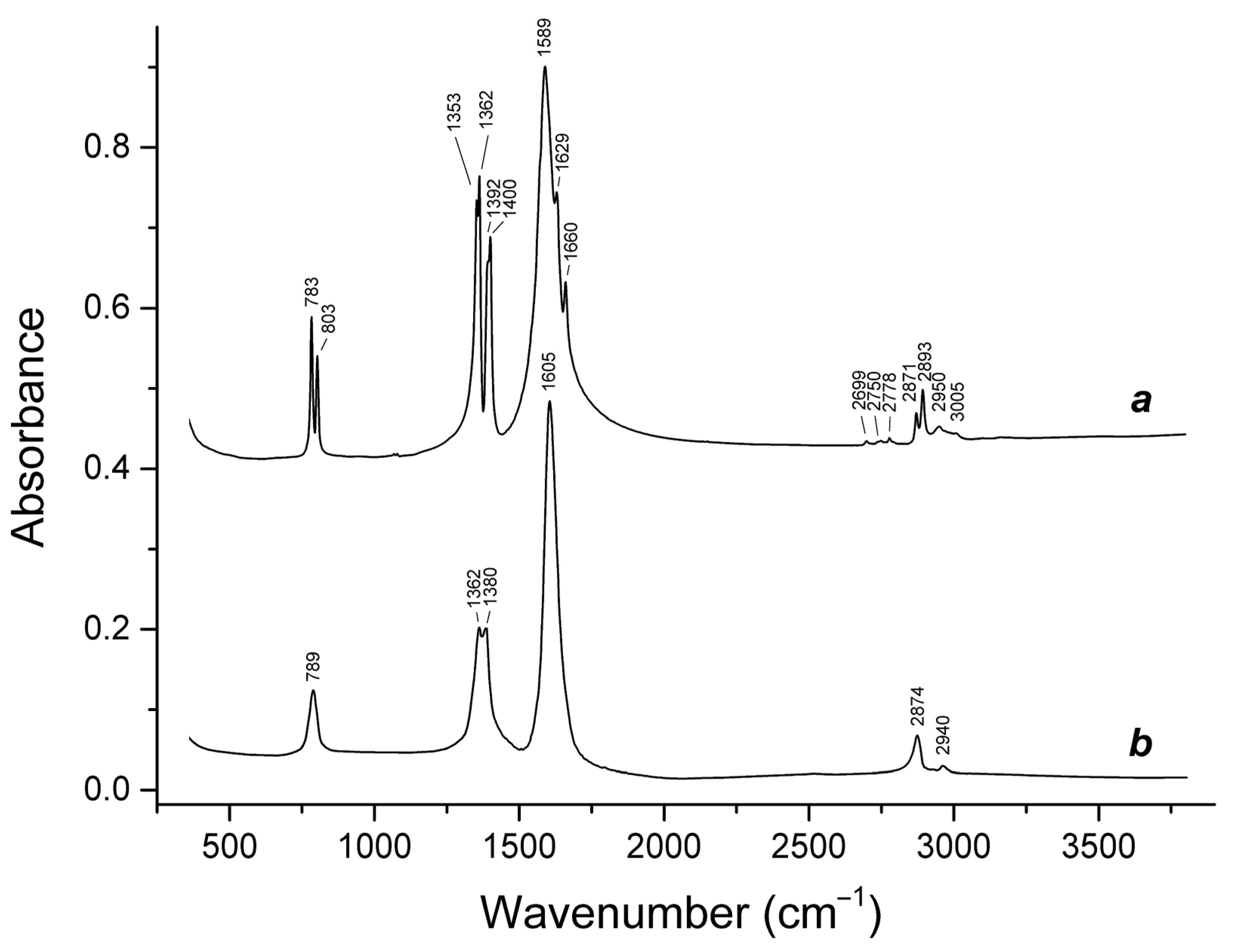
3.1. Infrared Absorption Spectroscopy
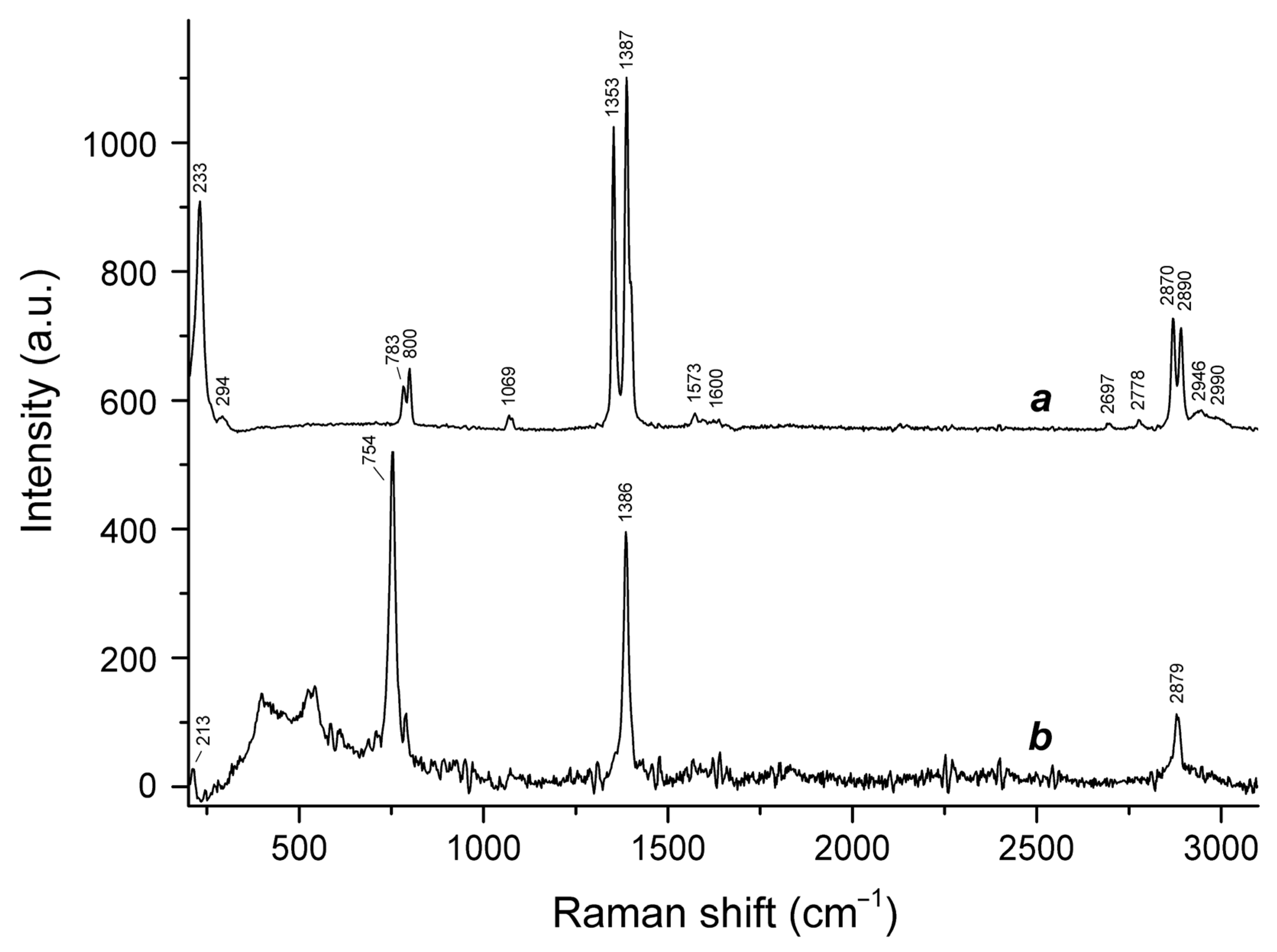
3.2. Raman Spectroscopy
- 2870 to 2890 cm−1, C–H stretching vibrations;
- 1573 to 1600 cm−1, antisymmetric stretching vibrations of the –CO2 group;
- 1353 to 1387 cm−1, symmetric stretching vibrations of the –CO2 group;
- 1069 cm−1, in-plane H–C–O bending mode;
- 754 to 800 cm−1, bending vibrations of the –CO2 group combined with O–C–H bending vibrations;
- 213 and 233 cm−1, stretching vibrations involving Ca···O ionic bonds.
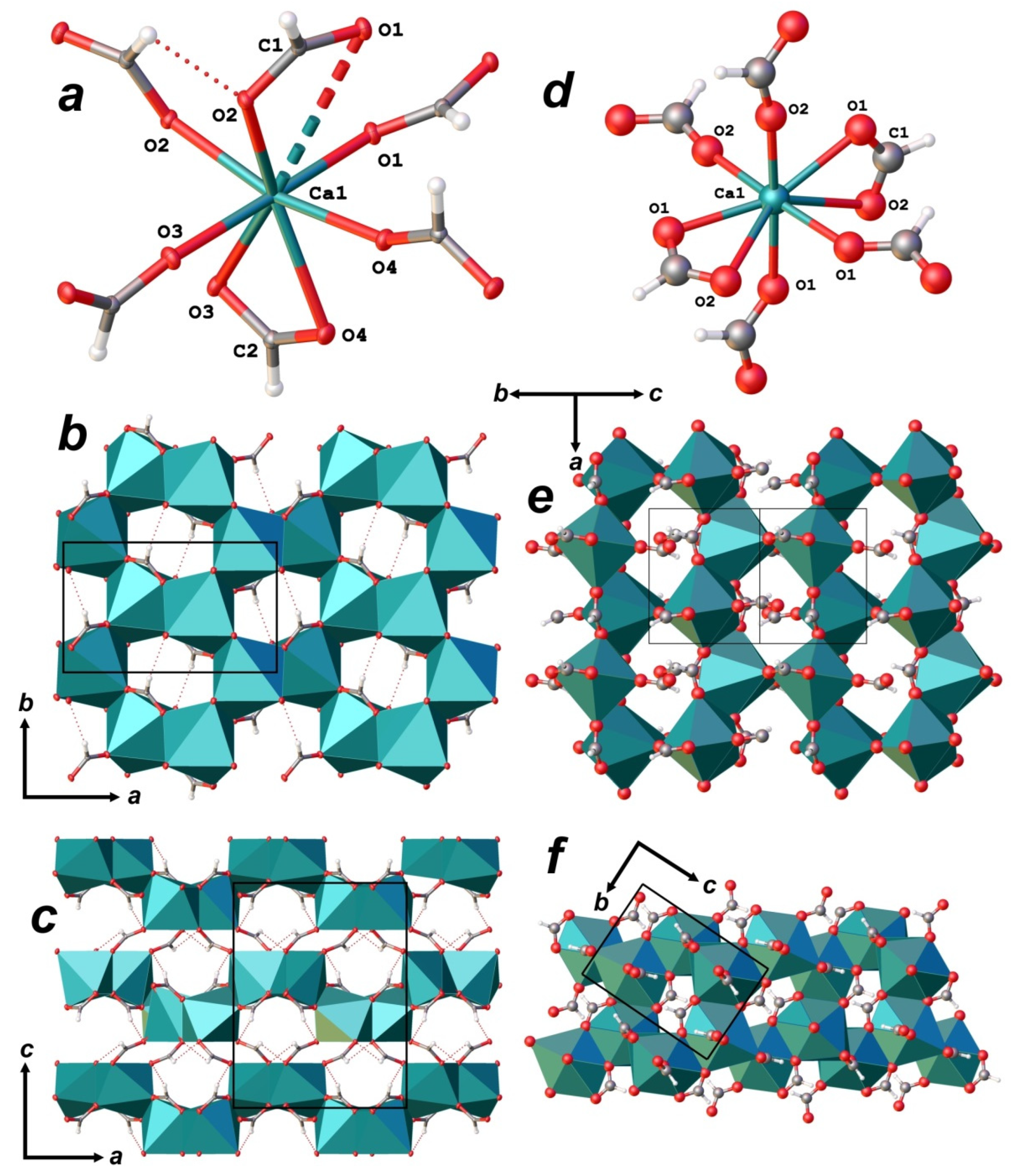
3.3. X-ray Diffraction Data and Crystal Structure
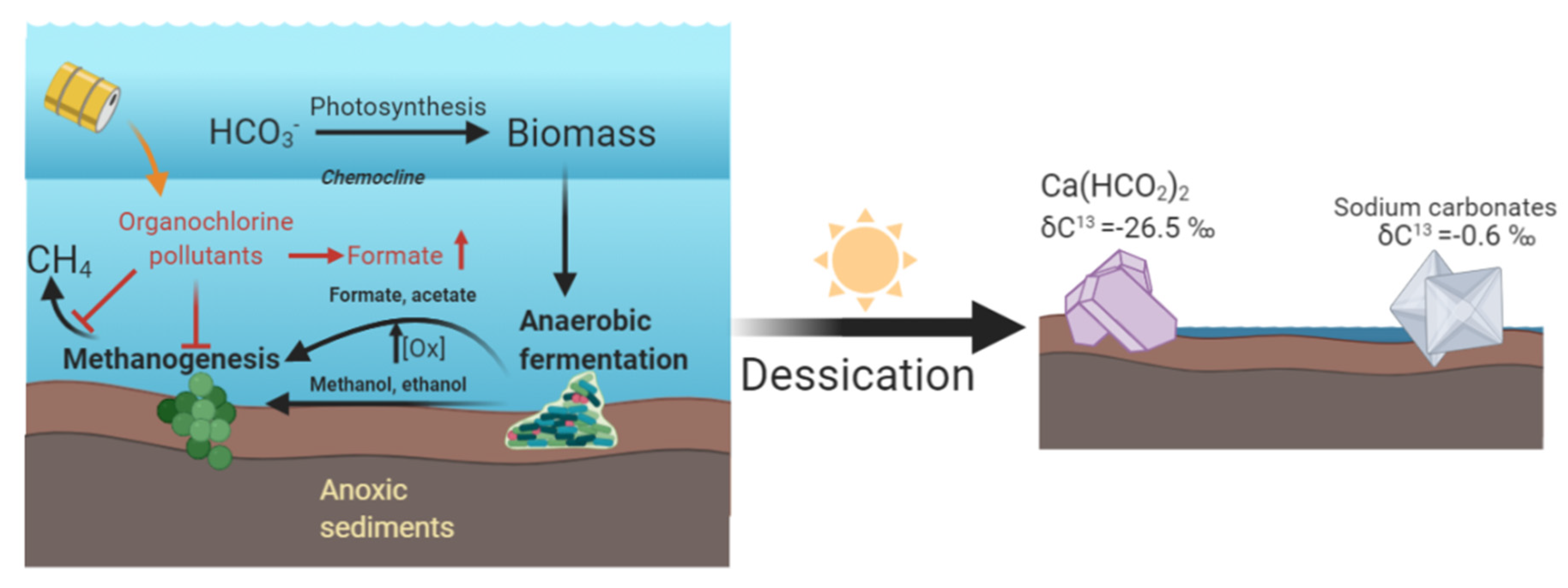
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chukanov, N.V.; Malinko, S.V.; Lisitsyn, A.E.; Dubinchuk, V.T.; Kuz’mina, O.V.; Zadov, A.E. Formicaite, Ca(HCO2)2, a new mineral. Zap. Vseross. Miner. Obs. (Proc. Russ. Miner. Soc.) 1999, 128, 43–48. (In Russian) [Google Scholar]
- Chukanov, N.V.; Belakovskiy, D.I.; Malinko, S.V.; Organova, N.I. Dashkovaite, Mg(HCO2)2·2H2O, a new formate mineral. Zap. Vseross. Miner. Ova. (Proc. Russ. Miner. Soc.) 2000, 129, 49–53. (In Russian) [Google Scholar]
- Comel, C.; Mentzen, B.F. Comparative study of the polymorphic species of strontium and calcium formates. I. Differential Thermal Analysis (DTA). J. Solid State Chem. 1974, 9, 210–213. [Google Scholar] [CrossRef]
- Mentzen, B.F.; Comel, C. Comparative study of the polymorphic species of strontium and calcium formates. II. X-Ray diffraction. J. Solid State Chem. 1974, 9, 214–223. [Google Scholar] [CrossRef]
- Matsui, M.; Watanabé, T.; Kamijo, N.; Lapp, R.L.; Jacobson, R.A. The structures of calcium formate β-Ca(HCOO)2 and δ-Ca(HCOO)2, and the tetragonal mixed crystals Ca(HCOO)2–Sr(HCOO)2. Acta Crystallogr. 1980, B36, 1081–1086. [Google Scholar] [CrossRef]
- Nitta, I.; Osaki, K. Crystal structure of calcium formate. X-Sen Osaka Univ. 1948, 5, 37–42. [Google Scholar] [CrossRef][Green Version]
- Burger, N.; Fuess, H.; Mason, S.A. Neutron diffraction of α-calcium formate at 100 and 296 K. Acta Crystallogr. 1977, B33, 1968–1970. [Google Scholar] [CrossRef]
- Bargouth, M.O.; Will, G. Calcium formate Ca(HCOO)2 (neutron). Cryst. Struct. Commun. 1980, 9, 605–613. [Google Scholar]
- Fuess, H.; Burger, N.; Bats, J.W. Deformationsdichteverteilung in Salzen komplexer Anionen I: X–N-Dichte in α-Calciumformiat bei 100 K und 296 K. Z. Kristallogr. 1981, 156, 219–232. [Google Scholar] [CrossRef]
- Watanabé, T.; Matsui, M. A redetermination of the crystal structures of α-calcium formate, α-strontium formate and barium formate by X-ray analyses. Acta Crystallogr. 1978, B34, 2731–2736. [Google Scholar] [CrossRef]
- Silaev, V.I.; Rakin, V.I.; Shanina, S.N.; Petrovskiy, V.A.; Shiryaeva, L.L. To mineralogy of the crystallic calcium formiate. Ural. Geol. Zhurnal (Ural Geol. J.) 2005, 46, 107–123. (In Russian) [Google Scholar]
- WINXPOW; Stoe & Cie: Darmstadt, Germany, 2004.
- CrysAlisPro Software System, Version 1.171.40.50a; Rigaku Oxford Diffraction: Oxford, UK, 2019.
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal structure determination. Acta Cryst. 2015, A71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Ito, K.; Bernstein, H.J. The vibrational spectra of the formate, acetate, and oxalate ions. Can. J. Chem. 1956, 34, 170–178. [Google Scholar] [CrossRef]
- Krishnan, R.S.; Ramanujam, P.S. Raman spectrum of calcium formate. J. Raman Spectrosc. 1973, 1, 533–538. [Google Scholar] [CrossRef]
- Wang, S.; Kong, P.; Zhang, Z.; Sun, H.; Li, P.; Chen, R.; Gu, B.; Ungar, G.; Wu, X.; Cheng, L.; et al. Structure, morphology, and nonlinear optical properties of orthorhombic α-Ca(HCOO)2 single crystals. Opt. Mater. Express 2018, 8, 2238–2245. [Google Scholar] [CrossRef]
- Gagné, O.C.; Hawthorne, F.C. Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Cryst. 2015, B71, 561–578. [Google Scholar] [CrossRef]
- Sazanova, K.V.; Vlasov, D.Y.; Osmolovskay, N.G.; Schiparev, S.M.; Rusakov, A.V. Significance and regulation of acids production by rock-inhabited fungi. In Biogenic-Abiogenic Interactions in Natural and Anthropogenic Systems; Frank-Kamenetskaya, O.V., Panova, E.G., Vlasov, D.Y., Eds.; Springer: Zug, Switzerland, 2016; pp. 379–392. [Google Scholar] [CrossRef]
- Frank-Kamenetskaya, O.V.; Ivanyuk, G.Y.; Zelenskaya, M.S.; Izatulina, A.R.; Kalashnikov, A.O.; Vlasov, D.Y.; Polyanskaya, E.I. Calcium Oxalates in Lichens on Surface of Apatite-Nepheline Ore (Kola Peninsula, Russia). Minerals 2019, 9, 656. [Google Scholar] [CrossRef]
- Vlasov, D.Y.; Frank-Kamenetskaya, O.V.; Zelenskaya, M.S.; Sazanova, K.V.; Rusakov, A.D.; Izatulina, A.R. The use of Aspergillus niger in modeling of modern mineral formation in lithobiotic systems. In Aspergillus niger: Pathogenicity, Cultivation and Uses; Baughan, E., Ed.; Nova Science Publishers: New York, NY, USA, 2020; pp. 1–123. [Google Scholar]
- Frank-Kamenetskaya, O.V.; Zelenskaya, M.S.; Izatulina, A.R.; Gurzhiy, V.V.; Rusakov, A.V.; Vlasov, D.Y. Oxalate formation by Aspergillus niger on manganese ore minerals. Am. Miner. (in press). [CrossRef]
- Li, Z.; Bai, T.; Dai, L.; Wang, F.; Tao, J.; Meng, S.; Hu, Y.; Wang, S.; Hu, S. A study of organic acid production in contrasts between two phosphate solubilizing fungi: Penicillium oxalicum and Aspergillus niger. Sci. Rep. 2016, 6, 25313. [Google Scholar] [CrossRef] [PubMed]
- Thiele, J.H.; Zeikus, J.G. Control of Interspecies Electron Flow during Anaerobic Digestion: Significance of Formate Transfer versus Hydrogen Transfer during Syntrophic Methanogenesis in Flocs. Appl. Environ. Microbiol. 1988, 54, 20–29. [Google Scholar] [CrossRef]
- Crain, A.V.; Broderick, J.B. Pyruvate formate-lyase and its activation by pyruvate formate-lyase activating enzyme. J. Biol. Chem. 2014, 289, 5723–5729. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.; Mentel, M.; van Hellemond, J.J.; Henze, K.; Woehle, C.; Gould, S.B.; Yu, R.-Y.; van der Giezen, M.; Tielens, A.G.M.; Martin, W.F. Biochemistry and Evolution of Anaerobic Energy Metabolism in Eukaryotes. Microbiol. Mol. Biol. Rev. 2012, 76, 444–495. [Google Scholar] [CrossRef]
- Atteia, A.; Van Lis, R.; Tielens, A.G.M.; Martin, W.F. Anaerobic energy metabolism in unicellular photosynthetic eukaryotes. Biochim. Biophys. Acta Bioenerg. 2013, 1827, 210–223. [Google Scholar] [CrossRef]
- Wolfe, A.J. The Acetate Switch. Microbiol. Mol. Biol. Rev. 2005, 69, 12–50. [Google Scholar] [CrossRef] [PubMed]
- Antony, C.P.; Kumaresan, D.; Hunger, S.; Drake, H.L.; Murrell, J.C.; Shouche, Y.S. Microbiology of Lonar Lake and other soda lakes. ISME J. 2013, 7, 468–476. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, G.; Jiang, H.; Yu, B.; Chapman, L.R.; Lucas, C.R.; Fields, M.W. Microbial diversity in sediments of saline Qinghai Lake, China: Linking geochemical controls to microbial ecology. Microb. Ecol. 2006, 51, 65–82. [Google Scholar] [CrossRef]
- Eugster, H.P.; Hardie, L.A. Saline Lakes. In Lakes; Lerman, A., Ed.; Springer: New York, NY, USA, 1978; pp. 237–293. [Google Scholar] [CrossRef]
- Oremland, R.S.; Des Marais, D.J. Distribution, abundance and carbon isotopic composition of gaseous hydrocarbons in Big Soda Lake, Nevada: An alkaline, meromictic lake. Geochim. Cosmochim. Acta 1983, 47, 2107–2114. [Google Scholar] [CrossRef]
- Kendall, M.M.; Boone, D.R. The Order Methanosarcinales. In The Prokaryotes; Dworkin, M., Falkow, S., Rosenberg, E., Schleifer, K.H., Stackebrandt, E., Eds.; Springer: New York, NY, USA, 2006; pp. 244–256. [Google Scholar] [CrossRef]
- Liu, Y.; Boone, D.R.; Choy, C. Methanohalophilus oregonense sp. nov. a methylotrophic methanogen from an alkaline, saline aquifer. Int. J. Syst. Bacteriol. 1990, 40, 111–116. [Google Scholar] [CrossRef]
- Pankow, J.F.; Isabelle, L.M.; Barofsky, D.F. The identification of chlorophenoxyphenols in soil and water samples by solvent extraction and field desorption mass spectrometry. Anal. Chim. Acta 1981, 124, 357–364. [Google Scholar] [CrossRef]
- Maltseva, O.; McGowan, C.; Fulthorpet, R.; Oriel, P. Degradation of 2,4-dichlorophenoxyacetic acid by haloalkaliphilic bacteria. Microbiology 1996, 142, 1115–1122. [Google Scholar] [CrossRef]
- Young, A.L.; Calcagni, J.A.; Thalken, C.E.; Tremblay, J.W. The toxicology, environmental fate, and human risk of herbicide orange and its associated dioxin. In U.S. Air Force OEHL Technical Report; United States Air Force Occupational and Environmental Health Laboratory, Aerospace Medical Division (AFSC), Brooks Air Force Base: San Antonio, TX, USA, 1978; TR-78-92. [Google Scholar]
- Johnson, R.L.; Brillante, S.M.; Isabella, L.M.; Houck, J.E.; Pankow, J.F. Migration of Chlorophenolic Compounds at the Chemical Waste Disposal Site at Alkali Lake, Oregon-1. Site Description and Ground-Water Flow. Groundwater 1984, 22, 593–601. [Google Scholar] [CrossRef]
- Johnson, R.L.; Brillante, S.M.; Isabella, L.M.; Houck, J.E.; Pankow, J.F. Migration of Chlorophenolic Compounds at the Chemical Waste Disposal Site at Alkali Lake, Oregon-2. Contaminant Distributions, Transport, and Retardation. Groundwater 1985, 23, 652–666. [Google Scholar] [CrossRef]
- Puyol, D.; Sanz, J.L.; Rodriguez, J.J.; Mohedano, A.F. Inhibition of methanogenesis by chlorophenols: A kinetic approach. New Biotechnol. 2012, 30, 51–61. [Google Scholar] [CrossRef] [PubMed]
- Aeppli, C.; Tysklind, M.; Holmstrand, H.; Gustafsson, O. Use of Cl and C isotopic fractionation to identify degradation and sources of polychlorinated phenols. Environ. Sci. Technol. 2013, 47, 790–797. [Google Scholar] [CrossRef]
- Gies, H. Studies on clathrasils. III. Crystal structure of melanophlogite, a natural clathrate compound of silica. Z. Kristallogr. 1983, 164, 247–257. [Google Scholar] [CrossRef]
- Golovina, N.I.; Raevskiy, A.V.; Chukanov, N.V.; Korsunskiy, B.L.; Shilov, G.V.; Atovmyan, L.O.; Aldoshin, S.M. Density of crystals of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane, a potential ligand. Ross. Khimicheskiy Zhurnal (Russian Chem. J.) 2004, 48, 41–48. (In Russian) [Google Scholar]
- Bennion, J.C.; Chowdhury, N.; Kampf, J.W.; Matzger, A.J. Hydrogen peroxide solvates of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane. Angew. Chem. 2016, 128, 13312–13315. [Google Scholar] [CrossRef]

| Modification | Sp. Gr.* | a, Å/α, ° | b, Å/β, ° | c, Å/γ, ° | V, Å3/ ρ, g/cm3 | Reference |
|---|---|---|---|---|---|---|
| α | Pbca | 10.229(1) | 6.256(1) | 13.243(1) | 847.47(2)/2.040 | This work |
| 10.163–10.228(3) | 6.261(3)–6.288(1) | 13.238(5)–13.407(2) | 847.73–858.81/2.008– 2.038 | [6,7,8,9,10] | ||
| β (synt) | P41212 | 6.776(2) | 6.776(2) | 9.453(5) | 434.03/1.991 | [5] |
| β (Formicaite) | 6.77(1) | 6.77(1) | 9.46(1) | 434(1)/1.990 | [1] | |
| γ | P2, Pm or P2/m | 6.75/90 | 6.705/119.47 | 5.78/90 | 227.75/1.897 | [4] |
| δ | I41/amd | 6.75(1) | 6.75(1) | 10.04(2) | 457.45/1.889 | [5] |
| Crystal System | Orthorhombic |
|---|---|
| Space group | Pbca |
| a (Å) | 10.22943(12) |
| b (Å) | 6.25587(9) |
| c (Å) | 13.24297(18) |
| V (Å3) | 847.471(19) |
| Molecular weight | 130.12 |
| μ (mm–1) | 11.986 |
| Temperature (K) | 100(2) |
| Z | 8 |
| Dcalc (g/cm3) | 2.040 |
| Crystal size (mm3) | 0.16 × 0.11 × 0.08 |
| Radiation | CuKα |
| Total reflections | 6597 |
| Unique reflections | 806 |
| Angle range 2θ (°) | 13.37–140.00 |
| Reflections with |Fo| ≥ 4σF | 802 |
| Rint | 0.0461 |
| Rσ | 0.0188 |
| R1 (|Fo| ≥ 4σF) | 0.0195 |
| wR2 (|Fo| ≥ 4σF) | 0.0542 |
| R1 (all data) | 0.0195 |
| wR2 (all data) | 0.0542 |
| S | 1.090 |
| ρmin, ρmax, e/Å3 | −0.296, 0.408 |
| CSD | 2070226 |
| Atom | x | y | z | Ueq |
|---|---|---|---|---|
| Ca1 | 0.63497(2) | 0.46904(4) | 0.60687(2) | 0.00687(15) |
| O1 | 0.47731(8) | 0.28344(15) | 0.70119(7) | 0.0118(2) |
| O2 | 0.29850(8) | 0.28148(15) | 0.79756(7) | 0.0104(2) |
| O3 | 0.79847(8) | 0.63126(15) | 0.51242(7) | 0.0131(2) |
| O4 | 0.96604(8) | 0.80824(15) | 0.45160(7) | 0.0125(2) |
| C1 | 0.37446(11) | 0.3653(2) | 0.73323(10) | 0.0091(3) |
| H1 | 0.3486(15) | 0.503(3) | 0.7099(14) | 0.014(4) |
| C2 | 0.88857(12) | 0.6535(2) | 0.44933(10) | 0.0102(3) |
| H2 | 0.9009(18) | 0.547(3) | 0.3972(12) | 0.012(4) |
| Bond * | BVS | Angle | ||
|---|---|---|---|---|
| Ca1–O1 | 2.3472(9) | 0.341 | O1–Ca1–O4 | 87.42(3) |
| Ca1–O2 | 2.4036(9) | 0.297 | O1–Ca1–O4 | 87.90(3) |
| Ca1–O2 | 2.4260(9) | 0.281 | O2–Ca1–O2 | 85.60(2) |
| Ca1–O3 | 2.5482(10) | 0.209 | O2–Ca1–O3 | 70.59(3) |
| Ca1–O3 | 2.3220(9) | 0.363 | O2–Ca1–O3 | 148.13(3) |
| Ca1–O4 | 2.3510(9) | 0.338 | O2–Ca1–O4 | 121.46(3) |
| Ca1–O4 | 2.5115(9) | 0.228 | O2–Ca1–O4 | 149.91(3) |
| <Ca1–O> | 2.416 | 2.057 | O3–Ca1–O1 | 176.17(3) |
| Ca1···O1 ** | 3.413(1) | 0.025 | O3–Ca1–O2 | 74.15(3) |
| O3–Ca1–O2 | 89.75(3) | |||
| C1–O1 | 1.2447(15) | O3–Ca1–O3 | 84.58(3) | |
| C1–O2 | 1.2667(15) | O3–Ca1–O4 | 91.74(3) | |
| C1–H1 | 0.952(19) | O3–Ca1–O4 | 95.34(3) | |
| C2–O3 | 1.2518(16) | O4–Ca1–O2 | 84.29(3) | |
| C2–O4 | 1.2512(17) | O4–Ca1–O2 | 166.99(3) | |
| C2–H2 | 0.969(17) | O4–Ca1–O3 | 51.39(3) | |
| O4–Ca1–O3 | 121.75(3) | |||
| Angle | O4–Ca1–O4 | 70.45(4) | ||
| O1–Ca1–O2 | 108.28(3) | O1–C1–O2 | 125.26(13) | |
| O1–Ca1–O2 | 87.51(3) | O3–C2–O4 | 122.44(13) | |
| O1–Ca1–O3 | 91.98(3) | |||
| dmeas | Imeas | Icalc | dcalc | hkl | dmeas | Imeas | Icalc | dcalc | hkl |
|---|---|---|---|---|---|---|---|---|---|
| 6.692 | 5 | 7 | 6.656 | 002 | 4 | 1.922 | 511 | ||
| 5.596 | 100 | 100 | 5.577 | 102 | 1.916 | 11 | 13 | 1.917 | 231 |
| 4.965 | 60 | 57 | 4.963 | 111 | 1.865 | 9 | 14 | 1.859 | 306 |
| 3.952 | 2 | 3 | 3.962 | 210 | 3 | 1.812 | 026 | ||
| 3.793 | 15 | 18 | 3.798 | 211 | 1.807 | 1 | 4 | 1.809 | 423 |
| 3.426 | 20 | 18 | 3.415 | 113 | 1.791 | 5 | 7 | 1.784 | 126 |
| 3.406 | 96 | 94 | 3.405 | 212 | 2 | 1.782 | 316 | ||
| 3.058 | 21 | 21 | 3.056 | 021 | 3 | 1.775 | 233 | ||
| 2.961 | 87 | 82 | 2.955 | 213 | 1.767 | 11 | 19 | 1.767 | 331 |
| 2.928 | 4 | 3 | 2.927 | 121 | 2 | 1.746 | 134 | ||
| 3 | 2.920 | 311 | 1.722 | 9 | 6 | 1.722 | 332 | ||
| 2.839 | 23 | 7 | 2.839 | 022 | 11 | 1.714 | 217 | ||
| 29 | 2.826 | 114 | 1.704 | 3 | 2 | 1.703 | 600 | ||
| 2.739 | 15 | 18 | 2.736 | 122 | 5 | 1.702 | 424 | ||
| 2.674 | 3 | 4 | 2.675 | 220 | 1.678 | 5 | 6 | 1.675 | 406 |
| 4 | 2.554 | 400 | 2 | 1.674 | 234 | ||||
| 2.546 | 4 | 2 | 2.548 | 214 | 1.655 | 1 | 4 | 1.658 | 522 |
| 2.490 | 12 | 13 | 2.486 | 123 | 2 | 1.642 | 108 | ||
| 2.483 | 15 | 14 | 2.481 | 313 | 1.632 | 1 | 4 | 1.631 | 611 |
| 12 | 2.383 | 115 | 1.627 | 4 | 2 | 1.627 | 027 | ||
| 2.291 | 20 | 24 | 2.284 | 024 | 5 | 1.624 | 135 | ||
| 2.272 | 1 | 3 | 2.274 | 321 | 1.598 | 3 | 4 | 1.595 | 612 |
| 2.234 | 16 | 12 | 2.229 | 124 | 1.591 | 2 | 2 | 1.589 | 425 |
| 2.229 | 19 | 20 | 2.225 | 314 | 3 | 1.589 | 118 | ||
| 2.218 | 4 | 2 | 2.219 | 006 | 2 | 1.582 | 208 | ||
| 3 | 2.210 | 215 | 2 | 1.541 | 141 | ||||
| 2.180 | 17 | 19 | 2.181 | 322 | 1.538 | 5 | 11 | 1.541 | 613 |
| 3 | 2.168 | 106 | 1.511 | 2 | 4 | 1.511 | 142 | ||
| 2 | 2.048 | 323 | 1.480 | 2 | 5 | 1.480 | 043 | ||
| 2.026 | 11 | 2 | 2.027 | 131 | 2 | 1.478 | 426 | ||
| 2.001 | 2 | 10 | 2.026 | 404 | 5 | 1.470 | 028 | ||
| 1.994 | 16 | 6 | 1.992 | 125 | 1.421 | 2 | 3 | 1.426 | 119 |
| 22 | 1.989 | 315 | 3 | 1.420 | 044 | ||||
| 1.978 | 13 | 19 | 1.981 | 420 | 1.409 | 1 | 6 | 1.413 | 711 |
| 5 | 1.960 | 132 | 1.398 | 1 | 3 | 1.394 | 408 | ||
| 1.948 | 8 | 12 | 1.953 | 502 | 1.358 | 2 | 4 | 1.357 | 237 |
| 1.936 | 4 | 6 | 1.937 | 230 | 6 | 1.356 | 526 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chukanov, N.V.; Menor-Salvan, C.; Gurzhiy, V.V.; Izatulina, A.R.; Pekov, I.V.; Vigasina, M.F.; Ksenofontov, D.A.; Britvin, S.N. Biogenic Orthorhombic α-Calcium Formate from Sediments of Alkali Lake, Oregon, USA. Minerals 2021, 11, 448. https://doi.org/10.3390/min11050448
Chukanov NV, Menor-Salvan C, Gurzhiy VV, Izatulina AR, Pekov IV, Vigasina MF, Ksenofontov DA, Britvin SN. Biogenic Orthorhombic α-Calcium Formate from Sediments of Alkali Lake, Oregon, USA. Minerals. 2021; 11(5):448. https://doi.org/10.3390/min11050448
Chicago/Turabian StyleChukanov, Nikita V., Cesar Menor-Salvan, Vladislav V. Gurzhiy, Alina R. Izatulina, Igor V. Pekov, Marina F. Vigasina, Dmitry A. Ksenofontov, and Sergey N. Britvin. 2021. "Biogenic Orthorhombic α-Calcium Formate from Sediments of Alkali Lake, Oregon, USA" Minerals 11, no. 5: 448. https://doi.org/10.3390/min11050448
APA StyleChukanov, N. V., Menor-Salvan, C., Gurzhiy, V. V., Izatulina, A. R., Pekov, I. V., Vigasina, M. F., Ksenofontov, D. A., & Britvin, S. N. (2021). Biogenic Orthorhombic α-Calcium Formate from Sediments of Alkali Lake, Oregon, USA. Minerals, 11(5), 448. https://doi.org/10.3390/min11050448










