Structural and High-Pressure Properties of Rheniite (ReS2) and (Re,Mo)S2
Abstract
1. Introduction
2. First-Principles Calculations
3. Experimental Methods
4. Results and Discussion
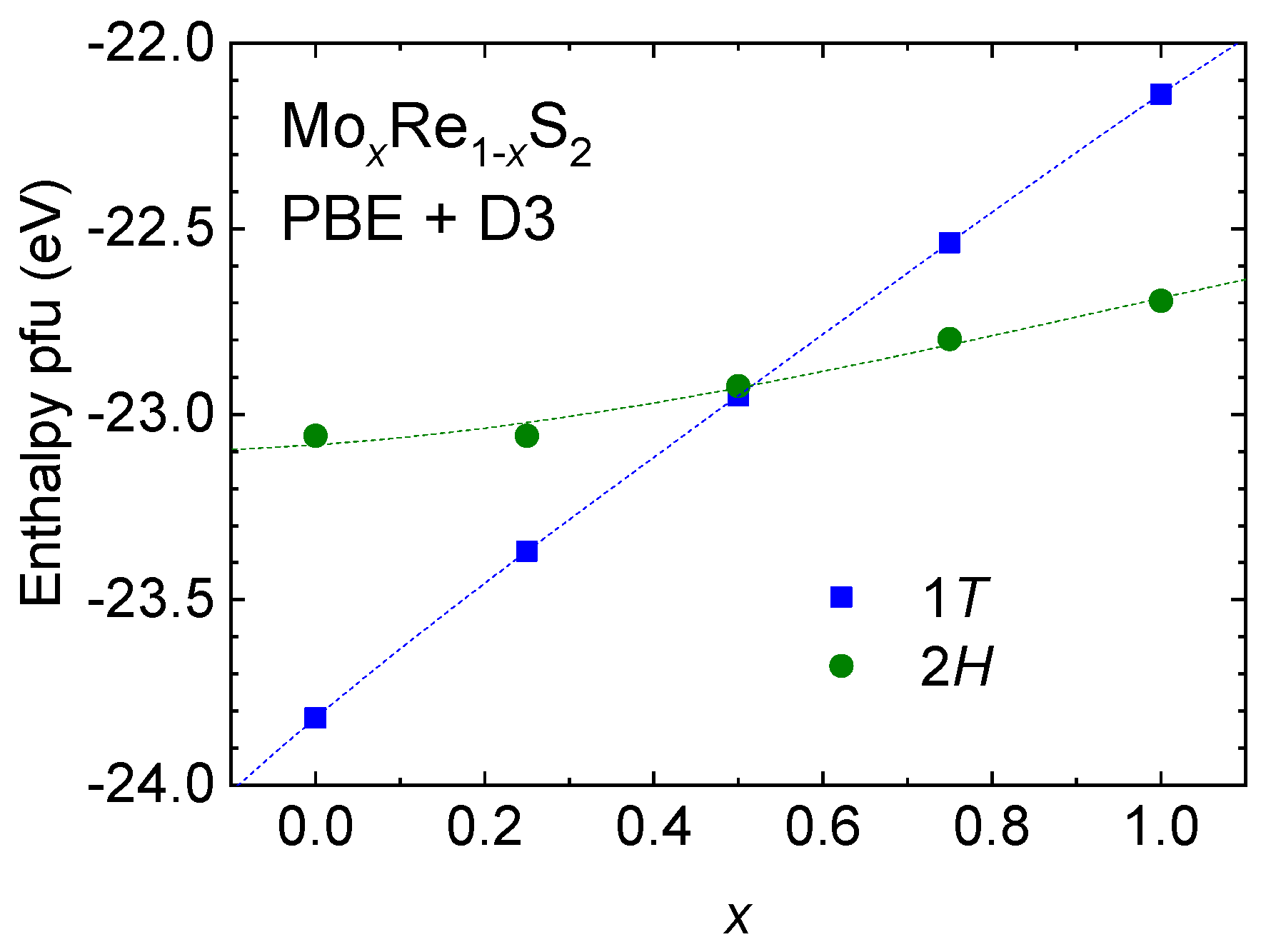
4.1. The Re1−xMoxS2 Solid Solution
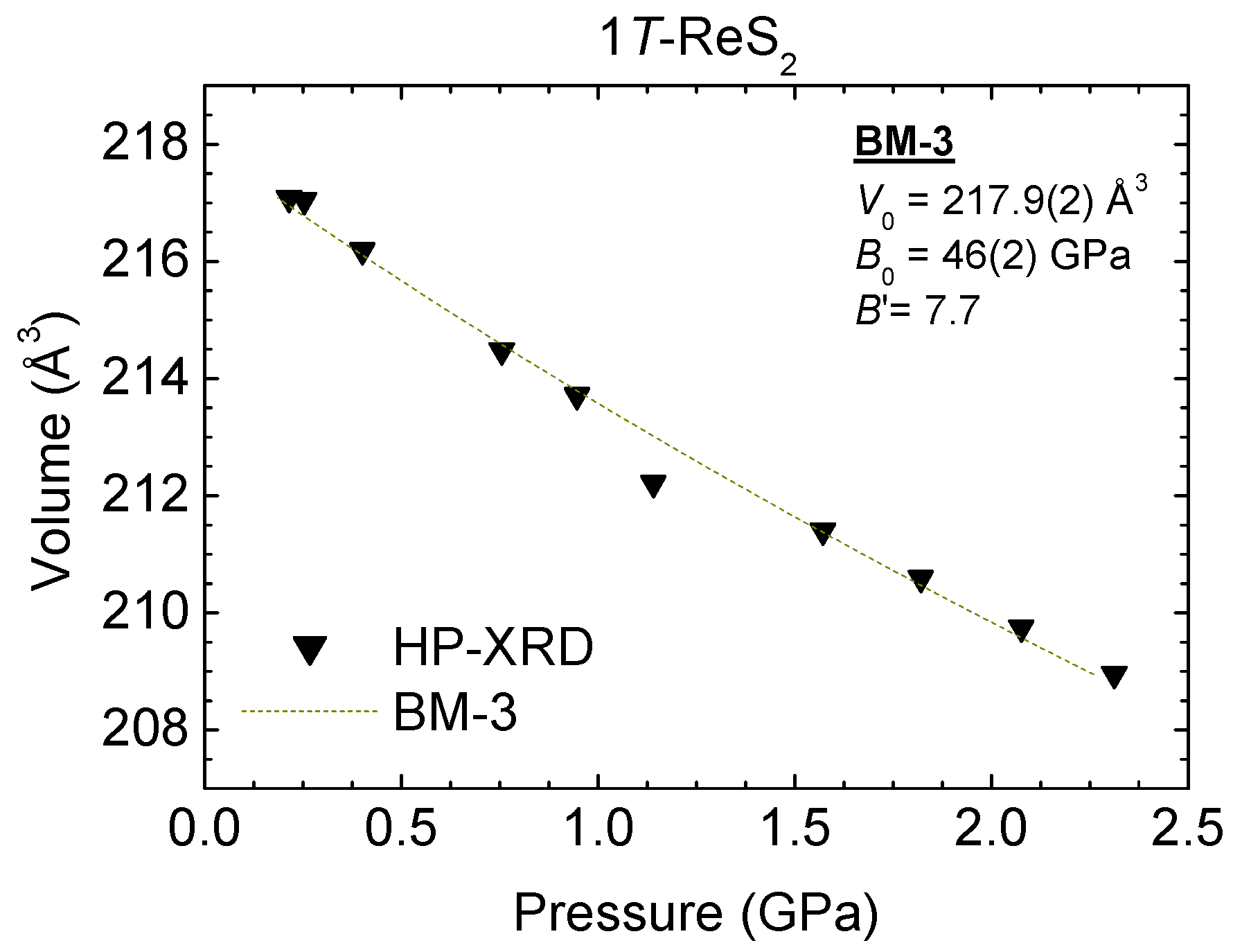
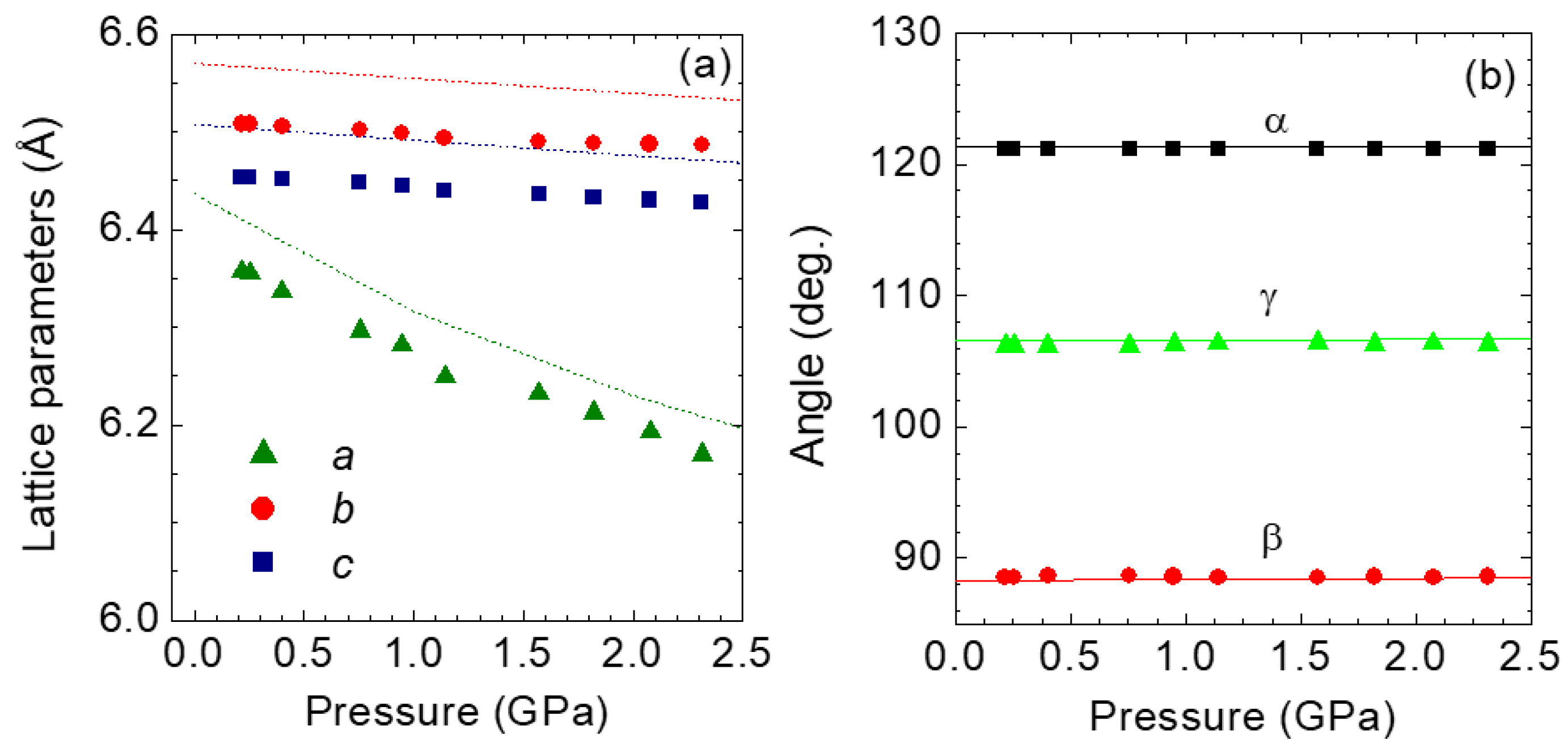
4.2. 1T-ReS2 and Re1−xMoxS2 under Pressure
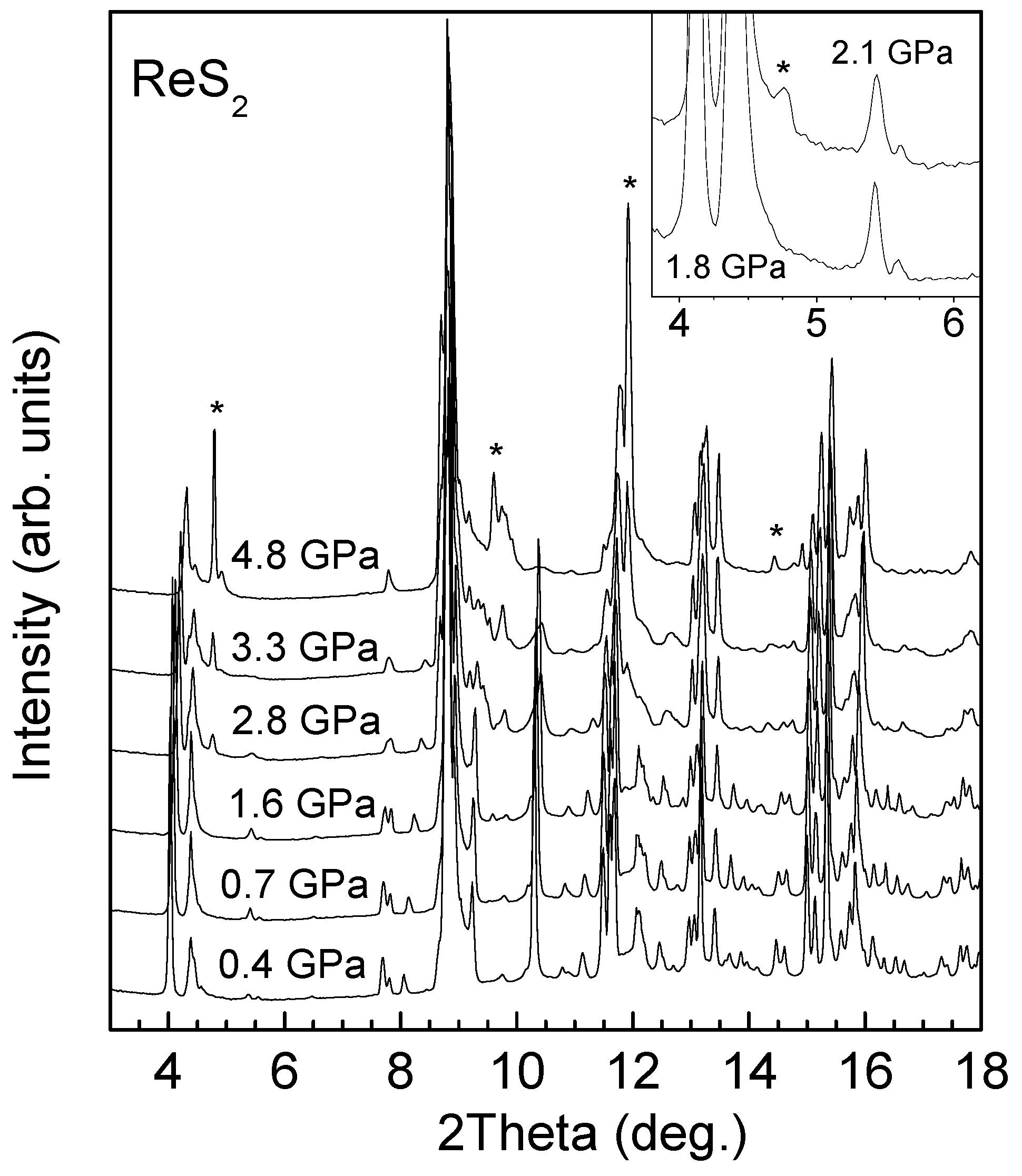
4.3. High-Pressure XRD of 1T-ReS2
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korzhinsky, M.A.; Tkachenko, S.I.; Shmulovich, K.I.; Taran, Y.A.; Steinberg, G.S. Discovery of a pure rhenium mineral at Kudriavy volcano. Nature 1994, 369, 51–52. [Google Scholar] [CrossRef]
- Znamensky, V.S.; Korzhinsky, M.A.; Steinberg, G.S.; Trachenko, S.I.; Yakushev, A.I.; Laputina, I.P.; Bryzgalov, I.A.; Samotoin, N.D.; Magazina, L.O.; Kuzmina, O.V.; et al. Rheniite, ReS2, the natural rhenium disulphide from fumaroles of of Kudryavy volcano, Iturup Island, Kurile Islands. Proc. Russ. Mineral. Soc. 2005, 134, 32–40. [Google Scholar]
- Voudouris, P.C.; Melfos, V.; Spry, P.G.; Bindi, L.; Kartal, T.; Arikas, K.; Moritz, R.; Ortelli, M. Rhenium-rich molybdenite and rheniite in the Pagoni Rachi Mo-Cu-Te-Ag-Au prospect, northern Greece: Implications for the re geochemistry of porphyry-style Cu-Mo and Mo mineralization. Can. Mineral. 2009, 47, 1013–1036. [Google Scholar] [CrossRef]
- Voudouris, P.; Melfos, V.; Spry, P.G.; Bindi, L.; Moritz, R.; Ortelli, M.; Kartal, T. Extremely re-rich molybdenite from porphyry Cu-Mo-Au prospects in northeastern Greece: Mode of occurrence, causes of enrichment, and implications for gold exploration. Minerals 2013, 3, 165–191. [Google Scholar] [CrossRef]
- Newberry, R.J.J. Polytypism in molybdenite (I): A non-equilibrium impurity-induced phenomenon. Am. Mineral. 1974, 64, 758–767. [Google Scholar]
- Newberry, R. Polytypism in molybdenite (II); Relationships between polytypism, ore deposition/alteration stages and rhenium contents. Am. Mineral. 1979, 64, 768–775. [Google Scholar]
- Frisenda, R.; Niu, Y.; Gant, P.; Muñoz, M.; Castellanos-Gomez, A. Naturally occurring van der Waals materials. npj 2D Mater. Appl. 2020, 4, 1–13. [Google Scholar] [CrossRef]
- Murray, H.H.; Kelly, S.P.; Chianelli, R.R.; Day, C.S. Structure of Rhenium Disulfide. Inorg. Chem. 1994, 33, 4418–4420. [Google Scholar] [CrossRef]
- Lamfers, H.J.; Meetsma, A.; Wiegers, G.A.; De Boer, J.L. The crystal structure of some rhenium and technetium dichalcogenides. J. Alloys Compd. 1996, 241, 34–39. [Google Scholar] [CrossRef]
- Kertesz, M.; Hoffmann, R. Octahedral vs. Trigonal-Prismatic Coordination and Clustering in Transition-Metal Dichalcogenides. J. Am. Chem. Soc. 1984, 106, 3453–3460. [Google Scholar] [CrossRef]
- Whangbo, M.H.; Canadell, E. Analogies between the Concepts of Molecular Chemistry and Solid-State Physics concerning Structural Instabilities. Electronic Origin of the Structural Modulations in Layered Transition-Metal Dichalcogenides. J. Am. Chem. Soc. 1992, 114, 9587–9600. [Google Scholar] [CrossRef]
- Choi, J.H.; Jhi, S.H. Origin of distorted 1T-phase ReS2: First-principles study. J. Phys. Condens. Matter 2018, 30, 105403. [Google Scholar] [CrossRef]
- Tongay, S.; Sahin, H.; Ko, C.; Luce, A.; Fan, W.; Liu, K.; Zhou, J.; Huang, Y.S.; Ho, C.H.; Yan, J.; et al. Monolayer behaviour in bulk ReS2 due to electronic and vibrational decoupling. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Biswas, D.; Ganose, A.M.; Yano, R.; Riley, J.M.; Bawden, L.; Clark, O.J.; Feng, J.; Collins-Mcintyre, L.; Sajjad, M.T.; Meevasana, W.; et al. Narrow-band anisotropic electronic structure of ReS2. Phys. Rev. B 2017, 96, 085205. [Google Scholar] [CrossRef]
- Oliva, R.; Laurien, M.; Dybala, F.; Kopaczek, J.; Qin, Y.; Tongay, S.; Rubel, O.; Kudrawiec, R. Pressure dependence of direct optical transitions in ReS2 and ReSe2. npj 2D Mater. Appl. 2019, 3, 20. [Google Scholar] [CrossRef]
- Nayak, A.P.; Bhattacharyya, S.; Zhu, J.; Liu, J.; Wu, X.; Pandey, T.; Jin, C.; Singh, A.K.; Akinwande, D.; Lin, J.-F. Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun. 2014, 5, 3731. [Google Scholar] [CrossRef]
- Selvi, E.; Ma, Y.; Aksoy, R.; Ertas, A.; White, A. High pressure x-ray diffraction study of tungsten disulfide. J. Phys. Chem. Solids 2006, 67, 2183–2186. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H.; Yuan, H.; Wang, S.; Lin, Y.; Zeng, Q.; Xu, G.; Liu, Z.; Solanki, G.K.; Patel, K.D.; et al. Pressure induced metallization with absence of structural transition in layered molybdenum diselenide. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Zhou, D.; Zhou, Y.; Pu, C.; Chen, X.; Lu, P.; Wang, X.; An, C.; Zhou, Y.; Miao, F.; Ho, C.H.; et al. Pressure-induced metallization and superconducting phase in ReS2. npj Quantum Mater. 2017, 2, 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X.; Zhou, Y.; Park, C.; An, C.; Zhou, Y.; Zhang, R.; Gu, C.; Yang, W.; Yang, Z. Pressure-induced iso-structural phase transition and metallization in WSe2. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; Ma, Y.; Du, J.; Yan, J.; Ji, C.; Zhu, H. High pressure X-ray diffraction study of ReS2. J. Phys. Chem. Solids 2010, 71, 1571–1575. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Y.; Qu, J.; Zhu, Q.; Yang, W.; Zhu, J.; Wang, L.; Zhang, W.; He, D.; Zhao, Y. Pressure-induced structural and electronic transitions, metallization, and enhanced visible-light responsiveness in layered rhenium disulphide. Phys. Rev. B 2018, 97, 1–9. [Google Scholar] [CrossRef]
- Saha, P.; Ghosh, B.; Mazumder, A.; Glazyrin, K.; Dev Mukherjee, G. Pressure induced lattice expansion and phonon softening in layered ReS2. J. Appl. Phys. 2020, 128, 085904. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, E.; Feng, X.; Liu, H.; Redfern, S.A.T.; Kanchana, V.; Liu, G.; Wang, H. Phase transition and superconductivity in ReS2, ReSe2 and ReTe2. Phys. Chem. Chem. Phys. 2018, 20, 29472–29479. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Zhang, J.; Sumpter, B.G.; Tan, Q.H.; Tan, P.H.; Meunier, V. Low-Frequency Shear and Layer-Breathing Modes in Raman Scattering of Two-Dimensional Materials. ACS Nano 2017, 11, 11777–11802. [Google Scholar] [CrossRef]
- Zhuang, Y.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Pu, C.; Hong, M.; Liu, P. Deviatoric stresses promoted metallization in rhenium disulfide. J. Phys. D Appl. Phys. 2018, 51, aab5a7. [Google Scholar] [CrossRef]
- Yan, Y.; Jin, C.; Wang, J.; Qin, T.; Li, F.; Wang, K.; Han, Y.; Gao, C. Associated Lattice and Electronic Structural Evolutions in Compressed Multilayer ReS2. J. Phys. Chem. Lett. 2017, 8, 3648–3655. [Google Scholar] [CrossRef]
- Sheremetyeva, N.; Tristant, D.; Yoshimura, A.; Gray, J.; Liang, L.; Meunier, V. First-principles study of the thermodynamic and vibrational properties of ReS2 under pressure. Phys. Rev. B 2019, 100, 214101. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ruzsinszky, A.; Perdew, J. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar]
- Peng, H.; Yang, Z.H.; Perdew, J.P.; Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef]
- Ibáñez, J.; Woźniak, T.; Dybala, F.; Oliva, R.; Hernández, S.; Kudrawiec, R. High-pressure Raman scattering in bulk HfS2: Comparison of density functional theory methods in layered MS2 compounds (M = Hf, Mo) under compression. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Oliva, R.; Woźniak, T.; Dybala, F.; Tołłoczko, A.; Kopaczek, J.; Scharoch, P.; Kudrawiec, R. Valley polarization investigation of GeS under high pressure. Phys. Rev. B 2020, 101, 235205. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Van De Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.L.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Efficient stochastic generation of special quasirandom structures. Calphad Comput. Coupling Phase Diagr. Thermochem. 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Fauth, F.; Peral, I.; Popescu, C.; Knapp, M. The new material science powder diffraction beamline at ALBA synchrotron. In Proceedings of the Powder Diffraction; Cambridge University Press: Cambridge, UK, 2013; Volume 28, pp. S360–S370. [Google Scholar]
- Sahu, R.; Bhat, U.; Batra, N.M.; Sharona, H.; Vishal, B.; Sarkar, S.; Assa Aravindh, S.; Peter, S.C.; Roqan, I.S.; Costa, P.M.F.J.; et al. Nature of low dimensional structural modulations and relative phase stability in RexMo(W)1−xS2 transition metal dichalcogenide alloys. J. Appl. Phys. 2017, 121, 105101. [Google Scholar] [CrossRef]
- Gupta, D.; Chauhan, V.; Kumar, R. A comprehensive review on synthesis and applications of molybdenum disulfide (MoS2) material: Past and recent developments. Inorg. Chem. Commun. 2020, 121, 108200. [Google Scholar] [CrossRef]
- Dalmatova, S.A.; Fedorenko, A.D.; Mazalov, L.N.; Asanov, I.P.; Ledneva, A.Y.; Tarasenko, M.S.; Enyashin, A.N.; Zaikovskii, V.I.; Fedorov, V.E. XPS experimental and DFT investigations on solid solutions of Mo1−xRexS2 (0 < x < 0.20). Nanoscale 2018, 10, 10232–10240. [Google Scholar] [PubMed]


| V0 (Å3) | B0 (GPa) | B′ | B″ | EoS | |
|---|---|---|---|---|---|
| PBE+D3 | 224.9 (5) | 44 (2) | 7.7 (5) | - | BM-3 |
| PBE+D3 | 222.92 (3) | 35.1 (2) | 13.2 (1) | −3.7 (1) | BM-4 |
| HP-XRD | 217.8 (2) | 49 (2) | - | - | BM-2 |
| HP-XRD | 217.9 (2) | 46 (2) | 7.7 1 | - | BM-3 |
| HP-XRD | 217.9 (2) | 41.3 (2) | 13.2 1 | −3.7 1 | BM-4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibáñez-Insa, J.; Woźniak, T.; Oliva, R.; Popescu, C.; Hernández, S.; López-Vidrier, J. Structural and High-Pressure Properties of Rheniite (ReS2) and (Re,Mo)S2. Minerals 2021, 11, 207. https://doi.org/10.3390/min11020207
Ibáñez-Insa J, Woźniak T, Oliva R, Popescu C, Hernández S, López-Vidrier J. Structural and High-Pressure Properties of Rheniite (ReS2) and (Re,Mo)S2. Minerals. 2021; 11(2):207. https://doi.org/10.3390/min11020207
Chicago/Turabian StyleIbáñez-Insa, Jordi, Tomasz Woźniak, Robert Oliva, Catalin Popescu, Sergi Hernández, and Julian López-Vidrier. 2021. "Structural and High-Pressure Properties of Rheniite (ReS2) and (Re,Mo)S2" Minerals 11, no. 2: 207. https://doi.org/10.3390/min11020207
APA StyleIbáñez-Insa, J., Woźniak, T., Oliva, R., Popescu, C., Hernández, S., & López-Vidrier, J. (2021). Structural and High-Pressure Properties of Rheniite (ReS2) and (Re,Mo)S2. Minerals, 11(2), 207. https://doi.org/10.3390/min11020207








