Towards Consistent Interpretations of Coal Geochemistry Data on Whole-Coal versus Ash Bases through Machine Learning
Abstract
1. Introduction
2. Compositional Data Transformation
2.1. Additive Log-Ratio (alr) Transformation
2.2. Centered Log-Ratio (clr) Transformation
2.3. Isometric Log-Ratio (ilr) Transformation
3. Improved Additive Log-Ratio and Correlation Analysis
3.1. Improved Additive Log-Ratio Transformation
3.2. Correlation Analysis of Different Transformation Methods
3.3. Correlation Replaced by Stability
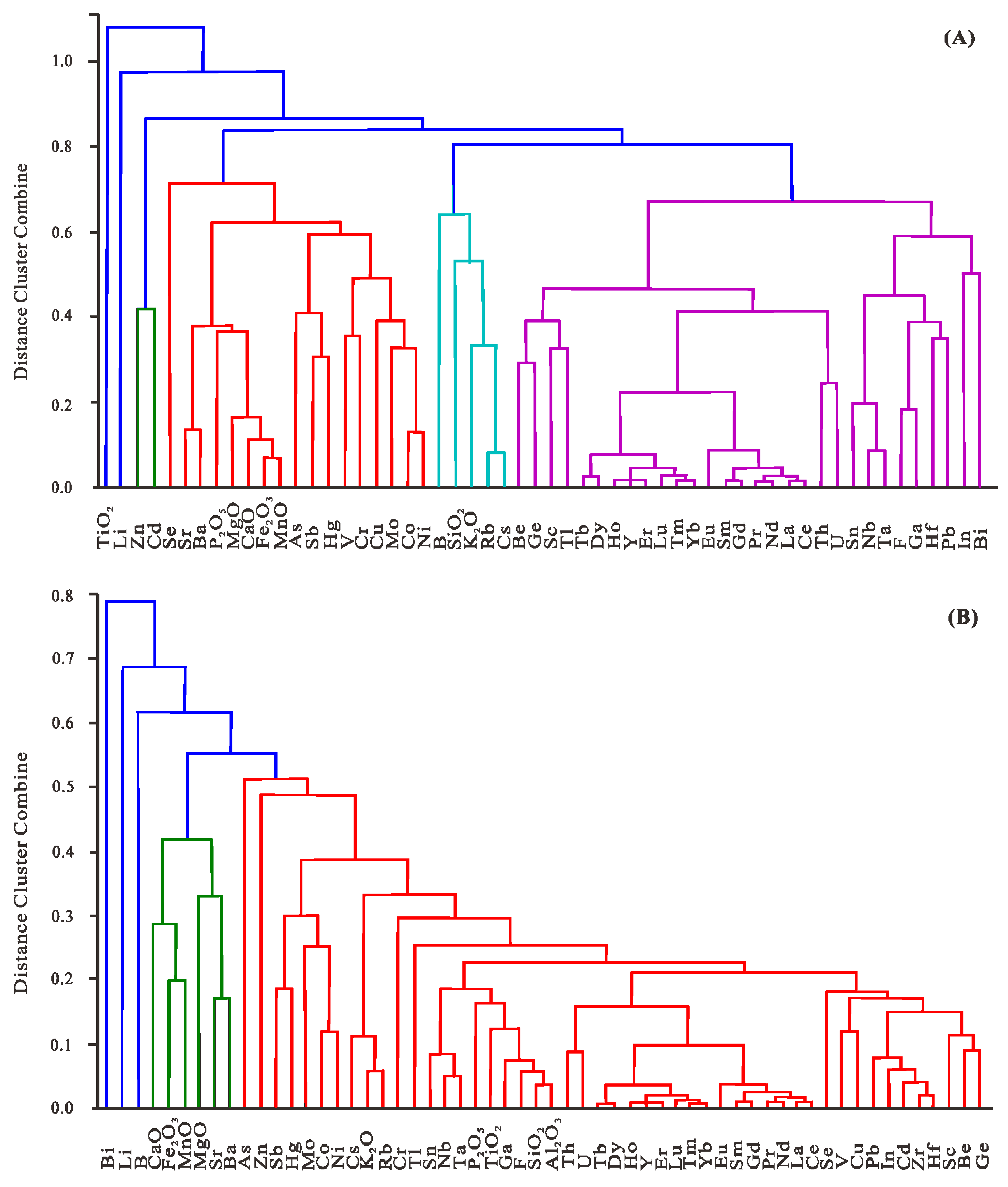
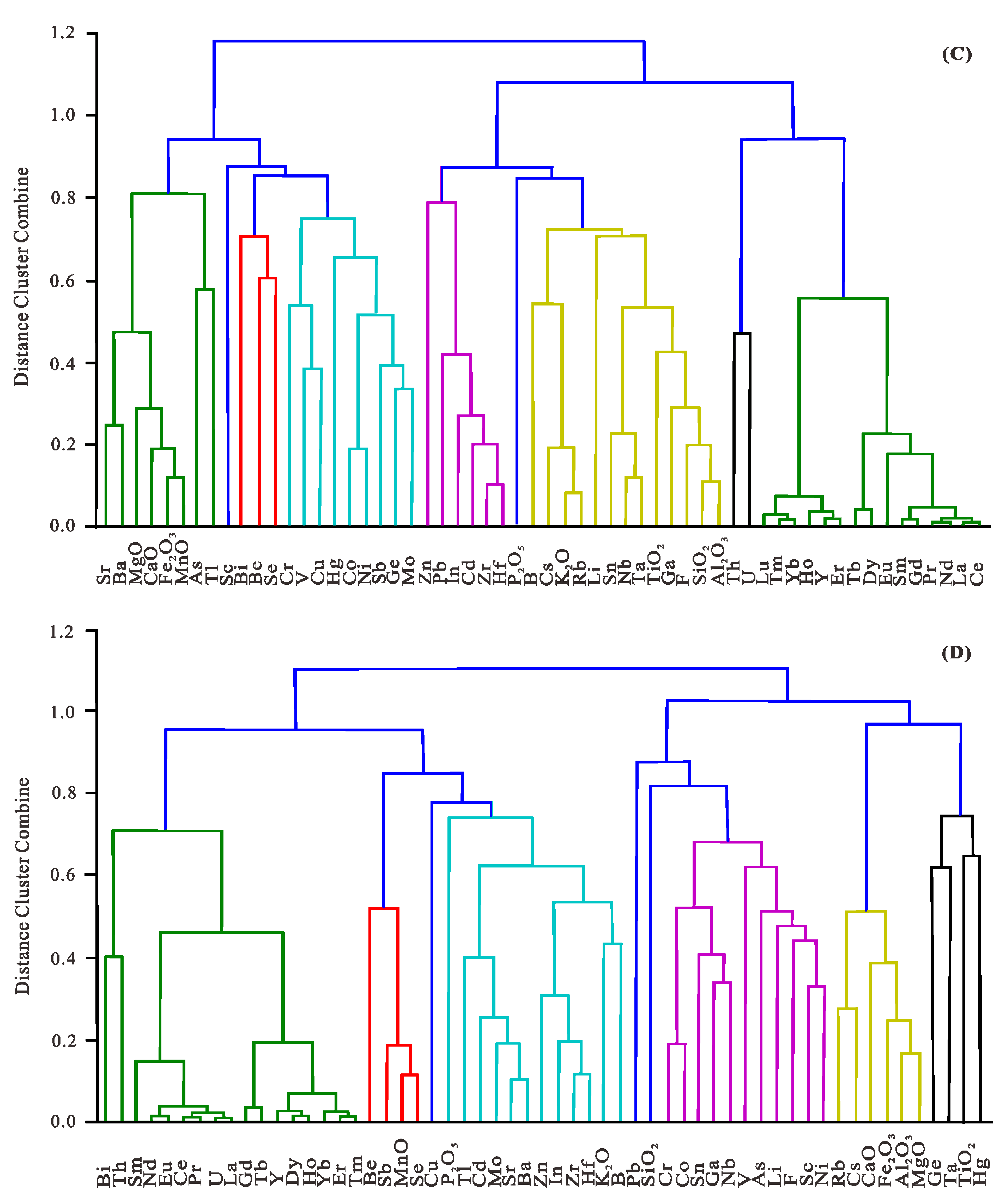
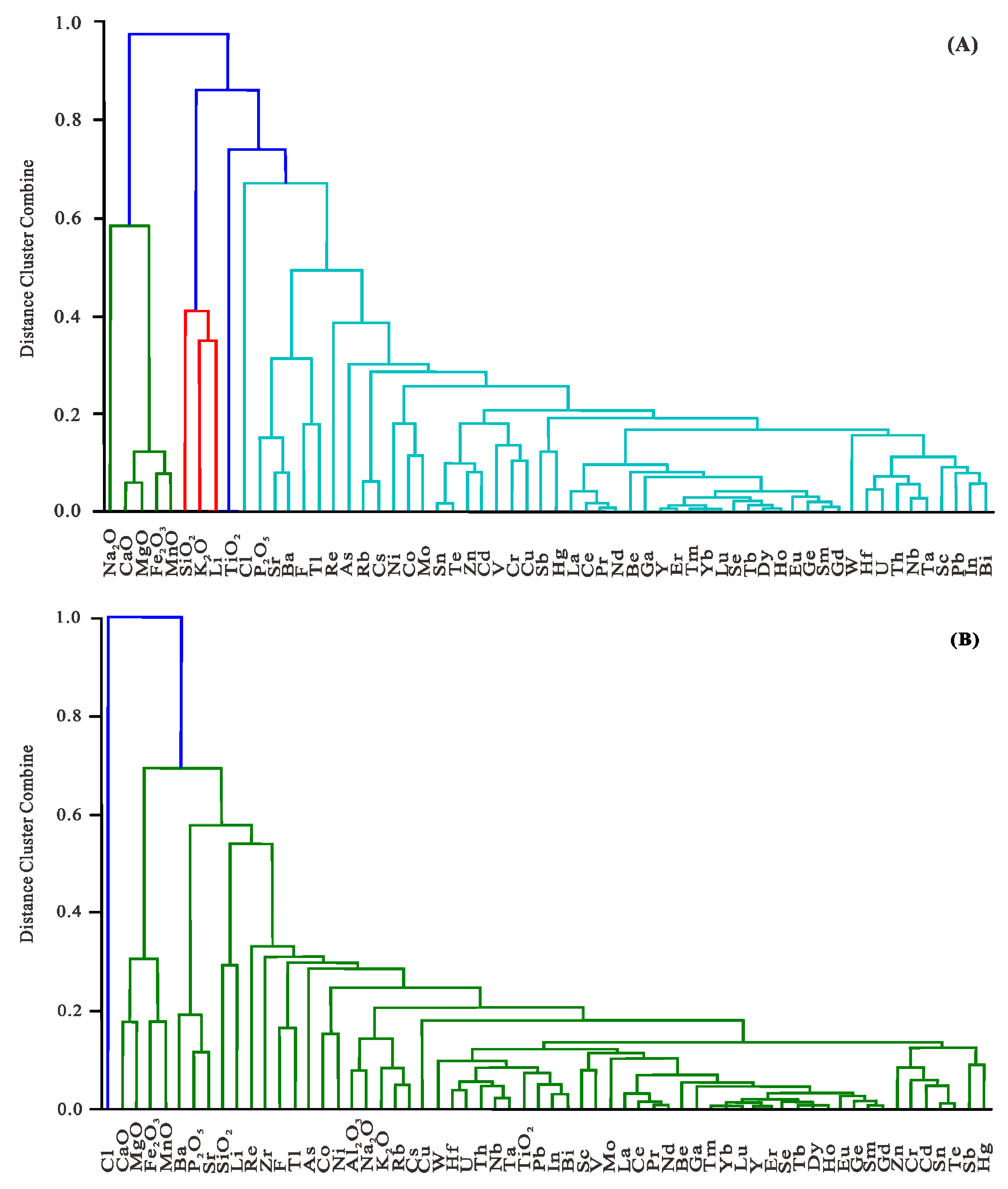
4. Prediction for Occurrence Mode of Element in Coal Based on Hierarchy Clustering
4.1. Hierarchical Clustering
4.2. Similarities Analysis between the Elements in Coal
4.3. Agglomerative Clustering Algorithm for Prediction
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dai, S.; Hower, J.C.; Finkelman, R.B.; Graham, I.T.; French, D.; Ward, C.R.; Eskenazy, G.; Wei, Q.; Zhao, L. Organic associations of non-mineral elements in coal: A review. Int. J. Coal Geol. 2020, 218, 103347. [Google Scholar] [CrossRef]
- Finkelman, R.B.; Palmer, C.A.; Wang, P. Quantification of the modes of occurrence of 42 elements in coal. Int. J. Coal Geol. 2018, 185, 138–160. [Google Scholar] [CrossRef]
- Querol, X.; Alastuey, A.; Zhuang, X.; Hower, J.; Lopez-Soler, A.; Plana, F.; Zeng, R. Petrology, mineralogy and geochemistry of the Permian and Triassic coals in the Leping area, Jiangxi Province, southeast China. Int. J. Coal Geol. 2001, 48, 23–45. [Google Scholar] [CrossRef]
- Dai, S.; Ren, D.; Chou, C.-L.; Finkelman, R.B.; Seredin, V.V.; Zhou, Y. Geochemistry of trace elements in Chinese coals: A review of abundances, genetic types, impacts on human health, and industrial utilization. Int. J. Coal Geol. 2012, 94, 3–21. [Google Scholar] [CrossRef]
- Swaine, D.J. Trace Elements in Coal; Butterworths: London, UK, 1990. [Google Scholar]
- Ward, C. Analysis and significance of mineral matter in coal seams. Int. J. Coal Geol. 2002, 50, 135–168. [Google Scholar] [CrossRef]
- Ward, C. Analysis, origin and significance of mineral matter in coal: An updated review. Int. J. Coal Geol. 2016, 165, 1–27. [Google Scholar] [CrossRef]
- Dai, S.; Finkelman, R.B. Coal as a promising source of critical elements: Progress and future prospects. Int. J. Coal Geol. 2018, 186, 155–164. [Google Scholar] [CrossRef]
- Dai, S.; Yan, X.; Ward, C.; Hower, J.C.; Zhao, L.; Wang, X.; Zhao, L.; Ren, D.; Finkelman, R. Valuable elements in Chinese coals: A review. Int. Geol. Rev. 2016, 60, 590–620. [Google Scholar] [CrossRef]
- Seredin, V.V.; Dai, S. Coal deposits as potential alternative sources for lanthanides and yttrium. Int. J. Coal Geol. 2012, 94, 67–93. [Google Scholar] [CrossRef]
- Dai, S.; Bechtel, A.; Eble, C.F.; Flores, R.M.; French, D.; Graham, I.T.; Hood, M.M.; Hower, J.C.; Korasidis, V.A.; Moore, T.A.; et al. Recognition of peat depositional environments in coal: A review. Int. J. Coal Geol. 2020, 219, 103383. [Google Scholar] [CrossRef]
- Finkelman, R.B.; Dai, S.; French, D. The importance of minerals in coal as the hosts of chemical elements: A review. Int. J. Coal Geol. 2019, 212, 103251. [Google Scholar] [CrossRef]
- Dai, S.; Zou, J.; Jiang, Y.; Ward, C.; Wang, X.; Li, T.; Xue, W.; Liu, S.; Tian, H.; Sun, X.; et al. Mineralogical and geochemical compositions of the Pennsylvanian coal in the Adaohai Mine, Daqingshan Coalfield, Inner Mongolia, China: Modes of occurrence and origin of diaspore, gorceixite, and ammonian illite. Int. J. Coal Geol. 2012, 94, 250–270. [Google Scholar] [CrossRef]
- Xu, N.; Finkelman, R.B.; Xu, C.; Dai, S. What do coal geochemistry statistics really mean? Fuel 2020, 267, 117084. [Google Scholar] [CrossRef]
- Zhao, L.; Dai, S.; Nechaev, V.P.; Nechaeva, E.V.; Graham, I.T.; French, D.; Sun, J. Enrichment of critical elements (Nb-Ta-Zr-Hf-REE) within coal and host rocks from the Datanhao mine, Daqingshan Coalfield, northern China. Ore Geol. Rev. 2019, 111, 102951. [Google Scholar] [CrossRef]
- Geboy, N.; Engle, M.; Hower, J.C. Whole-coal versus ash basis in coal geochemistry: A mathematical approach to consistent interpretations. Int. J. Coal Geol. 2013, 113, 41–49. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Filzmoser, P.; Hron, K.; Reimann, C. Univariate statistical analysis of environmental (compositional) data: Problems and possibilities. Sci. Total. Environ. 2009, 407, 6100–6108. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric Logratio Transformations for Compositional Data Analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Xu, R.; WunschII, D. Survey of Clustering Algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Arbuzov, S.I.; Chekryzhov, I.; Finkelman, R.; Sun, Y.; Zhao, C.; Il’Enok, S.; Blokhin, M.; Zarubina, N. Comments on the geochemistry of rare-earth elements (La, Ce, Sm, Eu, Tb, Yb, Lu) with examples from coals of north Asia (Siberia, Russian far East, North China, Mongolia, and Kazakhstan). Int. J. Coal Geol. 2019, 206, 106–120. [Google Scholar] [CrossRef]
- Erkoyun, H.; Kadir, S.; Huggett, J. Occurrence and genesis of tonsteins in the Miocene lignite, Tunçbilek Basin, Kütahya, western Turkey. Int. J. Coal Geol. 2019, 202, 46–68. [Google Scholar] [CrossRef]
- Ribeiro, J.; Machado, G.; Moreira, N.; Suárez-Ruiz, I.; Flores, D. Petrographic and geochemical characterization of coal from Santa Susana Basin, Portugal. Int. J. Coal Geol. 2019, 203, 36–51. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Pan, Z.; Pan, W.; Yin, X.; Chai, P.; Pan, S.; Yang, Q. Mineralogical and geochemical characteristics of the Permian coal from the Qinshui Basin, northern China, with emphasis on lithium enrichment. Int. J. Coal Geol. 2019, 214, 103254. [Google Scholar] [CrossRef]
- Dai, S.; Hower, J.C.; Ward, C.; Guo, W.; Song, H.; O’Keefe, J.M.; Xie, P.; Hood, M.M.; Yan, X. Elements and phosphorus minerals in the middle Jurassic inertinite-rich coals of the Muli Coalfield on the Tibetan Plateau. Int. J. Coal Geol. 2015, 144, 23–47. [Google Scholar] [CrossRef]
- Dai, S.; Ren, D.; Tang, Y.; Yue, M.; Hao, L. Concentration and distribution of elements in Late Permian coals from western Guizhou Province, China. Int. J. Coal Geol. 2005, 61, 119–137. [Google Scholar] [CrossRef]
- Liu, J.; Song, H.; Dai, S.; Nechaev, V.P.; Graham, I.T.; French, D.; Nechaeva, E.V. Mineralization of REE-Y-Nb-Ta-Zr-Hf in Wuchiapingian coals from the Liupanshui Coalfield, Guizhou, southwestern China: Geochemical evidence for terrigenous input. Ore Geol. Rev. 2019, 115, 103190. [Google Scholar] [CrossRef]
- Spiro, B.F.; Liu, J.; Dai, S.; Zeng, R.; Large, D.; French, D. Marine derived 87Sr/86Sr in coal, a new key to geochronology and palaeoenvironment: Elucidation of the India-Eurasia and China-Indochina collisions in Yunnan, China. Int. J. Coal Geol. 2019, 215, 103304. [Google Scholar] [CrossRef]
- Dai, S.; Ward, C.; Graham, I.T.; French, D.; Hower, J.C.; Zhao, L.; Wang, X. Altered volcanic ashes in coal and coal-bearing sequences: A review of their nature and significance. Earth-Science Rev. 2017, 175, 44–74. [Google Scholar] [CrossRef]
- Dai, S.; Seredin, V.V.; Ward, C.; Hower, J.C.; Xing, Y.; Zhang, W.; Song, W.; Wang, P. Enrichment of U–Se–Mo–Re–V in coals preserved within marine carbonate successions: Geochemical and mineralogical data from the Late Permian Guiding Coalfield, Guizhou, China. Miner. Deposita 2014, 50, 159–186. [Google Scholar] [CrossRef]
- Chelgani, S.C. Investigating the occurrences of valuable trace elements in African coals as potential byproducts of coal and coal combustion products. J. Afr. Earth Sci. 2019, 150, 131–135. [Google Scholar] [CrossRef]
- Kuppusamy, V.K.; Holuszko, M. Rare earth elements in flotation products of coals from East Kootenay coalfields, British Columbia. J. Rare Earths 2019, 37, 1366–1372. [Google Scholar] [CrossRef]
- Li, B.; Zhuang, X.; Querol, X.; Li, J.; Moreno, N.; Córdoba, P.; Shangguan, Y.; Zhou, J.; Ma, X.; Liu, S. Geological controls on enrichment of Mn, Nb (Ta), Zr (Hf), and REY within the Early Permian coals of the Jimunai Depression, Xinjiang Province, NW China. Int. J. Coal Geol. 2019, 215, 103298. [Google Scholar] [CrossRef]
- Medunić, G.; Grigore, M.; Dai, S.; Berti, D.; Hochella, M.F.; Mastalerz, M.; Valentim, B.; Guedes, A.; Hower, J.C. Characterization of superhigh-organic-sulfur Raša coal, Istria, Croatia, and its environmental implication. Int. J. Coal Geol. 2020, 217, 103344. [Google Scholar] [CrossRef]
- Dai, S.; Wang, X.; Seredin, V.V.; Hower, J.C.; Ward, C.; O’Keefe, J.M.; Huang, W.; Li, T.; Li, X.; Liu, H.; et al. Petrology, mineralogy, and geochemistry of the Ge-rich coal from the Wulantuga Ge ore deposit, Inner Mongolia, China: New data and genetic implications. Int. J. Coal Geol. 2012, 90, 72–99. [Google Scholar] [CrossRef]
- Dai, S.; Graham, I.T.; Ward, C. A review of anomalous rare earth elements and yttrium in coal. Int. J. Coal Geol. 2016, 159, 82–95. [Google Scholar] [CrossRef]
- Filzmoser, P.; Hron, K.; Reimann, C. The bivariate statistical analysis of environmental (compositional) data. Sci. Total. Environ. 2010, 408, 4230–4238. [Google Scholar] [CrossRef]
- Cohen-Addad, V.; Kanade, V.; Mallmann-Trenn, F.; Mathieu, C. Hierarchical Clustering: Objective Functions and Algorithms. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial & Applied Mathematics (SIAM), New Orleans, LA, USA, 7–10 January 2018; pp. 378–397. [Google Scholar]
- Wang, X.; Dai, S.; Sun, Y.; Li, D.; Zhang, W.; Zhang, Y.; Luo, Y. Modes of occurrence of fluorine in the Late Paleozoic No. 6 coal from the Haerwusu Surface Mine, Inner Mongolia, China. Fuel 2011, 90, 248–254. [Google Scholar] [CrossRef]
- Dai, S.; Ren, D.; Chou, C.-L.; Li, S.; Jiang, Y. Mineralogy and geochemistry of the No. 6 Coal (Pennsylvanian) in the Junger Coalfield, Ordos Basin, China. Int. J. Coal Geol. 2006, 66, 253–270. [Google Scholar] [CrossRef]
- Dai, S.; Li, D.; Chou, C.-L.; Zhao, L.; Zhang, Y.; Ren, D.; Ma, Y.; Sun, Y. Mineralogy and geochemistry of boehmite-rich coals: New insights from the Haerwusu Surface Mine, Jungar Coalfield, Inner Mongolia, China. Int. J. Coal Geol. 2008, 74, 185–202. [Google Scholar] [CrossRef]
- Dai, S.; Zhao, L.; Peng, S.; Chou, C.-L.; Wang, X.; Zhang, Y.; Li, D.; Sun, Y. Abundances and distribution of minerals and elements in high-alumina coal fly ash from the Jungar Power Plant, Inner Mongolia, China. Int. J. Coal Geol. 2010, 81, 320–332. [Google Scholar] [CrossRef]
- Li, L.; Ota, K.; Dong, M. Deep Learning for Smart Industry: Efficient Manufacture Inspection System with Fog Computing. IEEE Trans. Ind. Inform. 2018, 14, 4665–4673. [Google Scholar] [CrossRef]
- Chen, M.; Wang, T.; Ota, K.; Dong, M.; Zhao, M.; Liu, A. Intelligent resource allocation management for vehicles network: An A3C learning approach. Comput. Commun. 2020, 151, 485–494. [Google Scholar] [CrossRef]
- Feng, B.; Fu, Q.; Dong, M.; Guo, N.; Li, Q. Multistage and Elastic Spam Detection in Mobile Social Networks through Deep Learning. IEEE Netw. 2018, 32, 15–21. [Google Scholar] [CrossRef]

| SiO2 | TiO2 | Al2O3 | Fe2O3 | MgO | CaO | MnO | K2O | P2O5 | Li | Be | B | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | 1 | 0.890 | 0.964 | 0.310 | 0.346 | 0.213 | 0.206 | 0.835 | 0.828 | 0.419 | 0.803 | 0.551 | 0.940 | 0.804 | 0.647 | 0.669 | 0.481 | 0.572 | 0.734 | 0.606 | 0.932 | 0.734 |
| TiO2 | 0.890 | 1 | 0.875 | 0.297 | 0.316 | 0.206 | 0.206 | 0.670 | 0.817 | 0.451 | 0.805 | 0.470 | 0.834 | 0.828 | 0.696 | 0.675 | 0.470 | 0.555 | 0.774 | 0.544 | 0.903 | 0.714 |
| Al2O3 | 0.964 | 0.875 | 1 | 0.302 | 0.322 | 0.214 | 0.204 | 0.757 | 0.821 | 0.431 | 0.795 | 0.513 | 0.942 | 0.803 | 0.597 | 0.597 | 0.440 | 0.531 | 0.688 | 0.590 | 0.944 | 0.709 |
| Fe2O3 | 0.310 | 0.297 | 0.302 | 1 | 0.764 | 0.773 | 0.802 | 0.263 | 0.478 | 0.116 | 0.395 | 0.159 | 0.364 | 0.503 | 0.438 | 0.403 | 0.508 | 0.508 | 0.418 | 0.269 | 0.371 | 0.502 |
| MgO | 0.346 | 0.316 | 0.322 | 0.764 | 1 | 0.689 | 0.502 | 0.352 | 0.456 | 0.120 | 0.419 | 0.217 | 0.399 | 0.469 | 0.435 | 0.396 | 0.459 | 0.457 | 0.437 | 0.286 | 0.398 | 0.512 |
| CaO | 0.213 | 0.206 | 0.214 | 0.773 | 0.689 | 1 | 0.652 | 0.165 | 0.365 | 0.059 | 0.328 | 0.088 | 0.270 | 0.371 | 0.313 | 0.269 | 0.428 | 0.401 | 0.337 | 0.207 | 0.276 | 0.422 |
| MnO | 0.206 | 0.206 | 0.204 | 0.802 | 0.502 | 0.652 | 1 | 0.152 | 0.338 | 0.088 | 0.301 | 0.089 | 0.237 | 0.400 | 0.331 | 0.320 | 0.408 | 0.407 | 0.320 | 0.185 | 0.267 | 0.406 |
| K2O | 0.835 | 0.670 | 0.757 | 0.263 | 0.352 | 0.165 | 0.152 | 1 | 0.644 | 0.350 | 0.560 | 0.571 | 0.803 | 0.579 | 0.473 | 0.535 | 0.341 | 0.416 | 0.531 | 0.480 | 0.716 | 0.515 |
| P2O5 | 0.828 | 0.817 | 0.821 | 0.478 | 0.456 | 0.365 | 0.338 | 0.644 | 1 | 0.354 | 0.775 | 0.461 | 0.872 | 0.821 | 0.684 | 0.656 | 0.571 | 0.649 | 0.726 | 0.572 | 0.841 | 0.758 |
| Li | 0.419 | 0.451 | 0.431 | 0.116 | 0.120 | 0.059 | 0.088 | 0.350 | 0.354 | 1 | 0.385 | 0.223 | 0.389 | 0.376 | 0.299 | 0.425 | 0.162 | 0.271 | 0.324 | 0.213 | 0.449 | 0.294 |
| Be | 0.803 | 0.805 | 0.795 | 0.395 | 0.419 | 0.328 | 0.301 | 0.560 | 0.775 | 0.385 | 1 | 0.382 | 0.790 | 0.889 | 0.753 | 0.741 | 0.654 | 0.743 | 0.890 | 0.493 | 0.866 | 0.908 |
| B | 0.551 | 0.470 | 0.513 | 0.159 | 0.217 | 0.088 | 0.089 | 0.571 | 0.461 | 0.223 | 0.382 | 1 | 0.514 | 0.387 | 0.335 | 0.351 | 0.232 | 0.262 | 0.342 | 0.292 | 0.477 | 0.371 |
| F | 0.940 | 0.834 | 0.942 | 0.364 | 0.399 | 0.270 | 0.237 | 0.803 | 0.872 | 0.389 | 0.790 | 0.514 | 1 | 0.792 | 0.602 | 0.608 | 0.471 | 0.566 | 0.700 | 0.586 | 0.904 | 0.721 |
| Sc | 0.804 | 0.828 | 0.803 | 0.503 | 0.469 | 0.371 | 0.400 | 0.579 | 0.821 | 0.376 | 0.889 | 0.387 | 0.792 | 1 | 0.824 | 0.772 | 0.648 | 0.712 | 0.864 | 0.505 | 0.877 | 0.886 |
| V | 0.647 | 0.696 | 0.597 | 0.438 | 0.435 | 0.313 | 0.331 | 0.473 | 0.684 | 0.299 | 0.753 | 0.335 | 0.602 | 0.824 | 1 | 0.846 | 0.691 | 0.725 | 0.883 | 0.413 | 0.677 | 0.804 |
| Cr | 0.669 | 0.675 | 0.597 | 0.403 | 0.396 | 0.269 | 0.320 | 0.535 | 0.656 | 0.425 | 0.741 | 0.351 | 0.608 | 0.772 | 0.846 | 1 | 0.648 | 0.768 | 0.799 | 0.420 | 0.700 | 0.770 |
| Co | 0.481 | 0.470 | 0.440 | 0.508 | 0.459 | 0.428 | 0.408 | 0.341 | 0.571 | 0.162 | 0.654 | 0.232 | 0.471 | 0.648 | 0.691 | 0.648 | 1 | 0.881 | 0.728 | 0.349 | 0.524 | 0.745 |
| Ni | 0.572 | 0.555 | 0.531 | 0.508 | 0.457 | 0.401 | 0.407 | 0.416 | 0.649 | 0.271 | 0.743 | 0.262 | 0.566 | 0.712 | 0.725 | 0.768 | 0.881 | 1 | 0.767 | 0.373 | 0.617 | 0.776 |
| Cu | 0.734 | 0.774 | 0.688 | 0.418 | 0.437 | 0.337 | 0.320 | 0.531 | 0.726 | 0.324 | 0.890 | 0.342 | 0.700 | 0.864 | 0.883 | 0.799 | 0.728 | 0.767 | 1 | 0.475 | 0.784 | 0.877 |
| Zn | 0.606 | 0.544 | 0.590 | 0.269 | 0.286 | 0.207 | 0.185 | 0.480 | 0.572 | 0.213 | 0.493 | 0.292 | 0.586 | 0.505 | 0.413 | 0.420 | 0.349 | 0.373 | 0.475 | 1 | 0.593 | 0.485 |
| Ga | 0.932 | 0.903 | 0.944 | 0.371 | 0.398 | 0.276 | 0.267 | 0.716 | 0.841 | 0.449 | 0.866 | 0.477 | 0.904 | 0.877 | 0.677 | 0.700 | 0.524 | 0.617 | 0.784 | 0.593 | 1 | 0.811 |
| Ge | 0.734 | 0.714 | 0.709 | 0.502 | 0.512 | 0.422 | 0.406 | 0.515 | 0.758 | 0.294 | 0.908 | 0.371 | 0.721 | 0.886 | 0.804 | 0.770 | 0.745 | 0.776 | 0.877 | 0.485 | 0.811 | 1 |
| SiO2 | TiO2 | Fe2O3 | MgO | CaO | MnO | K2O | P2O5 | Li | Be | B | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | 1 | 0.386 | 0.150 | 0.270 | 0.074 | 0.099 | 0.668 | 0.263 | −0.173 | −0.162 | 0.102 | −0.183 | −0.217 | 0.253 | 0.398 | 0.192 | 0.154 | 0.204 | −0.030 | −0.328 | −0.007 |
| TiO2 | 0.386 | 1 | 0.147 | 0.148 | 0.107 | 0.152 | 0.029 | 0.398 | −0.020 | −0.154 | −0.224 | −0.457 | −0.094 | 0.286 | 0.172 | 0.017 | −0.028 | 0.223 | −0.248 | −0.365 | −0.173 |
| Fe2O3 | 0.150 | 0.147 | 1 | 0.885 | 0.913 | 0.930 | 0.123 | 0.676 | −0.295 | −0.022 | −0.252 | −0.229 | 0.236 | 0.379 | 0.258 | 0.522 | 0.452 | 0.228 | −0.061 | −0.299 | 0.386 |
| MgO | 0.270 | 0.148 | 0.885 | 1 | 0.871 | 0.758 | 0.327 | 0.577 | −0.333 | −0.058 | −0.144 | −0.235 | 0.060 | 0.287 | 0.167 | 0.412 | 0.322 | 0.176 | −0.082 | −0.332 | 0.314 |
| CaO | 0.074 | 0.107 | 0.913 | 0.871 | 1 | 0.864 | 0.015 | 0.664 | −0.429 | 0.059 | −0.369 | −0.226 | 0.167 | 0.269 | 0.116 | 0.512 | 0.414 | 0.252 | −0.053 | −0.296 | 0.431 |
| MnO | 0.099 | 0.152 | 0.930 | 0.758 | 0.864 | 1 | −0.015 | 0.628 | −0.253 | −0.005 | −0.350 | −0.304 | 0.256 | 0.331 | 0.266 | 0.490 | 0.431 | 0.215 | −0.099 | −0.305 | 0.406 |
| K2O | 0.668 | 0.029 | 0.123 | 0.327 | 0.015 | −0.015 | 1 | 0.077 | 0.060 | −0.181 | 0.403 | 0.196 | −0.129 | 0.080 | 0.300 | 0.022 | 0.039 | 0.034 | 0.079 | −0.012 | −0.114 |
| P2O5 | 0.263 | 0.398 | 0.676 | 0.577 | 0.664 | 0.628 | 0.077 | 1 | −0.218 | −0.047 | −0.125 | −0.143 | 0.082 | 0.361 | 0.225 | 0.422 | 0.366 | 0.190 | −0.033 | −0.312 | 0.216 |
| Li | −0.173 | −0.020 | −0.295 | −0.333 | −0.429 | −0.253 | 0.060 | −0.218 | 1 | 0.207 | 0.138 | 0.282 | 0.176 | −0.067 | 0.356 | −0.250 | 0.049 | −0.056 | −0.003 | 0.395 | −0.148 |
| Be | −0.162 | −0.154 | −0.022 | −0.058 | 0.059 | −0.005 | −0.181 | −0.047 | 0.207 | 1 | −0.002 | 0.509 | 0.658 | 0.240 | 0.317 | 0.449 | 0.545 | 0.629 | 0.092 | 0.554 | 0.709 |
| B | 0.102 | −0.224 | −0.252 | −0.144 | −0.369 | −0.350 | 0.403 | −0.125 | 0.138 | −0.002 | 1 | 0.433 | 0.013 | −0.130 | 0.005 | −0.116 | −0.117 | −0.225 | 0.111 | 0.289 | −0.062 |
| F | −0.183 | −0.457 | −0.229 | −0.235 | −0.226 | −0.304 | 0.196 | −0.143 | 0.282 | 0.509 | 0.433 | 1 | 0.512 | −0.035 | 0.098 | 0.076 | 0.199 | 0.177 | 0.420 | 0.815 | 0.285 |
| Sc | −0.217 | −0.094 | 0.236 | 0.060 | 0.167 | 0.256 | −0.129 | 0.082 | 0.176 | 0.658 | 0.013 | 0.512 | 1 | 0.480 | 0.412 | 0.434 | 0.464 | 0.528 | 0.125 | 0.590 | 0.633 |
| V | 0.253 | 0.286 | 0.379 | 0.287 | 0.269 | 0.331 | 0.080 | 0.361 | −0.067 | 0.240 | −0.130 | −0.035 | 0.480 | 1 | 0.645 | 0.545 | 0.511 | 0.641 | −0.132 | −0.119 | 0.396 |
| Cr | 0.398 | 0.172 | 0.258 | 0.167 | 0.116 | 0.266 | 0.300 | 0.225 | 0.356 | 0.317 | 0.005 | 0.098 | 0.412 | 0.645 | 1 | 0.473 | 0.627 | 0.460 | −0.016 | 0.135 | 0.390 |
| Co | 0.192 | 0.017 | 0.522 | 0.412 | 0.512 | 0.490 | 0.022 | 0.422 | −0.250 | 0.449 | −0.116 | 0.076 | 0.434 | 0.545 | 0.473 | 1 | 0.871 | 0.639 | 0.055 | 0.042 | 0.670 |
| Ni | 0.154 | −0.028 | 0.452 | 0.322 | 0.414 | 0.431 | 0.039 | 0.366 | 0.049 | 0.545 | −0.117 | 0.199 | 0.464 | 0.511 | 0.627 | 0.871 | 1 | 0.604 | 0.024 | 0.164 | 0.625 |
| Cu | 0.204 | 0.223 | 0.228 | 0.176 | 0.252 | 0.215 | 0.034 | 0.190 | −0.056 | 0.629 | −0.225 | 0.177 | 0.528 | 0.641 | 0.460 | 0.639 | 0.604 | 1 | −0.029 | 0.145 | 0.556 |
| Zn | −0.030 | −0.248 | −0.061 | −0.082 | −0.053 | −0.099 | 0.079 | −0.033 | −0.003 | 0.092 | 0.111 | 0.420 | 0.125 | −0.132 | −0.016 | 0.055 | 0.024 | −0.029 | 1 | 0.366 | 0.046 |
| Ga | −0.328 | −0.365 | −0.299 | −0.332 | −0.296 | −0.305 | −0.012 | −0.312 | 0.395 | 0.554 | 0.289 | 0.815 | 0.590 | −0.119 | 0.135 | 0.042 | 0.164 | 0.145 | 0.366 | 1 | 0.318 |
| Ge | −0.007 | −0.173 | 0.386 | 0.314 | 0.431 | 0.406 | −0.114 | 0.216 | −0.148 | 0.709 | −0.062 | 0.285 | 0.633 | 0.396 | 0.390 | 0.670 | 0.625 | 0.556 | 0.046 | 0.318 | 1 |
| SiO2 | TiO2 | Al2O3 | Fe2O3 | MgO | CaO | MnO | K2O | P2O5 | Li | Be | B | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | 1 | 0.625 | 0.891 | −0.635 | −0.512 | −0.687 | −0.649 | 0.737 | 0.241 | 0.325 | 0.041 | 0.486 | 0.786 | −0.026 | −0.303 | −0.137 | −0.495 | −0.418 | −0.233 | 0.306 | 0.709 | −0.382 |
| TiO2 | 0.625 | 1 | 0.617 | −0.593 | −0.559 | −0.627 | −0.555 | 0.292 | 0.285 | 0.422 | 0.168 | 0.264 | 0.429 | 0.242 | 0.008 | −0.021 | −0.431 | −0.374 | 0.096 | 0.148 | 0.639 | −0.331 |
| Al2O3 | 0.891 | 0.617 | 1 | −0.537 | −0.499 | −0.551 | −0.535 | 0.538 | 0.329 | 0.369 | 0.157 | 0.387 | 0.822 | 0.148 | −0.370 | −0.308 | −0.529 | −0.444 | −0.290 | 0.291 | 0.832 | −0.313 |
| Fe2O3 | −0.635 | −0.593 | −0.537 | 1 | 0.789 | 0.848 | 0.880 | −0.306 | 0.043 | −0.333 | −0.393 | −0.289 | −0.343 | 0.087 | 0.032 | −0.055 | 0.350 | 0.286 | −0.199 | −0.114 | −0.511 | 0.104 |
| MgO | −0.512 | −0.559 | −0.499 | 0.789 | 1 | 0.772 | 0.579 | −0.046 | −0.104 | −0.343 | −0.343 | −0.095 | −0.251 | −0.147 | −0.021 | −0.122 | 0.220 | 0.124 | −0.178 | −0.091 | −0.440 | 0.083 |
| CaO | −0.687 | −0.627 | −0.551 | 0.848 | 0.772 | 1 | 0.773 | −0.429 | 0.029 | −0.498 | −0.190 | −0.435 | −0.333 | −0.005 | −0.057 | −0.205 | 0.375 | 0.268 | −0.093 | −0.094 | −0.483 | 0.249 |
| MnO | −0.649 | −0.555 | −0.535 | 0.880 | 0.579 | 0.773 | 1 | −0.449 | −0.014 | −0.255 | −0.251 | −0.390 | −0.435 | 0.225 | 0.062 | 0.045 | 0.367 | 0.325 | −0.097 | −0.136 | −0.447 | 0.257 |
| K2O | 0.737 | 0.292 | 0.538 | −0.306 | −0.046 | −0.429 | −0.449 | 1 | 0.123 | 0.247 | −0.301 | 0.549 | 0.651 | −0.278 | −0.315 | −0.052 | −0.437 | −0.376 | −0.339 | 0.193 | 0.369 | −0.542 |
| P2O5 | 0.241 | 0.285 | 0.329 | 0.043 | −0.104 | 0.029 | −0.014 | 0.123 | 1 | 0.063 | −0.282 | 0.193 | 0.475 | −0.077 | −0.250 | −0.314 | −0.199 | −0.179 | −0.441 | 0.164 | 0.140 | −0.408 |
| Li | 0.325 | 0.422 | 0.369 | −0.333 | −0.343 | −0.498 | −0.255 | 0.247 | 0.063 | 1 | 0.178 | 0.142 | 0.230 | 0.121 | −0.048 | 0.360 | −0.404 | −0.072 | −0.065 | −0.033 | 0.438 | −0.287 |
| Be | 0.041 | 0.168 | 0.157 | −0.393 | −0.343 | −0.190 | −0.251 | −0.301 | −0.282 | 0.178 | 1 | −0.186 | 0.005 | 0.277 | 0.004 | 0.015 | 0.093 | 0.176 | 0.427 | −0.206 | 0.201 | 0.449 |
| B | 0.486 | 0.264 | 0.387 | −0.289 | −0.095 | −0.435 | −0.390 | 0.549 | 0.193 | 0.142 | −0.186 | 1 | 0.383 | −0.209 | −0.153 | −0.066 | −0.292 | −0.334 | −0.311 | 0.059 | 0.242 | −0.249 |
| F | 0.786 | 0.429 | 0.822 | −0.343 | −0.251 | −0.333 | −0.435 | 0.651 | 0.475 | 0.230 | 0.005 | 0.383 | 1 | −0.060 | −0.483 | −0.381 | −0.506 | −0.408 | −0.375 | 0.253 | 0.595 | −0.413 |
| Sc | −0.026 | 0.242 | 0.148 | 0.087 | −0.147 | −0.005 | 0.225 | −0.278 | −0.077 | 0.121 | 0.277 | −0.209 | −0.060 | 1 | 0.316 | 0.121 | 0.030 | −0.018 | 0.220 | −0.209 | 0.202 | 0.243 |
| V | −0.303 | 0.008 | −0.370 | 0.032 | −0.021 | −0.057 | 0.062 | −0.315 | −0.250 | −0.048 | 0.004 | −0.153 | −0.483 | 0.316 | 1 | 0.595 | 0.365 | 0.301 | 0.619 | −0.247 | −0.383 | 0.249 |
| Cr | −0.137 | −0.021 | −0.308 | −0.055 | −0.122 | −0.205 | 0.045 | −0.052 | −0.314 | 0.360 | 0.015 | −0.066 | −0.381 | 0.121 | 0.595 | 1 | 0.268 | 0.448 | 0.333 | −0.183 | −0.181 | 0.147 |
| Co | −0.495 | −0.431 | −0.529 | 0.350 | 0.220 | 0.375 | 0.367 | −0.437 | −0.199 | −0.404 | 0.093 | −0.292 | −0.506 | 0.030 | 0.365 | 0.268 | 1 | 0.812 | 0.404 | −0.175 | −0.506 | 0.451 |
| Ni | −0.418 | −0.374 | −0.444 | 0.286 | 0.124 | 0.268 | 0.325 | −0.376 | −0.179 | −0.072 | 0.176 | −0.334 | −0.408 | −0.018 | 0.301 | 0.448 | 0.812 | 1 | 0.317 | −0.263 | −0.423 | 0.314 |
| Cu | −0.233 | 0.096 | −0.290 | −0.199 | −0.178 | −0.093 | −0.097 | −0.339 | −0.441 | −0.065 | 0.427 | −0.311 | −0.375 | 0.220 | 0.619 | 0.333 | 0.404 | 0.317 | 1 | −0.214 | −0.196 | 0.341 |
| Zn | 0.306 | 0.148 | 0.291 | −0.114 | −0.091 | −0.094 | −0.136 | 0.193 | 0.164 | −0.033 | −0.206 | 0.059 | 0.253 | −0.209 | −0.247 | −0.183 | −0.175 | −0.263 | −0.214 | 1 | 0.219 | −0.253 |
| Ga | 0.709 | 0.639 | 0.832 | −0.511 | −0.440 | −0.483 | −0.447 | 0.369 | 0.140 | 0.438 | 0.201 | 0.242 | 0.595 | 0.202 | −0.383 | −0.181 | −0.506 | −0.423 | −0.196 | 0.219 | 1 | −0.180 |
| Ge | −0.382 | −0.331 | −0.313 | 0.104 | 0.083 | 0.249 | 0.257 | −0.542 | −0.408 | −0.287 | 0.449 | −0.249 | −0.413 | 0.243 | 0.249 | 0.147 | 0.451 | 0.314 | 0.341 | −0.253 | −0.180 | 1 |
| SiO2 | TiO2 | Al2O3 | Fe2O3 | MgO | CaO | MnO | K2O | P2O5 | Li | Be | B | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | 1 | −0.598 | −0.014 | −0.104 | 0.019 | 0.073 | −0.344 | 0.171 | 0.173 | 0.143 | −0.188 | −0.271 | 0.366 | 0.333 | 0.143 | 0.035 | 0.022 | 0.337 | −0.147 | 0.016 | 0.036 | −0.222 |
| TiO2 | −0.598 | 1 | −0.030 | −0.088 | 0.047 | −0.031 | 0.029 | −0.021 | −0.019 | −0.056 | 0.018 | 0.336 | −0.135 | −0.473 | −0.478 | −0.219 | −0.186 | −0.400 | 0.134 | 0.294 | −0.030 | 0.217 |
| Al2O3 | −0.014 | −0.030 | 1 | 0.795 | 0.834 | 0.783 | −0.737 | −0.633 | −0.545 | −0.553 | −0.480 | −0.754 | −0.197 | −0.034 | −0.111 | 0.323 | 0.227 | −0.285 | −0.266 | −0.768 | 0.028 | 0.257 |
| Fe2O3 | −0.104 | −0.088 | 0.795 | 1 | 0.715 | 0.408 | −0.464 | −0.688 | −0.519 | −0.462 | −0.271 | −0.642 | −0.380 | −0.069 | −0.157 | 0.207 | 0.084 | −0.221 | −0.222 | −0.654 | 0.042 | 0.047 |
| MgO | 0.019 | 0.047 | 0.834 | 0.715 | 1 | 0.644 | −0.795 | −0.509 | −0.638 | −0.307 | −0.592 | −0.578 | −0.125 | −0.060 | −0.192 | 0.381 | 0.264 | −0.107 | −0.183 | −0.598 | 0.221 | 0.248 |
| CaO | 0.073 | −0.031 | 0.783 | 0.408 | 0.644 | 1 | −0.738 | −0.485 | −0.315 | −0.374 | −0.509 | −0.702 | 0.073 | 0.030 | 0.057 | 0.299 | 0.261 | −0.173 | −0.248 | −0.577 | 0.147 | 0.226 |
| MnO | −0.344 | 0.029 | −0.737 | −0.464 | −0.795 | −0.738 | 1 | 0.351 | 0.419 | 0.105 | 0.603 | 0.649 | −0.222 | −0.155 | 0.069 | −0.411 | −0.324 | −0.036 | 0.209 | 0.470 | −0.358 | −0.218 |
| K2O | 0.171 | −0.021 | −0.633 | −0.688 | −0.509 | −0.485 | 0.351 | 1 | 0.360 | 0.301 | 0.342 | 0.567 | 0.082 | 0.048 | 0.017 | −0.157 | −0.081 | 0.075 | 0.191 | 0.395 | −0.123 | −0.041 |
| P2O5 | 0.173 | −0.019 | −0.545 | −0.519 | −0.638 | −0.315 | 0.419 | 0.360 | 1 | 0.247 | 0.169 | 0.213 | 0.083 | 0.008 | 0.354 | −0.386 | −0.072 | 0.049 | −0.032 | 0.410 | −0.214 | −0.300 |
| Li | 0.143 | −0.056 | −0.553 | −0.462 | −0.307 | −0.374 | 0.105 | 0.301 | 0.247 | 1 | 0.083 | 0.324 | 0.540 | 0.354 | 0.299 | 0.257 | 0.304 | 0.672 | −0.036 | 0.365 | 0.584 | −0.054 |
| Be | −0.188 | 0.018 | −0.480 | −0.271 | −0.592 | −0.509 | 0.603 | 0.342 | 0.169 | 0.083 | 1 | 0.305 | −0.244 | −0.098 | −0.052 | −0.263 | −0.327 | −0.144 | 0.074 | 0.242 | −0.153 | −0.123 |
| B | −0.271 | 0.336 | −0.754 | −0.642 | −0.578 | −0.702 | 0.649 | 0.567 | 0.213 | 0.324 | 0.305 | 1 | 0.006 | −0.224 | −0.219 | −0.337 | −0.263 | 0.063 | 0.313 | 0.636 | −0.135 | −0.048 |
| F | 0.366 | −0.135 | −0.197 | −0.380 | −0.125 | 0.073 | −0.222 | 0.082 | 0.083 | 0.540 | −0.244 | 0.006 | 1 | 0.565 | 0.338 | 0.247 | 0.177 | 0.553 | −0.142 | 0.189 | 0.460 | 0.103 |
| Sc | 0.333 | −0.473 | −0.034 | −0.069 | −0.060 | 0.030 | −0.155 | 0.048 | 0.008 | 0.354 | −0.098 | −0.224 | 0.565 | 1 | 0.669 | 0.450 | 0.387 | 0.673 | −0.181 | −0.263 | 0.359 | 0.100 |
| V | 0.143 | −0.478 | −0.111 | −0.157 | −0.192 | 0.057 | 0.069 | 0.017 | 0.354 | 0.299 | −0.052 | −0.219 | 0.338 | 0.669 | 1 | 0.339 | 0.494 | 0.406 | −0.153 | −0.158 | 0.223 | 0.036 |
| Cr | 0.035 | −0.219 | 0.323 | 0.207 | 0.381 | 0.299 | −0.411 | −0.157 | −0.386 | 0.257 | −0.263 | −0.337 | 0.247 | 0.450 | 0.339 | 1 | 0.812 | 0.389 | −0.162 | −0.458 | 0.430 | 0.367 |
| Co | 0.022 | −0.186 | 0.227 | 0.084 | 0.264 | 0.261 | −0.324 | −0.081 | −0.072 | 0.304 | −0.327 | −0.263 | 0.177 | 0.387 | 0.494 | 0.812 | 1 | 0.313 | −0.250 | −0.390 | 0.307 | 0.270 |
| Ni | 0.337 | −0.400 | −0.285 | −0.221 | −0.107 | −0.173 | −0.036 | 0.075 | 0.049 | 0.672 | −0.144 | 0.063 | 0.553 | 0.673 | 0.406 | 0.389 | 0.313 | 1 | −0.047 | 0.075 | 0.460 | 0.006 |
| Cu | −0.147 | 0.134 | −0.266 | −0.222 | −0.183 | −0.248 | 0.209 | 0.191 | −0.032 | −0.036 | 0.074 | 0.313 | −0.142 | −0.181 | −0.153 | −0.162 | −0.250 | −0.047 | 1 | 0.237 | −0.198 | −0.063 |
| Zn | 0.016 | 0.294 | −0.768 | −0.654 | −0.598 | −0.577 | 0.470 | 0.395 | 0.410 | 0.365 | 0.242 | 0.636 | 0.189 | −0.263 | −0.158 | −0.458 | −0.390 | 0.075 | 0.237 | 1 | 0.020 | −0.207 |
| Ga | 0.036 | −0.030 | 0.028 | 0.042 | 0.221 | 0.147 | −0.358 | −0.123 | −0.214 | 0.584 | −0.153 | −0.135 | 0.460 | 0.359 | 0.223 | 0.430 | 0.307 | 0.460 | −0.198 | 0.020 | 1 | −0.047 |
| Ge | −0.222 | 0.217 | 0.257 | 0.047 | 0.248 | 0.226 | −0.218 | −0.041 | −0.300 | −0.054 | −0.123 | −0.048 | 0.103 | 0.100 | 0.036 | 0.367 | 0.270 | 0.006 | −0.063 | −0.207 | −0.047 | 1 |
| Al2O3 | SiO2 | CaO | Fe2O3 | K2O | MgO | MnO | Na2O | P2O5 | TiO2 | Li | Be | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al2O3 | 1 | 0.614 | 0.258 | 0.411 | 0.817 | 0.187 | 0.284 | 0.924 | 0.422 | 0.866 | 0.515 | 0.908 | 0.820 | 0.806 | 0.811 | 0.854 | 0.709 | 0.752 | 0.713 | 0.746 | 0.922 | 0.842 |
| SiO2 | 0.614 | 1 | 0.097 | 0.159 | 0.729 | 0.060 | 0.099 | 0.693 | 0.117 | 0.581 | 0.708 | 0.503 | 0.342 | 0.543 | 0.512 | 0.461 | 0.352 | 0.416 | 0.389 | 0.348 | 0.565 | 0.514 |
| CaO | 0.258 | 0.097 | 1 | 0.724 | 0.174 | 0.825 | 0.681 | 0.324 | 0.181 | 0.221 | 0.095 | 0.289 | 0.341 | 0.261 | 0.286 | 0.395 | 0.424 | 0.387 | 0.333 | 0.355 | 0.292 | 0.295 |
| Fe2O3 | 0.411 | 0.159 | 0.724 | 1 | 0.272 | 0.739 | 0.823 | 0.469 | 0.204 | 0.387 | 0.172 | 0.448 | 0.458 | 0.409 | 0.434 | 0.565 | 0.480 | 0.547 | 0.469 | 0.451 | 0.434 | 0.435 |
| K2O | 0.817 | 0.729 | 0.174 | 0.272 | 1 | 0.119 | 0.182 | 0.794 | 0.307 | 0.804 | 0.622 | 0.752 | 0.620 | 0.726 | 0.661 | 0.676 | 0.534 | 0.585 | 0.546 | 0.571 | 0.772 | 0.694 |
| MgO | 0.187 | 0.060 | 0.825 | 0.739 | 0.119 | 1 | 0.634 | 0.238 | 0.145 | 0.165 | 0.063 | 0.205 | 0.247 | 0.182 | 0.194 | 0.289 | 0.287 | 0.293 | 0.235 | 0.228 | 0.201 | 0.199 |
| MnO | 0.284 | 0.099 | 0.681 | 0.823 | 0.182 | 0.634 | 1 | 0.328 | 0.151 | 0.248 | 0.111 | 0.320 | 0.367 | 0.266 | 0.291 | 0.408 | 0.318 | 0.349 | 0.333 | 0.363 | 0.307 | 0.318 |
| Na2O | 0.924 | 0.693 | 0.324 | 0.469 | 0.794 | 0.238 | 0.328 | 1 | 0.353 | 0.785 | 0.606 | 0.824 | 0.739 | 0.754 | 0.765 | 0.837 | 0.706 | 0.779 | 0.684 | 0.705 | 0.859 | 0.794 |
| P2O5 | 0.422 | 0.117 | 0.181 | 0.204 | 0.307 | 0.145 | 0.151 | 0.353 | 1 | 0.320 | 0.126 | 0.414 | 0.590 | 0.326 | 0.313 | 0.388 | 0.454 | 0.396 | 0.300 | 0.422 | 0.413 | 0.381 |
| TiO2 | 0.866 | 0.581 | 0.221 | 0.387 | 0.804 | 0.165 | 0.248 | 0.785 | 0.320 | 1 | 0.513 | 0.894 | 0.695 | 0.907 | 0.884 | 0.862 | 0.668 | 0.736 | 0.776 | 0.718 | 0.891 | 0.853 |
| Li | 0.515 | 0.708 | 0.095 | 0.172 | 0.622 | 0.063 | 0.111 | 0.606 | 0.126 | 0.513 | 1 | 0.410 | 0.351 | 0.425 | 0.464 | 0.450 | 0.352 | 0.402 | 0.381 | 0.363 | 0.476 | 0.436 |
| Be | 0.908 | 0.503 | 0.289 | 0.448 | 0.752 | 0.205 | 0.320 | 0.824 | 0.414 | 0.894 | 0.410 | 1 | 0.785 | 0.890 | 0.850 | 0.916 | 0.734 | 0.791 | 0.816 | 0.830 | 0.952 | 0.924 |
| F | 0.820 | 0.342 | 0.341 | 0.458 | 0.620 | 0.247 | 0.367 | 0.739 | 0.590 | 0.695 | 0.351 | 0.785 | 1 | 0.623 | 0.650 | 0.784 | 0.703 | 0.689 | 0.626 | 0.781 | 0.758 | 0.728 |
| Sc | 0.806 | 0.543 | 0.261 | 0.409 | 0.726 | 0.182 | 0.266 | 0.754 | 0.326 | 0.907 | 0.425 | 0.890 | 0.623 | 1 | 0.923 | 0.860 | 0.728 | 0.765 | 0.820 | 0.696 | 0.915 | 0.886 |
| V | 0.811 | 0.512 | 0.286 | 0.434 | 0.661 | 0.194 | 0.291 | 0.765 | 0.313 | 0.884 | 0.464 | 0.850 | 0.650 | 0.923 | 1 | 0.913 | 0.778 | 0.795 | 0.875 | 0.780 | 0.922 | 0.896 |
| Cr | 0.854 | 0.461 | 0.395 | 0.565 | 0.676 | 0.289 | 0.408 | 0.837 | 0.388 | 0.862 | 0.450 | 0.916 | 0.784 | 0.860 | 0.913 | 1 | 0.819 | 0.872 | 0.899 | 0.891 | 0.922 | 0.910 |
| Co | 0.709 | 0.352 | 0.424 | 0.480 | 0.534 | 0.287 | 0.318 | 0.706 | 0.454 | 0.668 | 0.352 | 0.734 | 0.703 | 0.728 | 0.778 | 0.819 | 1 | 0.847 | 0.770 | 0.757 | 0.776 | 0.725 |
| Ni | 0.752 | 0.416 | 0.387 | 0.547 | 0.585 | 0.293 | 0.349 | 0.779 | 0.396 | 0.736 | 0.402 | 0.791 | 0.689 | 0.765 | 0.795 | 0.872 | 0.847 | 1 | 0.780 | 0.748 | 0.810 | 0.798 |
| Cu | 0.713 | 0.389 | 0.333 | 0.469 | 0.546 | 0.235 | 0.333 | 0.684 | 0.300 | 0.776 | 0.381 | 0.816 | 0.626 | 0.820 | 0.875 | 0.899 | 0.770 | 0.780 | 1 | 0.831 | 0.832 | 0.844 |
| Zn | 0.746 | 0.348 | 0.355 | 0.451 | 0.571 | 0.228 | 0.363 | 0.705 | 0.422 | 0.718 | 0.363 | 0.830 | 0.781 | 0.696 | 0.780 | 0.891 | 0.757 | 0.748 | 0.831 | 1 | 0.824 | 0.842 |
| Ga | 0.922 | 0.565 | 0.292 | 0.434 | 0.772 | 0.201 | 0.307 | 0.859 | 0.413 | 0.891 | 0.476 | 0.952 | 0.758 | 0.915 | 0.922 | 0.922 | 0.776 | 0.810 | 0.832 | 0.824 | 1 | 0.964 |
| Ge | 0.842 | 0.514 | 0.295 | 0.435 | 0.694 | 0.199 | 0.318 | 0.794 | 0.381 | 0.853 | 0.436 | 0.924 | 0.728 | 0.886 | 0.896 | 0.910 | 0.725 | 0.798 | 0.844 | 0.842 | 0.964 | 1 |
| SiO2 | CaO | Fe2O3 | K2O | MgO | MnO | Na2O | P2O5 | TiO2 | Li | Be | F | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | Ge | As | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | 1 | −0.301 | −0.349 | 0.595 | −0.364 | −0.360 | 0.508 | −0.613 | 0.167 | 0.587 | −0.210 | −0.471 | 0.043 | −0.027 | −0.237 | −0.258 | −0.159 | −0.172 | −0.376 | −0.069 | −0.069 | −0.411 |
| CaO | −0.301 | 1 | 0.875 | −0.182 | 0.942 | 0.854 | 0.471 | 0.235 | −0.011 | −0.242 | 0.020 | 0.186 | 0.024 | 0.088 | 0.311 | 0.383 | 0.308 | 0.247 | 0.293 | 0.015 | 0.086 | 0.127 |
| Fe2O3 | −0.349 | 0.875 | 1 | −0.247 | 0.927 | 0.923 | 0.398 | 0.094 | 0.115 | −0.208 | 0.031 | 0.122 | 0.046 | 0.096 | 0.315 | 0.250 | 0.316 | 0.238 | 0.198 | −0.017 | 0.069 | 0.156 |
| K2O | 0.595 | −0.182 | −0.247 | 1 | −0.217 | −0.242 | 0.198 | −0.139 | 0.374 | 0.653 | 0.346 | 0.119 | 0.404 | 0.262 | 0.239 | 0.102 | 0.158 | 0.133 | 0.148 | 0.347 | 0.298 | 0.201 |
| MgO | −0.364 | 0.942 | 0.927 | −0.217 | 1 | 0.853 | 0.435 | 0.253 | 0.017 | −0.244 | 0.027 | 0.188 | 0.022 | 0.061 | 0.314 | 0.327 | 0.321 | 0.227 | 0.211 | 0.001 | 0.055 | 0.151 |
| MnO | −0.360 | 0.854 | 0.923 | −0.242 | 0.853 | 1 | 0.356 | 0.112 | 0.011 | −0.217 | 0.035 | 0.187 | −0.015 | 0.044 | 0.282 | 0.172 | 0.201 | 0.203 | 0.261 | −0.011 | 0.085 | 0.148 |
| Na2O | 0.508 | 0.471 | 0.398 | 0.198 | 0.435 | 0.356 | 1 | −0.185 | −0.087 | 0.260 | −0.420 | −0.349 | −0.247 | −0.242 | −0.152 | −0.078 | 0.020 | −0.172 | −0.239 | −0.313 | −0.255 | −0.452 |
| P2O5 | −0.613 | 0.235 | 0.094 | −0.139 | 0.253 | 0.112 | −0.185 | 1 | −0.186 | −0.200 | 0.287 | 0.593 | 0.127 | 0.098 | 0.274 | 0.453 | 0.325 | 0.152 | 0.428 | 0.254 | 0.249 | 0.351 |
| TiO2 | 0.167 | −0.011 | 0.115 | 0.374 | 0.017 | 0.011 | −0.087 | −0.186 | 1 | 0.173 | 0.276 | −0.082 | 0.472 | 0.449 | 0.324 | 0.116 | 0.195 | 0.389 | 0.184 | 0.215 | 0.307 | 0.365 |
| Li | 0.587 | −0.242 | −0.208 | 0.653 | −0.244 | −0.217 | 0.260 | −0.200 | 0.173 | 1 | 0.240 | 0.202 | 0.362 | 0.408 | 0.344 | 0.254 | 0.332 | 0.295 | 0.194 | 0.404 | 0.338 | 0.082 |
| Be | −0.210 | 0.020 | 0.031 | 0.346 | 0.027 | 0.035 | −0.420 | 0.287 | 0.276 | 0.240 | 1 | 0.684 | 0.869 | 0.765 | 0.848 | 0.656 | 0.723 | 0.773 | 0.730 | 0.918 | 0.880 | 0.771 |
| F | −0.471 | 0.186 | 0.122 | 0.119 | 0.188 | 0.187 | −0.349 | 0.593 | −0.082 | 0.202 | 0.684 | 1 | 0.477 | 0.483 | 0.686 | 0.644 | 0.604 | 0.508 | 0.706 | 0.644 | 0.606 | 0.591 |
| Sc | 0.043 | 0.024 | 0.046 | 0.404 | 0.022 | −0.015 | −0.247 | 0.127 | 0.472 | 0.362 | 0.869 | 0.477 | 1 | 0.909 | 0.820 | 0.684 | 0.719 | 0.794 | 0.575 | 0.902 | 0.858 | 0.641 |
| V | −0.027 | 0.088 | 0.096 | 0.262 | 0.061 | 0.044 | −0.242 | 0.098 | 0.449 | 0.408 | 0.765 | 0.483 | 0.909 | 1 | 0.874 | 0.739 | 0.744 | 0.857 | 0.679 | 0.889 | 0.852 | 0.613 |
| Cr | −0.237 | 0.311 | 0.315 | 0.239 | 0.314 | 0.282 | −0.152 | 0.274 | 0.324 | 0.344 | 0.848 | 0.686 | 0.820 | 0.874 | 1 | 0.794 | 0.853 | 0.897 | 0.840 | 0.865 | 0.857 | 0.751 |
| Co | −0.258 | 0.383 | 0.250 | 0.102 | 0.327 | 0.172 | −0.078 | 0.453 | 0.116 | 0.254 | 0.656 | 0.644 | 0.684 | 0.739 | 0.794 | 1 | 0.840 | 0.750 | 0.710 | 0.729 | 0.652 | 0.513 |
| Ni | −0.159 | 0.308 | 0.316 | 0.158 | 0.321 | 0.201 | 0.020 | 0.325 | 0.195 | 0.332 | 0.723 | 0.604 | 0.719 | 0.744 | 0.853 | 0.840 | 1 | 0.751 | 0.676 | 0.758 | 0.743 | 0.572 |
| Cu | −0.172 | 0.247 | 0.238 | 0.133 | 0.227 | 0.203 | −0.172 | 0.152 | 0.389 | 0.295 | 0.773 | 0.508 | 0.794 | 0.857 | 0.897 | 0.750 | 0.751 | 1 | 0.799 | 0.796 | 0.814 | 0.678 |
| Zn | −0.376 | 0.293 | 0.198 | 0.148 | 0.211 | 0.261 | −0.239 | 0.428 | 0.184 | 0.194 | 0.730 | 0.706 | 0.575 | 0.679 | 0.840 | 0.710 | 0.676 | 0.799 | 1 | 0.727 | 0.768 | 0.735 |
| Ga | −0.069 | 0.015 | −0.017 | 0.347 | 0.001 | −0.011 | −0.313 | 0.254 | 0.215 | 0.404 | 0.918 | 0.644 | 0.902 | 0.889 | 0.865 | 0.729 | 0.758 | 0.796 | 0.727 | 1 | 0.946 | 0.653 |
| Ge | −0.069 | 0.086 | 0.069 | 0.298 | 0.055 | 0.085 | −0.255 | 0.249 | 0.307 | 0.338 | 0.880 | 0.606 | 0.858 | 0.852 | 0.857 | 0.652 | 0.743 | 0.814 | 0.768 | 0.946 | 1 | 0.685 |
| As | −0.411 | 0.127 | 0.156 | 0.201 | 0.151 | 0.148 | −0.452 | 0.351 | 0.365 | 0.082 | 0.771 | 0.591 | 0.641 | 0.613 | 0.751 | 0.513 | 0.572 | 0.678 | 0.735 | 0.653 | 0.685 | 1 |
| Al2O3 | SiO2 | CaO | Fe2O3 | K2O | MgO | MnO | Na2O | P2O5 | TiO2 | Li | Be | F | Cl | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al2O3 | 1 | 0.544 | −0.434 | −0.289 | 0.519 | −0.341 | −0.310 | 0.672 | 0.063 | 0.326 | 0.355 | 0.342 | 0.335 | −0.213 | −0.060 | −0.049 | −0.182 | −0.212 | −0.172 | −0.325 | −0.246 | 0.439 |
| SiO2 | 0.544 | 1 | −0.417 | −0.399 | 0.732 | −0.437 | −0.419 | 0.724 | −0.464 | 0.433 | 0.760 | 0.070 | −0.299 | 0.013 | 0.307 | 0.192 | −0.220 | −0.267 | −0.102 | −0.181 | −0.415 | 0.448 |
| CaO | −0.434 | −0.417 | 1 | 0.820 | −0.470 | 0.927 | 0.803 | −0.003 | 0.043 | −0.609 | −0.349 | −0.519 | 0.117 | −0.087 | −0.395 | −0.256 | 0.245 | 0.368 | 0.240 | 0.059 | 0.121 | −0.611 |
| Fe2O3 | −0.289 | −0.399 | 0.820 | 1 | −0.455 | 0.903 | 0.898 | 0.042 | −0.100 | −0.354 | −0.255 | −0.351 | 0.079 | −0.156 | −0.278 | −0.172 | 0.360 | 0.140 | 0.306 | 0.072 | −0.024 | −0.568 |
| K2O | 0.519 | 0.732 | −0.470 | −0.455 | 1 | −0.436 | −0.449 | 0.464 | −0.115 | 0.480 | 0.612 | 0.146 | −0.027 | 0.047 | 0.172 | −0.118 | −0.401 | −0.368 | −0.294 | −0.414 | −0.387 | 0.249 |
| MgO | −0.341 | −0.437 | 0.927 | 0.903 | −0.436 | 1 | 0.812 | 0.035 | 0.097 | −0.460 | −0.339 | −0.453 | 0.121 | −0.195 | −0.361 | −0.281 | 0.285 | 0.269 | 0.281 | 0.045 | −0.013 | −0.605 |
| MnO | −0.310 | −0.419 | 0.803 | 0.898 | −0.449 | 0.812 | 1 | −0.010 | −0.068 | −0.467 | −0.273 | −0.321 | 0.182 | −0.057 | −0.394 | −0.260 | 0.287 | 0.013 | 0.082 | 0.034 | 0.129 | −0.523 |
| Na2O | 0.672 | 0.724 | −0.003 | 0.042 | 0.464 | 0.035 | −0.010 | 1 | −0.154 | 0.040 | 0.612 | −0.096 | 0.080 | −0.144 | −0.171 | −0.123 | −0.022 | −0.076 | 0.116 | −0.286 | −0.275 | 0.123 |
| P2O5 | 0.063 | −0.464 | 0.043 | −0.100 | −0.115 | 0.097 | −0.068 | −0.154 | 1 | −0.370 | −0.328 | −0.109 | 0.592 | −0.048 | −0.373 | −0.457 | −0.314 | 0.254 | 0.028 | −0.343 | 0.113 | −0.171 |
| TiO2 | 0.326 | 0.433 | −0.609 | −0.354 | 0.480 | −0.460 | −0.467 | 0.040 | −0.370 | 1 | 0.349 | 0.320 | −0.199 | 0.009 | 0.552 | 0.427 | 0.019 | −0.352 | −0.182 | 0.069 | −0.320 | 0.248 |
| Li | 0.355 | 0.760 | −0.349 | −0.255 | 0.612 | −0.339 | −0.273 | 0.612 | −0.328 | 0.349 | 1 | −0.251 | −0.124 | 0.185 | 0.016 | 0.170 | −0.008 | −0.128 | −0.010 | −0.069 | −0.182 | 0.155 |
| Be | 0.342 | 0.070 | −0.519 | −0.351 | 0.146 | −0.453 | −0.321 | −0.096 | −0.109 | 0.320 | −0.251 | 1 | −0.046 | −0.267 | 0.226 | −0.146 | −0.110 | −0.446 | −0.306 | −0.015 | −0.047 | 0.333 |
| F | 0.335 | −0.299 | 0.117 | 0.079 | −0.027 | 0.121 | 0.182 | 0.080 | 0.592 | −0.199 | −0.124 | −0.046 | 1 | −0.005 | −0.628 | −0.495 | −0.091 | 0.068 | −0.107 | −0.339 | 0.252 | −0.353 |
| Cl | −0.213 | 0.013 | −0.087 | −0.156 | 0.047 | −0.195 | −0.057 | −0.144 | −0.048 | 0.009 | 0.185 | −0.267 | −0.005 | 1 | 0.037 | 0.001 | −0.275 | 0.129 | 0.131 | −0.081 | −0.066 | −0.128 |
| Sc | −0.060 | 0.307 | −0.395 | −0.278 | 0.172 | −0.361 | −0.394 | −0.171 | −0.373 | 0.552 | 0.016 | 0.226 | −0.628 | 0.037 | 1 | 0.611 | −0.072 | −0.093 | −0.075 | 0.249 | −0.503 | 0.409 |
| V | −0.049 | 0.192 | −0.256 | −0.172 | −0.118 | −0.281 | −0.260 | −0.123 | −0.457 | 0.427 | 0.170 | −0.146 | −0.495 | 0.001 | 0.611 | 1 | 0.384 | 0.138 | 0.070 | 0.498 | −0.042 | 0.456 |
| Cr | −0.182 | −0.220 | 0.245 | 0.360 | −0.401 | 0.285 | 0.287 | −0.022 | −0.314 | 0.019 | −0.008 | −0.110 | −0.091 | −0.275 | −0.072 | 0.384 | 1 | 0.145 | 0.308 | 0.578 | 0.415 | −0.207 |
| Co | −0.212 | −0.267 | 0.368 | 0.140 | −0.368 | 0.269 | 0.013 | −0.076 | 0.254 | −0.352 | −0.128 | −0.446 | 0.068 | 0.129 | −0.093 | 0.138 | 0.145 | 1 | 0.505 | 0.245 | 0.145 | −0.232 |
| Ni | −0.172 | −0.102 | 0.240 | 0.306 | −0.294 | 0.281 | 0.082 | 0.116 | 0.028 | −0.182 | −0.010 | −0.306 | −0.107 | 0.131 | −0.075 | 0.070 | 0.308 | 0.505 | 1 | 0.182 | −0.027 | −0.258 |
| Cu | −0.325 | −0.181 | 0.059 | 0.072 | −0.414 | 0.045 | 0.034 | −0.286 | −0.343 | 0.069 | −0.069 | −0.015 | −0.339 | −0.081 | 0.249 | 0.498 | 0.578 | 0.245 | 0.182 | 1 | 0.373 | 0.032 |
| Zn | −0.246 | −0.415 | 0.121 | −0.024 | −0.387 | −0.013 | 0.129 | −0.275 | 0.113 | −0.320 | −0.182 | −0.047 | 0.252 | −0.066 | −0.503 | −0.042 | 0.415 | 0.145 | −0.027 | 0.373 | 1 | −0.200 |
| Ga | 0.439 | 0.448 | −0.611 | −0.568 | 0.249 | −0.605 | −0.523 | 0.123 | −0.171 | 0.248 | 0.155 | 0.333 | −0.353 | −0.128 | 0.409 | 0.456 | −0.207 | −0.232 | −0.258 | 0.032 | −0.200 | 1 |
| Al2O3 | SiO2 | CaO | Fe2O3 | K2O | MgO | MnO | Na2O | P2O5 | TiO2 | Li | Be | F | Cl | Sc | V | Cr | Co | Ni | Cu | Zn | Ga | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al2O3 | 1 | −0.533 | −0.599 | 0.395 | −0.530 | −0.502 | 0.468 | −0.493 | 0.290 | 0.715 | −0.089 | −0.521 | 0.108 | 0.199 | 0.102 | −0.212 | −0.274 | −0.103 | −0.100 | −0.351 | 0.146 | 0.116 |
| SiO2 | −0.533 | 1 | 0.765 | −0.810 | 0.924 | 0.696 | −0.893 | −0.109 | −0.771 | −0.722 | −0.537 | −0.135 | −0.086 | −0.452 | −0.357 | −0.074 | 0.203 | 0.023 | −0.053 | 0.029 | −0.617 | −0.414 |
| CaO | −0.599 | 0.765 | 1 | −0.743 | 0.824 | 0.795 | −0.835 | −0.200 | −0.532 | −0.611 | −0.399 | −0.163 | −0.142 | −0.310 | −0.246 | 0.031 | −0.034 | 0.116 | −0.003 | −0.060 | −0.521 | −0.323 |
| Fe2O3 | 0.395 | −0.810 | −0.743 | 1 | −0.808 | −0.685 | 0.681 | 0.310 | 0.688 | 0.589 | 0.486 | 0.235 | 0.177 | 0.340 | 0.149 | −0.055 | −0.202 | −0.178 | −0.075 | 0.016 | 0.465 | 0.262 |
| K2O | −0.530 | 0.924 | 0.824 | −0.808 | 1 | 0.637 | −0.858 | −0.112 | −0.749 | −0.714 | −0.599 | −0.215 | −0.227 | −0.438 | −0.372 | −0.059 | 0.126 | 0.074 | −0.071 | −0.106 | −0.589 | −0.431 |
| MgO | −0.502 | 0.696 | 0.795 | −0.685 | 0.637 | 1 | −0.759 | −0.227 | −0.583 | −0.532 | −0.352 | −0.035 | −0.007 | −0.436 | −0.326 | −0.072 | −0.219 | −0.195 | −0.048 | 0.091 | −0.460 | −0.231 |
| MnO | 0.468 | −0.893 | −0.835 | 0.681 | −0.858 | −0.759 | 1 | 0.255 | 0.593 | 0.686 | 0.470 | 0.225 | 0.084 | 0.315 | 0.299 | 0.108 | 0.020 | 0.108 | 0.035 | 0.084 | 0.540 | 0.336 |
| Na2O | −0.493 | −0.109 | −0.200 | 0.310 | −0.112 | −0.227 | 0.255 | 1 | 0.078 | −0.159 | 0.299 | 0.669 | 0.057 | 0.023 | −0.042 | 0.009 | 0.330 | 0.111 | −0.083 | 0.268 | 0.202 | 0.120 |
| P2O5 | 0.290 | −0.771 | −0.532 | 0.688 | −0.749 | −0.583 | 0.593 | 0.078 | 1 | 0.501 | 0.716 | 0.163 | 0.184 | 0.679 | 0.612 | 0.313 | −0.043 | 0.060 | 0.359 | 0.133 | 0.556 | 0.473 |
| TiO2 | 0.715 | −0.722 | −0.611 | 0.589 | −0.714 | −0.532 | 0.686 | −0.159 | 0.501 | 1 | 0.046 | −0.116 | 0.247 | 0.079 | 0.168 | −0.086 | −0.189 | −0.103 | −0.014 | −0.113 | 0.157 | 0.072 |
| Li | −0.089 | −0.537 | −0.399 | 0.486 | −0.599 | −0.352 | 0.470 | 0.299 | 0.716 | 0.046 | 1 | 0.360 | 0.052 | 0.672 | 0.522 | 0.482 | 0.122 | 0.176 | 0.461 | 0.438 | 0.716 | 0.666 |
| Be | −0.521 | −0.135 | −0.163 | 0.235 | −0.215 | −0.035 | 0.225 | 0.669 | 0.163 | −0.116 | 0.360 | 1 | 0.110 | −0.151 | −0.082 | 0.068 | 0.138 | −0.075 | −0.059 | 0.410 | 0.090 | 0.097 |
| F | 0.108 | −0.086 | −0.142 | 0.177 | −0.227 | −0.007 | 0.084 | 0.057 | 0.184 | 0.247 | 0.052 | 0.110 | 1 | −0.227 | −0.258 | −0.556 | −0.136 | −0.174 | −0.271 | −0.264 | −0.345 | −0.281 |
| Cl | 0.199 | −0.452 | −0.310 | 0.340 | −0.438 | −0.436 | 0.315 | 0.023 | 0.679 | 0.079 | 0.672 | −0.151 | −0.227 | 1 | 0.817 | 0.546 | 0.220 | 0.242 | 0.581 | 0.129 | 0.729 | 0.654 |
| Sc | 0.102 | −0.357 | −0.246 | 0.149 | −0.372 | −0.326 | 0.299 | −0.042 | 0.612 | 0.168 | 0.522 | −0.082 | −0.258 | 0.817 | 1 | 0.721 | 0.354 | 0.312 | 0.697 | 0.358 | 0.684 | 0.628 |
| V | −0.212 | −0.074 | 0.031 | −0.055 | −0.059 | −0.072 | 0.108 | 0.009 | 0.313 | −0.086 | 0.482 | 0.068 | −0.556 | 0.546 | 0.721 | 1 | 0.353 | 0.452 | 0.755 | 0.662 | 0.506 | 0.562 |
| Cr | −0.274 | 0.203 | −0.034 | −0.202 | 0.126 | −0.219 | 0.020 | 0.330 | −0.043 | −0.189 | 0.122 | 0.138 | −0.136 | 0.220 | 0.354 | 0.353 | 1 | 0.500 | 0.362 | 0.278 | 0.088 | −0.010 |
| Co | −0.103 | 0.023 | 0.116 | −0.178 | 0.074 | −0.195 | 0.108 | 0.111 | 0.060 | −0.103 | 0.176 | −0.075 | −0.174 | 0.242 | 0.312 | 0.452 | 0.500 | 1 | 0.318 | 0.150 | 0.106 | 0.194 |
| Ni | −0.100 | −0.053 | −0.003 | −0.075 | −0.071 | −0.048 | 0.035 | −0.083 | 0.359 | −0.014 | 0.461 | −0.059 | −0.271 | 0.581 | 0.697 | 0.755 | 0.362 | 0.318 | 1 | 0.544 | 0.402 | 0.507 |
| Cu | −0.351 | 0.029 | −0.060 | 0.016 | −0.106 | 0.091 | 0.084 | 0.268 | 0.133 | −0.113 | 0.438 | 0.410 | −0.264 | 0.129 | 0.358 | 0.662 | 0.278 | 0.150 | 0.544 | 1 | 0.329 | 0.468 |
| Zn | 0.146 | −0.617 | −0.521 | 0.465 | −0.589 | −0.460 | 0.540 | 0.202 | 0.556 | 0.157 | 0.716 | 0.090 | −0.345 | 0.729 | 0.684 | 0.506 | 0.088 | 0.106 | 0.402 | 0.329 | 1 | 0.844 |
| Ga | 0.116 | −0.414 | −0.323 | 0.262 | −0.431 | −0.231 | 0.336 | 0.120 | 0.473 | 0.072 | 0.666 | 0.097 | −0.281 | 0.654 | 0.628 | 0.562 | −0.010 | 0.194 | 0.507 | 0.468 | 0.844 | 1 |
| Input: The similarities graph . Output: Print hierarchy clustering records. Begin: Initialize: Elements clusters , Minimum distance Cluster index . While do . For ) do For do Calculate the distance between and : If then . End for End for Merge cluster and : .Delete and from . Append to Print elements . End While End |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, N.; Peng, M.; Li, Q.; Xu, C. Towards Consistent Interpretations of Coal Geochemistry Data on Whole-Coal versus Ash Bases through Machine Learning. Minerals 2020, 10, 328. https://doi.org/10.3390/min10040328
Xu N, Peng M, Li Q, Xu C. Towards Consistent Interpretations of Coal Geochemistry Data on Whole-Coal versus Ash Bases through Machine Learning. Minerals. 2020; 10(4):328. https://doi.org/10.3390/min10040328
Chicago/Turabian StyleXu, Na, Mengmeng Peng, Qing Li, and Chuanpeng Xu. 2020. "Towards Consistent Interpretations of Coal Geochemistry Data on Whole-Coal versus Ash Bases through Machine Learning" Minerals 10, no. 4: 328. https://doi.org/10.3390/min10040328
APA StyleXu, N., Peng, M., Li, Q., & Xu, C. (2020). Towards Consistent Interpretations of Coal Geochemistry Data on Whole-Coal versus Ash Bases through Machine Learning. Minerals, 10(4), 328. https://doi.org/10.3390/min10040328





