Effect of Stress Path on the Failure Envelope of Intact Crystalline Rock at Low Confining Stress
Abstract
1. Introduction
2. Background
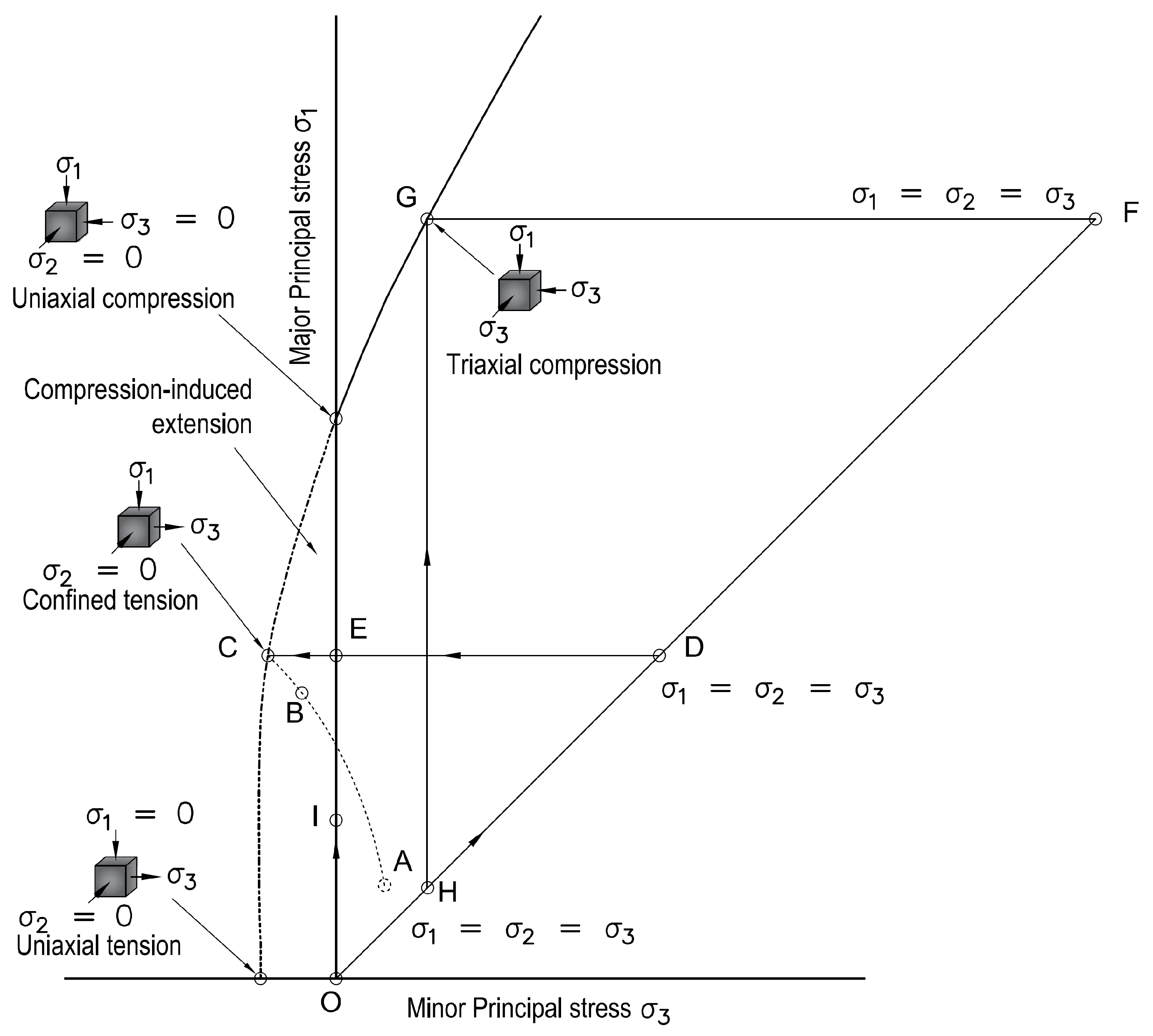
2.1. Stress Paths Observed in the Field and in Typical Low Confinement Laboratory Tests
2.2. Laboratory-Confined Extension Test on Rock
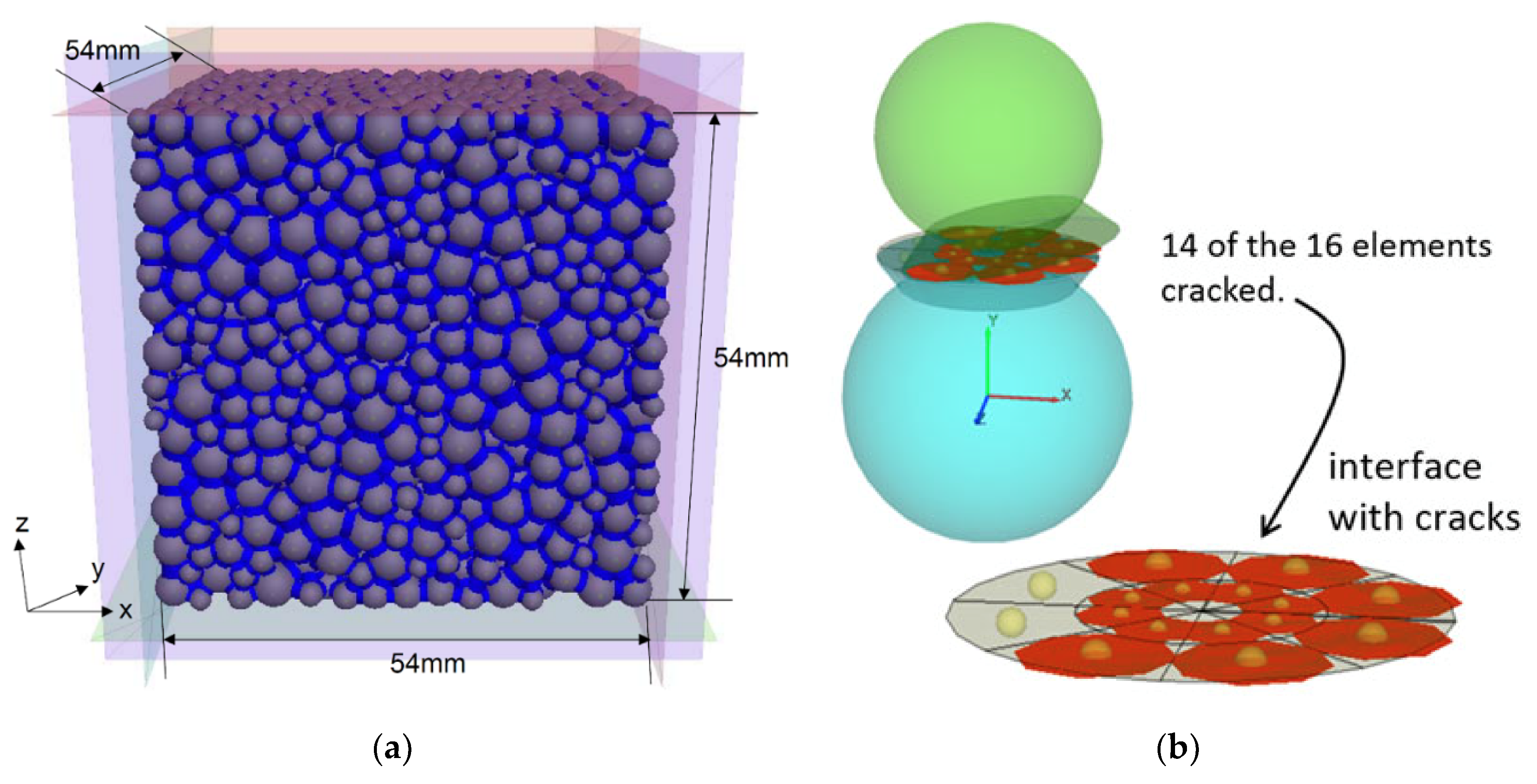
2.3. Flat-Jointed Bonded Particle Model
3. Calibration of Microparameters for Lac du Bonnet Granite for the BPM
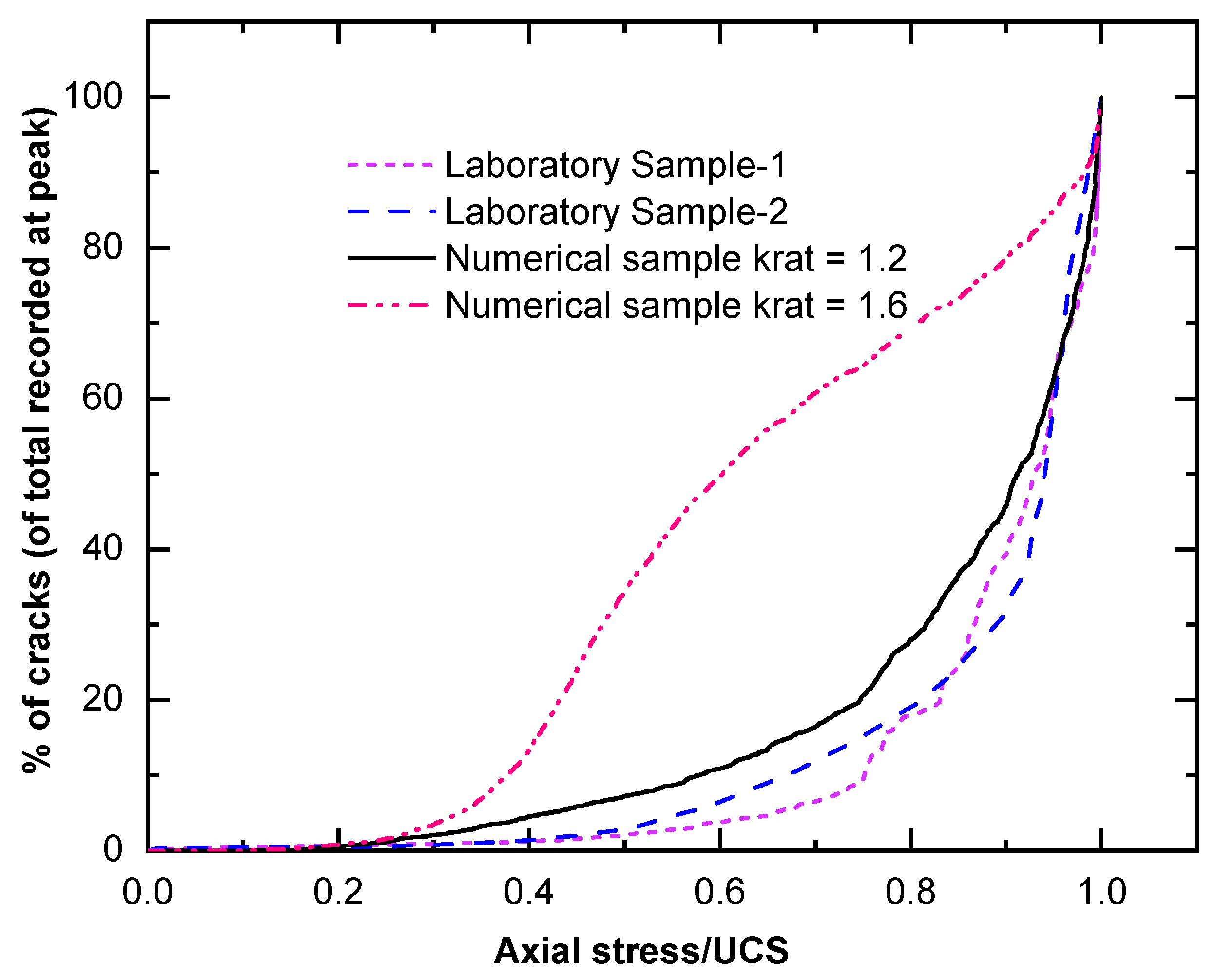
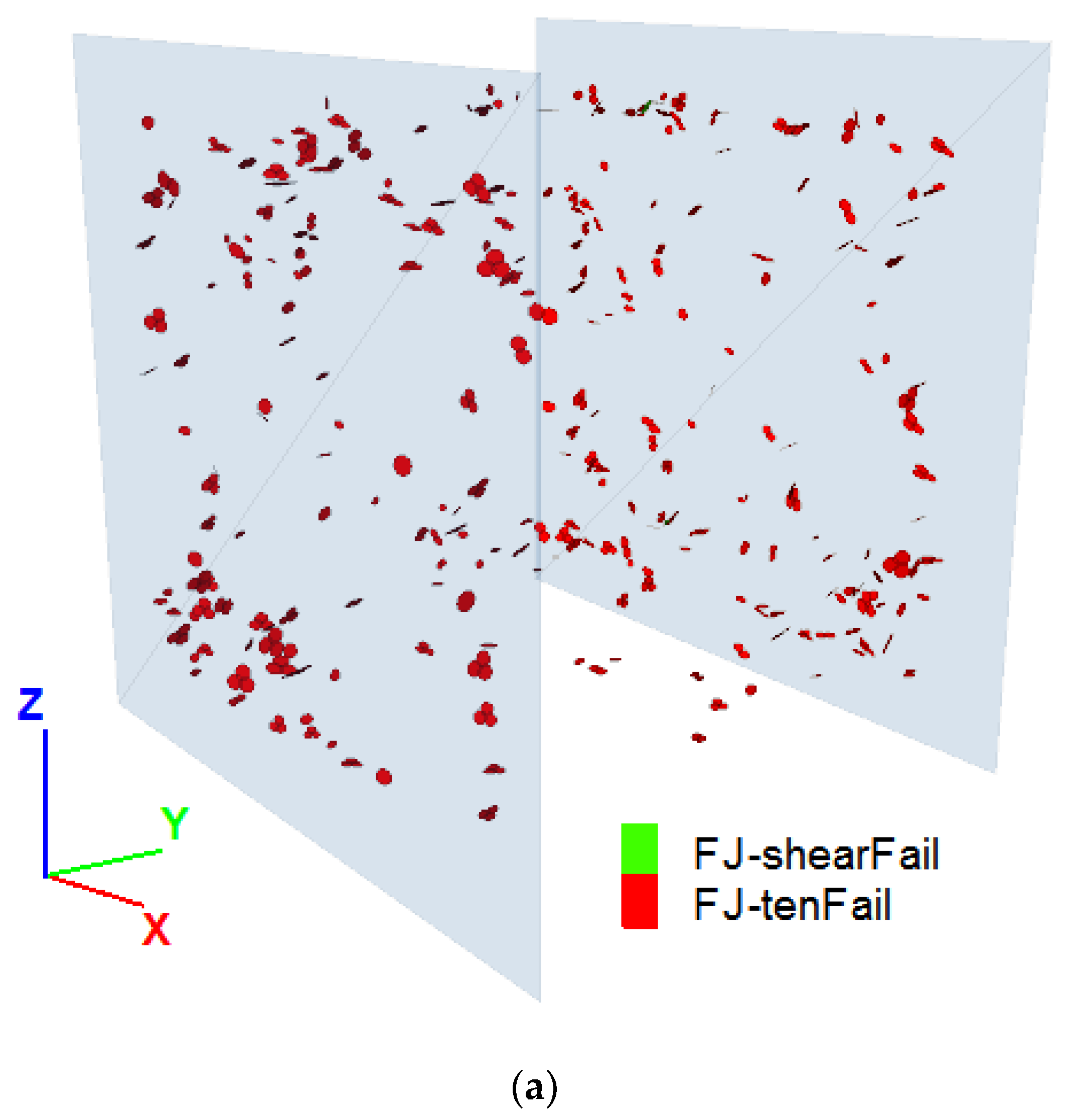
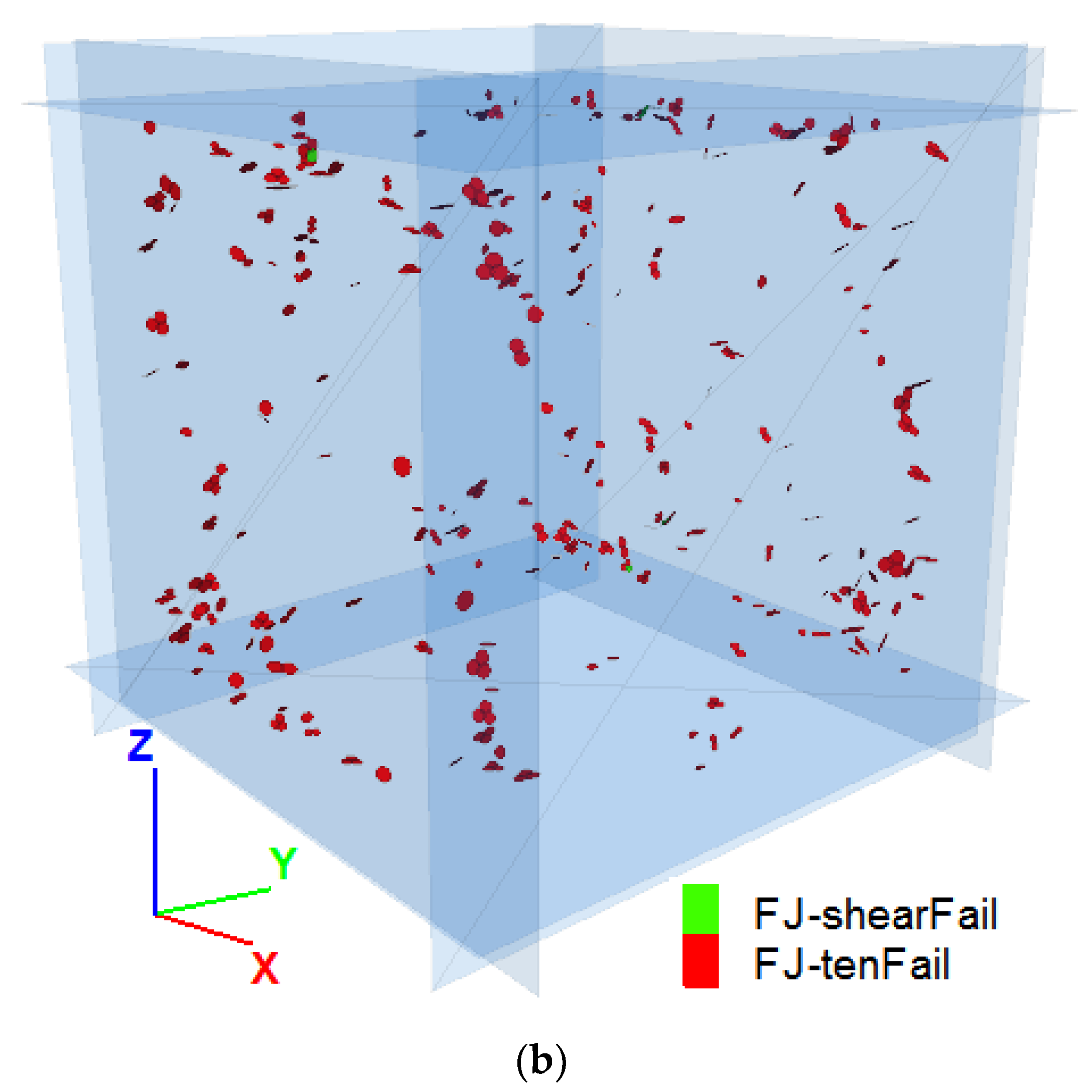
3.1. Intergranular Stiffness Ratio and the Formation of Microcracks in the Sample
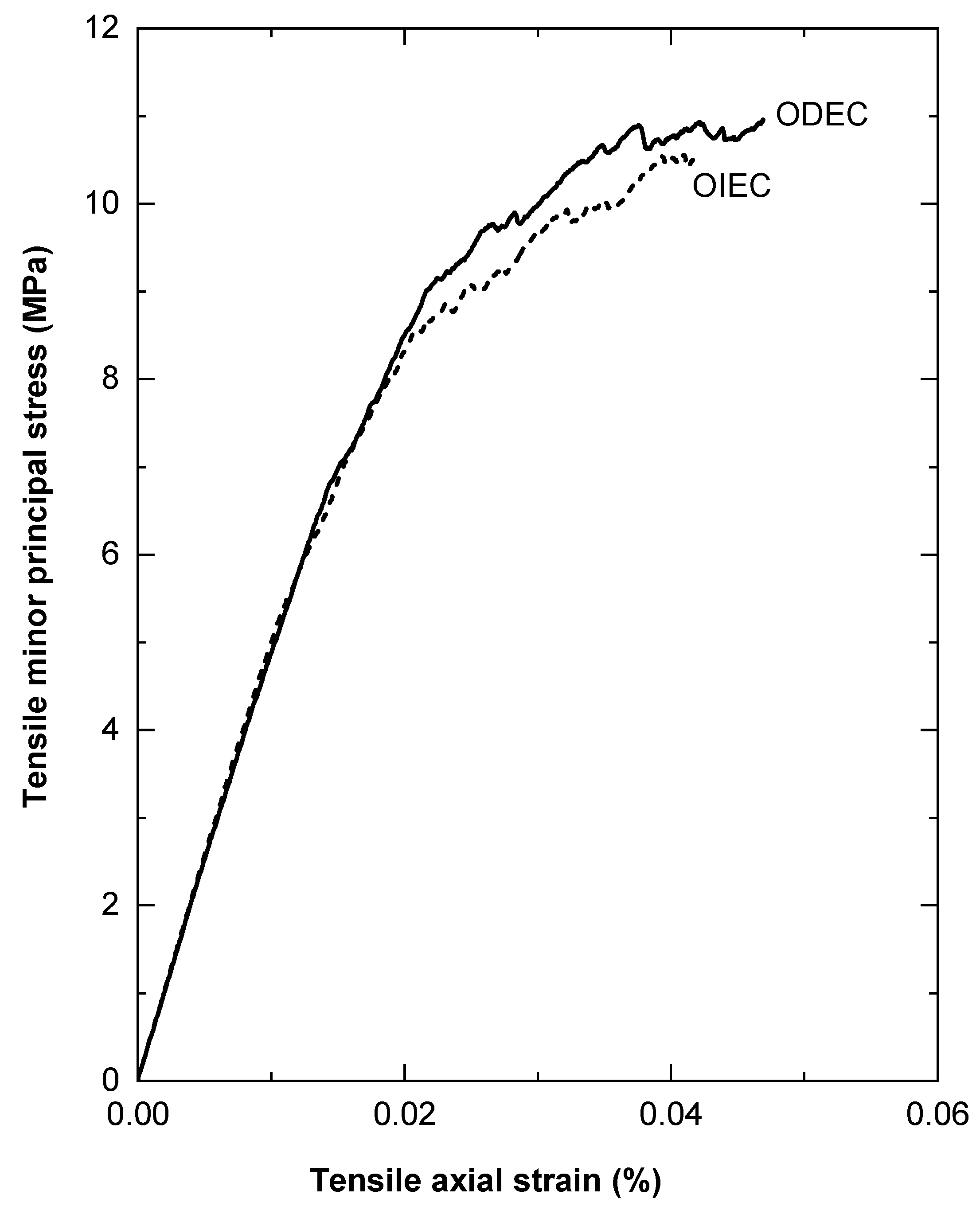
3.2. Comparison of Laboratory Response of the Lac du Bonnet Granite Sample with the FJ Numerical Sample for the UCS Test
4. Confined Extension Test Using the FJ BPM
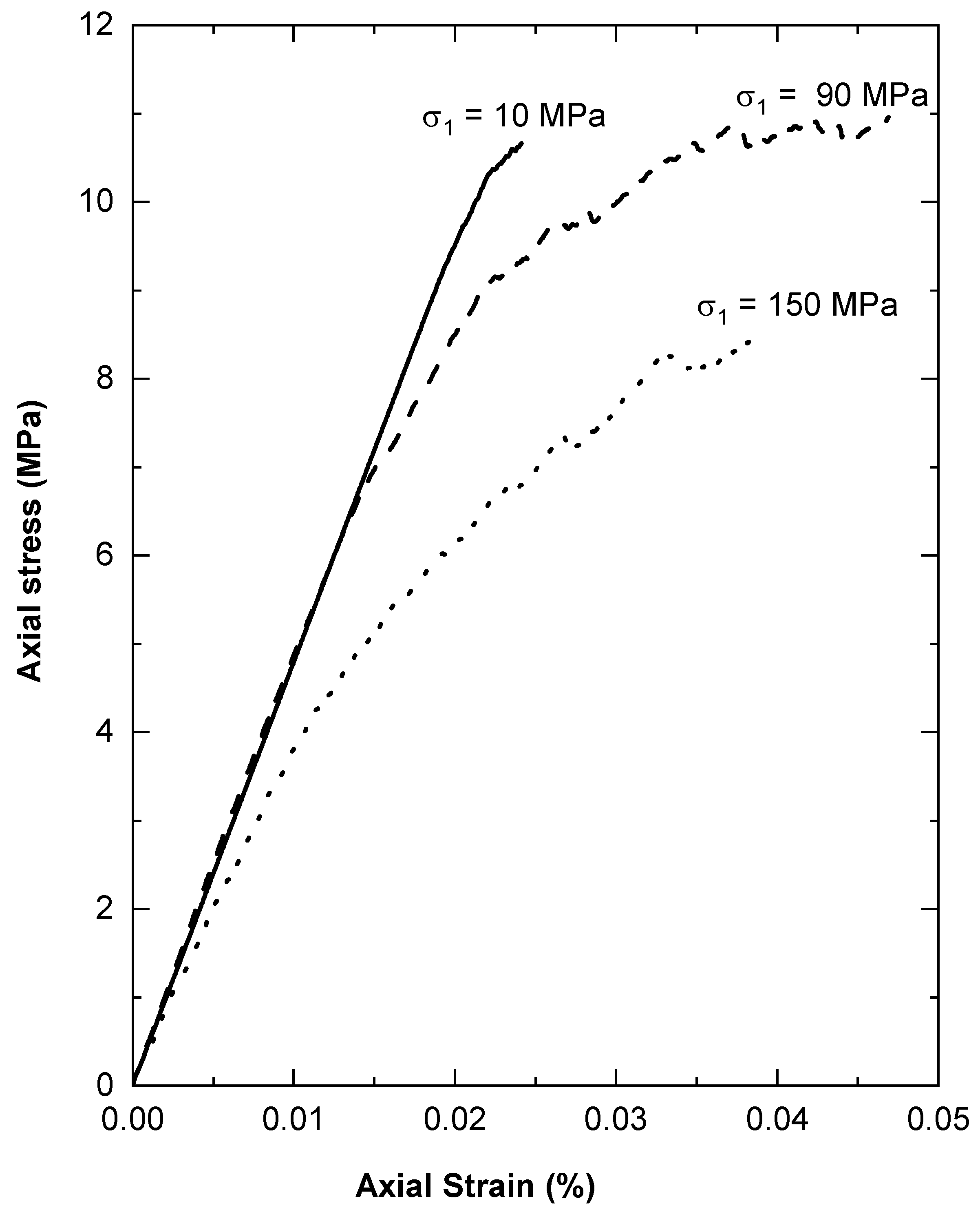
5. Results of FJ Modelling
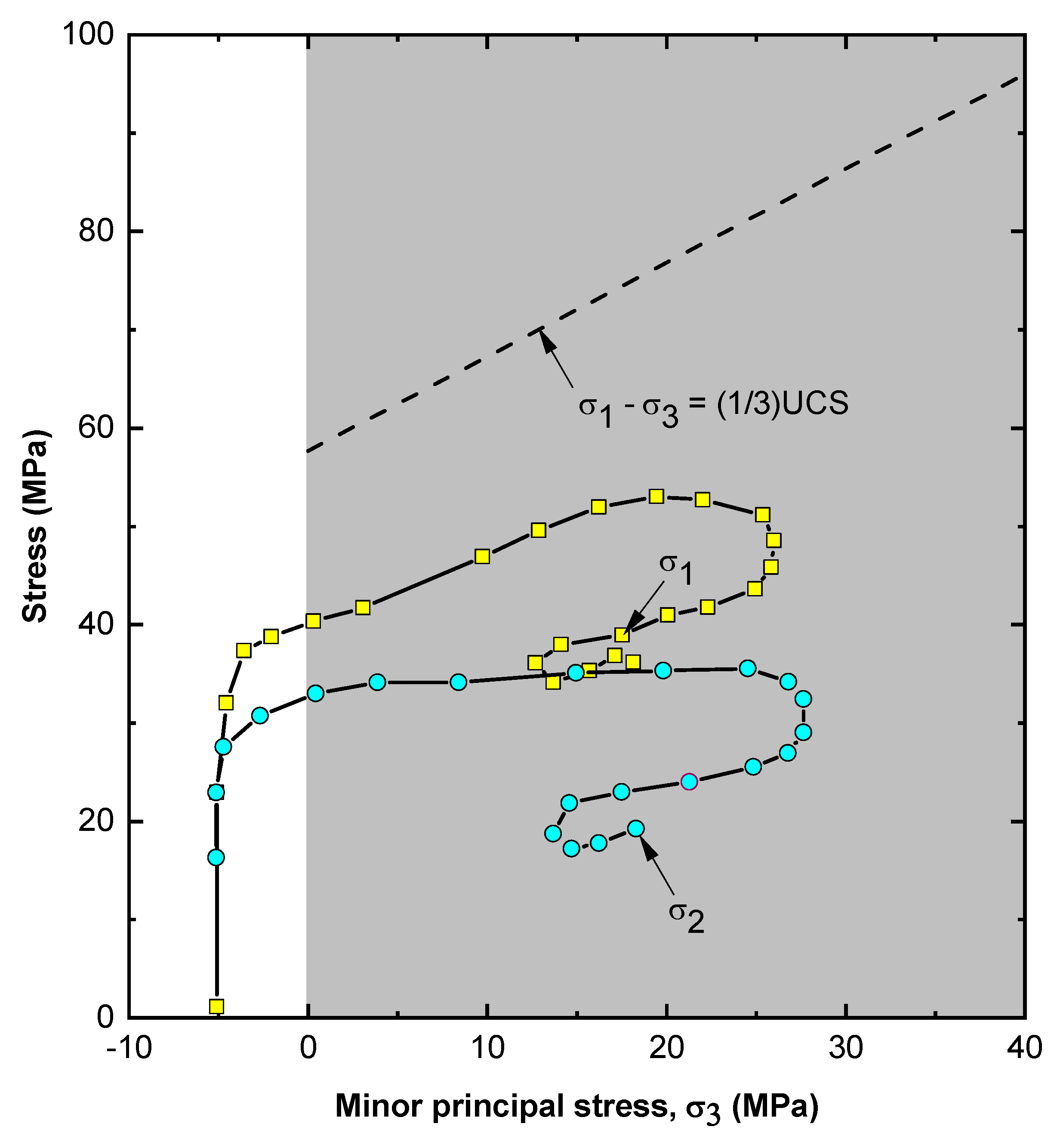
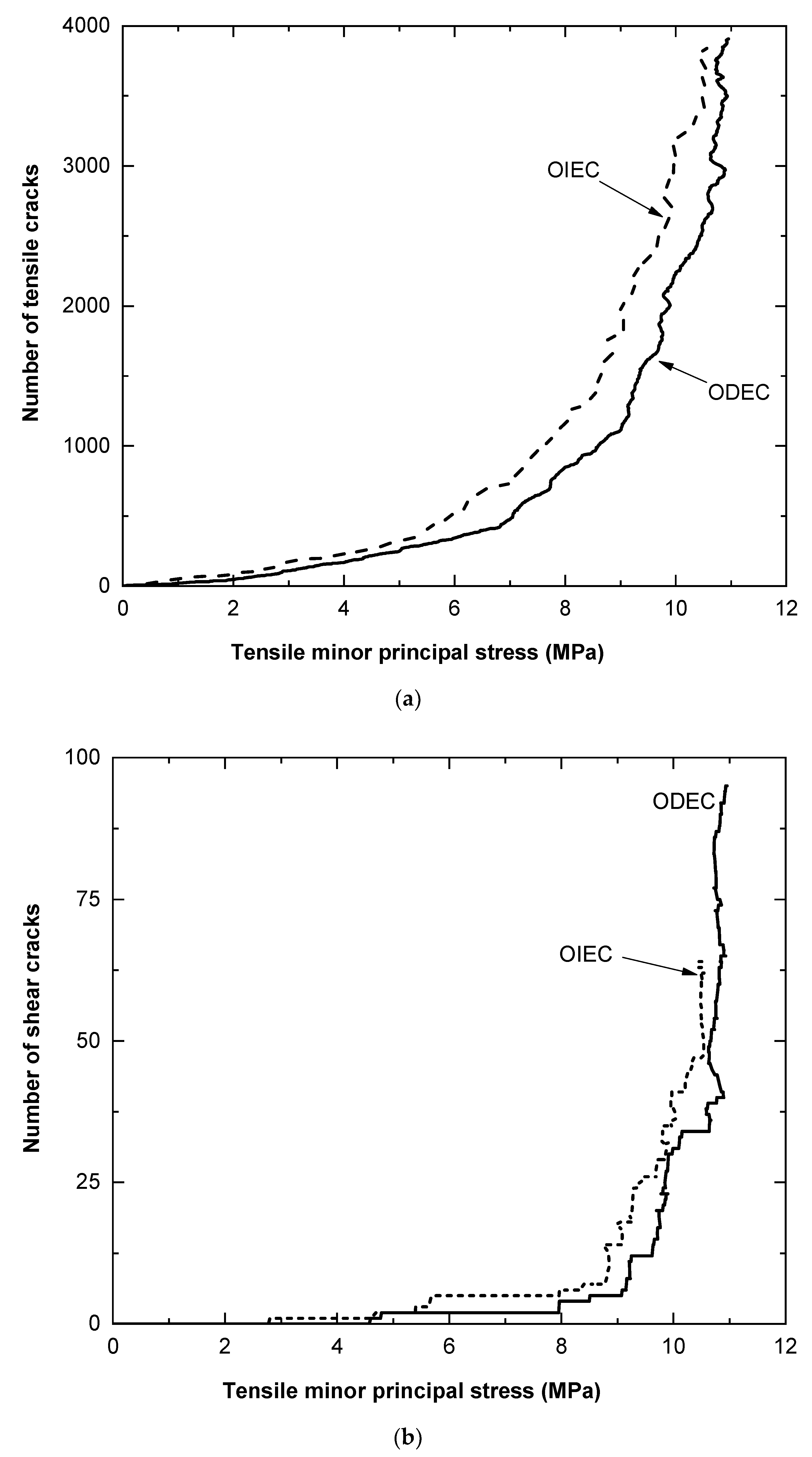
5.1. Influence of Stress Path on a Confined Extension Test
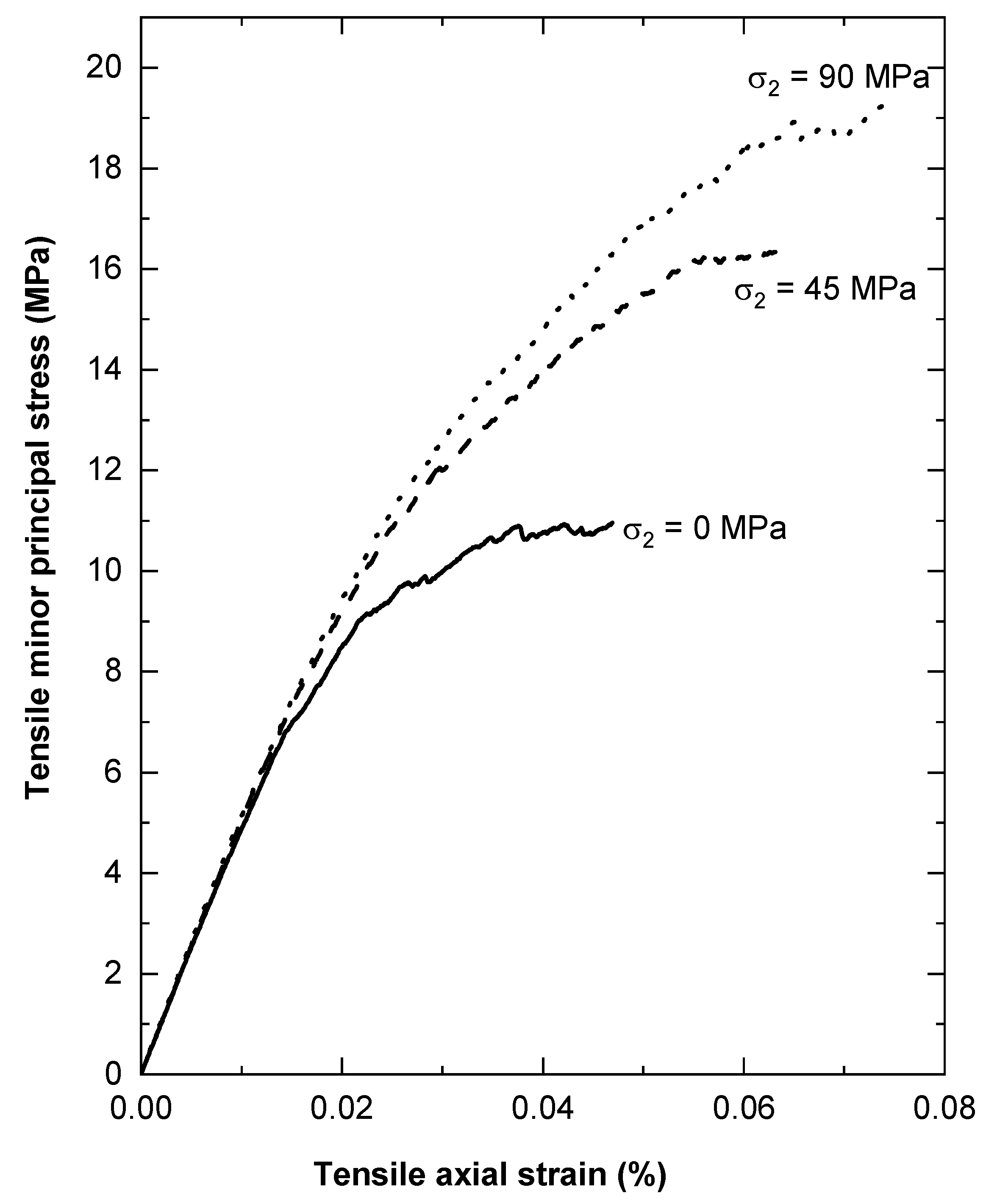
5.2. Results of the Confined Extension Test with σ2 = 0
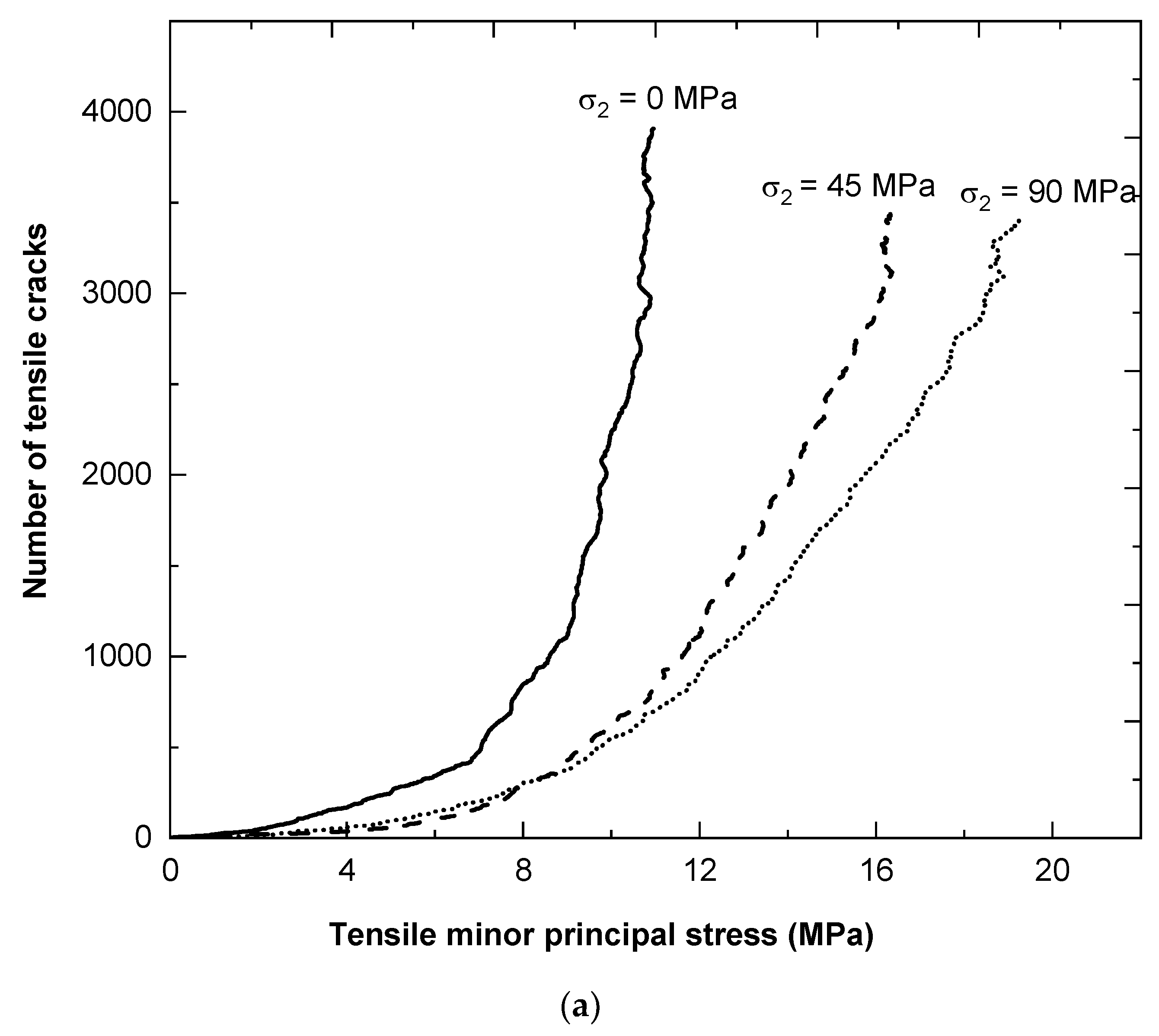
5.3. Impact of σ2 on the Confined Extension Test
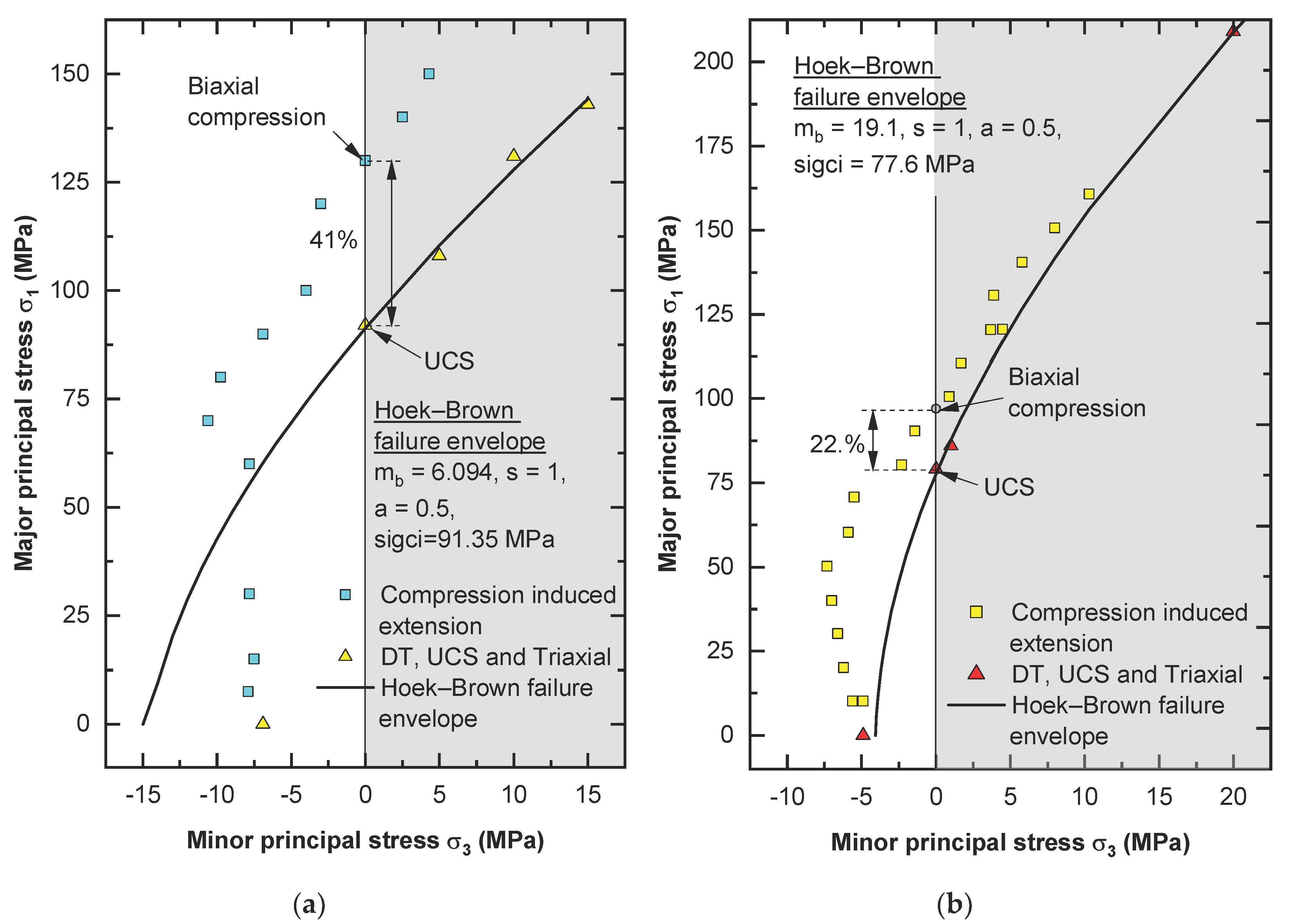
6. Failure Envelope for Lac du Bonnet Granite
7. Conclusions
- By changing the code, it was possible to study the behavior of the rock in confined extension at σ2 = 0. When compared with the Hoek–Brown failure criterion, the actual strength values obtained from the numerical samples in confined extension were higher than data points from the Hoek–Brown criterion; however, the Hoek–Brown failure envelope overestimated the peak strength obtained from the laboratory tests in confined extension, e.g., as in the case of Carrara marble (Figure 4a).
- The data points obtained from the Brazilian and flattened Brazilian tests were close to the values from the numerical analysis.
- Limited data available from laboratory testing (Brazilian and flattened Brazilian tests) and data from the numerical analysis indicate a tensile cutoff for Lac du Bonnet granite, as suggested by Hoek and Martin [2].
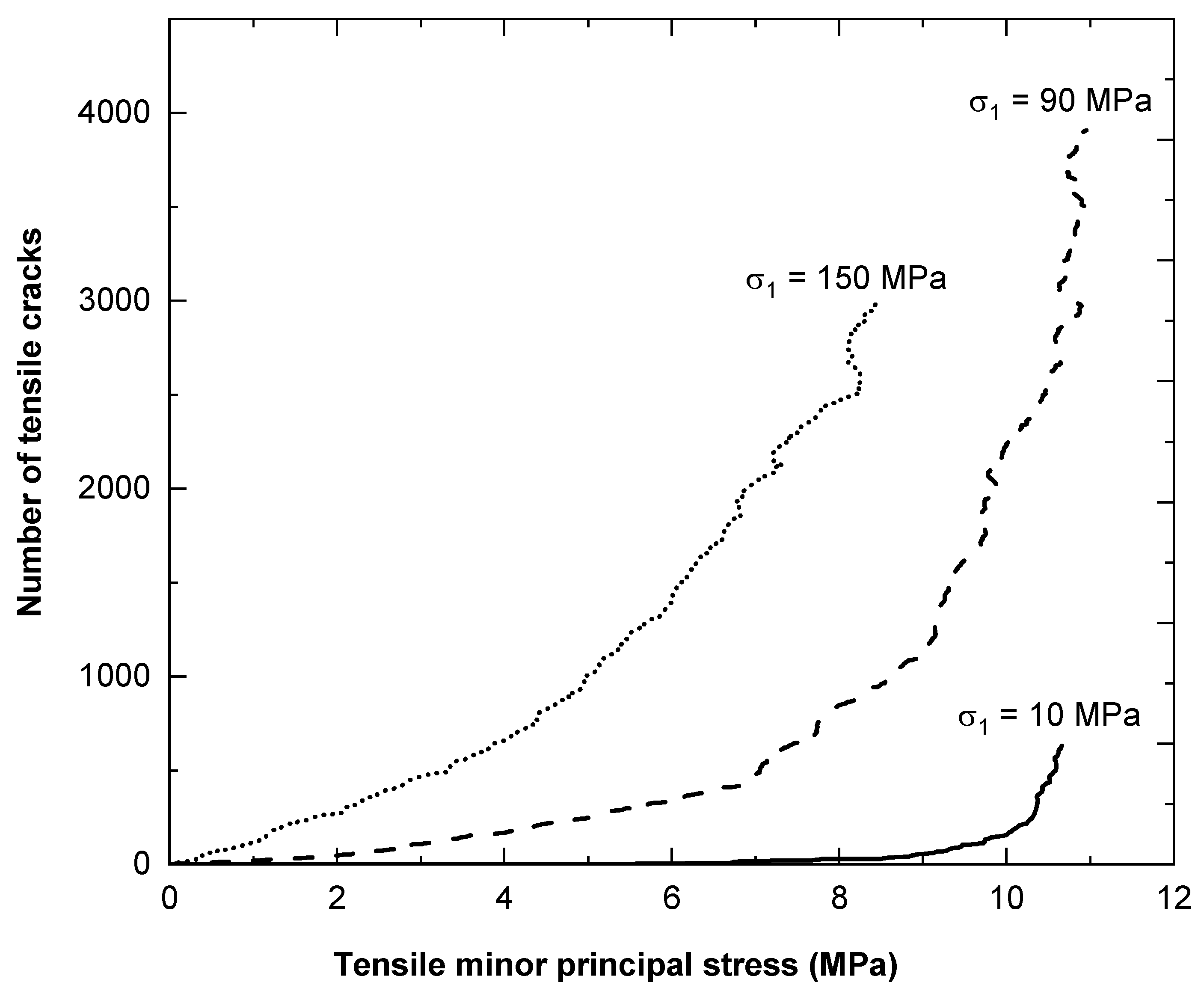
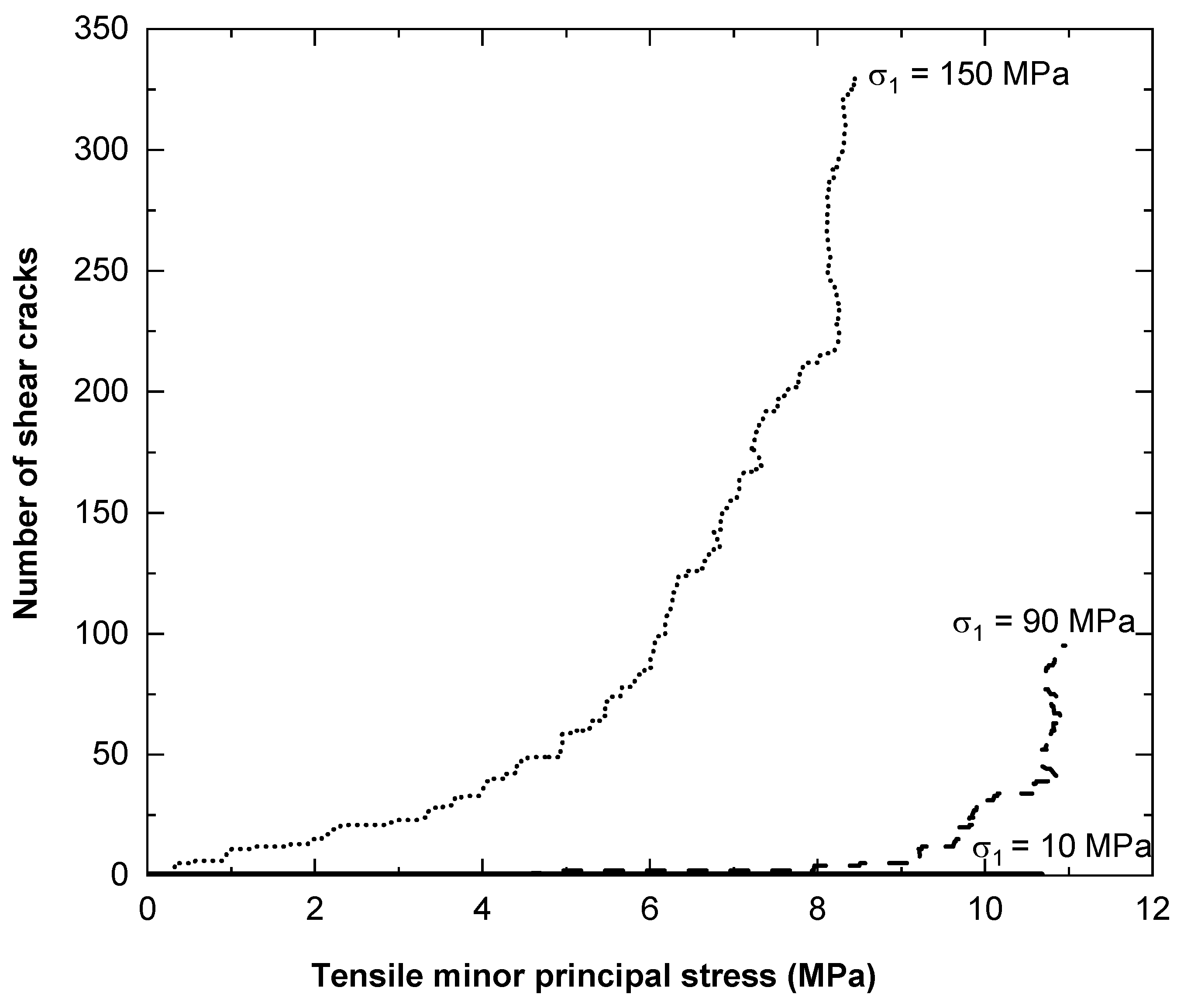
- For the numerical investigation on confined extension, the stress paths investigated have a minor impact on peak strength. However, microfracture formation was found to be path dependent.
- The numerical sample shows a clear impact of σ2 in the confined extension test. Rock with 90 MPa confinement for both σ1 and σ2 produced ~76% higher strength compared to the sample with σ2 = 0. This requires a review of the present methodology to test dog-bone-shaped specimens in confined extension.
- Further investigations should consider simultaneous stress rotation along with the stress path to better understand its impact on strength reduction in field conditions compared to the laboratory.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| σci | Crack initiation stress |
| σcd | Crack damage stress |
| σ1, σ2, σ3 | Major, intermediate, and minor principal stress |
| DT | Direct tension test |
| BT | Brazilian tensile test |
| FB | Flattened Brazilian test |
| UCS | Uniaxial compressive strength |
References
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining; Kluwer Academic Publishers: New York, NY, USA, 2005. [Google Scholar]
- Hoek, E.; Martin, C.D. Fracture initiation and propagation in intact rock—A review. J. Rock Mech. Geotech. Eng. 2014, 6, 287–300. [Google Scholar] [CrossRef]
- Hamdi, P.; Stead, D.; Elmo, D. Characterizing the influence of stress-induced microcracks on the laboratory strength and fracture development in brittle rocks using a finite-discrete element method-micro discrete fracture network FDEM-μDFN approach. J. Rock Mech. Geotech. Eng. 2015, 7, 609–625. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Yazici, S.; Maloney, S. Mining-induced stress change and consequences of stress path on excavation stability—A case study. Int. J. Rock Mech. Min. Sci. 2001, 38, 167–180. [Google Scholar] [CrossRef]
- Bahrani, N.; Valley, B.; Kaiser, P.K. Numerical simulation of drilling-induced core damage and its influence on mechanical properties of rocks under unconfined condition. J. Rock Mech. Min. Sci. 2015, 80, 40–50. [Google Scholar] [CrossRef]
- Martin, C.D.; Tannant, D.D.; Kaiser, P.K. Stress path and instability around mine openings Cheminement de contraintes et instabilité d’effort autour des ouvertures de mine Spannungsweg und-instabilität um Grube Hohlräume. In Proceedings of the 9th ISRM Congress, Paris, France, 25–28 August 1999. [Google Scholar]
- Diederichs, M.S. Instability of Hard Rockmasses, the Role of Tensile Damage and Relaxation. PhD Thesis, University of Waterloo, Waterloo, ON, Canada, 2000. [Google Scholar]
- Andersson, J.C.; Martin, C.D.; Stille, H. The Äspö Pillar Stability Experiment: Part II-Rock mass response to coupled excavation-induced and thermal-induced stresses. Int. J. Rock Mech. Min. Sci. 2009, 46, 879–895. [Google Scholar] [CrossRef]
- Martin, C.D. Seventeenth Canadian Geotechnical Colloquium: The effect of cohesion loss and stress path on brittle rock strength. Can. Geotech. J. 1997, 34, 698–725. [Google Scholar] [CrossRef]
- Read, R.S.; Chandler, N.A.; Dzik, E.J. In situ strength criteria for tunnel design in highly-stressed rock masses. J. Rock Mech. Min. Sci. 1998, 35, 261–278. [Google Scholar] [CrossRef]
- Harrison, J.P.; Hudson, J.A. Visualising and understanding the stress path for rock mechanics modelling and testing, and rock engineering design. In Proceedings of the 10th ISRM Congress, Sandton, South Africa, 8–12 September 2003; pp. 487–492. [Google Scholar]
- Diederichs, M.S.; Kaiser, P.K.; Eberhardt, E. Damage initiation and propagation in hard rock during tunnelling and the influence of near-face stress rotation. J. Rock Mech. Min. Sci. 2004, 41, 785–812. [Google Scholar] [CrossRef]
- Cantieni, L.; Anagnostou, G. The Effect of the Stress Path on Squeezing Behavior in Tunneling. Rock Mech. Rock Eng. 2009, 42, 289–318. [Google Scholar] [CrossRef]
- Potyondy, D.O. A Flat-Jointed Bonded-Particle Material for Hard Rock. In 46th U.S. Rock Mechanics/Geomechanics Symposium; Available online: https://www.onepetro.org/conference-paper/ARMA-2012-501 (accessed on 1 January 2012).
- Potyondy, D.O. A Flat-Jointed Bonded-Particle Model for Rock. In 52nd U.S. Rock Mechanics/Geomechanics Symposium; American Rock Mechanics Association: Seattle, WA, USA, 2018. [Google Scholar]
- Patel, S.; Martin, C.D. Impact of the initial crack volume on the intact behavior of a bonded particle model. Comput. Geotech. 2020, 127, 103764. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for determining tensile strength of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 99–103. Available online: https://www.isrm.net (accessed on 25 November 2020). [CrossRef]
- Bieniawski, Z.T.; Bernede, M.J. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 137–140. [Google Scholar] [CrossRef]
- Brace, W.F. Brittle failure of rock: State of stress in the earth’s crust. In Brittle Failure of Rock: State of Stress in the Earth’s Crust; Judd, W.R., Ed.; American Elsevier: New York, NY, USA, 1964; pp. 111–180. [Google Scholar]
- Ramsey, J.M.; Chester, M.F. Hybrid fracture and the transition from extension fracture to shear fracture. Nature 2004, 428, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Bobich, J.K. Experimental Analysis of the Extension to Shear Fracture Transition in Berea Sandstone. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2005. [Google Scholar]
- Patel, S.; Martin, C.D. Application of Flattened Brazilian Test to Investigate Rocks under Confined Extension. Rock Mech. Rock Eng. 2018, 51, 3719–3736. [Google Scholar] [CrossRef]
- Ramsey, J.M. Experimental study of the transition from brittle shear fractures to joints. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2003. [Google Scholar]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosystem Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Davoodi, A.; Asbjörnsson, G.; Hulthén, E.; Evertsson, M. Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance. Minerals 2019, 9, 788. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. and Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Potyondy, D. Material-Modeling Support in PFC [fistPkg25]. 2017. Available online: https://www.itascacg.com/software/pfc (accessed on 22 November 2020).
- Patel, S. Impact of Confined Extension on the Failure Envelope of Intact Low-Porosity Rock. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2018. [Google Scholar]
- Martin, C. The Strength of Massive Lac du Bonnet Granite around Underground Openings. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 1993. [Google Scholar]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Brace, W.F.; Paulding, B.W.; Scholz, C. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part II—Experimental studies. Mech. Eng. 1967, 4, 407–423. [Google Scholar]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The impact of porosity and crack density on the elasticity, strength and friction of cohesive granular materials: Insights from DEM modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 250–261. [Google Scholar] [CrossRef]
- Huang, H.; Ma, Y. DEM Analysis of Intact Rock Strength under Confined Tension. Available online: http://itasca-downloads.s3.amazonaws.com/documents/Itasca%20symposia/2020/ExtendedAbstracts/02-02.pdf (accessed on 1 January 2012).
- Mogi, K. Effect of the intermediate principal stress on rock failure. J. Geophys. Res. 1967, 72, 5117–5131. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Associated with grain size distribution: | |
| Minimum grain diameter | 2.2 mm |
| Grain-size ratio | 2.3 |
| Associated with material genesis: | |
| Width of sample | 54 mm |
| Height–width ratio | 1 |
| Associated with FJ material group: | |
| Installation gap | 1.31 mm |
| Bonded fraction | 0.65 |
| Gapped fraction | 0.35 |
| Slit fraction, derived | 0 |
| Initial surface-gap distribution, mean | 0.002 mm |
| Initial surface-gap distribution, standard deviation | 0 |
| Elements in radial direction | 1 |
| Elements in circumferential direction | 3 |
| Radius-multiplier code | 0 |
| Radius-multiplier value | 0.577 |
| Effective modulus | 135.8 GPa |
| Stiffness ratio | 1.2 |
| Friction coefficient | 1.4 |
| Tensile-strength distribution, mean | 41.6 MPa |
| Tensile-strength distribution, standard deviation | 0 |
| Cohesion distribution, mean | 203 MPa |
| Cohesion distribution, standard deviation | 0 |
| Friction angle | 43.2° |
| Associated with the linear material group: | |
| Effective modulus | 135.8 GPa |
| Stiffness ratio | 1.2 |
| Friction coefficient | 2.2 mm |
| Case | Ec (GPa) | νc | σci (MPa) | σcd (MPa) | UCS (MPa) | Et (GPa) | σt (MPa) | Et/Ec |
|---|---|---|---|---|---|---|---|---|
| Lab | 70.5 | 0.26 | 88.6 | 163.3 | 221.7 | 45.8 | 10.6 | 0.65 |
| Numerical | 69.3 | 0.1 | 97.7 | 208.1 | 219.6 | 47.7 | 10.8 | 0.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, S.; Martin, C.D. Effect of Stress Path on the Failure Envelope of Intact Crystalline Rock at Low Confining Stress. Minerals 2020, 10, 1119. https://doi.org/10.3390/min10121119
Patel S, Martin CD. Effect of Stress Path on the Failure Envelope of Intact Crystalline Rock at Low Confining Stress. Minerals. 2020; 10(12):1119. https://doi.org/10.3390/min10121119
Chicago/Turabian StylePatel, Shantanu, and C. Derek Martin. 2020. "Effect of Stress Path on the Failure Envelope of Intact Crystalline Rock at Low Confining Stress" Minerals 10, no. 12: 1119. https://doi.org/10.3390/min10121119
APA StylePatel, S., & Martin, C. D. (2020). Effect of Stress Path on the Failure Envelope of Intact Crystalline Rock at Low Confining Stress. Minerals, 10(12), 1119. https://doi.org/10.3390/min10121119





