Removal of Salicylic and Ibuprofen by Hexadecyltrimethylammonium-Modified Montmorillonite and Zeolite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sorbents Preparation and Characterization
2.3. Sorption Isotherm of Pharmaceuticals onto HM and HZ
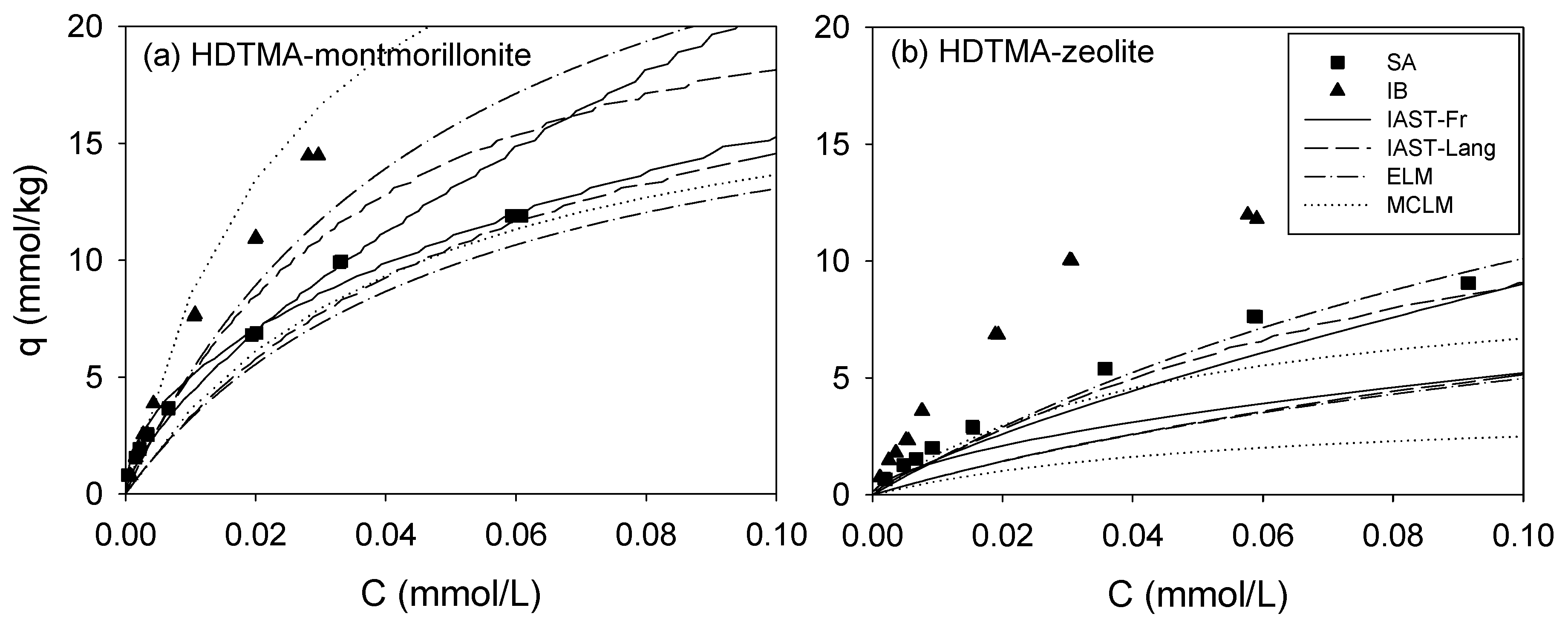
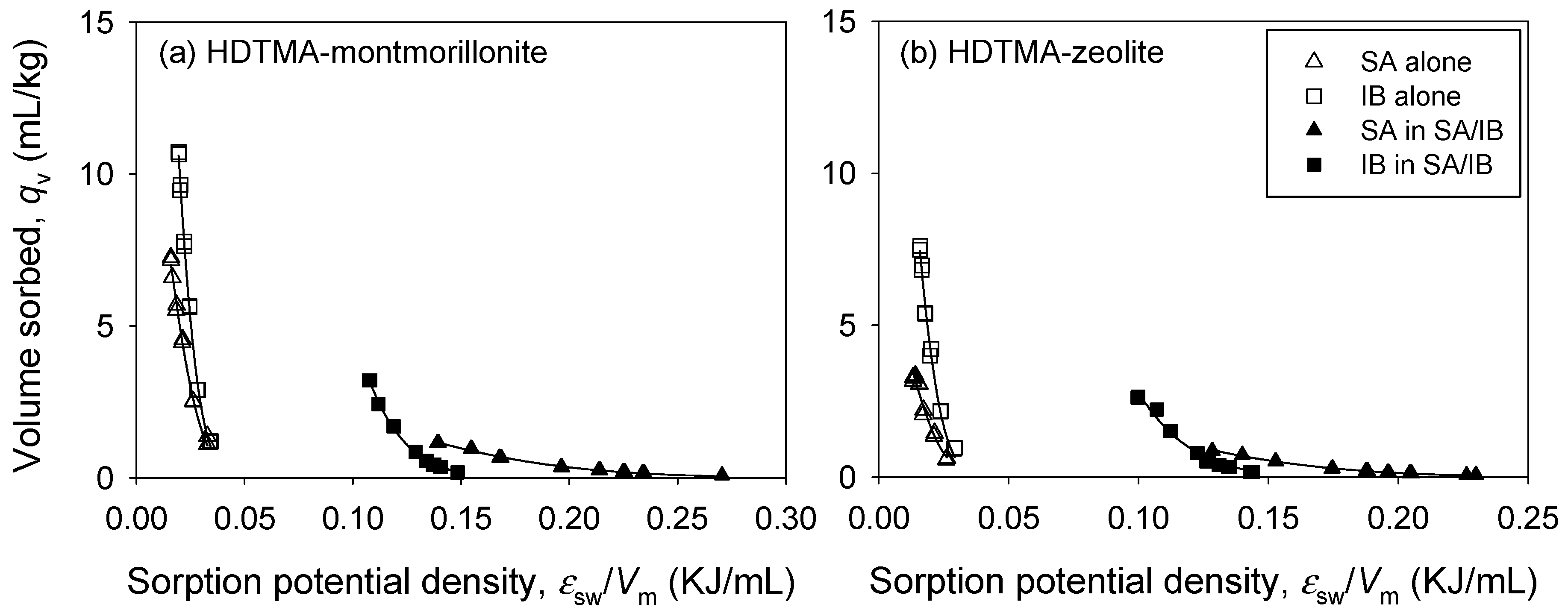
3. Results and Discussion
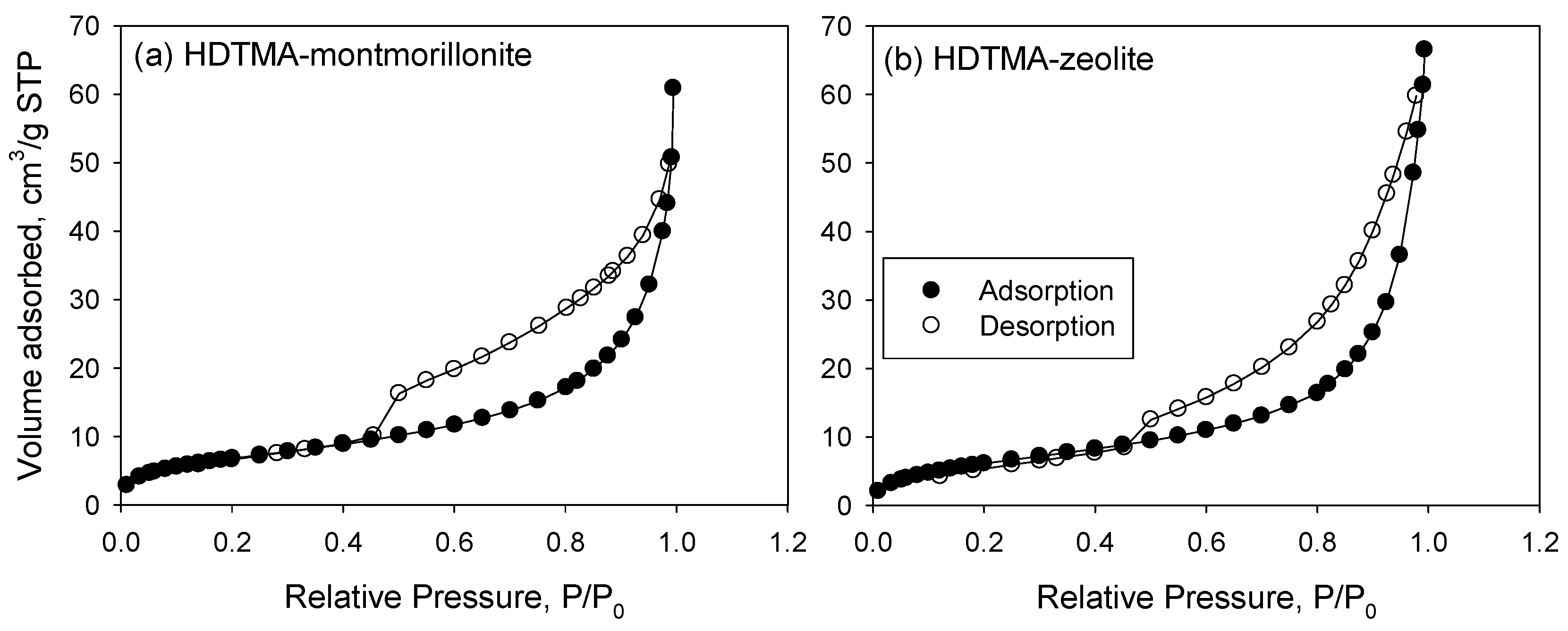
3.1. Characterization of the Sorbents
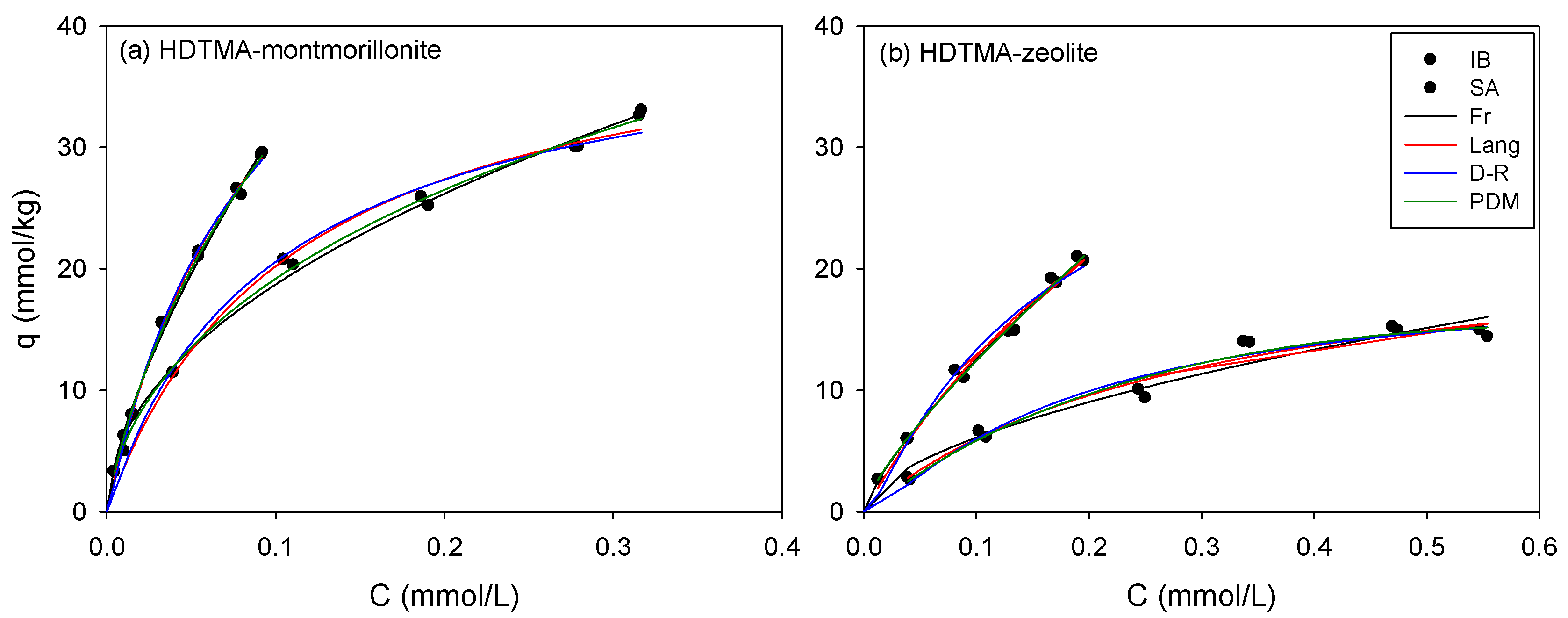
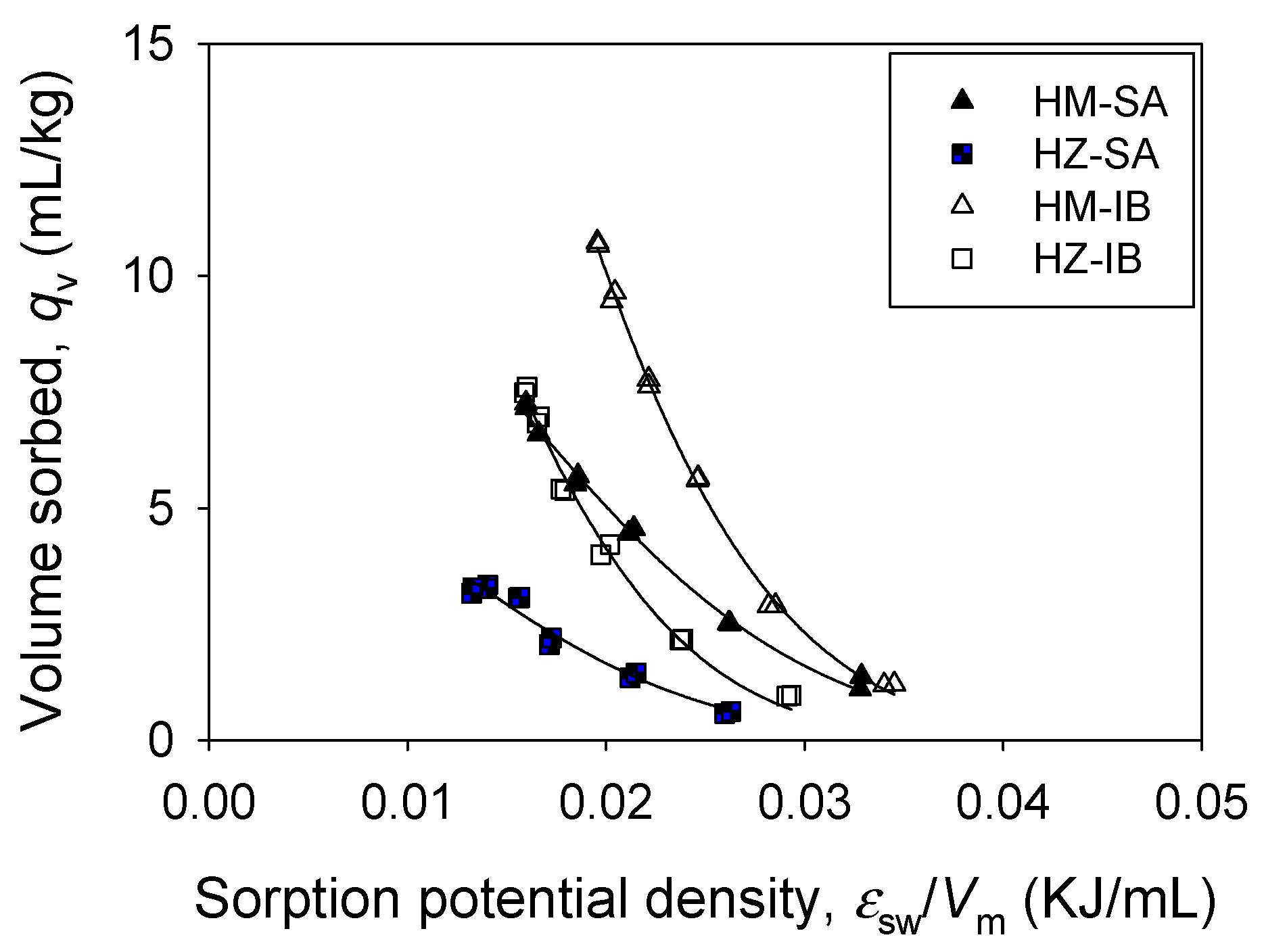
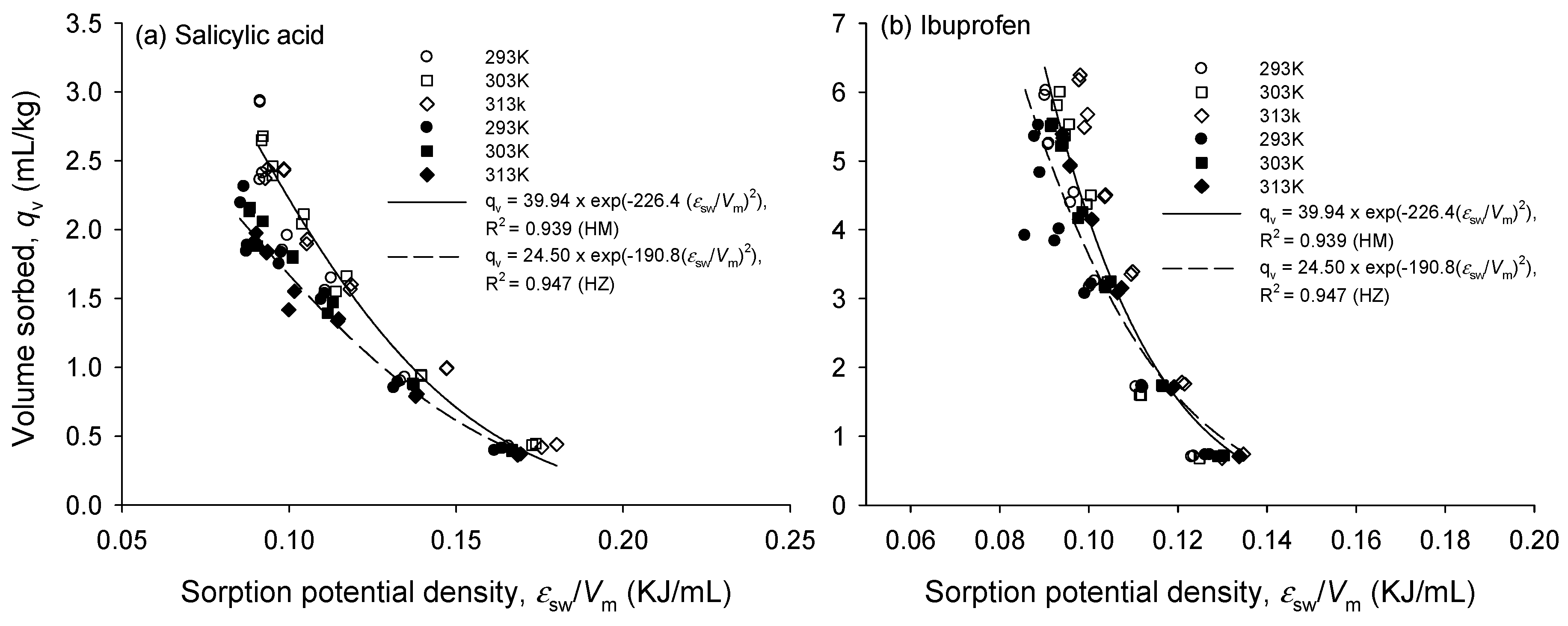
3.2. Single Sorption
3.3. Binary Sorption
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a ((mL)b+1(mol·Jb)−1) | fitting parameters |
| A | interfacial area between the solution and solid sorbent |
| b (−) | fitting parameters |
| bL (L/mmol) | site energy factor |
| βD (mol2/J2) | Dubinin–Radushkevich constant |
| E (kJ/mol) | mean free energy |
| ε (J/mol) | sorption potential (=RT ln(1 + 1/C)) |
| εsw (J/mol) | effective sorption potential, Polanyi potential (=RT ln(Sw/C)) |
| KF ((mmol/kg)/(mmol/L)) | Freundlich sorption coefficient (sorption affinity) |
| NF | linearity coefficient |
| ηi | constant interaction factor |
| qm (mL/kg) | maximum sorption capacity |
| qmD (mg/kg) | the theoretical saturation capacity |
| qmL (mmol/kg) | maximum sorption capacity |
| qmL,i(mmol/kg) and bL,i (L/mmol) | Langmuir model parameters obtained from single sorption |
| R (J/mol·K) | ideal gas constant |
| Sw (mmol/L) | solute solubility in water |
| T (K) | absolute temperature |
| Vm (mL/mol) | molar volume of solute |
| π | spreading pressure |
References
- Dionísio, R.; Daniel, D.; Arenas, F.; Campos, J.C.; Costa, P.C.; Nunes, B.; Correia, A.T. Effect of pH on salicylic acid toxicity in terms of biomarkers determined in the marine gastropod Gibbula umbilicalis. Mar. Environ. Res. 2020, 158, 104995. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Coimbra, R.N.; Escapa, C.; Figueiredo, S.A.; Freitas, O.M.; Otero, M. Green microalgae Scenedesmus Obliquus utilization for the adsorptive removal of nonsteroidal anti-inflammatory drugs (NSAIDs) from water samples. Int. J. Environ. Res. Public Health 2020, 17, 3707. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-M.; Wei, C.-W.; Zhang, Y.; Wang, D.-S.; Liu, Y.-N. Investigation of competitive binding of ibuprofen and salicylic acid with serum albumin by affinity capillary electrophoresis. J. Chromatogr. 2011, B879, 1934–1938. [Google Scholar] [CrossRef] [PubMed]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J.C. Thermodynamic analysis of acetaminophen and salicylic acid adsorption onto granular activated carbon: Importance of chemical surface and effect of ionic strength. Thermochim. Acta 2020, 683, 178467. [Google Scholar] [CrossRef]
- Essandoh, M.; Kunwat, B.; Pittman Charles, U., Jr.; Mohan, D.; Mlsna, T. Sorptive removal of salicylic acid and ibuprofen from aqueous solutions using pine wood fast pyrolysis biochar. Chem. Eng. J. 2015, 265, 219–227. [Google Scholar] [CrossRef]
- Park, J. Pharmaceuticals in the Environment and Management Approaches in Korea; Korea Environment Institute (KEI): Seoul, Korea, 2005. [Google Scholar]
- Raskin, I. Role of salicylic acid in plants. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1992, 43, 439–463. [Google Scholar] [CrossRef]
- Nakdong River Water Environment Research Institute. A Survey on the Monitoring of Potentially Hazardous Compounds and Contamination Routes in Tributary of the Nakdong River System; 3rd year report; National Institute of Environmental Research (NIER): Daegu, Korea, 2015.
- Wang, J.; Wang, S. Removal of pharmaceuticals and personal care products (PPCPs) from wastewater: A review. J. Environ. Manag. 2016, 182, 620–640. [Google Scholar] [CrossRef]
- Mailler, R.; Gasperi, J.; Conquet, Y.; Deshayes, S.; Zedek, S.; Cren-Olivé, C.; Cartiser, N.; Eudes, V.; Bressy, A.; Caupos, E.; et al. Study of a large scale powdered activated carbon pilot: Removals of a wide range of emerging and priority micropollutants from wastewater treatment plant effluents. Water Res. 2015, 72, 315–330. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, E.; Campinas, M.; Acero, J.; Rosa, M.J. Investigating PPCP removal from wastewater by powdered activated carbon/ultrafiltration. Water Air Soil Pollut. 2016, 227, 1–4. [Google Scholar] [CrossRef]
- Oliveira, T.D.; Fernandez, E.; Fougère, L.; Destandau, E.; Boussafir, M.; Sohmiya, M.; Sugahara, Y.; Guégan, R. Competitive association of antibiotics with a clay mineral and organoclay derivatives as a control of their lifetimes in the environment. ACS Omega 2018, 3, 15332–15342. [Google Scholar] [CrossRef] [Green Version]
- Maia, G.S.; de Andrade, J.R.; da Silva, M.G.C.; Vieira, M.G.A. Adsorption of diclofenac sodium onto commercial organoclay: Kinetic, equilibrium and thermodynamic study. Powder Technol. 2019, 345, 140–150. [Google Scholar] [CrossRef]
- Xu, S.; Boyd, S.A. Cationic surfactant adsorption by swelling and non-swelling layer silicates. Langmuir 1995, 11, 2508–2514. [Google Scholar] [CrossRef]
- Koh, S.-M.; Dixon, J.B. Preparation and application of organo-minerals as sorbents of phenol, benzene, and toluene. Appl. Clay Sci. 2001, 18, 111–122. [Google Scholar] [CrossRef]
- Saitoh, T.; Shibayama, T. Removal and degradation of b-lactam antibiotics in water using didodecyldimethylammonium bromide-modified montmorillonite organoclay. J. Hazard. Mater. 2016, 317, 677–685. [Google Scholar] [CrossRef]
- Crocker, F.H.; Guerin, W.F.; Boyd, S.A. Bioavailability of naphthalene sorbed to cationic surfactant-modified smectite clay. Environ. Sci. Technol. 1995, 29, 2953–2958. [Google Scholar] [CrossRef]
- Li, Z.; Bowman, R.S. Sorption of perchloroethylene by surfactant-modified zeolite as controlled by surfactant loading. Environ. Sci. Technol. 1998, 32, 2278–2282. [Google Scholar] [CrossRef]
- Reeve, P.J.; Fallowfield, H.J. Natural and surfactant modified zeolites: A review of their applications for water remediation with a focus on surfactant desorption and toxicity towards microorganisms. J. Environ. Manag. 2018, 205, 253–261. [Google Scholar] [CrossRef]
- Akçay, M. Characterization and adsorption properties of tetrabutylammonium montmorillonite (TBAM) clay: Thermodynamic and kinetic calculations. J. Colloid Interf. Sci. 2006, 296, 16–21. [Google Scholar] [CrossRef]
- Akçay, G.; Akçay, M.; Yurdakoç, K. The characterization of prepared organomontmorillonite (DEDMAM) and sorption of phenoxyalkanoic acid herbicides from aqueous solution. J. Colloid Interf. Sci. 2006, 296, 428–433. [Google Scholar] [CrossRef]
- Fuller, M.; Smith, J.A.; Burns, S.E. Sorption of nonionic organic solutes from water to tetraalkylammonium bentonites: Mechanistic considerations and application of the Polanyi–Manes potential theory. J. Colloid Interf. Sci. 2007, 313, 405–413. [Google Scholar] [CrossRef]
- Long, C.; Li, A.; Wu, H.; Liu, F.; Zhang, Q. Polanyi-based models for the adsorption of naphthalene from aqueous solutions onto nonpolar polymeric adsorbents. J. Colloid Interf. Sci. 2008, 319, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Anggraini, M.; Kurniawan, A.; Ong, L.K.; Martin, M.A.; Liu, J.-C.; Soetaredjo, F.E.; Indraswati, N.; Ismadji, S. Antibiotic detoxification from synthetic and real effluents using a novel MTAB surfactant-montmorillonite (organoclay) sorbent. RSC Adv. 2014, 4, 16298. [Google Scholar] [CrossRef] [Green Version]
- Ghemit, R.; Makhloufi, A.; Djebri, N.; Flilissa, A.; Zerroual, L.; Boutahala, M. Adsorptive removal of diclofenac and ibuprofen from aqueous solution by organobentonites: Study in single and binary systems, Groundw. Sustain. Dev. 2019, 8, 520–529. [Google Scholar] [CrossRef]
- Kim, J.-H.; Shin, W.S.; Song, D.-I.; Choi, S.J. Multi-step competitive sorption and desorption of chlorophenols in surfactant modified montmorillonite. Water Air Soil Pollut. 2005, 166, 367–380. [Google Scholar] [CrossRef]
- Xia, G.; Ball, W.P. Adsorption-partitioning uptake of nine low-polarity organic chemicals on a natural sorbent. Environ. Sci. Technol. 1999, 33, 262–269. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (US EPA). Cation-Exchange Capacity of Soils (Sodium Acetate)–Test Methods for the Evaluation of Solid Waste: Laboratory Manual Physical Chemical Methods; US EPA: Washington, DC, USA, 2014. Available online: https://www.epa.gov/hw-sw846/sw-846-test-method-9081-cation-exchange-capacity-soils-sodium-acetate (accessed on 9 October 2020).
- Appel, C.; Ma, L.Q.; Rhue, R.D.; Kennelley, E. Point of zero charge determination in soils and minerals via traditional methods and detection of electroacoustic mobility. Geoderma 2003, 113, 77–93. [Google Scholar] [CrossRef] [Green Version]
- Allen-King, R.M.; Grathwohl, P.; Ball, W.P. New modeling paradigms for the sorption of hydrophobic organic chemicals to heterogeneous carbonaceous matter in soils, sediments, and rocks. Adv. Water Resour. 2002, 25, 985–1016. [Google Scholar] [CrossRef]
- Long, C.; Lu, J.D.; Li., A.; Hu, D.; Liu, F.; Zhang, Q. Adsorption of naphthalene onto the carbon adsorbent from waste ion exchange resin: Equilibrium and kinetic characteristics. J. Hazard. Mater. 2008, 150, 656–661. [Google Scholar] [CrossRef]
- Kleineidam, S.; Schüth, C.; Grathwohl, P. Solubility-normalized combined adsorption-partitioning sorption isotherms for organic pollutants. Environ. Sci. Technol. 2002, 36, 4689–4697. [Google Scholar] [CrossRef]
- Choy, K.K.H.; Porter, J.F.; McKay, G. Langmuir Isotherm Models Applied to the Multicomponent Sorption of Acid Dyes from Effluent onto Activated Carbon. J. Chem. Eng. Data 2000, 45, 575–584. [Google Scholar] [CrossRef]
- Bellot, J.C.; Condoret, J.S. Modelling of liquid chromatography equilibrium. Process Biochem. 1993, 28, 365–376. [Google Scholar] [CrossRef]
- Ghaedi, N.; Jajjati, S.; Mahmudi, Z.; Tyagi, I.; Agarwal, S.; Maity, A.; Gupta, V.K. Modeling of competitive ultrasonic assisted removal of the dyes—Methylene blue and Safranin-O using Fe3O4 nanoparticles. Chem. Eng. J. 2015, 268, 28–37. [Google Scholar] [CrossRef]
- Radke, C.J.; Prausnitz, J.M. Thermodynamics of multi-solute adsorption from dilute liquid solutions. AIChE J. 1972, 18, 761–768. [Google Scholar] [CrossRef]
- Yen, C.Y.; Singer, P.C. Competitive Adsorption of Phenols on Activated Carbon. J. Environ. Eng. 1984, 110, 976–989. [Google Scholar] [CrossRef]
- Shin, W.S. Competitive sorption of anionic and cationic dyes onto cetylpyridinium-modified montmorillonite. J. Environ. Sci. Health Part A 2008, 43, 1459–1470. [Google Scholar] [CrossRef]
- Song, D.-I.; Choi, J.; Shin, W.S. The modified Song isotherm model: Application to multisolute sorption of phenols in organoclays using the ideal adsorbed solution theory. Environ. Technol. 2019, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Groisman, L.; Rav-Acha, C.; Gerstl, Z.; Mingelgrin, U. Sorption of organic compounds of varying hydrophobicities from water industrial wastewater by long- and short-chain organoclays. Appl. Clay Sci. 2004, 24, 159–166. [Google Scholar] [CrossRef]
- Zhou, Q.; Frost, R.L.; He, H.; Xi, Y. Changes in the surfaces of adsorbed para-nitrophenol on HDTMA organoclay-The XRD and TG study. J. Colloid Interf. Sci. 2007, 307, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Ko, C.H.; Fan, C.; Chiang, P.N.; Wang, M.K.; Lin, K.C. p-nitrophenol, phenol and aniline sorption by organo-clays. J. Hazard. Mater. 2007, 149, 275–282. [Google Scholar] [CrossRef]
- Thanos, A.G.; Katsou, E.; Malamis, S.; Psarras, K.; Pavaltou, E.A.; Haralambous, K.J. Evaluation of modified mineral performance for chromate sorption from aqueous solutions. Chem. Eng. J. 2012, 211–212, 77–88. [Google Scholar] [CrossRef]
- Kumar, K.V.; Gadipelli, S.; Wood, B.; Ramisetty, K.A.; Stewart, A.A.; Howard, C.A.; Brett, D.J.L.; Rodriguez-Reinoso, F. Characterization of the adsorption site energies and heterogeneous surfaces of porous materials. J. Mater. Chem. A 2019, 7, 10104. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, A.S.; Sakaria, P.L.; Vasudevan, M.; Pawar, R.R.; Sudheesh, N.; Bajaj, H.C.; Mody, H.M. Adsorption of an anionic dye from aqueous medium by organoclays: Equilibrium modeling, kinetic and thermodynamic exploration. RCS Adv. 2012, 2, 8663–8671. [Google Scholar] [CrossRef]
- McKay, G.; Al Duri, B. Prediction of multicomponent adsorption equilibrium data using empirical correlations. Chem. Eng. J. 1989, 41, 9–23. [Google Scholar] [CrossRef]
- Sun, K.; Shi, Y.; Wang, X.; Li, Z. Sorption and retention of diclofenac on zeolite in the presence of cationic surfactant. J. Hazard. Mater. 2017, 323, 584–592. [Google Scholar] [CrossRef]
- Septian, A.; Oh, S.; Shin, W.S. Sorption of antibiotics onto montmorillonite and kaolinite: Competition modelling. Environ. Technol. 2019, 40, 2940–2953. [Google Scholar] [CrossRef]
- El-Kamash, A.M. Evaluation of zeolite A for the sorptive removal of Cs+ and Sr2+ ions from aqueous solutions using batch and fixed bed column operations. J. Hazard. Mater. 2008, 151, 432–445. [Google Scholar] [CrossRef]
- Stapleton, M.G.; Sparks, D.L.; Dentel, S.K. Sorption of pentachlorophenol to HDTMA-clay as a function of ionic strength and pH. Environ. Sci. Technol. 1994, 28, 2330–2335. [Google Scholar] [CrossRef]
- Kim, J.-H.; Shin, W.S.; Song, D.-I.; Choi, S.J. Sequential competitive sorption and desorption of chlorophenols in organoclay. Korean J. Chem. Eng. 2006, 23, 63–70. [Google Scholar] [CrossRef]
- Dong, Y.; Wu, D.; Chen, X.; Lin, Y. Adsorption of bisphenol A from water by surfactant-modified zeolite. J. Colloid Interf. Sci. 2010, 348, 585–590. [Google Scholar] [CrossRef]
- Xie, J.; Meng, W.; Wu, D.; Zhang, Z.; Kong, H. Removal of organic pollutants by surfactant modified zeolite: Comparison between ionizable phenolic compounds and non-ionizable organic compounds. J. Hazard. Mater. 2012, 231–232, 57–63. [Google Scholar] [CrossRef]
- Krajišnik, D.; Kaković, A.; Milojević, M.; Malenović, A.; Kragović, M.; Bogdanović, D.B.; Dondur, V.; Milić, J. Properties of diclofenac sodium sorption onto natural zeolite modified cetylpyridinium chloride. Colloids Surf. B 2011, 83, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Zhu, L.; Xing, B. Adsorption of polycylic aromatic hydrocarbons by carbon nanomaterials. Environ. Sci. Technol. 2006, 40, 1855–1861. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liu, F.; Jing, X.; Ling, P.; Li, A. Displacement mechanism of binary competitive adsorption for aqueous divalent metal ions onto a novel IDA-chelating resin: Isotherm and kinetic modeling. Water Res. 2011, 45, 1177–1188. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Salicylic Acid (SA) | Ibuprofen Sodium (IB) |
|---|---|---|
| Molecular structure | 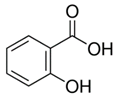 | 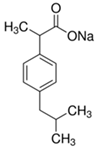 |
| Molar mass (g/mol) | 138.12 | 228.26 |
| Water solubility (mg/mL) | 1.8 | 100 |
| Molar volume (cm3/mol) 1 | 95.717 | 221.61 |
| log Kow at 20 °C | 2.3 | 3.5 |
| log Dow at pH 7 | −1.13 | 2.82 |
| Density (g/cm3) | 1.443 | 1.03 |
| pKa | 2.97 | 4.91 |
| Molecular size (Å) | 8.6 | 6.7 |
| Model/Equation | ||
|---|---|---|
| Single-Solute Sorption Isotherm | Equation | Ref. |
| Freundlich | (1) | - |
| Langmuir | (2) | - |
| Dubinin-Radushkevich (DR) | (3) | [20,21] |
| (4) | ||
| Polanyi−Dubinin−Manes (PDM) | (5) | [23,30,31,32] |
| Bi-Solute Sorption Isotherm | Equation | Ref. |
| Extended Langmuir model (ELM) | (6) | [33] |
| Modified Langmuir competitive model (MLCM) | (7) | [34,35] |
| IAST | (8) | [36,37,38,39] |
| Parameter | HM | HZ |
|---|---|---|
| Organic carbon content (foc, %) | 7.71 | 2.03 |
| CEC (meq/100 g) | 23.33 | 61.5 |
| BET surface area (ABET, m2/g) | 25.39 | 24.17 |
| Pore size (Å) | 97.31 | 124.2 |
| Pore volume (cm3/g) | 0.095 | 0.103 |
| pH | 3.6 | 4.9 |
| PZC | <1.9 | 6.2 |
| Freundlich | Sorbent | Solute | KF ((mmol/kg)/(mmol/L)) | NF (-) | R2 | SSE | |
| HM | SA | 57.148 ± 1.5973 | 0.4850 ± 0.0168 | 0.9942 | 6.6340 | ||
| IB | 153.10 ± 9.0869 | 0.6868 ± 0.0216 | 0.9956 | 4.6873 | |||
| HZ | SA | 22.371 ± 1.4158 | 0.5643 ± 0.0580 | 0.9484 | 13.311 | ||
| IB | 73.983 ± 3.9861 | 0.7719 ± 0.0276 | 0.9946 | 2.7769 | |||
| Langmuir | Sorbent | Solute | qmL (mmol/kg) | b (L/mmol) | R2 | SSE | SF |
| HM | SA | 42.400 ± 2.1476 | 9.1078 ± 1.2636 | 0.9844 | 17.780 | 0.5233 | |
| IB | 59.319 ± 2.8827 | 10.465 ± 0.8633 | 0.9976 | 2.5771 | 0.4887 | ||
| HZ | SA | 23.773 ± 2.3076 | 3.3703 ± 0.7250 | 0.9679 | 8.2896 | 0.7479 | |
| IB | 59.373 ± 9.2778 | 2.7424 ± 0.6062 | 0.9916 | 4.3682 | 0.7848 | ||
| DR | Sorbent | Solute | qmD (mmol/kg) | βD (mol2/J2) | R2 | SSE | E (KJ/mol) |
| MM | SA | 39.185 ± 1.2220 | 1.8253E−08 ± 1.2547E-09 | 0.9829 | 19.520 | 5.234 | |
| IB | 56.520 ± 1.6017 | 1.7807E−08 ± 5.5576E-09 | 0.9964 | 3.8266 | 5.299 | ||
| HZ | SA | 18.750 ± 0.7977 | 3.2292E−08 ± 3.1121E-09 | 0.9658 | 8.8333 | 3.935 | |
| IB | 35.042 ± 2.0262 | 2.7385E−08 ± 2.0399E-09 | 0.9818 | 9.4266 | 4.273 | ||
| PDM | Sorbent | Solute | qm (mmol/kg) | a (mL2/J2) | R2 | SSE | |
| HM | SA | 63.966 ± 1.9805 | 7.458E−5 ± 2.544E-6 | 0.9950 | 5.698 | ||
| IB | 412.08 ± 28.383 | 2.942E−4 ± 7.077E-6 | 0.9976 | 2.574 | |||
| HZ | SA | 31.435 ± 2.6393 | 1.037E−4 ± 9.417E-6 | 0.9634 | 9.454 | ||
| IB | 307.55 ± 37.217 | 3.623E−4 ± 1.504E-5 | 0.9932 | 3.505 |
| Sorbent | Solute | qV,m (mL/kg) | α (-) | R2 | SSE |
|---|---|---|---|---|---|
| HM | SA | 6.123 ± 0.190 | 74.51 ± 2.541 | 0.9950 | 0.0522 |
| IB | 91.32 ± 6.290 | 294.0 ± 7.070 | 0.9976 | 0.1264 | |
| HZ | SA | 3.009 ± 0.253 | 103.6 ± 9.408 | 0.9634 | 0.0866 |
| IB | 68.16 ± 8.248 | 361.9 ± 15.03 | 0.9932 | 0.1721 | |
| HM | SA in SA/IB | 3.668 ± 0.175 | 59.20 ± 1.884 | 0.9936 | 0.0143 |
| IB in SA/IB | 69.87 ± 4.306 | 266.4 ± 4.841 | 0.9979 | 0.0367 | |
| HZ | SA in SA/IB | 3.293 ± 0.123 | 79.50 ± 1.793 | 0.9966 | 0.0044 |
| IB in SA/IB | 32.28 ± 4.959 | 245.4 ± 13.42 | 0.9780 | 0.2723 |
| Model | Parameters | HM | HZ |
|---|---|---|---|
| ELM | R2 SSE RMSE | 0.8115/0.9468 118.35/44.263 3.0172/1.8452 | 0.7180/0.7275 104.86/170.40 2.8401/3.6204 |
| MLCM | η1 η2 R2 SSE RMSE | 0.8711 ± 0.1769 0.5317 ± 0.0801 0.9368/0.9792 15.440/6.670 1.0150/0.6900 | 0.3412 ± 0.0144 0.2774 ± 0.0366 0.9976/0.9821 0.3362/4.5010 0.1497/0.5478 |
| IAST-Fr | R2 SSE RMSE | 0.9942/0.8553 3.6540/120.36 0.5302/3.0428 | 0.7903/0.6645 77.967/209.80 2.4490/4.0172 |
| IAST-Lang | R2 SSE RMSE | 0.9676/0.9293 20.355/58.762 1.2513/2.1261 | 0.7263/0.7004 101.77/187.34 2.7980/3.7961 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Shin, W.S. Removal of Salicylic and Ibuprofen by Hexadecyltrimethylammonium-Modified Montmorillonite and Zeolite. Minerals 2020, 10, 898. https://doi.org/10.3390/min10100898
Choi J, Shin WS. Removal of Salicylic and Ibuprofen by Hexadecyltrimethylammonium-Modified Montmorillonite and Zeolite. Minerals. 2020; 10(10):898. https://doi.org/10.3390/min10100898
Chicago/Turabian StyleChoi, Jiyeon, and Won Sik Shin. 2020. "Removal of Salicylic and Ibuprofen by Hexadecyltrimethylammonium-Modified Montmorillonite and Zeolite" Minerals 10, no. 10: 898. https://doi.org/10.3390/min10100898
APA StyleChoi, J., & Shin, W. S. (2020). Removal of Salicylic and Ibuprofen by Hexadecyltrimethylammonium-Modified Montmorillonite and Zeolite. Minerals, 10(10), 898. https://doi.org/10.3390/min10100898







