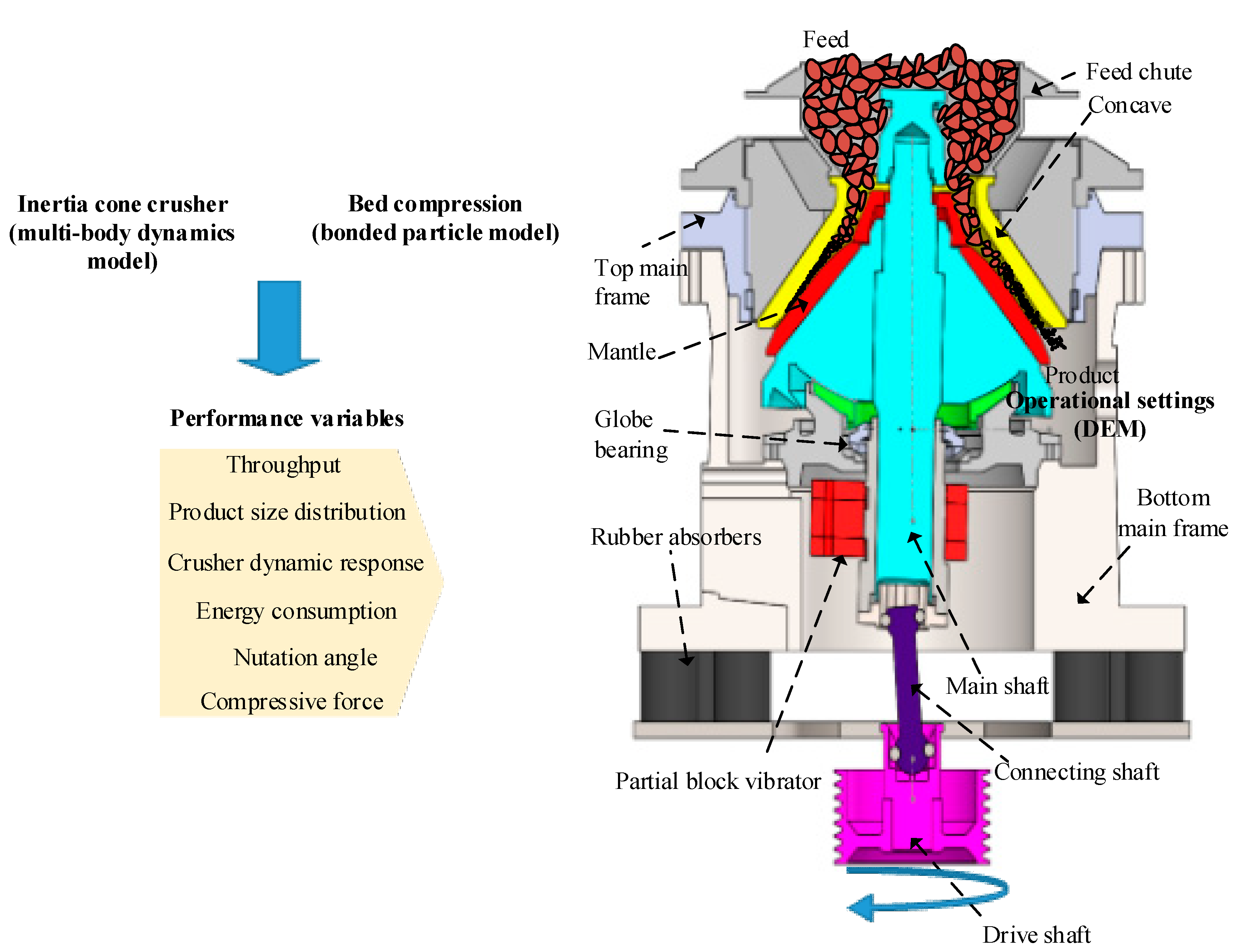
A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling
Abstract
:1. Introduction
2. Mathematical Model for the Inertia Cone Crusher with Bonded Particles
- All components of the inertia cone crusher are taken as rigid bodies.
- The drive speed is stable.
- The values for the stiffness and the damping for the rubber absorbers are invariant.
- The feed particles have the same material properties and uniform sizes.
- The particles are uniformly distributed in the chamber which is filled with broken particles.
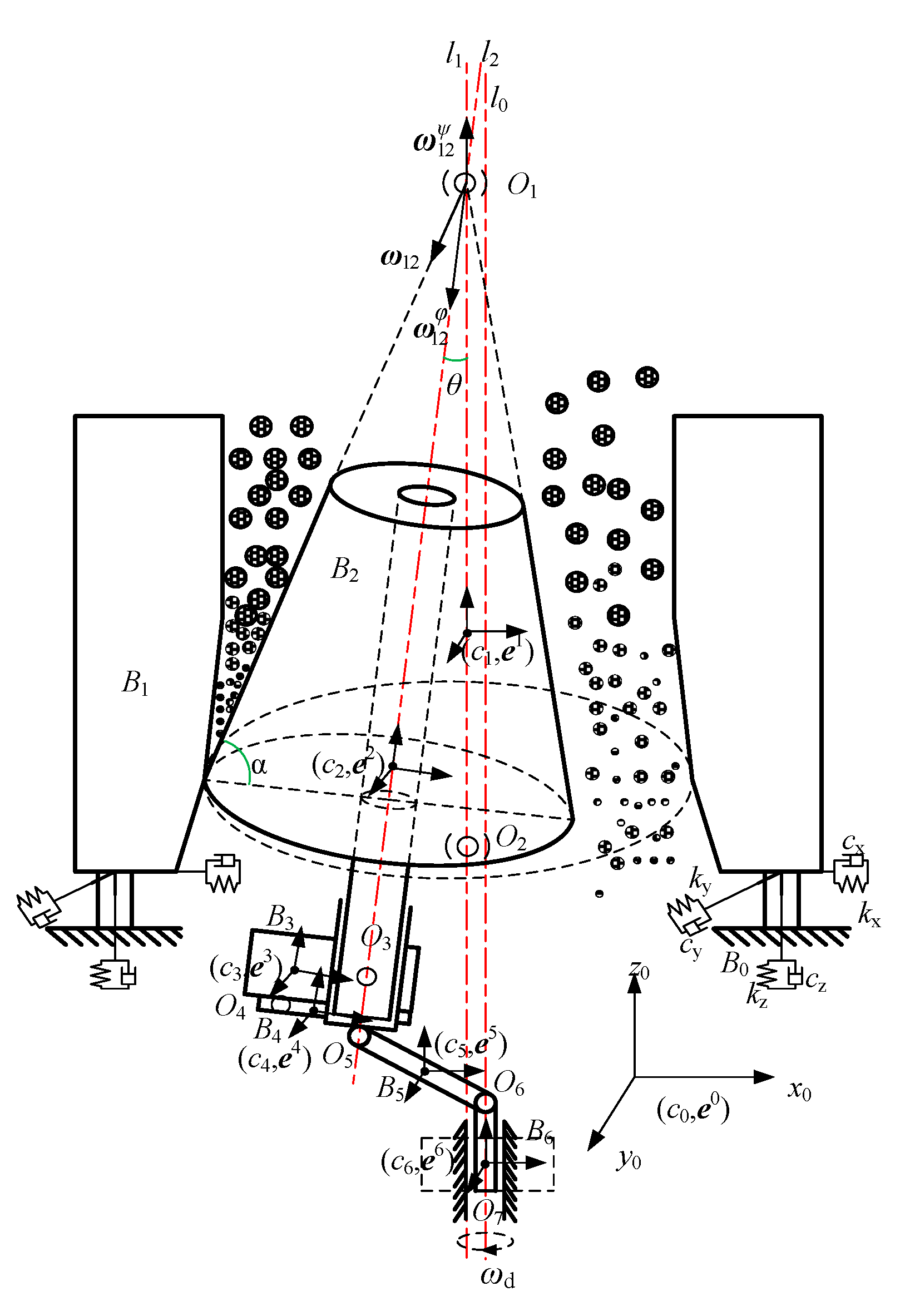
2.1. Cartesian Coordinate Method Formulation
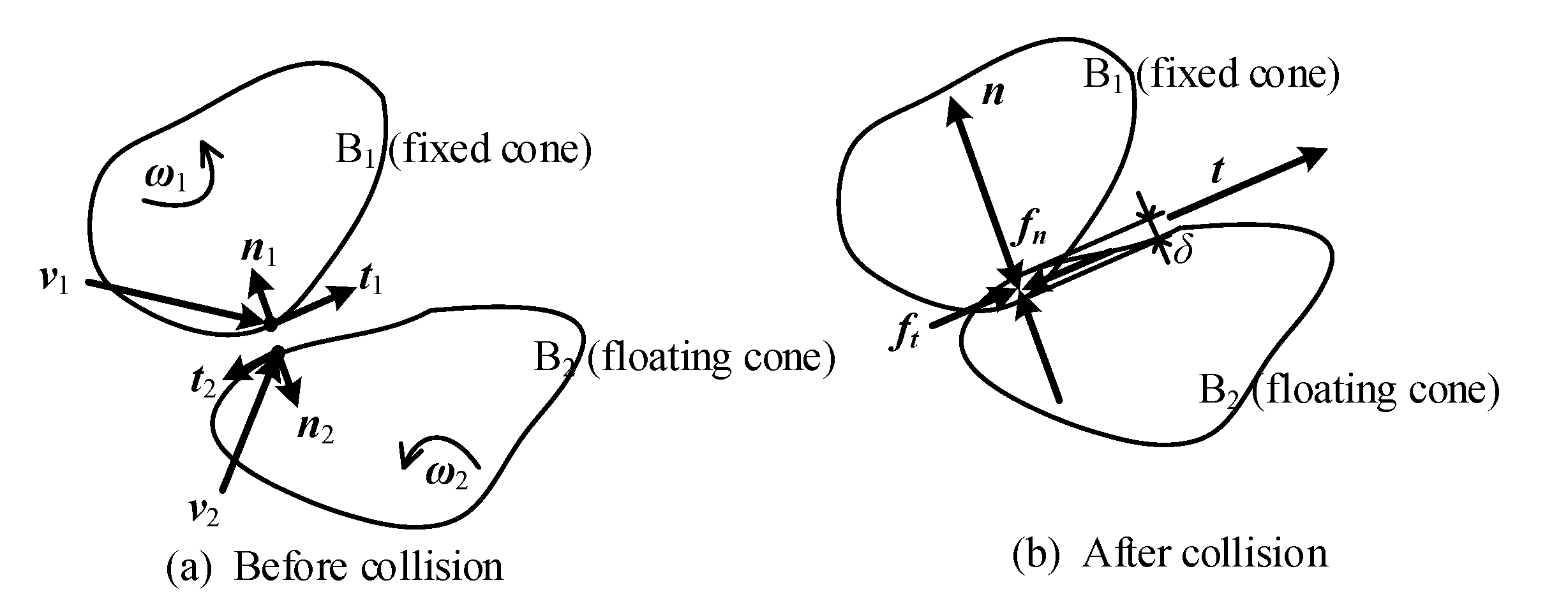
2.2. Nonlinear Contact Model
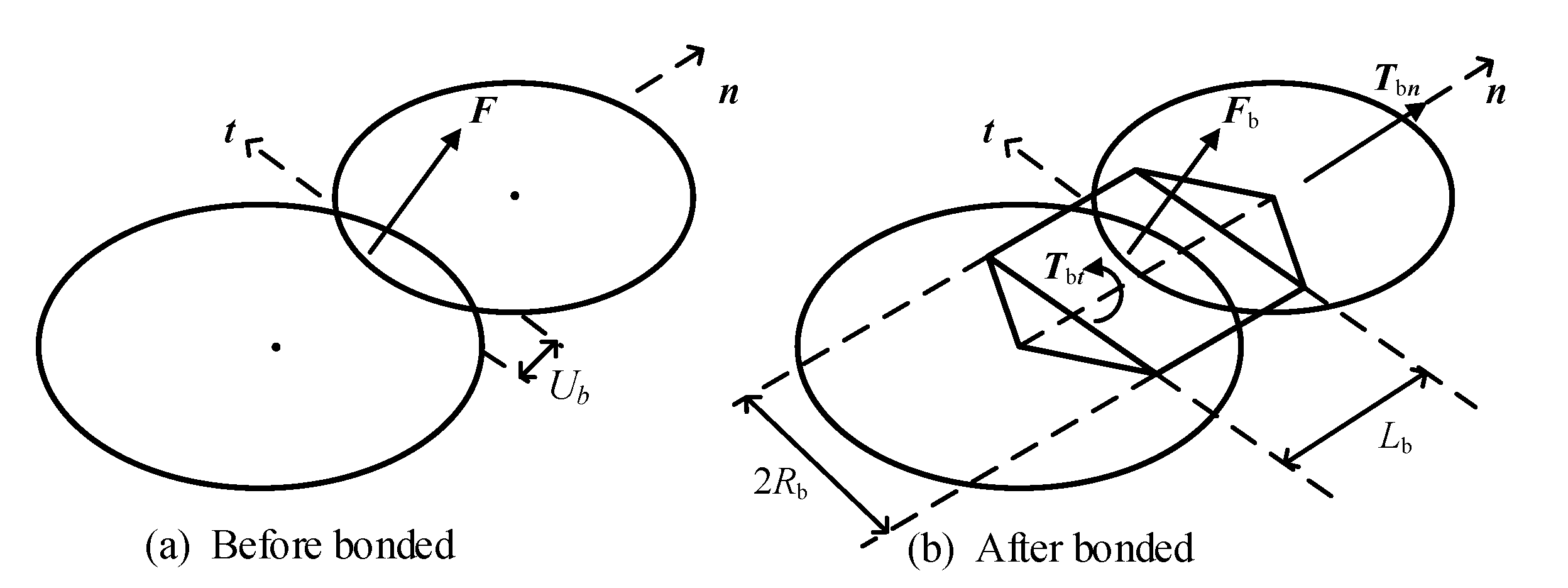
2.3. Particle Compression Model Using DEM
2.4. The Bonded Particle Model Calibration
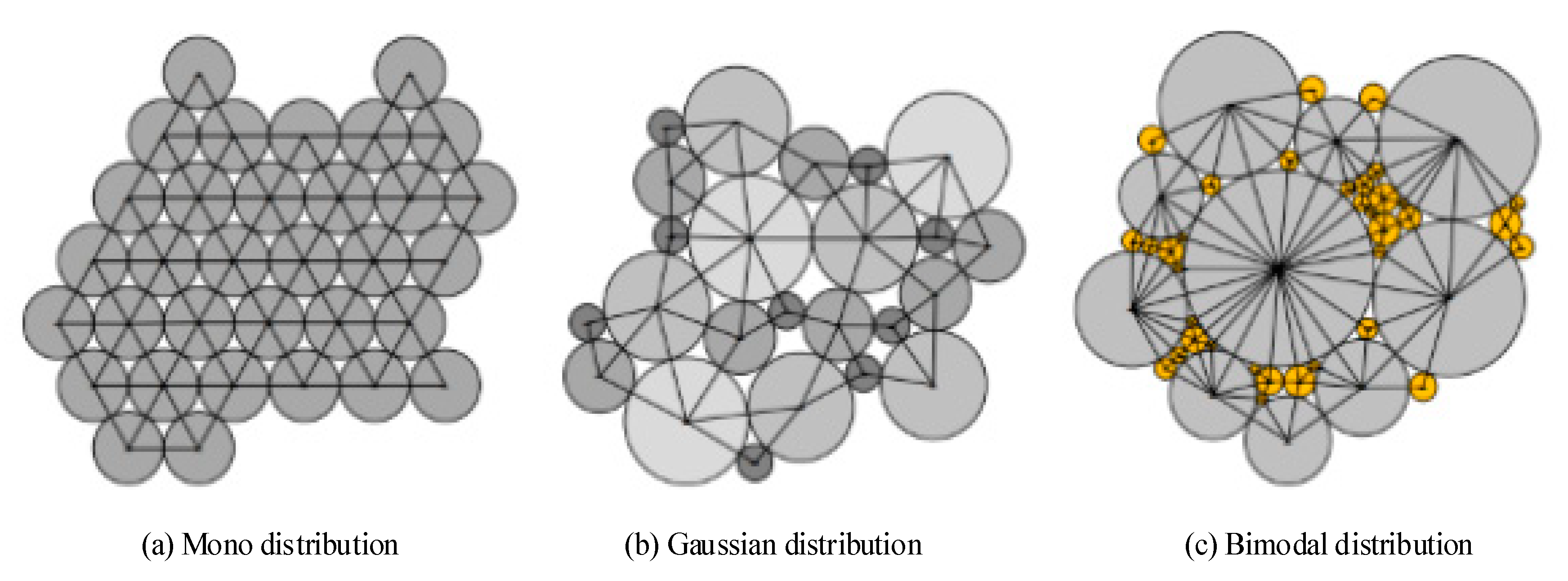
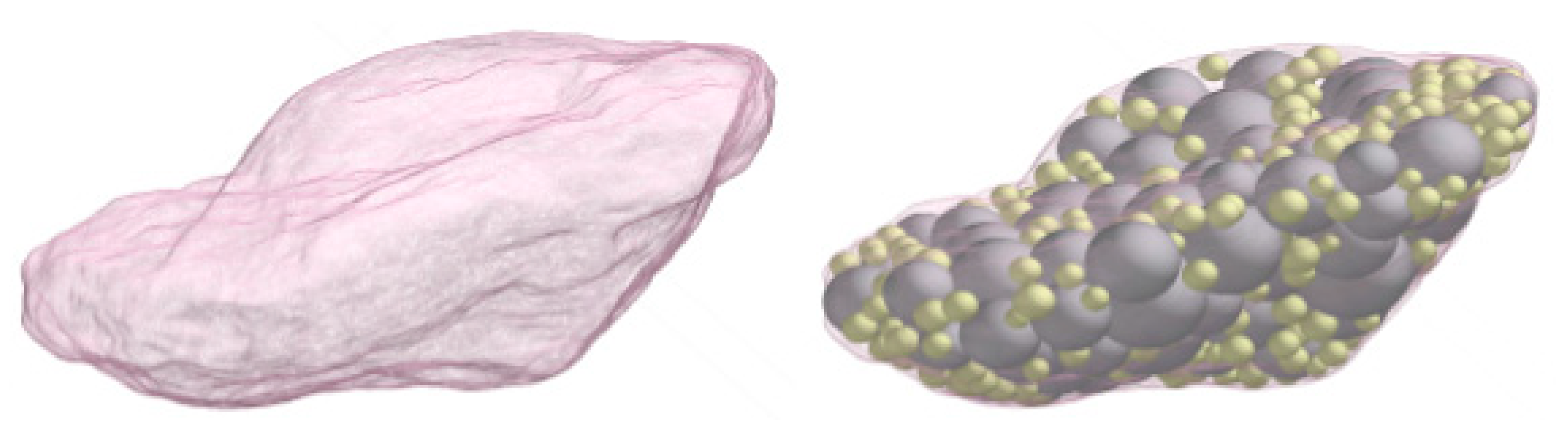
2.4.1. A Bimodal Particle Packing Cluster
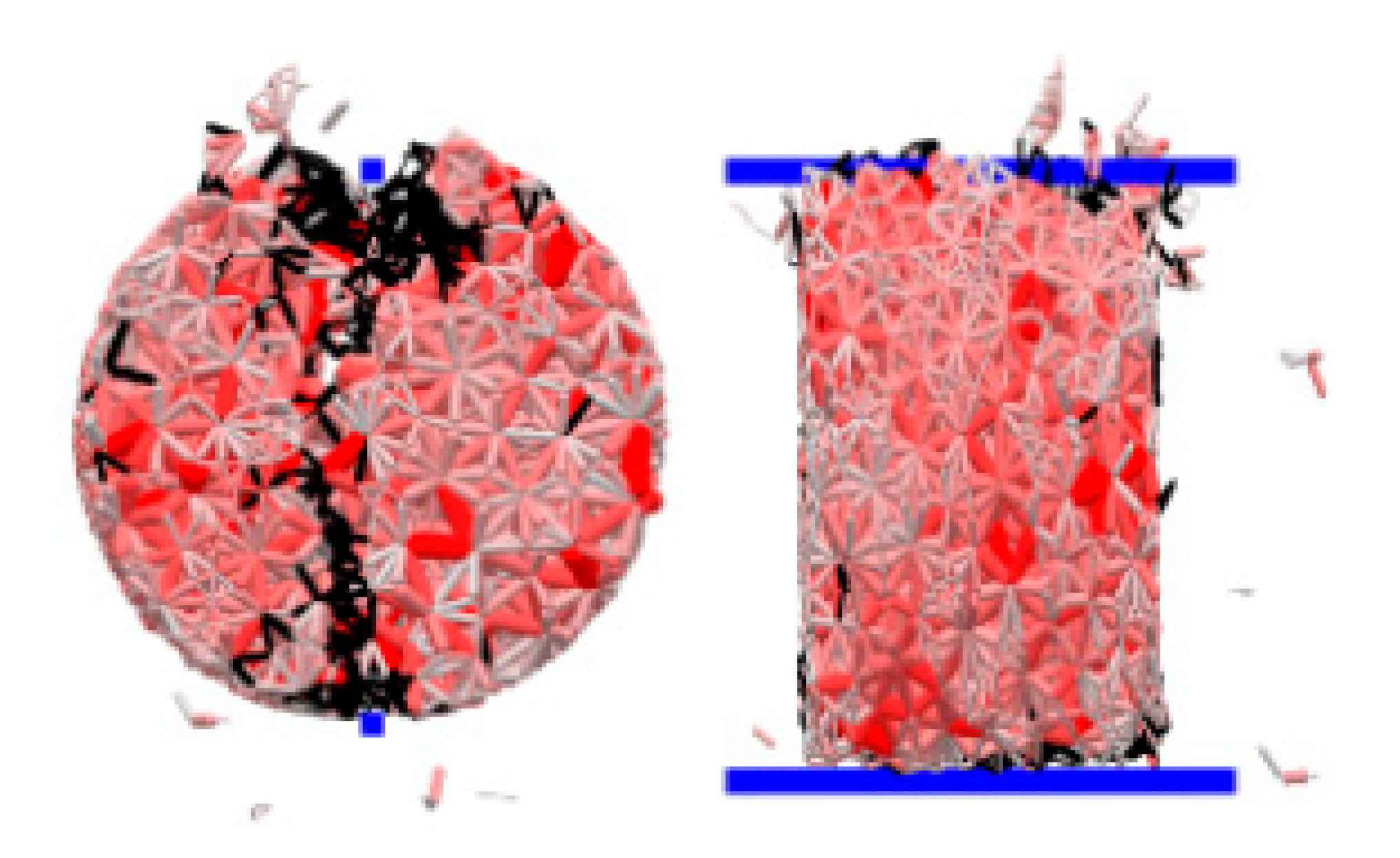
2.4.2. Laboratory Breakage Experiments
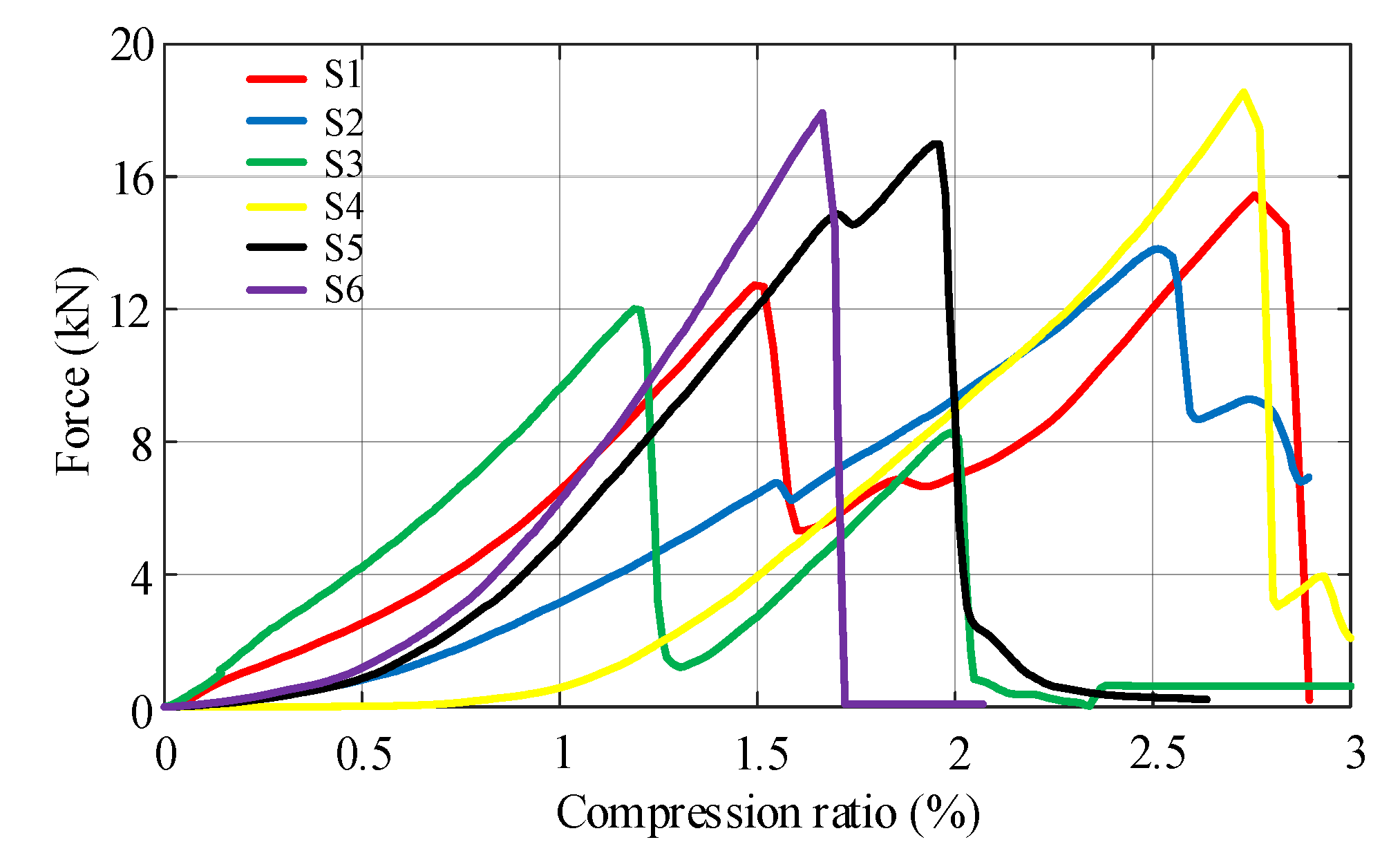
2.4.3. Breakage Simulations Established Using DOE
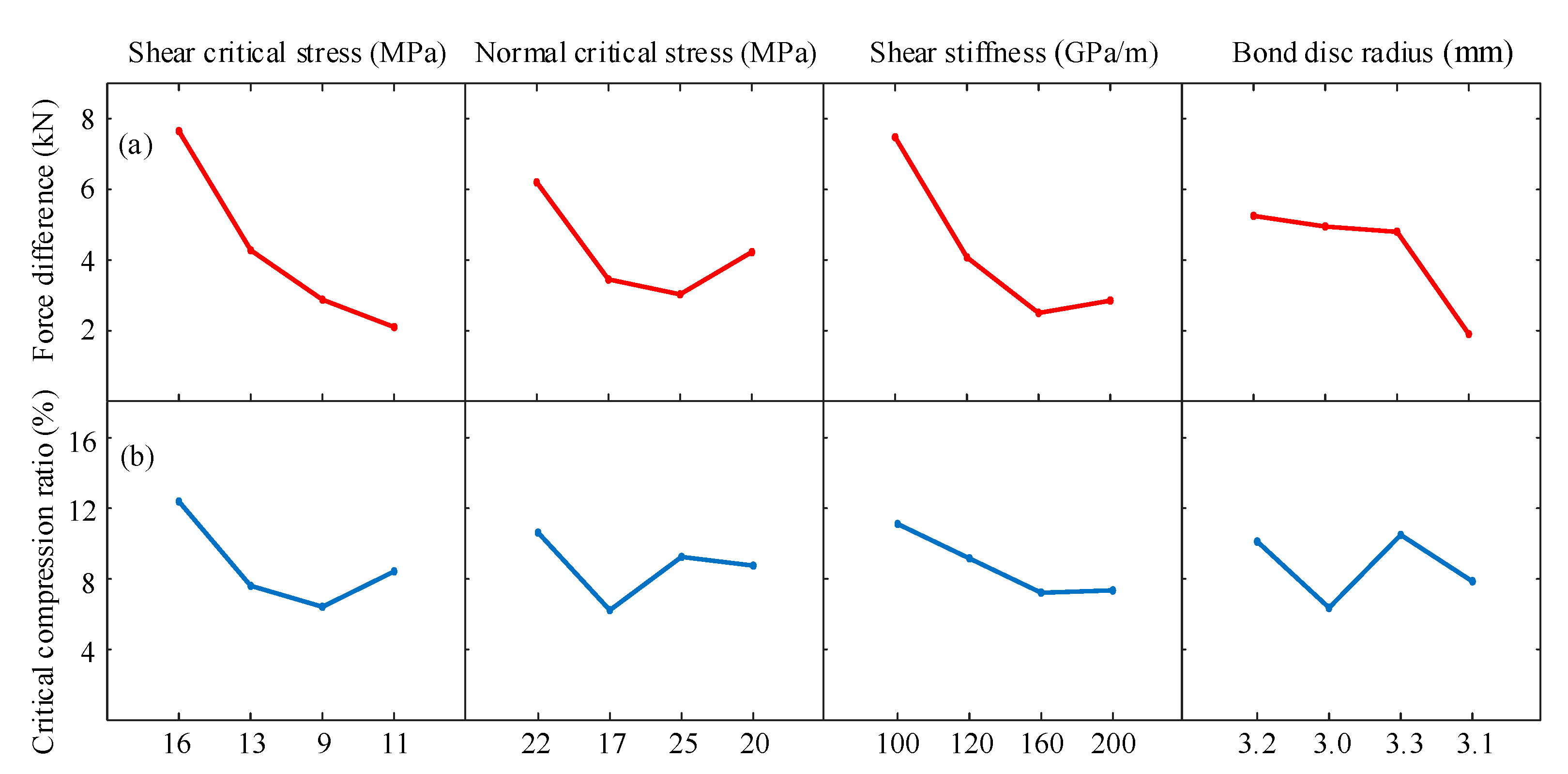
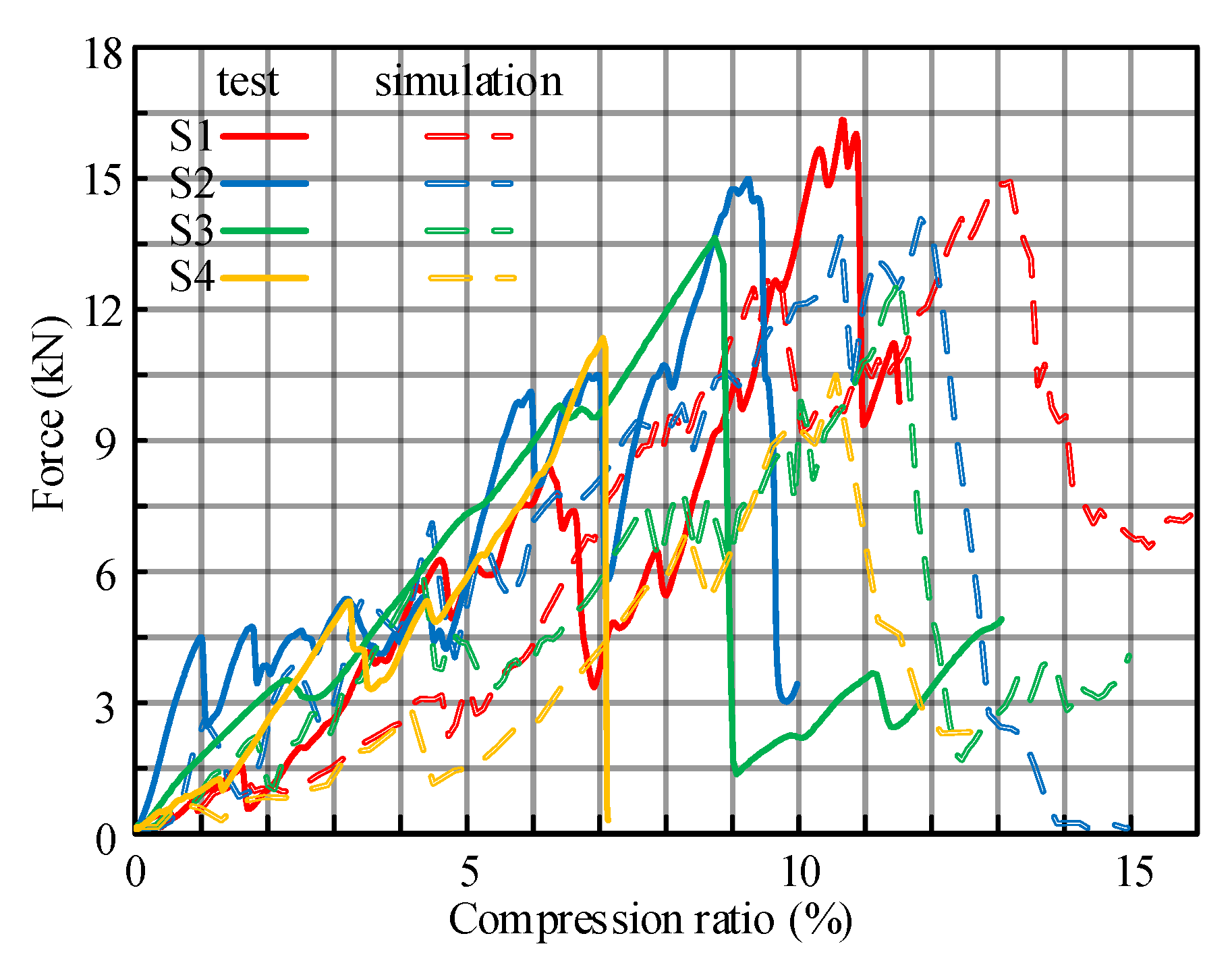
2.4.4. The Optimum BPM Parameters
3. Simulation Scheme for the Coupled Model and Validation for Industrial Experiments
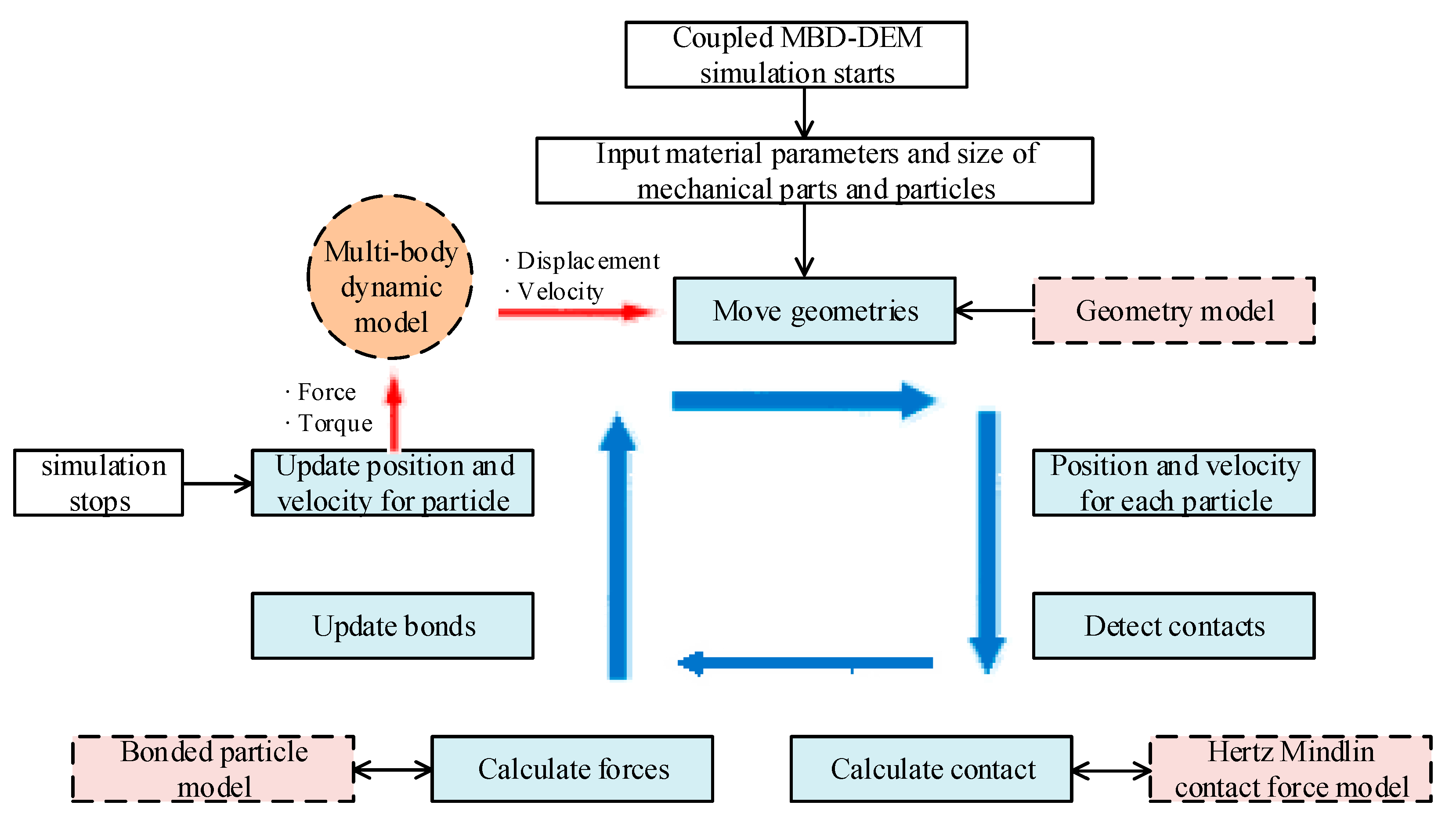
3.1. Numerical Calculation Flow Chart for Coupling of MBD–DEM
3.2. Industrial Experiments
4. Results and Discussion
4.1. Coupled Model Validation
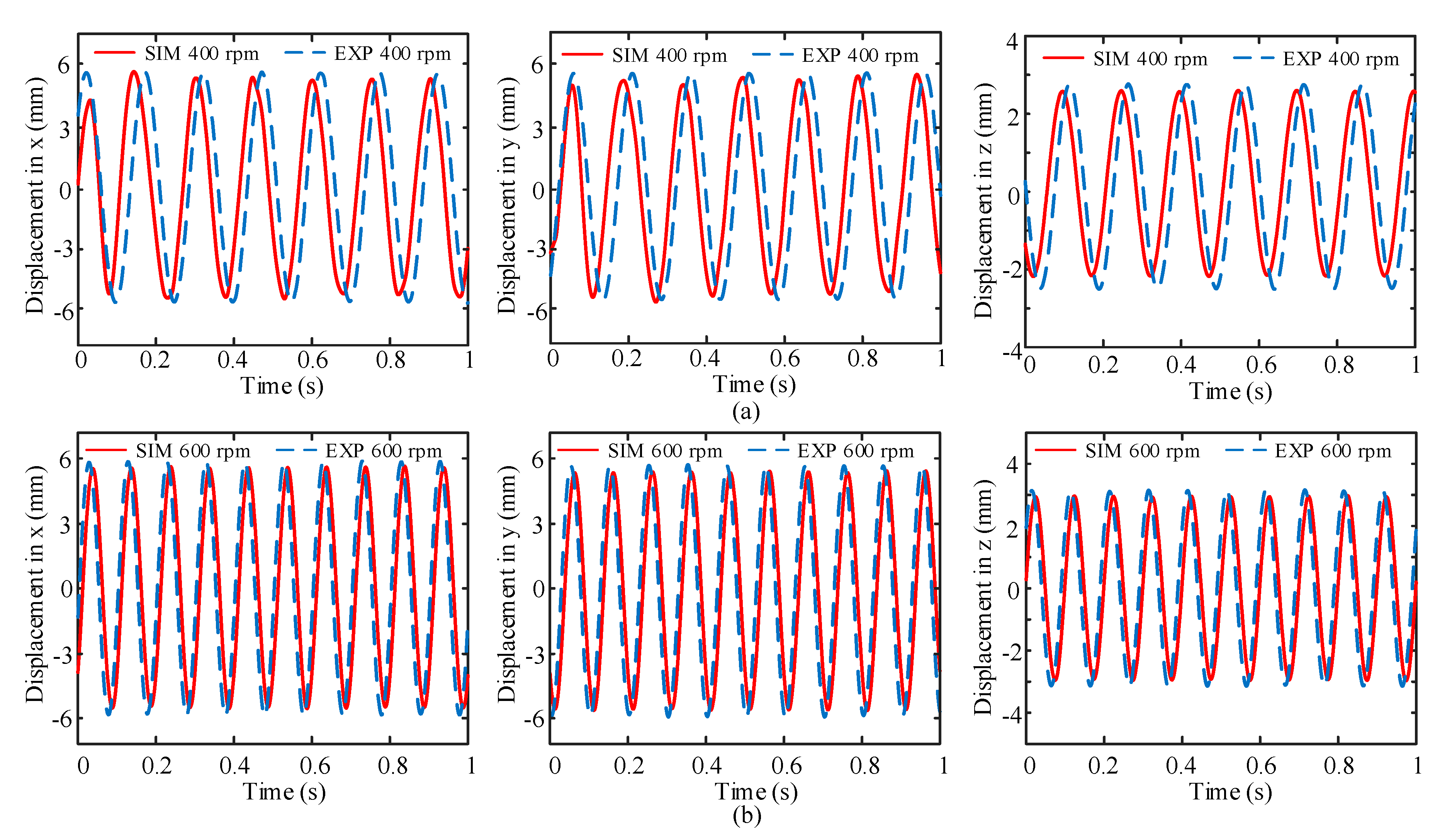
4.1.1. The Displacements of the Test Point
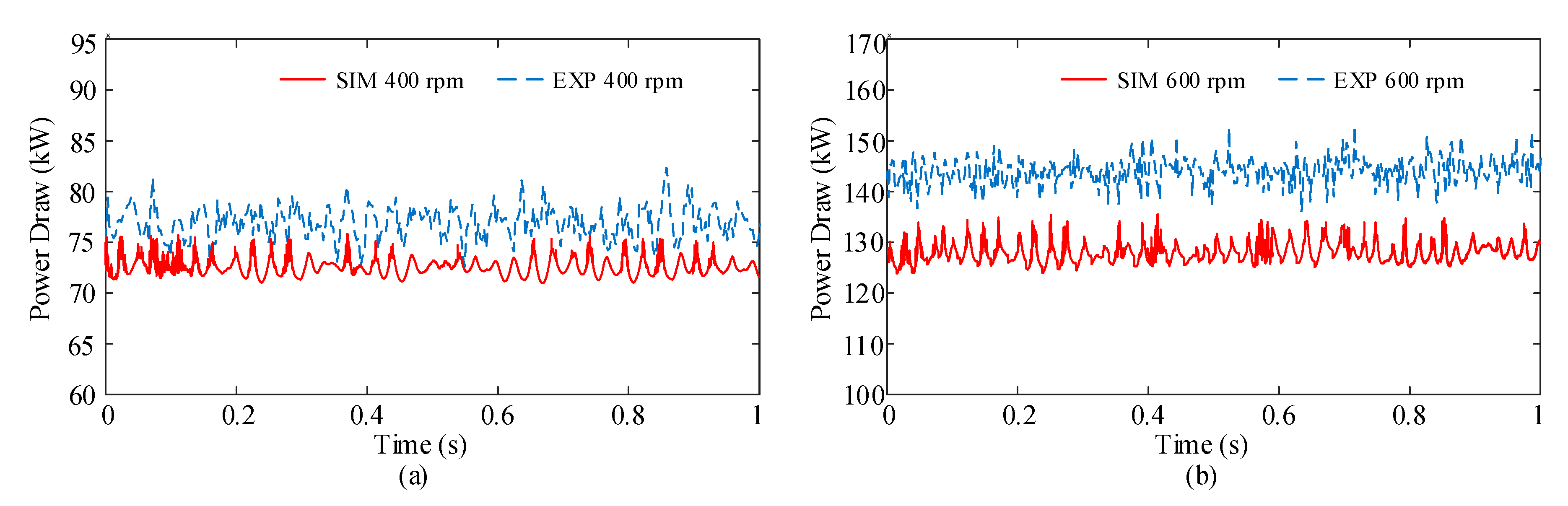
4.1.2. Power Draw
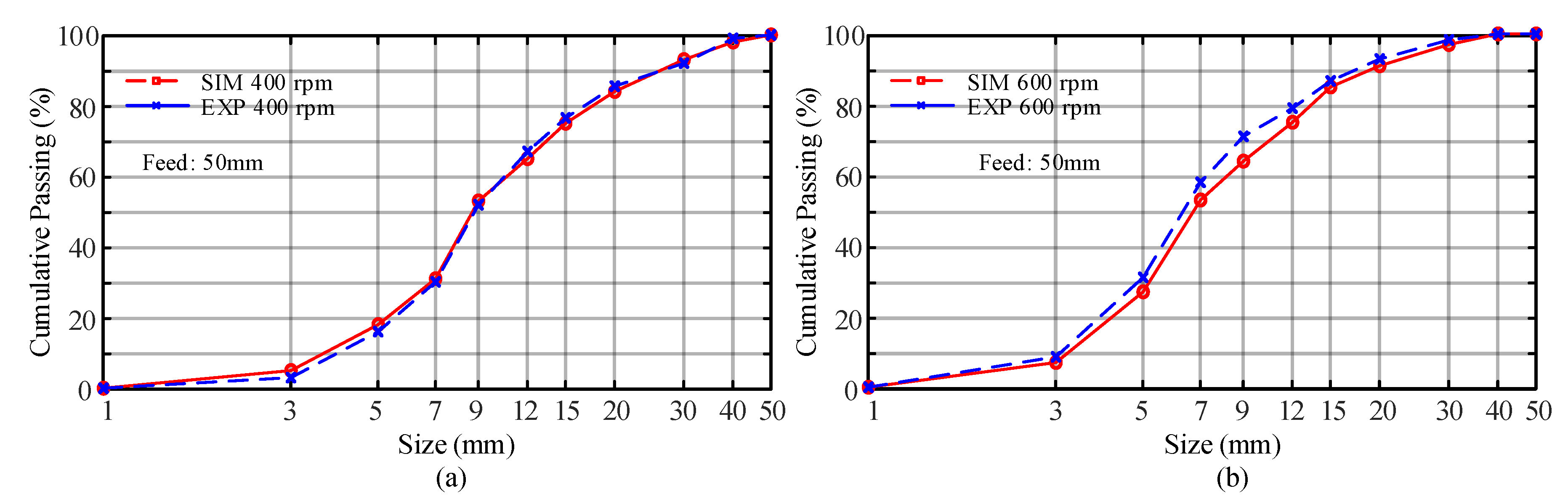
4.1.3. Product Size Distribution and Throughput Capacity
4.2. Simulated Results
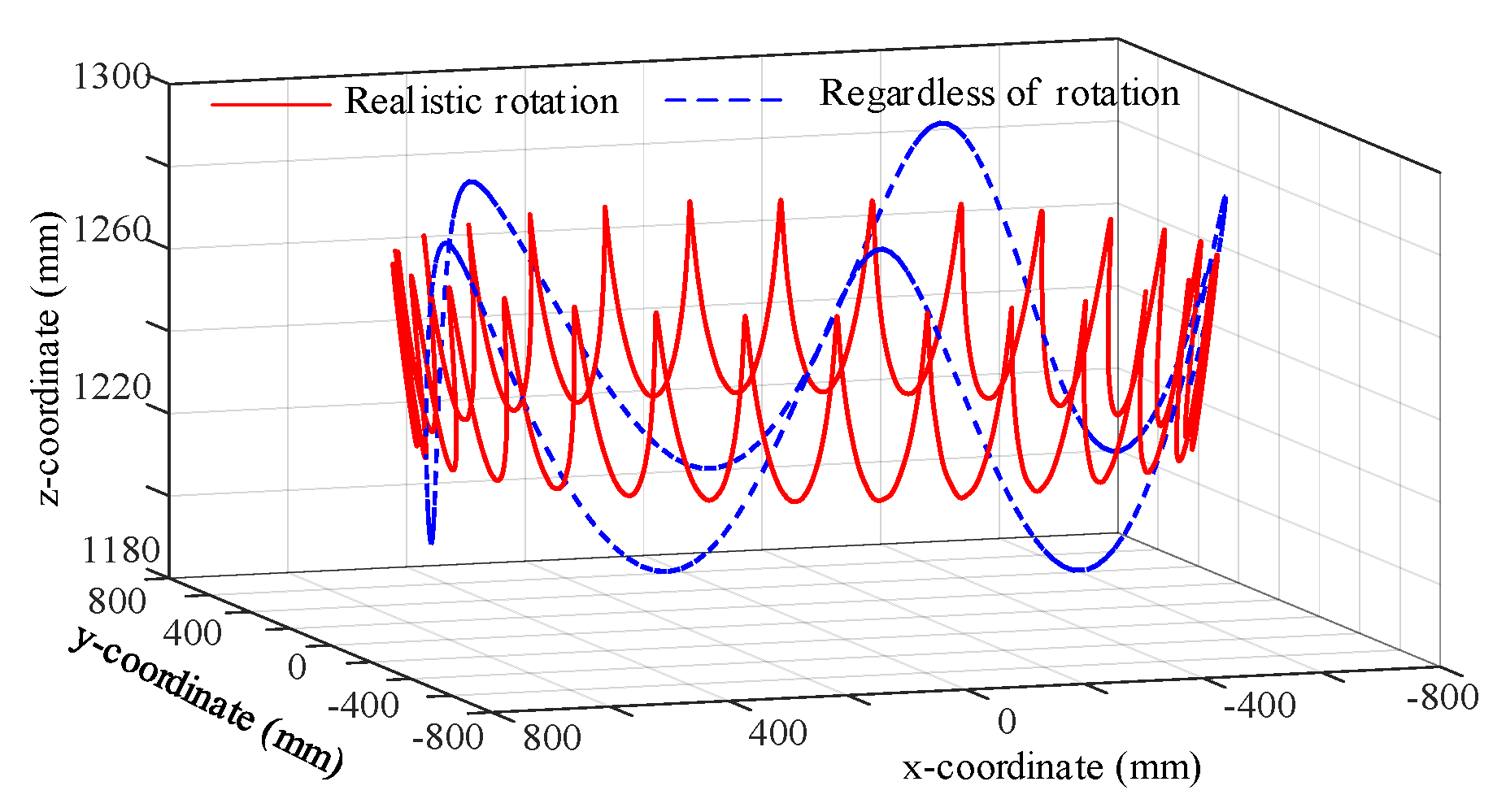
4.2.1. Trajectory of Fixed Point in the Mantle Surface
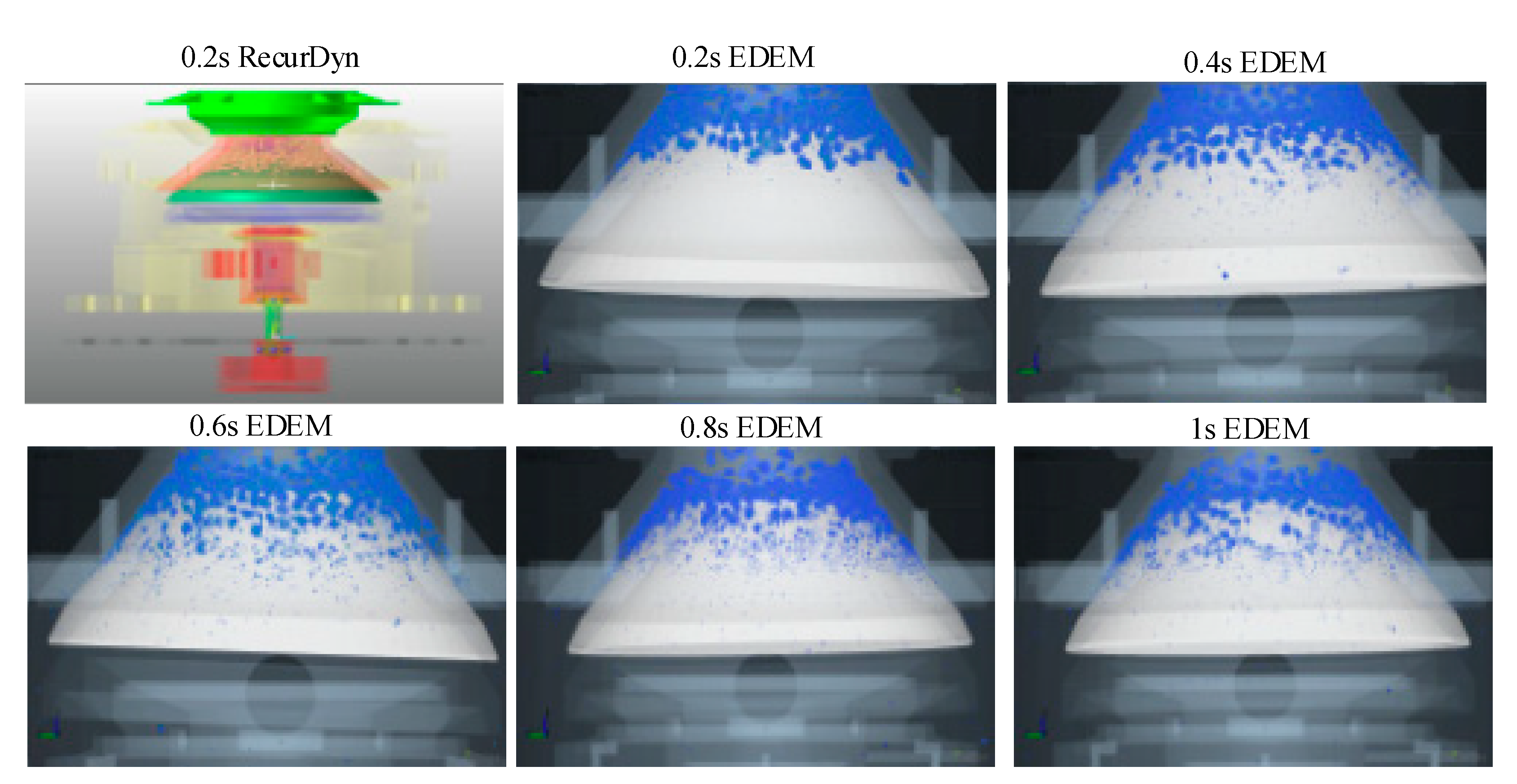
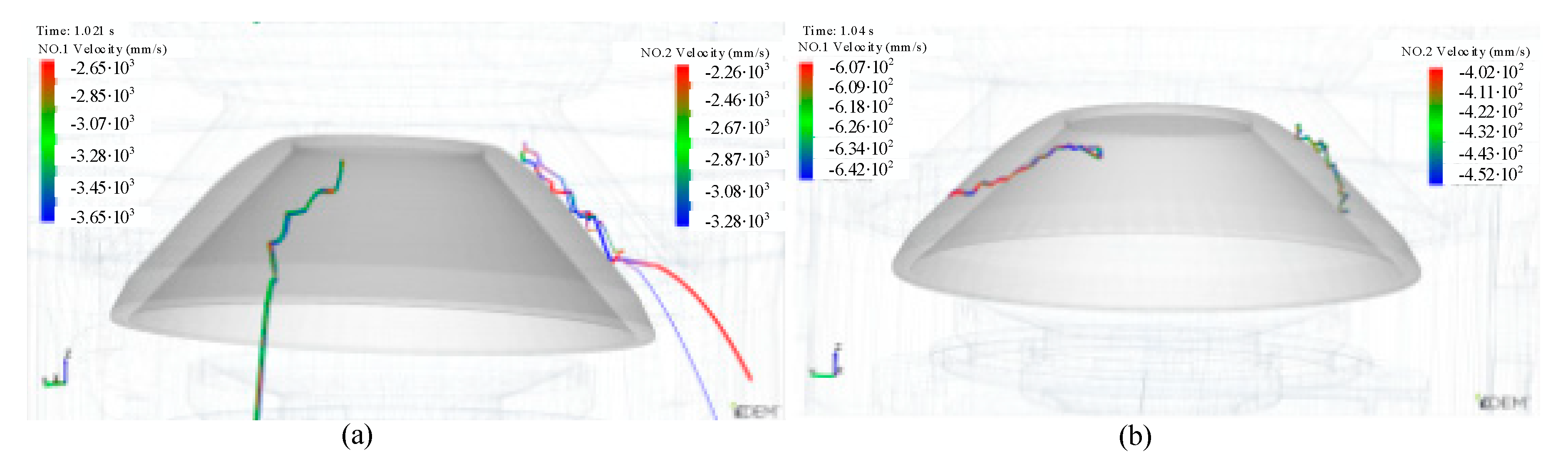
4.2.2. Behavior of the Particle Flow
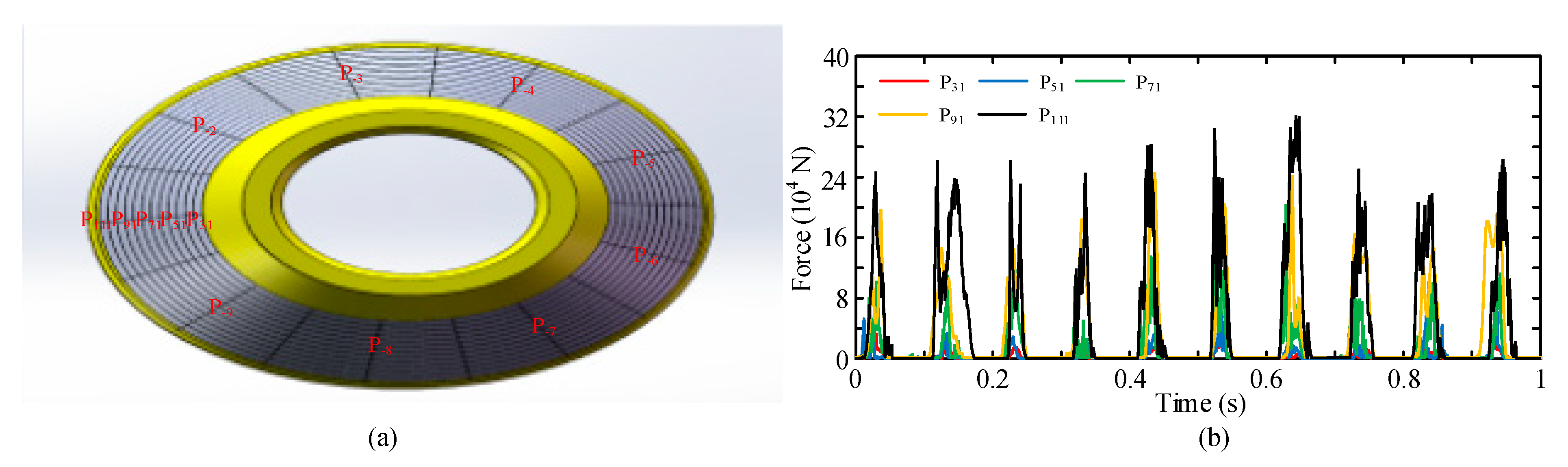
4.2.3. Crushing Force Distribution in the Concave Surface
4.3. Influence of Fixed Cone Mass and Drive Speed on Crusher Performance
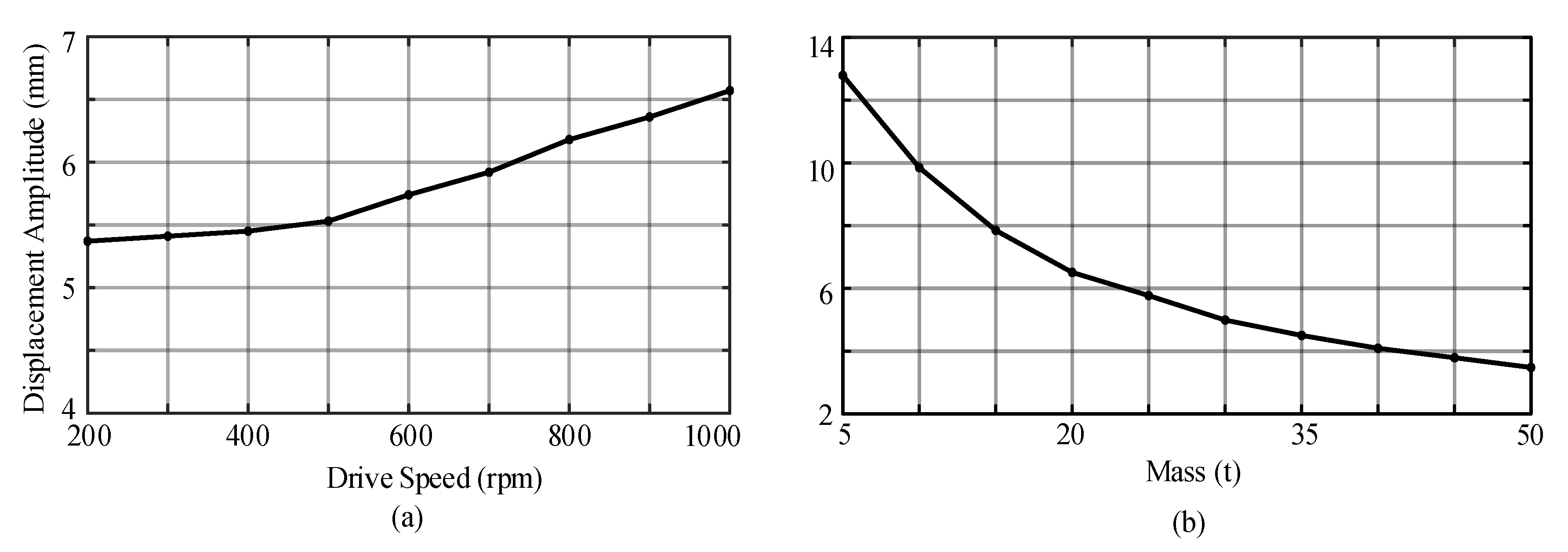
4.3.1. Influence on Displacement Amplitude
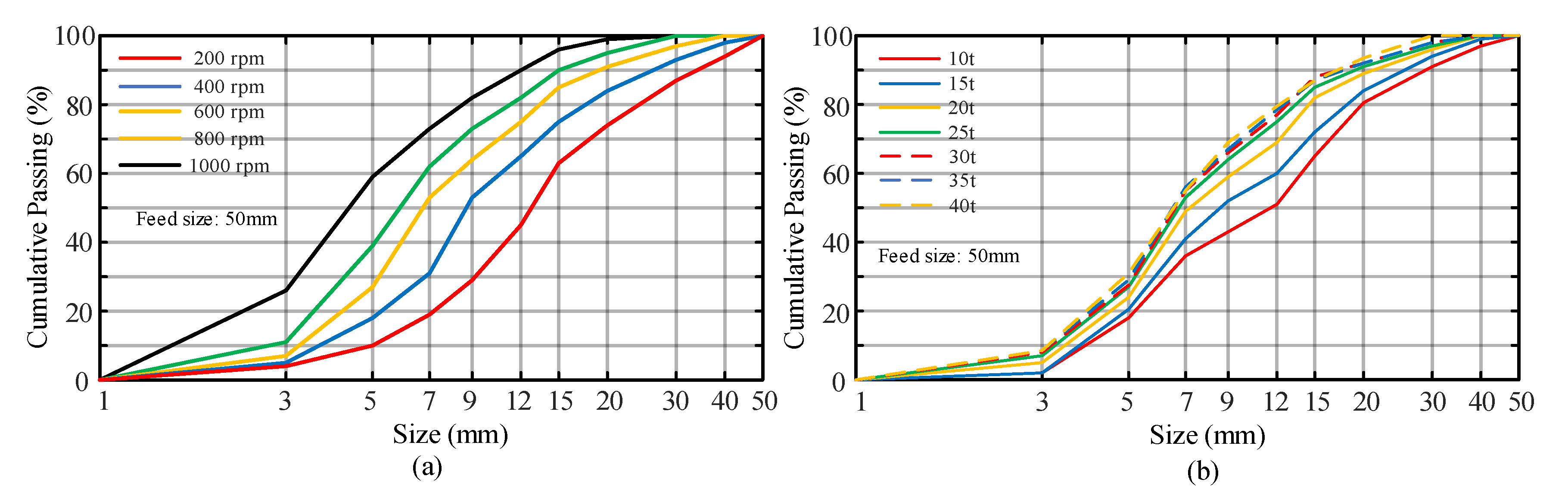
4.3.2. Influence on Product Size Distribution
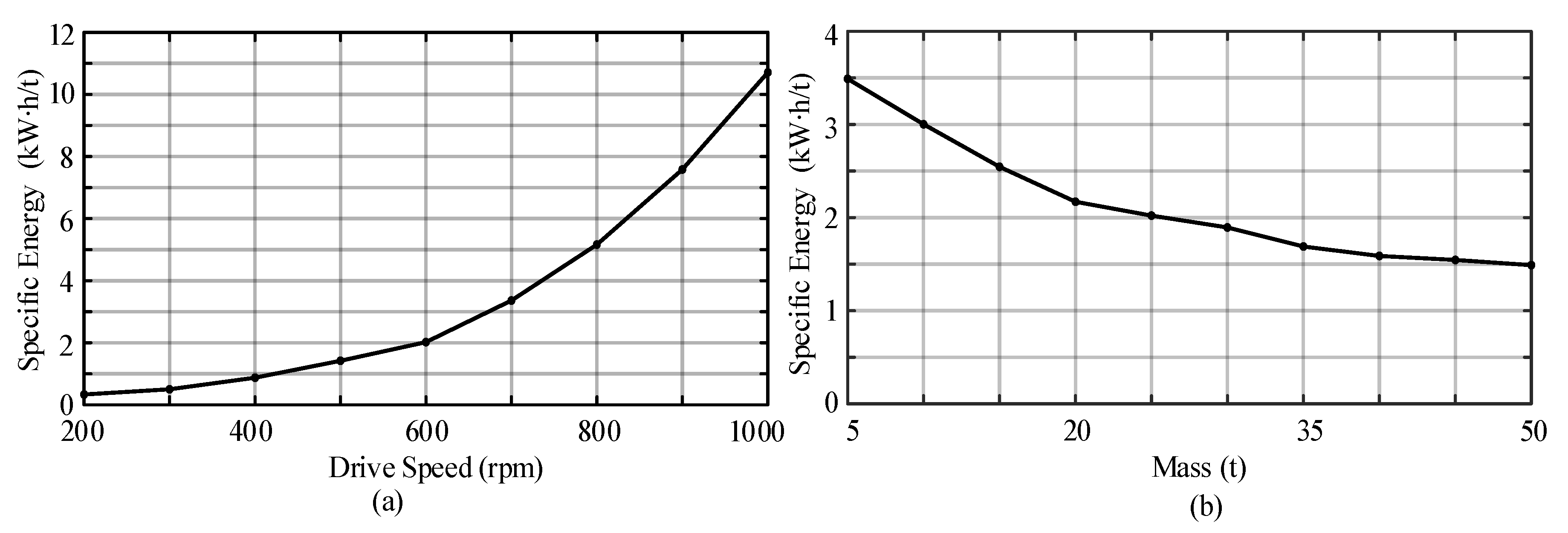
4.3.3. Influence on Specific Energy Consumption
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Z.; Ren, T.; Cheng, J.; Jin, X. The improved model of inter-particle breakage considering the transformation of particle shape for cone crusher. Miner. Eng. 2017, 112, 11–18. [Google Scholar] [CrossRef]
- Safronov, A.N.; Kazakov, S.V.; Shishkin, Y.V. New trends in inertia cone crusher studies. Miner. Process. J. 2012, 5, 40–42. [Google Scholar]
- Evertsson, C.M. Modelling of flow in cone crushers. Miner. Eng. 1999, 12, 1479–1499. [Google Scholar] [CrossRef]
- Babaev, R.M.; Kishchenko, V.L. The effect of KID-1500 inertia cone crusher parameters upon preset crushed stone size fraction yield. Miner. Process. J. 2012, 1, 22–24. [Google Scholar]
- Savov, S.; Nedyalkov, P.; Minin, I. Crushing force theoretical examination in one cone inertial crusher. J. Multidiscipl. Eng. Sci. Technol. 2015, 2, 430–437. [Google Scholar]
- Savov, S.; Nedyalkov, P. Layer crushing in one cone inertial crusher. J. Multidiscipl. Eng. Sci. Technol. 2015, 2, 2619–2626. [Google Scholar]
- Bogdanov, V.S.; Fadin, Y.M.; Vasilenko, O.S.; Demchenko, C.E.; Trubaeva, V.A. Analytical dependences of motion of working part in inertial cone crusher. IOP Conf. Ser. Mater. Sci. Eng. 2018, 327, 042113. [Google Scholar] [CrossRef]
- Xu, L. An approach for calculating the dynamic load of deep groove ball bearing joints in planar multibody systems. Nonlinear Dyn. 2012, 70, 2145–2161. [Google Scholar] [CrossRef]
- Langerholc, M.; Cesnik, M.; Slavic, J.; Boltear, M. Experimental validation of a complex, large-scale, rigid-body mechanism. Eng. Struct. 2012, 36, 220–227. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1980, 30, 331–336. [Google Scholar] [CrossRef] [Green Version]
- Quist, J.; Evertsson, C.M. Cone crusher modelling and simulation using DEM. Miner. Eng. 2016, 85, 92–105. [Google Scholar] [CrossRef]
- Li, H.; McDowell, D.; Lowndes, I. Discrete element modelling of a rock cone crusher. Powder Technol. 2014, 263, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D.; Cummins, S.; Delaney, G.W. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM. Miner. Eng. 2017, 100, 49–70. [Google Scholar] [CrossRef]
- Andre, F.P.; Tavares, L.M. Simulating a laboratory-scale cone crusher in DEM using polyhedral particles. Powder Technol. 2020, 372, 362–371. [Google Scholar] [CrossRef]
- Kazakov, S.V.; Shishkin, E.V. Upon dynamic analysis of vibratory cone crusher based on three-mass system. Miner. Process. J. 2016, 4, 43–47. [Google Scholar] [CrossRef]
- Jing, J.; Han, Q.; Li, C.; Yao, H.; Liu, S. Nonlinear dynamics of a vibratory cone crusher with hysteretic force and clearances. Shock Vib. 2011, 18, 3–12. [Google Scholar] [CrossRef]
- Li, G.; Shi, B.; Liu, R. Dynamic modeling and analysis of a novel 6-DOF robotic crusher based on movement characteristics. Math. Probl. Eng. 2019, 2019, 2847029. [Google Scholar] [CrossRef]
- Liu, R.; Shi, B.; Shen, Y.; Li, G. Prediction model for liner wear considering the motion characteristics of material. Math. Probl. Eng. 2018, 2018, 9278597. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; Tavares, L.M. A preliminary model of high pressure roll grinding using the discrete element method and multi-body dynamics coupling. Int. J. Miner. Process. 2016, 156, 32–42. [Google Scholar] [CrossRef]
- Chung, Y.C.; Wu, Y.R. Dynamic modeling of a gear transmission system containing damping particles using coupled multi-body dynamics and discrete element method. Nonlinear Dyn. 2019, 98, 129–149. [Google Scholar] [CrossRef]
- Nikravesh, P.E.; Haug, E.J. Generalized Coordinate Partitioning for Analysis of Mechanical Systems with Nonholonomic Constraints. J. Mech. Trans. Autom. 1983, 105, 379–384. [Google Scholar] [CrossRef]
- Orin, D.E.; McGhee, R.B.; Vukobratovic, M.; Hartoch, G. Kinematic and kinetic analysis of open-chain linkages utilizing Newton-Euler methods. Math. Biosci. 1972, 43, 107–130. [Google Scholar] [CrossRef]
- Flores, P.; Leine, R.; Glocker, C. Modeling and analysis of rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody Dyn. 2009, 23, 165–190. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dyn. 1994, 5, 193–207. [Google Scholar]
- Hertz, H. On the contact of elastic solids. J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Cha, H.; Choi, J.; Han, S.; Choi, J. Stick-slip algorithm in a tangential contact force model for multi-body system dynamics. J. Mech. Sci. Technol. 2011, 25, 1687–1694. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 231–250. [Google Scholar] [CrossRef]
- Chung, Y.C.; Wu, C.W.; Kuo, C.Y.; Hsiau, S.S. A rapid granular chute avalanche impinging on a small fixed obstacle: DEM modeling, experimental validation and exploration of granular stress. Appl. Math. Model. 2019, 74, 540–568. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Brouwers, H.J.H. Particle-size distribution and packing fraction of geometric random packings. Phys. Rev. E 2006, 74, 031309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Groot, R.D.; Stoyanov, D.S. Close packing density and fracture strength of adsorbed polydisperse particle layers. Soft Matter. 2011, 7, 4750–4761. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Huang, H. DEM analysis of failure mechanisms in the intact Brazilian test. Int. J. Rock Mech. Min. Sci. 2018, 102, 109–119. [Google Scholar] [CrossRef]
- Hanley, K.J.; Sullivan, C.O.; Oliveira, J.C.; Cronin, K.; Byrne, E.P. Application of Taguchi methods to DEM calibration of bonded agglomerates. Powder Technol. 2011, 210, 230–240. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Taguchi, G. System of Experimental Design; UNIPUB/Kraus International Publications: New York, NY, USA, 1987. [Google Scholar]
- Wang, Y.; Tonon, F. Modeling Lac du Bonnet granite using a discrete element model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1124–1135. [Google Scholar] [CrossRef]
- Mütze, T. Energy dissipation in particle bed comminution. Int. J. Miner. Process. 2015, 136, 15–19. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Machine | ||
| Crusher model | GYP1200 | - |
| Mantle cone angle | 50 | (deg) |
| Eccentric vibrator speed | (400,600) | (rpm) |
| Fixed cone mass | 24,124.4 | (kg) |
| Floating cone mass | 4495.1 | (kg) |
| Eccentric vibrator mass | 784.5 | (kg) |
| Rubber absorber properties | ||
| Spring coefficient (kx,ky,kz) | (320,320,970) | (N/mm) |
| Damping coefficient (cx,cy,cz) | (100,100,100) | (N·s/mm) |
| Nonlinear contact parameters | ||
| Stiffness coefficient | 105 | (N/mm) |
| Damping coefficient | 50 | (N·s/mm) |
| Stiffness exponent | 1.5 | - |
| Damping exponent | 1 | - |
| Indentation exponent | 2 | - |
| Dynamic threshold coefficient | 0.25 | - |
| Static threshold coefficient | 0.3 | - |
| Dynamic threshold velocity | 10 | (mm/s) |
| Static threshold velocity | 1 | (mm/s) |
| Control Factors | Levels | Column Assigned | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Normal critical stress (MPa) | 22 | 17 | 25 | 20 | 1 |
| Shear critical stress (MPa) | 16 | 13 | 9 | 11 | 2 |
| Shear stiffness (GPa/m) | 100 | 120 | 160 | 200 | 4 |
| Bond disk radius (mm) | 3.2 | 3.0 | 3.3 | 3.1 | 5 |
| Error - | 3 | ||||
| Force Difference | Critical Compression Ratio | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Factor | DF | SS | MS | P | Factor | DF | SS | MS | P | ||||
| Shear critical stress | 3 | 72.29 | 24.10 | 0.133 | Normal critical stress | 3 | 22.348 | 7.449 | 0.185 | ||||
| Shear stiffness | 3 | 61.83 | 20.61 | 0.125 | Shear critical stress | 3 | 20.041 | 9.680 | 0.174 | ||||
| Bond disk radius | 3 | 18.46 | 6.15 | 0.001 | Shear stiffness | 3 | 12.051 | 4.017 | 0.002 | ||||
| Normal critical stress | Equivalent errors | 3 | 6 | 5.64 | 13.06 | 1.88 | 4.35 | Bond disk radius | 3 | 20.135 | 6.717 | 0.102 | |
| Error | 3 | 7.42 | 2.47 | Error | 3 | 3.653 | 1.218 | ||||||
| Total | 15 | 165.64 | Total | 15 | |||||||||
| Parameter | Value | Unit | |
|---|---|---|---|
| DEM material properties | |||
| Rock | Steel | ||
| Density | 2600 | 7800 | (kg/m3) |
| Shear stiffness | 5.08∙108 | 7.0∙1010 | (Pa) |
| Poisson’s ratio | 0.35 | 0.3 | - |
| Rock-Rock | Rock-Steel | ||
| Static friction coefficient | 0.5 | 0.7 | - |
| Restitution coefficient | 0.15 | 0.2 | - |
| Rolling friction coefficient | 0.001 | 0.001 | - |
| BPM parameters | |||
| Normal stiffness | 400 | (GPa/m) | |
| Shear stiffness | 160 | (GPa/m) | |
| Normal critical stress | 25 | (MPa) | |
| Shear critical stress | 9 | (MPa) | |
| Bond disk radius | 3.1 | (mm) | |
| Simulation | |||
| Time step | 1.3∙10−7 | (s) | |
| Frequency | 1000 | (Hz) | |
| Number of particles | 229,409 | - | |
| Simulation time (400 rpm) | 1080 | (CPUH) | |
| Simulation time (600 rpm) | 1370 | (CPUH) | |
| CPU clock frequency | 4.32 | (GHz) | |
| CPU cores | 24 | - | |
| Performance | Analysis | SIM 400 rpm | EXP 400 rpm | SIM 600 rpm | EXP 600 rpm |
|---|---|---|---|---|---|
| Amplitude in x (mm) | Mean | 5.25 | 5.46 | 5.57 | 5.74 |
| Std Dev | 0.121 | 0.099 | 0.136 | 0.159 | |
| Power draw (kW) | Mean | 73.8 | 76.8 | 128.7 | 146.2 |
| Std Dev | 3.12 | 3.97 | 6.79 | 7.81 | |
| Throughput (t/h) | Mean | 84.4 | 80.8 | 63.7 | 51.8 |
| Specific energy (kW∙h/t) | 0.87 | 0.95 | 2.02 | 2.82 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Ren, T.; Zhang, Z.; Liu, D.; Jin, X. A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling. Minerals 2020, 10, 862. https://doi.org/10.3390/min10100862
Cheng J, Ren T, Zhang Z, Liu D, Jin X. A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling. Minerals. 2020; 10(10):862. https://doi.org/10.3390/min10100862
Chicago/Turabian StyleCheng, Jiayuan, Tingzhi Ren, Zilong Zhang, Dawei Liu, and Xin Jin. 2020. "A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling" Minerals 10, no. 10: 862. https://doi.org/10.3390/min10100862
APA StyleCheng, J., Ren, T., Zhang, Z., Liu, D., & Jin, X. (2020). A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling. Minerals, 10(10), 862. https://doi.org/10.3390/min10100862





