The Bridgmanite–Akimotoite–Majorite Triple Point Determined in Large Volume Press and Laser-Heated Diamond Anvil Cell
Abstract
1. Introduction
2. Methods
2.1. Large-Volume Press (LVP)
2.2. Laser-Heated Diamond Anvil Cell (LHDAC)
3. Results
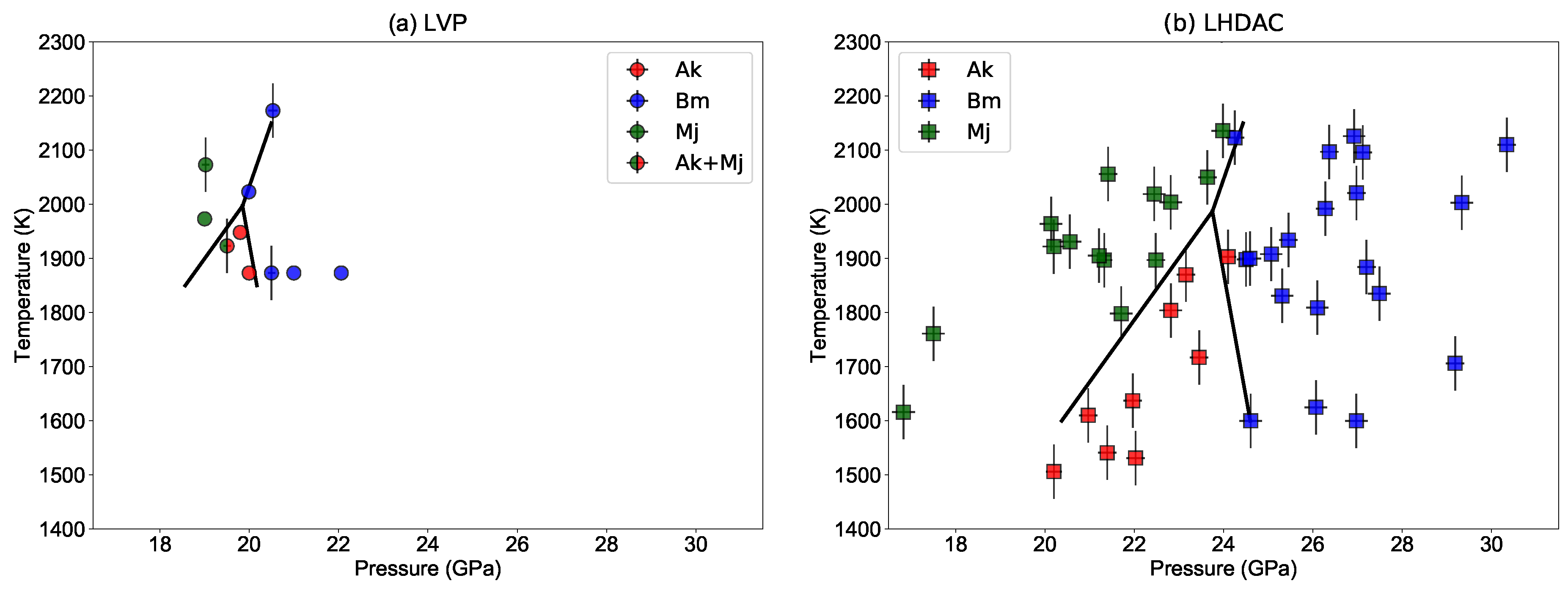
3.1. Large-Volume Press
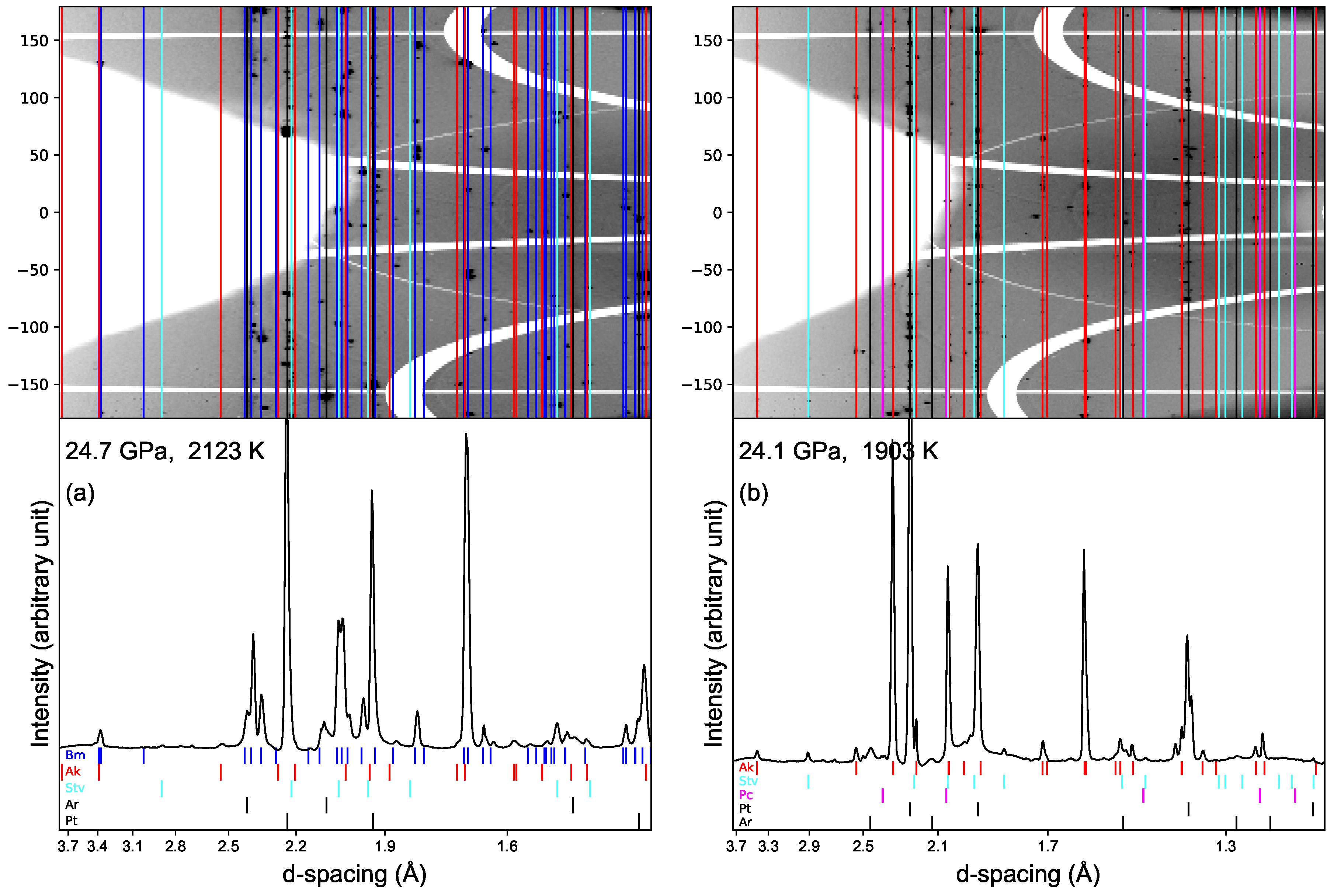
3.2. Laser-Heated Diamond Anvil Cell
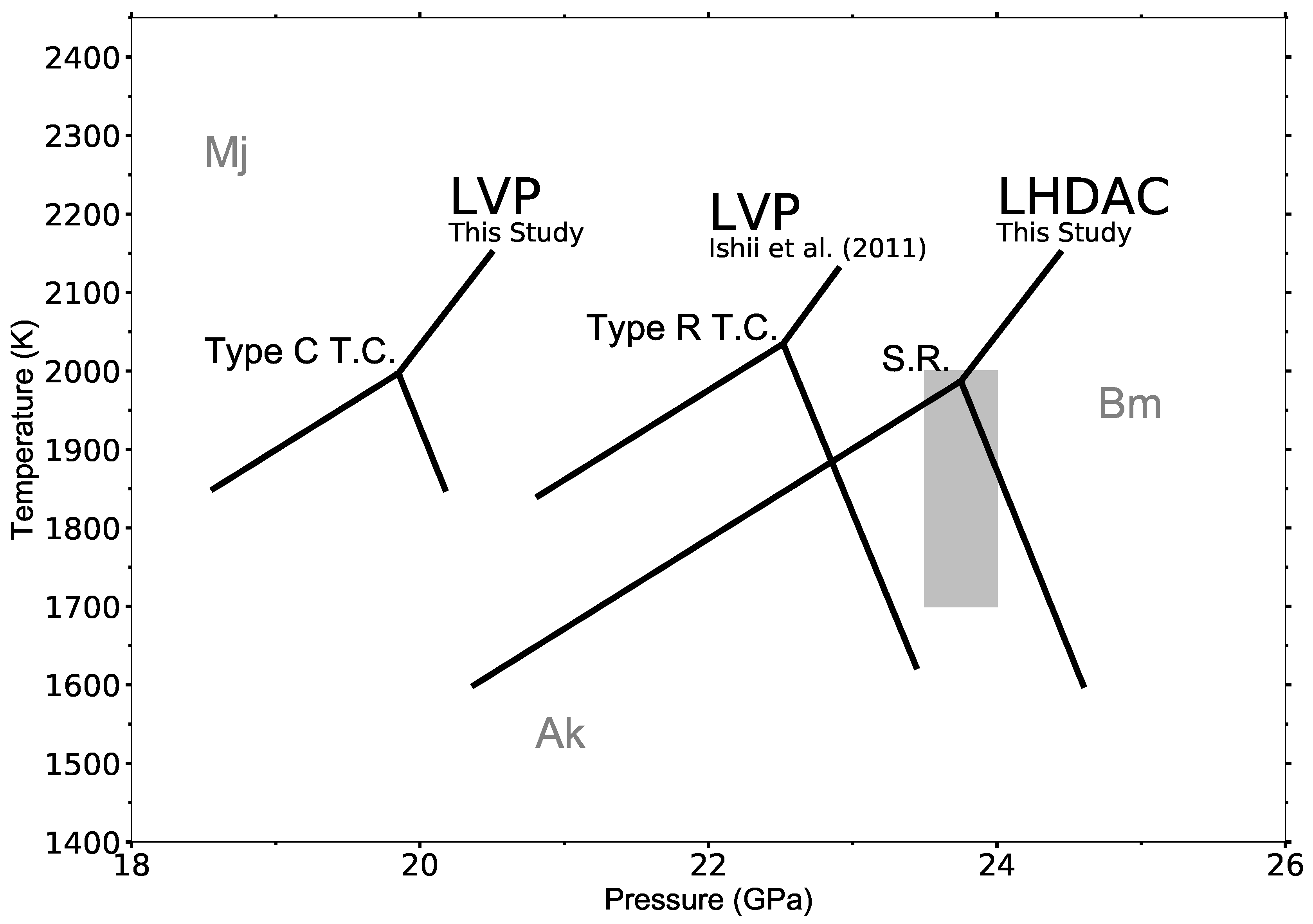
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| P | Pressure |
| T | Temperature |
| LVP | Large-volume press |
| LHDAC | Laser-heated diamond anvil cell |
| Ak | Akimotoite |
| Mj | Majorite |
| Bm | Bridgmanite |
| BAM | Bridgmanite–Akimotoite–Majorite |
References
- Anderson, O.L. The Grüneisen ratio for the last 30 years. Geophys. J. Int. 2000, 143, 279–294. [Google Scholar] [CrossRef]
- Irifune, T.; Nishiyama, N.; Kuroda, K.; Inoue, T.; Isshiki, M.; Utsumi, W.; Funakoshi, K.i.; Urakawa, S.; Uchida, T.; Katsura, T.; et al. The postspinel phase boundary in Mg2SiO4 determined by in situ X-ray diffraction. Science 1998, 279, 1698–1700. [Google Scholar] [CrossRef] [PubMed]
- Shim, S.H.; Duffy, T.S.; Shen, G. The post-spinel transformation in Mg2SiO4 and its relation to the 660-km seismic discontinuity. Nature 2001, 411, 571. [Google Scholar] [CrossRef] [PubMed]
- Hirose, K.; Komabayashi, T.; Murakami, M.; Funakoshi, K.I. In situ measurements of the majorite-akimotoite-perovskite phase transition boundaries in MgSiO3. Geophys. Res. Lett. 2001, 28, 4351–4354. [Google Scholar] [CrossRef]
- Katsura, T.; Yamada, H.; Shinmei, T.; Kubo, A.; Ono, S.; Kanzaki, M.; Yoneda, A.; Walter, M.J.; Ito, E.; Urakawa, S.; et al. Post-spinel transition in Mg2SiO4 determined by high P − T in situ X-ray diffractometry. Phys. Earth Planet. Inter. 2003, 136, 11–24. [Google Scholar] [CrossRef]
- Fei, Y.; Van Orman, J.; Li, J.; Van Westrenen, W.; Sanloup, C.; Minarik, W.; Hirose, K.; Komabayashi, T.; Walter, M.; Funakoshi, K.I. Experimentally determined postspinel transformation boundary in Mg2SiO4 using MgO as an internal pressure standard and its geophysical implications. J. Geophys. Res. Solid Earth 2004, 109, B02305. [Google Scholar] [CrossRef]
- Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an internally consistent pressure scale. Proc. Nat. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef]
- Sinogeikin, S.; Bass, J.; Prakapenka, V.; Lakshtanov, D.; Shen, G.; Sanchez-Valle, C.; Rivers, M. Brillouin spectrometer interfaced with synchrotron radiation for simultaneous X-ray density and acoustic velocity measurements. Rev. Sci. Instrum. 2006, 77, 103905. [Google Scholar] [CrossRef]
- Li, B.; Kung, J.; Uchida, T.; Wang, Y. Simultaneous equation of state, pressure calibration and sound velocity measurements to lower mantle pressures using multi-anvil apparatus. In Advances in High-Pressure Technology for Geophysical Applications; Elsevier: Amsterdam, The Netherlands, 2005; pp. 49–66. [Google Scholar]
- Ye, Y.; Gu, C.; Shim, S.H.; Meng, Y.; Prakapenka, V. The postspinel boundary in pyrolitic compositions determined in the laser-heated diamond anvil cell. Geophys. Res. Lett. 2014, 41, 3833–3841. [Google Scholar] [CrossRef]
- Ye, Y.; Prakapenka, V.; Meng, Y.; Shim, S.H. Intercomparison of the gold, platinum, and MgO pressure scales up to 140 GPa and 2500 K. J. Geophys. Res. Solid Earth 2017, 122, 3450–3464. [Google Scholar] [CrossRef]
- Getting, I.; Kennedy, G. Effect of pressure on the emf of chromel-alumel and platinum-platinum 10% rhodium thermocouples. J. Appl. Phys. 1970, 41, 4552–4562. [Google Scholar] [CrossRef]
- Nishihara, Y.; Fuke, K.; Tange, Y.; Higo, Y. Determination of pressure effect on thermocouple electromotive force using multi-anvil apparatus. High Press. Res. 2016, 36, 121–139. [Google Scholar] [CrossRef]
- Nishihara, Y.; Doi, S.; Kakizawa, S.; Higo, Y.; Tange, Y. Effect of pressure on temperature measurements using WRe thermocouple and its geophysical impact. Phys. Earth Planet. Inter. 2019, 298, 106348. [Google Scholar] [CrossRef]
- Boehler, R. High-pressure experiments and the phase diagram of lower mantle and core materials. Rev. Geophys. 2000, 38, 221–245. [Google Scholar] [CrossRef]
- Shen, G.; Rivers, M.L.; Wang, Y.; Sutton, S.R. Laser heated diamond cell system at the Advanced Photon Source for in situ X-ray measurements at high pressure and temperature. Rev. Sci. Instrum. 2001, 72, 1273–1282. [Google Scholar] [CrossRef]
- Kavner, A.; Panero, W.R. Temperature gradients and evaluation of thermoelastic properties in the synchrotron-based laser-heated diamond cell. Phys. Earth Planet. Inter. 2004, 143, 527–539. [Google Scholar] [CrossRef]
- Deng, J.; Du, Z.; Benedetti, L.R.; Lee, K.K. The influence of wavelength-dependent absorption and temperature gradients on temperature determination in laser-heated diamond-anvil cells. J. Appl. Phys. 2017, 121, 025901. [Google Scholar] [CrossRef]
- Lin, J.F.; Sturhahn, W.; Zhao, J.; Shen, G.; Mao, H.K.; Hemley, R.J. Absolute temperature measurement in a laser-heated diamond anvil cell. Geophys. Res. Lett. 2004, 31, L14611. [Google Scholar] [CrossRef]
- Bullen, K. The problem of the Earth’s density variation. Bull. Seismol. Soc. Am. 1940, 30, 235–250. [Google Scholar]
- Ai, Y.; Zheng, T.; Xu, W.; He, Y.; Dong, D. A complex 660 km discontinuity beneath northeast China. Earth Planet. Sci. Lett. 2003, 212, 63–71. [Google Scholar] [CrossRef]
- Day, E.A.; Deuss, A. Reconciling PP and P′P′ precursor observations of a complex 660 km seismic discontinuity. Geophys. J. Int. 2013, 194, 834–838. [Google Scholar] [CrossRef][Green Version]
- Leinenweber, K.D.; Tyburczy, J.A.; Sharp, T.G.; Soignard, E.; Diedrich, T.; Petuskey, W.B.; Wang, Y.; Mosenfelder, J.L. Cell assemblies for reproducible multi-anvil experiments (the COMPRES assemblies). Am. Mineral. 2012, 97, 353–368. [Google Scholar] [CrossRef]
- Walker, D.; Carpenter, M.; Hitch, C. Some simplifications to multianvil devices for high pressure experiments. Am. Mineral. 1990, 75, 1020–1028. [Google Scholar]
- Tangeman, J.A.; Phillips, B.L.; Navrotsky, A.; Weber, J.R.; Hixson, A.D.; Key, T.S. Vitreous forsterite (Mg2SiO4): Synthesis, structure, and thermochemistry. Geophys. Res. Lett. 2001, 28, 2517–2520. [Google Scholar] [CrossRef]
- Shim, S.H.; Catalli, K. Compositional dependence of structural transition pressures in amorphous phases with mantle-related compositions. Earth Planet. Sci. Lett. 2009, 283, 174–180. [Google Scholar] [CrossRef]
- Hixson, R.; Fritz, J. Shock compression of tungsten and molybdenum. J. Appl. Phys. 1992, 71, 1721–1728. [Google Scholar] [CrossRef]
- Hernlund, J.; Leinenweber, K.; Locke, D.; Tyburczy, J.A. A numerical model for steady-state temperature distributions in solid-medium high-pressure cell assemblies. Am. Mineral. 2006, 91, 295–305. [Google Scholar] [CrossRef]
- Dorogokupets, P.; Dewaele, A. Equations of state of MgO, Au, Pt, NaCl-B1, and NaCl-B2: Internally consistent high-temperature pressure scales. High Press. Res. 2007, 27, 431–446. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Shim, S.H. PeakPo—A python software for X-ray diffraction analysis at high pressure and high temperature. Zenodo 2017. Available online: https://zenodo.org/record/3376238#.Xhn22S2ZM1I (accessed on 14 January 2020).
- Dan Shim, S.-H. Pytheos—A Python Tool Set For Equations Of State. 2017. Available online: https://zenodo.org/record/802392#.Xhn2iC2ZM1I (accessed on 14 January 2020).
- Williams, Q.; Jeanloz, R.; McMillan, P. Vibrational spectrum of MgSiO3 perovskite: Zero-pressure Raman and mid-infrared spectra to 27 GPa. J. Geophys. Res. Solid Earth 1987, 92, 8116–8128. [Google Scholar] [CrossRef]
- Gillet, P.; Guyot, F.; Wang, Y. Microscopic anharmonicity and equation of state of MgSiO3-perovskite. Geophys. Res. Lett. 1996, 23, 3043–3046. [Google Scholar] [CrossRef]
- Rauch, M.; Keppler, H.; Häfner, W.; Poe, B.; Wokaun, A. A pressure-induced phase transition in MgSiO3-rich garnet revealed by Raman spectroscopy. Am. Mineral. J. Earth Planet. Mater. 1996, 81, 1289–1292. [Google Scholar]
- Okada, T.; Narita, T.; Nagai, T.; Yamanaka, T. Comparative Raman spectroscopic study on ilmenite-type MgSiO3 (akimotoite), MgGeO3, and MgTiO3 (geikielite) at high temperatures and high pressures. Am. Mineral. 2008, 93, 39–47. [Google Scholar] [CrossRef]
- Ishii, T.; Kojitani, H.; Akaogi, M. Post-spinel transitions in pyrolite and Mg2SiO4 and akimotoite–perovskite transition in MgSiO3: Precise comparison by high-pressure high-temperature experiments with multi-sample cell technique. Earth Planet. Sci. Lett. 2011, 309, 185–197. [Google Scholar] [CrossRef]
- Millett, J.; Gray III, G.; Bourne, N. Measurement of the shear strength of pure tungsten during one-dimensional shock loading. J. Appl. Phys. 2007, 101, 033520. [Google Scholar] [CrossRef]
- He, D.; Duffy, T.S. X-ray diffraction study of the static strength of tungsten to 69 GPa. Phys. Rev. B 2006, 73, 134106. [Google Scholar] [CrossRef]
- Lebedev, S.; Chevrot, S.; van der Hilst, R.D. Seismic evidence for olivine phase changes at the 410-and 660-kilometer discontinuities. Science 2002, 296, 1300–1302. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Brown, J.; Shankland, T. Thermodynamic parameters in the Earth as determined from seismic profiles. Geophys. J. Int. 1981, 66, 579–596. [Google Scholar] [CrossRef]
- Kennett, B.L.; Engdahl, E.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Katsura, T.; Yoneda, A.; Yamazaki, D.; Yoshino, T.; Ito, E. Adiabatic temperature profile in the mantle. Phys. Earth Planet. Inter. 2010, 183, 212–218. [Google Scholar] [CrossRef]
- Sawamoto, H. Phase diagram of MgSiO3 at pressures up to 24 GPa and temperatures up to 2200 °C: Phase stability and properties of tetragonal garnet. High Press. Res. Miner. Phys. 1987, 209, 219. [Google Scholar]
- Ishii, T.; Huang, R.; Fei, H.; Koemets, I.; Liu, Z.; Maeda, F.; Yuan, L.; Wang, L.; Druzhbin, D.; Yamamoto, T.; et al. Complete agreement of the post-spinel transition with the 660-km seismic discontinuity. Sci. Rep. 2018, 8, 6358. [Google Scholar] [CrossRef] [PubMed]
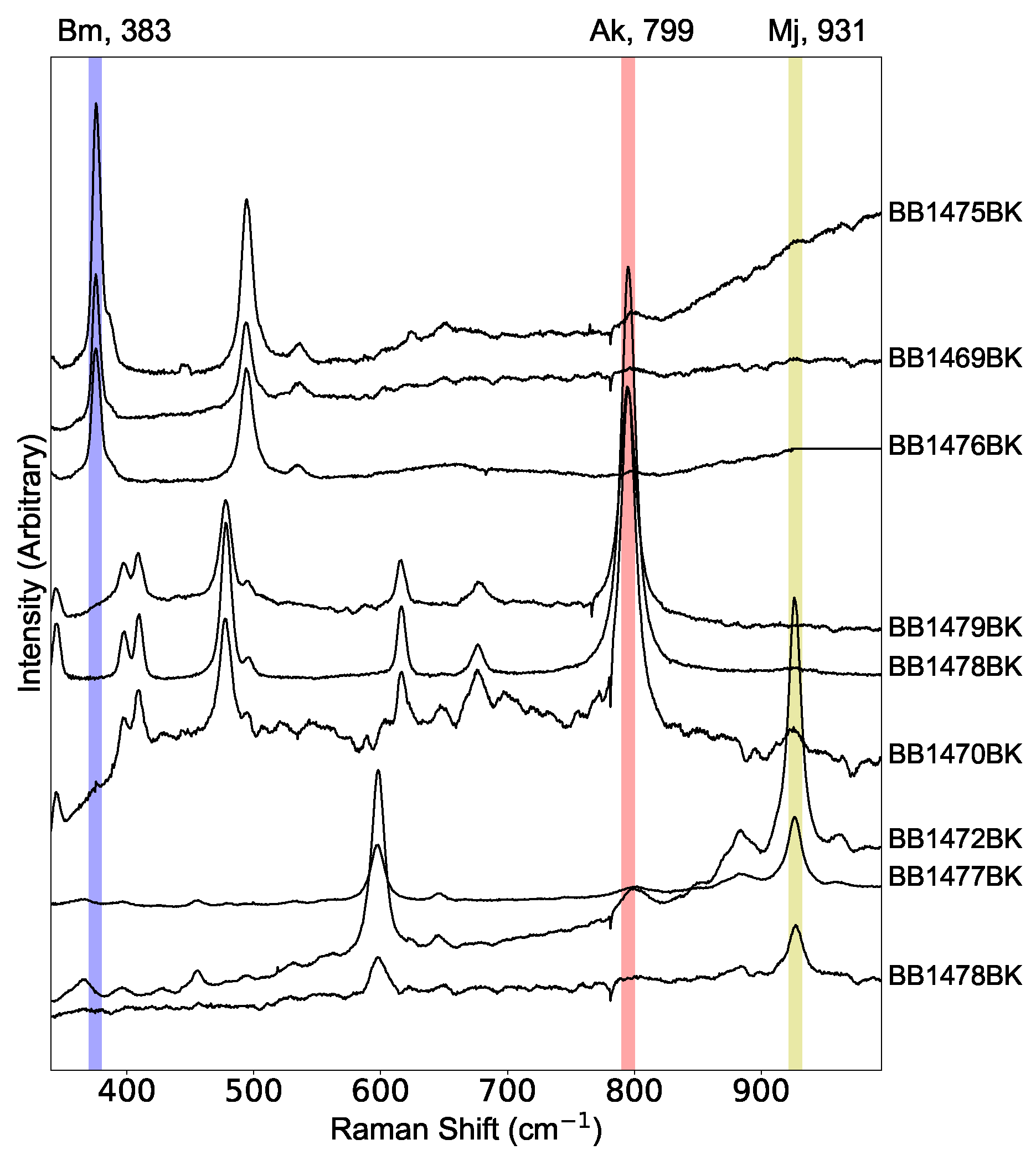
| Run ID | T (K) | O.P. (psi) | P (GPa) | F(ton) | t (min) | Product |
|---|---|---|---|---|---|---|
| BB1434JD | 2173 ± 5 | 5000 | 20.5 | 515 | 30 | Bm |
| BB1438JD | 2023 ± 5 | 4500 | 20.0 | 463 | 30 | Bm |
| BB1469BK | 1873 ± 5 | 4937 | 22.0 | 611 | 60 | Bm |
| BB1470BK | 1873 ± 5 | 4365 | 20.0 | 449 | 60 | Ak |
| BB1472BK | 2073 ± 50 | 4103 | 19.0 | 421 | 30 | Mj |
| BB1475BK | 1873 ± 5 | 4892 | 21.0 | 504 | 60 | Bm |
| BB1476BK | 1875 ± 50 | 4609 | 20.5 | 475 | 60 | Bm |
| BB1477BK | 1973 ± 5 | 4025 | 19.0 | 414 | 30 | Mj |
| BB1478BK | 1923 ± 50 | 4192 | 19.5 | 432 | 30 | Ak + Mj |
| BB1479BK | 1948 ± 5 | 4344 | 20.0 | 447 | 30 | Ak |
| DAC ID | Setting | Spot ID | P (GPa) | T (K) | Product |
|---|---|---|---|---|---|
| #1 | PM: Ar | 1 | 20.2 | 1506 | Ak |
| SM: Gl | 2 | 21.3 | 1897 | Mj | |
| XE: 37 keV | 3 | 24.1 | 1903 | Ak | |
| 4 | 21.0 | 1610 | Ak | ||
| 5 | 21.4 | 2056 | Mj | ||
| 6 | 22.0 | 1531 | Ak | ||
| 7 | 23.2 | 1870 | Ak | ||
| 8 | 30.3 | 2110 | Bm | ||
| 9 | 26.4 | 2097 | Bm | ||
| 10 | 24.5 | 1717 | Bm | ||
| 11 | 27.2 | 1884 | Bm | ||
| 12 | 23.5 | 1717 | Ak | ||
| 13 | 29.2 | 1706 | Bm | ||
| 14 | 24.3 | 2123 | Bm | ||
| 15 | 27.1 | 2096 | Bm | ||
| 16 | 26.3 | 1992 | Bm | ||
| 17 | 27.0 | 2021 | Bm | ||
| 18 | 25.5 | 1934 | Bm | ||
| 19 | 21.4 | 1541 | Ak | ||
| 20 | 22.5 | 1897 | Mj | ||
| 21 | 23.6 | 2050 | Mj | ||
| 22 | 22.0 | 1637 | Ak | ||
| #2 | PM: NaCl | 1 | 16.8 | 1616 | Mj |
| SM: Ak | 2 | 17.5 | 1761 | Mj | |
| XE: 30 keV | 3 | 22.4 | 2019 | Mj | |
| 4 | 20.1 | 1964 | Mj | ||
| 5 | 24.0 | 2349 | Mj | ||
| 6 | 20.6 | 1931 | Mj | ||
| 7 | 24.0 | 2136 | Mj | ||
| 8 | 20.2 | 1922 | Mj | ||
| 9 | 21.2 | 1905 | Mj | ||
| 10 | 26.1 | 1809 | Bm | ||
| 11 | 21.7 | 1798 | Mj | ||
| 12 | 22.8 | 1804 | Ak | ||
| 13 | 22.8 | 2004 | Mj | ||
| 14 | 27.5 | 1835 | Bm | ||
| 15 | 29.3 | 2003 | Bm | ||
| #3 | PM: NaCl | 1 | 26.1 | 1625 | Bm |
| SM: Ak | 2 | 27.0 | 1600 | Bm | |
| XE: 30 keV | 3 | 24.6 | 1900 | Bm | |
| 4 | 25.3 | 1831 | Bm | ||
| 5 | 25.1 | 1908 | Bm | ||
| 6 | 24.6 | 1600 | Bm | ||
| 7 | 26.9 | 2126 | Bm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulka, B.L.; Dolinschi, J.D.; Leinenweber, K.D.; Prakapenka, V.B.; Shim, S.-H. The Bridgmanite–Akimotoite–Majorite Triple Point Determined in Large Volume Press and Laser-Heated Diamond Anvil Cell. Minerals 2020, 10, 67. https://doi.org/10.3390/min10010067
Kulka BL, Dolinschi JD, Leinenweber KD, Prakapenka VB, Shim S-H. The Bridgmanite–Akimotoite–Majorite Triple Point Determined in Large Volume Press and Laser-Heated Diamond Anvil Cell. Minerals. 2020; 10(1):67. https://doi.org/10.3390/min10010067
Chicago/Turabian StyleKulka, Britany L., Jonathan D. Dolinschi, Kurt D. Leinenweber, Vitali B. Prakapenka, and Sang-Heon Shim. 2020. "The Bridgmanite–Akimotoite–Majorite Triple Point Determined in Large Volume Press and Laser-Heated Diamond Anvil Cell" Minerals 10, no. 1: 67. https://doi.org/10.3390/min10010067
APA StyleKulka, B. L., Dolinschi, J. D., Leinenweber, K. D., Prakapenka, V. B., & Shim, S.-H. (2020). The Bridgmanite–Akimotoite–Majorite Triple Point Determined in Large Volume Press and Laser-Heated Diamond Anvil Cell. Minerals, 10(1), 67. https://doi.org/10.3390/min10010067





