p-Curve and Selection Methods as Meta-Analytic Supplements for Biologists: A Demonstration of Effect Size Estimation in Studies of Human Fluctuating Asymmetry

Abstract

Fluctuating asymmetry is hypothesized to predict developmental instability (DI) and fitness outcomes. While published studies largely support this prediction, publication bias remains an issue. Biologists have increasingly turned to meta-analysis to estimate true support for an effect. Van Dongen and Gangestad (VD&G) performed a meta-analysis on studies of fluctuating asymmetry (FA) and fitness-related qualities in humans. They found an average robust effect size, but estimates varied widely. Recently, psychologists have identified limitations in traditional meta-analyses and popular companion adjustments, and have advocated for alternative meta-analytic techniques. P-curve estimates true mean effects using significant published effects; it also detects the presence of p-hacking (where researchers exploit researcher “degrees of freedom”), not just publication bias. Alternative selection methods also provide a means to estimate average effect size correcting for publication bias, but may better account for heterogeneity in effect sizes and publication decisions than p-curve. We provide a demonstration by performing p-curve and selection method analyses on the set of effects from VD&G. We estimate an overall effect size range (r = 0.08–0.15) comparable to VD&G, but with notable differences between domains and techniques. Results from alternative estimation methods can provide corroborating evidence for, as well as insights beyond, traditional meta-analytic estimates.

1. Introduction

Developmental instability (DI) is the imprecise expression of a developmental “plan” due to genetic or environmental perturbations such as mutations, non-adaptive gene complexes, infection, or toxins [1,2]. While a number of physiological or immunological aberrations may signal DI [3], the most widely used measure of individual differences in organisms’ DI is fluctuating asymmetry (FA)—deviation from perfect symmetry in bilateral traits that are symmetrical at the population level [4]. In theory, asymmetry in such traits results from developmental noise. The correlation between the asymmetry arising from two hypothetical “developments” of individuals’ levels on a particular trait (the repeatability of a single trait’s FA) is estimated to be very low—less than 0.1 [5,6,7]. Hence, a single trait’s FA is a very poor measure of individual differences in proneness to DI underlying the asymmetry (estimated validity coefficient less than 0.3 [5]). If a predisposition to DI is shared across multiple traits, however, a composite of multiple traits’ FA can potentially capture meaningful variance in individual differences in DI (e.g., a composite of 10 traits’ FA may typically have a validity coefficient >0.5 [5,8]).

DI may reveal poor overall “quality” of an individual, perhaps due to poor environmental conditions during development, or genotypes that are less efficient in terms of translating effort into reproductive success [1]. A main prediction stemming from this literature, then, is that indicators of DI (including FA) should relate negatively to fitness outcomes such as sexual attractiveness, fecundity, survival, and longevity. Qualitative reviews of published findings provided preliminary evidence consistent with this prediction (e.g., [1]). However, qualitative reviews may not provide precise information about the existence or strength of an effect. Within the past 20 years, meta-analyses have become a preferred tool to investigate the true strength and nature of findings in the biological sciences (e.g., [9,10]). Provided a meta-analyst is given access to the entirety of published and unpublished studies, these studies provide the advantage of transforming the results of studies into a common metric (effect size), which allows for unbiased conclusions about the overall strength of a relationship. The meta-analysis is an invaluable tool for any biologist who studies small effects within the innumerable influences acting upon an organism. Small effects are perhaps expected within much of non-molecular biology; Jennions and Møller [11], as a demonstration, used meta-analysis analytic procedures to estimate effect sizes for subfields themselves, and found small but significant average effects in behavioral ecology, physiological ecology, and evolutionary biology studies.

Within the DI literature, more studies have examined associations between FA and outcomes pertaining to fitness—e.g., physical/psychological health, reproductive outcomes, mate attractiveness—in humans than any other species. Van Dongen and Gangestad [2] (hereafter VD&G) performed a meta-analysis of 96 studies on humans. The average correlation between FA and these outcomes (weighted by standard errors) was r = 0.18. However, scholars argue that publication bias leads to an overestimation of population effect sizes in any scientific discipline with incentive structures that heavily favor statistically significant results [12]—and this includes biology [13]. VD&G thus applied multiple procedures to correct for publication bias: trim-and-fill [14], estimated effect size at large sample size (150) (for a related procedure, see [15] on PET-PEESE), and estimated effect size for all studies with N > 150. These corrected estimates averaged about r = 0.10. Although small (albeit highly statistically significant), this value underestimates the true correlation between underlying DI and these outcomes, due to lack of perfect validity of FA as a measure of DI. VD&G’s best estimate of this disattenuated correlation was about 0.3 (with a large confidence interval). No difference in effect size across six broad categories of outcomes—attractiveness, health, fetal outcomes, hormonal outcomes, psychological maladaptation, and reproductive outcomes—was detected, though power to do so was limited. Within these less heterogeneous domain-specific subsets, corrected effect sizes averaged about 0.12. Effect sizes were estimated to be close to 0.2 in some specific domains (e.g., schizophrenia/schizotypy, maternal risk factors, male number of sex partners) and near 0 in others (e.g., facial attractiveness).

Revisiting Van Dongen and Gangestad (2011) with New Meta-Analytic Techniques

Recently, scholars have identified potential sources of bias in estimates generated from traditional meta-analytic practices. On the one hand, some features systematically lead to the underestimation of true effect sizes. In particular, the most common means of adjusting for publication bias—trim-and-fill—is known to over-adjust for publication bias when true effect sizes are heterogeneous, leading true effect sizes to be underestimated [16]. PET-PEESE often over-adjusts as well [17,18].

On the other hand, other features systematically lead to the overestimation of true effect sizes. p-hacking occurs when researchers make post-hoc decisions about data analysis (e.g., they might engage in data-peeking to determine when to stop data collection; selectively choose to report analyses on particular measures; selectively choose covariates to control for based on results [19]), preferring analyses that return significant effects. Like biased reporting of significant effects subject to sampling variability (publication bias), p-hacking leads the published literature to overestimate true effect sizes. Given evidence of publication bias within biology [13], it is plausible that p-hacking also occurs. Trim-and-fill and PET-PEESE cannot adjust adequately for p-hacking [19].

The p-curve is a procedure developed to detect p-hacking [20,21]. It examines only statistically significant published p-values which range from ~0 to 0.05. A p-curve is the distribution of these values. In the absence of true non-zero effects, the p-curve is expected to be flat (e.g., with the same proportion of values falling between 0 and 0.01 as between 0.04 and 0.05). When true effects exist, the p-curve is expected to be right-skewed, with p-values over-representatively <0.01 (e.g., over 40% of p-values will, on average, be <0.01 when mean power is only 0.3; when mean power is 0.7, nearly 70% of p-values will be <0.01). When p-hacking operates and no true non-zero effects exist, by contrast, the p-curve is—under the assumption that researchers have modest ambitions and report the first p-value <0.05 they find—expected to be modestly left-skewed, with values close to 0.05 over-represented—this is because researchers choose to report analyses, out of multiple ones, that yield significant values (often barely so) rather than analyses that yield non-significant values (even if barely non-significant; see simulations in [20]). Preceding the development of p-curve, Ridley et al. [22] examined the distribution of p-values from biological science papers published in top journals. They found an overrepresentation of p-values just at or below thresholds conventionally used to determine statistical significance.

The p-curve is only one method within a larger set of methods known as selection methods, a class of techniques with a long history in the psychological literature [23,24]. Both p-curve and other selection models can assess whether a set of published effects yield evidential value. They can also yield estimates of true effect size underlying a set of published findings. p-curve estimates true effect size based only on statistically significant published results. However, within the larger class of selection methods, one can include non-significant published results, and either assume or estimate the probability that a non-significant result will be published (relative to the probability a significant one will be). Selection methods thereby permit an estimation of average effect size while accounting for degrees of publication bias. A recent paper reviewing selection methods [25] identified limitations to using p-curve and related approaches (i.e., p-uniform [26]) to estimate mean effect size. In addition to considering only statistically significant published studies in the predicted direction, these analyses also treat effects as homogeneous across a domain of studies. When this assumption is violated—as is likely often the case (see [27])—the p-curve may provide biased estimates, underestimating when non-significant results compose part of the published literature, and overestimating the mean in a population of effects when effects are heterogeneous (Figures 2 and 3, [25]). Thus, alternative selection methods that account for both (1) chance publication of non-significant and/or negative published results and (2) effect size heterogeneity are yet other important tools for meta-analysts looking to extract estimates of the true mean effect from a set of studies.

While the extent to which p-curve analyses and other selection methods should replace—or merely supplement—traditional meta-analyses remains a matter of debate [25,26,27], psychologists have established the usefulness of these techniques. In spite of this, biologists’ usage of these kinds of alternative analyses has been incomplete and preliminary. As one example, Head et al. [28] examined p-curves of effects in 12 different meta-analyses of effects in domains of evolution and ecology. Uniformly, p-curves were right-skewed, indicative of true effects. At the same time, some evidence for p-hacking emerged, as p-curves in some domains revealed notable “bumps” in frequency of p-values close to 0.05. Potentially, then, traditional meta-analysis in some domains overestimated true effects due to p-hacking. However, Head et al. [28] did not use p-curve to estimate mean effect sizes. Other selection methods are mentioned within the biological literature but are not widely used. Nakagawa and Santos [29] speculate that selection methods are the most preferable approach to correct for publication bias in biology meta-analyses, but believe their implementation is too technical for the typical meta-analyst. With the advent of recently developed packages in the open-source statistical software R (Version 3.4.0, R Core Team, Vienna, Austria), we believe this is no longer the case, and that biologists can easily perform p-curve and alternative selection model analyses on their own meta-analytic datasets. No one approach to meta-analysis may be definitive. By considering multiple approaches based on different assumptions, including multiple kinds of selection models, one may be able to evaluate the sensitivity of estimates to meta-analytic assumptions.

We apply p-curve and selection method analyses to VD&G’s dataset. We report the extent of evidence for p-hacking in the FA literature, similar to [28]. However, our primary focus in performing these analyses is to generate effect size estimates and compare them with values VD&G reported. We thereby offer a novel illustration of the ability of these techniques to generate effect size estimates, which may be of interest to FA researchers, and biologists more generally.

2. Methods

FA in VD&G’s sample examined asymmetries on dermatoglyphic, dental, facial, and body traits. Dermatoglyphic traits are set in early fetal development and were not included in VD&G’s “restricted” sample. Dental and facial features may not aggregate into composites that validly tap organism-wide DI, and VD&G hence also analyzed “body FA only” studies separately. We too focused on these same two subsets. Because facial symmetry may directly affect facial attractiveness (rather than tap underlying DI, which may then affect attractiveness), we did not include effects of facial FA on facial attractiveness.

VD&G listed 64 studies in their restricted sample, yielding 182 individual effect sizes; 48 studies examined body FA, 133 effects. Thirty-four studies had significant effects. p-curve analysis assumes that all effects are independent [21], so when multiple significant effects were reported in a single study, we identified a single effect that best reflected the aim of the study. Thirty-two effects concerned body FA (67% of the body FA sample from VD&G); two concerned dental FA.

Table 1. p-curve tests for evidential value and p-uniform tests for publication bias. FA: fluctuating asymmetry.

Domain	k	Evidence for Real Effects?	Stouffer’s Z	p-Value	p-Uniform Publication Bias Test (z)	p-Value
All	34	Yes	−3.19	<0.001	0.94	0.174
Body FA only	32	Yes	−3.00	0.001	0.77	0.221
p < 0.025 only	20	Yes	−6.55	<0.001	0.57	0.283
Attractiveness	5	No	−0.12	0.55	0.82	0.205
Health and disease	4	No	0.87	0.19	1.88	0.030
Fetal outcomes	5	Yes	−1.80	0.04	0.46	0.323
Hormonal	2
Psychological outcomes	11	Yes	−3.44	<0.001	0.46	0.322
Reproductive outcomes	7	Yes	−1.88	0.03	0.08	0.470

reports the breakdown of studies in p-curve analyses. We performed analyses for three “overall” domains: all 34 significant effects, the 32 “body FA” effects, and the 20 effects with p < 0.025 (which Simonsohn et al. [30] suggest provides an additional test of robustness). We also performed analyses for five individual domains, omitting one from VD&G (hormonal outcomes), as it contained only two significant effects (though these effects are included in the overall p-curve analysis). See Supplementary Materials for a full p-curve disclosure table [21]. p-curve analyses consisted of three components: first, analyses intended to detect the presence of p-hacking, performed using the online p-curve app (version 4.05) found at www.p-curve.com; second, a test of publication bias using the “puniform” R package, which employs a procedure nearly identical to p-curve (p-uniform; see [27] for details) to test for the presence of publication bias based on statistically significant effects; and third, analyses to estimate effect size, performed using the code provided in [20].

The other main category of analyses—which we refer to as “Alternative Selection Models”—included non-significant and/or negative effects in addition to the significant, independent effects used in p-curve analyses. We used R code provided by [25] to estimate effect size in all six individual domains with a variant of Hedges’ [23] original selection model that accounts for effect size heterogeneity (τ) and the relative chance of publication for non-significant and/or negative effects (q). This model estimates τ from the data provided, whereas the user specifies values for q. We provide estimates in each domain when q = 0.2 and q = 0.4. See the SOM for the exact R code used to generate these estimates.

3. Results

3.1. All Significant Independent Effects

The p-curve for all 34 effects is strongly right-skewed, reflecting real effects, Z = −3.19, p = 0.0007. Thirty-eight percent of all p-values are <0.01, approximately double that expected under null effects; see Figure 1. There is not significant evidence for publication bias in this set of statistically significant effects, z = 0.94, p = 0.174. The average true effect size estimated by p-curve is r = 0.12 (95% Confidence Interval (CI): 0.09–0.19). This estimate is slightly higher than VD&G’s “best” overall estimate of 0.10; however, it is appreciably lower than their estimate uncorrected for publication bias (0.21). Mean power is estimated to be 0.28. See

Table 2. Effect size estimates: p-curve effect size estimates (minimization of Kolmogorov–Smirnov (K-S) statistic and Stouffer’s Z); Hedges [23] selection model; alternative selection models; Van Dongen and Gangestad [2] meta-analytic estimates. All estimates scaled as r.

Domain	p-Curve Estimates				Hedges [23]			Alternative Selection Models							Van Dongen & Gangestad Restricted		Range of Plausible Mean Est.
	k	K-S	Stouffer’s Z	95% CI	k	r	95% CI	k	q = 0.2		q = 0.4		Est.	Median N	Mean	SE
									r	95% CI	r	95% CI	τ
All	34	0.12	0.14	0.09–0.19	34	0.13	0.09–0.17	61	0.08	0.05–0.11	0.11	0.08–0.14	0.14–0.16	94	0.21 a	0.02	0.08–0.14
Body FA only	32	0.13	0.15	0.09–0.20	32	0.14	0.10–0.19	59	0.08	0.05–0.11	0.11	0.08–0.14	0.15–0.17	94			0.08–0.15
p < 0.025 only	20		0.17	0.11–0.22
All (N > 150)															0.10	0.02
Attractiveness	5	b	0.02	−0.41–0.28	5	0.16	−0.07–0.39	21	0.05	0.01–0.09	0.07	0.03–0.11	<0.001	79	0.13	0.03	0.02–0.13
Health and Disease	4	−0.11	−0.14	−0.28–0.11	4	−0.16	−0.24–0.08	7	0.06	0.00–0.11	0.08	0.01–0.12	<0.001	203	0.09	0.04	0.06–0.09
Fetal	5	0.11	0.11	−0.01–0.19	5	0.09	0.00–0.19	6	0.09	0.02–0.15	0.10	0.04–0.16	0.06–0.07	208	0.17	0.03	0.09–0.17
Hormonal	2	b						5	0.05	-0.05–0.14	0.07	−0.03–0.17	0.12–0.14	141	0.08	0.04	0.05–0.08
Psychological	11	0.21	0.19	0.10–0.27	11	0.21	0.14–0.28	12	0.18	0.08–0.27	0.21	0.12–0.28	0.21–0.22	105	0.13	0.03	0.13–0.21
Reproductive	7	0.17	0.18	0.00–0.30	7	0.21	0.09–0.33	10	0.11	0.01–0.20	0.15	0.05–0.24	0.20–0.21	69	0.17	0.03	0.11–0.17

^a Estimate uncorrected for publication bias; ^b Kolmogorov–Smirnov test failed to converge on single value; see [19] or supplemental online materials (SOM) for details.

.

Simonsohn et al. [30] suggest an additional robustness analysis: p-curve applied to only those effects significant at p < 0.025. These analyses address “ambitious p-hacking,” which arises when researchers do not settle for a p-value less than 0.05 but rather look for p-values less than a smaller threshold (e.g., 0.04 or 0.035). This analysis also yields strong evidence for a mean non-zero effect size, here with an estimated effect size of 0.17 (95% CI: 0.11 to 0.22).

3.2. All Significant Independent Effects, Excluding Dental FA

This p-curve is similarly right-skewed, Z = −3.00, p = 0.0013; this set of effects also shows little evidence of publication bias, z = 0.77, p = 0.221. p-curve’s average effect size estimate is r = 0.13 (95% CI: 0.09–0.20).

3.3. All Effects, Including Non-Significant and Negative Effects

Next, we performed alternative selection models on the overall set of effects, including non-significant and negative effects. In one set of analyses, we used an approach comparable to p-curve: we used only significant effects, and assumed homogeneous effects [23]. These models generated mean effect size very similar to those generated by p-curve: 0.13 for the total set of effects and 0.14 for effects for body FA only. As McShane et al. [25] note, these estimates are actually superior to p-curve’s. Though both are similarly unbiased as estimates of effects of published mean effects and similarly biased by heterogeneity in estimating mean effect size in the population of effects, Hedge’s [23] model has less mean error (as reflected by smaller confidence intervals; see Figure 2). Hence, these results should be given more weight than p-curve’s (though both sets are very similar).

We also ran models that assume heterogeneity and use non-significant effects. They generated the same two estimates for both the total set of effects (N = 61) and the set of effects for body FA only (N = 59): r = 0.08 when q = 0.2, r = 0.11 when q = 0.4. These models detected moderate levels of heterogeneity, τ = 0.14–0.17 (see Table 2). This heterogeneity may explain why these estimates are slightly less than estimates from analyses that assume homogeneity.

3.4. Individual Domains

In Table 1, we examine p-curves (and p-uniform tests for publication bias) separately for each of five fitness-relevant domains. For three domains (psychological, fetal, and reproductive), the p-curve is significantly right-skewed and indicative of true effects. For the domains of health and attractiveness, p-curves yield inconclusive results: there is neither compelling evidence for real effects, nor indication of p-hacking (Z = −0.87, p = 0.19 and Z = 0.12, p = 0.55 for health and attractiveness, respectively). Tests reveal evidence for publication bias only in the health domain.

Table 2 contains four different effect size estimates per domain: two from p-curve analyses (Kolmogorov–Smirnov statistic minimization and Stouffer’s Z score; for details of estimation, see [19]), and two from selection methods (q = 0.2 and 0.4). These values are compared to VD&G’s “restricted” estimates. Our effect size estimates for reproductive outcomes, ranging from 0.11–0.18, are relatively close to VD&G’s estimate (0.17); the same is true for hormonal outcomes (our estimates: 0.05–0.07; VD&G: 0.08). Our estimates for fetal outcomes (0.09–0.11) fall short of VD&G’s (difference in r = 0.06–0.08). For psychological outcomes, our estimates exceed the meta-analytic estimates (difference in r = 0.05–0.08). Estimates for health and attractiveness are based on a very small number of significant effects (four and five, respectively), so p-curve analyses provide unstable estimates and wide confidence intervals (see Table 2); however, alternative selection method estimates fall short of VD&G’s for both domains, with estimates being more concordant for health than attractiveness (health: difference in r = 0.01–0.03; attractiveness: difference in r = 0.06–0.08).

4. Discussion

The results we provide from p-curve and alternative selection methods add to the understanding of human FA associations. First, they provide evidence for true evidential value in the overall set of FA effects, and for three of the five individual domains analyzed. Despite ubiquitous publication bias [12], it is not the sole source of positive effects in this literature. Additionally, although p-curve estimates are often biased downward when results have been p-hacked, our results do not reflect this pattern (even when accounting for ambitious p-hacking by examining only p-values < 0.025), and p-curve yielded no evidence of p-hacking (we cannot rule out p-hacking, but p-curve analysis does not detect it; it is possible that more aggressive forms of p-hacking operate [27,30]). This conclusion reinforces VD&G’s: when considered in aggregate, FA does appear to predict variance in fitness outcomes.

Second, our analyses speak to the strength of these effects, offering a supplement or alternative to traditional meta-analyses. For the overall set of effects (both including and excluding dental FA), Figure 2 provides a visual comparison of our effect size estimates to those derived from the original VD&G meta-analysis. Our range of effect size estimates, 0.08–0.15, resembles closely what VD&G consider the “best” possible estimate range (0.10–0.15), but falls short of their uncorrected estimates, suggesting some influence of publication bias. Within techniques, our estimate range based on p-curve (0.12–0.15) slightly exceeds that from alternative selection methods (0.08–0.11), suggesting an influence of effect size heterogeneity missed by p-curve [25]; this is corroborated by our estimates of τ (Table 2). A mean effect size for body FA of 0.12 yields an estimated effect size for underlying DI that is meaningful: in a typical study design, ~0.3. However, VD&G note that “there exists a great deal of variability across studies and, perhaps, outcomes” ([2], p. 396)—and this observation is consistent with the different techniques yielding different estimates in our overall set of effects. Not only does this suggest a need to analyze effects by domain, but it also calls into question the use of traditional meta-analytic procedures such as trim and fill, which overcorrect for publication bias that does not exist, especially in the presence of heterogeneity [16,31]. Our analyses have the advantage of providing alternative means to assess average effect size while accounting for publication bias and heterogeneity. We provide estimates within domains that depart, modestly but notably, from VD&G’s, likely due to differing influences of heterogeneity and publication bias between outcomes. We note as well that some heterogeneity may be due to methodological differences. For instance, VD&G found that FA measures that aggregated bodily asymmetry in a larger number of traits yielded larger effect size, likely because they tapped DI with greater validity. For this reason, estimates from methods that ignore heterogeneity (and hence estimate mean effects in studies yielding significant results) are not meaningless. Rather than advocating that any one set of estimates be seen as the “final word” regarding the strength of FA associations, we echo McShane et al. [25] and view our estimates as part of an overall sensitivity analysis, in which we provide a range of plausible estimates, given various assumptions regarding the body of effects analyzed (see Table 2).

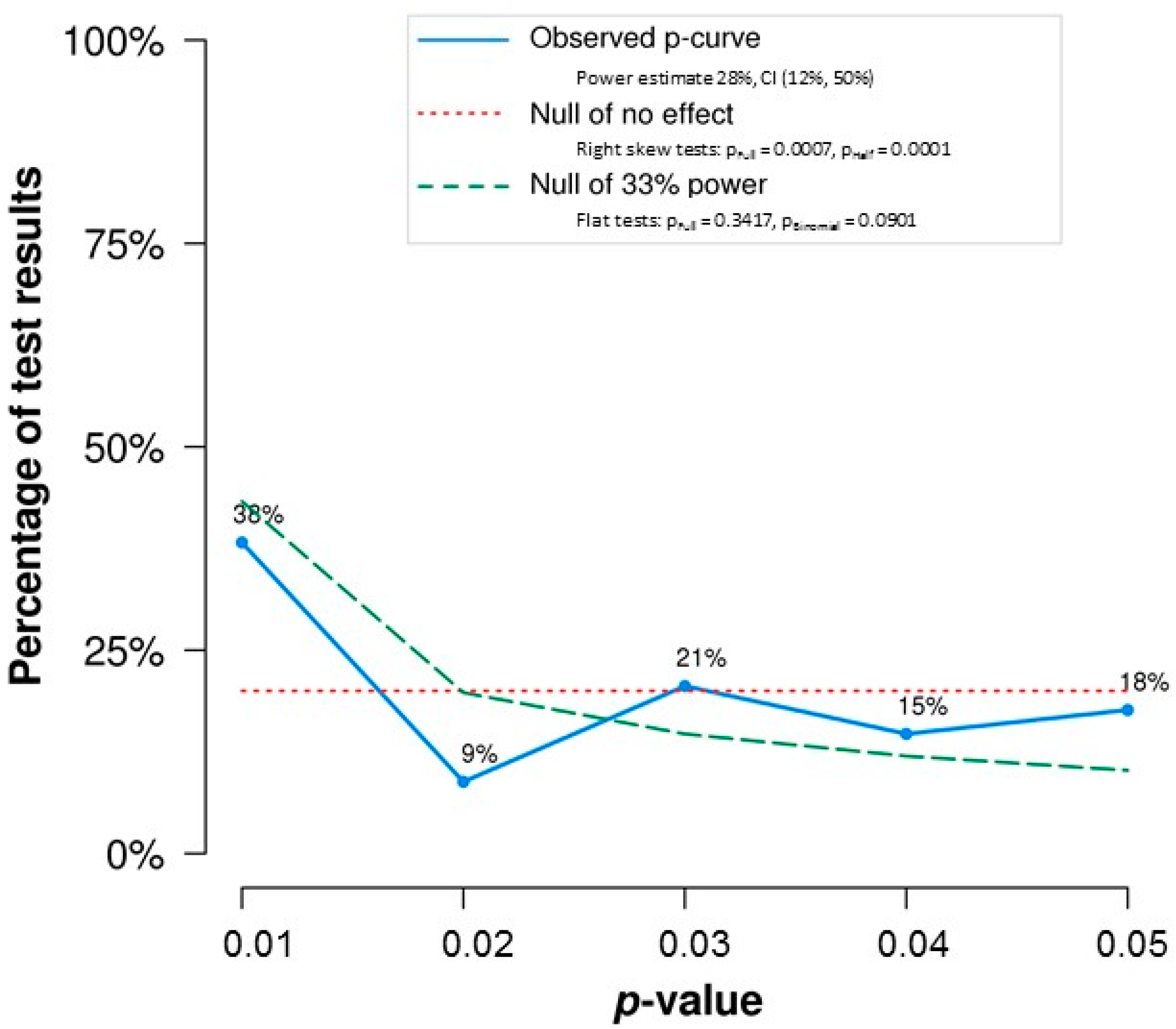
Third, our analyses reinforce a theme of VD&G’s conclusions, which is that the typical study in this literature is underpowered. In the overall set of significant effects, p-curve estimated mean power of just 28% (see Figure 1). Given a true correlation of 0.12, a sample size of 500+ is needed to ensure 80% power. By contrast, median sample size in our set of studies yielding significant effects fell short of 100 (median sample size for studies yielding non-significant effects was very similar). Indeed, only one study had sufficient sample size. Low power to detect real but meaningful effects very likely contributes strongly to the very mixed nature of literature on FA and DI.

As McShane et al. [25] document, selection models in the tradition of Hedges [23] and Hedges and Vevea [24] offer better estimates of effect size. Both p-curve and Hedges’s [23] model assume homogeneous effects. All else being equal, studies examining true effects larger than average are more likely to generate significant results, so these methods may overestimate the effect size in that domain of studies. However, they nonetheless provide unbiased true effect size estimate for effects that were detected as significant (see also [20]). Hedges’s model simply does so with less mean error (again, see Figure 2). Selection models that include non-significant results offer more efficient estimates than either p-curve or Hedges [23]; they can also account for heterogeneity in true effect size. In our approach, we assumed two different values of q, each in a range of plausible values. Estimates based on the two assumptions differed modestly (0.08 vs. 0.11). Of all 61 effects in our analysis, 56% were significant. Based on mean estimated power (28%), a q of just over 0.3—between the two values we used in our sensitivity analyses—would generate this proportion of significant effects. A best estimate of mean effect size in the population of effects, assuming heterogeneity, then, is about 0.1—very similar to VD&G’s.

Though we detected no p-hacking, p-hacking could have of course influenced results in individual studies. Researchers are advised to guard against the many ways p-hacking can occur [32]. We recommend adequately powered, pre-registered studies for the future.

In addition to adding to the literature on FA, our analyses illustrate the utility of p-curve and alternative selection methods for biology. They promise to be useful additions to the biologist’s toolbox as supplements to traditional meta-analyses. They are simply applied. They yield unbiased estimates of effect size across a range of conditions, and while these techniques may be biased under certain circumstances (e.g., when significant results have been p-hacked, or when effects are heterogeneous), applying these techniques jointly helps establish a plausible range of effect size estimates.