1. Introduction
In real word, a lot of available data may be imprecise, incomplete, and uncertain for numerous reasons, such as the incompleteness of our observations, measurements, and estimations, or due to the existing disturbances and uncertainties in the statistical processes. As an extension of classical statistics, Smarandache [
1,
2,
3] first presented neutrosophic statistics, which deals with set values instead of crisp values. In classical statistics, all data are determinate; while in neutrosophic statistics, the data may be ambiguous, vague, imprecise, incomplete, and even indeterminate. This is the distinction between neutrosophic statistics and classical statistics. In many cases, when indeterminacy is zero, neutrosophic statistics coincide with classical statistics.
In neutrosophic statistics, Smarandache [
1,
2,
3] first proposed concepts of neutrosophic probability, which are described as the truth-probability, indeterminacy-probability, and falsity-probability. It is important how to get indeterminacy in the whole set of
n trials. He defined an indeterminacy threshold
V, which is the number of trials whose outcome is indeterminate for
V ∈ {0, 1, 2, …,
n}.
The cases with a threshold < V will belong to the indeterminate part, while cases with a threshold ≥ V will belong to the determinate part. Thus, let PT be the chance that a particular trial results in a success, PI be the chance that a particular trial results in an indeterminacy (i.e., neither a success nor a failure), and PF be the chance that a particular trial results in a failure.
However, this partially indeterminate and partially determinate set of n trials depends on the problem that one needs to solve and on the expert’s point of view.
In classical statistics, all data are determined; while neutrosophic statistics refers to a set of data wherein a part of data is determinate/indeterminate/false in some degree.
In neutrosophic statistics, Smarandache [
1,
2,
3] also proposed the concept of a neutrosophic number (NN)
z = s + uI, which consists of its determinate part
s and its indeterminate part
uI for s,
u ∈
R (all real numbers) and
I ∈ [
inf I,
sup I] (indeterminacy). It is obvious that it can describe determinate and/or indeterminate information. For example, assume a
NN is
z = 5 + 2
I for
I ∈ [0, 0.6]. Thus, its determinate part is 5, its indeterminate part is 2
I, and then the NN is
z = [5, 6.2] for
I ∈ [0, 0.6] to express the possible range of
z. In actual applications, one can also adjust the range of indeterminacy
I to satisfy some specified requirements. Obviously, NN is very suitable for the expression of determinate and/or indeterminate information in indeterminate environments. Hence, NNs have been applied to decision making [
4,
5,
6] and fault diagnosis [
7,
8] in recent years.
Although neutrosophic statistics was defined by Smarandache in 1996 [
1,
2,
3], it has not been developed since then. Unfortunately, the existing theory of neutrosophic probability and statistics introduced in [
1,
2,
3] encounters a great deal of difficulties in engineering applications. In fact, the neutrosophic probability and statistics in [
1,
2,
3] is very difficult to be used for engineering applications in the current form. Therefore, it is necessary to propose new neutrosophic probability and a statistical method to be easily used for engineering applications. Motivated by the Smarandache’s neutrosophic probability and NN, in the original study, this paper firstly proposes a new concept of neutrosophic probability in neutrosophic interval distributions, which is called neutrosophic interval probability (NIP), and then originally introduces the NN with the confidence degree of NIP, which is called a neutrosophic interval statistical number (NISN). Finally, in an actual case, NISNs are used for the expressions of joint roughness coefficient (JRC) values with indeterminate information because determining the JRC value effectively is a key parameter in the shear strength between rock joint surfaces in geotechnical engineering [
9]. The main advantage of the new neutrosophic interval statistical method is that it is more suitable for engineering applications and expressions to solve the difficult problems of existing neutrosophic/classical statistical problems under indeterminate environments.
To realize the study, this article is organized as follows.
Section 2 gives the definition of NIP based on neutrosophic possibility in an interesting range.
Section 3 presents NISN based on combining NN with the confidence degree of NIP. In
Section 4, by an actual case, NISNs are used for expressing the JRC values with indeterminate information as an engineering application in geotechnical mechanics. In
Section 5, conclusions and future research directions are presented.
2. Neutrosophic Interval Probability
In this section, we give the definition of NIP based on neutrosophic probability in an interesting range.
Definition 1. Let a = [xL, xU] be an interesting range of all the sample individuals. A NIP can be defined as P = <[xL, xU], (PT, PI, PF)>, where PT is a truth-probability belonging to the determinate range, PI is an indeterminacy-probability belonging to the indeterminate range, and PF is a falsity-probability belonging to the almost impossible/failure range. Then, the sum of the three probabilities satisfies PT + PI + PF = 1.
Let us consider n samples with the same sizes as the same trials corresponding to some trial characteristic. By statistical analysis for the n trial data, we can obtain the maximum value xU (upper bound) and the minimum value xL (lower bound) in all trial data and the average value xm and standard deviation σ. Based on these statistical results, we propose the following calculation methods of NIP.
First, the interesting range of all the sample individuals is represented by the interval value a = [xL, xU] according to the maximum and minimum values (i.e., the upper and lower bounds) of the trial data. Then, in the interesting range of all the sample individuals we can calculate the truth-probability PT = nT/n, the indeterminacy-probability PI = nI/n, and the falsity-probability PF = nF/n from a statistical viewpoint, where nT implies the frequency in the robust/credible interval [xm − σ, xm + σ], nI implies the frequency in the indeterminate/uncertain intervals [xm − 3σ, xm − σ) and (xm + σ, xm + 3σ], and nF indicates the frequency in the remaining/incredible intervals [xL, xm − 3σ) and (xm + 3σ, xU].
Let us consider the following example to show the calculation of NIP.
Example 1. Assume that 100 samples (n = 100) with the same sizes are taken to measure some mechanical characteristic of the sample individuals. For the obtained measuring data, the distributions of the statistical data are shown in Table 1. From
Table 1, we can determinate the NIP by the following procedures:
First, the interesting range of all the sample individuals is a = [0, 5].
Then, we can calculate the truth-probability, the indeterminacy-probability, and the falsity-probability, respectively, as follows:
PT = nT/n = 70/100 = 0.7, PI = nI/n = 25/100 = 0.25, and PF = nF/n =5/100 = 0.05.
Thus, the NIP is P = <[xL, xU], (PT, PI, PF)> = <[0,5], (0.7, 0.25, 0.05)>.
From the example, we can see that the existing classical/neutrosophic probability cannot represent such a probability problem. Hence, the NIP contains much more information and demonstrates its advantage in such an expressed case.
3. Neutrosophic Interval Statistical Number
By combining a NN with the confidence degree of NIP, we present NISN for effectively expressing some statistical characteristic of trial data with indeterminate information.
Let a NIP be
P = <[
xL,
xU], (
PT,
PI,
PF)> and the ideal NIP be
P* = <[
xL,
xU], (1, 0, 0)>. Then, the cosine measure value between
P and
P* [
4] is defined as the confidence degree
Thus, NISN is presented as
where
xm is the average value/determinate part of
Ne and
I is indeterminacy. Here,
I may take the robust/credit interval [−
σ,
σ] based on a standard deviation
σ.
Obviously, if e = 1 for P = <[xL, xU], (1, 0, 0)>, then Ne = xm, which is degenerated to the classical average value (crisp value) xm with the maximum confidence degree; if e = 0 for P = <[xL, xU], (0, 0, 1)>, then Ne = xm + I, which is degenerated to a NN without confidence degree. However, when 0 < e < 1, the confidence degree of e can affect the indeterminate part (1 − e)I of the NISN Ne.
For Example 1, by using Equation (2) the NISN is calculated as
If I = [−σ, σ] = [−0.5, 0.5], then Ne = [1.97, 2.03].
Obviously, the NISN can indicate the interval range of actual measuring data effectively and reasonably under indeterminate environments, while the classical statistical method is only a crisp value xm, which is a specialty of the proposed neutrosophic interval statistical method.
4. Joint Roughness Coefficient Values Expressed by Using Neutrosophic Interval Statistical Number in Geotechnical Mechanics
Statistical analysis of geotechnical engineering is an important mathematical tool for modeling and quantifying uncertainties of geotechnical mechanics parameters. It is one of the initial and essential procedures because a lot of subsequent evaluations of risk and reliability depend on these parameters. In nature, the mechanical properties of geological bodies are very complex, and its various mechanical parameters are vague, incomplete, imprecise, and indeterminate [
9]. However, it is difficult to describe the indeterminacy of geotechnical parameters by the classical statistical method. Clearly, NISNs can effectively describe the incompleteness, uncertainty, and indeterminacy of geotechnical parameters by combining a NN with the confidence degree of NIP. In this section, we apply NISNs to express the indeterminate value of JRC because determining the JRC value effectively is a key parameter in the shear strength between rock joint surfaces.
To show the effectiveness and rationality of the proposed neutrosophic interval statistical method, we chose natural rock joint surface samples, with collected data from Changshan County, Zhejiang province, China. Here, as an actual case, we select a set of data measured by taking 10 groups of samples with the lengths of 10, 20, … 100 cm. According to the proposed neutrosophic interval statistical method, we use NISNs to express the JRC values.
Firstly, we give the total number of
n samples, the mean value
xm and the standard deviation
σ of each length
L, and then the results of their statistical analysis are shown in
Table 2.
Then, the frequency distributions in the different JRC intervals for each length
L are shown in
Figure 1. It is clear that most of the data are in the range of the truth probability, a small number of data is distributed on both sides of the truth range as the part of the indeterminacy, and the frequency of both sides is almost equal. Also there are a few data belonging to the false probability. Generally, all the distributions are almost in normal distribution, deflecting to left.
By taking the sample length L = 100 cm as an example, the calculation process is indicated by the following steps.
First, NIP is calculated as
Then by using Equation (2), the NISN is calculated as
Assume that I = [−σ, σ] = [−1.0050, 1.0050] is specified as the robust/credit interval, then Ne = [7.6929, 7.7421].
For other lengths of the data, we also obtain these results by above similar calculation steps, which are shown in
Table 3.
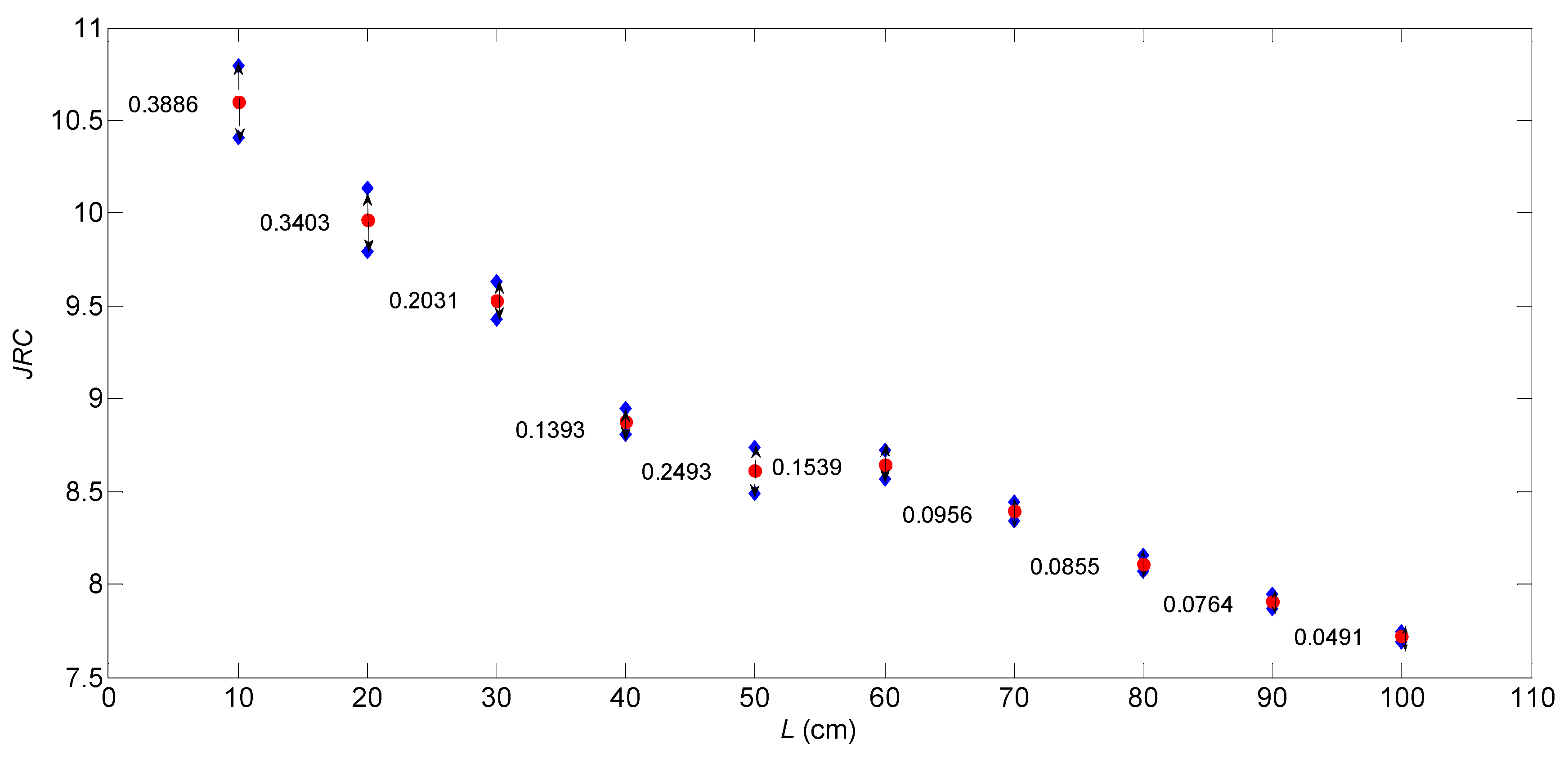
In
Figure 2, there are JRC values in each length
L expressed by using NISNs. Obviously, the interval values indicate symmetry regarding the average values, which imply their imprecise, uncertain information. Hence, we cannot give this indeterminate information just by the crisp statistical value such as an average value. That is to say, the classical statistical method ignores and loses some information which may be important and significant. However, we can use NISN to express it effectively and reasonably. In
Figure 2, we can also see that the NISNs can contain the average values (red points) and the black arrows show the indeterminate ranges indicted by numerical values. In general, when the sample length is increased, the indeterminate range is decreased. Clearly, NISNs can provide an effective and reasonable new way for the expression of JRC values under indeterminate environments.
In this original study, the superiority of the proposed neutrosophic interval statistical method over the existing neutrosophic statistical methods is in its ability to overcome the aforementioned drawback of Smarandache’s neutrosophic statistical method and to be more suitable for engineering applications under indeterminate environments. However, the classical statistical method cannot describe and deal with the indeterminate problems with the truth-probability, indeterminacy-probability, and falsity-probability, and then it only is a special case of the proposed neutrosophic interval statistical method in the determinate case, which may lose some useful information in engineering problems with indeterminate information; while the proposed neutrosophic interval statistical method can contain much more information and be easily applied in engineering areas under indeterminate environments. Therefore, it is more general and more feasible than the classical statistical method and the existing neutrosophic statistical method [
1,
2,
3].
5. Conclusions
This study first proposed the concepts of NIP and NISN, and then applied them to the JRC expressions by an actual case. However, NIP is an extension of the classical probability. In classical probability, the data are known and formed by crisp numbers (truth-probability), while in NIP, the data are composed of the truth-probability, indeterminacy-probability, and falsity-probability in different frequency distribution ranges. Since NISN consists of the determinate part and the indeterminate part with the confidence degree of NIP, NISN is very suitable for the expression of measuring data with indeterminate information such as JRC. Then in the classical statistical method, geotechnical mechanics parameters, such as JRC, are represented only by average values and/or standard deviations, but they cannot express indeterminate values and lose some useful information. It is obvious that NISN can effectively and reasonably express indeterminate information in engineering areas under indeterminate environments. In the future, we shall apply NISNs to the expression and analysis of engineering experimental/measuring data, economic data, fault diagnosis data, and medical diagnosis data.