Abstract
In order to improve the response performance of a proportion integration differentiation (PID) controller for magnetorheological fluids (MRF) brake and to reduce the braking fluctuation rate, an improved fruit fly optimization algorithm for PID controller parameters tuning of MRF brake is proposed. A data acquisition system for MRF brake is designed and the transfer function of MRF brake is identified. Moreover, an improved fruit fly optimization algorithm (IFOA) through integration of PID control strategy and cloud model algorithm is proposed to design a PID controller for MRF brake. Finally, the simulation and experiment are carried out. The results show that IFOA, with a faster response output and no overshoot, is superior to the conventional PID and fruit fly optimization algorithm (FOA) PID controller.
1. Introduction
As a new type of intelligent brake, magnetorheological fluids (MRF) brake uses MRF as a working medium, and its brake torque can be controlled by an external magnetic field [1,2,3]. Due to the well rheological properties of MRF, the control system of MRF brake is characterized by a simple structure, low power and fast response. However, with the passage of working time, the performance of MRF is changing [4]; it may result in worse control effects and lower level stabilization. Thus, the control technology with high accuracy, good stability and fast response for MRF brake has been an active area of research recently.
Although there are many control techniques, and new control theories and design methodologies are continually developed in the automatic control field, proportion integration differentiation (PID) control has been widely developed in the field of industrial control owing to the advantages of high dependability, strong robustness and supernal cost-benefit ratio [5]. There are many factors that influence the effect of PID control, among which selection of the three parameters P, I and D is one of the most important factors [6,7]. Parameter selection is a combinatorial optimization problem, and the result directly determines the effect of PID control; thus, parameters tuning would play an important role in evaluating the performance of a PID controller.
Fruit fly optimization algorithm (FOA), proposed by Professor Pan in 2011, is a global intelligent optimization algorithm based on the foraging behavior of the fruit fly [8]. FOA has some advantages; for example, it is easy to implement the program code with short running time, and it only needs to adjust four parameters which are the initial interval, the maximum number of iterations, the population amount and the flying distance range [9]. Since the FOA is proposed, it has been widely applied in financial parameter optimization [10], forecasting [11], scheduling [12], etc. However, similar to other optimization algorithms, the basic FOA also has the possibility of falling into local extremes due to its blind searching and fixed fly distance range [13].
Bearing the above observations in mind, we apply an improved fruit fly optimization algorithm (IFOA) to the problem of parameters tuning for PID controller of MRF brake and the rest of this paper is organized as follows. In Section 2, some related works are outlined based on the literature. In Section 3, some key techniques of the improved fruit fly optimization algorithm are presented. In Section 4, the simulation examples and experiments are carried out to verify the feasibility and efficiency of the proposed algorithm. Our conclusions and future works are summarized in Section 5.
2. Literature Review
Recent publications relevant to this paper are mainly concerned with two research streams: PID control methods and fruit fly optimization algorithms. In this section, we try to summarize the relevant literatures.
2.1. PID Control Methods
Due to the remarkable effectiveness, simple implementation and broad applicability, PID controller is becoming one of the most popular controllers and is widely used in industry. Oliveira et al. [14] used the Hermite-Biehler theorem to design PID controllers for a class of time delay systems, and obtained a stable PID controller. In [15], an improved conventional PID control scheme using linearization through a specified neural network was developed to control nonlinear processes, and the simulation results showed that the solution with nonlinear processes had a unique minimum that could be found directly. Fuzzy logic, genetic algorithms and neural networks were used to tune the PID parameters, and the results showed that the controller with a combination of these algorithms was better than the conventional controllers [16,17,18]. In [19], the variable universe fuzzy PID control for Landing Gear based on MRF damper was established; the results showed that the variable universe fuzzy PID control had a better control effect than the general fuzzy PID controller. In [20], a conventional PID controller was designed for a tension control, and the experiment results showed the feasibility and better control effect for tension control of a winch spooler system. In [21], the on-off and PID controller were proposed to evaluate the controller's effectiveness in braking the wheel shaft at 50, 100 and 150N in varying speeds of 300, 500, 700 and 900 rpm; the simulation and experiment results showed that the PID controller had good performance compared with the on-off control.
2.2. Fruit Fly Optimization Algorithm
Since the FOA has been proposed, it has gained a lot of attention. In [22], FOA-based optimized PID (FOA-PID) was proposed; simulation results demonstrated that the best PID controller parameters could be obtained with the capability of providing satisfactory closed-loop performance. In [23], FOA was used to tune the parameters of fractional order fuzzy PID controller for electronic throttle; the simulation results showed that the proposed method had a more effective performance. In [10], FOA was adopted to optimize the general regression neural network (GRNN) model, and the analysis results showed that the FOA-optimized GRNN model had the best detection capacity compared with other intelligent optimization algorithms. Although the FOA had an extensive application in many fields, there still existed the possibility of getting into the local optima [13]; this was probably due to the blind searching and the fixed flying range of the fruit fly individuals, which may result in the algorithm escaping from the optimal solution and falling into the local optima. In [24], a novel modified fly optimization algorithm (MFOA) was proposed for determining the optimal PID controller parameter, in order to avoid local optima solution; an escape local optima factor was added into FOA and the simulation results showed that the MFOA-PID controller was better than the FOA-PID controller especially in terms of the optimal solution. Wang et al. [12] also proposed an improved FOA, which maintained the population diversity to enhance the exploration ability, and added a new parameter to avoid local optimal solution. In [25], an improved FOA, called linear generation mechanism of candidate solution fruit fly optimization algorithm (LGMS-FOA), was proposed. It redefined the smell concentration judgment value and added a parameter called inertia weight; simulation results showed that it could enhance searching efficiency and improve searching quality greatly.
2.3. Discussion
Many valuable control methods have been proposed in the above literatures and applied in recent decades, but there are still some shortcomings. Firstly, the conventional PID controller has a worse control effect than the PID controller designed with an intelligent algorithm. Secondly, due to the increase in working hours and the external magnetic disturbances, it is necessary to design a faster-responding and less-overshooting control system for MRF brake. Thirdly, adaptive methods based on some intelligent algorithms are also limited because of the great amount of calculation. Finally, compared with FOA, other optimization algorithms, such as particle swarm optimization (PSO), genetic algorithms (GA), ant colony optimization (ACO),Gravitational Search Algorithms (GSA) [26,27] et al., have the problem of high complexity of coding. FOA has great advantages in iteration rate and encoding efficiency, but it still has the probability of falling into local optima.
Therefore, a novel method, IFOA, is proposed to tune parameter for PID controller of MRF brake. The flying distance is redefined by the cloud model and proposed formula, which aims to reduce the blind searching and improve convergence precision. A simulation example is carried out to validate the effectiveness and the correctness of the proposed method, and a comprehensive comparison and discussion are conducted to demonstrate the superiority of IFOA in iteration speed and precision. Simulation and experimental results show that the proposed controller can achieve better response characteristics and control effects.
3. The Proposed Method
3.1. The Data Acquisition System of MRF Brake
A data acquisition system of MRF brake has been developed in our laboratory, as shown in Figure 1. It consists of three phase asynchronous, frequency converter, torque speed transmitter, PCI data acquisition card, self-designed MRF brake, DP811A programmable power supply, monitor and display interface. The frequency converter provides 200 rpm for the three phase asynchronous, the torque speed transmitter measures the torque which is generated by the input current provided by the DP811A programmable power supply, the PCI data acquisition card is used for collecting the identification data, and the display interface is designed based on LabVIEW which mainly includes torque acquisition module and excitation current generation module. The proper records of torque data is a critical step in MRF brake modeling, so in the excitation current generation module, the excitation current is added with 128Hz white Gaussian noise and a standard deviation of 0.02. Thus, the system dynamic characteristics can be fully demonstrated and the main device details are shown in Table 1, Table 2 and Table 3.

Figure 1.
Identification data acquisition platform of magnetorheological fluids (MRF) brake.

Table 1.
Main technical parameters of self-designed MRF brake.

Table 2.
Main technical parameters of PCI8735 acquisition card.

Table 3.
Main technical parameters of DP811A programmable power supply.
3.2. The Transfer Function of MFR Brake
MRF brake is controlled by the excitation current in real time, so it is expressed as a first order pure delay link: . The rheological effect of MRF is produced at the millisecond level, so τ is very small, the can be replaced by , therefore, the transfer function of MRF brake can be expressed: . Where Ko is the gain of MRF brake, Tp1 and Tp2 are the time constants. In this paper, the current-braking torque data are obtained by the data acquisition system and the system identification toolbox is used to identify the mathematical model of MRF brake in MATLAB. A group of excitation current and output torque data are used as identification data, and another group of excitation current and output torque data are used as inspection data. The system identification steps of the mathematical model can be described as follows: Importing data and setting the start time and sampling time; Data preprocessing in Operations/Preprocess and filtering out the interference signal; Dragging the inspection data to validation data box and Clicking Estimate/Process models to set the parameters; Obtaining the system identification result; Selecting the Model output to view the system identification result. Finally, the Best Fit is 90.89%; that is a good fitting degree, where Ko = 9.6167, Tp1 = 0.22867, Tp2 = 0.24287. Transfer function of MRF brake can be expressed as follows:
3.3. The Improved Fruit Fly Optimization Algorithm
FOA is a global intelligent optimization algorithm based on foraging behavior of the fruit fly andit is more suitable for the optimization of complex problems. The steps of basic FOA can be expressed as follows:
- Step 1
- Initialize the master parameters of FOA. The population amount (PA), the maximum iteration number (INmax), the random flying distance range (FR), the group location range (LR), and the initial location ( of fruit fly population are determined.
- Step 2
- Calculate the random direction and distance to search for food of the fruit fly individual.
- Step 3
- Calculate the distance between the fruit fly individual and the origin, and then calculate the flavor concentration parameter which is the reciprocal of the distance.
- Step 4
- Substitute into the fitness function, calculate the value of flavor concentration function and find out the best flavor concentration in the fruit fly population. The minimum value is taken as the best flavor concentration in this paper.
- Step 5
- Obtain the best flavor concentration value and the coordinates of , the fruit fly population flies to that location through vision at this point.
- Step 6
- When the smell concentration reaches the preset precision value or the iteration number reaches the maximal IN, the circulation stops. Otherwise, Steps 2 to 4 are repeated.
From the basic FOA, it can be seen that the parameter assignment of the fly distance depends largely on rand function. It has the possibility of falling into local extremes due to its greater blind searching. Furthermore, the step size of FOA is always a fixed value, which reduces the convergence precision in the later iteration.
In this paper, the cloud model algorithm is used to adjust adaptively the value of rand function on interval [0, 1]. It can be defined as follows: Let C is the concept of universe U, if x∈U is a stochastic realization of concept C, which is : U→[0, 1], ∀x∈U, the determinacy of x to C described by ∈[0, 1] is a random number with a stable tendency, which satisfies a distribution x~N (Ex, En'), En'~N (En, He), the determination of x on C is . Where a one-dimensional backward cloud algorithm is used to get Ex, En and He, one-dimensional forward cloud algorithm is used to obtain the value of rand function of contemporary fruit flies. Then adjust the step size adaptively according to the current iteration number; since the step size is too small to jump out of the local optimal, the minimum step size of the searching distance is set to improve the convergence precision. , Ex, En, He, Rand and step size adjustment formulae are presented as follows:
where FR, are the maximum and minimum step size of the fruit fly, respectively, is a positive integer, defines the uncertainty of , and the uncertainty of is smaller as is larger. For having a good balance between the ambiguity and randomness, = 1 is used in this paper.
The flowchart of IFOA is shown in Figure 2.
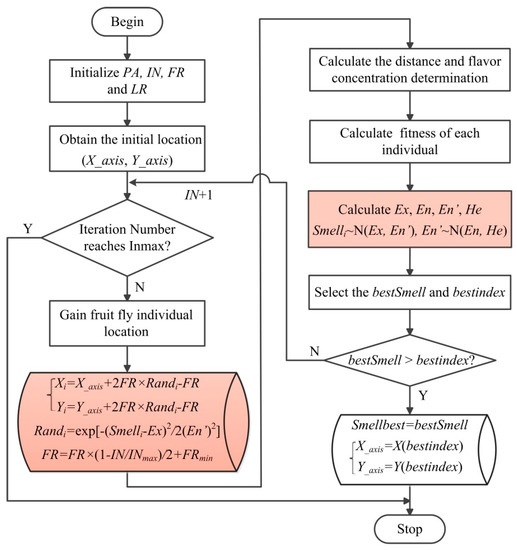
Figure 2.
Flowchart of the improved fruit fly optimization algorithm (IFOA).
The pseudo-code of IFOA can be summarized as follows:
| Begin Initialize PA, INmax, FR, LR and For (p: = 1; p < PA; p++) { ; ; ; ; ; } [bestSmell bestindex] = min (Smell); ; ; ; For (i: = 1; i< PA; i++) ; ; For (i: = 1; i< PA; i++) ; ; ; For (i: = 1; i < PA; i++) ; while (IN < INmax) { ; Update Xi; Yi; Disti; Si; Smelli; if (bestSmell < Smellbest) { ; ; bestS = S (bestindex,:); Smellbest = bestSmell; } ; ; Update Ex; En; He; Randi; IN = IN+1; } End |
3.4. Tuning the PID Parameters Based on IFOA
The principle of PID controller based on IFOA is shown in Figure 3. The output u(t) can be expressed as follows:
where is the proportional coefficient, is the integral coefficient, is the differential coefficient.
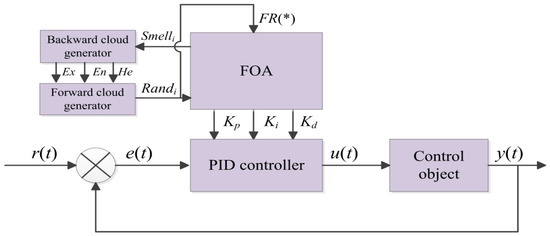
Figure 3.
Principle of proportion integration differentiation (PID) controller based on IFOA.
In order to tune parameters for the PID controller, the fitness function of IFOA must be established which can comprehensively evaluate all kinds of performance. The time integral performance index of the absolute value for the error (J) is used as the minimum objective function. In order to prevent excessive control of the energy, the square of u(t) is added to the objective function; in addition, a penalty function is used to avoid overshoot, so the overshoot will be taken as the optimal index once it is generated. The following formula is selected as the optimal index of parameters selection:
where , , and are weights, » , e(t) is the systematic error, e(t) = r(t) − y(t), u(t) is the controller output, and is the rise time.
The proposed method of PID parameters tuning based on IFOA is shown in Figure 4.
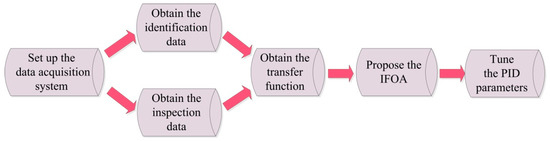
Figure 4.
Flowchart of the proposed method.
4. Simulation and Experimental Results
4.1. Simulation Analysis
In order to test the performance of the designed PID controller, a MRF brake system is used as the object to carry out simulation analysis. IFOA PID controller is compared with the conventional PID and FOA PID controller. The simulation of the conventional PID controller is carried out with the Signal Constraint module in MATLAB/Simulink. The IFOA and the FOA have the same parameters setting: PA = 50, INmax = 100, ∈ (0, 5), FR = 0.5, = 0.999, = 0.001, = 2.0, = 100.
The input of control system is unit step signal and the simulation time is 0.2s. The optimization process of comprehensive performance index function BestJ is shown in Figure 5, it can be seen that IFOA is superior to FOA in convergence speed and precision, which reveals its terrific global and local ability in parameter optimization. Figure 6 is the step response curve, the first curve is the target curve, the second curve is response of the conventional PID controller, the third curve is response of FOA PID controller, and the fourth curve is response of IFOA PID controller. PID parameters (, , ), the performance indicators of unit response (σ, , ) and consumption time (Ct) are shown in Table 4.
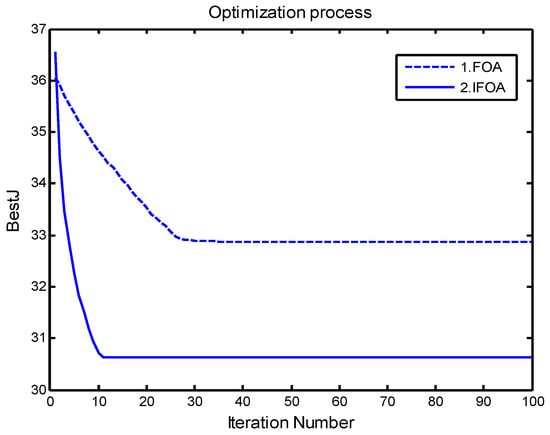
Figure 5.
Convergence trends of fruit fly optimization algorithm (FOA) and IFOA.
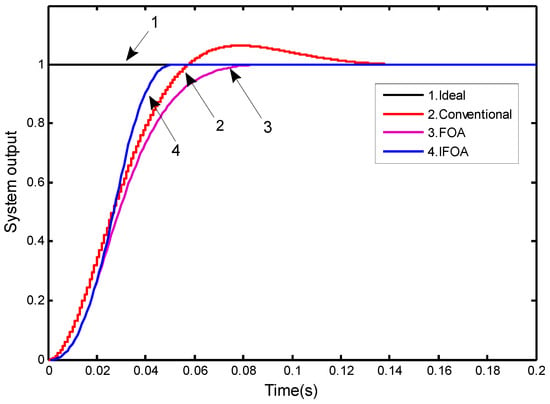
Figure 6.
Step response curves of the three controllers.

Table 4.
Performance indexes of the step response of the three controllers.
Compared with the conventional PID controller and FOA PID controller, the overshoot σ of IFOA PID controller is decreased from 6.5% to 0, the adjusting time has a decrease of 63.8% and 39.0%, respectively, and the rise time has a decrease of 45.8% and 50.0%, respectively. In terms of consumption time, because the conventional PID does not have the optimization part of the intelligent algorithm, it has the shortest time but the worst effect. In detail, the IFOA does not obviously vary from FOA in consumption time; the IFOA algorithm only increases 2.47% compared with the FOA algorithm, but it has a quicker response, showing a good calculation process. Simulation analyses of the step response show that IFOA PID controller has the advantages of quicker response, shorter adjusting times and no overshoot; it shows better response characteristics of a steady and dynamic state.
4.2. Experimental Results
Figure 7a,b show the experiment of 2A-200rpm and 3A-300rpm, respectively, to check MRF brake's ability of providing a constant braking torque. It can be seen that the conventional PID controller has the error of ±2% and has the overshoot of 5%, and the FOA PID controller and IFOA PID controller has the same error of ±1.5%, but the IFOA PID controller has quicker response and shorter adjusting times than the FOA PID controller. Experiment results prove that the conventional PID controller with optimization algorithm has a better comprehensive performance; IFOA PID controller is superior to the conventional PID and FOA PID controller.
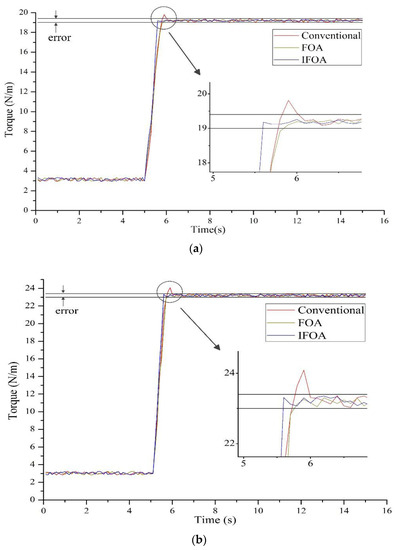
Figure 7.
Curve of braking stability of the three controllers. (a) 2A-200 rpm, (b) 3A-300 rpm.
5. Conclusions and Future Work
In this paper, an IFOA PID controller was designed to improve the control performance of MRF brake. The identification data acquisition system and transfer function of MRF brake were presented. In order to improve the characteristics of the proposed controller, PID control strategy, cloud model and IFOA were applied. Finally, simulations and experiments were carried out and the results showed that the self-designed controller was more ideal.
In future studies, other optimization algorithms and control strategies of MRF brake will be researched to get better response characteristics. The related experiments will be carried out continuously.
Acknowledgments
The support of National Natural Science Foundation of China (No. 51475454), National Natural Science Foundation of Jiangsu Province (No. BK20151144), Open Foundation of the State Key Laboratory of Tribology, Tsinghua University (No. SKLTKF14B06) and Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) in carrying out this research are gratefully acknowledged.
Author Contributions
Xinhua Liu wrote the paper; Yao Shi and Jing Xu designed the algorithm; Yao Shi carried out the simulations and experiments.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this article.
References
- Carlson, J.D.; Catanzarite, D.M.; St. Clair, K.A. Commercial magnetorheological fluid devices. Int. J. Mod. Phys. B 1996, 10, 2857–2865. [Google Scholar] [CrossRef]
- Duan, Y.F.; Ni, Y.Q.; Ko, J.M. Cable vibration control using magnetorheological dampers. Intell. Mater. Syst. Struct. 2006, 17, 321–325. [Google Scholar] [CrossRef]
- Tusset, A.M.; Balthazar, J.M. On the chaotic cuppression of both ideal and non-ideal duffing based vibrating systems, using a magnetorheological damper. Differ. Equ. Dyn. Syst. 2013, 21, 105–121. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Lu, H.; Wang, D.; Chen, Q.; Wang, Z. Effect of silicone oil viscosity on the properties of magnetorheological fluids. Optoelectron. Adv. Mater. Commun. 2015, 9, 226–230. [Google Scholar]
- Visioli, A. Practical PID Control; Springer Science & Business Media: London, UK, 2006. [Google Scholar]
- Liu, J.K. Advanced PID Control based on MATLAB; Publishing House of Electronics Industry: Beijing, China, 2011. [Google Scholar]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Pan, W.T. A new evolutionary computation approach: Fruit fly optimization algorithm. In Proceedings of the Conference on Digital Technology and Innovation Management, Taipei, Taiwan, 2011. [Google Scholar]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl. Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Lin, S.M. Analysis of service satisfaction in web auction logistics service using a combination of Fruit fly optimization algorithm and general regression neural network. Neural Comput. Appl. 2013, 22, 783–791. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Melt index prediction by least squares support vector machines with an adaptive mutation fruit fly optimization algorithm. Chemom. Intell. Lab. Syst. 2014, 141, 79–87. [Google Scholar] [CrossRef]
- Wang, L.; Shi, Y.; Liu, S. An improved fruit fly optimization algorithm and its application to joint replenishment problems. Expert Syst. Appl. 2015, 42, 4310–4323. [Google Scholar] [CrossRef]
- Pan, Q.K.; Sang, H.Y.; Duan, J.H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Oliveira, V.A.; Cossi, L.V.; Teixeira, M.C.; Silva, A.M. Synthesis of PID controllers for a class of time delay systems. Automatica 2009, 45, 1778–1782. [Google Scholar] [CrossRef]
- Chen, J.; Huang, T.C. Applying neural networks to on-line updated PID controllers for nonlinear process control. J. Process Control 2004, 14, 211–230. [Google Scholar] [CrossRef]
- Pelusi, D. On designing optimal control systems through genetic and neuro-fuzzy techniques. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology(ISSPIT), Bilbao, Spain, 14–17 December 2011; pp. 134–139. [Google Scholar]
- Pelusi, D. PID and intelligent controllers for optimal timing performances of industrial actuators. Int. J. Simul. Syst. Sci. Technol. 2012, 13, 65–71. [Google Scholar]
- Pelusi, D. Improving settling and rise times of controllers via intelligent algorithms. In Proceedings of the IEEE International Conference on Computer Modelling and Simulation (Uksim), Cambridge, UK, 28–30 March 2012; pp. 187–192. [Google Scholar]
- Zhu, S.X.; Chen, C.J. Study on variable universe fuzzy PID control for landing gear based on MRF (magneto-rheological fluid) damper. Appl. Mech. Mater. 2012, 233, 66–71. [Google Scholar] [CrossRef]
- Lee, J.H.; Yun, Y.W.; Hong, H.W.; Park, M.K. Tension control of wire rope in winch spooler using magneto rheological brake. Int. J. Precis. Eng. Manuf. 2016, 17, 157–162. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Zainordin, A.Z.; Hudha, K. Performance evaluation of shaft speed control using a magnetorheological brake. Int. J. Automot. Mech. Eng. 2015, 11, 2654–2663. [Google Scholar] [CrossRef]
- Han, J.; Wang, P.; Yang, X. Tuning of PID controller based on fruit fly optimization algorithm. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Chengdu, China, 5–8 August 2012; pp. 409–413. [Google Scholar]
- Sheng, W.; Bao, Y. Fruit fly optimization algorithm based fractional order fuzzy-PID controller for electronic throttle. Nonlinear Dyn. 2013, 73, 611–619. [Google Scholar] [CrossRef]
- Li, C.; Xu, S.; Li, W.; Hu, L. A novel modified fly optimization algorithm for designing the self-tuning proportional integral derivative controller. J. Converg. Inf. Technol. 2012, 7, 69–77. [Google Scholar]
- Shan, D.; Cao, G.H.; Dong, H.J. LGMS-FOA: An improved fruit fly optimization algorithm for solving optimization problems. Math. Probl. Eng. 2013, 2013, 1256–1271. [Google Scholar] [CrossRef]
- Pelusi, D.; Tivegna, M. Optimal trading rules at hourly frequency in the foreign exchangemarkets. In Mathematical and Statistical Methods for Actuarial Sciences and Finance; Perna, C., Sibillo, M., Eds.; Springer: Milan, Italy, 2012; pp. 341–348. [Google Scholar]
- Pelusi, D.; Mascella, R.; Tallini, L. Revised gravitationalsearch algorithms based on evolutionary-fuzzy systems. Algorithm 2017, 10, 44. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).