Solving Solar-Wind Power Station Location Problem Using an Extended Weighted Aggregated Sum Product Assessment (WASPAS) Technique with Interval Neutrosophic Sets
Abstract
:1. Introduction
2. Background
2.1. INs
- ,
2.2. INSs
- (1)
- The complement of is ,
- (2)
- (3)
- (4)
- ,
- (5)
- (1)
- (2)
- (3)
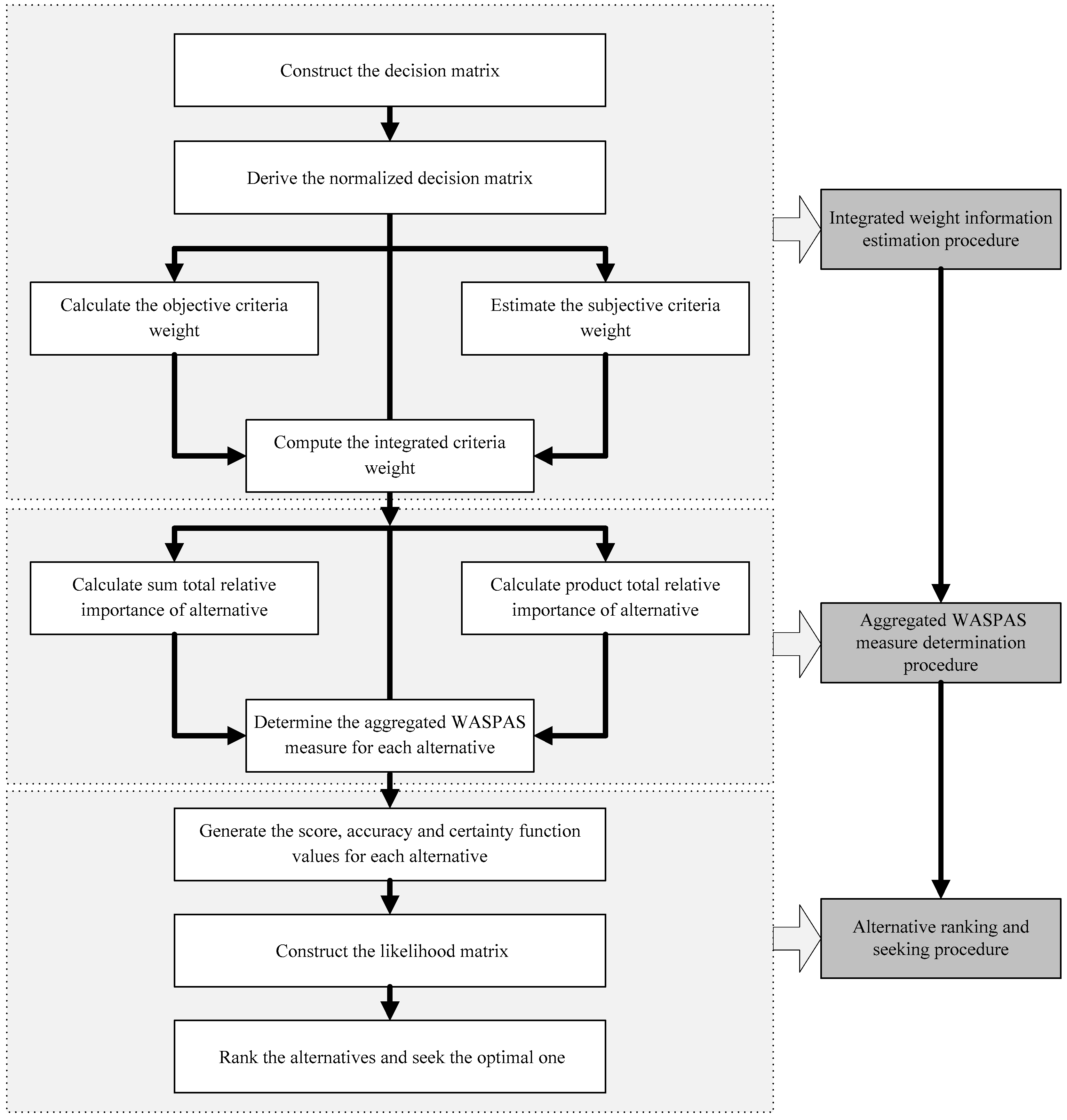
3. The Framework of an Extended WASPAS Technique
3.1. Maximizing Deviation Method for Objective Weight Estimating
3.2. G1 for Subjective Weight Estimating
- Step 1
- Determine the criteria ranking order relation.Let DMs provide the order relation of the set according to the importance of the criteria judging from their experience.
- Step 2
- Assign the relative importance degree index of adjacent criteria.Determine the relative importance degree index of the adjacent criteria and according to Table 1.
- Step 3
- Calculate the subjective weights of criteria by Equations (18) and (19).
3.3. An Extended WASPAS Technique with Integrated Criteria Weight Information
- Step 1.
- Construct the decision matrix.Let a DM provide performance estimation of every alternative with respect to all the criteria, which is shown as
- Step 2.
- Derive the normalized decision matrix.Utilize Equation (1) in Definition 4 to convert the evaluation under cost criteria to benefit criteria. For convenience, the normalized evaluations for the th alternative with respect to the th cost criteria are also denoted by .
- Step 3.
- Calculate the objective criteria weight.Use Equations (16) and (17) to calculate the objective weight for each criteria by the maximizing deviation method.
- Step 4.
- Estimate the subjective criteria weight.Conduct the procedures proposed in Section 3.2, and estimate the subjective criteria weight for each criteria.
- Step 5.
- Compute the integrated criteria weight.Combine the objective and subjective weights generated from Step 3 and Step 4, the integrated criteria weight is shown asin which is the aggregation parameter altering in .
- Step 6.
- Calculate sum total relative importance of alternative.Incorporate the INPWA operator defined in Equation (9), the sum total relative importance of alternative is calculated by Equation (21).
- Step 7.
- Calculate product total relative importance of alternative.Refer to the INPGWA operator in Equation (8), the product total relative importance for alternative is defined as
- Step 8.
- Determine the aggregated WASPAS measure for each alternative.Aggregate and , the final WASPAS measure can be determined by the equation as follows:in which is the parameter to adjust the proportion of WSM and WPM in the WASPAS technique altering in . When , the WASPAS technique is degenerated to WSM. When , the WASPAS technique is degenerated to WPM.
- Step 9.
- Generate the score, accuracy and certainty function values for each alternative.Obtain the score, accuracy and certainty function values , and for each alternative utilizing Equation (1) in Definition 7.
- Step 10.
- Construct the likelihood matrix.Construct the possibility matrix of the score function value according to Equation (2), which is shown as follows:whose elements represents the possibility degree of . If , then calculate the possibility degree of characterized by . If , then calculate the possibility degree of characterized by . Obtain the ranking vector according to Equation (4).
- Step 11.
- Rank the alternatives and select the good location.Rank all the alternatives and select the good location according to the descending order of .
4. Case Study
4.1. Problem Description
4.2. The Selection of Solar-Wind Power Station Location
- Step 1.
- Construct the decision matrix.The decision matrix is constructed by the illustration in Section 4.1, which is shown as above.
- Step 2.
- Derive the normalized decision matrix.Referring to the criteria description in Table 2, and are cost criteria. Utilize Equation (1) in Definition 4, the normalized decision matrix can be obtained as
- Step 3.
- Calculate the objective criteria weight.Use Equations (16) and (17), then the objective weight for each criteria can be calculated as
- Step 4.
- Estimate the subjective criteria weight.Assume that the aggregation parameter , and the order relation of all the criteria is judging from DMs’ subjective experience. Referring to the relative importance degree index among adjacent criteria in Table 1, the subjective criteria weight for each criteria is estimated as , , , and .
- Step 5.
- Compute the integrated criteria weight.Combine the objective and subjective weights generated from Step 3 and Step 4, the integrated weight of criteria is shown as , , , and .
- Step 6.
- Calculate sum total relative importance of alternative.Incorporate the INPWA operator defined in Equation (9), the sum total relative importance of all alternatives are
- Step 7.
- Calculate product total relative importance of alternative.Refer to the INPGWA operator in Equation (8), the product total relative importance for alternatives are
- Step 8.
- Determine the aggregated WASPAS measure for each alternative.Let , then the final WASPAS measure can be derived as
- Step 9.
- Generate the score, accuracy and certainty function values for each alternative.For each alternative, the score, accuracy and certainty function values , and are shown in Table 3.
- Step 10.
- Construct the likelihood matrix.Construct the possibility matrix of the score function value according to Equation (2), which is shown as follows:And the ranking vector can be obtained as , , and .
- Step 11.
- Rank the alternatives and select the good location.The ranking order of all the alternatives is and the good location is .
5. Sensitivity Analysis and Comparison Analysis
5.1. Sensitivity Analysis and Discussion
5.2. Comparison Analysis and Discussion
- (1)
- The method in [62] generates the selection result by implementing two steps. Firstly, confirm the ideal alternatives for different type of criteria. Subsequently, derive the result by similarity measures. According to the first similarity measure in that literature, the similarity measures are obtained as , , and .
- (2)
- In the method of [69], maximizing deviation method is utilized to derive objective weights. Then, based on the ideal of TOPSIS method, alternatives are ranked by the relative closeness coefficient. Conduct these procedures, relative closeness coefficient can be calculated as , , and .
- (3)
- The procedure of the method in [68] can be briefly classified into aggregation process and ranking process. The ranking procedure in [68] is identical with our proposed method. Based on weighted arithmetic aggregation operator or weighted geometric aggregation operator, the total score are obtained as or with the same ranking order .
- (4)
- Classical WASPAS method in [34] generates the final WASPAS measure by aggregating weighted arithmetic aggregation operator and weighted geometric aggregation operator. To better compare the classical WASPAS method with our method, the alternatives are ranked by the ranking procedure in our paper. Then, ranking vector can be obtained as , , and .
- (1)
- It can effectively manage the solar-wind power station location problem via embedding three procedures into the newly extended WASPAS technique. During the WASPAS technique implement process, a rational location selection result will be generated by incorporating the advantages of relevant methods in these procedures.
- (2)
- With the maximizing derivation method, objective criteria weights can be simply determined no matter under the criteria weights completely unknown or incomplete circumstances. Apart from the objective criteria weights, subjective weights, which fully reflect the subjective preference under practice, can be obtained with G1. The integrated criteria weight is the combination of the objective and subjective weights, and can adequately represent more realistic situation.
- (3)
- Different aggregation parameter and the proportion adjustment parameter facilitate the whole procedures a dynamic selection. The parameter setting is based on the requirement of real application and subjective preference of DMs, which makes the extended WASPAS technique feasible in dealing with the reality.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Khare, V.; Nema, S.; Baredar, P. Status of solar wind renewable energy in India. Renew. Sustain. Energy Rev. 2013, 27, 1–10. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P. Solar–wind hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Kazem, H.A.; Al-Badi, H.A.S.; Al Busaidi, A.S.; Chaichan, M.T. Optimum design and evaluation of hybrid solar/wind/diesel power system for Masirah Island. Environ. Dev. Sustain. 2016, 1–18. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Robinson, A.; Loizidou, M. Simulation and evaluation of a hybrid concentrating-solar and wind power plant for energy autonomy on islands. Renew. Energy 2016, 96, 863–871. [Google Scholar] [CrossRef]
- Jahangiri, M.; Ghaderi, R.; Haghani, A.; Nematollahi, O. Finding the best locations for establishment of solar-wind power stations in Middle-East using GIS: A review. Renew. Sustain. Energy Rev. 2016, 66, 38–52. [Google Scholar] [CrossRef]
- Lee, A.H.I.; Kang, H.Y.; Liou, Y.J. A hybrid multiple-criteria decision-making approach for photovoltaic solar plant location selection. Sustainability 2017, 9, 184. [Google Scholar] [CrossRef]
- Roy, B. Multicriteria Methodology for Decision Aiding; Springer Science & Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Roy, B. Paradigms and challenges. In Multiple Criteria Decision Analysis: STATE of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer: New York, NY, USA, 2005; Volume 78, pp. 3–24. [Google Scholar]
- Roy, B.; Słowiński, R. Questions guiding the choice of a multicriteria decision aiding method. EURO J. Decis. Process. 2013, 1, 69–97. [Google Scholar] [CrossRef]
- Abudeif, A.M.; Abdel Moneim, A.A.; Farrag, A.F. Multicriteria decision analysis based on analytic hierarchy process in GIS environment for siting nuclear power plant in Egypt. Ann. Nucl. Energy 2015, 75, 682–692. [Google Scholar] [CrossRef]
- Latinopoulos, D.; Kechagia, K. A GIS-based multi-criteria evaluation for wind farm site selection. A regional scale application in Greece. Renew. Energy 2015, 78, 550–560. [Google Scholar] [CrossRef]
- Liu, J.; Xu, F.; Lin, S. Site selection of photovoltaic power plants in a value chain based on grey cumulative prospect theory for sustainability: A case study in Northwest China. J. Clean. Prod. 2017, 148, 386–397. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, K.; Zeng, B.; Yang, M.; Li, L.; Zhang, H. A cloud decision framework in pure 2-tuple linguistic setting and its application for low-speed wind farm site selection. J. Clean. Prod. 2017, 142, 2154–2165. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Yuan, J.; Geng, S.; Zhang, H. Study of decision framework of offshore wind power station site selection based on ELECTRE-III under intuitionistic fuzzy environment: A case of China. Energy Convers. Manag. 2016, 113, 66–81. [Google Scholar] [CrossRef]
- Jun, D.; Tian-tian, F.; Yi-sheng, Y.; Yu, M. Macro-site selection of wind/solar hybrid power station based on ELECTRE-II. Renew. Sustain. Energy Rev. 2014, 35, 194–204. [Google Scholar] [CrossRef]
- Yunna, W.; Geng, S. Multi-criteria decision making on selection of solar-wind hybrid power station location: A case of China. Energy Convers. Manag. 2014, 81, 527–533. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Peng, H.G.; Wang, J.; Wang, J.Q. An extended outranking approach for multi-criteria decision-making problems with linguistic intuitionistic fuzzy numbers. Appl. Soft Comput. 2017, 59, 462–474. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Nie, R.; Wang, J.; Li, L. 2-tuple linguistic intuitionistic preference relation and its application in sustainable location planning voting system. J. Intell. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Cao, Y.X.; Zhou, H.; Wang, J.Q. An approach to interval-valued intuitionistic stochastic multi-criteria decision-making using set pair analysis. Int. J. Mach. Learn. Cybern. 2016, 1–12. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Wang, J.Q.; Zhang, H.Y. An improved MULTIMOORA approach for multi-criteria decision-making based on interdependent inputs of simplified neutrosophic linguistic information. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1998; pp. 1–105. [Google Scholar]
- Peng, H.; Zhang, H.; Wang, J. Probability multi-valued neutrosophic sets and its application in multi-criteria group decision-making problems. Neural Comput. Appl. 2016, 1–21. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Wang, J.Q.; Zhang, H.Y. Simplified neutrosophic linguistic multi-criteria group decision-making approach to green product development. Group Decis. Negot. 2017, 26, 597–627. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. Mult. Log. 1999, 8, 489–503. [Google Scholar]
- Liu, C. Interval neutrosophic fuzzy stochastic multi-criteria decision-making methods based on MYCIN certainty factor and prospect theory. Rev. Tec. Fac. Ing. Univ. Del Zulia 2017, 39, 52–58. [Google Scholar]
- Ma, H.; Hu, Z.G.; Li, K.Q.; Zhang, H.Y. Toward trustworthy cloud service selection: A time-aware approach using interval neutrosophic set. Parallel Distrib. Comput. 2016, 96, 75–94. [Google Scholar] [CrossRef]
- Reddy, R.; Reddy, D.; Krishnaiah, G. Lean supplier selection based on hybrid MCGDM approach using interval valued neutrosophic sets: A case study. Int. J. Innov. Res. Dev. 2016, 5, 291–296. [Google Scholar]
- Ma, Y.X.; Wang, J.Q.; Wang, J.; Wu, X.H. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2016, 1–21. [Google Scholar] [CrossRef]
- Tian, Z.P.; Zhang, H.Y.; Wang, J.; Wang, J.Q.; Chen, X.H. Multi-criteria decision-making method based on a cross-entropy with interval neutrosophic sets. Int. J. Syst. Sci. 2016, 47, 3598–3608. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Yang, L.J.; Qian, J. A novel multi-criteria group decision-making approach using simplified neutrosophic information. Int. J. Uncertain. Quantif. 2017. [Google Scholar] [CrossRef]
- Wu, X.H.; Wang, J.Q. Cross-entropy measures of multi-valued neutrosophic sets and its application in selecting middle-level manager. Int. J. Uncertain. Quantif. 2017, 2, 155–172. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Zhang, H.Y.; Wang, J.Q. Multi-criteria decision-making based on generalized prioritized aggregation operators under simplified neutrosophic uncertain linguistic environment. Int. J. Mach. Learn. Cybern. 2016, 1–17. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Electron. Electr. Eng. 2012, 122, 1–3. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kalibatas, D.; Kalibatiene, D. A multi-attribute assessment using WASPAS for choosing an optimal indoor environment. Arch. Civ. Mech. Eng. 2016, 16, 76–85. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Baušys, R.; Stanujkic, D.; Magdalinovic-Kalinovic, M. Selection of lead-zinc flotation circuit design by applying WASPAS method with single-valued neutrosophic set. Acta Montan. Slovaca 2017, 21, 85–92. [Google Scholar]
- Bagočius, V.; Zavadskas, E.K.; Turskis, Z. Multi-person selection of the best wind turbine based on the multi-criteria integrated additive-multiplicative utility function. J. Civ. Eng. Manag. 2014, 20, 590–599. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Baušys, R.; Lazauskas, M. Sustainable assessment of alternative sites for the construction of a waste incineration plant by applying WASPAS method with single-valued neutrosophic set. Sustainability 2015, 7, 15923–15936. [Google Scholar] [CrossRef]
- Baušys, R.; Juodagalvienė, B. Garage location selection for residential house by WASPAS-SVNS method. J. Civ. Eng. Manag. 2017, 23, 421–429. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Saparauskas, J.; Turskis, Z. MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions. Econ. Comput. Econ. Cybern. Stud. Res. 2013, 47, 5–20. [Google Scholar]
- Džiugaitėtumėnienė, R.; Lapinskienė, V. The multicriteria assessment model for an energy supply system of a low energy house. Eng. Struct. Technol. 2014, 6, 33–41. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Zolfani, S.H.; Derakhti, A.; Eshkalag, M.K. Assessment of regions priority for implementation of solar projects in Iran: New application of a hybrid multi-criteria decision making approach. Energy Convers. Manag. 2014, 86, 653–663. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Antuchevičienė, J. Assessment of third-party logistics providers using a CRITIC–WASPAS approach with interval type-2 fuzzy sets. Transport 2017, 32, 66–78. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Selecting a contractor by using a novel method for multiple attribute analysis: Weighted aggregated sum product assessment with grey values (WASPASG). Stud. Inform. Control. 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zakuan, N.; Loganathan, N.; Soheilirad, S.; Saman, M.Z.M.; Ibrahim, O. A systematic review and meta-Analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments. Appl. Soft Comput. 2017, 57, 265–292. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Razavi Hajiagha, S.H.; Hashemi, S.S. Extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF). Appl. Soft Comput. 2014, 24, 1013–1021. [Google Scholar] [CrossRef]
- Wei, G.W. Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting. Knowl. Based Syst. 2008, 21, 833–836. [Google Scholar] [CrossRef]
- Şahin, R.; Liu, P. Maximizing deviation method for neutrosophic multiple attribute decision making with incomplete weight information. Neural Comput. Appl. 2016, 27, 2017–2029. [Google Scholar] [CrossRef]
- Gitinavard, H.; Mousavi, S.M.; Vahdani, B. A new multi-criteria weighting and ranking model for group decision-making analysis based on interval-valued hesitant fuzzy sets to selection problems. Neural Comput. Appl. 2016, 27, 1593–1605. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl. Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, W. A new multiple attribute group decision making method in intuitionistic fuzzy setting. Appl. Math. Model. 2011, 35, 4424–4437. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Md, D.S.; Nukman, Y.; Aoyama, H.; Case, K. An integrated approach of fuzzy linguistic preference based AHP and fuzzy COPRAS for machine tool evaluation. PLoS ONE 2015, 10, e133599. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Xu, Y.; Wang, H. A consensus reaching model for 2-tuple linguistic multiple attribute group decision making with incomplete weight information. Int. J. Syst. Sci. 2016, 47, 389–405. [Google Scholar] [CrossRef]
- Ruan, C.; Yang, J. Software quality evaluation model based on weighted mutation rate correction incompletion G1 combination weights. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Zhou, Y. Interval number optimization for household load scheduling with uncertainty. Energy Build. 2016, 130, 613–624. [Google Scholar] [CrossRef]
- Xu, Z. Dependent uncertain ordered weighted aggregation operators. Inf. Fusion 2008, 9, 310–316. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Li, L. Multi-criteria decision-making method based on single-valued neutrosophic linguistic Maclaurin symmetric mean operators. Neural Comput. Appl. 2016, 1–19. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Li, L. Multi-criteria group decision-making method based on interdependent inputs of single-valued trapezoidal neutrosophic information. Neural Comput. Appl. 2016, 1–20. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. New operations on interval neutrosophic sets. J. New Theory 2015, 2, 62–71. [Google Scholar]
- Liu, P.; Wang, Y. Interval neutrosophic prioritized OWA operator and its application to multiple attribute decision making. J. Syst. Sci. Complex. 2015, 3, 681–697. [Google Scholar] [CrossRef]
- Liu, P.; Tang, G. Some power generalized aggregation operators based on the interval neutrosophic sets and their application to decision making. J. Intell. Fuzzy Syst. 2016, 30, 2517–2528. [Google Scholar] [CrossRef]
- Ye, J. Similarity measures between interval neutrosophic sets and their applications in multicriteria decision-making. J. Intell. Fuzzy Syst. 2014, 26, 165–172. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Yingming, W. Using the method of maximizing deviation to make decision for multiindices. J. Syst. Eng. Electron. 1997, 8, 21–26. [Google Scholar]
- Xu, F.; Liu, J.; Lin, S.; Yuan, J. A VIKOR-based approach for assessing the service performance of electric vehicle sharing programs: A case study in Beijing. J. Clean. Prod. 2017, 148, 254–267. [Google Scholar] [CrossRef]
- Chakraborty, S.; Zavadskas, E.K. Applications of WASPAS method in manufacturing decision making. Informatica 2014, 25, 1–20. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Q.; Zhu, L. Dual hesitant fuzzy power aggregation operators based on Archimedean t-conorm and t-norm and their application to multiple attribute group decision making. Appl. Soft Comput. 2016, 38, 23–50. [Google Scholar] [CrossRef]
- Zhao, A.; Du, J.; Guan, H. Interval valued neutrosophic sets and multi-attribute decision-making based on generalized weighted aggregation operator. J. Intell. Fuzzy Syst. 2015, 6, 2697–2706. [Google Scholar]
- Chi, P.; Liu, P. An extended TOPSIS method for the multiple attribute decision making problems based on interval neutrosophic set. Neutrosophic Sets Syst. 2013, 1, 63–70. [Google Scholar]
| Description | |
|---|---|
| 1.0 | is equally important as |
| 1.2 | is slightly more important than |
| 1.4 | is obviously more important than |
| 1.6 | is strongly more important than |
| 1.8 | is extremely more important than |
| Criteria | Description |
|---|---|
| Natural resources | Natural resources include various indicators related to wind and solar resources in the location. |
| Economic factors | Economic factors briefly measure the cost during the engineering construction, operation and maintenance procedures. |
| Traffic conditions | Traffic conditions reflect the traffic convenience to the location during the engineering construction, operation and maintenance procedures. |
| Environmental factors | Environmental factors reflect the environment destruction during the engineering construction and operation procedures. |
| Social factors | Social factors reflect the attitude of the local residents to the engineering. |
| Methods | Ranking Results |
|---|---|
| Similarity measure in [62] | |
| An extended TOPSIS method in [69] | |
| Method used weighted arithmetic aggregation operator in [68] | |
| Method used weighted geometric aggregation operator in [68] | |
| Classical WASPAS method in [34] | |
| The proposed method |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, R.-x.; Wang, J.-q.; Zhang, H.-y. Solving Solar-Wind Power Station Location Problem Using an Extended Weighted Aggregated Sum Product Assessment (WASPAS) Technique with Interval Neutrosophic Sets. Symmetry 2017, 9, 106. https://doi.org/10.3390/sym9070106
Nie R-x, Wang J-q, Zhang H-y. Solving Solar-Wind Power Station Location Problem Using an Extended Weighted Aggregated Sum Product Assessment (WASPAS) Technique with Interval Neutrosophic Sets. Symmetry. 2017; 9(7):106. https://doi.org/10.3390/sym9070106
Chicago/Turabian StyleNie, Ru-xin, Jian-qiang Wang, and Hong-yu Zhang. 2017. "Solving Solar-Wind Power Station Location Problem Using an Extended Weighted Aggregated Sum Product Assessment (WASPAS) Technique with Interval Neutrosophic Sets" Symmetry 9, no. 7: 106. https://doi.org/10.3390/sym9070106
APA StyleNie, R.-x., Wang, J.-q., & Zhang, H.-y. (2017). Solving Solar-Wind Power Station Location Problem Using an Extended Weighted Aggregated Sum Product Assessment (WASPAS) Technique with Interval Neutrosophic Sets. Symmetry, 9(7), 106. https://doi.org/10.3390/sym9070106





