Symmetry in Domination for Hypergraphs with Choice
Abstract
:1. Introduction
- (i)
- There is a directed edge from vertex v to vertex w if:i.e., if vertex w is never chosen in the presence of vertex v.
- (ii)
- There is a directed edge from vertex v to vertex w if:i.e., among the edges containing both v and w, v is chosen with greater frequency.
- (iii)
- There is a directed edge from vertex v to vertex w if:i.e., v is chosen for a majority of the edges containing both v and w.
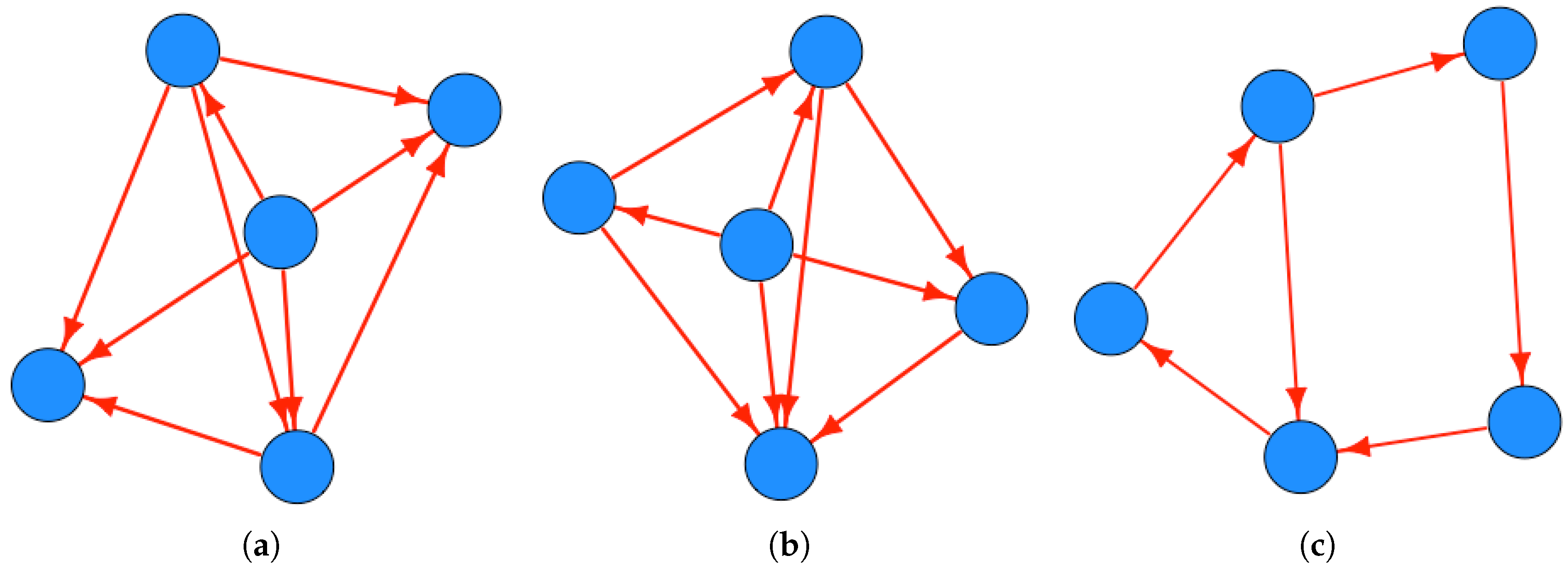
- What are the maximal and minimal number of edges possible for an -domination graph?
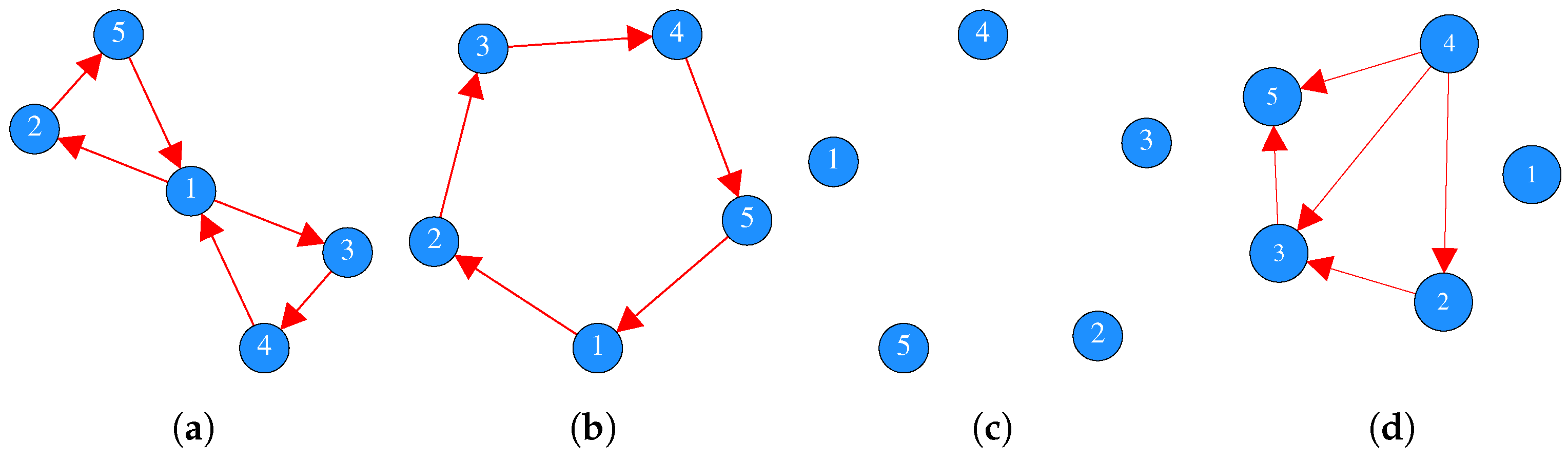
- What proportion of -domination graphs are strongly path connected (for example, Figure 3a,b?
- What is the distribution of the number of edges in the domination graph for a uniformly selected choice function on the edges of a k-hypergraph on n vertices?
- What is the number of non-isomorphic -domination graphs?
2. Proof of Theorems 1 and 2
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Berge, C.; Minieka, E. Graphs and Hypergraphs; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973; Volume 7. [Google Scholar]
- Johnson, M.R. Ideal structures of path independent choice functions. J. Econ. Theory 1995, 65, 468–504. [Google Scholar] [CrossRef]
- Moulin, H. Choice functions over a finite set: A summary. Soc. Choice Welf. 1985, 2, 147–160. [Google Scholar] [CrossRef]
- Beeler, K.E.; Berenhaut, K.S.; Cooper, J.N.; Hunter, M.N.; Barr, P.S. Deterministic walks with choice. Discret. Appl. Math. 2014, 162, 100–107. [Google Scholar] [CrossRef]
- Kayibi, K.; Khan, M.A.; Pirzada, S. Uniform sampling of k-hypertournaments. Linear Multilinear Algebra 2013, 61, 123–138. [Google Scholar] [CrossRef]
- Khan, M.A.; Pirzada, S.; Kayibi, K.K. Scores, inequalities and regular hypertournaments. J. Math. Inequal. Appl. 2012. [Google Scholar] [CrossRef]
- Pirzada, S.; Naikoo, T. On score sets in tournaments. Vietnam J. Math. 2006, 34, 157–161. [Google Scholar]
- Marshall, S. Properties of K-Tournaments. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 1994. [Google Scholar]
- Brookes, S. Fairness, resources, and separation. Electron. Notes Theor. Comput. Sci. 2010, 265, 177–195. [Google Scholar] [CrossRef]
- Cooper, C.; Ilcinkas, D.; Klasing, R.; Kosowski, A. Derandomizing random walks in undirected graphs using locally fair exploration strategies. Distrib. Comput. 2011, 24. [Google Scholar] [CrossRef]
- Jaeger, M. On fairness and randomness. Inf. Comput. 2009, 207, 909–922. [Google Scholar] [CrossRef]
- Krawczyk, M.W. A model of procedural and distributive fairness. Theory Decis. 2011, 70, 111–128. [Google Scholar] [CrossRef]
- Völzer, H.; Varacca, D. Defining fairness in reactive and concurrent systems. J. ACM 2012, 59. [Google Scholar] [CrossRef]
- Guofei, Z.; Tianxing, Y.; Kemin, Z. On score sequences of k-hypertournaments. Eur. J. Comb. 2000, 21, 993–1000. [Google Scholar] [CrossRef]
- Pirzada, S.; Chishti, T.; Naikoo, T. Score lists in [h-k]-bipartite hypertournaments. Discret. Math. Appl. 2009, 19, 321–328. [Google Scholar] [CrossRef]
- Koh, Y.; Ree, S. On k-hypertournament matrices. Linear Algebra Appl. 2003, 373, 183–195. [Google Scholar] [CrossRef]
- Pirzada, S.; Khan, M.A.; Guofei, Z.; Kayibi, K.K. On scores, losing scores and total scores in hypertournaments. Electron. J. Graph Theory Appl. 2015, 3, 8–21. [Google Scholar] [CrossRef]
- Landau, H. On dominance relations and the structure of animal societies: III The condition for a score structure. Bull. Math. Biol. 1953, 15, 143–148. [Google Scholar] [CrossRef]
- Pirzada, S.; Zhou, G. On k-hypertournament losing scores. Acta Univ. Sapientiae 2010, 2, 5–9. [Google Scholar]
- Surmacs, M. Regular hypertournaments and Arc-pancyclicity. J. Graph Theory 2017, 84, 176–190. [Google Scholar] [CrossRef]
- Gunderson, K.; Morrison, N.; Semeraro, J. Bounding the number of hyperedges in friendship r-hypergraphs. Eur. J. Comb. 2016, 51, 125–134. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Guo, Y.; Surmacs, M. On the vertex-pancyclicity of hypertournaments. Discret. Appl. Math. 2013, 161, 2749–2752. [Google Scholar] [CrossRef]
- Guo, Y.; Surmacs, M. Pancyclic out-arcs of a vertex in a hypertournament. Australas. J. Comb. 2015, 61, 227–250. [Google Scholar]
- Chao, W.; Guofei, Z. Note on the degree sequences of k-hypertournaments. Discret. Math. 2008, 308, 2292–2296. [Google Scholar] [CrossRef]

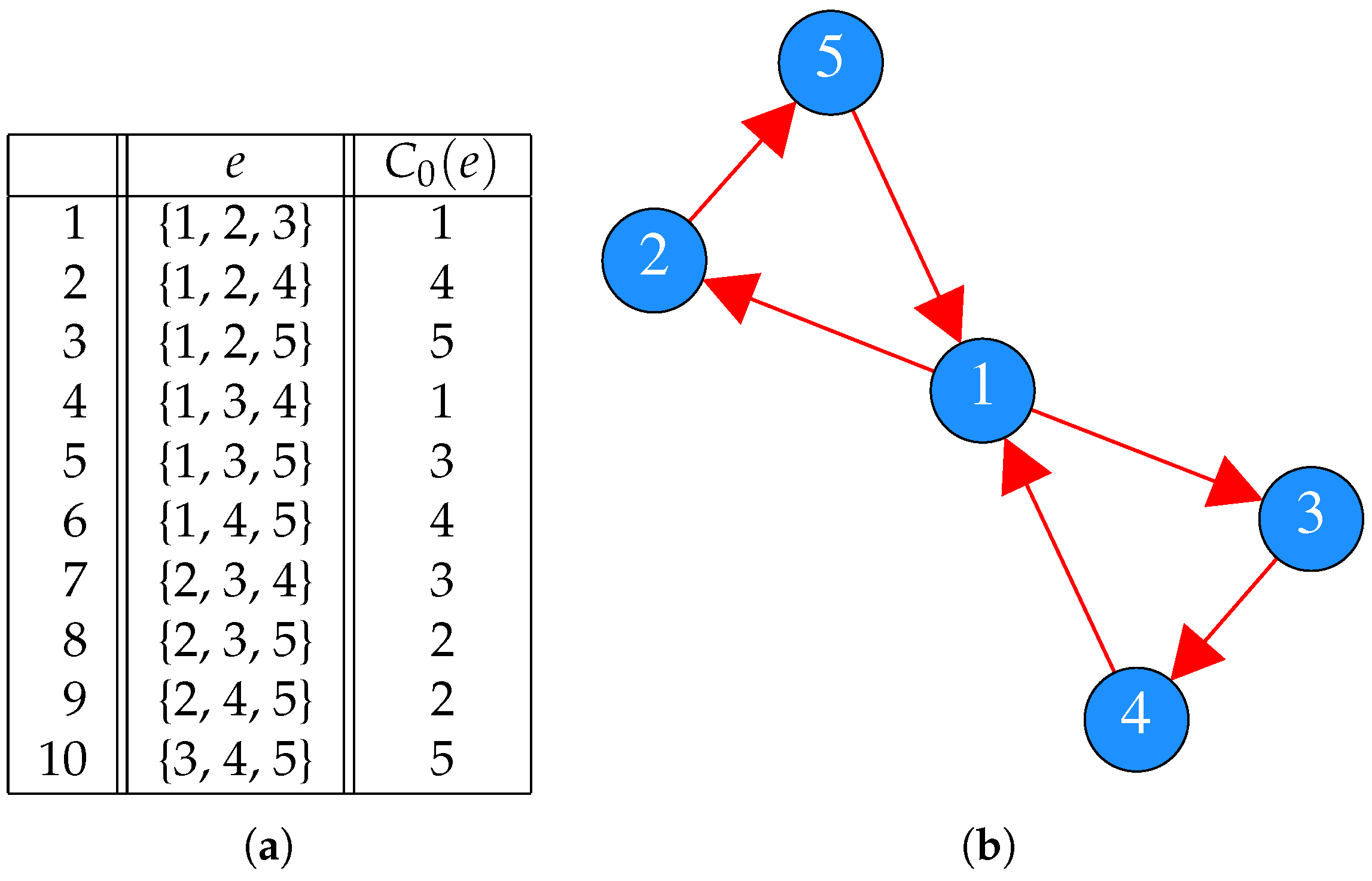
| e | |||||
|---|---|---|---|---|---|
| 1 | {1, 2, 3} | 1 | 1 | 1 | 1 |
| 2 | {1, 2, 4} | 4 | 1 | 2 | 2 |
| 3 | {1, 2, 5} | 5 | 5 | 5 | 5 |
| 4 | {1, 3, 4} | 1 | 3 | 4 | 4 |
| 5 | {1, 3, 5} | 3 | 5 | 3 | 3 |
| 6 | {1, 4, 5} | 4 | 4 | 1 | 1 |
| 7 | {2, 3, 4} | 3 | 2 | 3 | 4 |
| 8 | {2, 3, 5} | 2 | 2 | 2 | 2 |
| 9 | {2, 4, 5} | 2 | 4 | 4 | 4 |
| 10 | {3, 4, 5} | 5 | 3 | 5 | 3 |
| Edges | 0 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Frequency | 6 | 60 | 120 | 1035 | 3324 | 10080 | 15180 | 16920 | 9180 | 3144 |
| Components | 1 | 2 | 3 | 5 |
| Frequency | 3348 | 6630 | 11760 | 37311 |
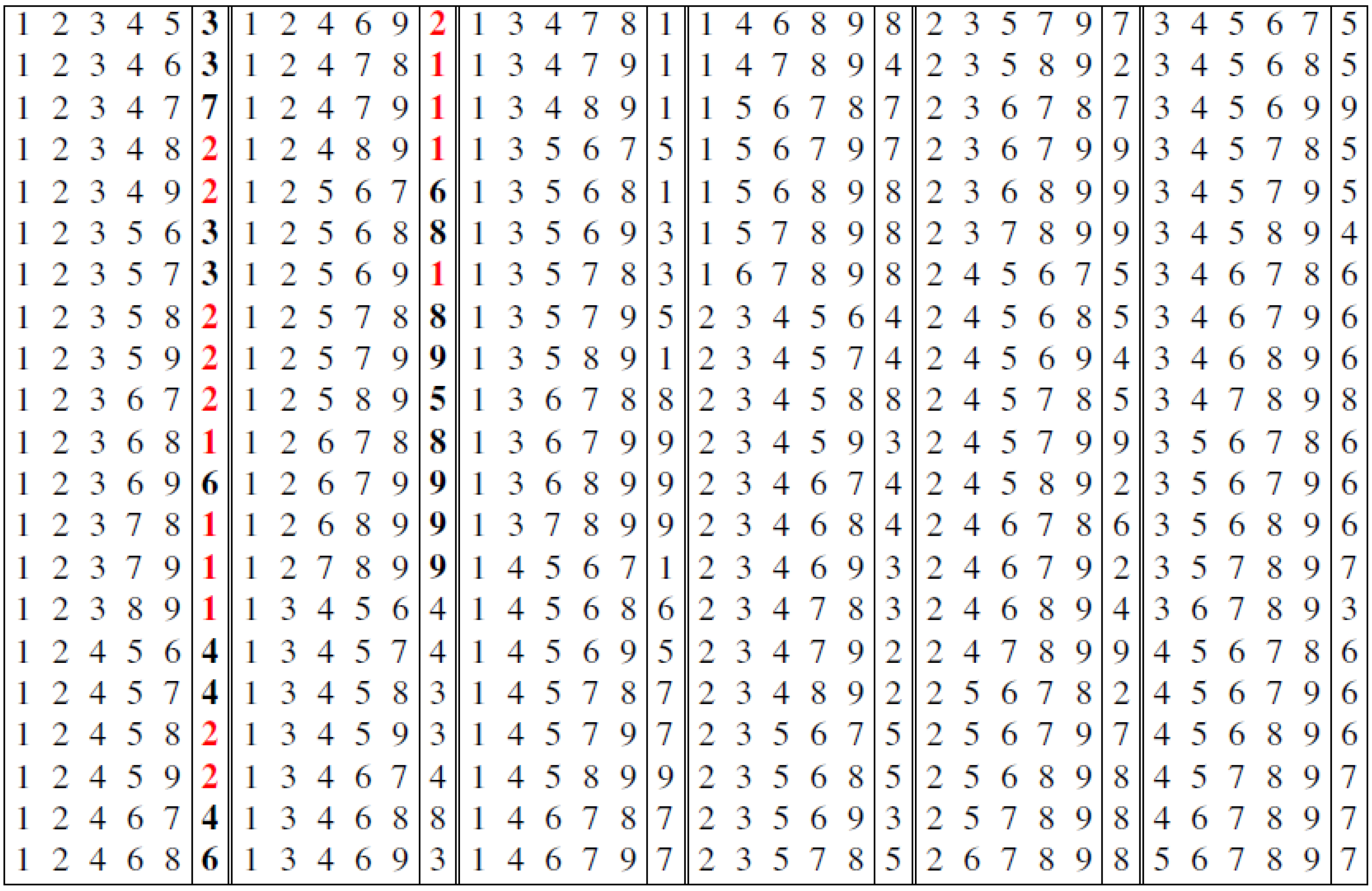
| Ind. | Freq. | Ind. | Freq. | Ind. | Freq. | Ind. | Freq. | Ind. | Freq. | Ind. | Freq. | Ind. | Freq. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1560 | 2 | 510 | 3 | 360 | 4 | 300 | 5 | 840 | 6 | 480 | 7 | 240 |
| 8 | 480 | 9 | 120 | 10 | 600 | 11 | 840 | 12 | 240 | 13 | 960 | 14 | 120 |
| 15 | 720 | 16 | 120 | 17 | 480 | 18 | 360 | 19 | 240 | 20 | 120 | 21 | 420 |
| 22 | 840 | 23 | 240 | 24 | 120 | 25 | 120 | 26 | 960 | 27 | 180 | 28 | 180 |
| 29 | 180 | 30 | 120 | 31 | 120 | 32 | 240 | 33 | 120 | 34 | 840 | 35 | 240 |
| 36 | 480 | 37 | 240 | 38 | 120 | 39 | 600 | 40 | 120 | 41 | 240 | 42 | 360 |
| 43 | 600 | 44 | 180 | 45 | 360 | 46 | 300 | 47 | 15 | 48 | 180 | 49 | 1200 |
| 50 | 720 | 51 | 1560 | 52 | 240 | 53 | 960 | 54 | 480 | 55 | 120 | 56 | 360 |
| 57 | 600 | 58 | 240 | 59 | 120 | 60 | 240 | 61 | 240 | 62 | 840 | 63 | 360 |
| 64 | 840 | 65 | 480 | 66 | 840 | 67 | 360 | 68 | 120 | 69 | 240 | 70 | 720 |
| 71 | 480 | 72 | 360 | 73 | 240 | 74 | 240 | 75 | 480 | 76 | 240 | 77 | 480 |
| 78 | 360 | 79 | 120 | 80 | 240 | 81 | 120 | 82 | 240 | 83 | 120 | 84 | 120 |
| 85 | 240 | 86 | 240 | 87 | 120 | 88 | 120 | 89 | 240 | 90 | 360 | 91 | 480 |
| 92 | 360 | 93 | 480 | 94 | 120 | 95 | 240 | 96 | 240 | 97 | 120 | 98 | 120 |
| 99 | 120 | 100 | 240 | 101 | 360 | 102 | 360 | 103 | 120 | 104 | 120 | 105 | 720 |
| 106 | 240 | 107 | 120 | 108 | 210 | 109 | 120 | 110 | 240 | 111 | 120 | 112 | 120 |
| 113 | 120 | 114 | 600 | 115 | 120 | 116 | 360 | 117 | 360 | 118 | 120 | 119 | 240 |
| 120 | 360 | 121 | 120 | 122 | 120 | 123 | 120 | 124 | 120 | 125 | 240 | 126 | 120 |
| 127 | 360 | 128 | 240 | 129 | 240 | 130 | 120 | 131 | 120 | 132 | 120 | 133 | 360 |
| 134 | 120 | 135 | 240 | 136 | 300 | 137 | 120 | 138 | 120 | 139 | 120 | 140 | 60 |
| 141 | 360 | 142 | 120 | 143 | 120 | 144 | 120 | 145 | 60 | 146 | 120 | 147 | 300 |
| 148 | 240 | 149 | 120 | 150 | 120 | 151 | 360 | 152 | 240 | 153 | 240 | 154 | 120 |
| 155 | 120 | 156 | 120 | 157 | 120 | 158 | 120 | 159 | 120 | 160 | 120 | 161 | 120 |
| 162 | 120 | 163 | 240 | 164 | 120 | 165 | 480 | 166 | 120 | 167 | 240 | 168 | 240 |
| 169 | 120 | 170 | 240 | 171 | 120 | 172 | 120 | 173 | 240 | 174 | 120 | 175 | 120 |
| 176 | 120 | 177 | 240 | 178 | 120 | 179 | 120 | 180 | 120 | 181 | 240 | 182 | 120 |
| 183 | 120 | 184 | 120 | 185 | 240 | 186 | 120 | 187 | 120 | 188 | 120 | 189 | 120 |
| 190 | 120 | 191 | 120 | 192 | 120 | 193 | 120 | 194 | 120 | 195 | 120 | 196 | 120 |
| 197 | 120 | 198 | 120 | 199 | 120 | 200 | 120 | 201 | 120 | 202 | 120 | 203 | 120 |
| 204 | 120 | 205 | 120 | 206 | 120 | 207 | 120 | 208 | 120 | 209 | 120 | 210 | 60 |
| 211 | 360 | 212 | 120 | 213 | 120 | 214 | 120 | 215 | 120 | 216 | 24 | 217 | 120 |
| 218 | 120 | 219 | 120 | 220 | 120 | 221 | 120 | 222 | 240 | 223 | 120 | 224 | 24 |
| 225 | 6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
S. Berenhaut, K.; P. Lidral-Porter, B.; H. Schoen, T.; P. Webb, K.
Symmetry in Domination for Hypergraphs with Choice
. Symmetry 2017, 9, 46.
https://doi.org/10.3390/sym9030046
S. Berenhaut K, P. Lidral-Porter B, H. Schoen T, P. Webb K.
Symmetry in Domination for Hypergraphs with Choice
. Symmetry. 2017; 9(3):46.
https://doi.org/10.3390/sym9030046
S. Berenhaut, Kenneth, Brendan P. Lidral-Porter, Theodore H. Schoen, and Kyle P. Webb.
2017. "Symmetry in Domination for Hypergraphs with Choice
" Symmetry 9, no. 3: 46.
https://doi.org/10.3390/sym9030046
S. Berenhaut, K., P. Lidral-Porter, B., H. Schoen, T., & P. Webb, K.
(2017). Symmetry in Domination for Hypergraphs with Choice
. Symmetry, 9(3), 46.
https://doi.org/10.3390/sym9030046






