New Operations of Picture Fuzzy Relations and Fuzzy Comprehensive Evaluation

Abstract

In this paper, some new operations and basic properties of picture fuzzy relations are intensively studied. First, a new inclusion relation (called type-2 inclusion relation) of picture fuzzy relations is introduced, as well as the corresponding type-2 union, type-2 intersection and type-2 complement operations. Second, the notions of anti-reflexive kernel, symmetric kernel, reflexive closure and symmetric closure of a picture fuzzy relation are introduced and their properties are explored. Moreover, a new method to solve picture fuzzy comprehensive evaluation problems is proposed by defining the new composition operation of picture fuzzy relations, and the picture fuzzy comprehensive evaluation model is built. Finally, an application example (about investment risk) of picture fuzzy comprehensive evaluation is given, and the effective experiment results are obtained.

1. Introduction

We meet many concepts in our everyday life. Most of them are vague than precise, and uncertainty is a common research topic of many branches of science (economics, engineering, environment, management science, medical science, and so on). However, uncertainty is an unintelligible expression without a straightforward description, and many theories were established, such as probability theory, fuzzy set theory [1,2,3], intuitionistic fuzzy set theory [4], hesitant fuzzy set theory [5,6,7,8], soft set theory [9,10,11,12], rough set theory [13,14,15,16,17], granular computing [18,19,20,21,22,23,24,25,26,27], et al.

Although an intuitionistic fuzzy set has been successfully applied in different areas, but there are situations that cannot be represented by it in real life, such as voting, we may face human opinions involving more answers of the type: yes, abstain, no and refusal. Thus, in 2013, B. C. Cuong proposed a new concept named picture fuzzy sets (PFSs) [28,29,30], which is an extension of fuzzy sets and intuitionistic fuzzy sets. Picture fuzzy sets give three degrees of an element named degree of positive membership, degree of neutral membership and degree of negative membership, respectively. The picture fuzzy set solved the voting problem successfully, and is applied to clustering [31], fuzzy inference [32], and decision-making [33,34].

Relations are a suitable tool for describing correspondences between objects. Crisp relations have served well in mathematical theories. However, there are some problems that can’t be solved through classic relationships, such as the relationship of two objects being vague. Therefore, after the fuzzy set was defined, the definition of fuzzy relations was also proposed by Zadeh in paper [1] as an extension of classic relationship. Then, some scholars study it and used it widely in many fields, such as decision making, clustering analysis [35,36,37,38], fuzzy comprehensive evaluation [39,40,41] and so on. Fuzzy relations can model vagueness; however, they cannot model uncertainty: there is no means to attribute reliability information to the membership degrees. Intuitionistic fuzzy sets, as defined by Atanassov [4], gave us a way to incorporate uncertainty in an additional degree. Burillo and Bustince gave the definition of intuitionistic fuzzy relations [42,43] and discussed some properties of them. Intuitionistic fuzzy relations are intuitionistic fuzzy sets in a Cartesian product of universes. In 2005, Lei et al. further researched intuitionistic fuzzy relations and composition operation of intuitionistic fuzzy relations [44]. Yang proposed the definition of kernels and closures of intuitionistic fuzzy relations and proved fourteen theorems of intuitionistic fuzzy relations [45]. B. C. Cuong proposed the notion of picture fuzzy relations and studied their operations and properties [28,29].

The rest of this paper is structured as follows. In Section 2, some basic notions and operations of picture fuzzy sets and picture fuzzy relations are provided. In Section 3, type-2 union, type-2 intersection, and type-2 complement operations of picture fuzzy relations are well described and their properties are studied. In Section 4 and Section 5, kernels and closures of a picture fuzzy relation are discussed. Their computational formulas and some properties are also obtained. Meanwhile, some examples are given. In Section 6, a new composition operation of picture fuzzy relations is investigated. Furthermore, according to the new composition operation, a new method to solve picture fuzzy comprehensive evaluation problems is proposed, and we also prove that this method is doable by an application example. The last section summarizes the conclusions.

2. Preliminary

2.1. Some Basic Concepts

In this section, several basic concepts and operations about picture fuzzy sets and picture fuzzy relations are provided.

Definition 1.

An intuitionistic fuzzy set (IFS) A on the universe X is an object of the form A = {(x, μ_A(x), ν_A(x)) | x ∈ X}, where μ_A(x) ∈ [0, 1] is called the “degree of membership of x in A”, ν_A(x) ∈ [0, 1] is called the “degree of non-membership of x in A”, and where μ_A(x) and ν_A(x) satisfy μ_A(x) + ν_A(x) ≤ 1 for all x ∈ X. In this paper, let IFS(X) denote the sets of all the intuitionistic fuzzy sets on X [4].

Definition 2.

A picture fuzzy set A on the universe X is an object of the form

$$A=\left\{\left(x,{\mu }_A\left(x\right),{\eta }_A\left(x\right),{\nu }_A\left(x\right)\right)|x\in X\right\},$$

where μ_A(x) ∈ [0, 1] is called the “degree of positive membership of x in A”, η_A(x) ∈ [0, 1] is called the “degree of neutral membership of x in A”, and ν_A(x) ∈ [0, 1] is called the “degree of negative membership of x in A”, and μ_A(x), η_A(x), ν_A(x) satisfy μ_A(x) + η_A(x) + ν_A(x) ≤ 1, for all x ∈ X. Then, ∀ x ∈ X, 1 − (μ_A(x) + η_A(x) + ν_A(x)) is called the “degree of refusal membership of x in A”. Let PFS(X) denote the set of all the picture fuzzy sets on a universe X [28].

Definition 3.

A picture fuzzy relation is a picture fuzzy subset of X × Y i.e., R given by

R = {((x, y), μ_R(x, y), η_R(x, y), ν_R(x, y))|x ∈ X, y ∈ Y},

where μ_R: X × Y → [0, 1], η_R: X × Y → [0, 1], and ν_R: X × Y → [0, 1] satisfy the condition 0 ≤ μ_R(x, y) + η_R(x, y) + ν_R(x, y) ≤ 1, for every (x, y) ∈ X × Y. PFR(X × Y) the set of all the picture fuzzy relations in X × Y is denoted [29].

Definition 4.

Let R ∈ PFR(X × Y). We define the inverse relation R⁻¹ between Y and X: μ_R⁻¹(y, x) = μ_R(x, y), η_R⁻¹(y, x) = η_R(x, y), ν_R⁻¹(y, x) = ν_R(x, y), ∀ (x, y) ∈ X × Y [29].

Definition 5.

Let R and P be two picture fuzzy relations between X and Y, for every (x, y) ∈ X × Y we define [29]:

(1)

R ⊆ P iff μ_R(x, y) ≤ μ_P(x, y), η_R(x, y) ≤ η_P(x, y), ν_R(x, y) ≥ ν_P(x, y);

(2)

R ∪ P = {((x, y), μ_R(x, y) ∨ μ_P(x, y), η_R(x, y) ∧ η_P(x, y), ν_R(x, y) ∧ ν_P(x, y)) | x ∈ X, y ∈ Y};

(3)

R ∩ P = {((x, y), μ_R(x, y) ∧ μ_P(x, y), η_R(x, y) ∧ η_P(x, y), ν_R(x, y) ∨ ν_P(x, y)) | x ∈ X, y ∈ Y};

(4)

R^c = {((x, y), ν_R(x, y), η_R(x, y), μ_R(x, y)) | x ∈ X, y ∈ Y}.

Proposition 1.

Let R, P, Q ∈ PFR(X × Y). Then [29],

• (a) (R⁻¹)⁻¹ = R;
• (b) R ⊆ P ⇒ R⁻¹ ⊆ P⁻¹;
• (c1) (R ∪ P)⁻¹ = R⁻¹ ∪ P⁻¹;
• (c2) (R ∩ P)⁻¹ = R⁻¹ ∩ P⁻¹;
• (d1) R ∩ (P ∪ Q) = (R ∩ P) ∪ (R ∩ Q);
• (d2) R ∪ (P ∩ Q) = (R ∪ P) ∩ (R ∪ Q);
• (e) R ∩ P ⊆ R, R ∩ P ⊆ P;
• (f1) If (R ⊇ P) and (R ⊇ Q), then R ⊇ P ∪ Q;
• (f2) If (R ⊆ P) and (R ⊆ Q), then R ⊆ P ∩ Q.

Definition 6.

Let E ∈ PFR(X × Y) and P ∈ PFR(Y × Z). Max-min composed relation PCE ∈ PFR(X × Z) is called to the one defined by [29]:

PCE = {((x, z), μ_PCE(x, z), η_PCE(x, z), ν_PCE(x, z))|x ∈ X, z ∈ Z},

where ∀ (x, z) ∈ X × Z:

$${\mu }_{PCE}\left(x,z\right)=\underset{y}{\vee }\left({\mu }_E\left(x,y\right)\wedge {\mu }_P\left(y,z\right)\right);$$

$${\eta }_{PCE}\left(x,z\right)=\underset{y}{\wedge }\left({\eta }_E\left(x,y\right)\wedge {\eta }_P\left(y,z\right)\right);$$

$${\nu }_{PCE}\left(x,z\right)=\underset{y}{\wedge }\left({\nu }_E\left(x,y\right)\vee {\nu }_P\left(y,z\right)\right).$$

Definition 7.

Let α = (μ_α, η_α, ν_α, ρ_α) be a picture fuzzy number, μ_α + η_α + ν_α ≤ 1, ρ_α = 1 − μ_α − η_α − ν_α. The score function S can be defined as S(α) = μ_α − ν_α, and the accuracy function H is given by H(α) = μ_α + η_α + ν_α, which S(α) ∈ [−1, 1], H(α) ∈ [0, 1]. Then, for two picture fuzzy numbers α and β [33],

(1)

if S(α) > S(β), then α is superior to β, denoted by α ⊱ β;

(2)

if S(α) = S(β), then

(i)  

if H(α) = H(β), implies that α is equivalent to β, denoted by α ~ β;

(ii) 

if H(α) > H(β), implied that α is superior to β, denoted by α ⊱ β.

We also use voting as a good example to explain the above definition, where S(α) = μ_α − ν_α represents goal difference and H(α) = μ_α + η_α + ν_α can be interpreted as the effective degree of voting. When S(α) increases, we can know that there are more people who vote for α and people who vote against α become less. When H(α) increases, we can know that there are more people who vote for or against α and people who refuse to vote become less. Therefore, H(α) depicts the effective degree of voting.

2.2. On Inclusion Relation of Picture Fuzzy Relations

Similar with [30], we consider the set D* defined by:

$$D^{*}=\left\{x=\left(x_1,x_2,x_3\right)|x\in {\left[0,1\right]}^3,x_1+x_2+x_3\le 1\right\}.$$

From now on, we will assume that if x, y ∈ D*, then x₁, x₂ and x₃ denote, respectively, the first, the second and the third component of x, i.e., x = (x₁, x₂, x₃). We denote the units of D* by 1_D* = (1, 0, 0) and 0_D* = (0, 0, 1), respectively.

Obviously, for every picture fuzzy set:

$$A=\left\{\left(x,{\mu }_A\left(x\right),{\eta }_A\left(x\right),{\nu }_A\left(x\right)\right)|x\in X\right\}.$$

It corresponds with a D*-fuzzy set, i.e., a mapping:

$$A:X\to D^{*}:x\mapsto \left({\mu }_A\left(x\right),{\eta }_A\left(x\right),{\nu }_A\left(x\right)\right).$$

The original inclusion relation of picture fuzzy relations is based on the following order relation on D*: ∀ x, y ∈ D*,

$$x{\le }_{1}y\iff \left(x_1\le y_1\right)\wedge \left(x_2\le y_2\right)\wedge \left(x_3\ge y_3\right).$$

The above “∧“ denote “and”. In this paper, above “≤₁” is called type-1 order relation and the original inclusion relation of picture fuzzy relations is called a type-1 inclusion relation, and denoted as the following:

R ⊆₁ P iff (∀ (x, y) ∈ X × Y, μ_R(x, y) ≤ μ_P(x, y), η_R(x, y) ≤ η_P(x, y), ν_R(x, y) ≥ ν_P(x, y)).

Accordingly, the union, intersection and complement operations in Definition 5 are called type-1 union, intersection and complement, and denoted as the following:

R ∪₁ P = {((x, y), μ_R(x, y) ∨ μ_P(x, y), η_R(x, y) ∧ η_P(x, y), ν_R(x, y) ∧ ν_P(x, y)) | x ∈ X, y ∈ Y}
      = {((x, y), (μ_R(x, y), η_R(x, y), ν_R(x, y)) ∨₁ (μ_P(x, y), η_P(x, y), ν_P(x, y))) | x ∈ X, y ∈ Y};

R ∩₁ P = {((x, y), μ_R(x, y) ∧ μ_P(x, y), η_R(x, y) ∧ η_P(x, y), ν_R(x, y) ∨ ν_P(x, y))} | x ∈ X, y ∈ Y}
      = {((x, y), (μ_R(x, y), η_R(x, y), ν_R(x, y)) ∧₁ (μ_P(x, y), η_P(x, y), ν_P(x, y))) | x ∈ X, y ∈ Y};

R^c₁ = {((x, y), ν_R(x, y), η_R(x, y), μ_R(x, y)) | x ∈ X, y ∈ Y} = {((x, y), (μ_R(x, y), η_R(x, y), ν_R(x, y))^c₁) | x ∈ X, y ∈ Y}.

Now, we introduce a new inclusion of picture fuzzy relations, and call it type-2 inclusion of picture fuzzy relations.

Definition 8.

Let R and P be two picture fuzzy relations between X and Y. The type-2 inclusion relation is defined as follows: R ⊆₂ P if and only if ∀ (x, y) ∈ X × Y, (μ_R(x, y) < μ_P(x, y), ν_R(x, y) ≥ ν_P(x, y)), or (μ_R(x, y) = μ_P(x, y), ν_R(x, y) > ν_P(x, y)), or (μ_R(x, y) = μ_P(x, y), ν_R(x, y) = ν_P(x, y) and η_R(x, y) ≤ η_P(x, y)).

In fact, type-2 inclusion relation is based on the following order relation on D* (see [5], and it is called a type-2 order relation in this paper):

$$x{\le }_{2}y\iff \left(\left(x_1<y_1\right)\wedge \left(x_3\ge y_3\right)\right)\vee \left(\left(x_1=y_1\right)\wedge \left(x_3>y_3\right)\right)\vee \left(\left(x_1=y_1\right)\wedge \left(x_3=y_3\right)\wedge \left(x_2\le y_2\right)\right).$$

The above “∧“ denote “and”, “∨“ denote “or”.

Remark 1.

In order not to cause confusion, the type-2 order relation on D* is denoted by “≤₂”, it is different from [30].

Note that, if for any x, y ∈ D* that neither x ≤₂ y nor y ≤₂ x, then x and y are incomparable, denoted as $x|{|}_{{\le }_2}y.$

3. New Operations and Properties of Picture Fuzzy Relations

In this section, we introduce some new operations named type-2 inclusion, type-2 union, type-2 intersection and type-2 complement operation of picture fuzzy relations and study their properties.

For any picture fuzzy relations R and P on X × Y, by Definition 8, we have:

R ⊆₂ P if and only if ∀ (x, y) ∈ X × Y, (μ_R(x, y), η_R(x, y), ν_R(x, y)) ≤₂ (μ_P(x, y), η_P(x, y), ν_P(x, y)).

From this, we can get the following proposition.

Proposition 2.

Let R, P and Q be picture fuzzy relations on X × Y, then

(1)

R ⊆₂ R;

(2)

(R ⊆₂ P, P ⊆₂ R) ⇒ R = P;

(3)

(R ⊆₂ P, P ⊆₂ Q) ⇒ R ⊆₂ Q.

Definition 9.

For every two PFRs R and P, the type-2 union, type-2 intersection, type-2 complement operators are defined as follows:

(1)

R ∪₂ P =

$$\{\begin{array}{l}\left\{\left(\left(x,y\right),{\mu }_R\left(x,y\right),{\eta }_R\left(x,y\right),{\nu }_R\left(x,y\right)\right)|\left(x,y\right)\in X\times Y\right\},ifP{\subseteq }_{2}R\hfill \\ \left\{\left(\left(x,y\right),{\mu }_P\left(x,y\right),{\eta }_P\left(x,y\right),{\nu }_P\left(x,y\right)\right)|\left(x,y\right)\in X\times Y\right\},ifR{\subseteq }_{2}P\hfill \\ \left\{\left(\left(x,y\right),{\mu }_R\left(x,y\right)\vee {\mu }_P\left(x,y\right),0,{\nu }_R\left(x,y\right)\wedge {\nu }_P\left(x,y\right)\right)|\left(x,y\right)\in X\times Y\right\},else;\hfill \end{array}$$

(2)

R ∩₂ P =

$$\{\begin{array}{l}\left\{\left(\left(x,y\right),{\mu }_R\left(x,y\right),{\eta }_R\left(x,y\right),{\nu }_R\left(x,y\right)\right)|\left(x,y\right)\in X\times Y\right\},ifR{\subseteq }_{2}P\\ \left\{\left(\left(x,y\right),{\mu }_P\left(x,y\right),{\eta }_P\left(x,y\right),{\nu }_P\left(x,y\right)\right)|\left(x,y\right)\in X\times Y\right\},ifP{\subseteq }_{2}R\\ \{(\left(x,y\right),{\mu }_R\left(x,y\right)\wedge {\mu }_P\left(x,y\right),1-\left({\mu }_R\left(x,y\right)\wedge {\mu }_P\left(x,y\right)\right)-\\ \left({\nu }_R\left(x,y\right)\vee {\nu }_P\left(x,y\right)\right),{\nu }_R\left(x,y\right)\vee {\nu }_P\left(x,y\right))|\left(x,y\right)\in X\times Y\},else;\end{array}$$

(3)

co(R) = R^c₂ =

$$\left\{\right(\left(x,y\right),{\nu }_R\left(x,y\right),1-{\mu }_R\left(x,y\right)-{\eta }_R\left(x,y\right)-{\nu }_R\left(x,y\right),{\mu }_R\left(x,y\right))|\left(x,y\right)\in X\times Y\}.$$

It is easy to verify that the type-2 union and type-2 intersection of PFRs satisfy commutative law and associative law.

Example 1.

Let X = {x₁, x₂}, Y = {y₁, y₂}. A picture fuzzy relation R in X × Y is given in

Table 1. A picture fuzzy relation R.

R	y1	y2
x1	(0.3, 0.2, 0.1)	(0.5, 0.1, 0.3)
x2	(0.2, 0.6, 0.2)	(0.2, 0.1, 0.5)

. By Definitions 5 and 9, we can compute R⁻¹ and R^c₂, which are given in

Table 2. The inverse R⁻¹ of R.

R−1	y1	y2
x1	(0.3, 0.2, 0.1)	(0.2, 0.6, 0.2)
x2	(0.5, 0.1, 0.3)	(0.2, 0.1, 0.5)

and

Table 3. The complement R^c₂ of R.

Rc2	y1	y2
x1	(0.1, 0.6, 0.3)	(0.2, 0, 0.2)
x2	(0.3, 0.2, 0.5)	(0.5, 0.3, 0.2)

, respectively.

Definition 10.

Let R ∈ PFR(X × Y).

(1)

If ∀ (x, y) ∈ X × Y, μ_R(x, y) = η_R(x, y) = 0 and ν_R(x, y) = 1, then R is called a null PFR, denoted by ∅_N.

(2)

If ∀ (x, y) ∈ X × Y, μ_R(x, y) = 1 and η_R(x, y) = ν_R(x, y) = 0, then R is called an absolute PFR, denoted by U_N.

(3)

If ∀ (x, y) ∈ X × Y, μ_R(x, y) = $\{\begin{array}{c}1,x=y\\ 0,x\ne y\end{array}$, η_R(x, y) = 0 and ν_R(x, y) = $\{\begin{array}{c}0,x=y\\ 1,x\ne y\end{array}$, then R is called an identity PFR, denoted by Id_N.

According the Definitions 9 and 10, we can get the Type-2 complement of Id_N denoted by (Id_N)^c₂ is a PFR satisfying: ∀ (x, y) ∈ X × Y,

$${\mu }_{{(I{d}_N)}^{c_2}}\left(x,y\right)=\{\begin{array}{c}0,x=y\\ 1,x\ne y\end{array},{\eta }_{{(I{d}_N)}^{c_2}}(x,y)=0,{\nu }_{{(I{d}_N)}^{c_2}}\left(x,y\right)=\{\begin{array}{c}1,x=y\\ 0,x\ne y\end{array}.$$

Definition 11.

Let R ∈ PFR(X × Y).

(1)

If ∀ x ∈ X, μ_R(x, x) = 1 and η_R(x, x) = ν_R(x, x) = 0, then R is called a reflexive PFR.

(2)

If ∀ (x, y) ∈ X × Y, μ_R(x, y) = μ_R(y, x), η_R(x, y) = η_R(y, x), ν_R(x, y) = ν_R(y, x), then R is called a symmetric PFR.

(3)

If ∀ x ∈ X, μ_R(x, x) = η_R(x, x) = 0 and ν_R(x, x) = 1, then R is called an anti-reflexive PFR.

Proposition 3.

Type-2 union and type-2 intersection of PFRs don’t satisfy distributive law, which means that ∀ R, P, Q ∈ PFR(X × Y):

(1)

(R ∩₂ P) ∪₂ Q ≠ (R ∪₂ Q) ∩₂ (P ∪₂ Q),

(2)

(R ∪₂ P) ∩₂ Q ≠ (R ∩₂ Q) ∪₂ (P ∩₂ Q).

Example 2.

X = {x₁, x₂}, Y = {y₁, y₂}. Picture fuzzy relations R, P, Q in X × Y are given in Table 1,

Table 4. A picture fuzzy relation P.

P	y1	y2
x1	(0.5, 0.2, 0.3)	(0.3, 0.2, 0.4)
x2	(0.6, 0.1, 0.2)	(0.7, 0.1, 0.1)

and

Table 5. A picture fuzzy relation Q.

Q	y1	y2
x1	(0.4, 0.1, 0.2)	(0.2, 0.1, 0.1)
x2	(0.2, 0.2, 0.5)	(0.1, 0.4, 0.2)

. Then (R ∩₂ P) ∪₂ Q, (R ∪₂ Q) ∩₂ (P ∪₂ Q), (R ∪₂ P) ∩₂ Q, (R ∩₂ Q) ∪₂ (P ∩₂ Q) in X × Y are given in

Table 6. The picture fuzzy relation (R ∩₂ P) ∪₂ Q.

(R ∩2 P) ∪2 Q	y1	y2
x1	(0.4, 0.1, 0.2)	(0.3, 0, 0.1)
x2	(0.2, 0.6, 0.2)	(0.2, 0, 0.2)

,

Table 7. The picture fuzzy relation (R ∩₂ Q) ∪₂ (P ∩₂ Q).

(R ∩2 Q) ∪2 (P ∩2 Q)	y1	y2
x1	(0.4, 0.4, 0.2)	(0.3, 0, 0.1)
x2	(0.2, 0.6, 0.2)	(0.2, 0, 0.2)

,

Table 8. The picture fuzzy relation (R ∪₂ P) ∩₂ Q.

(R ∪2 P) ∩2 Q	y1	y2
x1	(0.4, 0.1, 0.2)	(0.2, 0.5, 0.3)
x2	(0.2, 0.2, 0.5)	(0.1, 0.4, 0.2)

and

Table 9. The picture fuzzy relation (R ∩₂ Q) ∪₂ (P ∩₂ Q).

(R ∩2 Q) ∪2 (P ∩2 Q)	y1	y2
x1	(0.4, 0, 0.2)	(0.2, 0.5, 0.3)
x2	(0.2, 0.2, 0.5)	(0.1, 0.4, 0.2)

. Furthermore, according to Table 6, Table 7, Table 8 and Table 9, we can get the conclusion of Propositions 3 (1) and (2).

Proposition 4.

Let R, P, Q ∈ PFR(X × Y). Then, we have

(1)

R is symmetric iff R = R⁻¹;

(2)

(R^c₂)⁻¹ = (R⁻¹)^c₂;

(3)

(R^c₂)^c₂ = R, (R⁻¹)⁻¹ = R;

(4)

R ⊆₂ R ∪₂ P, P ⊆₂ R ∪₂ P;

(5)

R ∩₂ P ⊆₂ R, R ∩₂ P ⊆₂ P;

(6)

If R ⊆₂ P, then R⁻¹ ⊆₂ P⁻¹;

(7)

If R ⊆₂ P and Q ⊆₂ P, then R ∪₂ Q ⊆₂ P;

(8)

If P ⊆₂ R and P ⊆₂ Q, then P ⊆₂ R ∩₂ Q;

(9)

If R ⊆₂ P, then R ∪₂ P = P, R ∩₂ P = R;

(10)

(R ∪₂ P)⁻¹ = R⁻¹ ∪₂ P⁻¹, (R ∩₂ P)⁻¹ = R⁻¹ ∩₂ P⁻¹;

(11)

(R ∪₂ P)^c₂ = R^c₂ ∩₂ P^c₂, (R ∩₂ P)^c₂ = R^c₂ ∪₂ P^c₂.

Proof. 

Clearly, Labels (1) and (3)–(9) is hold. We only show Labels (2), (10) and (11).

(2) ∀ (x, y) ∈ X × Y, μ(Rc2)−1(x, y) = μRc2(y, x) = νR(y, x) = νR−1(x, y) = μ(R−1)c2(x, y); ν(Rc2)−1(x, y) = νRc2(y, x) = μR(y, x) = μR−1(x, y) = ν(R−1)c2(x, y); η(Rc2)−1(x, y) = ηRc2(y, x) = 1 − μR(y, x) − ηR(y, x) − νR(y, x) = 1 − μR−1(x, y) − ηR−1(x, y) − νR−1(x, y) = η(R−1)c2(x, y).

Therefore (R^c₂)⁻¹ = (R⁻¹)^c₂.

(10) If R ⊆₂ P, then R⁻¹ ⊆₂ P⁻¹, so (R ∪₂ P)⁻¹ = P⁻¹ = R⁻¹ ∪₂ P⁻¹; If P ⊆₂ R, then P⁻¹ ⊆₂ R⁻¹, so (R ∪₂ P)⁻¹ = R⁻¹ = R⁻¹ ∪₂ P⁻¹; If neither R ⊆₂ P nor P ⊆₂ R, then (R ∪₂ P)⁻¹ = {((x, y), μ_R(x, y) ∨ μ_P(x, y), 0, ν_R(x, y) ∧ ν_P(x, y)) | (x, y) ∈ X × Y }⁻¹ = {((y, x), μ_R⁻¹(x, y) ∨ μ_P⁻¹(x, y), 0, ν_R⁻¹(x, y) ∧ ν_P⁻¹(x, y)) | (x, y) ∈ X × Y }, R ⁻¹ ∪₂ P ⁻¹ = {((y, x), μ_R⁻¹(x, y), η_R⁻¹(x, y), ν_R⁻¹(x, y)) | (x, y) ∈ X × Y } ∪₂ {((y, x), μ_P⁻¹(x, y), η_P⁻¹(x, y), ν_P⁻¹(x, y)) | (x, y) ∈ X × Y } = {((y, x), μ_R⁻¹(x, y) ∨ μ_P⁻¹(x, y), 0, ν_R⁻¹(x, y) ∧ ν_P⁻¹(x, y)) | (x, y) ∈ X × Y } = (R ∪₂ P)⁻¹. Hence, (R ∪₂ P)⁻¹ = R⁻¹ ∪₂ P⁻¹. Similarly, we can show (R ∩₂ P)⁻¹ = R⁻¹ ∩₂ P⁻¹.

(11) If R ⊆₂ P, then P^c₂ ⊆₂ R^c₂, so (R ∪₂ P)^c₂ = P^c2 = R^c₂ ∩₂ P^c₂; If P ⊆₂ R, then R^c₂ ⊆₂ P^c₂, so (R ∪₂ P)^c₂ = R^c₂ = R^c₂ ∩₂ P^c₂; If neither R ⊆₂ P nor P ⊆₂ R, then neither R^c₂ ⊆₂ P^c₂ nor P^c₂ ⊆₂ R^c₂ and (R ∪₂ P)^c₂ = {((x, y), ν_R(x, y) ∧ ν_P(x, y), 1 – (μ_R(x, y) ∨ μ_P(x, y)) – (ν_R(x, y) ∧ ν_P(x, y)), μ_R(x, y) ∨ μ_P(x, y)) | (x, y) ∈ X × Y }, R^c₂ ∩₂ P^c₂ = {((x, y), ν_R(x, y), 1 – μ_R(x, y) – η_R(x, y) – ν_R(x, y), μ_R(x, y)) | (x, y) ∈ X × Y } ∩₂ {((x, y), ν_P(x, y), 1 – μ_P(x, y) – η_P(x, y) – ν_P(x, y), μ_P(x, y)) | (x, y) ∈ X × Y } = {((x, y), ν_R(x, y) ∧ ν_P(x, y), 1 – (μ_R(x, y) ∨ μ_P(x, y)) – (ν_R(x, y) ∧ ν_P(x, y)), μ_R(x, y) ∨ μ_P(x, y)) | (x, y) ∈ X × Y }. Hence, (R ∪₂ P)^c₂ = R^c₂ ∩₂ P^c₂. Similarly, we can get (R ∩₂ P)^c₂ = R^c₂ ∪₂ P^c₂. ☐

4. Kernels of Picture Fuzzy Relations

In this section, we will give the definition of anti-reflexive kernel and symmetric kernel about a PFR, and then study their properties.

Definition 12.

Let R ∈ PFR(X × Y).

(1)

The maximal anti-reflexive PFR contained in R is called anti-reflexive kernel of R, denoted by ar(R).

(2)

The maximal symmetric PFR contained in R is called symmetric kernel of R, denoted by s(R).

Proposition 5.

Let R ∈ PFR(X × Y). Then,

(1)

ar(R) = R ∩₂ (Id_N)^c₂.

(2)

s(R) = R ∩₂ R⁻¹.

Proof. 

(1) By Proposition 3 (5), R ∩₂ (Id_N)^c₂ ⊆₂ R. According the definition of Id_N, ∀ x ∈ X, we have μ_IdN(x, x) = 1 and η_IdN(x, x) = ν_IdN(x, x) = 0, then μ_(IdN)^c₂(x, x) = η_(IdN)^c₂(x, x) = 0 and ν_(IdN)^c₂(x, x) = 1. Hence, μ_(IdN)^c₂(x, x) ≤ μ_R(x, x), ν_(IdN)^c₂(x, x) ≥ ν_R(x, x), η_(IdN)^c₂(x, x) ≤ η_R(x, x). Therefore, (Id_N)^c₂ ⊆₂ R, μ_R∩2(IdN)^c₂(x, x) = η_R∩2(IdN)^c₂(x, x) = 0 and ν_R∩2(IdN)^c₂(x, x) = 1. According to Definition 11 (3), R ∩₂ (Id_N)^c₂ is an anti-reflexive PFR.

Suppose P is an anti-reflexive PFR and P ⊆₂ R. Obviously, P ⊆₂ (Id_N)^c₂. Hence, P ⊆₂ R ∩₂ (Id_N)^c₂. Therefore, ar(R) = R ∩₂ (Id_N)^c₂.

(2) By Proposition 3 (3) and Label (10), (R ∩₂ R⁻¹)⁻¹ = R⁻¹ ∩₂ (R⁻¹)⁻¹ = R⁻¹ ∩₂ R = R ∩₂ R⁻¹, which implies that R ∩₂ R⁻¹ is a symmetric PFR. According to Proposition 3 (5), R ∩₂ R⁻¹ ⊆₂ R.

Suppose P is a symmetric PFR and P ⊆₂ R. By Proposition 3 (6), P⁻¹ ⊆₂ R⁻¹. Then, by Proposition 3 (1) and (5), P = P⁻¹ ⊆₂ R ∩₂ R⁻¹. Therefore, s(R) = R ∩₂ R⁻¹. ☐

Example 3.

Let X = Y = {z₁, z₂, z₃}. A picture fuzzy relation R in X × Y is given in

Table 10. A picture fuzzy relation R.

R	z1	z2	z3
z1	(0.3, 0.2, 0.1)	(0.5, 0.1, 0.3)	(0.3, 0.2, 0.4)
z2	(0.2, 0.6, 0.2)	(0.2, 0.1, 0.5)	(0.6, 0.1, 0.2)
z3	(0.7, 0.1, 0.1)	(0.4, 0.1, 0.2)	(0.2, 0.2, 0.5)

. By Proposition 5, we can obtain ar(R) and s(R), which are given in

Table 11. The anti-reflexive kernel ar(R) of R.

ar(R)	z1	z2	z3
z1	(0, 0, 1)	(0.5, 0.1, 0.3)	(0.3, 0.2, 0.4)
z2	(0.2, 0.6, 0.2)	(0, 0, 1)	(0.6, 0.1, 0.2)
z3	(0.7, 0.1, 0.1)	(0.4, 0.1, 0.2)	(0, 0, 1)

and

Table 12. The symmetric kernel s(R) of R.

s(R)	z1	z2	z3
z1	(0.3, 0.2, 0.1)	(0.2, 0.5, 0.3)	(0.3, 0.2, 0.4)
z2	(0.2, 0.5, 0.3)	(0.2, 0.1, 0.5)	(0.4, 0.1, 0.2)
z3	(0.3, 0.2, 0.4)	(0.4, 0.1, 0.2)	(0.2, 0.2, 0.5)

, respectively.

Proposition 6.

The anti-reflexive kernel operator ar of the PFR has the following properties:

(1)

ar(∅_N) = ∅_N, ar((Id_N)^c₂) = (Id_N)^c₂;

(2)

∀ R ∈ PFR(X × Y), ar(R) ⊆₂ R;

(3)

∀ R, P ∈ PFR(X × Y), ar(R ∪₂ P) = ar(R) ∪₂ ar(P), ar(R ∩₂ P) = ar(R) ∩₂ ar(P);

(4)

∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, then ar(R) ⊆₂ ar(P);

(5)

∀ R ∈ PFR(X × Y), ar(ar(R)) = ar(R).

Proof. 

(1) By the definition of ∅_N, we can get ∅_N ⊆₂ (Id_N)^c₂. Therefore, ar(∅_N) = ∅_N ∩₂ (Id_N)^c₂ = ∅_N. ar((Id_N)^c₂) = (Id_N)^c₂ ∩₂ (Id_N)^c₂ = (Id_N)^c₂.

(2) ∀ R ∈ PFR(X × Y), by Proposition 5 (1) and Proposition 3 (5), ar(R) = R ∩₂ (Id_N)^c₂ ⊆₂ R.

(3) ar(R ∪₂ P) = (R ∪₂ P) ∩₂ (Id_N)^c₂, ar(R) ∪₂ ar(P) = (R ∩₂ (Id_N)^c₂) ∪₂ (P ∩₂ (Id_N)^c₂). ∀ (x, y) ∈ X × Y, when x = y, (Id_N)^c₂ = {((x, y), 0, 0, 1) | (x, y) ∈ X × Y }, so (Id_N)^c₂ ⊆₂ R, (Id_N)^c₂ ⊆₂ P, then ar(R ∪₂ P) = ar(R) ∪₂ ar(P) = (Id_N)^c₂; when x ≠ y, (Id_N)^c₂ = {((x, y), 1, 0, 0) | (x, y) ∈ X × Y }, so R ⊆₂ (Id_N)^c₂, P ⊆₂ (Id_N)^c₂, then ar(R ∪₂ P) = ar(R) ∪₂ ar(P) = R ∪₂ P. Hence, ar(R ∪₂ P) = ar(R) ∪₂ ar(P). ar(R ∩₂ P) = (R ∩₂ P) ∩₂ (Id_N)^c₂ = ((R ∩₂ (Id_N)^c₂) ∩₂ (P ∩₂ (Id_N)^c₂) = ar(R) ∩₂ ar(P).

(4) ∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, by Label (3) and Proposition 3 (4) and Label (9), ar(R) ⊆₂ ar(R) ∪₂ ar(P) = ar(R ∪₂ P) = ar(P).

(5) ∀ R ∈ PFR(X × Y), by Proposition 5 (1), ar(R) = R ∩₂ (Id_N)^c₂. Hence, ar(ar(R)) = ar(R ∩₂ (Id_N)^c₂) = (R ∩₂ (Id_N)^c₂) ∩₂ (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R). ☐

Proposition 7.

The symmetric kernel operator s of the PFR has the following properties:

(1)

s(∅_N) = ∅_N, s(U_N) = U_N, s(Id_N) = Id_N;

(2)

∀ R ∈ PFR(X × Y), s(R) ⊆₂ R;

(3)

∀ R, P ∈ PFR(X × Y), s(R ∩₂ P) = s(R) ∩₂ s(P);

(4)

∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, then s(R) ⊆₂ s(P);

(5)

∀ R ∈ PFR(X × Y), s(s(R)) = s(R).

Proof. 

(1) By the Definition 10 and Proposition 5, we have s(∅_N) = ∅_N, s(U_N) = U_N, s(Id_N) = Id_N.

(2) ∀ R ∈ PFR(X × Y), by Proposition 5 (2) and Proposition 3 (5), s(R) = R ∩₂ R ⁻¹ ⊆₂ R.

(3) ∀ R, P ∈ PFR(X × Y), by Proposition 5 (2) and Proposition 3 (10), we have

s(R ∩₂ P) = (R ∩₂ P) ∩₂ (R ∩₂ P)⁻¹ = (R ∩₂ P) ∩₂ (R⁻¹ ∩₂ P⁻¹) = (R ∩₂ R⁻¹) ∩₂ (P ∩₂ P⁻¹) = s(R) ∩₂ s(P).

(4) ∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, by Label (3) and Proposition 3 (5) and (9), s(R) = s(R ∩₂ P) = s(R) ∩₂ s(P) ⊆₂ s(P).

(5) ∀ R ∈ PFR(X × Y), by Proposition 5 (2), we have

s(s(R)) = s(R ∩₂ R ⁻¹) = (R ∩₂ R⁻¹) ∩₂ (R ∩₂ R⁻¹)⁻¹ = R ∩₂ R⁻¹ = s(R). ☐

5. Closures of Picture Fuzzy Relations

In this section, we give the concepts of reflexive closure and symmetric closure of a PFR, and investigate their properties.

Definition 13.

Let R ∈ PFR(X × Y). If O ∈ PFR(X × Y) satisfies the following conditions:

(1)

O is reflexive;

(2)

R ⊆₂ O;

(3)

∀ E ∈ PFR(X × Y), if E is reflexive and R ⊆₂ E, then O ⊆₂ E.

Then, O is called reflexive closure of R, denoted by $\overline{r}\left(R\right)$.

Definition 14.

Let R ∈ PFR(X × Y). If O ∈ PFR(X × Y) satisfies the following conditions:

(1)

O is symmetric;

(2)

R ⊆₂ O;

(3)

∀ E ∈ PFR(X × Y), if E is symmetric and R ⊆₂ E, then O ⊆₂ E.

Then, O is called symmetric closure of R, denoted by $\overline{s}\left(R\right)$.

Proposition 8.

Let R ∈ PFR(X × Y). Then,

(1) 

$\overline{r}$(R) = R ∪₂ Id_N.

(2) 

$\overline{s}$(R) = R ∪₂ R⁻¹.

Proof. 

(1) By Proposition 3 (4), R ⊆₂ R ∪₂ Id_N, Id_N ⊆₂ R ∪₂ Id_N. According the definition of Id_N, ∀ x ∈ X, we have μ_IdN(x, x) = 1 and η_IdN(x, x) = ν_IdN(x, x) = 0. Hence, μ_R(x, x) < μ_IdN(x, x), ν_R(x, x) ≥ ν_IdN(x, x), η_IdN(x, x) ≤ η_R(x, x) or μ_R(x, x) = μ_IdN(x, x) = 1, ν_R(x, x) = ν_IdN(x, x) = 0, η_IdN(x, x) = η_R(x, x) = 0. Therefore, R ⊆₂ Id_N or R = Id_N, so μ_R∪2IdN(x, x) = 1 and η_R∪2IdN(x, x) = ν_R∪2IdN(x, x) = 0. According to Definition 11 (1), R ∪₂ Id_N is a reflexive PFR.

Suppose P is a reflexive PFR and R ⊆₂ P. Obviously, Id_N ⊆₂ P. Hence, R ∪₂ Id_N ⊆₂ P. Therefore, $\overline{r}$(R)= R ∪₂ Id_N.

(2) By Proposition 3 (3) and Label (10), (R ∪₂ R⁻¹)⁻¹ = R⁻¹ ∪₂ (R⁻¹)⁻¹ = R⁻¹ ∪₂ R = R ∪₂ R⁻¹, which implies that R ∪₂ R⁻¹ is a symmetric PFR. According to Proposition 3 (4), R ⊆₂ R ∪₂ R ⁻¹.

Suppose P is a symmetric PFR and R ⊆₂ P. By Proposition 3 (6), R⁻¹ ⊆₂ P⁻¹. Then, by Proposition 3 (1) and Label (7), R ∪₂ R⁻¹ ⊆₂ P = P⁻¹. Therefore, $\overline{s}$(R) = R ∪₂ R⁻¹. ☐

Example 4.

Consider X, Y and R given in Example 3. By Proposition 8, we can obtain $\overline{r}$ (R) and $\overline{s}$(R), which are given in

Table 13. The reflexive closure $\overline{r}$ (R) of R.

$\overline{\mathit{r}}$(R)	z1	z2	z3
z1	(1, 0, 0)	(0.5, 0.1, 0.3)	(0.3, 0.2, 0.4)
z2	(0.2, 0.6, 0.2)	(1, 0, 0)	(0.6, 0.1, 0.2)
z3	(0.7, 0.1, 0.1)	(0.4, 0.1, 0.2)	(1, 0, 0)

and

Table 14. The symmetric closure $\overline{s}$ (R) of R.

$\overline{\mathit{s}}$(R)	z1	z2	z3
z1	(0.3, 0.2, 0.1)	(0.5, 0, 0.2)	(0.7, 0.1, 0.1)
z2	(0.5, 0, 0.2)	(0.2, 0.1, 0.5)	(0.6, 0.1, 0.2)
z3	(0.7, 0.1, 0.1)	(0.6, 0.1, 0.2)	(0.2, 0.2, 0.5)

, respectively.

Proposition 9.

The reflexive closure operator $\overline{r}$ has the following properties:

(1)

$\overline{r}$(U_N) = U_N, $\overline{r}$(Id_N) = Id_N;

(2)

∀ R ∈ PFR(X × Y), R ⊆₂ $\overline{r}$(R);

(3)

∀ R, P ∈ PFR(X × Y), $\overline{r}$(R ∪₂ P) = $\overline{r}$(R) ∪₂ $\overline{r}$(P), $\overline{r}$(R ∩₂ P) = $\overline{r}$(R) ∩₂ $\overline{r}$(P);

(4)

∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, then $\overline{r}$(R) ⊆₂ $\overline{r}$(P);

(5)

∀ R ∈ PFR(X × Y), $\overline{r}$($\overline{r}$(R)) = $\overline{r}$(R).

Proof. 

(1) By Definition 10, we can get Id_N ⊆₂ U_N. Therefore, $\overline{r}$(U_N) = U_N. $\overline{r}$(Id_N) = Id_N ∪₂ Id_N = Id_N.

(2) ∀ R ∈ PFR(X × Y), by Proposition 3 (4), we have R ⊆₂ R ∪₂ Id_N = $\overline{r}$(R).

(3) ∀ R, P ∈ PFR(X × Y),

$\overline{r}$(R ∪₂ P) = (R ∪₂ P) ∪₂ Id_N = (R ∪₂ Id_N) ∪₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∪₂ $\overline{r}$(P); $\overline{r}$(R ∩₂ P) = (R ∩₂ P) ∪₂ Id_N, $\overline{r}$(R) ∩₂ $\overline{r}$(P) = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N), ∀ (x, y) ∈ X × Y, when x = y, then by the definition of Id_N, we can get R ⊆₂ Id_N or R = Id_N, also we can get P ⊆₂ Id_N or P = Id_N, when x ≠ y, then we can get Id_N ⊆₂ R or R = Id_N, also we can get Id_N ⊆₂ P or P = Id_N. If R ⊆₂ Id_N and P ⊆₂ Id_N, then R ∩₂ P ⊆₂ Id_N, so $\overline{r}$(R ∩₂ P) = Id_N = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If R = Id_N and P ⊆₂ Id_N, then $\overline{r}$(R ∩₂ P) = Id_N = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If R ⊆₂ Id_N and P = Id_N, then $\overline{r}$(R ∩₂ P) = Id_N = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If R = Id_N and P = Id_N, then $\overline{r}$(R ∩₂ P) = R = P = Id_N = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If Id_N ⊆₂ R and Id_N ⊆₂ P, then by Proposition 3 (8), we have Id_N ⊆₂ R ∩₂ P, so $\overline{r}$(R ∩₂ P) = R ∩₂ P = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If Id_N = R and Id_N ⊆₂ P, then $\overline{r}$(R ∩₂ P) = Id_N = R = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P). If Id_N ⊆₂ R and Id_N = P, then $\overline{r}$(R ∩₂ P) = Id_N = P = (R ∪₂ Id_N) ∩₂ (P ∪₂ Id_N) = $\overline{r}$(R) ∩₂ $\overline{r}$(P).

Hence, $\overline{r}$(R ∩₂ P) = $\overline{r}$(R) ∩₂ $\overline{r}$(P).

(4) ∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, by Label (3) and Proposition 3 (4) and Label (9), we have $\overline{r}$ (R) ⊆₂ $\overline{r}$(R) ∪₂ $\overline{r}$(P) = $\overline{r}$(R ∪₂ P) = $\overline{r}$(P).

(5) ∀ R ∈ PFR(X × Y),

$\overline{r}$($\overline{r}$(R)) = ($\overline{r}$(R)) ∪₂ Id_N = (R ∪₂ Id_N) ∪₂ Id_N = R ∪₂ Id_N = $\overline{r}$(R). ☐

Proposition 10.

The symmetric closure operator $\overline{s}$ has the following properties:

(1)

$\overline{s}$(∅_N) = ∅_N, $\overline{s}$(U_N) = U_N, $\overline{s}$(Id_N) = Id_N;

(2)

∀ R ∈ PFR(X × Y), R ⊆₂ $\overline{s}$(R);

(3)

∀ R, P ∈ PFR(X × Y), $\overline{s}$(R ∪₂ P) = $\overline{s}$(R) ∪₂ $\overline{s}$(P);

(4)

∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, then $\overline{s}$(R) ⊆₂ $\overline{s}$(P);

(5)

∀ R ∈ PFR(X × Y), $\overline{s}$($\overline{s}$(R)) = $\overline{s}$(R);

Proof. 

(1) By the symmetry of ∅_N, U_N and Id_N, we have $\overline{s}$(∅_N) = ∅_N, $\overline{s}$(U_N) = U_N, $\overline{s}$(Id_N) = Id_N.

(2) ∀ R ∈ PFR(X × Y), by the Proposition 8 (2), R ⊆₂ R ∪₂ R⁻¹ = $\overline{s}$(R).

(3) ∀ R, P ∈ PFR(X × Y), by Proposition 8 (2) and Proposition 3 (10), we have

$\overline{s}$(R ∪₂ P) = (R ∪₂ P) ∪₂ (R ∪₂ P)⁻¹ = (R ∪₂ R⁻¹) ∪₂ (P ∪₂ P⁻¹) = $\overline{s}$(R) ∪₂ $\overline{s}$(P).

(4) ∀ R, P ∈ PFR(X × Y), if R ⊆₂ P, by Label (3) and Proposition 3 (4) and (9), $\overline{s}$(R) ⊆₂ $\overline{s}$(R) ∪₂ $\overline{s}$(P) = $\overline{s}$(R ∪₂ P) = $\overline{s}$(P).

(5) ∀ R ∈ PFR(X × Y),

$\overline{s}$($\overline{s}$(R)) = $\overline{s}$(R ∪₂ R⁻¹) = (R ∪₂ R⁻¹) ∪₂ (R ∪₂ R⁻¹)⁻¹ = R ∪₂ R⁻¹ = $\overline{s}$(R). ☐

Proposition 11.

∀ R ∈ PFR(X × Y), we have

(1)

($\overline{r}$(R^c₂))^c₂ = ar(R);

(2)

ar ($\overline{r}$(R)) = ar(R).

Proof. 

(1) By Proposition 8 (1), $\overline{r}$(R^c₂) = R^c₂ ∪₂ Id_N. By Proposition 3 (11) and Proposition 5 (1),

$${\left(\overline{r}\left(R^{{\mathrm{c}}_2}\right)\right)}^{{\mathrm{c}}_2}={\left(R^{{\mathrm{c}}_2}{\cup }_{2}I{d}_N\right)}^{{\mathrm{c}}_2}={\left(R^{{\mathrm{c}}_2}\right)}^{{\mathrm{c}}_2}{\cap }_2{\left(I{d}_N\right)}^{{\mathrm{c}}_2}=R {\cap }_2{\left(I{d}_N\right)}^{{\mathrm{c}}_2}=ar\left(R\right).$$

(2) By Propositions 5 and 8, ∀ (x, y) ∈ X × Y,

$$ar\left(\overline{r}\left(R\right)\right)=ar\left(R {\cup }_{2}I{d}_N\right)=\left(R{\cup }_{2}I{d}_N\right){\cap }_2{\left(I{d}_N\right)}^{{\mathrm{c}}_2},$$

(i)

If x = y and R = Id_N, then (Id_N)^c₂ ⊆₂ Id_N, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

(ii)

If x = y and R = (Id_N)^c₂, then (Id_N)^c₂ ⊆₂ Id_N, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = Id_N ∩₂ (Id_N)^c₂ = (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

(iii)

If x = y and (Id_N)^c₂ ⊆₂ R ⊆₂ Id_N, then (Id_N)^c₂ ⊆₂ Id_N, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = Id_N ∩₂ (Id_N)^c₂ = (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

(iv)

If x ≠ y and R = Id_N, then Id_N ⊆₂ (Id_N)^c₂, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

(v)

If x ≠ y and R = (Id_N)^c₂, then Id_N ⊆₂ (Id_N)^c₂, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

(vi)

If x ≠ y and Id_N ⊆₂ R ⊆₂ (Id_N)^c₂, then Id_N ⊆₂ (Id_N)^c₂, so ar ($\overline{r}$(R)) = (R ∪₂ Id_N) ∩₂ (Id_N)^c₂ = R ∩₂ (Id_N)^c₂ = ar(R);

Hence, ar ($\overline{r}$(R)) = ar(R). ☐

Proposition 12.

∀ R ∈ PFR(X × Y), we have

(1)

($\overline{s}$(R^c₂))^c₂ = s(R);

(2)

$\overline{s}$(s(R)) = s(R);

(3)

s($\overline{s}$(R)) = $\overline{s}$(R).

Proof. 

(1) By Proposition 8 (2), $\overline{s}$(R^c₂) = R^c₂ ∪₂ (R^c₂)⁻¹. By Proposition 3 (10) and Proposition 5 (2), we have

($\overline{s}$(R^c₂))^c₂ = (R^c₂ ∪₂ (R^c₂)⁻¹)^c₂ = ((R^c₂)^c₂) ∩₂ (((R^c₂)⁻¹)^c₂) = R ∩₂ R ⁻¹ = s(R).

(2) $\overline{s}$(s(R)) = $\overline{s}$(R ∩₂ R⁻¹) = (R ∩₂ R ⁻¹) ∪₂ (R ∩₂ R⁻¹)⁻¹ = R ∩₂ R⁻¹ = s(R).

(3) s($\overline{s}$(R)) = s(R ∪₂ R⁻¹) = (R ∪₂ R⁻¹) ∩₂ (R ∪₂ R⁻¹)⁻¹ = R ∪₂ R⁻¹ = $\overline{s}$(R). ☐

6. Picture Fuzzy Comprehensive Evaluation

In this section, we defined a new composition operation of picture fuzzy relations, and according to the new composition, we give a picture fuzzy comprehensive evaluation model about risk investment.

Definition 15.

Let R ∈ PFR(X × Y) and P ∈ PFR(Y × Z). Then, the composition of P and R is defined by

R ° P = {((x, z), μ_R°P(x, z), η_R°P(x, z), ν_R°P(x, z)) | (x, z) ∈ X × Z)},

where ∀ (x, z) ∈ X × Z

$$\left(R\circ P\right)\left(x,z\right)=\underset{y\in Y}{{\cup }_2}\left(R\left(x,y\right){\cap }_{2}P\left(y,z\right)\right),$$

$${\mu }_{\left(R\circ P\right)}\left(x,z\right)=\underset{y\in Y}{{\vee }_2}\left\{{\mu }_R\left(x,y\right){\wedge }_2{\mu }_P\left(y,z\right)\right\},$$

$${\nu }_{\left(R\circ P\right)}\left(x,z\right)=\underset{y\in Y}{{\wedge }_2}\left\{{\nu }_R\left(x,y\right){\vee }_2{\nu }_P\left(y,z\right)\right\},$$

whenever

0 ≤ μ_R°P(x, z) + η_R°P(x, z) + ν_R°P(x, z) ≤ 1, ∀ (x, z) ∈ X × Z.

Definition 16.

Let A = {A₁, A₂, …, A_n} ∈ PFS(X) and R ∈ PFR(X × Y), where A_i (i = 1, 2, …, n) is picture fuzzy set and

$$R=\left(\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1s}\\ r_{21}& r_{22}& \cdots & r_{2s}\\ \cdots & \cdots & \cdots & \cdots \\ r_{n1}& r_{n2}& \cdots & r_{ns}\end{array}\right);$$

Then, the composition of A and R is defined by

$$A\circ R=\left(B_1,B_2,\cdots ,B_s\right)=(\left(\underset{k=1}{\overset{n}{{\vee }_2}}\left(A_k{\wedge }_2{r}_{k1}\right)\right),\left(\underset{k=1}{\overset{n}{{\vee }_2}}\left(A_k{\wedge }_2{r}_{k2}\right)\right),\cdots ,\left(\underset{k=1}{\overset{n}{{\vee }_2}}\left(A_k{\wedge }_2{r}_{ks}\right)\right)),$$

where r_ij and B_j are picture fuzzy sets, i = {1, 2, …, n}, j = {1, 2, …, s}.

6.1. Picture Fuzzy Comprehensive Evaluation Model

Next, we will give the procedure of picture fuzzy comprehensive evaluation.

Step 1: Establish evaluation index system. According to the method of APH (Analytic Hierarchy Process), we classify various factors that influence evaluation and establish a hierarchical relationship of evaluation index. In this paper, we used two levels of evaluation indexes, where U_i (i = 1, 2, …, m) shows the first level evaluation index, u_j⁽ⁱ⁾ (j = 1, 2, …, n_i) shows the second level evaluation index. Let subscript sets I = {1, 2, …, m}, J^(I) = {1, 2, …, n_i}.

Step 2: Determine factor importance degree of evaluation indexes. In the evaluation index system, the importance degree of the various index of target is different. There are many ways to determine the factor importance degree, such as the Delphi method, Expert investigation method and so on. Suppose the importance degree of the first level evaluation index U_i relative to the total goal is W = (w₁, w₂, …, w_m), where w_k = (μ_k, η_k, ν_k), 0 ≤ μ_k ≤ 1, 0 ≤ η_k ≤ 1, 0 ≤ ν_k ≤ 1, 0 ≤ μ_k + η_k + ν_k ≤ 1(k = 1, 2, …, m), μ_k shows this evaluation index is useful for the total goal, η_k shows this evaluation index is dispensable for the total goal, and ν_k shows this evaluation index is not useful for the total goal. The importance degree of the second level evaluation index u_j⁽ⁱ⁾ (j ∈ J^(I)) relative to the first level evaluation index U_i is W⁽ⁱ⁾ = (w₁⁽ⁱ⁾, w₂⁽ⁱ⁾, …, w_ni⁽ⁱ⁾).

Step 3: Establish evaluation matrix. Let V = {v₁, v₂, …, v_s} be a natural language comment set, S = {1, 2, …, s}, and evaluation experts give the membership degree of waiting evaluation schemes relative to each comment according to the evaluation indexes. In this paper, let the five-level language review set V = {big risk, larger risk, general risk, smaller risk, small risk}. Suppose evaluation experts give evaluation matrix R⁽ⁱ⁾, which represents the picture fuzzy relation of factor sets and comment sets, and

$$R^{\left(i\right)}=\left(\begin{array}{cccc}{r}_{11}{}^{\left(i\right)}& r_{12}{}^{\left(i\right)}& \cdots & r_{1s}{}^{\left(i\right)}\\ r_{21}{}^{\left(i\right)}& r_{22}{}^{\left(i\right)}& \cdots & r_{2s}{}^{\left(i\right)}\\ \cdots & \cdots & \cdots & \cdots \\ r_{n_{i}1}{}^{\left(i\right)}& r_{n_{i}2}{}^{\left(i\right)}& \cdots & r_{n_{i}s}{}^{\left(i\right)}\end{array}\right),$$

where r_pq⁽ⁱ⁾ is a picture fuzzy set, i ∈ I, p ∈ J^(I), q ∈ S.

Step 4: The second level picture fuzzy comprehensive evaluation. According the evaluation matrix R⁽ⁱ⁾ and the importance degree W⁽ⁱ⁾, we can get evaluation vector of U_i (i ∈ I):

$$A^{\left(i\right)}=(a_1{}^{(i)},a_2{}^{(i)},\cdots ,a_s{}^{(i)})=W^{(i)}\circ R^{\left(i\right)}=(\left(\underset{k=1}{\overset{n_i}{{\vee }_2}}\left(w_k{}^{\left(i\right)}{\wedge }_2{r}_{k1}{}^{\left(i\right)}\right)\right),\left(\underset{k=1}{\overset{n_i}{{\vee }_2}}\left(w_k{}^{\left(i\right)}{\wedge }_2{r}_{k2}{}^{\left(i\right)}\right)\right),\cdots ,\left(\underset{k=1}{\overset{n_i}{{\vee }_2}}\left(w_k{}^{\left(i\right)}{\wedge }_2{r}_{ks}{}^{\left(i\right)}\right)\right)).$$

Step 5: The first level picture fuzzy comprehensive evaluation. Let the subset of factor sets as the element of total factor sets. Then, the picture fuzzy relation matrix of factor sets U and evaluation sets V is A = (A⁽¹⁾, A⁽²⁾, …, A^(m)). According to the factor importance degree vector W = (w₁, w₂, …, w_m) and the picture fuzzy relation matrix A, to calculate the first level comprehensive evaluation vector

$$B=(b_1,b_2,\cdots ,b_s)=W\circ A=(\left(\underset{k=1}{\overset{m}{{\vee }_2}}\left(w_k{\wedge }_2{a}_1{}^{\left(k\right)}\right)\right),\left(\underset{k=1}{\overset{m}{{\vee }_2}}\left(w_k{\wedge }_2{a}_2{}^{\left(k\right)}\right)\right),\cdots ,\left(\underset{k=1}{\overset{m}{{\vee }_2}}\left(w_k{\wedge }_2{a}_s{}^{\left(k\right)}\right)\right)).$$

Step 6: The risk assessment. All elements of B are picture fuzzy sets. Therefore, the evaluation vector B can be regarded as the picture fuzzy set of the evaluation scheme risk size of the evaluation set V, which comprehensively describe the picture fuzzy membership of the evaluation scheme about all the comments. In order to get the final evaluation result, we used the scoring function and accurate function in Definition 7 to compare the size of each element in B, and, according to the principle of maximum membership, the corresponding v_i in V of the maximum value b_i in the picture fuzzy comprehensive evaluation set B is selected as the final evaluation result. In this paper, the final evaluation result is to determine the risk level of the investment scheme.

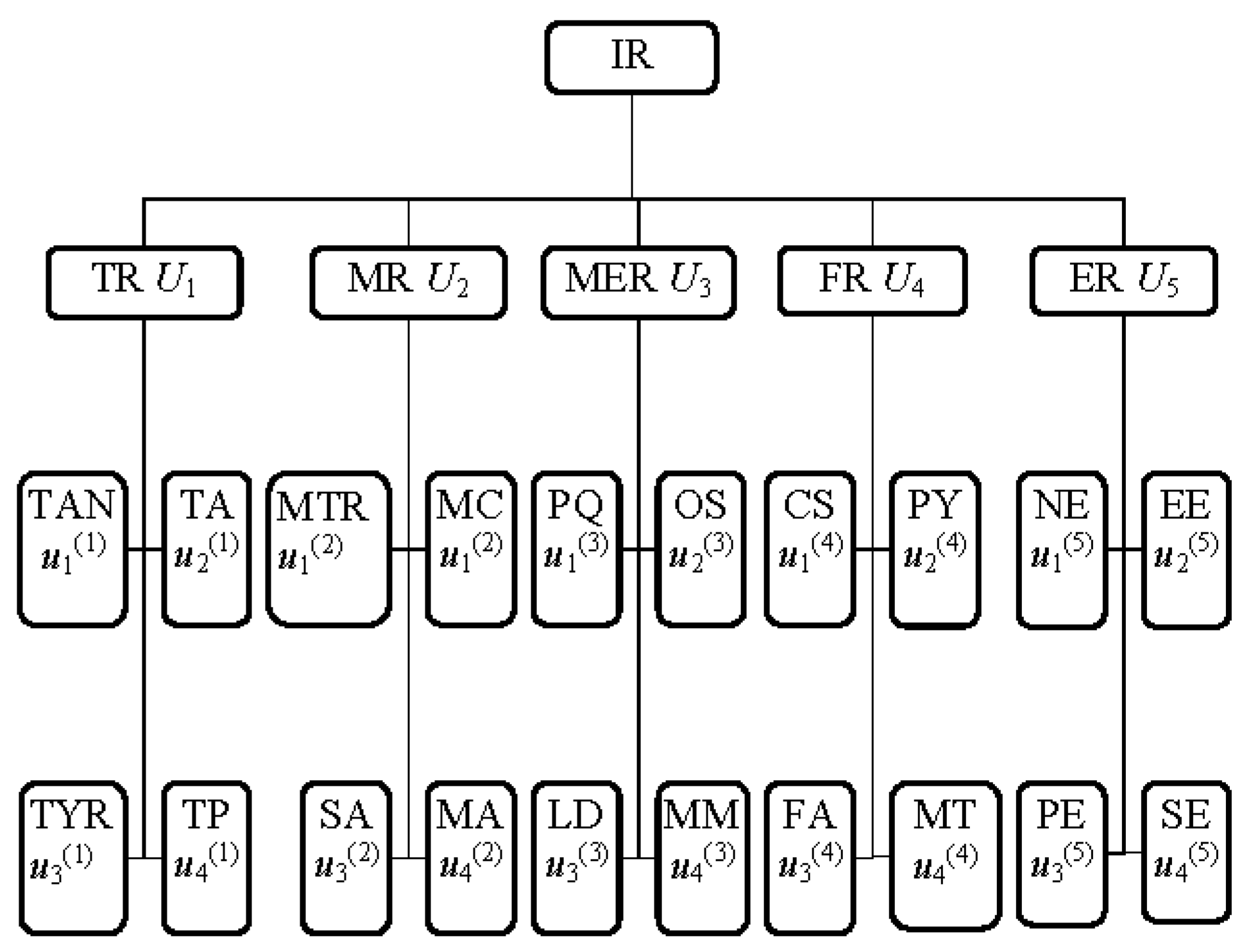
6.2. The Application Example

According to the principles of scientific nature, comparability and operability, we can get the investment risk multi-level evaluation index system as Figure 1 through the study of the structure and relationship analysis of venture capital investment risk factors, where IR-investment risk, TR-technical risk, MR-market risk, MER-manage risk, FR-financial risk, ER-environmental risk, TAN-technology advanced nature, TA-technology applicability, TYR-technology reliability, TP-technology periodicity, MTR-market requirement, MC-market competition, SA-sale ability, MA-market access, PQ-personnel quality, OS-organization structure, LD-leadership decision-making, MM-management mechanism, CS-capital structure, PY-profitability, FA-financing ability, MT-management ability, NE-natural environment, EE-economic environment, PE-political environment, and SE is social environment. According to the survey statistical method, we can get the factor importance degree vector W = {(0.5, 0.2, 0.1), (0.6, 0.1, 0.2), (0.4, 0.3, 0.3), (0.3, 0.1, 0.5), (0.3. 0.2, 0.3)}, W⁽¹⁾ = {(0.3, 0.1, 0.4), (0.4, 0.3, 0.2), (0.2, 0.3, 0.4), (0.4, 0.2, 0.2)}, W⁽²⁾ = {(0.2, 0.2, 0.5), (0.5, 0.1, 0.1), (0.2, 0.3, 0.3), (0.3, 0.4, 0.1)}, W⁽³⁾ = {5}, W⁽⁴⁾ = {(0.6, 0.1, 0.2), (0.4, 0.3, 0.1), (0.2, 0.6, 0.1), (0.3, 0.5, 0.2)}, W⁽⁵⁾ = {(0.5, 0.3, 0.1), (0.3, 0.2, 0.2), (0.4, 0.1, 0.2), (0.3, 0.4, 0.2)}, decision makers get the picture fuzzy evaluation matrix about a certain item risk investment projects through the information integration:

$$R^{\left(1\right)}=(\begin{array}{ccc}(0.3,0.2,0.1)& (0.7,0.1,0.1)& (0.1,0.2,0.6)\\ (0.2,0.6,0.1)& (0.5,0.1,0.3)& (0.6,0.1,0.2)\\ (0.6,0.1,0.1)& (0.5,0.3,0.1)& (0.2,0.1,0.5)\\ (0.5,0.1,0.2)& (0.5,0.1,0.3)& (0.6,0.2,0.1)\end{array}\begin{array}{cc}(0.4,0.1,0.2)& (0.4,0.1,0.4)\\ (0.4,0.2,0.3)& (0.1,0.6,0.1)\\ (0.6,0.1,0.2)& (0.3,0.2,0.4)\\ (0.3,0.4,0.2)& (0.3,0.1,0.4)\end{array});$$

$$R^{\left(2\right)}=\left(\begin{array}{ccc}(0.8,0.1,0)& (0.4,0.2,0.3)& (0.5,0.3,0)\\ (0.3,0.3,0.2)& (0.7,0.1,0.1)& (0.4,0.3,0.2)\\ (0.3,0.4,0.1)& (0.6,0.2,0.1)& (0.4,0.3,0.1)\\ (0.1,0.2,0.5)& (0.2,0.1,0.6)& (0.2,0.2,0.5)\end{array}\begin{array}{cc}(0.2,0.3,0.4)& (0.2,0.2,0.4)\\ (0.3,0.3,0.2)& (0.4,0,0.5)\\ (0.1,0.4,0.2)& (0.7,0.1,0.2)\\ (0.2,0.1,0.3)& (0.5,0.3,0.1)\end{array}\right);$$

$$R^{\left(3\right)}=(\begin{array}{ccc}(0.3,0.4,0.2)& (0.1,0.4,0.2)& (0.8,0,0.1)\\ (0.5,0.2,0.2)& (0.4,0.1,0.5)& (0.2,0.5,0.1)\\ (0.1,0.2,0.6)& (0.4,0.2,0.3)& (0.2,0.1,0.1)\\ (0.3,0.1,0.6)& (0.7,0.3,0)& (0.5,0.2,0.1)\end{array}\begin{array}{cc}(0.4,0.3,0.2)& (0.2,0.7,0.1)\\ (0.6,0.1,0.2)& (0.7,0.1,0.1)\\ (0.3,0.2,0.4)& (0.3,0.5,0.1)\\ (0.2,0.4,0.2)& (0.4,0.3,0.1)\end{array});$$

$$R^{\left(4\right)}=(\begin{array}{ccc}(0.6,0.1,0.2)& (0.1,0.1,0.6)& (0.1,0.4,0.3)\\ (0.4,0.2,0.3)& (0.2,0.3,0.4)& (0.3,0.3,0.2)\\ (0.3,0.1,0.5)& (0.2,0.2,0.4)& (0.6,0,0.3)\\ (0.2,0.1,0.3)& (0.3,0.4,0.2)& (0.1,0.4,0.2)\end{array}\begin{array}{cc}(0.5,0.2,0.2)& (0.4,0.1,0.5)\\ (0.2,0.2,0.4)& (0.4,0.2,0.3)\\ (0.7,0.3,0)& (0.5,0.2,0.3)\\ (0.4,0,0.3)& (0.8,0,0.1)\end{array});$$

$$R^{\left(5\right)}=(\begin{array}{ccc}(0.2,0.6,0.1)& (0.3,0.1,0.3)& (0.4,0.2,0.2)\\ (0.3,0.5,0.1)& (0.2,0.1,0.5)& (0.4,0.5,0)\\ (0.1,0.4,0.2)& (0.4,0.1,0.3)& (0.2,0.2,0.5)\\ (0.5,0.1,0.3)& (0.6,0.1,0.1)& (0.5,0.1,0.2)\end{array}\begin{array}{cc}(0.4,0.4,0.2)& (0.7,0.1,0.1)\\ (0.6,0.2,0.1)& (0.3,0.2,0.4)\\ (0.3,0.3,0.3)& (0.4,0.1,0.2)\\ (0.2,0.5,0.2)& (0.3,0.2,0.4)\end{array}).$$

Then, according to step 4, we can get the second level comprehensive evaluation vector:

A⁽¹⁾ = W⁽¹⁾ ° R⁽¹⁾ = {((0.3, 0.1, 0.4) ∧₂ (0.3, 0.2, 0.1)) ∨₂ ((0.4, 0.3, 0.2) ∧₂ (0.2, 0.6, 0.1)) ∨₂ ((0.2, 0.3, 0.4) ∧₂ (0.6, 0.1, 0.1)) ∨₂ ((0.4, 0.2, 0.2) ∧₂ (0.5, 0.1, 0.2)), ((0.3, 0.1, 0.4) ∧₂ (0.7, 0.1, 0.1)) ∨₂ ((0.4, 0.3, 0.2) ∧₂ (0.5, 0.1, 0.3)) ∨₂ ((0.2, 0.3, 0.4) ∧₂ (0.5, 0.3, 0.1)) ∨₂ ((0.4, 0.2, 0.2) ∧₂ (0.5, 0.1, 0.3)), ((0.3, 0.1, 0.4) ∧₂ (0.1, 0.2, 0.6)) ∨₂ ((0.4, 0.3, 0.2) ∧₂ (0.6, 0.1, 0.2)) ∨₂ ((0.2, 0.3, 0.4) ∧₂ (0.2, 0.1, 0.5)) ∨₂ ((0.4, 0.2, 0.2) ∧₂ (0.6, 0.2, 0.1)), ((0.3, 0.1, 0.4) ∧₂ (0.4, 0.1, 0.2)) ∨₂ ((0.4, 0.3, 0.2) ∧₂ (0.4, 0.2, 0.3)) ∨₂ ((0.2, 0.3, 0.4) ∧₂ (0.6, 0.1, 0.2)) ∨₂ ((0.4, 0.2, 0.2) ∧₂ (0.3, 0.4, 0.2)), ((0.3, 0.1, 0.4) ∧₂ (0.4, 0.1, 0.4)) ∨₂ ((0.4, 0.3, 0.2) ∧₂ (0.1, 0.6, 0.1)) ∨₂ ((0.2, 0.3, 0.4) ∧₂ (0.3, 0.2, 0.4)) ∨₂ ((0.4, 0.2, 0.2) ∧₂ (0.3, 0.1, 0.4))}
= {(0.4, 0.2, 0.2), (0.4, 0.3, 0.3), (0.4, 0.3, 0.2), (0.4, 0, 0.2), (0.3, 0, 0.2)}.

With the same way, we have

• A⁽²⁾ = {(0.3, 0.3, 0.2), (0.5, 0.1, 0.1), (0.4, 0.3, 0.2), (0.3, 0.3, 0.2), (0.4, 0, 0.1)};
• A⁽³⁾ = {(0.3, 0, 0.2), (0.3, 0.5, 0.1), (0.4, 0, 0.1), (0.4, 0, 0.2), (0.3, 0.5, 0.1)};
• A⁽⁴⁾ = {(0.6, 0.1, 0.2), (0.3, 0.4, 0.2), (0.3, 0.3, 0.2), (0.5, 0, 0.1), (0.4, 0, 0.2)};
• A⁽⁵⁾ = {(0.3, 0, 0.1), (0.4, 0, 0.2), (0.4, 0.2, 0.2), (0.4, 0.4, 0.2), (0.5, 0.3, 0.1)}.

Then, according to step 5, we can get the first level comprehensive evaluation vector:

B = W ° A

b₁ = ((0.5, 0.2, 0.1) ∧₂ (0.4, 0.2, 0.2)) ∨₂ ((0.6, 0.1, 0.2) ∧₂ (0.3, 0.3, 0.2)) ∨₂ ((0.4, 0.3, 0.3) ∧₂ (0.3, 0, 0.2)) ∨₂ ((0.3, 0.1, 0.5) ∧₂ (0.6, 0.1, 0.2)) ∨₂ ((0.3, 0.2, 0.3) ∧₂ (0.3, 0, 0.1)) = (0.4, 0.2, 0.2);

In addition, we have b₂ = (0.5, 0.3, 0.2); b₃ = (0.4, 0.3, 0.2); b₄ = (0.4, 0, 0.2); b₅ = (0.4, 0.4, 0.2).

Therefore, B = W ° A = {(0.4, 0.2, 0.2), (0.5, 0.3, 0.2), (0.4, 0.3, 0.2), (0.4, 0, 0.2), (0.4, 0.4, 0.2)}.

Next, we compare the size of each element in B by the scoring function and accurate function in Definition 7, and according to the principle of maximum membership, get the final evaluation result.

So, S(b₁) = 0.4 − 0.2 = 0.2, S(b₂) = 0.3, S(b₃) = 0.2, S(b₄) = 0.2, S(b₅) = 0.2. H(b₁) = 0.4 + 0.2 + 0.2 = 0.8, H(b₂) = 1, H(b₃) = 0.9, H(b₄) = 0.6, and H(b₅) = 1.

Therefore, we get b₂ ⊱ b₅ ⊱ b₃ ⊱ b₁ ⊱ b₄.

Hence, the risk rating for the evaluation scheme is “larger risk”.

7. Conclusions

In this paper, we investigate some new operations of picture fuzzy relations and discussed their properties. The kernels and closures of a picture fuzzy relation are defined and their properties are obtained. Then, we proposed a new composition operation of picture fuzzy relations and found a new method to solve picture fuzzy comprehensive evaluation problems. In addition, we prove it is feasible by an application example.

Future research will focus on other new methods for fuzzy comprehensive evaluation problems, especially applying some new granular computing techniques (see [18,19,20,21,22,23,24,25,26,27]) to develop a comprehensive evaluation model about investment risk.